Associação de Indutores e Capacitores

Associação de Indutores e Capacitores

1. Introdução

Capacitores e indutores são elementos que armazenam energia em circuitos elétricos e, a exemplo de resistores, podem ser do tipo linear, não-linear, varáveis ou invariáveis no tempo. Nesta apostila são descritas as regras e equações para associação série e paralela de capacitores e indutores lineares. Ao final é apresentado o comportamento dos mesmos em regime permanente em corrente contínua.

2. Relações Básicas

As relações de tensão e corrente para capacitores e indutores foram estudadas na apostila sobre conceitos básicos e são repetidas no que segue. As variáveis utilizadas são as seguintes:

q(t) - carga elétrica (coulomb , C)

( )

t

ψ - fluxo magnético concatenado (weber, Wb)

v(t) - tensão (volt, V)

i(t) - corrente (ampère, A)

p(t) - potência elétrica (watt, W)

W(t) - energia (joule, J)

L - indutância (henry, H)

L 1

=

Γ - indutância inversa (1/H)

C - capacitância (farad, F)

C 1

S= - elastância (capacitância inversa, 1/F)

2.1 Relação Tensão-Corrente no Indutor

Conforme visto anteriormente, para o indutor valem as seguintes relações (Figura 1):

( )

t =L⋅i

( )

t

ψ ⇒

( )

( )

( )

dt t di L t v dt

t d

⋅ = = ψ

(1)

Outra forma alternativa para a relação (1) é dada por:

( )

∫

τ ⋅ τ ⋅

= −

t

0

d v L 1 ) 0 ( i ) t ( i

( )

d i(0) v

L 1 ) t ( i

t

0

+ τ ⋅ τ ⋅

=

∫

(2)

A partir da expressão geral da potência, a potência associada ao indutor é dada pela relação:

( )

( ) ( )

( )

( )

dt t di L t i t i t v t

p = ⋅ = ⋅ ⋅ (3)

A energia armazenada no campo magnético do indutor linear é dada pela relação

( )

∫

( )

∫

( ) ( )

∫

( )

( )

⋅ τ = ⋅

∫

( )

τ ⋅ τ τ ⋅ ⋅ τ = τ ⋅ τ ⋅ τ = τ ⋅ τ = ) t ( i 0 t 0 t 0 t o di i L d d di L i d i v d p t W (4) 2 ) t ( i L ) t ( W 2 ⋅ = (5)

A energia magnética armazenada é, assim, diretamente relacionada ao valor da indutância e ao valor instantâneo da corrente.

2.2 Relação Tensão-Corrente no Capacitor

Para o capacitor valem as seguintes relações (Figura 2):

( )

t C v

( )

t

q = ⋅ ⇒

( )

( )

( )

dt t dv C t i dt t dq ⋅ =

= (6)

A equação anterior pode também ser expressa da seguinte forma:

( )

∫

τ ⋅ τ ⋅ = − t 0 d i C 1 ) 0 ( v ) t ( v (7)

( )

d v(0) i C 1 ) t ( v t 0 + τ ⋅ τ ⋅

=

∫

(8)

A partir da expressão geral da potência, pode-se determinar a potência associada com o capacitor:

( ) ( )

( )

( )

dt t dv C t v t i t v ) t (

p = ⋅ = ⋅ ⋅ (9)

A energia armazenada no campo elétrico do capacitor linear é dada pela relação:

( )

_∫

( ) ( )

_∫

( )

( )

_∫

( )

∫

⋅ τ= ⋅ τ ⋅

τ τ ⋅ ⋅ τ = τ ⋅ τ ⋅ τ = ⋅ τ = ) t ( v 0 t 0 t 0 t o dv v C d d dv C v d i v dt p ) t ( W

( )

2 t v C ) t ( W 2 ⋅ = (9)

Pelas últimas expressões pode-se ver que a potência e a quantidade de energia armazenada dependem diretamente do valor da capacitância.

+

_

v

i i i i

a

b

+ L1 - + L2 - + L3 - + Ln

-+

_

v

i

e

L

b a

Figura 3 - Indutância equivalente da associação série de indutores

3. Indutores em Série

Como no caso de resistores, quando dois ou mais indutores forem conectados em série, pode-se obter um indutor equivalente. Considerando a Figura 3, obtém-se pela LKC:

n 4

3 2

1 i i i i

i

i= = = = =⋯= (10)

Pela LKT obtém-se:

n 4

3 2

1 v v v v

v

v = + + + +⋯+ (11)

onde,

k

v = tensão no indutor k

k

i = corrente no indutor k

Utilizando a relação tensão-corrente do indutor, a última equação pode ser escrita como:

dt di L dt

di L dt di L dt di L dt di L

v = ₁⋅ 1 + ₂⋅ 2 + ₃⋅ 3 + ₄⋅ 4 +⋯+ _n⋅ n (12)

dt di L dt

di L dt di L dt di L dt

di L

v = ₁⋅ + ₂⋅ + ₃⋅ + ₄ ⋅ +⋯+ _n⋅ (13)

(

)

dt di L L

L L L

v = ₁+ ₂+ ₃ + ₄ +⋯+ _n ⋅ (14)

+

_

v

i

e L

a

b

+

v

_

i

1

L i1 L₂ i2 L₃ i3 Ln in

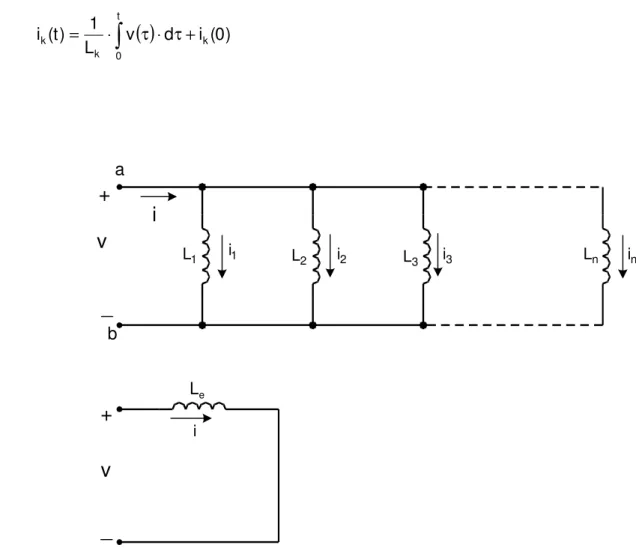
Figura 4 - Indutância equivalente da associação paralela de indutores

dt di L

v= _e⋅ (15)

Comparando-se as duas últimas equações obtém-se para a indutância equivalente dos n indutores em série, a partir dos terminais a-b, a seguinte expressão:

(

1 2 3 4 n

)

e L L L L L

L = + + + +⋯+ (16)

Deve ser observado que neste caso a LCK (equação 10) exige que em todos os instantes de tempo as correntes dos indutores sejam iguais. Ou seja, no momento da conexão dos indutores em série deve-se observar que a corrente inicial i(0) em todos seja a mesma.

4. Indutores em Paralelo

A indutância equivalente da associação paralela de indutores é obtida de forma análoga ao caso anterior. Neste caso, todos os indutores possuem a mesma tensão, sendo que todos estão conectados aos mesmos terminais a-b. Utilizando-se a LKT e LKC para a associação paralela mostrada na Figura 4, obtêm-se as seguintes relações:

n 4

3 2

1 v v v v

v

v = = = = =⋯= (17)

n 4

3 2

1 i i i i

i

i= + + + +⋯+ (18)

Utilizando a relação tensão-corrente, a última equação pode ser escrita da forma seguinte, sendo

k

L a indutância do indutor k:

( )

d i (0) v

L 1 ) t (

i _k

t

0 k

( )

( )

( )

( )

v

( )

d i (0)

L 1 ) 0 ( i d v L 1 ) 0 ( i d v L 1 ) 0 ( i d v L 1 t i n t 0 n 3 t 0 3 2 t 0 2 1 t 0 1 + τ ⋅ τ ⋅ + + + τ ⋅ τ ⋅ + + τ ⋅ τ ⋅ + + τ ⋅ τ ⋅ =

∫

∫

∫

∫

⋯ (19)

( )

v

( )

d i

( )

0 i

( )

0 i

( )

0 i

( )

0) L 1 L 1 L 1 L 1 t

i _{1 2 3 n}

t 0 n 3 2 1 + + + + + τ ⋅ τ ⋅       + + + +

= …

∫

⋯ (20)

Por outro lado, para a indutância equivalente vale a seguinte relação:

( )

v

( )

d i

( )

0 L 1 t i _e t 0 e + τ ⋅ τ ⋅

=

∫

(21)

Comparando-se as duas últimas equações, obtém-se a indutância equivalente da associação paralela de n indutores a partir dos terminais a-b:

      + + + + = n 3 2 1 e L 1 L 1 L 1 L 1 L 1 …       + + + + = n 3 2 1 e L 1 L 1 L 1 L 1 1 L … (22)

A corrente inicial equivalente será dada pela soma de todas as correntes iniciais:

( )

0 i

( )

0 i

( )

0 i

( )

0 i

( )

0

i_e = ₁ + ₂ + ₃ +⋯+ _n (23)

Pode-se também expressar a indutância equivalente a partir do conceito de indutância inversa equivalente da associação série:

n 4

3 2 1

e = Γ +Γ +Γ +Γ + +Γ

Γ ⋯ (24)

(

1 2 3 4 n

)

e e 1 1 L Γ + + Γ + Γ + Γ + Γ = Γ = ⋯ (25)

5. Capacitores em Série

Quando dois ou mais capacitores forem conectados em série, pode-se obter um capacitor equivalente da associação. Considerando a Figura 5, obtém-se pela LKC:

n 4

3 2

1 i i i i

i

i= = = = =⋯= (26)

Pela LKT obtém-se:

n 4

3 2

1 v v v v

v

v = + + + +⋯+ (27)

onde,

k

+

_

v

i i i i

a

b

+ - + - + - +

-1

C _{C2 C3}

n C

+

_

v

i e C b a

Figura 5 - Capacitância equivalente da associação série de capacitores

k

i = corrente no capacitor k

Utilizando a relação tensão-corrente do capacitor, a equação anterior pode ser escrita como:

( )

d v (0) i C 1 ) t ( v k t 0 k

k = ⋅

∫

τ ⋅ τ+

( )

( )

( )

( )

i

( )

d v (0)

C 1 ) 0 ( v d i C 1 ) 0 ( v d i C 1 ) 0 ( v d i C 1 t v n t 0 n 3 t 0 3 2 t 0 2 1 t 0 1 + τ ⋅ τ ⋅ + + + τ ⋅ τ ⋅ + + τ ⋅ τ ⋅ + + τ ⋅ τ ⋅ =

∫

∫

∫

∫

⋯ (28)

( )

( )

v (0) v (0) v (0) v (0)

C 1 C 1 C 1 C 1 d i t

v 1 2 3 n

n 3 2 1 t 0 + + + + +       + + + + ⋅ τ ⋅ τ

=

∫

⋯ ⋯ (29)

Por outro lado, para o indutor equivalente existe a seguinte relação:

( )

d v (0) i C 1 ) t ( v e t 0 e + τ ⋅ τ ⋅

=

∫

(30)

Comparando-se as duas últimas equações obtém-se para a capacitância equivalente dos n capacitores em série, a partir dos terminais a-b, a seguinte expressão:

a

b

+

v

_

i

1 C

1

i

2

C C₃ Cn

3

i

2

i _in

+

_

v

i

e

C

b a

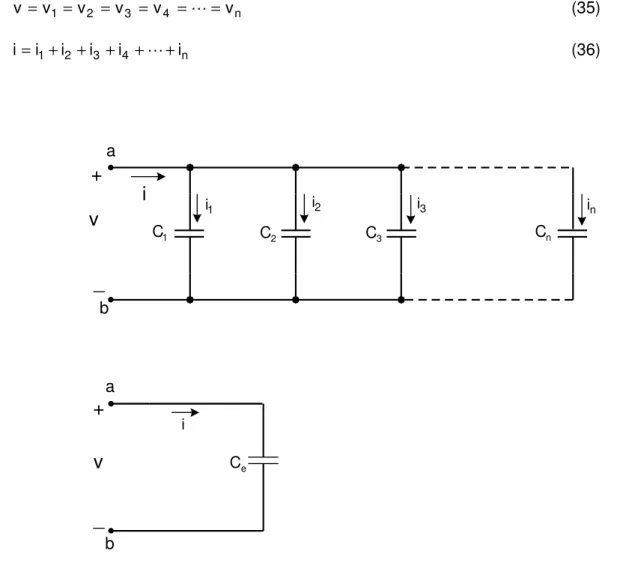
Figura 6 - Capacitância equivalente da associação paralela de capacitores

   

 

+ + + + =

n 3

2 1 e

C 1 C

1 C

1 C

1

1 C

…

(31)

A tensão inicial equivalente será dada pela soma de todas as tensões iniciais:

( )

0 v

( )

0 v

( )

0 v

( )

0 v

( )

0

v_e = ₁ + ₂ + ₃ +⋯+ _n (32)

Pode-se também expressar a capacitância equivalente a partir do conceito de elastância (capacitância inversa) equivalente da associação série:

n 4

3 2 1

e S S S S S

S = + + + +⋯+ (33)

(

1 2 3 4 n

)

e e

S S

S S S

1 S

1 C

+ + + + + = =

⋯

(34)

6. Capacitores em Paralelo

A capacitância equivalente da associação paralela de capacitores é obtida de forma análoga ao caso anterior, sendo que todos os capacitores possuem a mesma tensão, uma vez que todos estão conectados aos mesmos terminais a-b. Utilizando-se a LKT e LKC para a associação paralela mostrada na Figura 4, obtêm-se as seguintes relações:

n 4

3 2

1 v v v v

v

v = = = = =⋯= (35)

n 4

3 2

1 i i i i

i

Utilizando a relação tensão-corrente, a última equação pode ser escrita da forma seguinte, sendo

k

C a capacitância do capacitor k:

( )

( )

dt t dv C t

ik = k ⋅

( )

( )

( )

( )

( )

dt t dv C dt

t dv C dt

t dv C dt

t dv C t

i = 1⋅ + 2 ⋅ + 3 ⋅ +⋯+ n⋅ (37)

( )

[

]

( )

dt t dv C C

C C t

i = 1+ 2 + 3 +…+ n ⋅ (38)

Por outro lado, para a capacitância equivalente vale a seguinte relação:

( )

( )

dt t dv C t

i = e⋅ (39)

Comparando-se as duas últimas equações, obtém-se condutância equivalente da associação paralela de n resistores a partir dos terminais a-b:

n 3

2 1

e C C C C

C = + + +…+ (40)

Deve ser observado que neste caso a LTK (equação 35) exige que em todos os instantes de tempo as tensões dos capacitores sejam iguais. Ou seja, no momento da conexão dos capacitores em paralelo deve-se observar que a tensão inicial v(0) em todos seja a mesma.

7. Indutores e Capacitores em Regime Permanente CC

As equações que regem circuitos contendo resistores, indutores e capacitores são equações íntegro-diferenciais ou apenas diferenciais, cuja solução depende dos parâmetros do circuito e das características das fontes do circuito, especialmente a forma de onda de cada uma. Não é possível, portanto, determinar uma indutância ou capacitância equivalente do circuito quando o mesmo possui resistores, capacitores e fontes descritas por funções genéricas do tempo. A solução das equações diferenciais possui duas parcelas bem distintas: a solução transitória e a solução em regime permanente. A solução transitória é determinada pelas condições iniciais do circuito (energia armazenada nos indutores e capacitores) e a solução em regime permanente depende das fontes de alimentação. Pode-se, no entanto, baseado nas relações tensão-corrente do capacitor e do indutor, determinar o seu comportamento em regime permanente para o caso especial de todas as fontes independentes do circuito serem do tipo contínua. Este tipo de análise permite determinar a condição do circuito após o decaimento total da parcela transitória da solução, sendo por esse motivo chamado de regime permanente. Esta análise também é muito útil na solução de equações diferenciais de circuitos alimentados em corrente contínua, uma vez que parte da solução pode ser determinada de forma rápida pela análise do circuito, ao invés do processo matemático tradicional. Deve-se observar também que quando todas as fontes do circuito forem do tipo contínua, em regime permanente todas as correntes e tensões do circuito serão do tipo contínua.

7.1 Capacitor em Regime Permanente

Considerando a equação do capacitor para o caso particular que todas as tensões e correntes do circuito são contínuas, obtém-se:

( )

( )

0

dt t dv C

a

b

+

v

_

nF

1 3 µF

mH 2

mH 5

Ω

4 10 Ω 5 Ω

Ω

8

Figura 7 - Circuito em corrente contínua em regime permanente

Desta forma, a o capacitor em regime permanente comporta-se como um circuito aberto, uma vez que a corrente sobre o mesmo é zero. No entanto a tensão e a carga no capacitor não serão necessariamente nulas.

( )

d v(0) constante i

C 1 ) ( v

0

= + τ ⋅ τ ⋅ =

∞

∫

∞

(42)

O primeiro termo da equação é a integral de zero a infinito da corrente, a qual amortece com o tempo, fornecendo, portanto, um valor finito. A determinação do valor da tensão do capacitor deve ser feita considerando os demais elementos do circuito, sendo, no entanto, independente do valor da tensão inicial e da capacitância do mesmo.

7.2 Indutor em Regime Permanente

Considerando a equação do indutor também para o caso particular que todas as tensões e correntes do circuito são contínuas, obtém-se:

( )

( )

0

dt t di L

v ∞ = ⋅ = (43)

Desta forma, a o indutor em regime permanente comporta-se como um curto-circuito, uma vez que a tensão sobre o mesmo é zero. No entanto a corrente e o fluxo no indutor não serão necessariamente nulos, conforme pode ser comprovado:

( )

d i(0) constante v

L 1 ) ( i

0

= + τ ⋅ τ ⋅ =

∞

∫

∞

(44)

O primeiro termo da equação é a integral de zero a infinito da tensão, a qual amortece com o tempo, fornecendo, portanto, um valor finito. A determinação do valor da corrente do capacitor deve ser feita considerando os demais elementos do circuito, sendo também independente do valor inicial da corrente e da indutância.

8. Exercício Proposto

Considere o circuito mostrado na Figura 7 e determine o que segue:

a) circuito equivalente para o regime permanente CC;

b) valor das tensões e correntes nos indutores e capacitores em regime permanente, considerando que aos terminas a-b seja aplicada uma fonte de tensão v_ab =120 volts ;

9. Exercícios Recomendados

A seguir é apresentada uma lista de exercícios selecionados da bibliografia aconselhada para a disciplina. Aconselha-se que para uma melhor assimilação que todos os exercícios sejam resolvidos.