Método de captura e recaptura para a estimação da abundância de uma população: aplicação da metodologia Bootstrap

UNIVERSIDADE DE LISBOA

FACULDADE DE CIÊNCIAS

Departamento de Estatística e

Investigação Operacional

Métodos de Captura e Recaptura para a

Estimação da Abundância de uma População

Aplicação da Metodologia Bootstrap

Catarina Isabel Figueiredo Oliveira

Mestrado em Probabilidades e Estatística 2007

UNIVERSIDADE DE LISBOA

FACULDADE DE CIÊNCIAS

Departamento de Estatística e

Investigação Operacional

Métodos de Captura e Recaptura para a

Estimação da Abundância de uma População

Aplicação da Metodologia Bootstrap

Catarina Isabel Figueiredo Oliveira

Dissertação orientada pela Professora Doutora Teresa

Themido Pereira

Dissertação para a obtenção do grau de Mestre em Probabilidades e Estatística

Agradecimentos:

Agradeço aos meus pais pelo incentivo inicial e apoio constante; à minha orientadora; às minhas amigas Helenas; à grande amiga sempre presente Ana; aos meus primos Hugo e Lara; principalmente ao Francisco, a minha cara-metade. Agradeço a todos o apoio, a paciência e o incentivo constante que fizeram com que eu nunca desistisse, apesar de todos os contratempos que surgiram. Obrigada!

Resumo

Ao longo dos tempos foi crescendo a necessidade de estimar a dimensão de uma população, geralmente uma população animal, ou mesmo uma população humana ou um grupo de risco. Para tal, desenvolveram-se diferentes técnicas que se têm vindo a aperfeiçoar, tendo em conta a especificidade da população que se pretende estimar. Um dos métodos mais utilizados para a estimação da abundância de uma população é o método de captura e recaptura simples. Este método baseia-se na recolha de duas amostras aleatórias independentes representativas da população. Os indivíduos da primeira amostra recolhida são marcados e devolvidos à população e, depois de misturados com os restantes, é recolhida uma segunda amostra e são contabilizados os indivíduos marcados. A proporção de indivíduos marcados na segunda amostra é aproximadamente igual à proporção dos indivíduos da primeira amostra na população total e a estimativa do número total de indivíduos na população é retirada da relação existente entre estas proporções.

No caso de se recolherem mais do que duas amostras, utiliza-se o método de captura e recaptura múltipla. São vários os modelos considerados, tendo em conta as condições da população em estudo e de recolha das amostras; neste trabalho, estudar-se-á o modelo em que a probabilidade de captura é igual para cada um dos indivíduos e para cada uma das capturas.

Com a evolução dos computadores desenvolveram-se novas técnicas de reamostragem que utilizam algoritmos computacionais para obter estimativas e intervalos de confiança de uma forma mais rápida e acessível. Um exemplo disso é o método bootstrap que tem aplicação em diversas áreas da estatística e que foi aplicado, neste trabalho, quer ao método de captura e recaptura simples, quer ao método de captura e recaptura múltipla, com o objectivo de obter estimativas com menor viés e intervalos de confiança com menores amplitudes para a dimensão da população.

Palavras chave: Estimação da Dimensão de uma População, Método de Captura e Recaptura, Método Bootstrap, Intervalos de Confiança Bootstrap, Dimensão das Amostras.

Abstract

The need for estimating the size of a population, usually an animal population or even the population of a country or a risk-group in a certain city has been growing. In order to address this issue, different techniques have been developed, stemming from the characteristics of the population one wishes to estimate.

One of the most used methods of estimation of population abundance is the simple capture-recapture method. This method is based on the capture of two independent, random samples that represent the population. After taking the first sample, the individuals of the first sample are tagged and returned to the population. After all the individuals are mixed, a second sample is taken and the tagged individuals from the first sample are counted. The proportion of tagged individuals in the second sample is approximately the same as the proportion of tagged individuals in the overall population. The estimate of the population size is derived from the equality of these two proportions.

In situations when more than two samples are taken, the multiple capture-recapture method is used. Depending on the characteristics of the population under study and the conditions for sampling, different models can be considered; in this study, a model with equal probability of capture for all individuals and for all captures is considered.

The evolution of computing led to a development of new resampling techniques based on computational algorithms that deliver estimators and confidence intervals much more easily and faster than ever before. The bootstrap method is an example of such a technique, that has a widespread application in statistics and that was applied in this thesis to both the simple and multiple capture-recapture methods with the objective of obtaining more robust estimators and shorter length confidence intervals for the overall population size.

Keywords: Estimation of Population Size, Simple and Multiple Capture-Recapture Methods, Bootstrap Method, Bootstrap Confidence Intervals, Sample sizes.

ÍNDICE

1 INTRODUÇÃO...1

2 MÉTODO DE CAPTURA E RECAPTURA SIMPLES ...7

2.1 INTRODUÇÃO...7

2.2 PRESSUPOSTOS NECESSÁRIOS PARA A ESTIMAÇÃO DA DIMENSÃO DA POPULAÇÃO...8

2.3 ESTIMADORES DA DIMENSÃO DA POPULAÇÃO...11

2.3.1 Estimador de Petersen... 11

2.3.2 Estimador de Chapman ... 14

2.3.3 Estimador de Bailey... 16

2.3.4 Intervalos de Confiança... 17

2.4 DIMENSÃO DAS AMOSTRAS...21

2.5 ESTUDO COMPARATIVO...24

2.6 TABELAS DE CONTINGÊNCIA NA OBTENÇÃO DE INTERVALOS DE CONFIANÇA PARA A ABUNDÂNCIA DE UMA POPULAÇÃO...51

2.7 MÉTODO BOOTSTRAP NA OBTENÇÃO DE ESTIMATIVAS DA ABUNDÂNCIA DE UMA POPULAÇÃO61 2.7.1 Introdução Teórica ... 61

2.7.2 Estimativa bootstrap do erro padrão de um estimador ... 65

2.7.3 Intervalos de Confiança bootstrap ... 75

2.7.4 Aplicação Prática ... 79

2.8 CONCLUSÕES DAS VÁRIAS APLICAÇÕES PRÁTICAS. ...83

3 MÉTODO DE CAPTURA E RECAPTURA MÚLTIPLA ...87

3.1 INTRODUÇÃO...87

3.2 CENSO DE SCHNABEL...88

3.3 ESTUDO COMPARATIVO...95

3.4 MÉTODO BOOTSTRAP PARA A CAPTURA E RECAPTURA MÚLTIPLA...104

3.4.1 Intervalos de Confiança bootstrap ... 106

3.4.2 Exemplo prático... 108

3.5 MÉTODO ALTERNATIVO DE CAPTURA E RECAPTURA MÚLTIPLA...111

4 CONSIDERAÇÕES FINAIS ...115

ÍNDICE DE TABELAS ...123

BIBLIOGRAFIA ...125

1 Introdução

Em diversas áreas de conhecimento como é o caso da Ecologia, Biologia, … é necessário estimar a abundância de uma determinada população. Por exemplo, estimar o número de mamíferos de uma certa espécie, o número de plantas que se encontram numa região, o número de peixes num lago, o número de sem-abrigo de uma cidade ou região, o número de doentes de diabetes de um país, etc.

Ao longo dos anos foram desenvolvidas várias técnicas que se foram tornando cada vez mais específicas, tendo em conta a população e o objecto em estudo, já que, quando se trata de populações animais existem algumas dificuldades na estimação da dimensão da população devidas a alterações que podem ocorrer no seu habitat ou a modificações que podem ocorrer no comportamento dos animais em estudo. Efectuar estudos em populações animais sem que isso afecte o seu comportamento nem sempre é tarefa fácil, devendo, por isso, utilizar-se os modelos estatísticos com alguma precaução, pois deve ter-se em conta os pressupostos necessários para a sua aplicação, de forma a que os métodos utilizados sejam mais robustos e permitam obter estimativas mais precisas. Os primeiros trabalhos desenvolvidos para estimar a dimensão de uma população animal têm a sua proveniência em estudos desenvolvidos por Lincoln (1930) e Jackson (1933).

As várias técnicas empregues podem ser classificadas em duas categorias conforme se está perante uma população fechada ou uma população aberta, isto é, se existem alterações na população durante o período em estudo, tais como: nascimentos, mortes, imigrações, emigrações, entre outras.

Antes de se proceder a qualquer tipo de estudo devem ter-se em conta algumas condições iniciais que levam a uma escolha acertada do modelo a utilizar; isto porque, por vezes, pode ser preferível utilizar um método menos eficiente mas mais robusto, em vez dum método altamente eficiente mas com bastantes condições iniciais difíceis de controlar.

Entre os vários métodos desenvolvidos para estimar a dimensão de uma população encontram-se, o método da captura e recaptura (método que será estudado neste trabalho), band and tag return models (Laurs e Wetherall, 1981; Ebert, 1980; McCaughran, 1981), transect sampling models (Burnham, Andersen e Laake, 1980,

1981; Gates, 1980; Quinn e Gallucci, 1980; Franzeb, 1981; Seber, 1982; Buckland, 1985), quadrat and strip sampling removal (Thompson, 1982, 1990, 1991, 1992; Thompson, Ramsey e Seber, 1991), catch per unit effort models (Pollock, 1984; Butler e McDonal, 1979; Chapman, 1961; Paloheimo, 1961), change-in-ratio or selective removal models (Seber, 1982; Keller e Burnham, 1982; Pollock, 1991; Routledge, 1989), rádio tagging survival models (Amlaner e MacDonald, 1980; Thomas, 1980; White e Garrott, 1990) e aerial censusing (Seber, 1982; Besom, 1979; Ridpath e outros, 1983; Caughley e Grice, 1982).

Em alguns destes métodos é necessário capturar uma ou mais amostras da população, o que, por vezes, pode ser uma tarefa difícil pois depende de factores como a acessibilidade da população e os custos da recolha da(s) amostra(s), entre outros. A amostra recolhida deve ser tão representativa da população quanto possível, de modo a se realizarem inferências sobre a população com o menor enviesamento possível.

Em muitos estudos em que o objectivo é estimar a dimensão de uma população utiliza-se o método da captura e recaptura múltipla; este método foi inicialmente discutido por Schnabel (1938), tendo Cormack (1968)1 apresentado várias técnicas e Darroch (1958) e White e outros (1982), entre outros autores, contribuído para o desenvolvimento desses métodos. Geiger e Werner (1924) e Sekar e Deming (1949)2 foram dos primeiros autores a utilizar o método de captura e recaptura apresentando um exemplo para o caso de se recolherem duas amostras. Neyman (1938) foi também um dos primeiros a introduzir um método para a recolha de duas amostras denominado por two-phase sampling ou double sampling, e Stockford e Page (1984) utilizaram esse método para estimar a percentagem de veteranos que tinham realmente servido na guerra do Vietname através das listas dos hospitais de veteranos de guerra que intervieram na guerra do Vietname.

Com a evolução dos computadores criaram-se novos métodos de reamostragem que, através de programas de simulação, permitiram calcular estimativas e intervalos de confiança para um certo parâmetro ou característica populacional, de uma forma mais rápida e acessível. Exemplo disso são: o método jackknife (Maurice Quenouille, 1949;

1 _{Para maior detalhe consultar o artigo: Cormack, R. M. (1968) “The statistics of capture-recapture}

methods.” Oceanogr. Mar. Biol. Ann. Rev. 6, pág. 455-501.

Efron, 1979); o método bootstrap (Efron e Tibshirani, 1986; Buckland, 1984; Buckland e Garthwaite, 1991) e o método de Monte Carlo (Buckland, 1984).

No caso da população ser fechada, isto é, quando não há nascimentos, mortes e migrações durante o decorrer do estudo, as condições iniciais são mais fáceis de controlar e o número de parâmetros é menor. Normalmente o estudo é efectuado num curto período de tempo e alguns dos modelos utilizados assumem que todos os indivíduos da população têm a mesma probabilidade de captura. Nos casos em que isso não acontece, deve ter-se em conta, entre outros aspectos, a heterogeneidade da população e a diferente variação que pode existir na probabilidade de captura do indivíduo.

Nos casos da população ser aberta é necessário dispor de alguma informação adicional e devem considerar-se nascimentos, mortes e migrações, obtendo-se, desta forma, modelos mais complexos, com um maior número de condições iniciais assim como um maior número de parâmetros. Vários autores realizaram estudos nesse campo destacando-se como referências Seber (1982) e Pollock (1991) (Pollock apresenta num diagrama, uma perspectiva geral, dos métodos de captura e recaptura que se podem utilizar, ver anexo 1).

Este trabalho tem por objectivo estudar vários métodos para estimar a dimensão de uma população fechada considerando numa primeira referência, capítulo 2, o método de captura e recaptura simples. Para tal, a primeira coisa a ter em conta são os diferentes pressupostos necessários para estimar a dimensão da população fechada, secção 2.2., pressupostos que são considerados necessários para os vários métodos apresentados ao longo deste trabalho.

Neste capítulo consideram-se na secção 2.3., os estimadores da dimensão da população propostos por Petersen (1965), por Chapman (1951) e por Bailey (1951) e, na secção 2.3.4, os respectivos intervalos de confiança.

De forma a proceder ao estudo duma determinada população é necessário, em primeiro lugar, compreender a estrutura e a dinâmica dessa mesma população. Ao aplicar o método de captura e recaptura simples para estimar a dimensão de uma população fechada, o investigador precisa de recolher duas amostras e, para o efeito, deve apurar a dimensão de cada uma delas o mais adequadamente possível, pois uma escolha errada da dimensão de cada uma das amostras pode originar sobrestimativas nos resultados do estimador assim como grandes enviesamentos. Um dos métodos utilizados

para a escolha das dimensões a serem utilizadas no estudo é proposto por Robson e Regier (1964) no caso de se empregar o estimador de Petersen, secção 2.4..

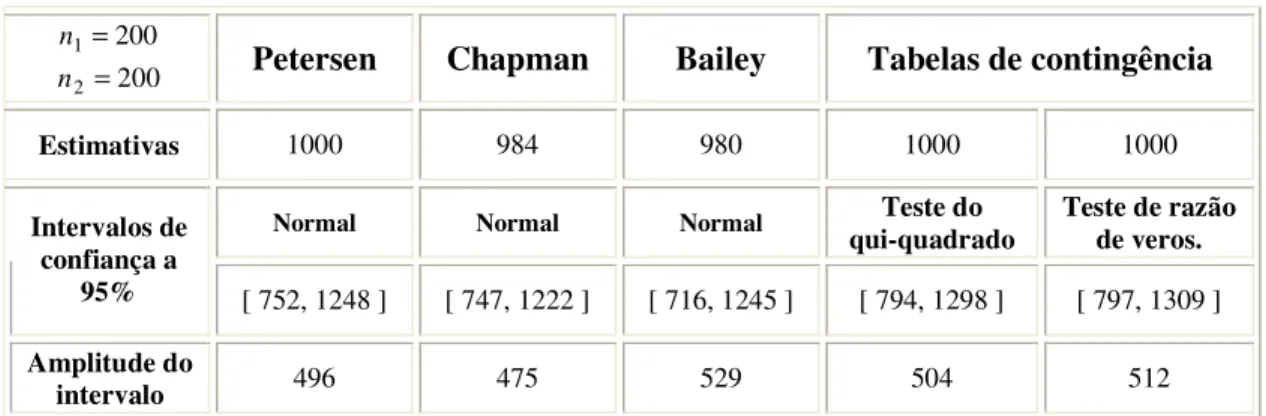
Uma outra abordagem para a estimação da abundância de uma dada população, usando o método de captura e recaptura simples, é sugerida por Fienberg (1972), secção 2.6.. A sua sugestão passa por recorrer à utilização de tabelas de contingência incompletas de margens fixas para o tratamento dos dados por forma a obter intervalos de confiança, sem haver necessidade de assumir que os estimadores têm distribuição aproximadamente Normal. Neste contexto, Cormack (1992) propõe a utilização do teste de independência do qui-quadrado de Pearson para a construção de intervalos de confiança para a dimensão da população. Com o mesmo objectivo é também utilizado o teste de razão de verosimilhanças.

Apesar de neste trabalho se considerarem tabelas de contingência apenas para o método de captura e recaptura simples, as mesmas podem aplicar-se no caso de haver recolha de mais do que duas amostras, tendo Fienberg (1972) e Cormack (1992) efectuado vários estudos nesse campo considerando sugestões dadas por outros autores. No método de captura e recaptura múltipla, a utilização de tabelas de contingência incompletas implica o recurso ao ajustamento de modelos loglineares que permitem avaliar a existência de independência entre as várias amostras. Obviamente que a célula com o valor em falta não poderá ser testada relativamente ao modelo que melhor se ajusta aos dados, mas, ainda assim, é possível utilizar esse modelo para obter uma estimativa da dimensão da população, e o respectivo intervalo de confiança.

O método de captura e recaptura múltipla utiliza-se quando existe disponibilidade de recolher mais do que duas amostras. No capítulo 3, estudar-se-á esse método no caso mais simples do modelo considerado ser o modelo M₀, em que a probabilidade de captura é a mesma para cada um dos indivíduos e não varia ao longo das várias capturas. Para esse modelo são referidas, ao longo do capítulo, diferentes alternativas para estimar a abundância de uma população fechada, nomeadamente o estimador de Schnabel e o estimador modificado de Petersen.

Tanto para o método de captura e recaptura simples como para o método de captura e recaptura múltipla é possível a aplicação da metodologia bootstrap de forma a obter estimativas mais precisas e com menor viés da dimensão da população, secção 2.7 e secção 3.4, respectivamente. Além disso podem construir-se intervalos de confiança

bootstrap para a abundância populacional que são mais robustos e de menor amplitude que os usuais, subsecção 2.7.3 e subsecção 3.4.1 respectivamente.

Quando se utilizam os censos para fazer o levantamento de certas características de uma população um dos resultados obtidos é o número de pessoas que integram essa população. No entanto, nem sempre se consegue obter o valor exacto da dimensão da população, pois alguns indivíduos podem não ser contabilizados. Por ser extremamente importante para certas medidas governamentais conhecer, o mais rigorosamente possível, a dimensão da população, desde a década de 1950 que se realizam estudos onde se utiliza o método de captura e recaptura, neste contexto designado por dual-system estimation, para ajustar a estimativa da dimensão da população obtida pelos censos. Este método gerou alguma controvérsia, tendo Fienberg (1992) realizado estudos sobre dual-system e discutido num seu artigo de 1994 sobre essa controvérsia. Por outro lado Hogan (1993) descreve no seu artigo o método utilizado para os censos Pos-Enumeration Survey realizados nos Estados Unidos da América em 1990, e Leo Breiman (1994) enumera razões que podem justificar alguns erros nos resultados desses mesmos censos.

Os vários estudos comparativos realizados neste trabalho, para os diferentes estimadores da dimensão da população tiveram como base a utilização de um algoritmo computacional gerador de amostras aleatórias de dados entre 1 e 1000. Nesses estudos consideraram-se duas ou mais amostras aleatórias com diferentes dimensões, conforme se aplicava o método de captura e recaptura simples ou o método de captura e recaptura múltipla. Para a construção das réplicas necessárias à utilização da metodologia bootstrap foi também utilizado este algoritmo.

2 Método de captura e recaptura simples

2.1 Introdução

O método de captura e recaptura surge da necessidade de se estimar o número total de indivíduos de uma determinada população. Este método consiste em obter uma amostra inicial de indivíduos que serão marcados ou identificados, dependendo da necessidade e do habitat da população em estudo, sendo, de seguida, devolvidos à população. Posteriormente é retirada uma segunda amostra, independente da primeira, na qual se contabilizam os indivíduos marcados da primeira amostra.

Este método assume que, no caso da segunda amostra ser representativa da população total, a proporção de indivíduos marcados na segunda amostra será aproximadamente igual à proporção dos indivíduos marcados na população total. A estimativa do número total de indivíduos na população é retirada da relação existente entre estas proporções.

Este tipo de método é muito utilizado para estimar a abundância de mamíferos, pássaros, peixes, répteis, insectos, entre outros, numa determinada região. Sendo útil também para estimar o número de acidentes de uma dada população, o número de viciados em cocaína ou qualquer outro tipo de grupo de risco que, de outra forma, seria impossível de estimar.

Para os casos em que, de alguma forma, seja possível avistar os indivíduos da população em estudo não se torna necessário haver captura, marcação e recaptura, pois, nesses casos, as amostras são obtidas exclusivamente por observação da região em estudo. No entanto, para todos os casos devem ter-se em conta alguns factores que podem prejudicar o estudo como, por exemplo, o tamanho do animal, a cobertura do terreno provocada pela vegetação, a actividade do animal, entre outros.

No caso do estudo ser realizado para uma população de humanos, consideram-se para as amostras diferentes listas de nomes. Por exemplo, para estimar o número de acidentes numa determinada cidade, considera-se a lista de acidentes contabilizados pelo sistema de saúde como a primeira amostra, e a lista de acidentes das seguradoras

como a segunda amostra, sendo o número de “marcados” os nomes que constam em ambas as listas.

O método de captura e recaptura não se limita a duas amostras, já que pode haver mais do que uma marcação ou mais do que uma captura, sendo, nesses casos, necessário contabilizar as marcas, distintas entre si, nas amostras retiradas nas diferentes capturas, caso que será analisado no capítulo 3.

Ao estimar a dimensão de uma população de animais podem surgir algumas complicações, sendo necessário ter em consideração que: o tipo de marca utilizada nos animais pode provocar a morte do animal; os animais ao serem devolvidos ao local em estudo poderão seguir caminhos diferentes dos seus hábitos, originando maior ou menor probabilidade de serem recapturados relativamente aos restantes elementos; o local escolhido para o uso de armadilhas deve ter em conta factores como o vento e o movimento dos animais;... Os resultados do estudo podem também variar muito de região para região ou podem inclusivamente sofrer alterações nas diferentes estações do ano.

2.2 Pressupostos necessários para a estimação da

dimensão da população

Os métodos utilizados no estudo de populações animais, nomeadamente no cálculo da estimativa da dimensão da população, devem ser utilizados com devido cuidado pois não existe controle da população animal, havendo factores que podem prejudicar gravemente o estudo pondo em causa os seus resultados. Daí a necessidade de considerar pressupostos para melhorar a precisão do estimador em causa.

O método de captura e recaptura simples é um dos métodos que se utiliza quando se pretende estimar a dimensão N de uma população. Para tal, recolhe-se uma primeira amostra aleatória de indivíduos de dimensão n1; estes indivíduos são

devidamente marcados para poderem ser identificados e, em seguida, são repostos na população. Algum tempo depois, de forma a possibilitar a mistura dos indivíduos marcados com os não marcados, retira-se uma segunda amostra aleatória de dimensão

2

n e contabiliza-se o número de indivíduos marcados nesta amostra, que se designa por

Para se proceder à recolha das duas amostras e para que se obtenha uma estimativa mais adequada da dimensão da população é necessário ter em consideração os seguintes pressupostos:

- A população é fechada, ou seja, não há entrada nem saída dos seus elementos, sendo que o valor de N é constante;

- Todos os elementos da população têm igual probabilidade de serem escolhidos, ou seja, é realizada uma amostragem aleatória simples da população;

- As duas amostras são independentes; os elementos da primeira amostra são recolocados na população originando igual probabilidade dos elementos serem escolhidos na segunda amostra, quer sejam elementos marcados ou não;

- A segunda amostra é uma amostra aleatória simples, isto é, cada uma das       2 n N

amostras possíveis tem igual probabilidade de ser escolhida;

- As marcas devem ser feitas e colocadas de forma a não se degradarem nem desaparecerem para não afectar a recaptura dos elementos da população.

Estes pressupostos dependem uns dos outros pois, para que a segunda amostra seja aleatória, é necessário que todos os elementos marcados na primeira recolha tenham probabilidade de ser escolhidos igual à probabilidade dos elementos não marcados. Assim, a recolha das amostras deve ser cumprida de forma a possibilitar a mistura dos indivíduos, sendo para tal necessário que a população seja fechada, visto que, no caso de haver migrações ou mortes, tal pressuposto não pode ser garantido. De igual modo, o tipo de marcas escolhidas para distinguir os indivíduos uns dos outros deve ter em conta que estas não os podem prejudicar, não devem alterar os seus hábitos, ou ser colocadas de forma a poderem perder-se ou degradar-se, alterando a probabilidade dos indivíduos serem novamente recolhidos.

Alguns destes pressupostos podem ser difíceis de cumprir em termos práticos, principalmente quando se trata de estudos realizados em populações animais, como é o caso do pressuposto da segunda amostra ser uma amostra aleatória simples. Uma forma de tentar resolver esse problema passa por escolher zonas da população onde os indivíduos tenham a mesma probabilidade de serem recolhidos (Leslie e outros (1953)); claro que, por vezes, isso pode não se verificar pois, para certas populações animais, o simples facto de se recolher uma primeira amostra vai desestabilizar toda a população e

afectar as futuras recapturas. Muitas vezes a probabilidade de captura varia em função de factores como a idade, o sexo, a espécie, entre outras, dos indivíduos em causa (Kikkawa (1964), Pucek (1969)).

Se, por exemplo, a primeira amostra não for uma amostra aleatória simples, por existirem na população indivíduos que são mais fáceis de recolher do que outros, esse facto determina que a segunda amostra também não seja aleatória pois, ao marcar todos os indivíduos da primeira amostra e ao colocá-los novamente na população, estes têm maior probabilidade de serem novamente recolhidos comparativamente com os indivíduos não marcados. Dificilmente se consegue ultrapassar este problema; no entanto, alguns autores sugerem o uso de diferentes formas de captura para cada amostra recolhida.

Da mesma forma, quando se trata de marcar os indivíduos em estudo, nomeadamente para populações animais, deve ter-se o cuidado de colocar marcas que não se degradem, não desapareçam e que não afectem a possível recaptura. Com o objectivo de minimizar este problema deve ter-se em consideração que: as marcas devem ser escolhidas de forma a não prejudicar o animal nem influenciar os seus hábitos; é necessário ter bastante cuidado ao capturar os animais e ao marcá-los para que estes recuperem e se devolvam à população sem alterações; o procedimento para a sua devolução à população deve ter em conta alterações no seu comportamento que devem ser minimizadas para não afectar a sua mistura com os restantes elementos da população. Um processo utilizado para evitar os problemas que surgem com a perda da marca é a utilização de duas marcas, havendo até estudos que determinam uma estimativa da probabilidade dos indivíduos perderem as duas marcas (Hubert, 1976).

Bohlin e Sundstrom (1977) quando utilizaram o método de captura e recaptura para estimar a dimensão de uma determinada população de peixes com o estimador proposto por Petersen, ver subsecção 2.3.1, aperceberam-se do efeito que as marcas tinham nessa população pois os peixes marcados tinham maior probabilidade de captura. De forma a confirmar as suas suspeitas, procederam a um novo estudo com uma população de dimensão conhecida dessa espécie de peixes, onde constataram que efectivamente a marca afectava a captura, aumentando a sua probabilidade, levando a uma sobrestimação do valor da dimensão da população.

Obviamente que todas estas considerações aos pressupostos exigidos dependem da população em estudo que, no caso dos animais, varia muito de espécie para espécie;

vários autores conduziram o seu estudo desenvolvendo técnicas para ajudar os investigadores no melhor caminho a seguir para a recolha e para a escolha da dimensão das amostras tendo em conta a espécie em estudo.

No caso destes pressupostos não serem válidos, o estimador da população pode sofrer algumas alterações ou haver necessidade de reformular o modelo considerado. No entanto, esta questão não irá ser abordada neste trabalho. Daqui em diante supõe-se que os pressupostos referidos anteriormente são verificados.

2.3 Estimadores da Dimensão da População

São várias as propostas para se estimar a dimensão de uma população utilizando o método de captura e recaptura simples, sendo que as mais utilizadas, e aqui referenciadas, são os estimadores de Petersen, de Chapman e de Bailey. Para todos eles é necessário a recolha de duas amostras e que os pressupostos referidos anteriormente (secção 2.2) sejam válidos, tanto quanto possível.

2.3.1 Estimador de Petersen

Supondo que se pretende estimar a dimensão N de uma população, recolhe-se uma primeira amostra aleatória de n₁ indivíduos; estes indivíduos são devidamente marcados para poderem ser identificados e, em seguida, são repostos na população. Algum tempo depois, de forma a possibilitar a mistura dos indivíduos marcados com os não marcados, retira-se uma segunda amostra aleatória de dimensão n da população e ₂ contabiliza-se o número de indivíduos marcados nesta amostra, que se designa por m .

Sabe-se então que a proporção de indivíduos marcados na segunda amostra é aproximadamente igual à proporção dos indivíduos da primeira amostra na população. A estimativa do número total de indivíduos na população é retirada da relação existente entre estas proporções,

N n n m ₁ 2 ≈ .

Desta forma, obtemos o estimador de Petersen (1965) da dimensão total da população, que é dado por

m n n Nˆ = 1 2 .

Exemplo 2-1:População de França: Laplace (1783)

Para estimar o total da população de França, Laplace considerou como primeira amostra, de dimensão n₁, os registos dos nascimentos de todo o país e como segunda amostra, de dimensão n2, o total de baptizados da população, sendo que o número de

indivíduos “marcados”, m , seria o número de nascimentos registados de entre os baptizados, o que não é mais do que uma aplicação do método de Petersen utilizado nos dias de hoje.

Sabendo que existem _      2 n N

amostras possíveis em n₂ extracções sem reposição

da população, o número m de indivíduos marcados na segunda amostratem distribuição Hipergeométrica, m∩H

(

N,n₂, p

)

. Ou seja, designando por P(m) a probabilidade de obter m indivíduos marcados (“sucessos”) na segunda amostra, tem-se:

                  − − = 2 1 2 1 ) ( n N m n m n n N m P , m=0,1,...,min

(

n₁,n₂

)

,

em que n₁ representa o número de indivíduos marcados da população com probabilidade de captura

N n

p= 1 e N −n1 representa o número de indivíduos não marcados.

Robson (1969)3 mostrou que no caso de não se verificar o pressuposto das duas amostras serem aleatórias, a probabilidade de obter m indivíduos marcados na segunda amostra tem igualmente uma distribuição Hipergeométrica, m∩H

(

N,n₂, p

)

, visto que esta distribuição é simétrica em n₁ e n₂.

O estimador de Petersen da dimensão da população coincide com o estimador de N obtido pelo método dos momentos. De facto, o método dos momentos consiste em

3 _{Para maior detalhe consultar artigo Robson, D. S. (1969) “Mark-recapture methods of population}

estimation.” Development in Survey Sampling, Eds N. L. Johnson and H. Smith, pág. 120-40. New York: 2-1

igualar momentos amostrais a momentos populacionais e, atendendo a que neste caso particular se tem apenas uma recaptura, isto é, m=m e E(m)=n₂×p, obtém-se

m N n n m m E( )= ⇔ ₂ 1 = , resultando m n n Nˆ = 1 2 .

Além disso, o estimador de máxima verosimilhança de N coincide com a parte inteira do estimador de Petersen (Thompson, pág. 216).

As propriedades do estimador de Petersen foram amplamente estudadas por Chapman (1951) 4 que mostrou que Nˆ tem uma distribuição assintoticamente Normal quando N →+∞, embora enviesada. Além disso, o viés de ˆN tende a ser muito elevado para valores pequenos de n₁ e n₂, tendo Chapman (1951) obtido uma sua estimativa.

Em populações de grande dimensão, se a dimensão da segunda amostra for

muito menor do que a dimensão da população, isto é, se n₂ <<N vem que 2 _≈0 N n , ou seja, 1 1 2 _≈ − − N n N

e a variância da distribuição Hipergeométrica, que é dada por

(

)

1 1 2 − − − N n N p p n em que N n

p= 1 , aproxima-se da variância da distribuição Binomial,

(

p

)

p

n 1− . Por outras palavras, quando a dimensão da segunda amostra é muito

diminuta em relação à dimensão da população, a distribuição Hipergeométrica pode ser aproximada pela distribuição Binomial e m segue aproximadamente uma distribuição

(

n p

)

b ₂, . Logo, m n m N n N n m n m P −       −             ≈ 2 1 1 2 ₁ ) ( , m=0,1,...,n₂.

Utilizando este modelo Binomial, o estimador de máxima verosimilhança de N é novamente o estimador de Petersen.

Por sua vez, quando a dimensão da segunda amostra, n , é elevada e a ₂ probabilidade de sucesso de cada prova,

N n

p= 1 , é pequena pode-se aproximar a

4 _{Para maior detalhe consultar o artigo de Chapman, D. G. (1951) “Some properties of the hypergeometric}

distribuição Binomial pela distribuição de Poisson com parâmetro λ =n2 p, ou seja, pode-se considerar que m tem aproximadamente distribuição P

(

n₂ p

)

. Logo,

m N n n N n n m e m P       ≈ − 2 1 ! ) ( 2 1 , m=0,1,....

De igual modo, utilizando o modelo Poisson, o estimador de máxima verosimilhança de N é o estimador de Petersen.

Um estimador para a variância do estimador de Petersen da dimensão da população foi proposto por Sekar & Deming (1949) e é dado por:

3 2 1 2 1 ( )( ) ) ˆ r( aˆ v m m n m n n n N = − − .

Note-se que pode acontecer que m= e, nesses casos, o estimador de Petersen 0 não pode ser utilizado, sendo que Chapman propõe outro estimador para a dimensão da população, conforme se faz referência a seguir.

2.3.2 Estimador de Chapman

Pode acontecer que não existam indivíduos marcados na segunda amostra, ou seja, m= e, nesses casos, a estimativa de Petersen da dimensão da população é 0 infinita. De forma a tentar minimizar este problema, e com o objectivo de encontrar outro estimador que tenha viés mais reduzido e com um estimador para a variância que seja centrado, Chapman (1951) propôs um novo estimador, baseado no estimador de Petersen, dado por:

(

)(

)

(

1

)

1 1 1 ~ 1 2 ₋ + + + = m n n N .

A proposta encontrada por Chapman para estimar a dimensão da população é um estimador centrado sempre que n₁+n₂ ≥ N, como se demonstra a seguir. Seja,

( )

(

)(

)

(

)

(

)(

)

1. 1 1 1 1 1 1 1 1 ~ 2 1 2 1 −       + + + =       − + + + = m E n n m n n E N E 2-4 2-5 2-6

Sabendo que       ∩ N n n N H m , ₂, 1 , tem-se que ( ) . 1 1 1 1 min 1, 2 0 2 1 2 1

∑

=                   − − × + =       + n n m n N m n m n n N m m E

Considerando m

,

= m+1 e notando que m

,

∈

{

1,...,min

(

n₁+1,n₂+1

)

}

, obtém-se, depois de algumas simplificações,

(

)(

)

( )

(

)

(

)(

)

. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 2 1 1 , 1 min 1 2 1 2 1 2 1 2 1 '

,

,

                    + +       + − − × + + + =       + +       +       − + − + + + =       +

∑

+ + = n N n n N n n N n N m n m n n N n n N m E n n m

Substituindo na expressão anterior 2-6 tem-se:

( )

(

)(

)

(

)

(

)(

)

(

)

. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ~ 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 1       + +       + − + − = −       + +       + − −       + +       + − − + = −                     + +       + − − × + + + × + + = n N n n N N N n N n n N n N n n N N N n N n n N n n N n n N E

Para o estimador ser centrado, deve ter-se que 0 1 2 1 =       + − n n N . Como se trata de

sempre que N <n1+n2+1, ou seja, n1+n2 > N−1⇔n1+n2 ≥N, tem-se 0 1 2 1 =       + − n n N

e o estimador N~ é centrado, conforme se pretendia demonstrar.

Seber (1970) e Wittes (1972) apresentam um estimador para a variância do estimador de Chapman da dimensão da população, da forma:

(

)(

)(

)(

)

(

1

) (

2

)

1 1 ) ~ r( aˆ v 1 2 ₂ 1 2 + + − − + + = m m m n m n n n N

Mesmo que m seja zero esta estimativa da variância é sempre finita, sendo centrada quando n₁+n₂ ≥N.

Por vezes não é possível fixar antecipadamente a dimensão da segunda amostra,

2

n , pois na prática esse valor pode depender do tempo ou do esforço necessário para a recolha da segunda amostra. No entanto, quando a dimensão da segunda amostra é uma variável aleatória e não um parâmetro fixo, a estimativa da dimensão da população proposta por Chapman, N~, expressão 2-5, continua a ser centrada, já que

[

]

[

]

[ ]

. , ~ ~ 2 2 1 2 1 N N E n n N E E n N E n n = = =

Da mesma forma se tem que a estimativa da variância, vaˆr(N , é uma estimativa ~) centrada da var

[

N~ n₁

]

, não existindo grandes diferenças no tratamento de n como um ₂ parâmetro fixo ou como uma variável aleatória, quando se pretende estimar a dimensão de uma população.

2.3.3 Estimador de Bailey

Como o estimador da dimensão da população proposto por Petersen (subsecção 2.3.1) é enviesado, Bailey (1951, 1952) propôs uma alteração ao estimador da dimensão da população no caso da distribuição Binomial, expressão 2-3, constituir uma boa aproximação da distribuição Hipergeométrica, dado por:

(

)

1 1 2 1 * + + = m n n N . 2-8 2-7

Bailey propõe para o respectivo estimador da variância, o seguinte:

(

)(

)

(

1

) (

2

)

1 ) r( aˆ v 2 ₂ 2 2 1 * + + − + ≈ m m m n n n N .

Nas situações em que a fracção amostral n2 N seja suficientemente pequena, de forma a ignorar-se o facto de, na recolha de amostras, existir ou não reposição, pode-se utilizar o estimador da dimensão da população proposto por Bailey, *

N , em vez do proposto por Chapman (2.3.2). Este estimador também pode ser o mais apropriado de entre os apresentados, nas situações em que não existe recolha de amostras, mas sim contagem dos indivíduos através da observação dos mesmos dentro do seu habitat, visto que, nesse caso, continua a ser válida a utilização da distribuição Binomial. No entanto, em termos práticos, não existem diferenças significativas entre o estimador proposto por Chapman e o proposto por Bailey.

2.3.4 Intervalos de Confiança

Nas subsecções anteriores foram fornecidas fórmulas para calcular estimativas pontuais da dimensão da população. No entanto, quando se pretende estimar um parâmetro θ desconhecido, além de calcular uma estimativa pontual, é de grande importância determinar um intervalo de confiança para o parâmetro. Sendo I um intervalo de confiança de 100

(

1−α

)

% para θ, pode afirmar-se que P(θ∈I)=1−α,

ou seja, a proporção dos intervalos de confiança que contêm o parâmetro θ é de

(

1

)%

100 −α .

Suponha-se que se tem uma amostra aleatória de valores x=

(

x1, x2,...,xn

)

, da distribuição de probabilidade F desconhecida e que θˆ=s(x) representa a estimativa do parâmetro θ =t(F). Em certas situações, quando a dimensão da amostra é elevada, a distribuição de θˆ é aproximadamente Normal com valor médio θ e variância ∧2

se , pelo que se pode afirmar que

( )

θ θ θ ˆ ˆ ∧ − = se

Z segue aproximadamente uma distribuição

) 1 , 0 ( N .

Para determinar um intervalo de confiança para o parâmetro θ, começa-se por definir um intervalo tal que

α − = < < ) 1 (linf Z lsup P ,

ou seja, determinar um intervalo

[

l_inf,l_sup

]

onde a variável aleatória Z pertença com probabilidade igual a 1−α, que se designa por grau de confiança do intervalo. Com o objectivo de minimizar a amplitude do intervalo e tendo em conta que a distribuição Normal é simétrica, deve considerar-se:

α α α _= −    _{− ≤ ≤} − − ₂ 1 ₂ 1 1 Z z z P , ou seja,

( )

θ α θ θ α α _= −        ≤ − ≤ − − ∧ − 1 ˆ ˆ 2 1 2 1 z se z P .

Resolvendo em ordem ao parâmetro θ, obtém-se

( )

θ θ θ

( )

θ α θ α α = −      × + ≤ ≤ × − ∧ − ∧ − ˆ ˆ ˆ 1 ˆ 2 1 2 1 se z se z P .

Logo, o intervalo a 100×(1−α)% de confiança para θ é dado por

( )

( )

_   × + × − ∧ − ∧ − θ θ θ θˆ α ˆ, ˆ α ˆ 2 1 2 1 se z se z , onde 2 1₋α

z é o quantil de probabilidade 1−α 2 da distribuição N

(

0,1

)

.

Chapman (1951) mostrou que a distribuição do estimador de Petersen é assintoticamente Normal, quando N →∞ e, portanto, considera-se o intervalo de (aproximadamente) 100(1−α)% de confiança para N dado por:

) ˆ r( aˆ v ˆ 2 1 N z N± ₋α .

Tal como o estimador de Petersen, também o estimador de Chapman tem distribuição assintoticamente Normal quando N →∞. Sendo assim, considera-se o intervalo (aproximado) de 100(1−α)% de confiança dado por:

) ~ r( aˆ v ~ 2 1 N z N _α − ± .

Igualmente para o estimador da dimensão da população proposto por Bailey se mostra que a distribuição do estimador é assintoticamente Normal, quando N →∞, considerando-se o intervalo de 100(1−α)% de confiança dado por:

) r( aˆ v * 2 1 * N z N _α − ± .

Estes intervalos de confiança, construídos a partir do facto da distribuição dos estimadores ser assintoticamente Normal, não satisfazem a necessidade de precisão necessária para alguns dos estudos, nomeadamente quando se trata de populações de pequena dimensão ou quando a dimensão das amostras não é muito elevada. Fienberg (1972) sugere uma nova abordagem para a construção dos intervalos de confiança através da utilização de tabelas de contingência incompletas, como se refere na secção 2.6.

Como para determinados valores de n , ₁ n e N a distribuição Hipergeométrica ₂ pode ser aproximada pela distribuição de Poisson, pela distribuição Binomial ou pela distribuição Normal, alguns autores sugerem algumas recomendações tendo em conta as dimensões das amostras e o número de indivíduos marcados na segunda amostra, m.

Seja N n p= 1 e considere-se 2 ˆ n m p= . Quando pˆ <0,1 e 0,1 1 < n m _{, a distribuição}

de Poisson é recomendada e pode considerar-se um intervalo de confiança para

N n n_{1 2} =

µ como proposto na tabela de Pearson e Hartley (1966: 227, m≤50), na tabela de Crow e Gardner (1959: m≤300) ou no gráfico de Adams (1951: m≤50). No entanto, para m≤50 pode utilizar-se a tabela proposta por Chapman (1948) onde se indica um intervalo, com menor amplitude, a 95% de confiança para

λ

N com λ =n1n2,

tabela que se encontra no anexo 2.

No caso de pˆ <0,1 e m>50 a proposta de Cochran (1963: 87) consiste na utilização da distribuição Normal na obtenção de um intervalo de confiança a 95% para p, sendo este dado por:

(

) (

)

(

)

          +       − − − ± 2 2 1 2 2 1 1 ˆ 1 ˆ 1 96 , 1 ˆ n n p p f p em que N n

f = 2 , que pode ser menosprezado se a sua estimativa

1

nm for inferior a 0,1. Muitas vezes o factor de correcção

2

2 1

n também é menosprezado. Com este intervalo de confiança para

N n

p= 1 obtém-se o respectivo intervalo de confiança para N.

Quando se verifica N >150, n₁ >50 e n₂ >50, m segue uma distribuição aproximadamente Normal e um intervalo de confiança a 95%, com maior precisão que o anterior, para a dimensão da população, é sugerido por Robson e Regier (1964) através do cálculo das duas maiores raízes da equação cúbica:

2 2 1 1 2 2 2 1 96 , 1 1 1 =       − −       − ×       − N n N N n N n n N n n m .

Para os casos em que pˆ >0,1 pode usar-se a aproximação Binomial, expressão 2-3, ou a distribuição Normal, tendo em conta que para valores pequenos da dimensão da segunda amostra se pode utilizar a expressão 2-9, seguindo a sugestão de Cochran (1963: 57) que se encontra na tabela seguinte:

pˆ (ou 1− ) pˆ 0,5 0,4 0,3 0,2 0,1

2

n 30 50 80 200 600

Se, por outro lado, não for possível utilizar a aproximação à distribuição Normal, pode obter-se um intervalo de confiança para p com o uso da distribuição Binomial, quando pˆ >0,1 pelos gráficos Clopper-Pearson propostos por Pearson e Hartley (1966: 228-229) e por Adams (1951) ou através das tabelas de Harvard Computation Laboratory (1955).

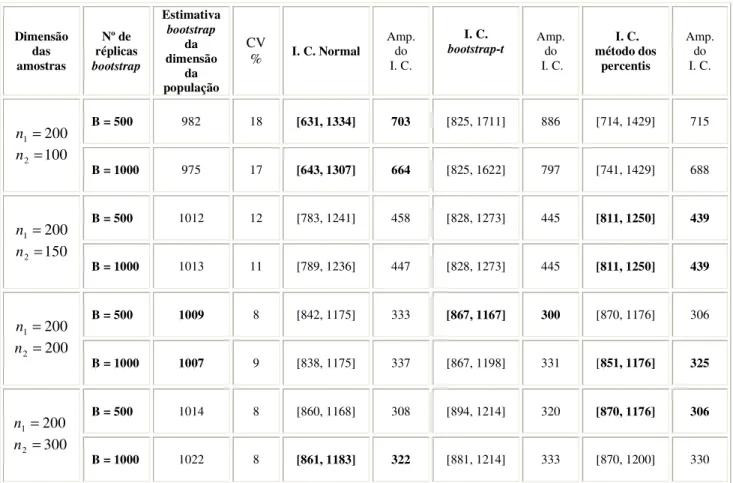
Nos casos em que a recolha de amostras não é muito acessível, um outro método foi desenvolvido para tornar os estimadores e os intervalos de confiança mais exactos e não tão enviesados, sem haver um esforço muito elevado na recolha de amostras. Esse método consiste em considerar apenas as duas amostras iniciais e criar um determinado número de réplicas da segunda amostra com a mesma dimensão, construindo a partir dessas novas amostras os cálculos necessários para a estimação do parâmetro e do respectivo intervalo de confiança. Este método denomina-se por método bootstrap e será analisado na secção 2.7.

2.4 Dimensão das amostras

Para estimar a dimensão de uma determinada população fechada, aplicando o método de captura e recaptura simples, é necessário recolher duas amostras. Para tal, é importante que a dimensão de cada uma das amostras seja a mais adequada, já que uma escolha errada da dimensão de cada amostra pode originar desvios importantes nos resultados obtidos. A recolha das amostras e a dimensão de cada uma delas deve ter em conta a população em estudo, a sua estrutura e a sua dinâmica.

Existem vários critérios nos quais um investigador se pode apoiar para proceder à escolha da dimensão das amostras a realizar, com vista a um cálculo mais preciso do estimador da dimensão total da população, N. Um dos métodos utilizados é proposto por Robson e Regier (1964) (para o caso de se querer empregar o estimador de Petersen, representado por Nˆ ) que principia pela escolha de um determinado valor de α e de A, de modo que a probabilidade do estimador da dimensão da população tenha um erro relativo inferior a A seja igual a

(

1−α

)

, isto é, de forma a que:

      < − < − ≤ − A N N N A ˆ Pr 1 α , onde N N Nˆ −

representa o erro relativo do estimador.

São sugeridos três valores para a escolha de α e de A:

1) 1−α =0,95, A=0,50, recomendado para estudos preliminares ou para situações em que apenas seja necessária uma ideia aproximada do tamanho da população;

2) 1−α =0,95, A=0,25, recomendado para estudos que necessitem de maior precisão;

3) 1−α =0,95, A=0,10, recomendado para estudos que necessitem de um resultado mais fiel da dimensão da população.

Robson e Regier criaram gráficos5 _{para os diferentes valores de}

_α

_{e de A tendo}

em conta a dimensão da população em estudo e a necessidade de precisão da estimativa, no caso de se utilizar o estimador de Petersen. Através da análise dos gráficos é possível

avaliar se a escolha da dimensão das amostras foi ou não a mais adequada. Para o caso em que basta um valor aproximado da estimativa da dimensão da população, A=0,50, é proposto no gráfico respectivo que a segunda amostra tenha dimensão inferior à primeira; para o caso em que A=0,25 e de modo que o estudo tenha alguma precisão é necessário que as dimensões das amostras sejam aproximadamente as mesmas; se, por outro lado, A=0,10, isto é quando se pretende que o estudo tenha bastante precisão, a dimensão da segunda amostra tem de ser superior à primeira.

Como seria de esperar, pode concluir-se que, quanto menor é o valor de A, maior é a necessidade da dimensão das duas amostras ser elevada (Seber, 1982). Os autores salientam que para os valores de n e 1 n dados pelos gráficos, o viés do estimador de 2

Petersen é apenas da ordem de 1%.

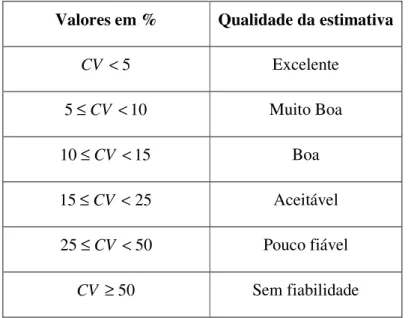
Uma medida que se pode considerar para avaliar a qualidade da estimativa da dimensão da população é o coeficiente de variação, CV, que é dado pelo quociente entre o erro padrão amostral e o valor amostral da estimativa. Em função do valor obtido para este coeficiente podem retirar-se conclusões acerca da fiabilidade da estimativa obtida. A seguinte tabela apresenta uma classificação da qualidade das estimativas:

Valores em % Qualidade da estimativa

5 < CV Excelente 10 5≤ CV < Muito Boa 15 10≤ CV < Boa 25 15≤ CV < Aceitável 50 25≤ CV < Pouco fiável 50 ≥ CV Sem fiabilidade

Tabela 2-1 – Qualidade da estimativa em função do coeficiente de variação

Supondo que numa primeira investigação se consideram dimensões para as duas amostras que originam maus resultados para a qualidade do estimador da dimensão da

população pode-se, de antemão, para um novo estudo escolher dimensões para as amostras que originem melhores resultados no coeficiente de variação obtendo assim uma estimativa com melhor qualidade e precisão.

Petersen propôs uma aproximação para o coeficiente de variação do seu estimador da dimensão da população no caso desta ser fechada. Assim, e considerando que todos os pressupostos referidos na secção 2.2. são satisfeitos e que a dimensão da segunda amostra é suficientemente elevada, o coeficiente de variação sugerido por Petersen de Nˆ , é: m n n N CV ˆ 1 2 1 ≈ ≈ .

Petersen refere também que para se obter CV <0,25 devem obter-se no mínimo 16 indivíduos marcados, isto é, m≥16.

Sabendo que o estimador de Petersen da dimensão da população é dado por

m n n

Nˆ = 1 2 e a respectiva estimativa da variância dada por

3 2 1 2 1 ( )( ) ) ˆ r( aˆ v m m n m n n n

N = − − , substituindo na definição do coeficiente de variação

( )

N N se CV ˆ ˆ = , obtém-se:

(

)(

)

. 1 2 2 1 1 2 1 2 1 2 1 2 1 2 1 n m n n m n m n n m m n m n n n m m m m n m n n n CV − × − × = × × − − = × − − =

Assim, constata-se que Petersen considera apenas m

1

para o coeficiente de

variação, assumindo que 1

2 2 1 1− _× − _≈ n m n n m n

o que nem sempre se verifica. Por outro

lado, a qualidade do estimador iria depender quase exclusivamente do valor de m, ou seja, dos indivíduos encontrados na segunda amostra que foram marcados na primeira amostra. Deste modo, o coeficiente proposto por Petersen produz piores resultados que

o coeficiente de variação usual e, por esse motivo, não será considerado nos exemplos que se seguem.

Tendo em conta os valores sugeridos para a escolha de α e de A, assim como os gráficos propostos por Robson e Regier que orientam os investigadores na escolha da dimensão das duas amostras, verifica-se que, para obter uma estimativa mais correcta e adequada à situação em causa, é necessário uma razoável proporção de indivíduos marcados. Assim, para o caso de n₁ =n₂ =n e considerando o valor de A anteriormente mencionado, podem considerar-se para a proporção de indivíduos necessários na recolha das amostras, tendo em conta a dimensão da população em estudo, os seguintes valores da tabela: A 0,5 0,25 0,1 0,5 0,25 0,1 0,5 0,25 0,1 N 50 50 50 100 100 100 1000 1000 1000 N n 100 40 54 74 32 43 64 13 20 40

Para alguns autores o ideal seria considerar para a dimensão da primeira amostra, isto é, o número de indivíduos que seriam marcados, aproximadamente metade da população em causa. Outros autores consideram que o estimador proposto por Petersen para a dimensão da população nem sempre é satisfatório, chegando a propor que, no caso de haver um uso exaustivo desse estimador no estudo duma determinada espécie, os resultados sejam comparados com estimativas calculadas anteriormente por outros processos ou, eventualmente, seja testado o estimador numa população conhecida.

2.5 Estudo Comparativo

Pretende-se com os exemplos aqui apresentados tirar algumas conclusões e confirmar algumas teorias no que respeita à dimensão das amostras necessárias para o cálculo dos diferentes estimadores da dimensão de uma dada população, assim como tentar avaliar qual o melhor estimador. Para tal, utilizou-se um algoritmo computacional gerador de amostras aleatórias de dados constituídos pelos números de 1 a 1000. Esse

algoritmo utilizou-se para todos os exemplos em que foi necessário gerar duas ou mais amostras de números e cada número representará um certo indivíduo da população em estudo.

Exemplo 2-2:

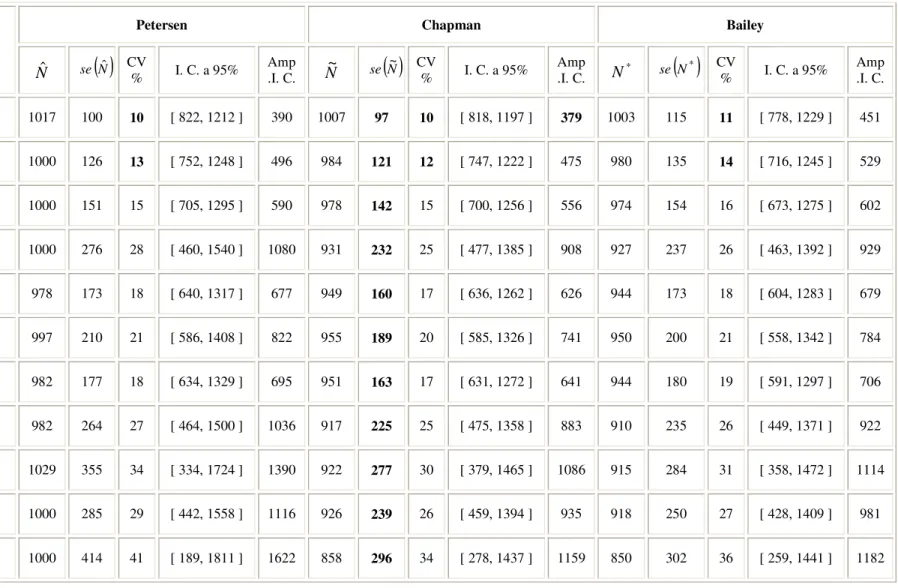
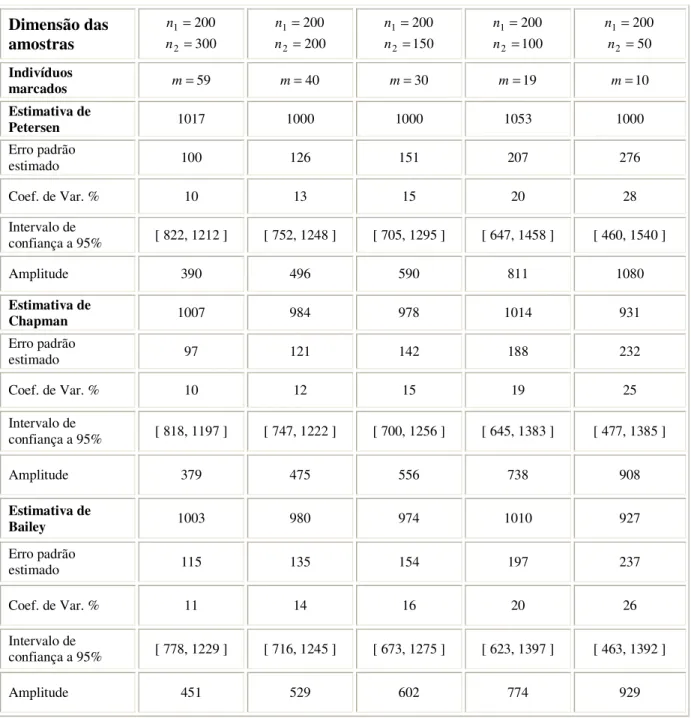
Com a utilização do algoritmo geram-se duas amostras aleatórias independentes com diferentes dimensões. Considera-se que os valores da primeira amostra gerada constituem os indivíduos da população que são marcados e, portanto, o número de indivíduos marcados na segunda amostra gerada é o número de valores repetidos nas duas amostras, que se designa por m. Num primeiro estudo foram realizadas várias simulações em que se fez variar a dimensão da primeira amostra e se considerou para a dimensão da segunda amostra, 150, 100, 75, 50 e 25% da dimensão da primeira, respectivamente, onde se registaram o número de indivíduos marcados para cada uma das simulações.

Foram realizadas quarenta e uma simulações para cada uma das variações realizadas às dimensões das amostras, obtendo-se para cada uma delas um determinado valor de m, e, consequentemente, os respectivos valores para a estimação da dimensão da população segundo as propostas de Petersen, de Chapman e de Bailey que se encontram nas tabelas seguintes e nos respectivos gráficos:

1º Caso: Dimensão da primeira amostra 100 indivíduos Dimensão da segunda

amostra 25 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

0 5 --- --- --- 1 10 2500 1312 1300 2 13 1250 874 867 3 9 833 656 650 4 4 625 524 520 Total 41

Dimensão da segunda

amostra 50 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

1 1 5000 2575 2550 2 6 2500 1716 1700 3 7 1667 1287 1275 4 6 1250 1029 1020 5 8 1000 858 850 6 4 833 735 729 7 3 714 643 638 8 6 625 571 567 Total 41 Dimensão da segunda

amostra 75 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

2 1 3750 2558 2533 3 1 2500 1918 1900 4 4 1875 1534 1520 5 7 1500 1278 1267 6 3 1250 1096 1086 7 8 1071 959 950 8 6 938 852 844 9 3 833 767 760 10 1 750 697 691 11 3 682 639 633 12 1 625 589 585 13 3 577 547 543 Total 41 Dimensão da segunda

amostra 100 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

5 2 2000 1699 1683 6 1 1667 1456 1443 7 3 1429 1274 1263 8 3 1250 1132 1122 9 10 1111 1019 1010 10 4 1000 926 918 11 5 909 849 842 12 6 833 784 777 13 5 769 728 721 16 1 625 599 594 17 1 588 566 561 Total 41

0 2 4 6 8 10 12 14 --- 1300 867 650 520 --- 1312 874 656 524 --- 2500 1250 833 625 F re q u ên ci a N N N ˆ ~ * Dimensão da segunda

amostra 150 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

10 2 1500 1385 1373 11 5 1364 1270 1258 12 3 1250 1172 1162 13 4 1154 1088 1079 14 3 1071 1016 1007 15 3 1000 952 944 16 4 938 896 888 17 5 882 846 839 18 2 833 802 795 19 2 789 762 755 20 2 750 725 719 21 3 714 692 686 22 2 682 662 657 27 1 556 544 539 Total 41

Gráficos do 1º Caso: Dimensão da primeira amostra 100 indivíduos Dimensão da segunda amostra 25 indivíduos

0 2 4 6 8 10 2550 1700 1275 1020 850 729 638 567 2575 1716 1287 1029 858 735 643 571 5000 2500 1667 1250 1000 833 714 625 F re q u ên ci a N N N ˆ ~ * 0 2 4 6 8 10 12 1683 1443 1263 1122 1010 918 842 777 721 594 561 1699 1456 1274 1132 1019 926 849 784 728 599 566 2000 1667 1429 1250 1111 1000 909 833 769 625 588 F re q u ên ci a N N N ˆ ~ * 0 1 2 3 4 5 6 7 8 9 2533 1900 1520 1267 1086 950 844 760 691 633 585 543 2558 1918 1534 1278 1096 959 852 767 697 639 589 547 3750 2500 1875 1500 1250 1071 938 833 750 682 625 577 F re q u ên ci a N N N ˆ ~ *

Dimensão da segunda amostra 50 indivíduos

Dimensão da segunda amostra 75 indivíduos

Dimensão da segunda amostra 100 indivíduos

0 4 8 1373 1258 1162 1079 1007 944 888 839 795 755 719 686 657 539 1385 1270 1172 1088 1016 952 896 846 802 762 725 692 662 544 1500 1364 1250 1154 1071 1000 938 882 833 789 750 714 682 556 F re q u ên ci a N N N ˆ ~ *

Dimensão da segunda amostra 150 indivíduos

2º Caso: Dimensão da primeira amostra 120 indivíduos Dimensão da

segunda amostra 30

indivíduos Estimativas

Valor de

m Frequência Petersen Chapman Bailey

0 1 --- --- --- 1 6 3600 1875 1860 2 11 1800 1249 1240 3 8 1200 937 930 4 8 900 749 744 5 4 720 624 620 6 2 600 535 531 7 1 514 468 465 Total 41

Dimensão da segunda amostra 60

indivíduos Estimativas

Valor de

m Frequência Petersen Chapman Bailey

2 1 3600 2459 2440 3 1 2400 1844 1830 4 2 1800 1475 1464 5 8 1440 1229 1220 6 5 1200 1053 1046 7 6 1029 922 915 8 5 900 819 813 9 3 800 737 732 10 4 720 670 665 11 1 655 614 610 12 1 600 567 563 13 3 554 526 523 14 1 514 491 488 Total 41 Dimensão da segunda

amostra 90 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

7 3 1543 1375 1365 8 4 1350 1222 1213 9 3 1200 1100 1092 10 9 1080 1000 993 11 2 982 917 910 12 6 900 846 840 13 3 831 786 780 14 4 771 733 728 15 3 720 687 683 16 4 675 647 642 Total 41

Dimensão da segunda amostra 120

indivíduos Estimativas

Valor de

m Frequência Petersen Chapman Bailey

8 1 1800 1626 1613 9 1 1600 1463 1452 10 2 1440 1330 1320 11 2 1309 1219 1210 12 6 1200 1125 1117 13 4 1108 1045 1037 14 3 1029 975 968 15 6 960 914 908 16 3 900 860 854 17 3 847 812 807 18 3 800 770 764 19 5 758 731 726 20 1 720 696 691 21 1 686 665 660 Total 41 Dimensão da segunda amostra 180 indivíduos Estimativas Valor de

m Frequência Petersen Chapman Bailey

14 2 1543 1459 1448 15 2 1440 1368 1358 16 1 1350 1287 1278 17 4 1271 1216 1207 18 2 1200 1152 1143 19 2 1137 1094 1086 20 6 1080 1042 1034 21 1 1029 995 987 22 7 982 951 944 23 6 939 912 905 24 3 900 875 869 25 2 864 841 835 26 1 831 810 804 27 2 800 781 776 Total 41

0 2 4 6 8 10 12 --- 1860 1240 930 744 620 531 465 --- 1875 1249 937 749 624 535 468 --- 3600 1800 1200 900 720 600 514 F re q u ên ci a N N N ˆ ~ * 0 1 2 3 4 5 6 7 8 9 2440 1830 1464 1220 1046 915 813 732 665 610 563 523 488 2459 1844 1475 1229 1053 922 819 737 670 614 567 526 491 3600 2400 1800 1440 1200 1029 900 800 720 655 600 554 514 F re q u ên ci a N N N ˆ ~ *

Gráficos do 2º Caso: Dimensão da primeira amostra 120 indivíduos Dimensão da segunda amostra 30 indivíduos

0 1 2 3 4 5 6 7 8 9 10 1365 1213 1092 993 910 840 780 728 683 642 1375 1222 1100 1000 917 846 786 733 687 647 1543 1350 1200 1080 982 900 831 771 720 675 F re q u ên ci a N N N ˆ ~ * 0 1 2 3 4 5 6 7 1613 1452 1320 1210 1117 1037 968 908 854 807 764 726 691 660 1626 1463 1330 1219 1125 1045 975 914 860 812 770 731 696 665 1800 1600 1440 1309 1200 1108 1029 960 900 847 800 758 720 686 F re q u ên ci a N N N ˆ ~ * 0 1 2 3 4 5 6 7 8 1448 1358 1278 1207 1143 1086 1034 987 944 905 869 835 804 776 1459 1368 1287 1216 1152 1094 1042 995 951 912 875 841 810 781 1543 1440 1350 1271 1200 1137 1080 1029 982 939 900 864 831 800 F re q u ên ci a N N N ˆ ~ *

Dimensão da segunda amostra 90 indivíduos

Dimensão da segunda amostra 120 indivíduos

3º Caso: Dimensão da primeira amostra 150 indivíduos Dimensão da segunda

amostra 38 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

2 2 2850 1962 1950 3 3 1900 1471 1463 4 6 1425 1177 1170 5 7 1140 981 975 6 7 950 840 836 7 7 814 735 731 8 5 713 653 650 9 1 633 588 585 10 2 570 534 532 11 1 518 490 488 Total 41 Dimensão da segunda

amostra 75 indivíduos Estimativas

Valor de m Frequência Petersen Chapman Bailey

6 1 1875 1638 1629 7 3 1607 1434 1425 8 5 1406 1274 1267 9 8 1250 1147 1140 10 6 1125 1042 1036 11 7 1023 955 950 12 1 938 882 877 13 6 865 819 814 16 2 703 674 671 17 2 662 637 633 Total 41