Análise e intervenção no ensino-aprendizagem de cônicas e suas aplicações: um estudo de caso

(1)

56 REnCiMa, v. 10, n.6, p. 56-75, 2019

ANÁLISE E INTERVENÇÃO NO ENSINO-APRENDIZAZEM DE CÔNICAS

E SUAS APLICAÇÕES: UM ESTUDO DE CASO

ANALYSIS AND INTERVENTION IN THE TEACHING-LEARNING OF CONIC SECTIONS AND THEIR APPLICATIONS: A CASE STUDY

Evando Santos Araújo

Universidade Federal do Vale do São Francisco - UNIVASF, Mestrado Profissional em Matemática – PROFMAT, evando.araujo@univasf.edu.br

Adriano Victor Lopes da Silva

Universidade Federal do Vale do São Francisco - UNIVASF, adriano.silva@univasf.edu.br

Waldiclecyo Souza Silva

Secretaria de Educação do Estado de Pernambuco, Gerência Regional de Educação – Sertão do Médio São Francisco, waldiclecyo.silva@educacao.pe.gov.br

Resumo

As cônicas são formas geométricas que recebem bastante atenção devido às inúmeras aplicações tecnológicas de suas propriedades em diversas áreas do conhecimento, o que destaca a busca pela melhoria do ensino-aprendizagem desse tema de matemática no ensino básico. Neste trabalho foi proposto um estudo de caso investigativo, com estudantes do Ensino Médio da rede pública estadual de ensino, relativo ao ensino-aprendizagem de cônicas e suas aplicações. O objetivo foi analisar a evolução da habilidade dos alunos em tópicos essenciais do conteúdo após minicurso com o uso de sinucas cônicas e construções geométricas com régua e compasso, em comparação com o aprendizado obtido através do ensino habitual na escola campo de estudo. Os dados foram coletados através de questionários, analisados e interpretados via modelo de Rasch dicotômico e técnicas estatísticas usuais, levando em consideração o balanço entre a dificuldade dos itens e a habilidade dos alunos com o tema. A aplicação do modelo permitiu o diagnóstico das dificuldades de forma direcionada e confirmou que as ações complementares às aulas usuais ajudaram a diminuir a hierarquia de dificuldade dos itens, com evolução significativa na proficiência dos alunos e consequente aumento da probabilidade de sucesso nos tópicos analisados.

Palavras-chave: Ensino-aprendizagem, Seções Cônicas, Materiais Manipuláveis, Metodologias Alternativas, Modelo de Rasch.

Abstract

The conic sections are geometric curves that receive a lot of attention due to technological applications of its properties in different areas of knowledge, which highlights the search

(2)

57 REnCiMa, v. 10, n.6, p. 56-75, 2019

for the improvement of teaching and learning of this mathematical topic in high school. In this work, a case-study (with secondary school students from the public education system) was proposed, concerning the teaching-learning of conics and their applications. The aim of the research was to analyze the evolution of the students' ability in essential topics of the theme after a mini-course with the use of conical snooker tables and geometric constructions with ruler and compass, compared to the traditional learning in the school. Data were collected through questionnaires, analyzed and interpreted according to the dichotomous Rasch model and of usual statistic techniques, taking into account the balance between the difficulty of the items and the ability of the students with the theme. The application of the model allowed the diagnosis of the difficulties in a directed way and confirmed that the actions complementary to the usual classes helped to decrease the hierarchy of difficulty of the items, with a significant evolution in the students' proficiency and consequent increase in the probability of success in the analyzed topics.

Keywords: Teaching-Learning Process, Conic Sections, Manipulable Materials, Alternative Methodologies, Rasch model.

Introdução

Metodologias alternativas que tornem mais significativo o processo ensino-aprendizagem de Matemática são cada vez mais discutidas em todo o mundo. O ensino de conteúdos com o auxílio de Jogos e Materiais Concretos (RODRIGUES; GAZIRE, 2012), da Interdisciplinaridade, da Resolução de Problemas, da Modelagem (MELO; FIREMAN, 2016) e de Novas Tecnologias (SANTOS; LORETO; GONÇALVES, 2010) são algumas das propostas pedagógicas atuais que vêm sendo utilizadas com esse propósito. As chamadas seções cônicas (ou simplesmente, cônicas) são curvas planas geradas a partir da intersecção entre um cone circular reto e um plano. Dependendo do ângulo entre o plano e o cone, elas podem ser classificadas como circunferência, elipse, hipérbole ou parábola. Essas três últimas se inserem como um tema atual de ensino e pesquisa em matemática e ciências, uma vez que suas propriedades geométricas e as relações entre seus parâmetros (foco, excentricidade e diretriz) podem ser utilizadas para desenvolver diversas aplicações tecnológicas e modelar fenômenos em diferentes áreas do conhecimento (KULOGLU, 2013; CHEN, 2013).

Diversas construções arquitetônicas (SAMPER; GONZÁLEZ; HERRERA, 2017), a trajetória de partículas, a melhoria da acústica de ambientes e os movimentos planetários e de satélites são alguns dos exemplos já bem conhecidos. Algumas das aplicações tecnológicas mais recentes das cônicas envolvem a detecção de agentes bioquímicos e a determinação da concentração e cinética de moléculas na superfície de materiais a partir de propriedades de dispersão da luz (LEPAGE et al., 2012), o desenvolvimento de novos algoritmos computacionais (CHERNOV; WIJEWICKREMA, 2013) e de novos aparelhos para avaliar a capacidade térmica do solo com menor custo de operação (BOUGHANMI

(3)

58 REnCiMa, v. 10, n.6, p. 56-75, 2019

De acordo com Lévy (2010, p.169), “os indivíduos toleram cada vez menos seguir cursos uniformes ou rígidos que não correspondem a suas necessidades reais e à especificidade de seu trajeto de vida”. Dessa forma, dada a parcela de importância das cônicas para despertar o pensamento crítico/científico nos alunos, é fundamental que o professor possa explorar os parâmetros e as propriedades dessas estruturas geométricas oferecendo-lhes momentos com potencial de permitir a construção do conhecimento de forma significativa, aliando a teoria à prática do dia-a-dia. Nesse contexto, os materiais concretos e as construções geométricas são consideradas ferramentas potenciais para se alcançar esses objetivos (MOREIRA, 2017; MACEDO; LAURINO, 2018; SILVA; LOPES, 2013).

Diante do exposto, o objetivo deste trabalho foi analisar a evolução da habilidade de alunos do 3º ano do ensino médio de uma escola da rede estadual de ensino com as cônicas, suas propriedades e aplicações tecnológicas, a partir de intervenção didática proposta com o uso de materiais concretos e construções geométricas, em comparação com o aprendizado obtido através do ensino habitual na escola campo de estudo. Em ambos os momentos da investigação, o modelo probabilístico de Rasch dicotômico (RASCH, 1980) foi utilizado como ferramenta estatística de análise e interpretação dos resultados.

Materiais concretos e construções geométricas

O material concreto pode ser entendido como qualquer instrumento, objeto palpável, manipulável (ou até imagens gráficas) utilizado com vista à melhoria do ensino-aprendizagem (MIORIM; FIORENTINI, 1990; LORENZATO, 2006, p. 23).

Lorenzato (2006, p.23) ainda diferencia o material concreto manipulável em estático e dinâmico. Diferente do estático (apenas para o manuseio e observação), o dinâmico admite alterações em sua estrutura física a partir de sua manipulação. Este último pode ainda admitir operações conferidas pelo indivíduo que o manipula com o objetivo de facilitar a percepção de determinadas propriedades. Assim, podem se mostrar com diversas propostas de trabalho, com características específicas e com diferentes usos em momentos distintos do processo ensino-aprendizagem.

Defende-se ainda que o conceito de “concreto” deve ir além do uso de um conjunto de objetos “abstratos” (sem qualquer relação com o real) desenvolvidos com a finalidade de ensino: este deve remeter a situações que o indivíduo possa se deparar socialmente. Em outras palavras, faz-se necessário que, por trás da utilização do material, haja uma proposta pedagógica que a justifique, alinhada à visão de mundo, do homem, de matemática e de educação que o material pode propor (CARRAHER, A.; CARRAHER, D; SCHILEMANN, 2001, p. 180).

Já as construções geométricas podem ser entendidas como manipulações criativas que podem promover a habilidade de pensar de forma clara e coerente, o que é de fundamental importância para o processo conceitual. A construção de entes geométricos como próprio material didático da aula, sua análise detalhada e posterior significação relacionada ao mundo real ajuda o aluno a melhorar o interesse pelas aulas de matemática, além de permitir uma maior interação entre professor e aluno.

(4)

59 REnCiMa, v. 10, n.6, p. 56-75, 2019

Assim, a introdução de régua e compasso nas aulas de matemática pode melhorar a habilidade do aluno na elaboração de figuras geométricas ao mesmo passo que amplia sua capacidade motora fina (diretamente relacionada à atenção e concentração), uma vez que este necessita de orientações verbais do mediador para executar a tarefa. Há então uma interação dinâmica entre professor e aluno, criando um ambiente de confiança e diversão propício ao ensino-aprendizagem (KALEFF, 2006; SILVA; LOPES, 2013; KULOGLU, 2013).

Piaget (1995) discorre que atividades lúdicas como as citadas anteriormente podem auxiliar o aluno no processamento e assimilação dos conceitos em questão. O autor continua seu discurso mostrando a importância de se trabalhar com variedades de aprendizagem. Ele destaca que quando se propõe o contato do aluno com o objeto do conhecimento, este indivíduo experimenta então uma conexão direta com seu material de estudo, o que proporciona uma melhor compreensão dos conceitos a partir do seu aprendizado.

Ao manipular materiais concretos ou construir figuras no papel utilizando ferramentas como régua e compasso aponta-se que olhos, mãos e cérebro do aluno se conectam de forma a estimular seu desenvolvimento psicológico e cognitivo, tornando o aprendizado criativo e divertido (TÉLLEZ; DIAZ; GOMEZ, 2007). A possibilidade de relacionar os estudantes na execução das ações reforça o destaque das práticas pedagógicas citadas. Estes últimos autores também citam Vigotsky para indicar que a interação entre os estudantes proporciona a relação entre seus conhecimentos, melhora suas relações interpessoais e a autoestima, com uma aprendizagem cooperativa, prática e motivadora. A utilização dessas práticas pedagógicas propiciam ainda o exercício psicomotor, a coordenação e a originalidade do aluno, bem como fornece ao docente, ferramentas alternativas para expor os assuntos e atingir os objetivos propostos.

O modelo de Rasch dicotômico

O modelo de Rasch dicotômico é um dos modelos mais utilizados e aceitos na Teoria de Resposta ao Item (TRI), a qual dispõe de ferramentas para análise de resultados de testes de conhecimento e amplamente empregada e aceita em avaliações educacionais em todo o mundo.

O modelo permite a análise particular dos indivíduos e dos itens do questionário ao invés de análises estatísticas apenas grupais (porcentagens de ocorrência de respostas positivas em cada item). Outro diferencial é a possibilidade de identificar, entre os que não obtiveram sucesso em um item, os subgrupos com maior ou menor tendência de sucesso na resposta ao item e direcionar intervenções didático/pedagógicas específicas, de acordo com as necessidades diagnosticadas. Na área de Matemática, pesquisadores têm utilizado o modelo de Rasch para identificar alunos ingressantes em universidades com necessidade de tutoria, avaliar universitários com relação ao nível de habilidade em modelagem, identificar respostas inesperadas de professores estagiários formandos em testes de proficiência, avaliar a evolução da habilidade algébrica de alunos do ensino básico ao longo do ano letivo após aplicação de intervenções didáticas, entre outros (CALLINGHAM; BOND, 2006; HAINES; CROUCH, 2001; EDWARDS; ALCOCK, 2010; RYAN; WILLIAMS, 2007; VAN STIPHOUT; DRIJVERS; GRAVEMEIJER, 2014).

(5)

60 REnCiMa, v. 10, n.6, p. 56-75, 2019

Pelo modelo de Rasch (1980), a análise das respostas dos indivíduos a um item está condicionada às respostas dadas por eles aos outros itens do questionário. Essa conexão, estabelecida a partir da aplicação do modelo, gera para cada variável um nível relativo de interferência no estudo em questão, denominado de dificuldade do item. Considerando como o parâmetro que expressa a dificuldade de um item = 1, 2, 3..., n e θj o parâmetro que expressa a habilidade de um indivíduo = 1,2,3..., m, dada uma combinação particular de e , ( ), o modelo de Rasch dicotômico retorna a probabilidade do indivíduo responder de forma satisfatória ao item , de acordo com a

Equação 1: (Eq. 1). Ao desenvolver a Eq. 1, considerando-se

j = e , obtém-se: (Eq. 2). Com a equação neste novo formato, a comparação entre e pode ser feita em uma mesma escala métrica de valores (chamada de logits ou log da chance de sucesso), no intervalo (-∞,∞), o que facilita a interpretação dos resultados: quando , a probabilidade de resposta correta ( ) será maior ou igual a 0,5. Em outras palavras, pelo modelo, um indivíduo conseguirá responder positivamente a um item quando sua habilidade ( ) for maior ou igual à dificuldade do item ( ). Quanto mais positivo for o valor estimado de de um item, maior a sua dificuldade e vice-versa; e, quanto mais positivo for o valor de θ para um ID, maior sua habilidade e vice-versa.

O modelo também pode ser representado graficamente pelas curvas P versus

( (Fig. 1). Os indivíduos (ID’s) (ou grupos de ID’s) estarão localizados sobre a

curva, obedecendo às combinações específicas dos parâmetros . A probabilidade mínima de resposta positiva ( 0,5 ou ) de um ID ocorre no ponto de inflexão da curva. ID’s localizados após o ponto de inflexão da sigmoide (Fig. 1a) possuem probabilidade de sucesso maior que 0,5.

Figura 1 - (a) Gráfico versus ( ). (b) Curvas Características dos Itens (CCI).

Fonte: adaptado de Edwards e Alcock (2010).

Outra forma de representar a relação entre as variáveis do modelo para cada item do questionário é através da Curva Característica do Item (CCI) (gráfico versus θ). Embora a dificuldade do item não seja explicitada na CCI, sabe-se que quando 0,5, e, dessa forma, a dificuldade de cada item pode ser mensurada no eixo das habilidades (θ) no ponto de inflexão da curva (Fig. 1b). Quanto maior a dificuldade de um

(6)

61 REnCiMa, v. 10, n.6, p. 56-75, 2019

item, mais deslocada para a direita estará a sua CCI em relação às curvas dos itens com menor dificuldade.

Metodologia

A pesquisa consistiu em um estudo de caso com abordagem predominantemente quantitativa e caráter exploratório (GIL, 2010). Para o maior controle das ações planejadas e eficácia do discurso do professor mediador aos alunos, a proposta de intervenção foi realizada em turma com número reduzido de alunos (BARBOZA; REGO; BARBOSA, 2013). A coleta dos dados foi obtida a partir de uma amostra aleatória de 20 ID’s, no software estatístico Minitab, de um universo de 80 alunos matriculados no 3° ano do ensino médio de uma escola estadual de tempo integral do estado de Pernambuco.

Após as aulas habituais, os ID’s participaram de um minicurso com duração de 8 h/a (divididas em 3 dias de atividades). Essa intervenção trabalhou as definições, elementos e propriedades focais das cônicas a partir do uso de sinucas não usuais com formas geométricas cônicas (ou “sinucas cônicas”) (Fig. 2) e de construções geométricas com régua e compasso, conforme orientações descritas por Moreira (2017), culminando com a apresentação e discussão de aplicações das propriedades das cônicas em problemas reais. Todas as ações do minicurso foram planejadas previamente e posteriormente aplicadas no laboratório de matemática da escola, com mediação de um dos autores da pesquisa e do professor responsável pela disciplina. As sinucas cônicas foram confeccionadas em madeira a partir de moldes das formas geométricas em destaque, produzidos no programa gráfico Geogebra.

Figura 2 - Sinucas cônicas produzidas em madeira: (a) elíptica, (b) parabólica e (c) hiperbólica.

Fonte: próprio autor.

O aprendizado dos alunos foi avaliado a partir de questionário de proficiência aplicado em duas oportunidades: após as aulas habituais (com o Questionário Q1); e, após a intervenção com o minicurso (Questionário Q2), complementar às aulas. Os estudantes tiveram cento e cinquenta minutos para responder tanto o Q1 quanto o Q2, individualmente e sem o auxílio de fontes de pesquisa.

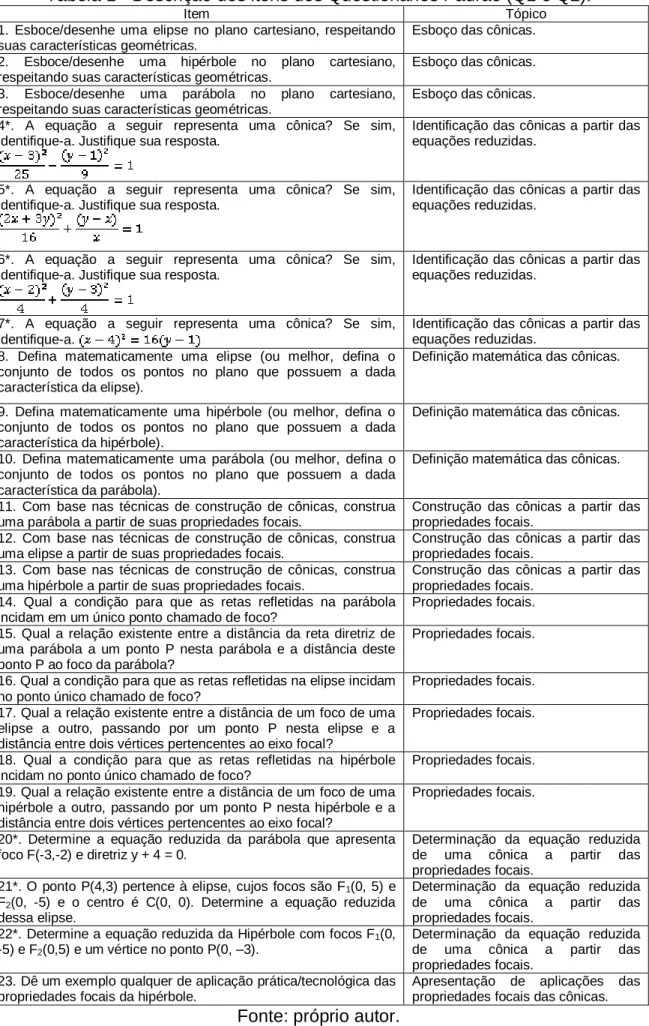
O Questionário de proficiência (Tab. 1) foi elaborado pelos autores a partir da revisão da literatura, com vinte e oito itens abordando tópicos representativos da definição, da identificação, da construção, das propriedades focais, das formas reduzidas e das aplicações das propriedades focais das cônicas (elipse, hipérbole e parábola).

(7)

62 REnCiMa, v. 10, n.6, p. 56-75, 2019

Tabela 1 - Descrição dos itens dos Questionários Padrão (Q1 e Q2).

Item Tópico

1. Esboce/desenhe uma elipse no plano cartesiano, respeitando suas características geométricas.

Esboço das cônicas. 2. Esboce/desenhe uma hipérbole no plano cartesiano,

respeitando suas características geométricas.

Esboço das cônicas. 3. Esboce/desenhe uma parábola no plano cartesiano,

respeitando suas características geométricas.

Esboço das cônicas. 4*. A equação a seguir representa uma cônica? Se sim,

identifique-a. Justifique sua resposta.

Identificação das cônicas a partir das equações reduzidas.

5*. A equação a seguir representa uma cônica? Se sim, identifique-a. Justifique sua resposta.

6*. A equação a seguir representa uma cônica? Se sim, identifique-a. Justifique sua resposta.

7*. A equação a seguir representa uma cônica? Se sim, identifique-a.

8. Defina matematicamente uma elipse (ou melhor, defina o conjunto de todos os pontos no plano que possuem a dada característica da elipse).

Definição matemática das cônicas.

9. Defina matematicamente uma hipérbole (ou melhor, defina o conjunto de todos os pontos no plano que possuem a dada característica da hipérbole).

10. Defina matematicamente uma parábola (ou melhor, defina o conjunto de todos os pontos no plano que possuem a dada característica da parábola).

11. Com base nas técnicas de construção de cônicas, construa uma parábola a partir de suas propriedades focais.

Construção das cônicas a partir das propriedades focais.

12. Com base nas técnicas de construção de cônicas, construa uma elipse a partir de suas propriedades focais.

13. Com base nas técnicas de construção de cônicas, construa uma hipérbole a partir de suas propriedades focais.

14. Qual a condição para que as retas refletidas na parábola incidam em um único ponto chamado de foco?

Propriedades focais. 15. Qual a relação existente entre a distância da reta diretriz de

uma parábola a um ponto P nesta parábola e a distância deste ponto P ao foco da parábola?

Propriedades focais.

16. Qual a condição para que as retas refletidas na elipse incidam no ponto único chamado de foco?

Propriedades focais. 17. Qual a relação existente entre a distância de um foco de uma

elipse a outro, passando por um ponto P nesta elipse e a distância entre dois vértices pertencentes ao eixo focal?

18. Qual a condição para que as retas refletidas na hipérbole incidam no ponto único chamado de foco?

Propriedades focais. 19. Qual a relação existente entre a distância de um foco de uma

hipérbole a outro, passando por um ponto P nesta hipérbole e a distância entre dois vértices pertencentes ao eixo focal?

20*. Determine a equação reduzida da parábola que apresenta foco F(-3,-2) e diretriz y + 4 = 0.

Determinação da equação reduzida de uma cônica a partir das propriedades focais.

21*. O ponto P(4,3) pertence à elipse, cujos focos são F1(0, 5) e F2(0, -5) e o centro é C(0, 0). Determine a equação reduzida dessa elipse.

22*. Determine a equação reduzida da Hipérbole com focos F1(0, -5) e F2(0,5) e um vértice no ponto P(0, –3).

23. Dê um exemplo qualquer de aplicação prática/tecnológica das propriedades focais da hipérbole.

Apresentação de aplicações das propriedades focais das cônicas. Fonte: próprio autor.

(8)

63 REnCiMa, v. 10, n.6, p. 56-75, 2019

Tabela 1. Continuação. 24. Dê um exemplo qualquer de aplicação prática/tecnológica das propriedades focais da elipse.

Apresentação de aplicações das propriedades focais das cônicas. 25. Dê um exemplo qualquer de aplicação prática/tecnológica das

propriedades focais da parábola.

Apresentação de aplicações das propriedades focais das cônicas. 26. As lâmpadas de faróis de carro podem ser colocadas no foco

de uma cônica que os modelam, para maximizar o direcionamento da luz. Nessas condições, qual deve ser essa cônica para que a fonte luminosa seja refletida sobre ela para então seguir um trajeto reto. Justifique sua resposta.

Identificação e solução de problemas com aplicações práticas/tecnológicas das propriedades focais das cônicas.

27. Em uma sala de reuniões temos um palestrante sem microfone em um ponto A e um ouvinte em um ponto B. Qual o melhor formato dessa sala para que o ouvinte consiga escutar as palavras do palestrante da melhor forma possível? Justifique sua resposta.

Identificação e solução de problemas com aplicações práticas/tecnológicas das propriedades focais das cônicas.

28. Na mesa de sinuca hiperbólica, qual o melhor lugar para posicionar a bola de modo que ela ricocheteie na tabela e siga uma trajetória retilínea em direção ao buraco (caçapa)? Justifique sua resposta.

Identificação e solução de problemas com aplicações práticas/tecnológicas das propriedades focais das cônicas. Fonte: próprio autor.

Os parâmetros foram estimados por máxima verossimilhança, no software de domínio público jMetrik 3.0, utilizando-se o algoritmo iterativo de Newton-Raphson, com o máximo de 150 iterações ou critério de convergência de 0,005. Com a estimativa dos parâmetros, as probabilidades de sucesso, , foram calculadas a partir da Eq. 1 em uma planilha do Excel.

A análise estatística dos dados foi realizada com o software Minitab. Os resultados amostrais (n = 20) de habilidade (como média amostral de habilidades ( ) e o seu desvio padrão ( )) foram interpretados através de técnicas estatísticas descritivas usuais. As médias populacionais de habilidade (média estimada para o total de alunos) antes e depois da aplicação da intervenção didática foram determinadas por inferência estatística,

em termos de intervalos de confiança ( ; ), com distribuição t de

Student, nível de significância do teste α = 0,05 (95% de confiança) e ( ) graus de liberdade. Para analisar se houve diferença significativa nas médias de habilidade dos ID’s, antes ( ) e após ( ) a intervenção, foi realizado um teste de hipóteses de comparação entre duas médias (teste t de Student para comparação de duas médias com variâncias populacionais diferentes e desconhecidas e 95 % de confiança).

Resultados e discussão

Dificuldade dos Itens

Segundo os planos de aula do professor responsável pela disciplina de matemática no campo de estudo, todo o conteúdo de cônicas foi ministrado com uma carga-horária de 6 h/a. Para cada cônica foram apresentadas a definição, a forma geométrica, seus elementos (centro, eixos, focos), equação reduzida, simetrias, excentricidade, propriedades focais e exercícios de fixação através de aulas expositivas, utilizando quadro branco e pincel e com o auxílio do livro didático adotado pela escola.

Em uma primeira análise das respostas da amostra de alunos ao Q1 (anterior ao minicurso), verificou-se que a maioria dos itens foi estimada com valores positivos na escala logits de dificuldade e que os estudantes não obtiveram sucesso na maioria dos

(9)

64 REnCiMa, v. 10, n.6, p. 56-75, 2019

tópicos sobre cônicas. Esse caso representa a situação em que a habilidade dos indivíduos é menor que a dificuldade dos itens. Em outras palavras, o conhecimento dos alunos adquirido a partir das aulas convencionais não foi suficiente para que estes obtivessem êxito em diversos itens do teste proposto. A quantidade usual de alunos por turma (40 alunos), a complexidade do conteúdo, a carga-horária para se trabalhar os assuntos, a falta de metodologias alternativas de ensino e materiais didáticos auxiliares são alguns dos fatores que interferiram diretamente no insucesso dos entrevistados. Passos e Nacarato (2018) também consideram a influência da própria formação inicial docente no baixo rendimento do aluno quando afirmam que muitos profissionais em atividade “provêm de cursos de formação que deixam sérias lacunas conceituais para o ensino de Matemática. Muitas vezes anseiam por programas de formação continuada que lhes deem subsídios para suprir essas lacunas”.

Em adição, como verificado nos planos de aula disponibilizados, o livro adotado pela escola era a única referência e fonte de consulta do professor para trabalhar os conteúdos em sala de aula. Teoricamente, o livro deveria ser utilizado como instrumento auxiliar e a busca por outras fontes metodológicas de pesquisa também deveriam naturalmente fazer parte da atividade pedagógica do professor, o que muitas vezes não ocorre na prática (FREITAG; MOTA; COSTA, 1997).

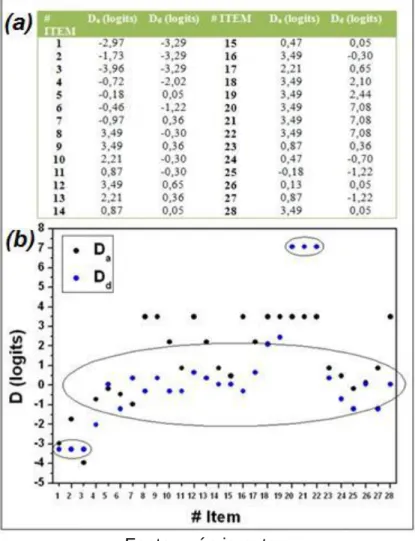
Na Fig. 3a são apresentados os valores estimados de dificuldade dos itens antes (Da) e depois (Dd) da aplicação da intervenção didática com o minicurso. No Q1, os itens relativos ao tópico “esboço/desenho das cônicas (elipse, hipérbole e parábola) no plano cartesiano” foram estimados com os valores mais negativos (Itens 1, 2 e 3 com pontuações -2,97, -1,73 e -3,96 logits, respectivamente), indicando que esse tópico do conteúdo foi considerado o mais fácil para os estudantes. O valor mais negativo (-3,96 logits) atribuído ao esboço da parábola pode está ligado ao fato dos alunos já terem um conhecimento preliminar da sua forma geométrica, a partir dos estudos de funções e equações do 2° grau, no 9° ano do ensino fundamental e no 1° ano do ensino médio. Do total de entrevistados, 90 %, 75 % e 95 % responderam corretamente os Itens 1, 2 e 3, respectivamente.

Já os Itens de 4 a 7 do Q1 (relativos à identificação das cônicas, dadas as suas equações reduzidas) receberam pontuações mais à direita na escala logits, entre 0,97 e -0,18, indicando que este tópico se mostrou com um nível de dificuldade maior do que o obtido no esboço das curvas (Fig. 3a). Quantificando este resultado, por exemplo, fazendo uma comparação com o Item 2 (D2 = -1,73 logits, com 75% de respostas positivas), o Item 5 foi calculado com uma dificuldade 1,55 logits maior (D5 = -0,18 logits), o que corresponde a uma redução de 25 % de acertos (apenas 50% dos ID’s obtiveram sucesso nesse item). Esse resultado pode estar ligado à dificuldade de se manipular algebricamente a equação na forma dada, na tentativa de transformá-la em uma das equações reduzidas conhecidas para que a análise pudesse ser realizada (BRUM; CURY, 2013).

Os demais itens do Q1 (do Item 8 ao 28) se mostraram com níveis de dificuldade muito altos, com insucesso de respostas variando entre 85 % e 100 %. Um fato importante observado é que em grande parte dos itens (relativos à definição

(10)

65 REnCiMa, v. 10, n.6, p. 56-75, 2019

matemática, à construção com régua e compasso, às propriedades focais, às equações reduzidas e às aplicações) o insucesso foi de 100%, com um valor D estimado em 3,49 logits (com uma amplitude de 7,45 na escala logits se comparado com o item considerado como mais fácil no Q1), como descrito na tabela da Fig. 3a. Com exceção da construção de cônicas com régua e compasso, todos os outros tópicos de cônicas propostos na pesquisa e trabalhados no Q1 estavam descritos no plano de aula do professor da disciplina, o que reforça ainda mais a necessidade de intervir para assegurar ao aluno a aprendizagem desses conceitos.

Figura 3 - (a) Estimativa dos valores de dificuldades dos itens, antes (Da) e depois (Dd) da aplicação do minicurso. (b) Distribuição de Da e Dd para o conjunto de itens do Q1 e Q2.

Após a aplicação do minicurso, com o Q2 foi possível inferir que houve uma evolução significativa na proficiência dos ID’s. É possível observar em destaque na Fig. 3b, uma quebra na hierarquia da dificuldade da maioria dos itens, visto que estes agora ocupam a mesma região central na escala logits de dificuldades no gráfico D versus #Item, em comparação com as dificuldades estimadas antes da intervenção. Este resultado evidencia que já não existem itens considerados muito fáceis e nem muito difíceis de serem respondidos pelos ID’s, como consequência de um maior nivelamento e assimilação dos conceitos trabalhados sobre cônicas a partir da aplicação do minicurso.

Essa evolução também pode ser confirmada a partir das curvas características dos itens (CCI), antes e depois da intervenção, representadas pelos gráficos (Fig. 4). Em

(11)

66 REnCiMa, v. 10, n.6, p. 56-75, 2019

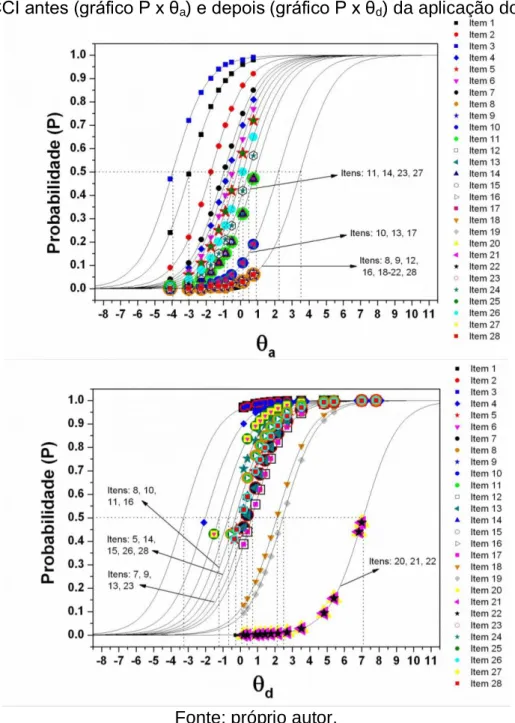
todas as CCI, cada ponto representa indivíduos (ou grupo de ID’s) do experimento, que foram avaliados com mesma habilidade para responder o item , a partir do ajuste dos dados experimentais ao modelo de Rasch (Eq. 1). Observa-se no Q1, que a maioria das CCI comporta pontos experimentais concentrados abaixo do ponto de inflexão das curvas (próximos à calda inferior da sigmóide) indicando que as probabilidades de sucesso dos indivíduos foram menores que 0,5. Nesses casos, os itens se mostraram com dificuldade superior à habilidade dos estudantes para respondê-los com êxito, o que corrobora com o que foi discutido anteriormente.

Figura 4 - CCI antes (gráfico P x θa) e depois (gráfico P x θd) da aplicação do minicurso.

Após a intervenção, há uma indicação clara de mudança no nível de proficiência dos entrevistados, visto o notável deslocamento da concentração dos indivíduos para regiões acima dos pontos de inflexão das CCI (gráfico x θd, Fig. 4) indicando que nesses casos os alunos adquiriram habilidades suficientes para responder corretamente esses itens ( ) e aumentar as probabilidades de sucesso ( ). Desses ID’s, os mais

(12)

67 REnCiMa, v. 10, n.6, p. 56-75, 2019

habilidosos estão localizados nas regiões onde 1 (próximo à calda superior das curvas).

No Q2, os Itens 1, 2 e 3 se apresentaram com o mesmo nível de dificuldade e com valor menor ( -3,29) que todos os outros itens: todos os vinte alunos esboçaram todas as cônicas corretamente o que mostra que não há mais hierarquia quanto à proficiência dos alunos nesse tópico das cônicas (com destaque para a evolução no esboço das hipérboles, antes com 75 % de acertos). A evolução na habilidade dos ID’s é discutida em detalhes a seguir.

Habilidades dos ID’s

Comparando os histogramas de frequência dos valores de habilidade amostrais (estimados via modelo de Rasch) antes (θa) e depois (θd) do minicurso (Fig. 5),

observa-se que no primeiro caso a distribuição de habilidades observa-se concentrava em uma região de valores negativos na escala logits.

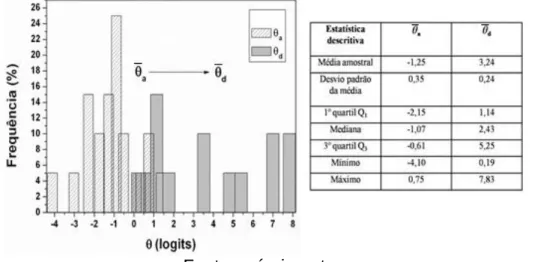
Figura 5 - Histogramas de frequências dos valores amostrais de θ dos ID’s antes (θa) e

depois (θd) da aplicação do minicurso. À direita, as estatísticas descritivas relacionadas.

Após a intervenção, houve um deslocamento para maiores valores na escala, em uma indicação de que os ID’s se tornaram mais preparados para lhe dar com o tema. Em adição, todas as estatísticas descritivas de θa e θd estudadas (Fig. 5) foram melhoradas, reforçando o indício de que a média de valores de θ evoluiu expressivamente. Como exemplo, podemos citar o ID1, que obteve o maior desenvolvimento de habilidade entre os selecionados com uma evolução de 11,93 logits (de -4,1 para 7,83). Esses diagnósticos individuais, que reforçam a aplicabilidade do modelo de Rasch, ampliam as possibilidades de estudo e acompanhamento dos resultados em detrimento de técnicas de análise convencionais que levam em conta apenas estatísticas grupais.

Para se ter uma análise mais ampla da situação, estimou-se os resultados de habilidade para a condição dos questionários serem aplicados a um número bem maior de ID’s de mesma característica (alunos do 3° ano do ensino médio da escola de tempo integral).

A média populacional de θa foi estimada no intervalo de (-1,81; -0,69) logits enquanto a média populacional de θd foi estimada em (2,05; 4,42) logits. O teste de

(13)

68 REnCiMa, v. 10, n.6, p. 56-75, 2019

hipóteses para a diferença entre as médias de habilidades retornou um p-valor = 0 (p-valor < α = 0,05), indicando que as médias de habilidades dos ID’s se mostraram significativamente diferentes, o que comprova que realmente houve uma evolução nesse quesito. Em outras palavras, se um maior número de alunos com a mesma característica amostral respondesse ao Q1, teríamos também indivíduos com níveis muito baixos de habilidade com as cônicas. Por outro lado, com a aplicação do minicurso, existiria uma grande possibilidade destes ID’s se tornarem mais habilidosos com o tema, o que demonstra a viabilidade da proposta.

Análise dos Gráficos P versus ( ) e Porcentagem de ID’s versus P

Embora as CCI mostrem que as dificuldades dos itens se tornaram mais niveladas, os gráficos relacionados não retornam informações da quantidade de ID’s contidos em cada ponto experimental. Em adição, as estatísticas que mostraram a evolução nas habilidades por si só não especificam quantitativamente o quanto um θj foi maior que um

Di na escala logits ou se as habilidades não foram suficientes para que os ID’s conseguissem responder a um dado item .

Por outro lado, o nível de evolução na proficiência dos entrevistados pode ser obtido a partir de uma análise do balanceamento entre e θj, do Q1 para o Q2, a partir dos gráficos experimentais de P versus ( ) e de Porcentagem de ID’s versus P. Esse último gráfico retorna a porcentagem acumulada de ID’s respondentes do item e também se mostra importante para a análise dos resultados uma vez que cada ponto experimental representa um único ID (diferente do gráfico anterior, onde cada ponto geralmente representa um conjunto de ID’s com mesma probabilidade de sucesso).

Como exemplo, podemos citar os resultados obtidos para os itens de 11 a 13, que trataram das construções geométricas da parábola, da elipse e da hipérbole a partir de suas propriedades focais (Fig. 6). Nos três casos, antes da intervenção, nenhum dos alunos conseguiu êxito na construção das curvas, embora tenham sido disponibilizados compasso e régua a cada ID.

A probabilidade de sucesso tendeu a zero (P 0) para a maioria dos ID’s nos itens 12 (elipse) e 13 (hipérbole). No Item 11 alguns dos ID’s ainda se deslocaram para regiões com probabilidades de sucesso entre 0,0 e 0,5, por apresentarem um valor de maior que os demais, mas ainda sem um θ suficiente para superar a dificuldade do item (θj ). Essa dificuldade era de certa forma esperada visto que o planejamento das aulas habituais do professor não contemplava a construção das cônicas pelos alunos utilizando algum tipo de material didático adequado para tal. As técnicas de construção foram utilizadas pelo professor apenas nos momentos de apresentação do conteúdo e eventualmente quando julgado necessário para ilustrar e (ou) auxiliar na resolução de exercícios propostos.

Trabalhando esse tópico no minicurso, as probabilidades de sucesso dos entrevistados cresceram abruptamente, com P→1 para a maioria dos ID’s. Nessa segunda fase da pesquisa, 100 %, 90 % e 95 % dos alunos respondeu corretamente os Itens 11, 12 e 13, respectivamente, como consequência do significativo avanço no balanço ( ). Os autores destacam que essa evolução expressiva na proficiência dos

(14)

69 REnCiMa, v. 10, n.6, p. 56-75, 2019

alunos está diretamente relacionada à intervenção didática com as sinucas cônicas e as construções geométricas com régua e compasso. As ações oportunizaram o diálogo, a formulação de perguntas, a elaboração de hipóteses e a realização de experimentações pelo aluno na busca pelas soluções dos problemas propostos, como sugere Passos e Nacarato (2018).

É importante destacar que nessa fase da pesquisa os erros se concentraram em apenas dois indivíduos: no ID6 (com insucesso nos Itens 12 e 13) e no ID19 (insucesso no Item 13). E, mesmo com insucesso, estes ID’s obtiveram probabilidades de sucesso próximas a 0,5, ou seja, próximas à probabilidade mínima de êxito (como verificado na Fig. 6).

Figura 6 - (À esquerda) Gráficos P versus (θ – D) e Porcentagem de ID’s versus P para os Itens 11, 12 e 13 no Q1 e no Q2 (antes e após o minicurso, respectivamente).

(15)

70 REnCiMa, v. 10, n.6, p. 56-75, 2019

Embora seja evidente a evolução na proficiência dos alunos com o minicurso, os itens de 20 a 22 ainda se mostraram com níveis de dificuldade muito altos (Fig. 7). Mesmo após a intervenção, todos os alunos continuaram sem conseguir determinar analiticamente as equações reduzidas das cônicas, dadas suas informações focais, o que fez com que o nível de dificuldade desses itens aumentasse significativamente em relação aos níveis desses mesmos itens obtidos no Q1 (de 3,49 logits no Q1 para 7,08 logits no Q2) e em relação aos demais itens do Q2. Nesse sentido, pode ser inferido que as ações propostas no minicurso não foram suficientes para que os selecionados assimilassem esse tópico do conteúdo e que outras intervenções podem ser planejadas na tentativa de reverter a situação.

Figura 7 - Gráficos P x (θ – D) e Porcentagem de ID’s x P, para os Itens 20, 21 e 22.

Uma evolução significativa também pode ser notada nas respostas aos Itens 18 e 19. No Q1, foi obtido 100 % de insucesso em ambos os itens, enquanto no Q2, 60 % e 55 % dos alunos responderam os quesitos com êxito, nessa ordem. Dos que não responderam, a maioria se localizou em regiões de probabilidade de sucesso entre 0,25 e 0,5.

No Q1, quando os alunos foram convidados a descrever exemplos prático-tecnológicos das propriedades focais das cônicas (Itens de 23 a 25), notou-se uma maior dificuldade para o caso da hipérbole (com valor estimado em 0,87) seguida pela elipse (0,47) e pela parábola (-0,18). Esse nível decrescente de dificuldades também se manteve quando se pediu para identificar e solucionar problemas envolvendo as propriedades focais (itens de 26 a 28), com destaque para a hipérbole com valor estimado em 3,49. Como esperado, esses resultados são consequências diretas do insucesso dos alunos na definição dessas cônicas, como observado nos itens de 8 a 10. Na intervenção, além de trabalhar as definições matemáticas e propriedades focais da elipse, da parábola e da hipérbole com o apoio dos materiais manipuláveis e das construções geométricas, outra ação em destaque foi apresentar aplicações tecnológicas conectadas à discussão das propriedades focais envolvidas em cada situação prática.

Com estas ações complementares às aulas habituais, notou-se que as dificuldades destes últimos itens deixaram de apresentar hierarquia com relação aos outros itens do questionário. Essa observação é resultado do aumento dos níveis de proficiência dos alunos, em uma indicação da melhoria do processo de ensino-aprendizagem no caso estudado. Os melhores resultados de proficiência, obtidos pelos ID’s nessa segunda

(16)

71 REnCiMa, v. 10, n.6, p. 56-75, 2019

análise, a partir da introdução das sinucas cônicas e das construções geométricas com régua e compasso estão de acordo com os resultados publicados por Kuloglu (2013) e Chen (2013). Os autores destacam que métodos alternativos de ensino das cônicas com o propósito de relacioná-las com situações reais, com o auxílio de materiais concretos e de técnicas de construção geométrica, ajudaram a aumentar a criatividade e a interação entre os alunos, além de levá-los a repensar o seu meio social e, consequentemente, a significar o sentido da aprendizagem em matemática.

A Fig. 8 mostra o score total de probabilidade dos ID’s (soma das probabilidades de sucesso em cada item, obtidas por um ID) dado como função de sua habilidade θ. Essa medida pode ser interpretada como a nota obtida pelos indivíduos da amostra em resposta aos vinte e oito itens do questionário, em uma escala normalizada de valores de 0,00 a 10,00. Os valores próximos aos pontos experimentais indicam o número de ID’s que obtiveram uma dada nota (ou soma de probabilidades) no teste (AZIZ, 2013).

No Q1, 50 % dos ID’s obtiveram nota menor que 2,00 e a maior nota foi estimada em 4,14. Já no Q2, a menor nota foi estimada em 5,33 e 50 % dos ID’s obtiveram nota maior que 8,05. A nota média obtida pelo grupo de alunos avaliado foi centrada em 2,02 ± 1,01 antes do minicurso e em 7,90 ± 1,31 após a intervenção, confirmando que houve uma expressiva evolução na proficiência dos alunos para lidar com cônicas.

Figura 8 - Score total de probabilidades normalizado dos ID’s com relação às respostas dadas aos itens de 1 a 28, antes e depois do minicurso.

Para mostrar outra aplicabilidade do modelo de Rasch no diagnóstico do insucesso no aprendizado e na escolha de ações que podem ser tomadas para reverter a situação, tomou-se como exemplo prático o caso dos Itens de 20 a 22. Como discutido anteriormente, nenhum dos alunos obteve êxito nesses itens mesmo após a participação no minicurso. Por outro lado, três desses ID’s obtiveram probabilidades de sucesso próximas a 0,5 (verificado na Fig. 6), indicando que estes estão na eminência de obter uma habilidade limear para dar uma resposta positiva a esses itens.

Para colocar novamente em prática a eficácia do discurso do professor (inversamente proporcional à quantidade de alunos atendidos) na ação de educar em

(17)

72 REnCiMa, v. 10, n.6, p. 56-75, 2019

matemática (BARBOZA; REGO; BARBOSA, 2013), planejou-se um segundo momento de intervenção (3ª. análise da pesquisa), particular para esses três alunos e três questões, utilizando-se os mesmos materiais didáticos usados na primeira intervenção, no laboratório de matemática. Nesse segundo momento de análise foi possível discutir as respostas anteriores desses alunos a esses itens no Q1 e no Q2, detectar os erros e trabalhá-los de forma mais direcionada para corrigi-los. Nessa terceira fase da pesquisa, todos os três ID’s responderam esses itens com sucesso, mostrando que as ações foram compatíveis com a proposta de se aumentar a habilidade dos alunos para que estes pudessem realizar as manipulações algébricas necessárias para determinar as equações reduzidas.

Considerações finais

A partir desse estudo de caso foi possível verificar que o aprendizado dos alunos não ocorreu de forma satisfatória a partir do ensino habitual na escola pesquisada. Por outro lado, o insucesso dos alunos foi revertido na maioria dos tópicos estudados, a partir das ações complementares de intervenção didática proposta com os materiais manipuláveis e construções geométricas.

A discussão das aplicações das cônicas, conectadas às suas propriedades focais, minimizou a hierarquia de dificuldade desses itens com relação aos demais, nivelando a proficiência dos alunos nesse aspecto. Em geral, observou-se uma grande evolução nas habilidades dos ID’s, com consequente aumento das probabilidades de sucesso desses indivíduos nas respostas aos itens.

A análise dos resultados mostrou uma maior facilidade dos alunos em assimilar conhecimentos geométricos do que analíticos sobre o tema. Alguns itens que necessitavam de uma abordagem analítica para a sua solução do problema continuaram com um nível de dificuldade muito alto, mesmo após a intervenção. Em uma segunda intervenção mais direcionada às dificuldades detectadas, essa situação foi revertida com sucesso para uma amostra de alunos, escolhida a partir dos resultados da análise de Rasch. Em resumo, o modelo de Rasch se mostrou como uma importante ferramenta de avaliação do processo de ensino-aprendizagem, proporcionando análises individuais das dificuldades dos itens e das habilidades dos alunos, o que o qualifica como promissor para avaliar diversos outros aspectos em educação matemática.

É importante destacar que as ações praticadas nesta pesquisa se fundamentaram nos princípios de Freire (1996), no sentido de que “faz parte da natureza da prática docente a indagação, a busca, a pesquisa. O de que se precisa é que, em sua formação permanente, o professor se perceba e se assuma, porque professor, como pesquisador”.

Uma vez que a matemática se mostra com um dos piores desempenhos dos alunos no ensino básico brasileiro atualmente, os resultados insatisfatórios obtidos no estudo das curvas cônicas têm grande chance de se repetirem em outros temas de geometria e outras unidades temáticas do currículo de matemática como álgebra, grandezas e medidas e probabilidade e estatística (PASSOS; NACARATO, 2018). Por outro lado, os bons resultados obtidos com a intervenção reforçam a possibilidade de ampliá-la para uma quantidade maior de alunos e para outras escolas da rede e de propor

(18)

73 REnCiMa, v. 10, n.6, p. 56-75, 2019

outros materiais manipuláveis para se trabalhar outros conteúdos matemáticos de interesse.

Diante do exposto, esse estudo foi importante para mostrar que pesquisas e intervenções relativas à melhoria do ensino-aprendizagem de matemática, em especial das seções cônicas, são atuais, viáveis e extremamente necessárias na busca por melhores resultados na educação matemática brasileira.

Agradecimentos

O presente trabalho foi realizado com apoio da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Código de Financiamento 001.

Referências

AZIZ, A. A. Insights into engineering education learning outcome’s assessment with Rasch model. Research Journal of Applied Sciences, Engineering and Technology, v. 6, n. 19, p. 3520-3526, 2013. https://doi.org/10.19026/rjaset.6.3555

BARBOZA, P. L.; REGO, R. M.; BARBOSA, J. C. Discurso do professor de matemática e suas implicações na compreensão dos alunos. Bolema, v. 27, n. 45, p. 55-74, 2013.

http://dx.doi.org/10.1590/S0103-636X2013000100004

BOUGHANMI, H.; LAZAAR, M.; FARHAT, A.; GUIZANI, A. Evaluation of soil thermal potential under Tunisian climate using a new conic basket geothermal heat exchanger: Energy and exergy analysis. Applied Thermal Engineering, v. 113, n. 25, p. 912-925, 2017. https://doi.org/10.1016/j.applthermaleng.2016.10.204

BRUM, L. D.; CURY, H. N. Análise de erros em soluções de questões de álgebra: uma pesquisa com alunos do ensino fundamental. RenCiMa, v. 4, n. 1, p. 45-62, 2013.

https://doi.org/10.26843/rencima.v4i1.560

CALLINGHAM, R.; BOND, T. Research in mathematics education and Rasch measurement. Mathematic Education Research Journal, v. 18, n. 2, p. 1-10, 2006.

https://doi.org/10.1007/BF03217432

CARRAHER, T.; CARRAHER, D.; SCHLIEMANN, A. Na vida dez, na escola zero. 11. ed. São Paulo: Cortez, 2001.

CHEN, W. H. Applying problem-based learning model and creative design to conic-sections teaching. International Journal of Education and Information Technologies, v. 7, n. 3, p. 73-80, 2013. http://naun.org/cms.action?id=6452

CHERNOV, N.; WIJEWICKREMA, S. Algorithms for projecting points onto conics. Journal of Computational and Applied Mathematics, v. 251, n. 15, p. 8-21, 2013.

https://doi.org/10.1016/j.cam.2013.03.031

EDWARDS, A.; ALCOCK, L. Using Rasch analysis to identify uncharacteristic responses to undergraduate assessments. Teaching Mathematics and its Applications, v. 29, n. 4, p. 165-175, 2010. https://doi.org/10.1093/teamat/hrq008

FREIRE, P. Pedagogia da autonomia: saberes necessários à prática educativa (Coleção Leitura). São Paulo: Paz e Terra, 1996.

(19)

74 REnCiMa, v. 10, n.6, p. 56-75, 2019

FREITAG, B.; MOTA, V. R.; COSTA, W. F. O livro didático em questão. São Paulo: Cortez, 1997.

Gil, A. C. Como elaborar projetos de pesquisa. São Paulo: Atlas, 2010.

HAINES, C.; CROUCH, R. Recognizing constructs within mathematical modelling. Teaching Mathematics and its Applications, v. 20, n. 3, p. 129-138, 2001.

https://doi.org/10.1093/teamat/20.3.129

KALEFF, A. M. M. R. Do fazer concreto ao desenho em geometria: ações e atividades desenvolvidas no laboratório de ensino de geometria da Universidade Federal Fluminense. In: LORENZATO, S. Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006, p. 113-134.

KULOGLU, S. I’m discovering conics and designing buildings with conics. Journal for the Education of the Young Scientist and Giftedness, v. 1, n. 2, p. 40-52, 2013.

LEPAGE, D.; JIMÉNEZ, A.; BEAUVAIS, J.; DUBOWSKI, J. Conic hyperspectral dispersion mapping applied to semiconductor plasmonics. Light: Science & Applications, v.1, p. 1-8, 2012. https://doi.org/10.1038/lsa.2012.28

LÉVY, P. Cibercultura. 3. ed. São Paulo: Ed. 34, 2010.

LORENZATO, S. Laboratório de ensino de matemática e materiais didáticos manipuláveis. In: LORENZATO, Sérgio. Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006, p. 3-38.

MACEDO, A. C. O.; LAURINO, D. P. Pensar o aprender Matemática no conversar com o estudante. Revista Eletrônica de Educação Matemática, v. 13, n. 2, p. 149-161, 2018. MELO, E. V.; FIREMAN, E. C. Ensino e aprendizagem de funções trigonométricas por meio do software Geogebra aliado à modelagem matemática. REnCiMa, v. 7, n. 5, p. 12-30, 2016. https://doi.org/10.26843/rencima.v7i5.1182

MIORIM, M. A.; FIORENTINI, D. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da matemática. Boletim da SBEM, v. 4, n. 7, p. 5-10, 1990.

MOREIRA, J. S. Construções das cônicas utilizando o desenho geométrico e instrumentos concretos. Dissertação (Programa de Pós-graduação em Matemática). Pontifícia Universidade Católica do Rio de Janeiro, 2017. 103 f.

PASSOS, C. L. B.; NACARATO, A. M. Trajetória e perspectivas para o ensino de Matemática nos anos iniciais. Estudos Avançados, v. 32, n. 94, p. 119-135, 2018.

http://dx.doi.org/10.1590/s0103-40142018.3294.0010

PIAGET, J. Seis estudos de psicologia. Trad. D’Amorim, M. A. M. e Silva, P. S. L. 21. ed. Rio de Janeiro: Forense Universitária, 1995.

RASCH, G. Probabilistic models for some intelligence and attainment tests. Chicago: University of Chicago Press, 1980.

RODRIGUES, F. C.; GAZIRE, E. S. Reflexões sobre uso de material didático manipulável no ensino de matemática: da ação experimental à reflexão. Revista Eletrônica de Educação Matemática, v. 7, n. 2, p. 187-196, 2012.

(20)

75 REnCiMa, v. 10, n.6, p. 56-75, 2019

RYAN, J.; WILLIAMS, J. Maths maps for diagnostic assessment with pre-service teachers: stories of mathematical knowledge. Mathematics education research, v. 9, n.1, p. 95-109, 2007. https://doi.org/10.1080/14794800008520173

SAMPER, A.; GONZÁLEZ, G.; HERRERA, B. Determination of the geometric shape which best fits an architectural arch within each of the conical curve types and hyperbolic-cosine curve types: The case of Palau Güell by Antoni Gaudí. Journal of Cultural Heritage, v. 25, p. 56-64, 2017. https://doi.org/10.1016/j.culher.2016.11.015

SANTOS, R.; LORETO, A. B.; GONÇALVES, J. L. Avaliação de softwares matemáticos quanto a sua funcionalidade e tipo de licença para uso em sala de aula. RenCiMa, v. 1, n. 1, p. 47-65, 2010. https://doi.org/10.26843/rencima.v1i1.4

SILVA, R. S.; LOPES, D. C. V. A construção de conceitos da geometria plana com o uso de materiais concretos e digitais: uma experiência com Tangram. Revista Eletrônica de Educação Matemática, v. 8, n. 1, p. 179-198, 2013.

TÉLLEZ, M. N. B.; DÍAZ, M. C.; GÓMEZ, A. R. Piaget y LS Vigotsky en el análisis de la relación entre educación y desarrollo. Revista Iberoamericana de Educación, v. 42, p. 7-25, 2007. https://dialnet.unirioja.es/ejemplar/158948

VAN STIPHOUT, I.; DRIJVERS, P.; GRAVEMEIJER, K. (2014). The Development of Students’ Algebraic Proficiency. International Electronic Journal of Mathematics Education, v.8, n. 2-3, p. 62-80, 2014. https://www.iejme.com/article/the-development-of-students-algebraic-proficiency