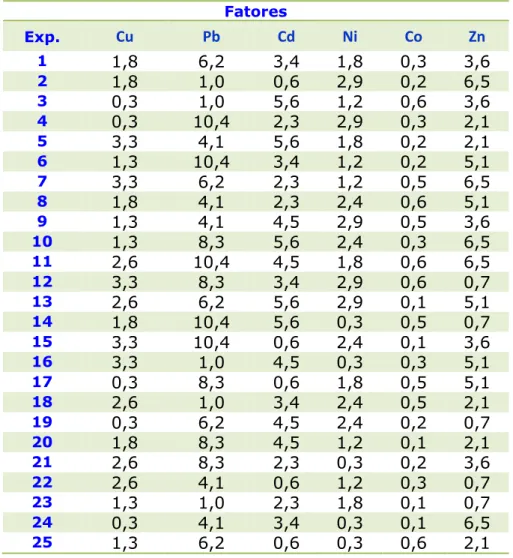
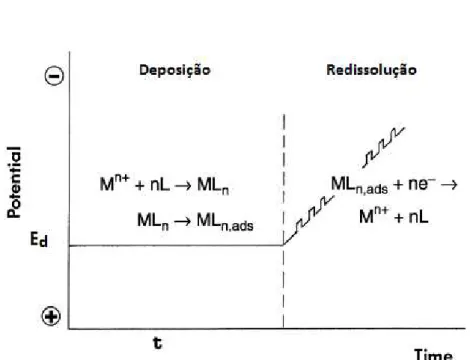
Determinação simultânea de Cu, Pb, Cd, Ni, Co e Zn em etanol combustível por voltametria de redissolução adsortiva e calibração multivariada.

CARMELLO 2009 afirma; que no mundo do trabalho ocorreram inúmeras mudanças não só no processo produtivo devido inovações tecnológicas, mas no impacto causado na saúde do

Para os objetivos desse estudo, nos detemos na avaliação do processo de trabalho dos ACS, através das concepções dos atores envolvidos no contexto da Estratégia

RESUMO – O semiárido cearense (SC) é marcado pela escassez de recursos hídricos subterrâneos e pela alta variabilidade interanual e sazonal das chuvas. Dessa forma, estabeleceu-se

RESUMO: O presente trabalho foi desenvolvido com o objetivo de determinar as relações entre o Teor de Uréia no Leite TUL e fatores nutricionais (Proteína Bruta (PB),

Este trabalho objetiva a divulgação dos principaisproblemas agronômi- cos atuais que afetam a cultura do dendê, a estruturação do Programa Nacional de Pesquisa de Dendê, os

Em todas as esferas da vida humana, temos conflito de sentidos, e os indivíduos ou grupos que detém o poder (legal/tradicional ou carismático) acabam impondo seu

Segundo Alcântara (2008), a criança necessita da presença dos pais, ou de alguém que lhe seja querida, sendo importante para o seu desenvolvimento mental e emocional, minimizando seu

Summarizing, in this study we combined different model’s parameters been, two family distributions for step length and two for turning angle, four temporal resolutions, five