Decaimento do potencial de um plasma numa matriz sólida em geometria plana

DECAIMENTO DO POTENCIAL DE UM PLASMA NUMA MATRIZ SOUDA EM GEOMETRIA PLANA

Alcione Silva F.ernancies

Dissertação apl'esentadii ao

Instituto

dt: Física e Químíca de São Carlos, para obtenção do título de mestre em Física Aplicada.

Orientador:

Or. GuilherrT'le F. Leal Ferreira

DECAIMENTO DO POTENCIAL DE UM PLASMA NUMA MATRIZ SDLIDA EM GEOMEfRIA PLANA

ALCIONE SILVA FERNANDES

Dissertação apresentada ao Instituto de Ftsica e Qul-mica de São Carlos. para obtenção do tltulo de mes-tre em Ffsica Aplicada.

Orientador:

Dr. Guilherme F. Leal Ferreira

-MEMBROS DA COMISS~O JULGADORA DA DISSERTAÇAO DE MESTRADO DE

--

de

ALCIONE SILVA FERNANDES

APRESENTADA AO INSTITUTO DE F1SICA E QU1MICA. DE SAO CARLOS, DA UNI

-VERSIDADE DE SAO PAULO, EM

-ll-

DE maio DE

19~.

COMISSAO JULGADORA:

Dr.Guilherme Fontes Leal Ferre1ra- Or1entador DFCM/IFQSC • USP

---~

/-4~?o4'

l~~/

'-- u_ 00_." ••0 .• -- .u_._u ..

Dr.Renê Armando Moreno Alfaro

DFCMJ IFQS~USP

I

A Nelma,

companheira em todos

08

momentos.

APROVAÇlo ••••••••••••••••• '•••••••••••••••••••••••••••••••••• III

RESUMO •••••••••••••••••••••••••• I ••••••••••••••••••••••••

IV

ABSTRACT •••••••••••••••••••••••••••••••••••••••••••••••••••. V

••••••••••••••••••••••••••••••••••••

A f~ação

do problema ••••••••••••••••••

O método das caracterlsticas •••••••••••••

INTRODuÇlo CAPITULO

I

•••••••••••••••••••••••••••••••••••••••••••••••••

A roJMD:N:lD DO PROBLEMA E O MATaDO DAS CARAC-TER!STICAS

1.1

1.2

i

1

1

6

CAPITULO

11-

BMPRBGO DO MI'1'ODO DAS CARACTER!STICAS NA

SO-LUÇlO DO CASO GERAL: RBCOMBINAç10 ENTRE OS

PORTADORES POSITIVOS E NEGATIVOS ••••••••••••••• 9

11.1 - solução para um tempo Mnor

que o tem

po de cruzamento •••••••••••••••••••••••• 10

II.1.a -

_{R!gião central de}

recombina-çao

••••••••••••••••••••••••••••

10

II.1.b - Região de carga espacial ne-

gativa

•••••••••••••••••••••••••

14

II.1.c - Região de carga espaCial po-

si

ti

va .•••••••••••••••••••••••••

19

11.2

-Solução para um tempo ••ior que o t~

po de cruzamento

••••••••••••••••••••••••

22

II.2.a

-Região central

sem carga

es-pacial

...

.,

...

23

II.2.b

-Região de carga espacial n.~

gativa

•••••••••••••••••••••••••

24

II.2.c

-Região de carga espacial

po-sitiva

111.1 - cálculo da difetença de potencial instantânea V(t) entre os eletro-dos para um tempo menor que o tem

pc de cruzamento ••••••••••••••••••••• 29

111.2 - Cálculo da diferença de potencial instantânea V(t) entre os eletro-dos para um tempo maior que o t8!

po de cruzamento ••••••••••••••••••••• 31

111.3 - cálculo da carga residual nos el!

trodos

...•...

43

CAPITULO IV - SOLUçOES PADA DOIS CASOS PARTICULARES DO PROBLEMA PROPOSTO: RELAçlo DE LANGEVIN E AuslNCIA DE RECOMBINAçlO ENTRE OS PORTADQ

RES ••••••••••••••••••••••••••••••••••••••••••

48

IV.l - Solução para um caso particular:

relação de Langevin •••••••••••••••••••

48

IV.l.l - Tempo menor que o tempo

de cruzamento •.•••••••••••••• 49

IV.l.l.a·- Região central

de recombinação ••••• 49 IV.l.l.b- Região de carga

. espacial negat!

va ....•...•.•.••••

50

IV.ll.c - Região de carga espacial posit!

va ••••••••••••••••••

51

IV.l.2 - Tempo maior que o tempo

de cruzamento •••••••••••••••• 52

IV.l.2.a- Região central sem carga

IV.l.3 - Carga residual nos eletrodos •• 57

IV.2 - solução para um caso particular, au-sência de recombinação entre os

por-tadores positivoS e negativos ••••••••••

58

IV.2.l - Tempo menor que o tempo de

cruzamento ••••••••••••••••••••

58

IV.2.l.a - Região central el.!,

tricamente neutra •••••

58

IV.2.l.b - Região de carga 81

pacial negativa •••••• 60 IV.2.l.c - Região de carga e!,

pacial positiva •••••• 60 IV.2.2 - Tempo maior que o tempo de

cruzamento ••••••••••••••••••••

61

IV.2.2.a - Região central sem

carga espacial •••••••

61

IV.2.2.b - Região de carga e!

pacial negativa •••••• 62 IV.2.2.c - Região de carga e.

pacial positiva

.7..•.

63 IV.2.3 - Carga residual nos eletrodos •• 66

CAPITULO V - ANALISE GRAFlCA DAS SOLUÇOES OBTIDAS ••••••••••••

68

APINDICE ••••••••••••••••••••••••••••••••.•••••••••••••••••••• 74

AGRADECIMENTOS

!

com grande satisfação que agradeço a todas as pessoas que, de uma forma ou outra, contribuiram para a realizaçio deste trabalho. De modo especial, agradeço

- ao Dr. Guilherme F.L. Ferreira, professor e.orienta -dor, pela orientação dedicada que me proporcionou, a par de gran-de amizagran-de demonstradaJ

- ao Dr. Bernard Gross e sua esposa Sra. Gertrudes ~ pela confiança com que me distinguiram num momento crueial da re! lizaçio deste trabalhoJ

- ao Dr. Luiz E. carrano de Almeida, pelo incentivo ~ tante e pela amizadeJ

- ao Prof. Marco Antonio S. Leite, colega e amigo, pelo otimismo encorajador que sempre me transmitiuJ

- aos Profs. Cleide Roberto Alves e Jordão Mlder Netto,

do Departamento de FIsica da UFP, pelo companheirismo e boa vont!

de;

- aos Profs. Rene Moreno; Milton Campos; Hari Gupta; J2 sé Giacometti; Roberto Faria e Mariangela Fi~edo , do Laborat2 rio de Eletretos, pelo cordial ambiente de trabalho proporcionado;

- à

Srta. Marta Regina Bastos Pereira pela solicitude e

presteza com que datilografou este trabalho;

- aos colegas, demais professores e funcionários

do

OFCM1

- a todos aqueles que, embora ausentes, sempre tiveram

RESUMO

Neste trabalho estudamos o decaimento do potencial de um plasma, inicialmente diatribuIdo de maneira uniforme num

sóli-do dielétrico, submetido a um potencial inicial conhecido. A pos-sibilidade de recombinação entre os portadores positivos e negat! vos constituintes do plasma é considerada.

Usando o método das caracter!sticas obtemos o potencial e a configuração espacial de portadores para qualquer instante bem como, a carga residual nos eletrodos ao final do processo.

Dois casos particulares são igualmente resolvidos: no primeiro, a mobilidade relativa dos portadores é relacionada ao coeficiente de recombinação entre eles através da relação de Lan-gevin e, no segundo, considera-se que os portadores não se recom-binam.

N~ desenvolvimento da solução ao problema surge, também,

ABSTRACT

In the present work we studied the decay of the potentia1 of a plasma wich ia initially uniformely distributed in a solid dieletric and the potential is initially know. The possibility of recombination between the positive and negative charge carriers of the plasma is a1so considered.

Using the method of characteristics, we obtained the po-tential and space distribution of charge carriers for any time and a1so residual charge in the electrodes at end of the process.

Two particular cases are considered. In the first case, the relative mobility of charge carriers is related to their recom-bination coeficient through Langevin's relation and, in the aecond case, the recombination of charge carrier is absent.

INTRODUÇAO

No presente trabalho estuda-se o decaimento no

poten-cial de uma mistura de cargas positivas e negativas (plasma) sub-metidas ao campo de um condensador plano carregado inicialmente a um dado potencial (circuito aberto, modo carga). Como se verá no

desenvolvimento que segue, ele

é

suscetlvel de uma anáiise compl~ ta empregando-se o método das caracterlsticas6• Já o mesmo probl~ ma sob a condição de voltagem aplicada (modo corrente) constante

é

muito mais diflcl, senão imposslvel, de tratamento analltico.

Problema similar foi abordado na referência 1. Além de~ se, na literatura podem ser encontrados trabalhos que se consti-tuem casos particulares do estudado aqui. Por exemplo, o trabalho de von Hippel et a1l2, que ilustra a formação de uma barreira de potencial j·~nto a um e1etrÕdio, considera a mobilidade de um dos portadores nula. Isto, aliás, permitiu que o problema fosse trat~ do no modo corrente embora seja relativamente simples aplicá-lo ao modo carga.

A interpretação de Hughes3 de suas experiências em an-traceno excitado por um poderoso pulso de radiação X - ele mediu o decaimento da corrente induzida - envolvendo a criação de port! dores, condução, recombinação e atrapamento, a menos deste último processo não inc1uldo em nossa análise, também se constitue um

C!

so particular do nosso em que o campo no interior da amostra pode

Os materiais eletrocrômicos - óxidos de tungstênio e m2 libdênio hidrogenados em proporção variável - apresentam natural-mente um plama formado por prótons e eletrons. No entanto, medi-das até agora só foram realizadas no modo corrente~.

Pelo que foi dito vê-se que não pudemos conferir ou aplicar os resultados obtidos

à

situações práticas. Mas não é

im-pos8ivel que isto possa ser feito no futuro desde que a.situação contemplada apresenta aspectos comumente empregados. Talvéz, para complementá-la, fosse necessário incluir o processo de

t~apping

de cargas o que, no entanto, complica consideravelmente o

proble-ma.

No desenvolvimento deste trabalho iniciamos, no capitu-lo I, com a formulação do problema e um rápido vôo conceitual so-bre o método das caracteristicas.

No capitulo 11 atacamos o problema na sua forma ampla , que chamamos caso geral, onde as mobilidades dos portadores e o coeficiente de recombinação entre eles são considerados ~~ • Analisamos os vários aspectos do problema bem como, um sistema de equações para a obtenção da configuração de portadores no dielé -trico para um dado instante,

é

conseguido.

O

decaimento do potencial com o tempo, ainda no caso g~ ral,

é

analisado com detalhes no capitulo 111 que também apresen-ta uma equação que fo~ a carga residual nos eletrodos ao final do processo como função dos vários parâmetros do problema.

vês da relação de Langevin, no segundo, a ausência de recombina -ção entre os portadores

é

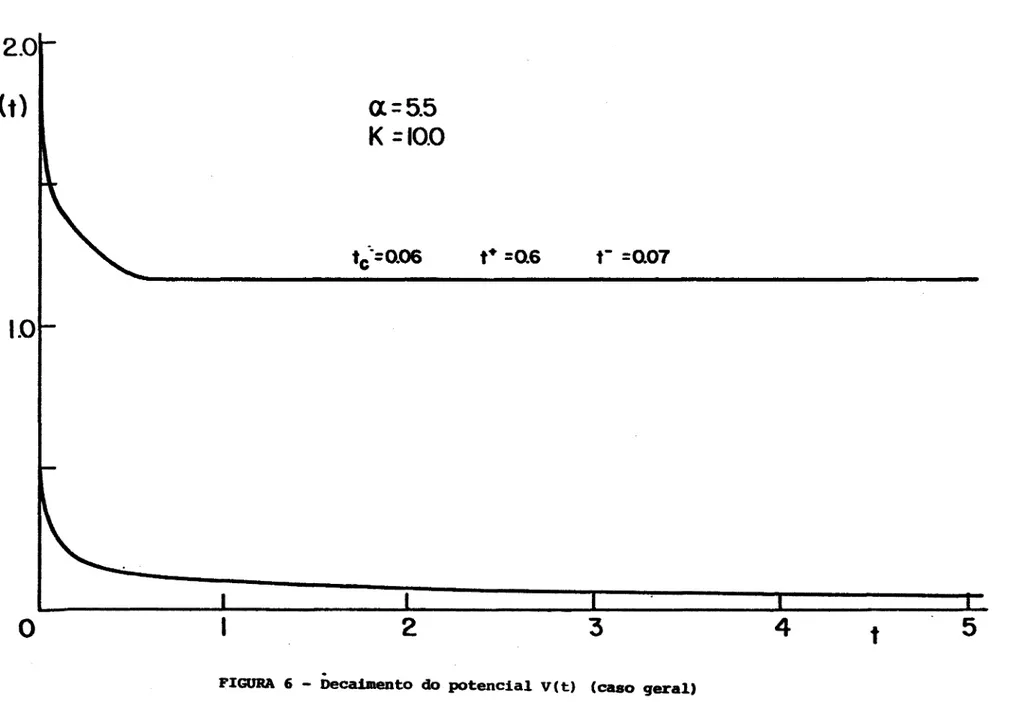
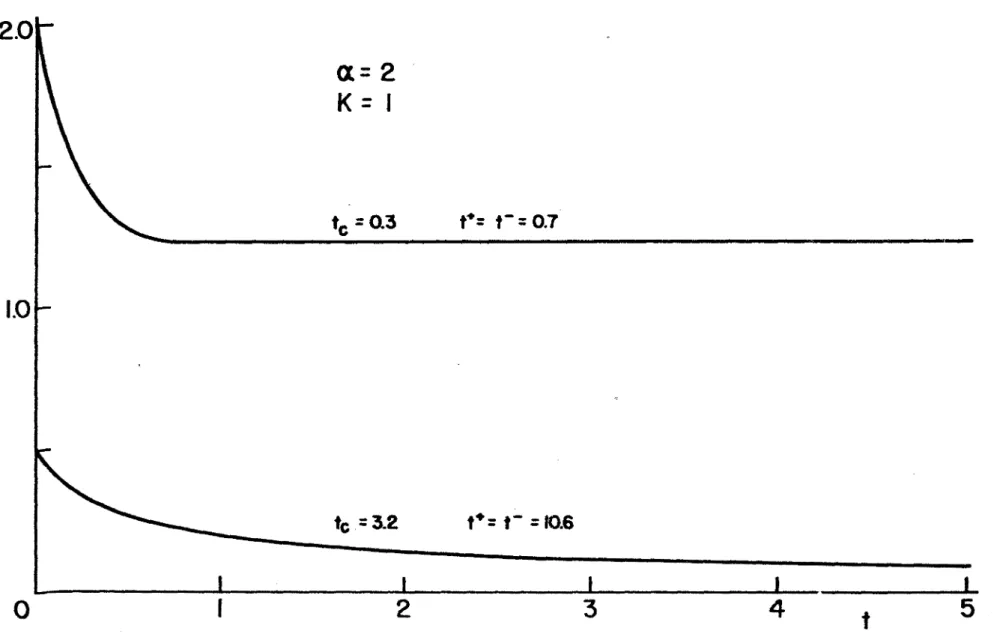
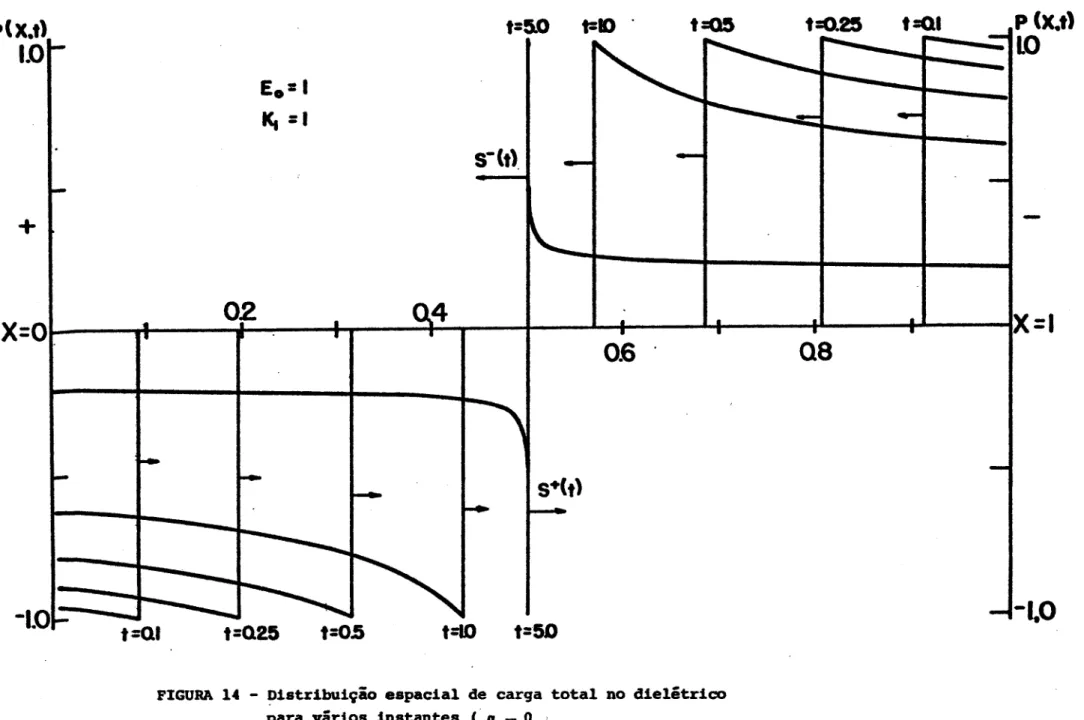
considerada.

No capItulo V ilustramos graficamente o decaimento do potencial com o tempo para diferentes valores dos parimetros

en-volvidos nos capItulos anteriores. A configuração espacial de po~ tadores no dielétrico para um dado instante e num caso particular,

é

apresentada.

CAPITULO 1

A FORMULAÇAO 00 PROBLEMA E O METODO DAS CARACTERtSTICAS

1.1 - FORMULAÇAO 00 PROBLEMA

Os aspectos gerais do problema que procuraremos

resol-ver são os seguintes: consideremos um dielétrico de espessura

g,

com simetria plana e ausência de traps colocado entre dois eletr2 dos desconectados (circuito aberto) e inicialmente descarregados.

O dielétrico apresenta densidades espaciais de cargas uniformemen te distribuídas em todo o seu volume, +p_o e -p_o ,de tal for.maque esteja eletricamente neutro (veja Fig. 1).

Por questão de generalidade vamos supor que as cargas positivas e negativas possam se recombinar proporcionalmente ao produto de suas densidades, em cada ponto. Isto permite abordar problemas em que as cargas em consideração foram criadas instant~ neamente, por exemplo, por um pulso interno de radiação.

Em t = O os eletrodos são instantaneamente carregados a uma diferença de potencial conhecida e posteriormente mantidos em circuito aberto. Em consequência, os portadores positivos da dis-tribuição espacial migrarão para o catodo (x=d) e os portadores negativos para o anodo

(x-O).

Procuraremos determinar:

a) a configuraçã~ espacial de portadores num dado instante;

b) o decaimento do potencial entre os eletrodos como função do tempo;

aE'

(x',tI)= p'(x' tI) - p'(x',tI)

e:

ax'

+'

_

(Fq. de Poisson)

(I .1)

aJ~+ ap~

(x'

,t')

± ax,-+ - at' = -a'p~ (x',tI) P_ (x',t') (Fq. da cxm tinuidadef

(I.2)

J~

_±(Xl,tl)=lJ+p~(Xl_{- -} ,t')E'(Xl,tI) (dens.cor. de oorxiução)

(I.3)

(dens.corrente total em circ. aberto)

(1.4)

A equação (1.4)

ê

obtida derivando-se parcialmente no tempo a eq. de POisson, usando-se a equação de continuidade e integrando-se em x', com a densidade de corrente total nula eM circuito aberto.

A diferença de potencial entre os eletrodos

ê

dada por

d

V

(t)

=

J

E'

(x' ,

t ')

dx'

o

Nas equações acima temos que:

x' - coordenada espacial;

(1.5)

t' - tempo;

E' (x',t') - campo elétrico na posição x' e no instante tI;

p~(X',tl) - densidade espacial de portadores positivos na posição x' e no instante t';

p~(x',t') - densidade espacial de portadores negativos na posição x' e no instante t' ;

E - constante dielétrica do dielétrico;

a' - coeficiente de recombinação entre portadores positivos e n! gativos.

Podemos liberar o sistema de equações (I.l) a (I.S) de alguns parâmetros, introduzindo o seguinte conjunto de unidades redUtidads àdiMertsioh'i~:

,

a=

,

,

a =

..f...

+

a'

II

,

p+=

.l..J'

_Po

₊

,

-.IL.

+

II

K =

,

x'

x=cr

v

11I

....f.-

V'

P

_o

d2

onde ±~ (t) é a densidade superficial de cargas existentes nos eletrodos no instante t.

As equações básicas em unidades reduzidas, tornam-se:

(Eq. de Poisson)

(1.6)

±

aJc

±

(x,t)

ãx

(Eq._t1nu1dader

da oon

(I.7)

Jc

₊

(x,t)= p+(x,t)E(x,t) (Dens.oorrente oondução p/ portadorespositivos)

(I.8)

(Dens.cor-

(I.10)

rente total

em circo aberto)

Jc

-

(x,t)= KP_(x,t)E(x,t) (Dens.

cm-rente

oondução p/ portadoresnegativos)

0= [p+(x,t)+KP_(X,t)]E(x,t)+ aE~x~t) ,

(I.9)

1

V

(t)

I&:

J

E

(x,

t)

dx

O

(I. 11)

Aplicada a diferença de potencial inicial Vo= ao entre os eletrodos, analisemos alguns aspectos do movimento dos portad2

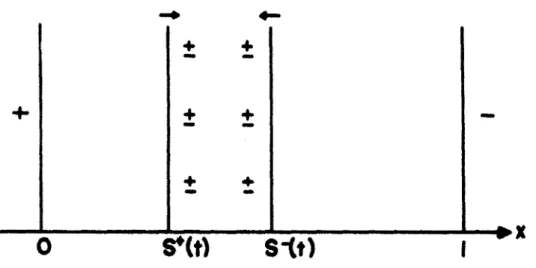
res em direção aos respectivos eletrodo~. Para isso, ~ s+(t)

à

posição instantanea do plano trazeiro de portadores positivos ,

e s-(~

â

posição instantanea do plano trazeiro de portadores neg~ tivos (veja Fig. 2).

+

O plano S (t), em seu movimento para a direita, deixa atrás de si uma região de carga espacial negativa que se extende até o anodo, enquanto que o movimento do plano S-(t) para a es-querda gera uma região de carga espacial positiva até o catodo.

Os movimentos destes planos trazeiros poderão apresen-tar diferentes situações dependendo do valor do potencial inicial

Vo entre os eletrodos, e do coeficiente de recombinação a. Assim, eles poderão ou não cruzar durante o processo e cruzando, atingi rem os respectivos eletrodos no mesmo instante (se K=l), ou em instantes diferentes (se K

'11) •

Desta forma, algumas previsões podem ser feitas com re-lação aos movimentos dos planos trazeiros, ou seja (suponhamos, para facilidade de racioclnio, que não haja recombinação entre os portadores, isto é, a = O):

ao

-

<

1

.

•

deve-se ao fato de que,

ã

medida que os portadores dianteiros das distribuições chegam aos eletrodos ai sendo neutralizados, dimi-nui o campo elétrico no interior do dielétrico fazendo com que os

portadores mais internos se desloquem mais e mais lentamente com o decorrer

do

tempo.

Além disso, como as quantidades de cargas depositadas nos eletrodos são menores que as correspondentes quantidades ini-ciais de cargas livres no dielétrico (O'

_o

< p

_o

= 1), podemos esperar também que a carga total em cada eletrodo seja totalmente neutra-lizada pelos portadores da distribuição que alcancem este eletro-do. Com isto, a diferença de potencial entre os eletrodos, que

inicialmente era V

_o

= O'

_o

, tenderá a um valor final nulo.

A configuração a que tendem as distribuições de portad2 res é mostrada na Fig.2-a, onde supôs-se maior mobilidade para os portadores negativos (K > 1> •

O' >

1

o :

Neste caso, o campo elétrico no interior do dielétrico é suficiente para causar o cruzamento dos planos trazeiros. Isto ocorrerá no instante t=t

_c

(instante de cruzamento), e na posição

+

-

~

8 (tc> =8 (tc> interior ao dieletrico.

Fica evidente que a carga total em cada um dos eletro

-dos, inicialmente ±o , não será totalmente_o neutralizada, o que

ocasionará uma diferença de potencial maior que zero entre os el! trodos ao final do processo.

A Figura 3, mostra a configuração espacial dos portado-res para t > t , mas num instante

_c

em que os planos trazeiros ainda não atingiram os eletrodos; aqui é suposto mobilidades iguais pa-ra os portadore~ positivos e negativos tK=l).

Nota-se que se a recombinação entre os portadores for considerada (a. > O) parte da carga inicialmente livre no dielétri-co sofrerá recOmbinação até o instante t = t , quando

_c

os planos trazeiros cruzam; desta forma a quantidade total de portadores que alcançará os eletrodos será menor que a correspondente ao

ca-so em que inexiste recombinação (a= O). Assim, para a > O teremos uma maior quantidade de carga residual nos eletrodos ao final do processo e, consequentemente, uma maior diferença de potencial f! nal entre eles.

Na seção III.3 voltamos a discutir estes aspectos com detalhes matemáticos.

1.11 - O METOCO DAS CARACTERTsTICAS

A solução do problema proposto será obtida com o empre-go do método das caracteristicas, usado inicialmente por Many-Ra-kavy5 na resolução de problema de carga espacial.

A utilização de tal método faz surgir o conceito de li-nha de corrente que expressa a posição dos portadores no

como função do tempo.

o

movimento dos portadores positivos em tais linhas de

corrente e em unidades reduzidas,

é

dado por

dx

+(

_dt

t)

= E

[x

+ (

t) , tJ

(I.12)

+

-onde x (t) expressa a posiçao dos portadores positivos que no in~ tante t estão sujei tos ao campo elétrico E [x+ (t) ,t]. As.sim, a ve-locidade dos portadores positivos, em cada instante, é igual ao campo elétrico a que estão submetidos.

Para os portadores negativos, temos:

(I.13)

A aceleração dos portadores positivos ao longo de uma linha de corrente,

é

obtida de

+

..A~+~

ax+ dt at

que com emprêgo de (I.6), (I.10) e (I.12), resulta:

(I.14)

Analogamente para os portadores negativos:

2 -

-d x ~t) = -(1 + K) p (x,t) dx (t). (I.15)

dt + dt

+

+

+

+

!!.e....

=

l.e...

₊

9lL

+

lL

=

dt ax dtat

•

,

das equações (I.7), (I.8) e (I.6), temos:

ap+ 3E ap+

- = -p

--E --

ap p

at + ax+ ax

+

+

-e portanto,

+

.2.e... =

dt

- p (p - p ) - ap p

+ +

-

+ -

(I.16)

A integração da eq. (I.16) fornece a densidade p+(t) na posição x+(t) que pode ser obtida da integração da eq. (I.14).

De maneira análoga obtemos para os portadores negativo~

dp

--=.

dt

= K P

-

(P - P )- ap p

₊

_-

₊

-que integrada fornece a densidade p-(t) na posição x-(t) da integração de (I.ls).

(I.17)

obtida

No capítulo II procuraremos obter a solução do problema proposto.

CAPITULO 11

EMPREGO DO MlTODO DAS CARACTER!STICAS NA SOLUÇAO

DO CASO GERAL: RECOMBINAÇ~O ENTRE OS PORTADORES

POSITIVOS E NEGATIVOS

Neste capítulo vamos aplicar o método das característi-cas no desenvolvimento da solUção geral do problema proposto, is-to

I,

quando há recombinação entre os portadores positivos e neg! tivos. Como suposto anteriormente, esta recombinação entre porta-dores ocorre, em cada ponto, proporcionalmente ao produto das dea sidades dos portadores positivos e negativos neste ponto.

Com o objetivo de maior clareza, vamos separar a solu

-ção em dois casos relativos ao instante de cruzamento (t=tc) dos

+

-planos trazeiros de cargas s (t) e s (t). Teremos:

11.1

11.2

-o < t < t

_c

: TEMPO MENOR QUE O TEMPO DE CRUZAMENTO, ISTO

!,

OS PLANOS TRAZEIROS N!O CRUZARAM

t >

t :

_c

TEMPO MAIOR QUE O TEMPO DE CRUZAMENTO, ISTO

!,

OS PLANOS TRAZEIROS

JA

CRUZARAM

Note-se que, se o potencial inicialmente aplicado entre

os eletrodos

vo'

para um dado a, for tal que os planos trazeiros nunca cruzam, a solução será dada integralmente pelo

pleta será dada pelos desenvolvimentos de II.l e II.2.

Passemos

à

solução de cada caso separadamente.

11.1 - SOLUÇ~O PARA uM TEMPO MENOR QUE O TEMPO DE CRUZAMENTO

Para O < t <

te

o die1êtI'ico apresenta três regiões dis-tintas de carga espacial, a saber (FIG. 2):

(à)

região central de recornbinação, s

+

(t) ~ x

$

s- (t)1

(b) região de carga espacial negativa, O< x < S

+

(t)1

(c) região de carga espacial posi tiva, s- (t)< x <

1

Analisemos cada urna destas regiões individualmente.

II.l.a - Região central de recornbinação

- .-

+-Esta regiao e limitada no espaço por s (t) ~ x ~ s (t) e no tempo por O<

_-

t< t • Aqui, ocorre

_c

a recornbinação de portadores, se a > O. A sua carga total é nula em qualquer instante, e as den-sidades de portadores positivos e negativos dependem do tempo mas não da posição (distribuição uniforme de portadores em

instante) •

qualquer

Devido

à

recombinação as densidades de portadores

deca-em com o tdeca-empo desde os valores iniciais ±l até os valores ±p± (t) =

±p(t) no instante t considerado.

Esta região deixará de existir no instante t = tc' se ocorrer o cruzamento dos planos trazeiros de cargas.

O

sistema de equações (I.6) a (I.IO), para esta região, escreve-se:

aE

(x,

t)

= O

dp (t) = _ap2 (t)

dt

J (t)= p(t)E(x,t)

c+

(Equação da continuidade)

(Den$idade de corrente de condução p/portado-res positivos)

(11.2)

(11.3)

J (t)=- K p(t)E(x,t)

c_ (Densidade do corren-'

te de cond. p/ porta-dores negativos)

(II.4)

0= (1+K) p(t)E(x,t) + aE(x,t) at

(Densidade de corrente to-tal em circo aberto)

(II.5)

A equação da continuidade (II.2) é obtida fazendo-se o

térmo aJc /ax_±

=

O na equação (I.7), já que nesta região as correa tes de condução independem da posição. Também com p± = p em (I.16) obtemos (II.2) •

A densidade de portadores, positivos ou negativos, obtida da integração da eq. (II.2):,

.•

e

p

(t)

=-

1

l+a.t

(II.6)

J

E

(t)

E!=

E

que resulta

- (1

+

1<:)

t

J

l+at

dt

o

,

E(t) =Eo(l + at)-(l+I<:)/a

(II.7)

onde E

_o

= V

_o

é o campo elétrico aplicado em t = O.

O

movimento do plano trazeiro de cargas positivas é da-do, segundo o método das caracter!sticas, por:

E

[x(t) ,t]

,

(II.8)

e integrando com o campo elétrico de (II.7),

s

+

(t)

J

ds+

(t)

=

Eo

o

que resulta

t

J

(1

+

at) -

(1+1<:)

Ia

o

dt

,

E

[

.

s+

(t)

=

_l+jl:-a

o

1- (1

+ at) -

(1

+I<:

- a)

I

a]

Para o plano trazeiro negativo, temos

e a integração

s (t) t

J

ds - (t) = - K E

_J

(1

_{+ at) - (l+K)Ia dt}

,

o

1

o

que resulta

[1- li + atl-ll+K-al/a]

KE

s-(t)

=1-o

_(II.10)

•

l+K-a

As equações (II.9) e (II.10) nos fornecem as posições

trazeiros instantaneas dos planos trazeiros de cargas para qualquer instan-te do ininstan-tervalo O <

_-

t <

_{- c}

t •

No instante de cruzamento, t= t , os planos

_c

de cargas ocupam a mesma posição, ou seja

que com as equaçõese (II.10), fornece:(II.9)

t

=

1

{exp

[_

a

t+-l+K-a )] I}

,

c

_{a l+K-a}

(l+K)Eo

-e, impomos a condição de que

(II.11)

>

1

,

(II.12)

o que assegura a existência do cruzamento, isto

é,

t

_c

> O. A condi

-, ou

e

a)

1

+

K >

a

ção (II.12)

é

verificada para:

~+K-a < 1

A condição (b) verifica de imediato a desigualdade (11.12)

qualquer valor finito de E

_o

> O. Das condições (a) temos que

para

Assim, se o campo elétrico inicialmente aplicado entre os eletrodos E

_o

*=V

_o

verificar a relação (11.13), haverá

cruzamen-to dos planos trazeitds no instante

t

=- tc > O, dado pela equação

(II.1i) •

II.l.b - Região de carga espacial negativa

Esta região consti tu!da de portadores negativos (p+= O)

é limitada no espaço por O < x <

S+

(t) para 0< t ~ tc' Os portadores

negativos que a constituem são deslocados para o anodo, por efei-to de campo elétrico, onde alguns ou todos serão neutralizados.

O sistema de equações básicas (1.6) a (1.10), ~~e:

aE (x,t)_ax = _p_- (x,t) (Equação de Poisson) (11.14)

aJ

(x,

t)

c_

ax

+

=0

(Eq. da conti-_nuidade) (11.15)

Jc

₊

(x,t)=0

(Dens. de corrente p/porto (11.16) positivos)

J

_c

-

(x,t) = K' P

_-

(x,t)E(x,t) (Dens. de cor. (11.17) p/porto negativos)

0= Kp_(x,t)E(x,t)

+

aE(x,t)

_at (Dens. de cor-rente total)

Vamos designar por tempo de emissão (~) para um conjun to de portadores negativos desta região, ao instante em que a po-sição desse conjunto de portadores coincide com o plano trazeiro

+

positivo s (tE). Concentremo-mos agora, no movimento do conjunto de portadores negativos, em suas respectivas linhas de corrente ,

.

+

que cruzaram o plano s (t) no instante t

=

tE; tudo se passa como

se as

linhas

de

co.t'rÊlht~s

de~st!!s

t)ortadb:t'es

nascessem

sm t:

=

tE

'

sendo x- (~)

=

s+ (tE) as suas posições iniciais. Para reforçar a imagem deste quadro imaginemos que no instante t = tE' quando o

+

plano s (t) coincide com um determinado plano de portadores neg!

tivos, esses portadores negativos são emitidos da posição s+(~) e evoluem, com o passar do tempo, em direção ao anodo.

Desta maneira, a cada posição ocupada pelo plano traze!

+

ro positivo s (t), teremos um conjunto de portadores ~ativos sen

Va-do emi tidosI com um tempo caracterIstico de emissão t = tE. riando tE continuamente no intervalo O ~ tE ~

t,

onde t designa instante em que o plano trazeiro se encontra na posição s+(t),

o

ob

-temos todas as posições iniciais das diferentes linhas de

corren-te, x- (tE).

!

claro que tE está limitado no intervalo O ~ tE ~ tc • Segundo o método das características, a equação para o movimento dos portadores negativos ao longo das linhas de

corren-te, é de (

I •

13) ,

(11.19)

mobi-lidade relativa dos portadores e E[X-(tE) ,tE] o campo elétrico s2 bre os portadores no instante de emissão t=tE•

Justifica-se que os portadores evoluam na posição e no tempo, em suas respectivas linhas de corrente, sob a ação de um campo cortstante e igual

ao

êampo no respectivo instante de emis-são, analisando-se as variações do campo elétrico numa particular

l1nha de éortente caracterizada por sua posição inicial, x·(tE) , num instante genérico t > tE. Usando-se (II.14), (II.18) e (II.19) tem-se:

variação total com o tempo ª=

aE dx- aE -

---+-=

KpE- KpE=O

dt

ax- dt at

variação total com a posiçãodE dE aE dt

+

P = O

- = -

+ -- -

=-p

dX- ax- at

dx-mostrando assim, que o campo elétrico permanece constante sobre o conjunto de portadores emitidos no mesmo instante. Este campo é

obtido, fazendo-se t=tE na eq. (II.7):

•

(II.20)

Levando

(II.20)

em (II.19) e integrando:

t

= - K

E (1

+

cx

t )-(

1

+

K) / cx

J

o

E

dt

~

-

+

-

-onde x (tE) = s (~) e a posiçao inicial das linhas de corrente e dada por (11.10) com t = tE; assim, a inte9ra~ão resulta:

Ir

(t'lE) =

1:~ [1-

(li<1lE) -

(1

+lO-<I)

Ia

J-KEo (li<1lE) - (l+K)

Ia

(t-lE)

(11.21)

que é a equação das linhas de oorrentepara os portadoresElnitidoslX) insta!!, te t· tE.

A densidade espacial de portadores na linha de corrente

caradterizada pela posição inicial x-(~), obtém da inteqração da equação (1.17) com p+ = O, ou seja

p _

(t)

f~

p-p_

(tE)

que resulta;

= -I<:

t

,

(11.22)

onde p_(tE) é a densidade de portadores na posição inicial da li-nha de corrente considerada, e obtida da eq. (11.6) com t=tE:

(11.23)

com o auxIlio da (11.23), nos dá a densidade de portadores no

instante t. ao longo da linha de corrente caracterizada pela pos!

ção inicial x- (tE); podemos assim, fixàndo t -= T e tE' resolventCss';' multaneamente (11.22) e (11.21) para encontrar a densidade de po~

tadores P-(T,tE) na posição X-(T,tE); perdorrendo todos os

valo-res de

t~

dentro dos limites permt-idos para o instante T,

obter!

mos a configuração espaeiai de ~ortadores neste instahte. Vejamos

, ,

estes limites:

I '

I

i ,

- ~ limite superibr de ~ será dado por tE-T, que caractet1za o instante de emissão do último conjunto de portadores emitidos no intervalo 0< t <

..

T ~

- ~ limite inferior de tE' t~, corre.poderâ ao tempo de emissão do conjunto de portadores que no instante T estão se neutrali •• zando no anodo,

bU

seja, a solução

da

equação

ou, de (11.21):

com t = T

(11.24)

1

l+-K-a

=

1+

1

K-a

(1+

t') -

E

(l+K-a)Ia + K(l+

t!.) -

~

(l+K)Ia

(t-t..!.)

~

para resolvermos tE como função de t, consideremos tE=tE(t) e derivemos a equação anterior relativamente a t, para obter:

dt'

--!.

=

dt

K

- t

t')]

(1+.) [1+.

(l:"t!

(11.25)

t variando de O a T, nos dará o valor tE = tE da eq. (II.24)

II.l.c - Região de carga espacial positiva

Esta região é limitada no espaço por s- (t) < x < 1 para

.

-0< t ~ te' aqUi a densidade de portadores negativos e

nula

e os portadores positivos são deslocados para o catodo por efeito de campo elétrido, onde, alguns ou todos serão neutralizados.

O

sistema de equações (I.6) a (I.10) para essa região, escreve-se:

élE(x,t)_élx = p

₊

(x,t) (Eq. de POisson) (II.26)

ax

élP+(X,t)

+

----=0

at (Eq. da continui-dade)

(II.27)

J

(x,t) = p+ (x,t)E (x,t)

c+

.

(dens. corrente_{de cond. p/por-} (II.28)

tadores positivos)

Jc_

(x,

t)

= O (dens. corrente_{p/porto negativos)}de cond. (II.29)

+

O = p (x ,t)E (x,t)

+

é)E (x,t) at

(corrente total {II.30) em circo aberto)

O

procedimento a ser usado para esta região será

(II.31)

onde x+(t,~)

é a posição instantanea

dos portadores nas

linhas

- .

+-de corrente caracterizadas

pelas posiçoes iniciais

x (~)

=

s (~);

E[X+(tE),tEJ

é o campo elétrico

sobre os portadores

no instante

de emissão t

=

tE e dado por (II.7)

com t=- tE:

Integrando

(II.31)

com o emprego de (II.32):

(II.32)

+

x

(t,tE)

J

dx+(t)

=

E (1 + at )- (1+

o

E

k) /

a

s-

(tE)

ou

t

,

onde s- (tE) é obtida de (II.10)

com t

=

tE:

(t - ~)

,

- KE [ ]

s (tE) =1-

1

+K-a

o

1- (l+at

E

)-ll+.K-a)/a

'

que substituIdo

na equação anterior

resulta:

(II.33)

x+ (t, i;:l -

1- 1:';;' [1- (l.•••

i;:l - (1+<-a)

la]+

Eo(l.•••

i;:) -

(1

+I<l

Ia

(t-i;:l

(II.34)

tenp:>sde emissão t = tE •

A densidade espacial de portadores negativos nestas

li-nhas de corrente,

é

dada pela integração da eq.

(1.16)

com p_ = O , que resul ta: '

,

(11.35)

onde p+(tE)

é

a densidade de portadores na posição inicial x-(tE) da linha de corrente considerada, e no instante de emissão t

=

~7

assim, de

(11.6),

com t=tE:

(11.36)

A configuração espacial de portadores positivos para um dado instante t = T, O

_-

< T <

_{- c}

t ,

é

obtida da resolu~ão_T simultanea das

eqs.

(11.34)

e

(11.35)

para um particular conjunto de linhas de

-

+)-corrente caracterizadas pela posiçao inicial x (~ • s (tE). Va-riando-se tE dentro dos limites permitidos no instante T, enoontr~ remos a configuração espacial de portadores nesta região para t = T. Estes limites são:

- o limite superior de tE

é

dado por tE = T, que caracteriza o in!, tante de emissão do último conjunto de portadores emitidos no instante t = T7

- o limite inferior de tE' tE' correspoderá ao tempo de emissão do cojunto de portadores que no instante T está se neutralizan-do no anoneutralizan-do, ou seja, a solução da equação

+

e, substituindo (II.33)

ou

•

,

para resolvermos tE como função de t consideremos tE = tE(t) e derivemos a equação anterior relativamente a t, pàra obter:

dt"

E _

dt

-

1

t - tE) (1+IC) ( 1 + l+a.t;

(II.38)

A integração numérica desta equação, com tE variando de O a tE e t variando de O a T nos dará o valor tE = tE requerido pela equa-ção (II.37) •

11.2 - SOLUÇAO PARA UM TEMPO MAIOR QUE O TEMPO DE CRUZAMENTO

Pela análise da equação (II.ll) conclu!mos que, se o

potencial inicialmente aplicado entre os eletrodos Vo=Eo' verif! car a relação (II.13),

(11.13)

ocorrerá o cruzamento dos planos trazeiros de cargas.

(a) regiao central sem carga espacial, s (t)< x < s (t)1

(b) região de carga espacial negativa, (c) região de carga espacial positiva,

o <

x

$

s-

(t)

1

+

s

(t) ~

x

<

1.

A principal mudança na configuração das cargas espa-ciais em relação ao caso em que t< t , é a substituição

_c

da região central de recombinação por uma região sem carga espacial livre, mas também limitada pelos planos trazeiros.

Esta região aumenta a sua extensão com a evolução do tempo e compreenderá todo o dielétrico (O< x < 1) após os dois pl!. nos trazeiros atingirem os respectivos eletrodos. A partir deste instante, em que não há mais portadores livres no dielétrico, ha-verá uma diferença de potencial estacionária entre os eletrodos , cujo valor dependerá da carga residual que permanecer nos eletro-dos sem neutralização, ou seja (o - 1) •

_o

Analisemos cada uma das regiões do dielétrico separada-mente.

II.2.a - Região central sem carga espacial As equações para esta região, são:

ôE(x,t)

_ax

= O

J

(x,

t)

= O

c±

aE(x,t)

_at

=

O

(Eq ~ de Poisson)

(I)ens. de corrente de

cxmdução) (correntede

desloca-!tento)

(II.39)

(II.40) (II.41)

o

campo elétrico

é

constante nesta região, como

aparece no instante de cruzamento dos planos trazeiros e, portan-to, daOO pela

~.ão

(II.7) com t = t :

_c

E(t ) =E

_c

_o

(l+at

_c

)-(l+K)/a

com tc dado pela equação (II.ll).

(11.42)

II.2.b - Região de carga espacial negativa

Chamemos de t- o tempo de transito do plano s-(t) que

corresponde ao instante em que s- (t) ••O. Assim, para tc < t< t- e!, ta região está limitada por O< x <

-

s- (t), e para t

-

> t- ela desapa

-rece.

As equações básicas para esta região são as mesmas que compoem o sistema de equações (II.14) a (11.18).

A equação para as linhas de corrente

é

dada por (11.21).

O

movimento do plano trazeiro s-(t), corno função do tem

po de cruzamento tc' e para tc ~ t ~ t-,

é

obtido de

ds-

(t)

dt

= - te:: E

(t )

c

onde E(t )

_c

é

o campo constante que atua sobre o plano trazeiro ao longo de seu movimento, e dado por (II.42), integrando esta equa-ção com o emprego de (II.42),

s-

(t)

t

JdS-<t)

=

-KEoCl+ "tC)-<l+K)/"

Jdt

,

s-

(tc>

ou

,

onde a posição de cruzamento s-(tc)

é

obtida de (II.10) com t=tc' que resulta para a equação anterior,

Podemos, com o auxilio da equação (II.ll), mostrar que

(1 + at )- (l+K-a)

_c

Ia

= 1 _ l+K-a

(l+dE o

o que permite escrever que:

,

(II.43)

s-

(t)

_{= 1 ~ K - K Eo (1 + atc) - (1+1<)}

_I

_{a (t - tc)} (II.44)

Para t=t- os portadores do plano s-(t) estão sendo ne~ tralizados no anodo, o que corresponde

à

condição

que com a substituição da equação (II.44), forma:

(II.45)

Assim, equação (II.45) nos dá o instante em que plano trazeiro ne gativo s-(t) alcança o catodo, isto é, o instante em que despare-ce a região de portadores negativos no dielétrico.

A densidade espacial de portadores nas linhas de corren

~

-

+

instan-te t,

é

dada pela equação (11.22) com o aux!lio de (11.23).

A configuração espacial de portadores para o instante T,

tc < T < t-,

é

encontrado de modo idêntico ao empregado para o caso em que t<tc' na seção (II.1.b), ou seja, a resolução conjunta das equações (11.21), (11.22) e (11.23), para cada valor de tE m2 difica-se, apenas, o intervalo de variação de tE' tc ~ tE ~

tE'

0!l

de ~ = tc

é

o instante em que o último conjunto de port~dores ne-gativos

é

emitido (o conjunto de portadores que formam o

s-(t».

tE

é

dado pela integração numérica de (11.25).

plano

I1.2.c - Região de carga espacial positiva

+

+

Chamemos t o tempo de transito do plano s (t) que

cor-+ + +

responde ao instante em que s (t > = 1. Assim, para t < testa

re--

~ 1

+

+

d

giao esta imitada por s (t) ~ x ~ 1 1 para t ~ tela esaparece. As equações básicas para esta região, são as mesmas que compoem o sistema (11.26) a (11.30).

A equação para as linhas de corrente dos portadores

ca-racterizadas pelo tempo de emissão tE' é dada por (11.34).

O movimento do plano trazeiro de portadores positivos ,

como função do tempo de cruzamento te' para tc < t ~ t+ , é obtido

de

ds+(t>

dt

=

E(tc) (11.46)

e usando a equação (11.9) com t == t

c

para obtermos s+ (t ), e o em-

c

prego de (11.43):

s+(t) = rl-K + Eo(l+atc)-(l+K)/a e(t-tc) • (11.47)

Para t = t+ os portadores que compoem o plano s+ (t) estão sendo neutralizados no catodo o que corresponde

à

condição

s+(t+)=l

que com a substituição de (11.47), fornece:

(11.48)

..

e

Esta equação nos dá, portanto, o instante em que o plano trazeiro positivo s+(t) alcança o catodo ou seja, o instante em que desap~ rece a região de carga espacial positiva.

Observe-se que, para mobilidades iguais dos portadores positivos e negativos (K=l), as equaçõ.s (11.45) e (11.48) coin-cidem, como esperado.

A densidade espacial de portadores nas linhas de corren

te caracterizadas pelo instante de e~issão tE' no instante t, dada pela equação (11.35) com o auxIlio de (11.36).

A configuração espacial de portadores, nesta região, p~

ra o instante T, te ~ T < t+,

é

encontrada de modo análogo ao empr!, gado para t <t

_c

na seção (II.l.c), ou seja, a resolução conjunta

das equações (11.34), (11.35) e (11.36) para cada valor de tE. A única modificação está no intervalo de variação de tE' que passa

ocorre para t

=

tc:

tE

é

dado pela integração mInima da

(II.38) •

equação

No capItulo

III

procuraremos calcular o decaimento

do

potencial como função do tempo, V(t), para os diferentes

casos

CAPITULO 111

CALCULOS DA DIFERENÇA DE POTENCIAL INST~NTANEA V(t)

ENTRE OS ELETRODOS E DA CARGA RESIDUAL NOS ELETRODOS

Neste capItulo vamos realizar os cálculos para determi-nar a diferença de potencial instantânea V(t) entre os eletrodos bem como a carga residual nos eletrodos.

De inIcio calcularemos V (t) para um instante O ~ t < tc ' isto

é,

numa situação em que o cruzamento dos planos trazeiros de dárgas não ocorreu.

Em 'eguida, faremos o cálculo para V(t) dom

t

>

t

_c

ou

lIe

-ja, num instante após o cruzamento dos planos trazeiros. Esta si-tuação só ocorrerá se a condição dada por (II.l3) for satisfeita, conforme discutido na seção (II.l.a).

111.1 - CALCULO DA DIFERENÇA DE POTENCIAL INSTANT~NEA V(t), ENTRE

OS ELETRODOS PARA UM TEMPO MENOR QUE O TEMPO DE

CRUZAMEN-TO.

A diferença de potencial instantânea entre os eletrodos

é

dada pela equação (I.ll),

1

V (

t)

=

J

_o

E (x,

t)

dx

(I.ll)

Como vimos anteriormente, para t < tc há três regiões di.!, tintas de carga espacial no dielétrico, a saber: região de carga

ga espacial positiva; a equação (I.ll) escrita para estas diferen_... tes regiões, torna-se:

s+

(t)

V(tl"

LE[X-(t.tr;:),t]

_o

clx- +

1

+

J

_s

_E

_(t)

fjc+

(t'l:p;l,t]

clx+

à-

(t)

f

_s+

_(t)

E(X,t)dx +

(III.l)

onde E[X-(t,tE) ,t] e E [x+(t,tE) ,t] representam os campos elé-tricos nas várias linhas de corrente nas regiões de carga espa-cial negativa e positiva, respectivamente, e E(x,t) =E(t) o campo elétrico na região central de recornbinação. Assim, ao realizarmos as integrais do primeiro e terceiro termos do segundo membro de

(III.l) devemos ter o cuidado de levar em conta todas as linhas

de corrente da região a que a integral se refere. A individualiz! ção das linhas de corrente numa região pode ser conseguida se co~ siderarmos que, de um modo geral, estas linhas de corrente são

funções do tempo t e do parâmetro tE:

,

(III.2)

e a variação total de x:

dx = d~X_E dtE (111.3) Tendo em conta (111.3), vamos calcular cada uma das integrais de

(111.1) separadamente.

Região de carga espacial negativa

O potencial nesta região é dado pelo primeiro. têrmo de

(111.1), que com o emprego da equação (111.3), torna-se:

s

+ (t)

t

J

E dx-

J

dx-= E dtE dtE

o

tI

E

onde a mudança na variável de integração permite-nos _(111.4)

considerar

todas as linhas de corrente existentes na região negativa para o

instante t; tE' como já discutido na seção (II.l.b),

é

dado pela integração numérica da equação (11.25). O têrmo dX-/dtE é obtido

da derivação parcial em relação a tE da equação (11.21), ou seja:

:: =

(1 h) Eo [l1"",'il) - (1+K)

Ia

+ Klt-'il) (l"",'il) - (1_)

/0].

(111.5)

com o campo elétrico, para cada conjunto de linhas de corrente ca

racterizadas por tE' dado por (11.20). Substituindo (111.5) e

(11.20) em (111.4):

t

J

(1

+

"'il)

-2 (1

+te) /"

d~

~

t

+ (1 + <)< E~.t

J

(1 + a~) - [2(1+<) + a]/a

d~

tE .

t

- (1+ K)K E~

J

(1+ a~) - [2(l+K)+ a]Ia ~. d~

tE

(111.6)

A primeira e segunda integrais do segundo membro são imediatas e

resultam:

e

t

J

(1+ at-)-2 (l+K)Ia

t:

d~ - -

_ (1+ at-)- [2(l+K)-aJ/a

t:

tE

2 (1

+

K) -

a

t

,

t

J

(1+ a~) - [2(1+<) +a]/a

ti

d~ __ (l+a~)-2(1+<)/a

₂₍₁

₊

K)

t

•

I

a terceira integral

é

calculada considerando-se a fórmula de int~

gração:

J

l-a

x (1

+

x) - a dx

=

(1 - x)

_l-a

e pondo-se x 11I atE e a = [2 (l+K) + aJ/a I

(

x -

2="ã

l+X)

para se obter

(111.7)

t

J

(1+ at-)- [2(l+K)+a]Ia

t:

*l: d~ -

(1+ at-)-2 (l+K)Ia

t:

•

a

tE

--

2(1+<)

•

e, a equação (III.6) pode ser escrita,

t

+

substituindo os limites de integração e rearranjando os termos tem-se:

,

+ )

2

s (t (l+K)Eo

J

E dx- = 2(1+K)-a

o

_ 2 (l+K)-a1 + atE ] (1+ atE)-2 (l+K)Ia (III.S)

Assim, a equação (III.S)

é

a contribuição ao potencial entre os eletrodos devida

ã

região com carga ·espacial negativa.

Região central de recombinação

s-

(t)

J

E(x,t)dx

=

EO(l+ Clt)-(1+<)/Cl [s-(tl

-s+(tl]

•

s

+

(i:)

-

+

com s (t) e s (t) dados por (11.10) e (11.9), o que resulta

• Eo (1+ at)- (l+K)Ia (111.9)

Região de carga espacial positiva

O cálculo para esta região

é

análogo ao da região nega-tiva devido

ã

similaridade das duas regiões. Tendo em conta a ~ ção (111.3), a terceira integral do segundo membro de (111.1), ~ na-se:

1

til

/

_t

(111.10)

onde o limite superior tE

é

obtido da integração numérica da equ! ção (11.38), conforme discutido na seção (II.l.c). O têrmo dx+/d~

é

dado pela derivação parcial relativamente a tE da equação (II.3~,

dx+

e o campo elétrico, para cada conjunto de linhas de corrente ca

-racterizadas por tE' dado por (II.32). Substituindo (II.32) e (III.ll) em (III.10), temos:

1

J

E dx+ - -(l+~)E~

s-

(1;)

ti

J

(1ttl~)-2(1+i<l~d~_

t

ti

-(l+~)E~

t

J

_t

(l+a~)-

~(l"",)-aJla

d~

+

!E

+(l+KlE~

J

_t

(l+a~)-I?(l"",)-<>]/a

~ d~

•

(III.12)

De modo análogo ao cálculo do potencial para a região negativa

,

as duas primeiras integrais do segundo membro de (III.12) são ime... diatas e a terceira pode ser integrada com o emprego de (III.7), o que resulta:

1

J

E dx+ _ (l+~)~

s-

(t)

(1+ a~) - [2(l+K)-aJIa

t

+

t

E2

2(~K) (1+a~)-2(1+K)/a [~ - 1- 2 (l+K)l+a~ ]

ItE

't

,

substituindo os limites de integração e rearranjando os têrmos tem-se:

,

1

I

E dx+

=

(~+K)E~

s-

(t)

1

+

atE

]

- 2(1

+ K)

-a

(1

+

atE)

-2

(l+K)

/0.

(±íI.14)

que

é,

portanto, a contribuição ao potencial entre os eletrodos devida

ã

região de carga espacial positiva.

Assim, a diferença de potencial entre os eletrodos para

o instnte O ~ t < tc

é

obtido pela substituição das equações (III. 8), (III.9) e (III.14) na equação (III.l), que resulta:

• (1

+

atiP

-2

(l+K)

/0.

t > t>

_c

_-

O

com tE e tE dados pelas integrações numéricas de (11.25) e (11.38), respectivamente.

111.2 - CALCuLo DA DIFERENÇA DE POTENCIAL INSTANTANEA V(t) ENTRE

OS ELETRODOS PARA UM TEMPO MAIOR QUE O TEMPO DE

CRUZAMEN-TO.

A diferença de potencial instantânea, dada pela equação (1.11), pode ser escrita para este caso, de modo similar à equa-ção (111.1):

s-

(t)

V(t)

=

fE[X-(t,~) ,tJ dx-+E(tcl [s+(tl - s-(tl] +

o

+

1

fE[X+(t'~l ,t] dx+

s

+

(t)

,

(111.16)

onde E[X-(t,tE),t] e E [x+(t,tE) ,t] são os campos elétricos nas diferentes linhas de corrente nas regiões negativa e positiva, ~

pectivamente, e E(tc) o campo elétrico constante, dado pela equa-ção (11.42), existente na região central sem carga espacial.

Os três têrmos do segundo membro de (11.65) são as con-tribuições ao potencial devidas às três diferentes regiões exis

-d

-

+

tentes no ieletrico, para t

_c

< t

_-

< t- •

Novamente, observemos que ao realizarmos as duas inte-grais de (III.16), deveremos ter o cuidado de incluir as

conseguido, pela troca da variável de integração x por tE' atra-vés da equação (III.3).

Calculemos cada uma das contribuições de (III.36), sep~ radamente.

Região de carga espacial negativa

Usando (í±í.3), podemos $ScreVét

á

~riMeirá irite~ral de (III.16), como:

s- (t) t

f

E

dX-c

=

f

E dx-

dtE

,

(III.17)

dtE

o

ti E

onde

tE = tc' é o instante de emissão para o plano trazeiro de negativas S-(t)7

cargas

~

=tE

'

é

o tempo de emissão para o conjunto de portadores que no instante t estão sendo neutralizados no anodo, isto é,

a solução da equação (II.24)

é

dada pela integração num! rica de (II.25).

o

campo elétrico ao longo da linha de corrente

caracte-rizada pela posição inicial X-(tE) é dado pela equação (II.20). O têrmo dX-/dtE

ê

dado pela equação (III.5).

s

-

(t)

t

e

JE

dx-

= (l+K)E~

J

(1 +a~) -2 (1+t<)

Ia

d~

+

o

tE

te

+ (l+K)K E~t

J

(l+a~)-[2(1+K)+aJ/a

• d~

-tE

te

- (1 + K)K E~

J

(1 + a~) - [2 (l+K)+a]

Ia

. ~

d~

(IlI.18)

tE

comparando (III.18) eom a equação (III.6), notamos apenas a

muda~

ça do limite superior de integração; usando os cálculos já

reali-zados para a obtenção da equação (III.8), eoncluimos que:

K E2

+

--2

2

[

_tc

-

t

+ 2 (1

1

₊+.

_at

K)-a

_]

(1

+

atc) -2 (l+K)

Ia

+

l+atE

- 2(1 + K)-a ] (1 + ai! )-2

(l+K)Ia

,

(II1.l9)

Região Qentral sem carga espact.l

Nêstâ

t.~1ãb;

a

~ort~ki~ul~lo

ao potenêiái

é

dada pelo segundo têrmo do segundo membro da equação (111.16),

,

+

-

-com o campo constante E(tc) dado por (11.42); s (t) e s (t) sao dados por (11.47) 3 (11.44), substituindo estas equações na equa-ção anterior temosl

±

para t > t > te •

-

+

+

-Para t > t ~ t , pondo s (t) - 1 e s

(t)

dado pela

equa-ção

(11.44):

+

-

+

-Para

t ~

t

"t , com s

(t)

dado por (11.47) e pOrxb s(t). • O, temos:

E (te) s

+

(t) • :~~

(1 +

Clte)

-(1+14 /

Cl

[1+

(l+IÓEo

(1+

Clt:d -

(1"",)/

Cl •

•

(t-te)]

•

(III.22)

Região de carqa espacial positiva

onde

,

(111.23)

; • tc

é

o instante de emissão para os portadores que compÕem o

+

plano s (t), e

~.

tE

é

o instante de emissão para os portadores positivos que no instante t estão sendo neutralizados no catodo, isto

é,

a solução da equação (II.37) dada pela integração numéri-ca de (1I.38).

o

campo elétrico ao longo da linha de corrente

caracte-rizada pela posição inicial x+ (tE) • s- (;)

é

dado pela equação (II.32).

o

têrmo dX+/dtE

é

dado pela equação (III.ll).

Substituindo as equações (II.32) e (III.11) na (111.23), temos:

1

J

E dx+ • -(1+~)~

s+(t)

t!;

J

(l+ai!) 2 (1+0:)/ a di!

-tc

ti

- (l+Kl~

t

f

(1+a i!) -

(2

(1+~)-a]la

di! +

ti

+ (1+Kl~

f

(1+a'E1-[2(l+l<l-a]/a

'E.d'E

tc

(III.24)

(1+IC)E2 [

• '2 (1+"1 ~

(1+ ali l- ~ (l+K).•••]/a

- (1+ ate>- ~(l+l<l.•••]/a ]

+

(III.25)

(1 + at )

_c

-2

(l+tc)

Ia

(1 + atE )

-2

(1+1C)

Ia

1 +atc

]

[tc-t

+ 2/1+1<)

.•••

[

t-t.!! - "

""E

2 (1+1C)-a

1+

atE ]

~

+-

₂

A comparação de (111.24) com (III.12) mostra que apenas os limi-tes interior •• das integrais são diferentes, repetindo os cálCU-los que

coftdu.l~~

1

(IIÍ.14), temos

i

1

fE~

s+(~

que

é

a contribuição ao potencial devida

i

região com distribui -ção de portadores positivos.

O potencial instantâneo V(t) será obtido pela substitu! ção das contribuições ao potencial dadas pelas equações (III.19),

(III.20) e (III.25) na (III.16), que resulta:

[

tc

-

t + 21l+lC)=a

1 +at

]

(1 +

atc)

-2

(l+tc)

Ia

+

IC~

+--2

₂

+ (1+K)E2 (t-t ) (l+at )-2(1+K)/a

_o

_c

_c

2

(l+K)Eo + 2(1+K)-a

•

• [(1+

"i!)- ~

(1+te)-u] / •• - (1+ ••

td

-12

(1+te)-u

1/••]

+ 2

So [

.

l+a~

]

+

T

t-

ti -

2(1+K)-a (l+ati )-2(1+K)/a +

2

Eõ [

1+

at ]

+ -2 .

t

c

-t + ~

(l+K)-a

c (l+at )-2(1+K)/a

c

(111.26)

Note-se que a equação (111.26) fornece o potencial para cada

ins-tante t± > t > tc' sendo t± os tempos de trânsito dos planos tra-ze1ros.

+

-

-

•..

Para t > t > t as equaçoes (111.19) e (111.20) serao r!, tiradas da equação (111.26) com a inclusÃo da equação (1II.22)IP!

-

+

.•....

ra t > t > t serao retiradas as equaçoes (111.25) e (111.20) com a inclusÃo de (111.21) na equação (111.26).

111.3 - CALCULO DA CARGA RESIDUAL NOS ELETRODOS

Procuraremos agora, determ~nar a quantidade de carga que permanecerá nos eletrodos ao final do processo sem neutra11z~ ção, isto é, a carga residual nos eletrodos.

Para efeito do cálculo, raciocinemos em têrmos da quan-tidade de carga negativa que, durante o decorrer do processo, al-cança o anodo aI se neutralizando. A carga residual neste

dual do citodo será simétrica

ã

do anodo.

A carga negativa total que alcançará o anodo será

a me.

-ma que, no decorrer do processo, atravessará o plano s+(t), em seu movimento pâra a direita com velocidade ds+/dt. (veja Figura 2). Calculemos essa quarttidade de carga.

A

corrente devida aos portadores negativos que

atraves-sam o

plabô s+(tl

co~

!unçãb

do

tempo

é:

d~~t) • -p(t)v(t)

,

(III.27)

onde p(t) é a densidade de portadores na posição s+(t) e dada por

p(t)·

--..!

,

(III.28)

e v(t) a velocidade dos portadores negativos relativamente ao pl!

no s+(t)

+

v (t)· ~t

+

K E (t) • (1 + K) E (t) ,

sendo E(t) o campo elétrico na região central,

assim,

E (t) • Eo (1

+

at) - (l+K)Ia

,

(II.7)

•

(III.29)

q (t) ••-Eo (1 + te)

J

(1 + at) - (l+te-a)

Ia

dt

o

que resulta

q

(tI •

-Eo [1 - (1

+ utl- (1+~)

lU]

,

(III.30)

que fornece a quantidade de carga q(t) que atravessou o plano s+(t) até o instante t, e será posteriormente neutralizada no an2

do.

Como vimos no capItulo

II,

a condição para que ocorra o cruzamento dos planos trazeiros

é

que

(II.13)

Se esta condição não se verificar, os planos trazeiros tenderãp a

pOSições 1imites

para t

+

00' nesta situação, a carga negativa total que cruzará o plano s+(t) e, posteriormente, será neutralizada no anodo é, da EqUaÇão

(III. 30),

fazendo t

+

00

q

(00)

"-E

_o

,

que é igual

à

quantidade de carga positiva

0'0"

Eo depositada ini-cialmente no anodo. Assim, para t

+

00 a carga residual nos eletro-dos será

,

(III.31)

e, consequentemente, uma diferença de potencial residual V(oo) -O permanecerá entre os eletrodos.

re-gião central pois, da equa9ão (II.6),

p(llO) = O •

Passemos agora ao caso em que a desigualdade (II.13)

é

verificadâ, isto

é,

os plartos trazeirol crUzam. A equação (III.30) escreve-sé:

q

(te) • ~l!!o[

1- (1

+

"te) -

(l+l<l/á ]

;

(tIl. ;)2)

já

que no instante t· t

_c

cessa o fluxo de port.adores negativos

a--

+

-

1

traves do plano s (t), assim, para t > t a carga residua no

ano-do

é,

qr • Eo + q (t ) • E (1

c

o

+

at )- (l+ldIa

c

que

é

também a expressão para a diferença de potencial

(III.33)

residual entre os eletrodos. Notamos assim, que o potencial residual pode ser obtido, de imediato, pelo produto do campo constante que exi~ tirá no dielétrico após os planos trazeiros terem sido neutraliz~ dos nos eletrodos e dado pela equação

E(t)

_c

=E

_o

(l+at

_c

)-(l+ld/a

(II.42)

e o comprimento d. 1 do dielétrico, o que result.a a própria

equa-ção anterior (ou, a equação

(III. 33».

Ainda, o valor t· t.c

i

da-do pela equação

t

_c

=

.!

_a

a

l+K-a

CAPTTULOIV

SOLUÇDES PARA DOIS CASOS PARTICULARES DO PROBLEMA

PROPOSTO: RELAtAo

~t

LANGEVIN E AUSrNCIA DE RECOM

BINAÇ~O ENTRE OS PORTADORES.

Neste capItulo vamos obter as soluções para dois casos particulares do problema proposto tendo em conta os resultados g~ rais dos CapItulos 11 e 111.

IV.l - SOLUÇ~O PARA UM CASO PARTICULAR: RELAÇ~O DE LANGEVIN

A dependência entre as mobilidades dos portadores posi-tivos e negaposi-tivos e o coeficiente de recombinação a', escreve-se

a,_lJ++lJ-

_t

,

(IV.l)

conhecida como Relação de Langevin (apêndice). Em unidades reduz! das ela torna-se

0.-1+1(

_(IV.2)

Desta forma, as equações para a solução do problema, s~. rão obtidas pela substituição da relação

(IV.2)

nas equações ge-rais desenvolvidas nos capItulos II e III.