Modelo de regressão para um processo de renovação Weibull com termo de fragilida...

(1)

Escola Superior de Agricultura “Luiz de Queiroz”

Modelo de regress˜

ao para um processo de renova¸c˜

ao Weibull com

termo de fragilidade

Jos´

e Carlos Fogo

Tese apresentada para obten¸cão do t´ıtulo de Doutor em Agronomia. Área de concentra¸cão: Estat´ıstica e Experimenta¸cão Agronômica

(2)

Estat´ıstico

Modelo de regress˜ao para um processo de renova¸c˜ao Weibull com termo de

fragilidade

Orientadora:

Prof. Dr. CLARICE G. B. DEM ´ETRIO

Tese apresentada para obten¸cão do t´ıtulo de Doutor em Agronomia. Área de concentra¸cão: Estat´ıstica e Experimenta¸cão Agronômica

Piracicaba

(3)

DadosInternacionais de Catalogação na Publicação (CIP) DIVISÃO DE BIBLIOTECA E DOCUMENTAÇÃO - ESALQ/USP

Fogo, José Carlos

Modelo de regressão para um processo de renovação Weibull com termo de fragilidade / José Carlos Fogo. - - Piracicaba, 2007.

184 p. : il.

Tese (Doutorado) - - Escola Superior de Agricultura Luiz de Queiroz, 2007. Bibliografia.

1. Análise de sobrevivência 2. Processos estocásticos pontuais 3. Simulação (Estatística) I. Título

CDD 519.536

(4)

`

A minha esposa Elza pelo amor, pela compreensão, pelo apoio e por ser o pilar que dá sustenta¸cão à nossa fam´ılia com sua for¸ca e determina¸cão.

(5)

AGRADECIMENTOS

Com a conclusão do trabalho e obten¸cão do sucesso almejado, todos os mo-mentos passados retornam em nossas mentes: pessoas, lugares, sensa¸cões, tudo fica na lembran¸ca valorizando ainda mais o nosso feito. A todas as pessoas que, direta ou indi-retamente, contribu´ıram para que esse projeto alcan¸casse êxito, deixo, aqui, meus sinceros agradecimentos.

`

A Profa _Dra _{Clarice Garcia Borges Dem´etrio a orienta¸c˜ao sempre dedicada, a}

amizade, confian¸ca e incentivo em todo o decorrer do trabalho.

Ao Profo _{Francisco Louzada Neto a valiosa colabora¸c˜ao no projeto.}

`

A Universidade Federal de São Carlos e professores do Departamento de Es-tat´ıstica a confian¸ca, proporcionando as condi¸cões necessárias para a realiza¸cão do trabalho. Aos professores Wagner Borges, Roseli Aparecida Leandro e José Antonio Frizzoni as valiosas sugestões e comentários quando da realiza¸cão do meu exame de quali-fica¸cão.

Aos professores e funcionários do Departamento de Ciências Exatas da ESALQ/USP que me propiciaram as condi¸cões para a realiza¸cão do trabalho.

Aos colegas e amigos de doutorado Beth, Ana Maria, Denise, Genevile e Pedro a for¸ca, a amizade, a troca de experiências e a aten¸cão recebida em todos os momentos que estivemos juntos, momentos esses que ficarão para sempre.

A Todos os colegas do Departamento de Estat´ıstica deixo meus sinceros agra-decimentos pela colabora¸c˜ao e confian¸ca, em especial `as Profas _{Cristina e Vera e ao Prof.}

Luiz Milan, os valiosos conselhos e sugest˜oes.

Ao Sr. Valério e D. Lurdes, que no papel de avô e avó, dedicaram tanto carinho ao meu filho durante minhas ausências.

`

A minha mãe Antonia, meu pai Vilézio e toda minha fam´ılia, o carinho e a compreensão, sempre rezando por mim e acreditando no meu trabalho.

(6)

SUM ´ARIO

RESUMO . . . 8

ABSTRACT . . . 9

LISTA DE FIGURAS . . . 10

LISTA DE TABELAS . . . 13

1 INTRODUC¸ ˜AO . . . 17

2 CONCEITOS INICIAIS . . . 20

2.1 Eventos terminais e recorrentes . . . 20

2.2 Popula¸cões homogêneas e heterogêneas . . . 21

2.3 Observa¸c˜oes dos dados . . . 23

2.4 Censura . . . 23

2.4.1 Tipos de censuras . . . 25

2.5 Modelos de sobrevivˆencia cont´ınuos . . . 27

2.5.1 Algumas considera¸c˜oes sobre a fun¸c˜ao de risco . . . 30

2.5.2 A fun¸c˜ao de verossimilhan¸ca . . . 32

2.6 Modelos discretos . . . 34

2.7 Modelos de regress˜ao . . . 35

2.7.1 Modelos de regress˜ao param´etricos . . . 38

2.7.1.1 Modelo exponencial . . . 38

2.7.1.2 Modelo de Weibull . . . 39

2.7.2 Modelos de regress˜ao semiparam´etricos . . . 40

2.7.2.1 Modelo de regress˜ao de Cox . . . 40

2.8 Processos de contagem . . . 43

2.8.1 No¸c˜oes b´asicas de processos de contagem . . . 43

2.8.2 Processos de Poisson . . . 51

2.8.2.1 Processo de Poisson homogˆeneo (HPP) . . . 52

2.8.2.2 Processo de Poisson n˜ao homogˆeneo (NHPP) . . . 53

2.8.3 Processos de renova¸c˜ao . . . 54

2.9 Modelo de fragilidade . . . 61

(7)

2.9.2 A distribui¸c˜ao para a fragilidade . . . 66

3 MODELO DE REGRESS ÃO PARA UM PROCESSO DE RENOVAÇ ÃO . . . 68

3.1 Modelo de regressão para um processo de renova¸cão limitado pelo número de falhas 68 3.2 Modelo de regressão para um processo de renova¸cão limitado pelo tempo . . . 69

3.3 Modelo de fragilidade para um processo de renova¸c˜ao limitado pelo tempo . . . . 71

3.3.1 Modelo de regress˜ao para um processo de renova¸c˜ao com fragilidade gama . . . 72

4 M´ETODOS . . . 76

4.1 Simula¸cão de um modelo de regressão para um processo de renova¸cão com distri-bui¸cão Weibull, limitado pelo número de falhas . . . 76

4.2 Simula¸cão de um modelo de regressão para um processo de renova¸cão com distri-bui¸cão Weibull, limitado pelo tempo . . . 79

4.3 Simula¸cão de um modelo de regressão para um processo de renova¸cão com distri-bui¸cão Weibull, com censuras, limitado pelo número de falhas . . . 80

4.3.1 Corre¸c˜ao do v´ıcio de ˆβ0 pelo processo de “bootstrap” . . . 81

4.4 Simula¸cão de um modelo de regressão para um processo de renova¸cão com distri-bui¸cão Weibull, com termo de fragilidade com distridistri-bui¸cão gama . . . 83

5 RESULTADOS . . . 86

5.1 Simula¸cão de um modelo de regressão para um processo de renova¸cão com distri-bui¸cão Weibull . . . 86

5.1.1 An´alise das variˆancias dos estimadores. . . 94

5.1.2 Processo de renova¸c˜ao limitado pelo tempo . . . 104

5.1.3 Conclus˜ao . . . 105

5.2 Simula¸cão de um modelo de regressão para um processo de renova¸cão com distri-bui¸cão Weibull e dados censurados . . . 107

5.2.1 Variância das estimativas, para um processo de renova¸cão com dados censurados 113 5.2.2 Corre¸cão do v´ıcio nas estimativas deβ0 . . . 126

5.2.3 Conclus˜ao . . . 128

(8)

5.3.1 Análise das variâncias das estimativas para as simula¸cões do modelo com termo

de fragilidade . . . 130

5.3.2 Conclus˜ao . . . 133

REFERˆENCIAS . . . 146

APˆENDICES . . . 150

(9)

RESUMO

Modelo de regress˜ao para um processo de renova¸c˜ao Weibull com termo de

fragilidade

Processsos de renova¸cão são um caso especial de processos pontuais envolvendo eventos recorrentes nos quais um item ou unidade, após a ocorrência de uma falha, é reco-locado na mesma condi¸cão de novo. Devido a essa propriedade os tempos entre ocorrências para um processo de renova¸cão são independentes e a sua fun¸cão intensidade é dada pela fun¸cão de risco. Fatores que interferem nos tempos de recorrência de unidades distintas, ou indiv´ıduos, e que não são observados, podem ser modelados com a inclusão de um termo de fragilidade no modelo. Neste trabalho é apresentado o desenvolvimento de um modelo de regressão para um processo de renova¸cão com tempos entre ocorrências com distribui¸cão de Weibull. Na modelagem foi considerada, ainda, a presen¸ca de censuras e a inclusão de um termo de fragilidade para explicar a rela¸cão existente entre os tempos de recorrências de uma unidade. A metodologia é desenvolvida para o caso em que várias unidades são acometidas por eventos recorrentes. Nas simula¸cões realizadas foram analisadas as probabilidades de co-bertura emp´ıricas do intervalo de confian¸ca normal assintótico e também o comportamento das variâncias dos estimadores. A presen¸ca de censuras na amostra inflacionou as variâncias dos estimadores de máxima verossimilhan¸ca além de produzir estimativas viciadas para um dos parâmetros da regressão, sendo que o v´ıcio do estimador foi corrigido por meio de um processo ”bootstrap”. Na modelagem sem termo de fragilidade, os resultados das análises das probabilidades de cobertura emp´ırica dos intervalos de confian¸ca assintóticos mostraram uma boa aproxima¸cão com os valores esperados, mas com certos cuidados a serem toma-dos, especialmente nos procedimentos baseados na simetria das distribui¸cões emp´ıricas. A inclusão de um termo de fragilidade na modelagem, por sua vez, causou uma perturba¸cão na estima¸cão máxima verossimilhan¸ca com um aumento nas variâncias dos estimadores di-retamente associados à variabilidade do termo de fragilidade. Além disso, as coberturas emp´ıricas dos intervalos de confian¸ca assintóticos foram, na grande maioria superestimadas, com resultados satisfatórios apenas para o parâmetro de forma da distribui¸cão Weibull.

(10)

ABSTRACT

Regression model for a Weibull renewall process distribution with a frailty effect

Renewal Processes are a special case of point processes involving recurrent events in which a unit, after a failure, is restored to the like new condition. Due to that property the times between occurrences for a renewal process are independent and its in-tensity function is given by the hazard function. Random factors not observed, that affects the recurrence times of the units, can be explained by a frailty term added in the model. In this work a regression model is presented for a renewal process with Weibull distribution for the times between occurrences. The modeling considers censored times and a frailty variable to explain the relationship among the recurrence times of a unit. The methodo-logy was developed for the situation where several units are submitted by recurrent events. The empirical probabilities of coverage of the asymptotic normal confidence interval and the behavior of the variances of the estimators were analyzed in the simulations performed. The presence of censures in the sample inflated the variances of the maximum likelihood estimators besides to produce biased estimates for the regression parameters. The bias of the estimator was corrected by ”bootstrap” procedure. The analysis of the probability of empirical coverage of the asymptotic confidence intervals, without frailty, presented a good approximation to the nominal values, but some observations about procedures have to be made on the symmetry of the empirical distributions. The frailty term incorporated at the modeling disturbed the maximum likelihood estimation increasing estimators’ variability, directly associated to the variance of the fragility term. In the most of the cases, the empi-rical coverages of the asymptotic confidence intervals were overestimated, with satisfactory results just for the shape parameter of the Weibull distribution.

(11)

LISTA DE FIGURAS

Figura 1 - Representa¸c˜ao gr´afica para dados terminais e recorrentes, respectivamente 22

Figura 2 - Representa¸cão gráfica de censuras à direita, de tipo I e tipo II . . . 27

Figura 3 - A esquerda, fun¸c˜oes de densidade Weibull para δ = 0,8; 1,0 e 2,0 e a direita, respectivas fun¸c˜oes de risco . . . 30

Figura 4 - Tipos diferentes de fun¸c˜oes de risco . . . 32

Figura 5 - Representa¸c˜ao gr´afica de um processo de contagem . . . 44

Figura 6 - Representa¸c˜ao gr´afica individual, de falha (x) e censura (o), na forma de processo de contagem . . . 49

Figura 7 - Processo de renova¸c˜ao com tempo limite . . . 60

Figura 8 - Processo de renova¸c˜ao com tempo limitetL (as linhas horizontais indicam

as unidades e as marcas sobre as linhas, as recorrˆencias do evento) . . . . 62

Figura 9 - Decaimento das variˆancias de ˆδ, ˆβ0 e ˆβ1, com n fixo, para δ= 0,8 . . . 98

Figura 12 - Decaimento das variˆancias de ˆδ, ˆβ0 e ˆβ1, com m fixo, para δ= 0,8 . . . . 101

Figura 15 - Decaimento das variˆancias de ˆδ, ˆβ0 e ˆβ1, comδ = 2,0, para o caso limitado

pelo tempo . . . 106

Figura 16 - Decaimento das variˆancias de ˆδ, ˆβ0 e ˆβ1, com n fixo, para δ = 2,0 e

propor¸c˜ao de censuras p= 0.30 . . . 118

Figura 20 - Decaimento das variˆancias de ˆδ, ˆβ0 e ˆβ1, com m fixo, para δ = 2,0 e

(12)

Figura 24 - Decaimento das variˆancias de ˆα, para α= 0,2 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com n fixo . . . 155

Figura 25 - Decaimento das variˆancias de ˆδ, para α= 0,2 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com n fixo . . . 156

Figura 26 - Decaimento das variˆancias de ˆβ0, para α = 0,2 e δ = 0,8, 1,0 e 2,0,

respectivamente, com n fixo . . . 157

Figura 28 - Decaimento das variˆancias de ˆα, para α= 0,2 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com m fixo . . . 159

Figura 29 - Decaimento das variˆancias de ˆδ, para α= 0,2 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com m fixo . . . 160

respectivamente, com m fixo . . . 161

Figura 32 - Decaimento das variˆancias de ˆα, para α= 0,5 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com n fixo . . . 163

Figura 33 - Decaimento das variˆancias de ˆδ, para α= 0,5 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com n fixo . . . 164

(13)

Figura 36 - Decaimento das variˆancias de ˆα, para α= 0,5 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com m fixo . . . 167

Figura 37 - Decaimento das variˆancias de ˆδ, para α= 0,5 e δ = 0,8, 1,0 e 2,0, respec-tivamente, com m fixo . . . 168

(14)

LISTA DE TABELAS

Tabela 1 - Resultados das simula¸c˜oes para ˆδ, geradas com δ = 0,8 . . . 88

Tabela 4 - Resultados das simula¸c˜oes para ˆβ0, geradas com δ= 0,8 . . . 90

Tabela 10 -Coeficientes angulares de log[ ˆvar(.)] x log(m) para n fixo . . . 96

Tabela 11 -Coeficientes angulares de log[ ˆvar(.)] x log(n), para m fixo . . . 97

Tabela 12 -Resultados das simula¸c˜oes com δ = 2,0, para para o caso limitado pelo tempo . . . 104

Tabela 13 -Coeficiente angular de log[ ˆvar(.)] x log(m), para o caso limitado pelo tempo105 Tabela 14 -Resultados das simula¸c˜oes para ˆδ, com δ = 2,0 e propor¸c˜ao de censuras p= 0,30 . . . 108

Tabela 15 -Resultados das simula¸c˜oes para ˆδ, com δ = 2,0 e propor¸c˜ao de censuras p= 0,20 . . . 109

Tabela 18 -Resultados das simula¸c˜oes para ˆβ1, com δ = 2,0 e propor¸c˜ao de censuras p= 0,30 . . . 111

Tabela 19 -Resultados das simula¸c˜oes para ˆβ1, com δ = 2,0 e propor¸c˜ao de censuras p= 0,20 . . . 112

(15)

Tabela 21 -Resultados das simula¸c˜oes para ˆβ1, com δ = 2,0 e propor¸c˜ao de censuras

p= 0,01 . . . 113

Tabela 22 -Raz˜ao entre as variˆancias das esimativas com e sem censuras . . . 114

Tabela 23 -Coeficientes angulares de log[ ˆvar(.)] x log(m) para n fixo, na presen¸ca de censuras . . . 116

Tabela 24 -Coeficientes angulares de log[ ˆvar(.)] x log(n) para m fixo, na presen¸ca de censuras . . . 117

Tabela 25 -V´ıcio do estimador de m´axima verossimilhan¸ca deβ0, para dados censurados126

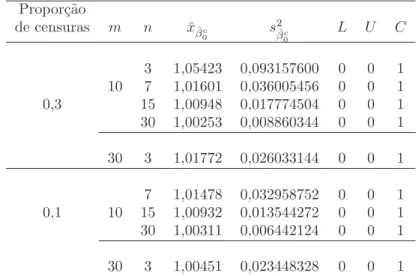
Tabela 26 -Probabilidade de cobertura do estimador corrigido ˆβc

0, para m fixo e δ =

2,0, com dados censurados . . . 128

Tabela 27 -Raz˜ao entre as variˆancias de ˆβc

0 e variˆancia das estimativas sem censuras . 128

Tabela 28 -Médias das razões das variâncias do modelo com fragilidade e do modelo sem fragilidade e sem censuras, em rela¸cão aos parâmetros α e δ . . . 132

Tabela 29 -Resultados das simula¸c˜oes para ˆα, comδ = 0,8 e parˆametro de fragilidade

α = 0,2 . . . 134

α = 0,2 . . . 135

Tabela 32 -Resultados das simula¸c˜oes para ˆδ, comδ = 0,8 e parˆametro de fragilidade

α = 0,2 . . . 135

α = 0,2 . . . 136

Tabela 35 -Resultados das simula¸c˜oes para ˆβ0, comδ= 0,8 e parˆametro de fragilidade

α = 0,2 . . . 137

(16)

α = 0,2 . . . 138

α = 0,2 . . . 139

α = 0,5 . . . 140

α = 0,5 . . . 141

α = 0,5 . . . 142

α = 0,5 . . . 143

α = 0,5 . . . 144

(17)

α = 0,5 . . . 145

Tabela 53 -Coeficientes angulares de log[ ˆvar(.)] x log(m) para o parˆametro da distri-bui¸c˜ao da fragilidade igual a 0,2 e 0,5 . . . 151

Tabela 54 -Coeficientes angulares de log[ ˆvar(.)] x log(n) para o parˆametro da distri-bui¸c˜ao da fragilidade igual a 0,2 e 0,5 . . . 152

Tabela 55 -Raz˜ao entre as variˆancias do modelo com fragilidade e do modelo sem fragilidade e sem censuras . . . 153

Tabela 56 -Médias das razões entre as variâncias do modelo com fragilidade e do modelo sem fragilidade e sem censuras, em rela¸cão ao número de unidades

m . . . 154

(18)

1 INTRODUC¸ ˜AO

Processsos de renova¸cão (RP) são um caso especial de processos pontuais, nos quais um item ou unidade, após a ocorrência de uma falha, é recolocado na mesma condi¸cão de novo (ou tão bom quanto novo) por meio de uma a¸cão corretiva ou de manuten¸cão. Em fun¸cão disso, segue-se que os tempos entre as ocorrências são iid segundo uma intensidade

λ(.). A literatura para eventos recorrentes é bastante ampla e tem crescido muito nos últimos anos, acompanhando o desenvolvimento computacional. Ascher e Feingold (1984) e Rigdon e Basu (2000) apresentam detalhes da teoria. Klein e Moeschberger (1997) e Andersen et al. (1993) apresentam a teoria para eventos recorrentes sob o enfoque de processos de contagem. Dados de eventos recorrentes são estudados através de modelos de fragilidade, conforme pode-se observar em Klein e Moeschberger (1997) e Colosimo e Giolo (2006).

O modelo para dados de sobrevivência na forma de processos pontuais mais explorado é o modelo introduzido por Cox (1972b), também conhecido como processo de

renova¸c˜ao modulado, ou RPM, o qual engloba diferentes tipos de processos conforme a

defini¸cão dos parâmetros envolvidos. Gill (1984) apresenta o modelo de Cox (1972a) sob o enfoque da teoria de processos de contagem multivariados, extendendo a teoria assintótica por meio de martingales. Lawless e Thiagarajah (1996) apresentam um modelo misto que engloba tanto um termo detendência, como um termo derenova¸cão e Lindqvist et al. (2003) unificaram oito tipos de modelos similares ao de Lawless e Thiagarajah, considerando o processo transformado para as intensidades acumuladas. Em seu modelo, Lindqvist engloba os processos de Poisson, de renova¸cão e os modelos mistos, o qual chamou de processo de

renova¸c˜ao e tendˆencia TRP (trend renewal process), bem como esses mesmo modelos com

a incorpora¸cão de um termo de heterogeneidade, ou fragilidade. Mais recentemente, Guo et al. (2006) apresentaram um modelo misto, alternativo ao modelo de Lawless e Thiagarajah, no qual o termo referente à renova¸cão foi substitu´ıdo pelo número esperado de falhar do processo N(t), visando simplicar a aplica¸cão do modelo na prática.

(19)

apresenta um estudo comparativo de modelos de regressão em processos de Poisson e em Silva (2001), têm-se detalhes da teoria para modelos de regressão sob o enfoque de processos de contagem.

A estima¸cão dos parâmetros por meio do método de máxima verossimilhan¸ca, na maior parte das situa¸cões, considera a aproxima¸cão assintótica dos estimadores na cons-tru¸cão de intervalos de confian¸ca ou em teste de hipótese. A teoria estat´ıstica, no entanto, apresenta inúmeros exemplos de casos nos quais as propriedades assintóticas não funcionam conforme o esperado, especialmente quando se trabalha com dados censurados. Johnson et al. (1995) citam um exemplo no qual o estimador de máxima verossimilhan¸ca do parâmetro de forma do modelo de Weibull apresenta um v´ıcio quando se incorporam dados censurados. Em estudos com eventos recorrentes, como é o caso dos processos de renova¸cão, pode existir uma dependência nos dados referente a um fator aleatório, não mensurável e que pode levar a v´ıcios nas estimativas dos parâmetros do modelo. Além disso, a não inclusão de covariáveis importantes na modelagem pode causar um aumento significativo na heterogeneidade não observada, o que pode afetar as inferências sobre as covariáveis presentes no modelo (COLOSIMO E GIOLO, 2006). Os modelos de fragilidade têm sido desenvolvidos com o intuito de minizar os efeitos decorrentes dessas situa¸cões. Os modelos mais difundidos consideram um termo de fragilidades w agindo de forma multiplicativa na fun¸cão de risco

Este trabalho tem como objetivo o desenvolvimento de de um modelo de re-nova¸cão para eventos recorrentes para uma quantidade de unidades em teste, introduzindo na modelagem a presen¸ca de um termo de fragilidade explicando o relacionamento entre as recorrências de uma unidade ou um indiv´ıduo. Pretende-se, ainda, estudar o comportamento assintótico dos estimadores de máxima verossimilhan¸ca pela quantifica¸cão da probabilidade de cobertura dos intervalos asintóticos, em situa¸cões nas quais observam-se dados censu-rados; avaliar o decaimento das variâncias dos estimadores com o aumento do número de unidades e da quanridade de recorrências por unidade e estudar o efeito da fragilidade na va-riabilidade dos estimadoresnas e nas probabilidades de coberturas dos inervalos de confian¸ca asintóticos.

(20)

(21)

2 CONCEITOS INICIAIS

Análise de Sobrevivência é formada pelo conjunto de técnicas estat´ısticas

uti-lizadas para o estudo de dados de tempos de vida de um indiv´ıduo, item ou componente. Este tempo de vida é uma medida contada a partir de um tempo inicial, bem definido, até a ocorrência de um evento em particular, o qual se deseja estudar. O intervalo de tempo que vai do instante inicial até a ocorrência do evento de interesse poderá ser chamado de

tempo de sobrevivˆenvia ou de sobrevida, tempo de falha ou simplesmente tempo de vida.

A análise de tempos de vida tem sido aplicada preferencialmente na pesquisa médica, onde recebe o nome de análise de sobrevivência e na área industrial, onde compõe um conjunto de técnicas denominadas de análise de confiabilidade.

Em análise de sobrevivência, o tempo de origem corresponde ao instante de entrada de um indiv´ıduo em um estudo. Esse instante pode coincidir com o instante do diagnóstico de uma doen¸ca; in´ıcio de um tratamento; ocorrência de um evento adverso (por exemplo infarto); recorrência de uma doen¸ca; etc. O tempo final pode ser o tempo até a cura, também chamado de tempo de remissão; até a primeira manifesta¸cão da doen¸ca; tempo de recorrência ou, se tratando de doen¸ca terminal, tempo até a morte do paciente. Se o tempo final culminar com a morte do paciente, então, o dado resultante será de fato um tempo de sobrevivência. Dados não terminais são chamados de tempo até o evento

(COLLETT, 2003).

Em análise de confiabilidade, o equivalente ao tempo de sobrevivência é co-nhecido como tempo de falha, quando um componente ou sistema deixa de operar satifato-riamente.

2.1 Eventos terminais e recorrentes

(22)

terminal quando se tem interesse em observá-lo uma única vez, como é o caso da primeira gravidez ou cura de uma doen¸ca. Note que no segundo caso o tempo ser, ou não, terminal depende da defini¸cão do estudo que se está realizando.

Eventos não terminais, por sua vez, ocorrem quando a observa¸cão não se encerra com a ocorrência do evento de interesse, podendo o mesmo acontecer por diversas vezes durante o per´ıodo de observa¸cão e são conhecidos por eventos recorrentes. Eventos recorrentes são muito comuns em confiabilidade quando se observa a ocorrência de falhas de um equipamento, ou máquina, durante um estudo ou durante a sua vida útil (RIGDON E BASU, 2000). Na pesquisa médica, podem-se encontrar dados de eventos recorrentes quando se estuda a reincidência de doen¸cas ou sintomas, como por exemplo em estudos sobre a AIDS. Em Barreto et al. (1994), é apresentado um estudo da recorrência de diarréia infantil com dados da Universidade Federal da Bahia.

Uma caracter´ıstica importante dos dados de eventos recorrentes é a de-pendência temporal, ou estocástica, permitindo a modelagem desses dados através de métodos de sobrevivência em processos de contagem (AALEN, 1978).

Na Figura 1, tem-se a representa¸cão gráfica para dados terminais e recorrentes. Para os dados terminais, o s´ımbolo “x” representa a ocorrência do evento, no caso a morte ou falha e indica o final da observa¸cão. Para os dados recorrentes, o s´ımbolo “x” representa as recorrências do evento e o s´ımbolo “o” indica que a observa¸cão já se encerrou, porém outras ocorrências do evento poderão ocorrer além daquele instante (que serão definidos

comotempos de censuras).

2.2 Popula¸cões homogêneas e heterogêneas

(23)

0 5 10 15

1

2

3

4

Tempo

Indivíduos

x x

0 5 10 15 20 25

1

2

3

4

Tempo

Indivíduos

x x x x

x x x

x x

Figura 1 - Representa¸c˜ao gr´afica para dados terminais e recorrentes, respectivamente

dispon´ıveis juntamente com o tempo até o evento. Essas variáveis ou, covariáveis, rece-berão o nome de variáveis explanatórias ou explicativas, pois descrevem as caracter´ısticas individuais de cada paciente. Quando os tempos de sobrevivência estão relacionados com as covariáveis, diz-se que a popula¸cão dos ind´ıviduos, ou unidades, é uma popula¸cão

hete-rogˆenea.

Normalmente, as covariáveis são medidas uma única vez ao longo do estudo sendo, portanto, consideradas fixas. Contudo, podem-se encontrar conjuntos de dados em que as covariáveis também variam com o tempo, uma vez que seus valores se modificam durante o per´ıodo de observa¸cão.

(24)

experi-mentos com cobaias, criadas em laboratórios exclusivamente para ensaios cl´ınicos ou, então, na indústria, em que os componentes em teste podem ser considerados todos “iguais”.

2.3 Observa¸c˜oes dos dados

Na literatura de análise de sobrevivência são apresentados basicamente dois mecanismos para a observa¸cão de dados. No primeiro caso, tem-se uma popula¸cão infinita, com parâmetros desconhecidos, que devem ser estimados através de uma amostra. As caracter´ısticas associadas a cada indiv´ıduo são fixas, mas podem variar entre os mesmos, originando uma distribui¸cão populacional cujos parâmetros são aqueles que se quer conhecer (CARVALHO et al., 2005).

O segundo mecanismo pressupõe que as caracter´ısticas individuais obedecem a uma lei estocástica, comum a todos. Uma mesma caracter´ıstica poderá ser mensurada repetidas vezes para um mesmo indiv´ıduo, ou item, possuindo uma distribui¸cão desconhe-cida, que se deseja determinar. Portanto, essas caracter´ısticas não são fixas, podendo variar com o tempo.

Geralmente, tem-se apenas um conjunto de observa¸cões para cada indiv´ıduo, o que impede a descri¸cão da distribui¸cão individual, contudo, as inferências poderão ser obtidas considerando-se que os indiv´ıduos são homogêneos e independentes (CARVALHO et al., 2005).

Os dois mecanismos descritos permitem generaliza¸cões. Assim, a popula¸cão infinita, que serve de fonte para a amostra em estudo, pode ser formada de misturas de popula¸cões com diferentes distribui¸cões. De forma análoga, as leis estocásticas que regem a distribui¸cão das medidas realizadas em um único indiv´ıduo não precisam ser necessariamente iguais, implicando numa amostra com indiv´ıduos heterogêneos entre si. Essas idéias darão origem aos modelos conhecidos como de efeitos aleatórios ou de fragilidade (CARVALHO et al., 2005).

2.4 Censura

(25)

maneira geral, ocorre quando o tempo até o evento para alguns indiv´ıduos, não é observado (LAWLESS, 1982). A censura ocorre porque, de alguma maneira, o indiv´ıduo deixa de ser acompanhado ou porque ele morre de uma causa não relacionada com o estudo ou tratamento.

Outra forma de censura ocorre quando o estudo, ou experimento, deve ser encerrado e ainda existem itens funcionando, ou indiv´ıduos vivos, cujos tempos de sobre-vivˆencia, obviamente, ainda n˜ao foram observados.

A falta de informa¸cão, ou censura, ocorre normalmente com rela¸cão ao tempo final do acompanhamento de um indiv´ıduo, ou grupo de indiv´ıduos. Nessa situa¸cão, nem todos os indiv´ıduos têm seus tempos de sobrevivência observados. A perda de informa¸cão também pode se dar no ´ıncio do estudo, quando não se conhece o tempo inicial de alguns dos indiv´ıduos. As causas de perda de informa¸cão são várias, sendo algumas delas:

i) ´obitos por causa n˜ao relacionada ao estudo;

ii) t´ermino do estudo;

iii) perda de contato com o paciente;

iv) recusa em continuar participando do estudo e conseq¨uente abandono por parte do paciente;

v) abandono do estudo devido a efeitos colaterais do tratamento.

Em confiabilidade, dentre as causas mais comuns, destaca-se a falha por um motivo não relacionado com o experimento; mudan¸cas nos procedimentos por descuido ou acidente e, principalmente, devido ao encerramento do experimento, já que neste caso, o monitoramento é constante.

(26)

2.4.1 Tipos de censuras

A censura, conforme já foi visto, ocorre de diversas maneiras influenciando a constru¸cão da fun¸cão de verossimilhan¸ca. Nesta se¸cão, serão apresentadas as principais formas de censura encontradas nos estudos de tempos de vida. Para se estudarem os tipos de censuras, no entanto, é necessário que se considere a forma como os dados são coletados e especialmente como o estudo (ou experimento) deverá ser encerrado. A seguir, serão apresentados os três tipos mais comuns de censuras.

i) Censura de tipo I: é mais comum em estudos médicos, em que os indiv´ıduos são

incorporados ao estudo no decorrer do per´ıodo de observa¸cão, conforme vão sendo recrutados. Também pode aparecer na área industrial quando a confiabilidade das unidades em teste é muito elevada, o que faz com que o tempo de observa¸cão seja muito longo. Na censura de tipo I o estudo, ou experimento, é conduzido até um tempo limite L, pré-fixado, quando o número de ocorrênciasr do evento é registrado. Como, na maioria dos estudos médicos, nem todos os pacientes entram em estudo ao mesmo tempo, cada indiv´ıduo tem o seu tempo de censuraLi,i= 1,2, ..., n(LAWLESS, 1982).

Dessa forma, os indiv´ıduos, cujas mortes forem observadas, terão seus tempos de vida registrados e, aqueles que ainda permacerem vivos, terão seus tempos censurados. Uma caracter´ıstica importante da censura de tipo I é que o número de falhas, ou mortes, é aleatório.

ii) Censura de tipo II: ´e mais comum em confiabilidade, principalmente quando o custo

do experimento é muito elevado. Nesse esquema de censura, fixa-se o número r de falhas e o experimento é conduzido com n unidades em teste,n > r, até que r dessas unidades tenham falhado. As n₋r unidades que ainda continuam em funcionamento após a ocorrência das r falhas, terão seus tempos de vida censurados em tr, em que

tr ´e o tempo de falha do r-´esimo item. Note que em censura de tipo II os tempos de

falhas s˜ao naturalmente ordenados, ou seja, T1 =T(1), T2 =T(2), ..., Tr =T(r).

iii) Censura aleatória: em alguns tipos de estudos na área médica, os pacientes podem ser

(27)

termina numa data pré-estabelecida, então, os tempos de censuras daqueles pacientes que ainda permacem vivos, ou sem terem experimentado o evento de interesse, serão aleatórios. Freqüentemente, nestes casos, consideram-se censuras de tipo I, assumindo dados condicionados nos tempos de censuras (LAWLESS, 1982).

Além dessa classifica¸cão, podem-se diferenciar as censuras conforme o instante de ocorrência. Normalmente, a censura ocorre no final do experimento, ou seja, numa posi¸cãoà direita na escala do tempo. No entanto, pode acontecer de a censura ser observada antes do in´ıcio do estudo propriamente dito, ou à esquerda e até mesmo dentro de um

intervalo de tempo.

a) Censura `a direita: ocorre quando o tempo de censura ´e menor do que o tempo real de

sobrevivência, não observado. Setcé o tempo de censura eT o tempo de sobrevivência,

ent˜ao, na censura `a direita T > tc. Por exemplo, um indiv´ıduo em tratamento

de-vido a uma doen¸ca terminal, deixa de ser acompanhado, porém sua última condi¸cão registrada o considera como “vivo”.

b) Censura à esquerda: ocorre quando não se conhece o momento exato da ocorrência de

um evento, mas sabe-se que este aconteceu antes de um tempo determinado, ou seja,

T < tc. Em estudos sobre o tempo do primeiro contato com as drogas, muitas vezes

os jovens não têm a resposta exata, mas sabe-se que é anterior a uma determinada data.

c) Censura por intervalo, ou intervalar: ao se realizar um estudo, muitas vezes o

acom-panhamento dos indiv´ıduos somente pode ser realizado em visitas ou entrevistas a intervalos de tempos regulares (semanais, quinzenais, mensais, etc...), quando se veri-fica a ocorrˆencia, ou n˜ao, do evento de interesse. Durante um visita, ao se constatar que o evento ocorreu, pode-se afirmar apenas que o mesmo aconteceu durante o inter-valo de tempo transcorrido entre a visita anterior, tk−1 e a visita atual,tk,k = 1,2, ....

O tempo de sobrevivˆencia, portanto, dever´a pertencer ao intervalo (tk−1;tk), ou seja,

(tk−1 < T < tk).

(28)

comum. No esquema de tipo II, a censura à direita é predominante. Na próxima sessão será apresentada a constru¸cão da fun¸cão de verossimilhan¸ca considerando censuras de tipo I, à direita. A constru¸cão da verossimilhan¸ca para casos de censuras à esquerda pode ser encontrada em Lawless (1982) e uma expressão geral para diversos tipos de censuras é apre-sentada por Klein e Moeschberger (1997). Na Figura 2, são apreapre-sentadas as representa¸cões gráficas dos esquemas de tipo I e tipo II, com censuras à direita.

Censura Tipo I

Tempo

Indivíduos

0 4 8 L

x

x x

x

Censura Tipo II

Tempo

Indivíduos

0 6 12 18 24

x x

x x x t₍1)

t₍2)

t(3)

t₍r−1)

t₍r)

Figura 2 - Representa¸cão gráfica de censuras à direita, de tipo I e tipo II

2.5 Modelos de sobrevivˆencia cont´ınuos

O tempo de sobrevivênciat de um indiv´ıduo pode ser considerado como uma observa¸cão de uma variável aleatóriaT, não negativa e comfdp f(t), representando os tem-pos de vida de uma popula¸cão. Esses dados de sobrevivência podem ser resumidos através de duas fun¸cões de central interesse em análise de sobrevivência: afun¸cão de sobrevivência

e a fun¸c˜ao de risco, ou “hazard” (COLLETT, 2003).

(29)

Considere uma variável aleatória T, não negativa, representando os tempos de vida dos indiv´ıduos de uma popula¸cão. Normalmente, T é assumida como sendo uma variável cont´ınua. Afun¸cão de distribui¸cão deT é definida como (BERGER E CASELLA, 2002)

F(t) =P (T _≤t),

e a fun¸c˜ao densidade de probabilidade (fdp) de T ´e dada por

f(t) = ∂

∂tF(T).

A fdp pode ainda ser representada em termos da probabilidade de ocorrˆencia de um evento num intervalo infinitesimal de tamanhodt. Em Lee (1980), tem-se que

f(t) = lim

dt→0

P(T _≤t+dt)₋P (T _≤t)

dt . (1)

Note que a defini¸cão (1) é, de fato, a defini¸cão da derivada de F(t).

A fun¸cão de sobrevivência, S(t), é definida como a probabilidade de que o tempo de vida T seja maior do que, ou igual, a um determinado valor t,

S(t) = P(T _≥t) =

Z ∞

t

f(u)du

ou ainda,

S(t) = 1₋F(t).

A fun¸cão de sobrevivência é uma medida da probabilidade de que um indiv´ıduo sobreviva, do instante inicial, a além do instantet (COLLETT, 2003).

A fun¸cão de risco é definida como sendo a probabilidade de ocorrência do evento de interersse num intervalo [t, t+dt), condicionada à sobrevivência no instante t, dividida pelo tamanho do intervalo, ou seja,

h(t) = lim

dt→0

P (t_≤T _≤t+dt_|T _≥t)

dt . (2)

A fun¸c˜ao de risco especifica a taxa instantˆanea de morte, ou falha, no instante

(30)

(COLLETT, 2003). Além disso, é importante observar que, apesar de se utilizar o termo risco, h(t) é uma taxa, e não uma probabilidade. Sua unidade é tempo−1 _{e pode assumir}

qualquer valor real positivo, n˜ao estando restrita ao intervalo [0,1].

Da defini¸c˜ao de probabilidade condicional pode-se obter a seguinte rela¸c˜ao:

h(t) = lim

dt→0

P (t _≤T _≤t+dt)

dt P(T _≥t)

= 1

P(T _≥t) dtlim→0

P (t _≤T _≤t+dt)

dt =

f(t)

S(t). (3)

Como ∂S(t)/∂t=₋f(t), pode-se ainda escrever

h(t) =₋∂

∂tlog[S(t)].

Integrando-se ambos os lados em rela¸cão at, obtém-se a fun¸cão de risco

acu-mulado, definida como

H(t) =₋log[S(t)],

de onde se pode escrever

S(t) = exp_{−H(t)_}. (4)

Uma forma alternativa de (4), bastante comum, ´e dada por

S(t) = exp

½

−

Z t 0

h(u)du

¾

. (5)

Das equa¸cões (3) e (5), pode-se obter uma expressão bastante útil para repre-sentar a fun¸cão de densidade da variável aleatóriaT,

f(t) = h(t) exp

½

−

Z t 0

h(u)du

¾

. (6)

Como exemplo, considere uma variável aleatória T, representando o tempo de vida de indiv´ıduos sujeitos a um certo tipo de tratamento. Suponha que T tenha uma distribui¸cão de probabilidade de Weibull com fdp

f(t) = λ δ tδ−1 exp©

−λ tδª

(31)

Então, a fun¸cão de risco para o modelo Weibull é dada por

h(t) = λ δ tδ−1. (8)

A distribui¸cão de Weibull é, talvez, a mais utilizada para dados de tempos de vida (LAWLESS, 1982), pois os seus dois parâmetrosλeδlhe dão uma grande flexibilidade, uma vez que permitem modelar diferentes tipos de taxas de falhas. Na Figura 3 são apre-sentadas fun¸cões densidades Weibull, com suas respectivas fun¸cões de risco, para diferentes valores deδ.

0.0 0.5 1.0 1.5 2.0 2.5

0.0

0.5

1.0

1.5

tempo

f

(

t

)

δ = 2.0 δ = 1.0 δ = 0.8

0.0 0.5 1.0 1.5 2.0

0.0

0.5

1.0

1.5

2.0

tempo

h

(

t

)

δ = 2.0

δ = 1.0

δ = 0.8

Figura 3 - A esquerda, fun¸c˜oes de densidade Weibull para δ = 0,8; 1,0 e 2,0 e a direita,

respectivas fun¸c˜oes de risco

Como caso especial, quando δ = 1, tem-se a distribui¸cão exponencial que historicamente foi o primeiro modelo aplicado em estudos de tempos de vida (FOGO, 1994). A distribui¸cão exponencial é conhecida pela sua propriedade de falta de memória, que pode ser representada pela sua taxa de risco constante. De fato, para δ = 1, de (8) tem-se

h(t) =λ.

2.5.1 Algumas considera¸c˜oes sobre a fun¸c˜ao de risco

(32)

propor¸c˜ao esperada de indiv´ıduos, com idade t, que poder˜ao falhar num pequeno intervalo de tempo [t;t+dt).

A fun¸cão de risco h(t) é bastante útil para se determinar a distribui¸cão dos tempos de sobrevivênvia e para descrever a maneira com que a chance de ocorrência de uma falha, ou morte, muda com o tempo (KLEIN E MOSCHBERGER, 1997). Diferentes tipos de fun¸cões de risco são observadas dependendo do formato do gráfico deh(t). Por exemplo, a taxa de ocorrência de um evento pode ser crescente, decrescente, constante, em forma de banheira (“bathtub-shaped”), em forma de “corcova” (“humpshaped”) ou possuindo alguma caracter´ıstica que descreve o mecanismo de falhas. A Figura 4 apresenta diferentes tipos de fun¸cões de risco.

Modelos com fun¸c˜ao de risco crescente, apresentado pela fun¸c˜ao h2(t) na

Fi-gura 4, surgem naturalmente em consequência do envelhecimento ou desgate de material. É também uma forma bastante comum no final da vida das pessoas ou da vida útil de pe¸cas ou equipamentos. Pode ser observada em pacientes em fase terminal e que não respondem mais ao tratamento. Taxas de risco decrescentes, h3(t), são menos comuns, mas podem ser

encontradas quando há uma chance grande de falha nos per´ıodos iniciais de vida, como em certos tipos de dispositivos eletrônicos. Também podem ser observadas em pacientes que se recuperam de cirurgias simples ou em bebês nos primeiros anos de vida. A fun¸cão de risco em forma de banheira, h1(t), é historicamente utilizada em demografia para representar a

taxa de mortalidade de popula¸cões com uma taxa inicial elevada, que cai até um determi-nado patamar, onde permanece constante por um longo per´ıodo de tempo, vindo a crescer drasticamente no final da vida. Pode também representar a taxa de falhas de máquinas que passam por um per´ıodo inicial de ajuste, mas que permanecem com taxas constantes durante todo o per´ıodo de vida útil, vindo a crescer rapidamente no per´ıodo final do tempo de vida. A fun¸cão de risco h4(t), em forma de “corcova”, pode ser observada em pacientes

(33)

cu-mum. Esse mecanismo de falha ´e encontrado durante per´ıodos isolados do tempo de vida de indiv´ıduos ou equipamentos, tal como apresentado pela fun¸c˜aoh1(t). Por exemplo, pode

ser usada para representar o risco de morte em indiv´ıduos entre 18 e 25 anos, quando a principal causa de morte ´e por acidente.

0 1 2 3 4 5 6

0.0

0.5

1.0

1.5

2.0

tempo

h

(

t

)

h1(t) h2(t) h3(t) h4(t) h5(t)

Figura 4 - Tipos diferentes de fun¸c˜oes de risco

2.5.2 A fun¸c˜ao de verossimilhan¸ca

Suponha o conjunto_D com os dados den indiv´ıduos. Considere que o tempo de vida doi-ésimo indiv´ıduo seja representado pela varável aleatória Xi e que, associado ao

i-´esimo indiv´ıduo existe um tempo de censura fixoLi.

(34)

indiv´ıduo tem um tempo de censura Li, tal que o tempo de vida do i-´esimo indiv´ıduo ´e

observado apenas quandoXi ≤Li, i= 1,2, ..., n. Os dados de sobrevivˆenvia do indiv´ıduo i

ser˜ao representados por pares do tipo (Ti, ci),i= 1,2, . . . , n, sendo que

Ti =min(Xi, Li) e ci =







1, seXi ≤Li,

0, seXi > Li.

Os tempos de sobrevivˆenviaT1, T2, ..., Tn ser˜ao assumidos iid, comfdp f(t|θ),

em queθé o vetor de paramêtros. Se ci = 1, então, Ti representa o tempo de sobrevivência

do indiv´ıduo ie se ci = 0, Ti, representa o seu tempo de censura e, como

P (Ti, ci = 1) =P (Ti|ci = 1)P (ci = 1) =f(ti|θ)

e

P(Ti =Li, ci = 0) =P(ci = 0) =S(ti|θ),

ent˜ao, afdp conjunta deTi e ci ´e dada por

f(ti, ci|θ) = [f(ti|θ)]ci[S(ti|θ)]1−ci.

Dessa forma, a fun¸cão de verossimilhan¸ca para dados sujeitos a censuras do tipo I, à direita, é obtida de

L(θ_{| D}) =

n

Y

i=1

f(ti, ci|θ)

=

n

Y

i=1

[f(ti|θ)]ci[S(ti|θ)]1−ci.

Utilizando as rela¸cões (5) e (6), obtém-se uma representa¸cão da fun¸cão de verossimilhan¸ca expressa unicamente em termos da fun¸cão de risco, ou seja,

L(θ_{| D}) =

( _n

Y

i=1

[h(ti|θ)]ci

)

exp

½

−

Z ti 0

h(u_|θ)du

¾

. (9)

Para popula¸cões heterogêneas, o conjunto _D é formado por

(35)

sendo que ti é o valor observado do tempo de sobrevivência, ci é a fun¸cão indicadora de

censura e zi é o vetor de covariáveis observadas para o indiv´ıduo i. A fun¸cão de risco

é dependente do vetor de parâmetros θ, acrescido dos parâmetros referentes ao vetor de covariáveisz, e a fun¸cão de verossimilhan¸ca, dada em (9), passa a ser expressa por

L(θ_{| D}) =

( _n

Y

i=1

[h(ti|zi,θ)]ci

)

exp

½

−

Z ti 0

h(u_|zi,θ)du

¾

. (10)

2.6 Modelos discretos

Apesar de não ser o enfoque deste texto, a modelagem discreta para tempos de vida será rapidamente apresentada nesta se¸cão.

Algumas vezes a variávelT pode indicar o “tempo de vida” de uma máquina pelo número de ciclos ou pelo número de realiza¸cões de alguma tarefa, como exemplo, para máquinas fotocopiadoras considera-se o número de cópias realizadas. Nestas situa¸cões, é mais conveniente tratarT como uma variável aleatória discreta, assumindo valores 0_≤1<

2< . . . com probabilidade

p(ti) =P (T =ti), i= 1,2, . . . ,

e fun¸c˜ao de sobrevivˆencia

S(ti) = P(T > ti) =

X

i:ti>t

p(ti).

Da mesma forma como no caso cont´ınuo, para o caso discreto S(t) também é monótona, decrescente, cont´ınua à esquerda, comS(0) = 1 e S(_∞) = limt→∞S(t) = 1.

A fun¸c˜ao de risco ´e definida por

h(ti) = P (T =ti|T ≥ti) =

p(ti)

S(ti−1)

, i= 1,2, . . . . (11)

Como p(ti) =S(ti−1)−S(ti), ent˜ao, pode-se reescrever (11) como

h(ti) = 1−

S(ti)

S(ti−1)

, i= 1,2, . . . , (12)

e, como a fun¸c˜ao de sobrevivˆencia pode ser escrita como o produto de probabilidades con-dicionais, ou seja,

S(t) = Y

i:ti≤t

S(ti)

S(ti−1)

(36)

então, de (12) e (13) a fun¸cão de sobrevivência está relacionada com a fun¸cão de risco através da expressão

S(t) = Y

i:ti≤t

[1₋h(ti)].

A fun¸c˜ao de risco acumulado pode ser definida como

H(t) = X

i:ti≤t

h(ti),

porém, neste caso a rela¸cão H(t) =₋log [S(t)] não é valida.

Cox e Oakes (1984) sugerem definir a fun¸c˜ao de risco acumulado por

H(t) = X

i:ti≤t

[1₋h(ti)],

pois essa forma preserva a rela¸c˜aoS(t) = exp_{−H(t)_}. Para valores pequenos de h(ti), os

resultados das duas expressões são muito próximos.

SeT é uma variável aleatória positiva com fun¸cão de risco h(t) definida pela soma de uma fun¸cão cont´ınua hc(t) e uma fun¸cão discreta hd(t), com massa nos tempos

0_≤t1 ≤t2 ≤. . ., então a fun¸cão de sobrevivência está relacionada com a taxa de falhas pelo

produto integral1 _{de [1}₋_h₍_t_)]_dt_{, definido como se segue (KLEIN E MOESCHBERGER,}

1997):

S(t) = Y

i:ti≤t

[1₋hd(ti)] exp

½Z t

0

hc(u)du

¾

.

2.7 Modelos de regress˜ao

Os resultados apresentados na se¸cão anterior referem-se a modelos univariados, com uma única distribui¸cão de probabilidade para os tempos de vida. Na prática, no entanto, muitas aplica¸cões envolvem a presen¸ca de um vetor z de variáveis concomitantes, ou covariáveis. Uma questão de especial relevância consiste em investigar a influência destas covariáveis nos tempos de vida dos componentes, ou pacientes, o que usualmente é feito por meio de modelos de regressão.

1

(37)

Em estudos com pacientes com câncer de pulmão, por exemplo, normalmente deseja-se medir a influência no tempo de vida dos pacientes de variáveis tais como sexo, estágio da doen¸ca ao ser diagnosticada, número de cigarros fumados por dia, outros casos na fam´ılia, etc. Em estudos na área industrial, pode-se querer medir a influência da varia¸cão de voltagem, temperatura e umidade do ambiente, material utilizado, procedência da matéria prima, dentre outras. Uma situa¸cão bastante comum na área industrial e que se utiliza de modelos de regressão ocorre no estudo de testes acelerados (NELSON, 1970).

A influência das covariáveis no tempo de vida de popula¸cões heterogêneas pode ser representada por meio da modelagem da fun¸cão de risco h(t). A literatura es-tat´ıstica apresenta uma ampla bilbiografia sobre os modelos de regressão. Em Collet (2003) e Carvalho et al. (2005), tem-se uma ênfase em modelos semiparamétricos, especialmente o modelo de riscos proporcionais de Cox. Modelos paramétricos são especialmente apresen-tados em Lawless (1982) e Klein e Moeschberger (1997). Os modelos de regressão podem, ainda, ser expressos através da teoria de processos de contagem, por meio do modelo de Aalen (1978), conforme apresentado em Gill (1984).

Considere um conjunto de dados de tempos de vida _D com n unidades in-dependentes e p covariáveis. Se T é uma variável aleatória que representa o tempo de ocorrência de um evento, o modelo de regressão estabelece que a fun¸cão de risco de um componente, ou indiv´ıduo, no tempot, dado o vetor de covariáveiszé

h(ti|zi) =h0(ti)g(zi|β), (14)

sendo que zi é o vetor de covariáveis do componentei, β é o vetor de parâmetros a serem

estimados eg(_·) uma fun¸cão positiva das covariáveis. A fun¸cãoh0(t) é conhecida porfun¸cão

de risco de base, sendo a fun¸c˜ao de risco de um componente para o qual g(z) = 1. A

fun¸c˜aog(zi) pode ser interpretada como um risco relativo de um componente com vetor de

covari´aveiszi, em rela¸c˜ao a um componente para o qual z=0 (COLLETT, 2003).

A fun¸cãoh0(t), assim como a fun¸cãog(z) pode envolver parâmetros

desconhe-cidos. Quando h0(t) é indexada por um, ou mais parâmetros, os modelos são considerados

paramétricos. Além disso, na regressão paramétrica, é necessário que uma distribui¸cão de

(38)

Uma propriedade importante do modelo (14) é que a razão entre os riscos de dois componentes não depende do tempo, ou seja, os riscos sãoproporcionais. Por exemplo, a razão de riscos de dois componentes com covariáveiszi e zj é dada por

h(ti|zi)

h(tj|zj)

= g(zi|β)

g(zj|β)

.

Devido a essa propriedade, o modelo (14) ´e conhecido como modelo de riscos

proporcionais.

Para a especifica¸cão do modelo (14), a fun¸cão g(z) deve ser não negativa e, assim, uma escolha apropriada consiste em fazer g(z) = exp_{β′z_}. Dessa forma, a fun¸cão de risco para o componentei, pode ser reescrita por

h(t_i|zi) =h0(ti) exp{β′zi}. (15)

Das rela¸c˜oes (5) e (14) tem-se que

S(t_|z) = exp

½

−

Z t 0

h0(u)g(z|β)du ¾

,

em que se segue que a fun¸cão de sobrevivência de T, dadas as covariáveis z é

S(t_|z) = [S0(t)]g(

z_|β)

, (16)

sendo que S0(t|z) = exp n

−Rt

0 h0(u)du

o

é a fun¸cão de sobrevivência de base de um com-ponente para o qualg(z_|β) = 1.

De (16), verifica-se uma ordena¸c˜ao na fam´ılia de riscos proporcionais, pois para dois componentes (ou indiv´ıduos) com vetores de covari´aveisz1 ez2, tem-se que, para

todot >0, S(t_|z1)≥S(t|z2), ou vice-versa (LAWLESS, 1982).

Nos modelos de riscos proporcionais, as variáveis concomitantes têm um efeito multiplicativo sobre a fun¸cão de risco, o que, na maioria das vezes parece bastante razoável. Em algumas situa¸cões, entretanto, o efeito das covariáveis é expresso aditivamente na fun¸cão de risco, como por exemplo

h(ti|zi) = h0(ti) +g(zi|β), (17)

(39)

Os modelos aditivos não são muito comuns, pois a estima¸cão dos parâmetros do modelo é, de certa forma, complicada. Geralmente, a estima¸cão é feita através de métodos não paramétricos, baseados em processos de contagem (TOMAZELLA, 2003). O modelo aditivo mais conhecido é o modelo de Aalen (1980). Uma versão paramétrica dos modelos de regressão aditivos foi apresentada por Andersen et al. (1993).

2.7.1 Modelos de regress˜ao param´etricos

Os modelos de regressão paramétricos ocorrem quando os tempos de sobre-vivência são assumidos como tendo uma distribui¸cão de probabilidade, indexada por um, ou mais, parâmetros. Como resultado direto dessa suposi¸cão, as estat´ısticas e inferências para o modelo considerado serão mais precisas.

Dentre os modelos paramétricos mais explorados na literatura podem-se des-tacar os modelos exponencial, de Weibull, gama e lognormal. A seguir, serão descritos os modelos exponencial e de Weibull, que pertencem à classe dos modelos de riscos proporcio-nais.

2.7.1.1 Modelo exponencial

SejaT uma variável aleatória representando o tempo de vida de componentes, ou indiv´ıduos, num estudo de sobrevivência e seja z um vetor de covariáveis associadas a esses componentes. O modelo exponencial deverá ser utilizado quando se assume que o risco é constante ao longo do tempo. No modelo exponencial, a fdp deT é da forma

f(t_|λ) = λ(z)e−λt, t_≥0 e λ >0.

O parâmetroλdepende das covariáveis através da rela¸cãoλ =g(z_|β) e como o risco no modelo exponencial é constante e igual aλ, entãoh(t_|z) =g(z_|β). Considerando a rela¸cão em (15), o modelo de regressão exponencial é definido por

h(t_|z) = exp_{β′z_}= exp_{β0+β1z1+. . .+βpzp}, (18)

sendo que β′ = (β0, β1, . . . , βp) é o vetor de parâmetros do modelo de regressão e o vetor

de covari´aveis ´e do tipo z′ _{= (1}_{, z}

1, . . . , zp). Inferências para os parâmetros do modelo são

(40)

Apesar de sua simplicidade, o modelo exponencial tem sido largamente utili-zado, especialmente na ´area industrial.

2.7.1.2 Modelo de Weibull

O modelo de Weibull é o modelo de regressão mais utilizado pela sua versa-tilidade em acomodar diversas situa¸cões práticas. A distribui¸cão de Weibull, dada em (7), apresenta um parâmetro de escala λ e um parâmetro de forma δ, sendo que o modelo de regressão mais comum considera apenas o parâmetro λ dependente das covariáveis. Desta forma, a fun¸cão de risco para o modelo de Weibull é definida por

h(t_|z) =λ δ tδ−1 =δ tδ−1g(z_|β), (19)

em que λ=g(z_|β) e h0(t) = δtδ−1.

Considerando g(z_|β) = exp_{β′z_}, a fun¸c˜ao de risco pode ser escrita por

h(t_|z) =δ tδ−1 exp_{β′z_}. (20)

e, considerando os vetores β e zcomo em (18), tem-se

h(t_|z) =δ tδ−1 exp_{β0+β1z1+. . .+βpzp}.

Pelo resultado (20), a razão dos riscos de dois componentes com vetores de covariáveisz1 e z2 é

h(t1|z1)

h(t2|z2)

= exp{β

′_z

1}

exp_{β′z2}

= exp_{β′(z1−z2)},

que n˜ao depende de t, o que caracteriza o modelo de Weibull como um modelo de riscos proporcionais.

Observe que as covariáveis têm um efeito multiplicativo no risco em (20), o que é uma caracter´ıstica dos modelos de riscos proporcionais. Contudo, quando se considera o logaritmo dos tempos de vida, ou seja, tomando Y = log(T), a distribui¸cão de Y dado z

´e da forma

f(y_|z) = 1

σ exp

½

y₋µ(z)

σ −exp

·

y₋µ(z)

σ

¸¾

, _−∞< y < _∞, (21)

(41)

Com a fun¸c˜ao assumida para g(z) em (15),µ(z) = ₋σβ′z. Assim, de (21), Y

pode ser representado na forma de um modelo log linear com

Y =µ(z) +σW =z′β∗+σW, (22)

sendo que β∗ = ₋σβ e W é uma variável de erro com distribui¸cão valor extremo padrão (JOHNSON et al., 1995).

O modelo (22) ´e um modelo do tipoloca¸c˜ao-escala com erroW, muito comum quando se utiliza o logaritmo do tempo de vida.

Estimativas e inferências para o modelo de Weibull, bem como para o modelo loca¸cão-escala (22), podem ser obtidas por meio da fun¸cão de verossimilhan¸ca (10). Outros modelos de regressão paramétricos podem ser encontrados em Lawless (1982) e Klein e Moeschberger (1997), que apresentam os métodos de estima¸cão para dados completos e censurados.

2.7.2 Modelos de regress˜ao semiparam´etricos

Na se¸cão anterior foram apresentados alguns modelos de regressão pa-ramétricos para dados de sobrevivência. Os modelos papa-ramétricos supõem uma fun¸cão de distribui¸cão de probabilidades para o tempo de vidaT, porém, algumas vezes, essa su-posi¸cão pode não ser adequada. Além disso, em muitas aplica¸cões práticas, pode-se ter o interesse de estimar os efeitos das covariáveis sobre o tempo de vida das unidades em teste ou sobre o tempo de vida de pacientes em estudo.

Sob esse enfoque, Cox (1972a) propˆos o modelo semiparam´etrico de riscos

proporcionais, que passou a ser conhecido como modelo de riscos proporcionais de Cox

ou, simplesmente, modelo de Cox. O modelo de Cox, devido a sua praticidade, alcan¸cou rapidamente um enorme sucesso entre os estat´ısticos, sendo o modelo mais utilizado na análise de dados de sobrevida na área médica.

2.7.2.1 Modelo de regress˜ao de Cox

(42)

princ´ıpio da proporcionalidade, podem-se estimar esses efeitos sem que seja necess´ario fazer qualquer suposi¸c˜ao a respeito dos tempos de vida. Foi pensando nisso que Cox (1972a) criou o modelo de riscos proporcionais.

Sejah0(t) uma fun¸c˜ao de risco de base arbrit´aria eβ′ = (β0, . . . , βp) um vetor

de parˆametros. O modelo proposto por Cox ´e da forma

h(ti|zi) =h0(ti) exp{β′zi}, (23)

que tem a mesma forma do modelo apresentado em (15), porém, o modelo de Cox é dito semiparamétrico pois não assume nenhuma distribui¸cão estat´ıstica parah0(t).

De fato, os modelos semiparamétricos são assim chamados pois assumem uma forma paramétrica apenas para os efeitos das covariáveis, representados pela fun¸cãog(z_|β). A fun¸cão de risco de base, neste caso, é tratada de uma forma não paramétrica.

O modelo de Cox comporta muito bem dados com censuras além de incor-porar naturalmente covariáveis com dependência no tempo. Adapta-se muito bem ao tipo de dado obtido em ensaios de tempos de vida, pois combina elegantemente as abordagens paramétricas e não paramétricas da inferência estat´ıstica (GILL, 1984). Por tudo isso, o modelo de riscos proporcionais proposto por Cox (1972a) se tornou muito popular, sendo exaustivamente explorado em aplica¸cões de dados de tempos de vida. Por ter sido muito estudado, um grande número de contribui¸cões têm sido verificadas desde a sua publica¸cão (LAWLESS, 1982). Hoje em dia, pode-se encontrar uma completa e ampla literatura so-bre o modelo de Cox, com destaques para Cox e Oakes (1984); Lawless (1982); Klein e Moeschberger (1997); Collett (2003), dentre outros.

Para a estimativa do vetor β, Cox introduziu o conceito da verossimilhan¸ca

parcial. Na verossimilhan¸ca parcial, considera-se apenas a informa¸c˜ao das unidades sob risco

no tempo t por meio do vetor de covariáveis z, pois a fun¸cão de risco de base é eliminada devido à propriedade de proporcionalidade. Essa formula¸cão é semelhante aos modelos não paramétricos, mas, neste caso, permite que os efeitos sejam estimados através da fun¸cão de verossimilhan¸ca.

(43)

em que r é o número de falhas observadas. A verossimilhan¸ca parcial, baseada no modelo de riscos proporcionais (23), é expressa por

L(β_|D) =

r

Y

i=1

exp©

β′z(i) ª

P

j∈R(t(i))exp{β

′_z

j}, (24)

sendo que R(t(i)) ´e o conjunto de unidades em risco no instante t(i), ou seja, ´e o conjunto

de unidades em opera¸c˜ao e n˜ao censuradas no instante imediatamente anterior at(i).

Considerando os dados na forma (Ti, ci,zi), a verossimilhan¸ca parcial dada em

(24) pode ser escrita na forma

L(β_|D) =

n

Y

i=1 "

exp_{β′zi}

P

j∈R(ti)exp{β

′_z

j}

#ci

, (25)

em que R(ti) ´e o conjunto em risco no instante ti.

As estimativas de máxima verossimilhan¸ca dos parâmetros β’s são obtidas maximizando-se o logaritmo de (25) por meio de métodos numéricos. Essa maximiza¸cão, geralmente, é alcan¸cada utilizando-se o método de Newton-Raphson.

Muitos autores buscaram demonstrar as propriedades assintóticas dos estima-dores do modelo, confirmando as conjecturas de Cox, mas em todos os casos os resultados foram restritos a situa¸cões especiais. Uma nova abordagem, no entanto, foi introduzida por Aalen (1978), apresentando o modelo Cox sob o enfoque de processos de contagem, em que a fun¸cão de risco pode ser descrita em termos da intensidade de um processo de contagem multivariado e que permitiu demonstrar as propriedades assintóticas do modelo de forma natural (GILL, 1984).

As aplica¸cões do modelo de Cox têm considerado, exclusivamente, a suposi¸cão de riscos proporcionais, em que as covariáveis têm um efeito multiplicativo sobre o tempo de vida dos indiv´ıduos ou unidades. Isso tem atendido satisfatoriamente a maioria dos casos abordados, porém, podem ocorrer situa¸cões nas quais a suposi¸cão de proporcionalidade não seja válida. Nestes casos, outros modelos semiparamétricos poderão ser considerados, tal como o modelo aditivo de Aalen (1980).

(44)

Tomazella (2003) obteve estimativas cl´assicas e Bayesianas utilizando-se de t´ecnicas com-putacionais como “bootstrap” e MCMC.

2.8 Processos de contagem

Uma forma alternativa na abordagem de dados de sobrevivência, através da teoria de processos de contagem, foi desenvolvida por Aalen (1978). Em seu trabalho, Aalen (1978) combinou elementos de integra¸cão estocástica, teoria de martingale para tempos cont´ınuos e teoria de processos de contagem numa metodologia que permite facilmente o desenvolvimento de técnicas de inferência para dados de sobrevivência na presen¸ca de censuras. A grande vantagem dessa formula¸cão é que permite acomodar com facilidade tanto dados com censuras, quanto situa¸cões mais complexas, tais como, covariáveis dependentes no tempo, eventos recorrentes e eventos múltiplos. Uma descri¸cão mais detalhada dessa teoria, pode ser encontrada em Andersen et al. (1993) e Fleming e Harmington (1991).

2.8.1 No¸c˜oes b´asicas de processos de contagem

Um processo de contagem_{N(t), t_≥0_}é o número de eventos de um processo pontual em [0, t], ou seja, N(t) é um processo estocástico que assume os valores 0,1,2, . . .

registrando um salto do valor i₋1 ao valor i, quando o evento de interesse ocorre pela

i-ésima vez,i= 0,1,2, . . . . N(t) é igual a zero até que se registre a primeira ocorrência do evento, quando então, salta para o valor 1. O processo cont´ınua até uma nova ocorrência do evento, quando é registrado um novo salto para o valor 2, e assim, vão se registrando saltos sucessivos, de tamanho 1, até o encerramento das observa¸cões, Figura 5.

Um processo de contagem _{N(t), t _≥0_}, ´e um processo estoc´astico com as seguintes propriedades

i) N(0) = 0;

ii) N(t)<_∞;

iii) N(t) ´e cont´ınuo `a direita;

(45)

0.0 0.2 0.4 0.6 0.8 1.0

0

5

10

15

20

tempo

N

(

t

)

Figura 5 - Representa¸c˜ao gr´afica de um processo de contagem

N(t) é, portanto, uma variável aleatória que representa o número de falhas no intervalo [0, t]. Para um intervalo qualquer (a, b] o número de falhas é definido por

N(a, b] =N(b)₋N(a),

Um processo_{N(t), t_≥0_}é dito terincrementos independentes se o número de falhas em intervalos disjuntos são independentes, ou seja, se para todo 0 _≤ t1 < t2 <

. . . < tk, as variáveis alatóriasN(t1)−N(t0), . . . , N(tk)−N(tk−1) são independentes.