UNIVERSIDADE DE SAO PAULO
INSTITUTO DE F
ISICA
M
ETODOS ESTOC
ASTICOS APLICADOS
A TRANSIC
~
AO DE FASE
Jose R. Novaes Chiappin
Tese apresentada ao Instituto de Fsia da
Universidade de S~ao Paulo para obten~ao
do ttulo de Doutor em Ci^enias.
Orientador Prof. Dr. Mario Jose de Oliveira
Bana Examinadora
Prof. Dr. Mario Jose de Oliveira (IFUSP)
Prof. Dr. J urgen Fritz Stilk (UFF)
Prof. Dr. Paulo Murilo C. de Oliveria (UFF)
Prof. Dr. Slvio Roberto de Azevedo Salinas (IFUSP)
Prof. Dr. Wagner Figueiredo (UFSC)
S~ao Paulo
Antonio Itamar e Glauo Cesar e a minha irm~a Maria Apareida
ao meu orientador s~ao profundos pois muito do que se enontra nesta tese aprendi
om ele, alem de ser o responsavel pelos meus primeiros trabalhos publiados em
fsia.
aos membros do grupo de Me^ania Estatstia, parte do qual foi onstrudo pelo
prof. Salinas,s~aoespeiaisporuma inu^eniadaqualnunapude enuna quisme
livrar eda quala busa poressa tese foi uma neessidade eo resultado.
aoOzorios~aomuitosn~aosopelaamizadequeonstrumosaopartilhar-mosamesma
sala mas tambem porsua sistematia einansavelajuda.
aoInstitutode Fsia,empartiular aoDepartamentode FsiaGeral, s~aoenormes
por proporionar minha forma~ao basia e uma infra-estrutura de funionamento
de 24 horas que tornou essa tese possvel pois boa parte dela foi feita nos sabados,
domingos edurante a noite.
ao meu Departamentoe olegaspelaonviv^enia.
a Maria por proporionar um ambiente de trabalho muito agradavel om sua
dis-posi~aoe seu uidado om a organiza~ao.
ao prof.Lira e sua equipe, ao Sergio e Valdir por terem onstrudo uma rede de
omputadores muito eiente daqual z uso intensivo e muito mebeneiei.
aoSr. Jo~aoeaoSlvioporteremproporionadonoturnodanoite,durantetodoesse
tempo, aerteza de queteramos sempre afe quente e a disposi~aopara pequenas
e desontradas onversas.
a Dire, Ivone e Silvana pelo apoio administrativo e ao Sr. Wilson e Dona Suely
pelaaten~aoe pelo afe.
ao pessoal da biblioteae da seretariada pos-gradua~ao que foramsempre muito
Apresentepesquisaserefereaaplia~aodosmetodosestoastiosparaestudarfen^omenos
rtiosemmodelosdesistemaslassiadosomodesordenados,queapresentamtransi~ao
de fase do tipo ordem-desordem. Essa pesquisa e denida tanto no quadro teorio da
Me^ania Estatstia dos fen^omenos rtios e transi~ao de fase de equilbrio e fora de
equilbrio, om os reursos assoiados a analise de esala de tamanho nito quanto no
quadrodosreursosaosproessosestoastiosmarkovianos,desritospelaequa~ao-mestra
e assoiados a tenias essenialmente numerias omo o metodo estoastio
omputa-ional de MonteCarlo.
Na primeira etapa desta pesquisa, os modelos estudados s~ao da lasse denominada
de votante majoritario. Eles s~ao indexados pelo numero z de vizinhos mais proximos,
om spin entral, t^em dois estados e s~ao onstrudos em redes quadradas. A evolu~ao
din^amia e dada pela regra da maioria junto om regra de desempate. Eles n~ao
satis-fazem apropriedadedoprinpiodobalaneamentodetalhado,portanto,s~aolassiados
omo desrevendo fen^omenos fora de equilbrio. Contudo, eles satisfazem a propriedade
de simetriade invers~ao de sinal, oqueos oloateoriamente nalassede universalidade
do modelode Ising. Destaforma,aevolu~aodin^amia desses modelose estudadaom os
reursos daequa~ao-mestra ouequa~ao de evolu~ao. Noentanto,essa abordagemteoria
efeitaapenasnaaproxima~aodeampomedio,aqualfornee,nasolu~aoestaionaria,os
valores lassios para os par^ametros relevantes. Em ontrapartida, os valores numerios
exatas para os valores do ponto rtio e dos expoentes rtios, que s~ao n~ao-lassios, e
dada pormeio doreursoaometodode simula~aoomputaionale aanalise de esalade
tamanho nito. Esses valoresonrmamoresultadoteorioquantoalassede
universali-dade paraadamodeloespeo. Nasequ^enia,estudam-seaspropriedadesdos modelos
resultantesdaombina~aoonvexadosmodelosdovotantemajoritario. Osresultadoss~ao
semelhantes aos anteriores. Umresultadoextra permitidoporessa ombina~aoonvexae
a onstru~aode umarela~aoontnuaentre ovalorrtiodoindutordatransi~aode fase
e o numero de vizinhos. Neste ontexto foi apresentada uma solu~aopara oproblema do
modelomais simples destalasse de modelos. Com omodelo mais simplesilustram-se as
ondi~oes universais de transi~aode fase,em partiular opapel dadimens~aodo sistema.
que, por analogiaom o modelo de Ising, tem omo estado fundamentala fase
antiferro-magnetia: a lasse dos modelos do votante minoritario. Essa lasse de modelos possue
as mesmaspropriedades dalasse de modelos dovotante majoritarioe porissoobtem-se
os mesmos resultados A analogia om o modelo de Ising e levada um pouo mais longe
om a onstru~ao de um analogo ao modelo de Ising J: a onstru~ao da ombina~ao
onvexa do votante majoritario om o minoritario. Para esse novo modelo onstroi-se
tanto o diagramaom as tr^esfases, ferromagnetia, paramagnetia e antiferromagnetia
quando as onentra~oes rtias que as distinguem. N~ao se obtem uma possvel fase de
vidrode spin. Umavez queosmodelosdovotantes~aooriginalmentetidos omosistemas
desordenados, omparam-se, para um mesmo modelo, resultados obtidos pela aplia~ao
de dois diferentes metodos de tratar os modelos de sistemas desordenados: o metodo
temperado -"quenhed"- e ometodoreozido -\annealed".
Na tereira etapa desta pesquisa e na mesma linha dos modelos estoastios
irre-versveis tratados anteriormente, estuda-se ainda outro modelo, lassiado omo jogo
espaial, om uma din^amia desrevendo a evolu~ao de N indivduos interagentes
loal-izados nos stios de uma rede quadrada. Simula~oes mostram que alem de dois estados
absorventes ha tambema presena de um estado ativodenido poruma densidade nita
de ooperadorese n~aoooperadoreseque essemodeloseenontranalasse de
universal-idade domodelo daperola~aodireionada. Nesta mesmaetapa,mas, agora,noontexto
da Me^ania Estatstia de Equilbrio, aborda-se o modelo de Ising qu^antio
unidimen-sional om ampo transverso por meio da simula~ao de Monte Carlo. Com o uso do
metodoestoastioepormeiodaurvadoolpasoalulam-se osvaloresdopontortio
This researh refers to the apliation of the stohasti methods to the study of the
ritialphenomenainmodels ofsystems lassiedasdisorderedthat undergophase
tran-sition of the order-disorder kind. This researh isdened as inthe theoretialframework
of the Statistial Mehanis of the equilibrium and non-equilibrium of the ritial
phe-nomena and phase transition, with the resoures assoiated to the analysis of nite-size
sale, as in the frame of the resoures of markovian stohasti proess desribed by the
master equationassoiated withessentiallynumerialtehniques suh asstohasti
om-putaional method ofMonte Carlo. In the rst stageof this researh,the studied models
belong to the lass of the majority voter. They are desribed by a lattie with spins in
eah site with two states. The dynami ofthese models is desribed by the majority rule
together with a rule for solving problems of indeision. These models do not obey the
prinipleofmirosopireversibilitythereforethey arelassiedasdesribingphenomena
of non-equilibrium. However, they satisfy the property of \up- down" symmetry whih
make them theoretially belong to the universality lass of the Ising model. The mean
eld approahtothe masterequationisdone andtheexat value ispursued by theuse of
themethodoftheomputationalsimulationwiththeuseoftheanalysisofnite-sizesale.
The resultsobtainedforthe ritialexponentssupportthe hipothesisof universality lass
of these models. There are onstrutions of the onvex ombination of these models. A
question israisedaboutthe simplestmodeland apossiblesolutionispresented. Thereis
a searh for another kind of majority voter, but with an antiferromagnetiground state,
whihleads tothe minorityvoter. It isalsotobelassiedinthe sameuniversality lass.
A natural unfold of this researh is making the onvex ombination of the minority and
majorityvotermodelsbyanalogywiththeIsingmodelJ andaskforthe phasediagram
relating the ritial value and the density. It is lose to that of the Ising model J.
Some results are also obtained by omparing the quenhed and annealed approah to a
same majorityvotermodel. Finally,therearetwomoreappliationsofthese methodsfor
obtainingritialpointand ritialexponents. The rst referstoamodelwith absorbing
state whih is lassied in the universality lass of diret perolation. The seond refers
1.1 Graodopar^ametrodeordem{magnetiza~ao{omoaraterstiadatransi~ao
ontnua parao tamanhoL resente. . . 21
1.2 Grao dasusetibilidadeomo araterstia datransi~aoontnua. . . 22
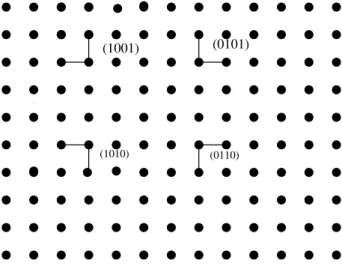
2.1 As oordenadas das formas geometriasde liga~oes. . . 33
2.2 As quatro possveisformas geometriasde liga~ao. . . 35
2.3 As seis possveis formas geometriasde liga~oes. . . 39
2.4 Os dois modelos basios (1100)e (0011) . . . 40
2.5 Os dois modelos basios (1100)e (0011) . . . 44
2.6 M omo fun~ao de 1=L para ada q. . . 49
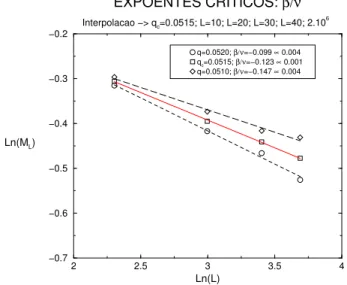
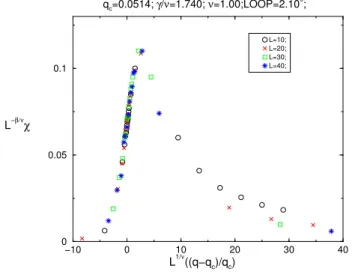
2.7 O metodo doumulante ! q =0:0514 para U =0:61. . . 50
2.8 Ometododamagnetiza~ao,M, versus q para diversos Leaontinuidade omo araterstia. . . 51
2.9 O metodo da susetibilidade, L , versus q e a diverg^enia omo ara-terstia. . . 51
2.10 Regress~ao linear! = =0:1220:003. . . 52
2.11 Metodo de interpola~ao! q =0:0514. . . 53
2.12 Regress~ao linear! = =1:742. . . 54
2.13 Regress~ao linear! = =1:737om os dados para max (L). . . 55
2.14 A hipotese de esala para ~ M e".~ . . . 56
2.15 A hipotese de esala para ~ L (q) versus ".~ . . . 56
2.16 A hipotese de esala para ~ U L =U L versus ".~ . . . 57
2.17 Grao de q versus densidade 1100 . . . 58
2.18 As quatro possveisformas geometriasde liga~oes. . . 60
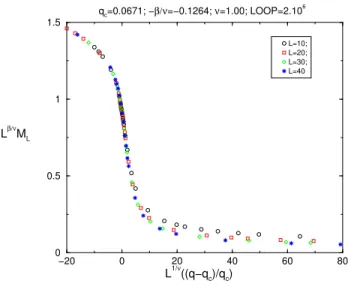
2.19 A forma geometriade liga~aoe (1001)om q =0:0671. . . 64
2.20 O metodo damagnetiza~ao,M L ,versus q. . . 65
2.21 Susetibilidade, L ,versus q om adiverg^enia araterstia. . . 66
2.22 O metodo de regress~aolinear ! = =0:12640:009. . . 66
2.23 Regress~ao linear! = =1:70360:0730. . . 67
2.25 A hipotese de esala para ~
M versus ".~ . . . 68
2.26 A hipotese de esala para ~ L versus ".~ . . . 69
2.27 A hipotese de esala para ~ U L versus "~ . . . 69
2.28 As duas formas geometriase simetrias de liga~oes (1010)e (0101). . . 71
2.29 As duas formas geometrias om simetria no eixo x, de liga~oes (1010) e (1001). . . 71
2.30 Grao darela~ao q versus 1001 . . . 72
2.31 Grao para arela~aoentre q versus 1010 .. . . 73
2.32 Grao dasuperposi~ao darela~ao q versus 1001 para os dois onjuntos. . 74
2.33 As seis possveis formas geometriasde liga~oes. . . 75
2.34 As liga~oes (0011)e (1010). . . 76
2.35 q versus 1010 . . . 76
2.36 Superposi~ao das rela~oes entre q eas densidades 0 s. . . 77
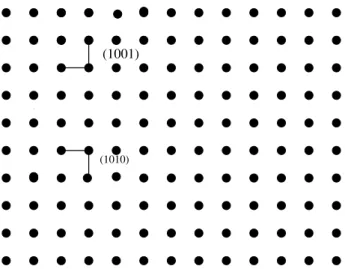
3.1 As quatro possveisformas geometriasde liga~oes . . . 81
3.2 O metodo doumulante e ovalorrtio q =0:0754. . . 84
3.3 Grao damagnetiza~aoM L versus q. . . 85
3.4 Grao dasusetibilidade L versus q. . . 85
3.5 Grao de lnM versus lnL e regress~ao linear ! = =0:12350:0058 . . 86
3.6 Grao de ln versus lnLe regress~aolinear ! = =1:74300:0161. . . 87
3.7 A hipotese de esala para ~ M L (q)versus ".~ . . . 87
3.8 A hipotese de esala para ~ L (q)versus "~ . . . 88
3.9 A hipotese de esala para U versus ".~ . . . 88
3.10 Conjunto(1011) e (0111). . . 89
3.11 Conjunto(1101) e (0111). . . 90
3.12 Superposi~ao dos graos q versus 0111 . . . 91
3.13 Metodo doumulante ! q =0:0800. . . 92
3.14 O onjunto (1111),um spin entral e quatro vizinhos. . . 92
3.15 Grao de U(L)versus q . . . 97
3.16 Grao damagnetiza~aoM L versus q. . . 98
3.17 Grao dasusetibilidade L versus q. . . 98
3.18 Regress~ao linear! = =0:1230:0025 . . . 99
3.19 Grao domaximodasusetibilidade, max , versus L. . . 99
3.20 A hipotese de esala para arela~ao ~ M versus ".~ . . . 100
3.21 A hipotese de esala para arela~ao~ L versus "~ . . . 101
3.22 A hipotese de esala para arela~ao ~ U versus ".~ . . . 101
3.23 As quatro formas geometriaspossveisom ino vizinhos. . . 102
3.25 Rela~aoentre magnetiza~ao,M, versus q para diversos z. . . 104
3.26 Rela~aoentre q e adensidade 1v . . . 107
3.27 As liga~oes geometrias(1100), (0011) e(0100). . . 108
3.28 Grao teorio da rela~aoq versus 2 . . . 112
3.29 Rela~aoentre q e 2v . . . 115
3.30 Rela~aoentre q e 2v . . . 115
3.31 Rela~aoentre q versus 1100 . . . 116
3.32 Da rela~aoentre q e 1100 tem-se que 1100 =0:99 ! q =0:0075. . . 117
3.33 Da rela~aoq e 2v tem-se que 2v =0:01 !q =0:000075. . . 119
4.1 Os dois modelos basios (1100)e (0011). . . 126
4.2 Cumulantede quarta ordem U L (q): interse~ao novalorrtio q =0:0514.133 4.3 Magnetiza~ao,M L (q),versusq para valores de L. . . 133
4.4 Susetibilidade, L (q),versus q para valores de L. . . 134
4.5 Regress~ao linear: expoentertio / =0:1210. . . 135
4.6 Regress~ao linear: expoentertio = =1:7632. . . 135
4.7 Regress~ao linear: expoentertio = =1:7753. . . 136
4.8 Fun~aouniversal L = M(q) omo fun~ao de L 1= (q q )=q . . . 137
4.9 Fun~aouniversal L = (q)omo fun~aode L 1= (q q )=q . . . 137
4.10 Fun~aouniversal U(q) omo fun~ao de L 1= (q q )=q . . . 138
4.11 O onjunto (1111),um spin entral e quatro vizinhos. . . 139
4.12 O metodo doumulante U L (q): a interse~ao novalorrtio q =0:0848. . 143
4.13 A magnetiza~ao M L (q) versus q para alguns valores de L. . . 144
4.14 A susetibilidade L versus q e tend^enia a diverg^enia emq =0:0848. . . 144
4.15 Regress~ao linear! = =0:1232. . . 145
4.16 Regress~ao linear! / =1:705.. . . 146
4.17 Regress~ao linear! = =1:741.. . . 146
4.18 Fun~aouniversal L = M(q) versus L 1= (q q )=q . . . 147
4.19 Fun~aouniversal L = (q)versus L 1= (q q )=q . . . 148
4.20 Fun~aouniversal U(q) versus L 1= (q q )=q . . . 148
5.1 Estes s~ao exemplos de plaquetas (I)n~ao frustradase de (II) frustradas.. . . 151
5.2 O grao q versus vmin . . . 156
5.3 O grao q versus vmin . . . 157
5.4 O grao q versus vmin . . . 158
5.5 O metodo doumulante obtemosq =0:0380 para vmaj =0:95. . . 159
5.6 A rela~aodamagnetiza~ao,M L ,om q. . . 160
5.7 A rela~aodasusetibilidade, L om q. . . 160
5.9 Grao log-logda susetibilidade
max
versus L. . . 162
5.10 Grao log-logda susetibilidade,
L (q
),versus L. . . 162
5.11 Fun~aoUniversal ~
M(q)=L =
M versus "~=L 1=
(q q
)=q
. . . 163
5.12 Fun~aouniversal (q)~ =L =
versus "~=L 1=
(q q
)=q
. . . 164
5.13 Fun~aouniversal U(q) versus "~=L 1=
(q q
)=q
. . . 164
5.14 Domnios (F) e (AF) domodelo onvexoVMAJ4VMIN4 om p>=0:5. . . 166
5.15 Domnios(AF)e(F)domodeloonvexo VMAJ4VMIN4om0:00 p0:5.166
5.16 Domnios(AF)e(F)domodeloonvexoVMAJ4VMIN4om0:00p1:00.167
5.17 O metodo doumulante, U
L
versus q,!
vmin
=0:08000:008. . . 168
5.18 O grao da magnetiza~ao(M(q=0))versus
vmin
. . . 169
5.19 O grao da susetibilidade((q=0))versus
vmin
. . . 169
5.20 O grao lnM(q = 0;
vmin =
)versus lnL. Dois valores simulados e
quatro valores interpolados !
=0:0806. . . 170
5.21 O grao lnM(q=0; =
)versus lnLda regress~aolinear. . . 171
5.22 O grao ln(q=0;=
)versus lnL daregress~ao linear.. . . 171
5.23 Fun~aouniversal L =
M(q=0;
vmin
) versus L 1= ( vmin )=
. . . 172
5.24 Fun~aouniversal L =
(q =0;
vmin
) versus L 1= ( vmin )=
. . . 173
5.25 Fun~aouniversal Uversus L 1= ( vmin )=
. . . 174
5.26 O grao do umulante de quarta ordem versus q. . . 175
5.27 O grao da magnetiza~aoM
L
versus q. . . 176
5.28 O grao da susetibilidade
L
versus q. . . 176
5.29 O grao da ln
max
versus lnL. . . 177
5.30 O grao do ln
q
versus lnL. . . 178
5.31 O grao do lnM
L
versus lnL. . . 178
5.32 O grao do olapsoL = M L versus L 1= (q q )=q
. . . 179
5.33 O grao do olapsoL = versus L 1= (q q )=q
. . . 180
5.34 O grao do olapsoU versus L 1=
(q q
)=q
. . . 180
5.35 Grao U
L
versus q omU
=0:61. . . 182
5.36 O grao da magnetiza~ao,M
L
versus q. . . 183
5.37 O grao da susetibilidade,
L
versus q. . . 183
5.38 O grao de lnM
L
versus lnL ! expoente =. . . 184
5.39 O grao da ln
q
versus lnL! expoente =. . . 185
5.40 O grao da ln
max
versus lnL ! expoente =. . . 185
5.41 O grao do olapso ~
M =L =
M versus "~=L 1=
(q q
)=q
. . . 186
5.42 O grao do olapso~=L =
versus "~=L 1=
(q q
)=q
. . . 187
5.43 O grao do olapso ~
U =U versus "~=L 1=
(q q
)=q
. . . 187
5.44 O valorde q
=0:066 para
1001
=0:98 pelo metodo \annealed". . . 188
5.47 A superposi~ao dos dois graos para
1001
=0:98.. . . 189
5.48 O grao da abordagem\quenhed" de q
versus
1001
. . . 190
5.49 O grao da superposi~aodos dois graos: \quenhed" e\annealed". . . . 191
6.1 Diagramadefasenoplano(r;)obtidodasimula~aonumeriaemumarede
quadrada. As tr^es fasess~ao o estado de plena oopera~ao (C) para oqual
=1,estadoativo(A)paraoqual0< <1,eestadode n~ao-oopera~ao
plena (D)para oqual=0. Aslinhas de transi~oes C-AeA-Ds~aolinhas
rtias embora alinha C-De uma linhade transi~aodesontnua. As tr^es
linhas enontra-se no ponto r==1. . . 199
6.2 Densidade do ooperador versus o par^ametro r para varios valores de ,
obtidosdas simula~oesnumerias. Da esquerdapara adireitaosvaloresde
s~ao 0;0:1;0:2;0:3;0:4;0:5;0:6;0:7; e0:9: . . . 200
6.3 Grao de ln versus lnr emque =r
r para o aso =0. As tr^es
linhasorrespondem,daesquerdaparaadireita,paravalorestentativasde
r
=0:798;0:800,e 0:802:Omelhor ajustelinearda r
=0:8000:001 eo
expoentertio =0:580:01:. . . 201
7.1 Cumulantedequarta ordemU
L
( ): interse~aonovalorrtio
=1:000
para o valorde U
L (
)=0:55. . . 209
7.2 Magnetiza~ao M omo fun~ao do par^ametro para varios valores L da
adeia. . . 210
7.3 Susetibilidade M omo fun~ao do par^ametro para varios valores L da
adeia. . . 211
7.4 Fun~aouniversal ~
M =L 1=8
M omo fun~aode L 1=
(
)=
.. . . 212
7.5 Fun~aouniversal ~=L 3=4
omo fun~aode L 1=
(
)=
. . . 213
7.6 Fun~aouniversal ~
U =U omo fun~aode L 1=
(
)=
1 INTRODUC ~
AO. 1
1.1 Metodos etenias para estudara natureza e
obter o valordo pontortio e expoentes rtios. . . 20
1.1.1 Metodos para identiar a natureza datransi~ao. . . 20
1.1.2 O metododoumulantede quarta ordem. . . 22
1.1.3 O metododamagnetiza~ao: valor, natureza e expoente rtio. . . . 23
1.1.4 O metododasusetibilidade: valor, natureza eexpoentes rtios. . 24
1.1.5 A fun~aode esala ea urvaolapso. . . 25
1.1.6 Roteiro da tese. . . 26
2 O MODELO DO VOTANTE MAJORIT ARIO - VMAJ. 29 2.1 Introdu~ao: os objetivos eproblemas. . . 29
2.2 O modelo do Votante Majoritario: desri~ao geral e espeia~ao dos ob-jetivos. . . 30
2.3 O modelo VMAJ1. . . 34
2.3.1 A desri~ao domodelo. . . 34
2.3.2 A abordagemteoria: a aproxima~aode ampo medio. . . 36
2.3.3 A simula~aoomputaional: resultados numerios e analise dos dados. . . 37
2.4 O modelo VMAJ2 eseus submodelos. . . 38
2.4.1 Desri~aodo modelo. . . 38
2.4.2 O modelo onvexo VMAJ2.1 sem spin entral: desri~aodo modelo. 39 2.4.3 A abordagemteoria: a aproxima~aode ampo medio. . . 41
2.4.4 Asimula~aoomputaional: resultadosnumerioseanalisedosdados. 43 2.4.5 O modelo onvexo VMAJ2.1 om spin entral: desri~aodo modelo. 43 2.4.6 A abordagemteoria: a aproxima~aode ampo medio. . . 45
2.4.7 Asimula~aoomputaional: resultadosnumerioseanalisedosdados. 48 2.4.8 O modelo onvexo VMAJ2.2 sem spin entral: desri~aodo modelo. 59 2.4.9 A abordagemteoria: aproxima~ao de ampomedio. . . 60
2.4.12 A abordagemteoria: a aproxima~aode ampo medio. . . 62
2.4.13 Asimula~aoomputaional: resultadosnumerioseanalisedosdados. 62 2.4.14 O modelo VMAJ2.2 puro: desri~ao domodelo. . . 63
2.4.15 A abordagemteoria: a aproxima~aode ampo medio. . . 63
2.4.16 A abordagemda simula~aoomputaional: resultados numerios e analise dos dados. . . 63
2.4.17 Os modelosVMAJ2.2.1 eVMAJ2.2 om spin entral: desri~ao do modelo. . . 70
2.4.18 A abordagemteoria: a aproxima~aode ampo medio. . . 72
2.4.19 A abordagem omputaional: resultados numerios e analise dos dados. . . 72
2.4.20 O modelo onvexo VMAJ2.3: desri~aodomodelo. . . 74
2.4.21 A abordagemteoria: a aproxima~aode ampo medio. . . 75
2.4.22 Asimula~aoomputaional: resultadosnumerioseanalisedosdados. 75 3 O MODELO DO VOTANTE MAJORIT ARIO E O MODELO MAIS SIMPLES. 79 3.1 Introdu~ao. . . 79
3.2 O modelo onvexo VMAJ3: desri~aodo modelo. . . 80
3.2.1 A abordagemteoria: a aproxima~aode ampo medio . . . 82
3.2.2 Asimula~aoomputaional: resultadosnumerioseanalisedosdados. 83 3.3 Os modelos VMAJ3.1e VMAJ3.2: desri~ao dos modelos. . . 89
3.3.1 A abordagemteoria: aproxima~ao de ampomedio. . . 90
3.3.2 A simula~aoomputaional: resultadosnumerioseanalisedos dados 90 3.4 O modelo VMAJ4 om spin entral. . . 90
3.4.1 Desri~aodo modelo. . . 90
3.4.2 A abordagemteoria: a aproxima~aode ampo medio. . . 93
3.4.3 Asimula~aoomputaional: resultadosnumerioseanalisedosdados. 97 3.5 Os outrosmodelos homog^eneos VMAJx. . . 102
3.6 Osmodelosheterog^eneos: arela~aoentre q e z . . . 104
3.7 O problema domodelo mais simples. . . 108
3.7.1 O modelo onvexo VMAJ2.1-VMAJ1.. . . 108
3.7.2 A abordagemteoria: o enfoquede ampo medio . . . 109
3.7.3 Asimula~aoomputaional: resultadosnumerioseanalisedosdados.113 3.7.4 A rela~aoentre q e . . . 115
3.7.5 O modelo mais simples. . . 116
4 O MODELO DO VOTANTE MINORIT
ARIO-VMIN. 123
4.1 Introdu~ao. . . 123
4.2 O modelo dovotante minoritario(VMIN) -A fase antiferromagnetia. . . 124
4.3 O modelo minoritarioVMIN2.1 sem spin entral. . . 125
4.3.1 Desri~aodo modelo. . . 125
4.3.2 A abordagemteoria: a aproxima~aode ampo medio. . . 127
4.3.3 Asimula~aoomputaional: resultadosnumerioseanalisedosdados.128 4.4 O modelo minoritarioVMIN2.1 om spin entral. . . 129
4.4.1 Desri~aodo modelo. . . 129
4.4.2 A abordagemteoria: a aproxima~aode ampo medio. . . 130
4.4.3 Asimula~aoomputaional: resultadosnumerioseanalisedosdados.132 4.5 O modelo minoritarioVMIN4 om spin entral. . . 138
4.5.1 Desri~aodo modelo. . . 138
4.5.2 A abordagemteoria: aproxima~ao de ampomedio. . . 140
4.5.3 A simula~ao omputaional: resultados numerios e a analise dos dados. . . 143
5 O MODELO CONVEXO DO VOTANTE MAJORIT ARIO-MINORIT ARIO:VMAJ4VMIN4. 149 5.1 Introdu~ao. . . 149
5.2 O modelo VMAJ4VMIN4. . . 150
5.2.1 Introdu~ao. . . 150
5.2.2 A desri~ao domodelo VMAJ4VMIN4. . . 151
5.2.3 O modelo VMAJ4VMIN4 om spin entral. . . 152
5.2.4 A abordagemteoria: a aproxima~aode ampo medio. . . 153
5.2.5 Asimula~aoomputaional: resultadosnumerioseanalisedosdados.158 5.2.6 O modelo VMAJ4VMIN4 eo valorrtio . . . 167
5.3 Os tiposde desordem: \annealed"e \quenhed". . . 174
5.3.1 O modelo VMAJ98AN: a abordagem\annealed". . . 174
5.3.2 O modelo VMAJ98Q: a abordagem\quenhed". . . 181
5.3.3 Asimula~aoomputaional: resultadosnumerioseanalisedosdados.181 5.3.4 O modelo VMAJANQ: q versus 1001 . . . 189
6 O PROBLEMA DA EMERGENCIA DA COOPERACAO
ENTRE INDIV
IDUOS INTERAGENTES. 193
6.1 Introdu~ao. . . 193
6.2 O modelo. . . 195
6.3 Simula~aonumeria. . . 198
6.4 Conlus~oes. . . 202
7 MODELO DE ISING COM CAMPO TRANSVERSO: MODELO QU ^ ANTICO. 203 7.1 Introdu~ao. . . 203
7.2 Formulas basias. . . 205
7.3 O metodo de Monte Carlo. . . 206
7.4 Algoritmo. . . 207
7.5 Resultados numerios. . . 208
INTRODUC ~
AO.
Apresentetesetemporobjetivoproporeresolverproblemasrelaionadosomfen^
ome-nos rtiosetransi~aodefase. Essesproblemasreferem-seaspropriedadesdemodelosde
sistemaslassiadosomodesordenados, om transi~aode fasedotipoordem-desordem.
A natureza geral desses problemas de fen^omenos rtios e transi~ao de fase enontra-se
tantonoontextodaTermodin^amiaquantonodaMe^aniaEstatstiadeEquilbrio. No
entanto, muitos destes reursos podem ser apliadospara transi~oes de fase em modelos
de n~ao-equilbrio, omo e o aso da maioria dos modelos dessa tese. O objetivo da T
er-modin^amiae onstruir quantidadesfsiasapropriadas, taisomo press~ao,temperatura,
variaveisde estados, desrevendo aspropriedadesmarosopiasdamateria,pormeiode
maroestados e estabeleer rela~oes entre essas quantidades, ou seja, formular equa~oes
de estados e as leis da Termodin^amia. Contudo, essas quantidades marosopias de
estados s~ao resultantes dos valores medios de propriedades mirosopias, tais omo
o-ordenadas emomentosdas partulasque onstituemamateria. OobjetivodaMe^ania
Estatstia de Equilbrio e o de expliar ou derivar as propriedades marosopias da
materiaapartirdasleisgovernandooomportamentodaspartulasindividuais. As
pro-priedades mirosopias s~ao expressas por meio de maroestados emtermos de variaveis
termodin^amias denominadas de energia, temperatura, press~ao, potenial qumio,
en-tropia, potenial termodin^amio, :::. Uma das maneiras de tratar essas propriedades
marosopias e explia-las diretamente por meio da Termodin^amia. Elapode ser
on-strudaemtermos axiomatiosa partir dos poteniais termodin^amiosom os prinpios
de maximiza~ao ou de minimiza~ao submetidos as restri~oes dadas pelas leis da
on-serva~ao da energia, dasegunda lei e da tereira lei daTermodin^amia. No ontexto da
Me^ania Estatstia de Equilbrio a desri~ao mirosopia dos estados das partulas,
representada pelos miroestados, e dada pela aplia~aodas leis da Me^ania Classia ou
daMe^aniaQu^antia aoestudodas intera~oesentre essaspartulas. Essas s~aodesritas
pormodelos. A explia~ao do omportamentomirosopio das partulase,ent~ao,
quan-estados marosopiosdamateria,s~ao denidas omovaloresmedios de quantidades
mi-rosopias, oordenadas emomentos, (q
, p
)determinando osmiroestados dosistema
de partulas onstituindo a materia. O espao apropriado para desrever, de maneira
mirosopia, esse sistema de partulas e o espao de fase. Cada ponto neste espao
orresponde a um estado mirosopio que e um miroestado do sistema. A evolu~ao
temporal do sistema orresponde a uma urva (q
(t), p
(t)) nesse espao de fase. Essa
urva e a trajetoria no espao de fase. Tal trajetoria e denida pelas leis da Me^ania
Classia expressas por meiodas equa~oes an^onias domovimento:
_ q
=
H
p
_ p
=
H
q
; (1.1)
em que a hamiltonianaH (q
(t);p
(t)) orresponde, noaso onservativo, a energia total
do sistema. Do mesmo modo outros observaveis g(q
(t);p
(t)) podem ser assoiados aos
pontos desrevendo a trajetoria determinada pelas equa~oes an^onias. Em um sistema
fehado, que pode ser denido pelas variaveis de maroestados V, N, a hamiltoniana
n~ao depende do tempo e e uma quantidade, E, que se onserva. Com esse reurso e
subdividindo-seoespaode faseemelulasdevolumeelementard 3N
qd 3N
p,pode-seent~ao
assoiar a um dado maroestados (E;V;N) um grandenumero (E;V;N) de diferentes
miroestados. Neste ontexto pode-se denirooneitode entropia, S,ea rela~ao
funda-mental entre os estados marosopios termodin^amios desritos pela entropia e a fsia
mirosopia desrita pelonumerode miroestados. Essa rela~aoe
S =kln(E;V;N): (1.2)
Emquekeaonstantede Boltzmann. Contudo, oelementooperaionaldestarela~ao
depende do alulo do numero de miroestados. Nesse ontexto se insere a \teoria dos
ensembles". Nesta se desenvolvem metodos efetivos para realizar esse alulo direta ou
indiretamente. Por meio deste metodo todas as quantidades termodin^amias, E, T, P,
:::, apareem ent~ao omo uma media de \ensemble" de uma quantidade mirosopia,
g(q
;p
), denida emtermos dos pontos doespaode fase. Nodomniodoespaode fase
de todos estados mirosopios possveis, o primeiro aspeto a observare que o aso de
umsistemafehadoimp~oequetodososseusmiroestadosonsistentesenontrem-sesobre
uma superfiede energiaE quedeneosistemafehado. Daquisegue-se apressuposi~ao
fundamentaldaMe^aniaEstatstiasobreaequiprobabilidadedos miroestadosemuma
superfie de energia para um sistema fehado. Desta forma, pode-se agora falar de um
espaode probabilidadepara o espao dos miroestados. Trata-sedo espao dos estados
om probabilidades assoiadas a eles ou om densidades de probabilidades (q
;p
) por
hgide um maroestado talque ada de seus miroestados ontribui om sua pondera~ao
dada peladensidade. De maneiraformal
hgi= Z
d 3N
qd 3N
p[g(q;p)(q;p)℄: (1.3)
A media do observavel aima e hamada de \media de ensemble" om a densidade
sendo a pondera~ao do \ensemble". Por sua vez este \ensemble" de miroestados om
essas araterstias e denominado de \ensemble miroan^onio". Deve haver, portanto,
uma rela~ao entre a media do \ensemble" dos observaveis, hgi, e o valor dos mesmos
observaveis, dependentedo tempo,alulado agora sobre atrajetoria(q
(t);p
(t)), omo
solu~ao das equa~oes de Hamilton. Segue-se, portanto, que estas ultimas quantidades
devem ser aluladas omomedias temporais
g = lim
T!1 1
T Z
T
0
g(q(t);p(t))dt: (1.4)
Boltzmann fez uma hipotese denominada hipotese ergodiga segundo a qual a media
temporalgeigualamediade\ensemble"hgi. Istosigniaqueatrajetoriadoobservavel
para o sistema fehado, que e determinada pelas equa~oes de Hamilton, perpassa ada
ponto da energia de superfie o mesmo numero de vezes. No entanto, onsidera-se que
ha pontos ainda ontroversos sobre a tentativa de dar uma fundamenta~ao estritamente
me^aniaateoriados\ensembles". Nestatentativadeelaborarmetodosompropositode
alular as quantidades marosopias termodin^amias a partir dos miroestados, v^e-se
que a abordagem dada pelo \ensemble miroan^onio" que e onstrudo para sistemas
fehados, emque a energia,E,eonstante e omplementada pelas variaveisde
maroes-tados V e N e tem a rela~ao S = kln(E;V;N) omo a onex~ao fundamental entre as
variaveisdosmaroestados, atermodin^amia,eafsia domiroestado. Oproblema om
esta representa~ao e a diuldade oloada pela ontagem dos miroestados, tornando
este reurso interessanteapenas paraasos bastante simples. Atentativade resolveresse
problema da ontagem levou a alternativa de onstruir outro tipo de \ensemble" onde
fosse mais failresolvero problema daontagem. Este novo\ensemble" eonstrudo
so-bre ahipotese de que aquantidade marosopia onstanten~aoe maisa energia,E,mas
atemperaturaT. Istoefeitopeloreursoapressuposi~aodosistemasubmetidoabanhos
termios proporionados por reservatorios que mantenham a temperatura onstante T.
Neste aso,o sistema,denido pelas variaveisT,V, N,e talqueseus diferentes
miroes-tados indexados por i apresentam diferentes energias E
i
om ertas probabilidades. O
problema a ser resolvidoaquionsiste, ent~ao,emahar aprobabilidadep
i
de enontrar o
sistema em um determinado miroestado orrespondente a pela energia E
i
.
Utilizando-se a representa~ao do \ensemble miroan^onio", pode-se resolver esse problema om a
p
i /
exp E
i
kT
P
i exp (
Ei
kT )
; (1.5)
emquea somaorresponde atodos osmiroestados. Denomina-seZ = P
i
exp ( E
i =kT)
afun~aodeparti~aoan^oniadosistema. Pode-sedesenvolveravers~aoontnuaparaessas
rela~oes bastando para isso substituir a soma pela integral, ou seja, P
i por
R
d 3N
qd 3N
p.
Obtem-se, ent~ao,
(q
;p
)=
exp [ H (q
;p
)℄
Z
: (1.6)
Nestenovo\ensemble",denominadodean^onio,todasaspropriedadesmarosopias
desritas pelas quantidades termodin^amias podem ser obtidas a partir dahamiltoniana
desrevendo os miroestados do sistema. A rela~ao om a termodin^amia e feita agora
pormeio do potenialtermodin^amio energialivre de Helmholtz,
F(T;V;N)= 1
lnZ(T;V;N): (1.7)
Neste ontexto, se g(x) e uma quantidade fsia e x representa uma ongura~ao
mirosopia possvel, ent~ao o valor medio de uma fun~ao dessa quantidade A g(x)
e
dado por
D
A g(x)
E
T =
1
Z Z
dxexp h
H (x)
kT i
A(g(x)): (1.8)
Com isso am bem araterizadas a estrutura e os omponentes da Me^ania
Es-tatstia de Equilbrio e a propria natureza estatstia dessa Me^ania que e o alulo
de valores medios. Outros tipos de \ensembles" s~ao possveis e mais adequados para
outros tipos de invari^anias, no entanto n~ao e esse o interesse desta pesquisa, e sim o
de mostrar, om o \ensemble" miroan^onio e an^onio, omo a Me^ania Estatstia
onstroi a onex~ao entre as desri~oes mirosopias e a desri~ao marosopia dos
sis-temas fsios. No ontexto da\teoria dos ensembles", o \ensemble an^onio"e bastante
apropriado para araterizar o prinipalproblema da Me^ania Estatstia de Equilbrio
omo sendo aquele de expliar o omportamento dos fen^omenos rtios e das transi~oes
de fase. Oprimeiropassosobreesteassuntoeadeni~aode pontode transi~aode faseno
ontexto deste\ensemble". Pontodetransi~aode faseedenidoomosendoum pontode
n~ao-analitiidadedafun~aode parti~ao. Comose expressaThompson (Thompson,1972)
sobre esse ponto:
any nonanalyti point of the anonial free energy
f(v;T)= lim
N;V!1
v= V
N xed
N 1
lnZ(V;N;T):::; (1.9)
ouringfor real positiveT, v,...isalled a phase transitionpoint 1
.
1
deTayloremtornodesseponto. Masparatertransi~aodefase,matematiamentefalando,
e preiso primeiro tomar o limite termodin^amio, ou seja, N, V ! 1 om a densidade
v =N=V xada, portanto onsiderando apenas sistemas no limite termodin^amio. Para
N e V nitos, afun~aoparti~aoeuma fun~aoompletamenteanaltia de T.
Para os propositos dessa tese, o modelo adequado para representar as partulas e o
modelo de gasde rede. Este modelo onsisteem ter em ada um dos seus N stios uma
variavelestoastiaom dois estados
i
=1eregras quedenem qualoestado de ada
stio,dependendo daintera~aoourela~ao omosvizinhos mais proximos. Ha 2 N
estados
mirosopios possveis que onstitui o espao de probabilidade. Com a hamiltoniana
H (x), fun~ao das x ongura~oes, tem-se a desri~ao dos estados aessveis do modelo
entre os estados possveis. A hamiltoniana do sistema introduz uma restri~ao no espao
dos estados possveis. O modelo de Ising e o sistema mais simples que apresenta uma
transi~ao de faseeservede paradigma para amaioriados outros modelose investiga~oes
naMe^ania Estatstia deEquilbrio. Esse modeloedesritoporuma redeom spins
i
no stio i om dois estados1. Umaongura~ao fge espeiada porN variaveisde
spin
i
. Em uma ongura~aofg aenergia de intera~ao oua hamiltonianae dada por
Efg= J X
<i;j>
i
j h
X
i
i
; (1.10)
em queo smbolo<i;j >signiavizinhos mais proximos, o smboloJ ea onstantede
aoplamento eh e oampomagnetioexterno.
Ha tr^es maneiras de abordar o problema da transi~ao de fase neste modelo: a
abor-dagem de ampomedio, asolu~aoexata para h=0 omd =2,e aabordagemdin^amia.
Essas tr^esabordagens revelamaspetosimportantesdosfen^omenosrtiosetransi~aode
fase. Contudo,aabordagemdin^amiatrazaideiadeestaareaultrapassarosproprios
on-tornos da Me^ania Estatstia de Equilbrio. A abordagemde ampo medio do modelo
de Ising revelaa exist^enia de uma temperatura rtia, T
, e desreve o omportamento
da magnetiza~aoe da susetibilidadenas proximidades deste ponto, por meio de leis de
pot^enias om expoentes denominados de lassios. A solu~ao deste modelo para h = 0
om d=2 feitapor meio dos reursos da matrizde transfer^enia a qual desreve o
om-portamentoorretodamagnetiza~aoedasusetibilidadepara qualquer temperatura,em
partiular, permitindoalularosvaloresexataosparaatemperaturartiaedesrevero
omportamentodo sistemanas proximidadesdo ponto rtio. Os expoentes rtios das
leisde pot^enia,ontudo,s~aodiferentesdos anterioreseforamdenominadosde expoentes
n~ao-lassios. As transi~oes de fase do equilbrio s~ao denominadas de transi~oes de fase
estatias. Os valores aima s~ao denominados de expoentes rtios estatios. O modelo
de Isingeum modeloestatio,e,portanto,um modelo paradesreveraspropriedadesde
de Ising. A pressuposi~ao basia do modelo de Glaubere que ha uma probabilidade de
transi~ao por unidade de tempo, w
j (
j
) de apliar o metodo do \single spin-ip", ou
seja, de substituir oestado davariavelestoastia
j
dostioj, esolhido aleatoriamente
por
j
, segundo a probabilidade w
j (
j
). Com esta propriedade se onstroi a equa~ao
do movimento para a distribui~ao de probabilidade naforma de uma equa~ao-mestra de
ganhos e perdas (de Oliveirae T^ania Tome,2001):
dP(;t)
dt = N X j=1 fw j ( j )P( j
;t) w
j
()P(;t)g; (1.11)
em que a ongura~ao j
e obtida da ongura~ao pela troa de
j
por
j
. Desta
equa~ao pode-se mostrar, por exemplo, que a equa~ao para a evolu~ao da media h
j i e
dada por(de Oliveira eT^ania Tome,2001)
dh j i dt = 2h j w j ()i: (1.12)
As propriedadesdomodelo de Glaubers~aodeterminadas, uma vez queprobabilidade
de transi~ao,w
j
,eespeiada. Contudo,aonex~aoentreesta ultimaequa~aoeomodelo
de Isingvemdaimposi~aode queasolu~aoestaionariadestaequa~aosatisfazoprinpio
do balaneamentodetalhado, ou seja,que
w j ( j )P eq ( j
)=w
j ()P
eq
(); (1.13)
emqueP
eq
denotaadistribui~aode probabilidadedo\ensemblean^onio"assoiadoom
a hamiltonianade Isingaima (h=0):
P
eq
=exp fK X <i;j> i j g: (1.14)
emqueK =J. Glaubermostrou(Glauber,1963)que,aosepressuporqueataxade
transi~ao w
j
() satisfaz o prinpiodobalaneamento detalhado, tem-separa sua forma
w j ()= 2 [1 j tanh(K X Æ i+Æ )℄: (1.15)
Neste ontexto, pode-se evideniar(deOliveira eT^ania Tome,2001)que oalgoritmo,
proessoestoastiomarkovianoomaprobabilidadedetransi~aoaima,paraasimula~ao
domodelodeGlauber,podeserinterpretadoomoummetododeMonteCarloparaa
sim-ula~aodo modelo de Isingem equilbrio. A unia diferenae que adin^amiade Glauber
seenontranolugardadin^amiadeMetropolis. Asolu~aodomodelodeGlauber,modelo
inetio de Ising, fornee as mesmas propriedadesestaionarias domodelo de Ising. Em
quantoaosigniadodaexig^eniaqueataxadeprobabilidadede transi~aow
j (
j
)ouque
as regras mirosopias denindo a din^amia do sistema, obedeam ao prinpio do
bal-aneamentodetalhado. Oprimeirosigniadoequeessa exig^eniagarantequeosistema
evolua, para tempos suientemente longos, para o equilbrio alem da estaionariedade.
Osegundo signiadoequegraas aessaexig^eniatorna-sepossvelaonstru~aode uma
hamiltoniana dosistema assoiada as regrasmirosopias. Portanto, oprinpiodo
bal-aneamentodetalhadoeaondi~aoparapassardasregrasmirosopias,noasodesrito
por w
j (
j
), a qual dene a din^amia do sistema e faz om que este sistema evolua para
tempos suientemente longos em dire~ao ao estado estaionario, para a onstru~ao da
hamiltoniana do sistema que dene a ondi~ao de equilbrio. A ondi~ao de equilbrio e
expressa por uma distribui~ao de probabilidade dos estados dependente do valor da
en-ergia eda temperatura. A rela~aoentre as regras mirosopiasdenindo adin^amiado
sistema e aonstru~ao dahamiltonianadenindo as ondi~oes de equilbrioe o prinpio
do balaneamento detalhado. Como foi mostrado, o exemplo bem-suedido deste
em-preendimento e o modelo din^amio, din^amia de Glauber, do modelo de Ising. Alem
desta tentativade onstruir uma din^amia parao modelo de Ising,que levou ao
entendi-mento do uso de proessos estoastios markovianos para a abordagem de sistemas em
equilbrio e fora do equilbrio outra fonte do uso dos proessos estoastios markovianos
em Me^ania Estatstia de equilbrio foramas proprias diuldadesenontradasna
ten-tativa de resolver o problema basio da Me^ania Estatstia de Equilbrio, que onsiste
em alular a fun~ao de parti~ao e as quantidades termodin^amias omo valores medios
dos estados mirosopios. Essas diuldades levaram ao uso de metodos estoastios
numerios ou metodos de Monte Carlo que onsistem em proessos estoastios
marko-vianos, mas um pouo diferentes dos metodos de Monte Carlo usuais. Esses metodos
estoastios numerios(de Oliveira, 1996) s~aousados para alularsomas dotipo
hfi= X
s
f(s)P(s); (1.16)
emquef(s)eumafun~aodada,orrespondendoaonossog(q
(t);p
(t))menionado
ante-riormenteeP(s)euma distribui~aode probabilidadea priori. No ontexto daMe^ania
Estatstia de Equilbrio disutido anteriormente pode-se ver a relev^ania desse metodo
para alular seus valores medios das quantidades fsias. A probabilidade P(s) no
\en-semble" an^onio e, ent~ao, dada pela distribui~aode Gibbs. Esse metodo, om a
proba-bilidadede Gibbs,eutilizadoparagerar osestadosmaisprovaveisentre todos osestados
aessveis do sistema. Desenvolveu-se assim o metodo de Monte Carlo om o algoritmo
de Metropolisque onsisteemum proesso estoastio markovianoreversvel om ataxa
The Monte Carlo method (by importane sampling) omprises the
sam-pling ofM statess
1 , s
2 ,s
3 ...,s
M
,eah onebeinggenerated withprobability
P(s), and the alulation of the arithmeti mean
f = 1
M M
X
i=1
f(s) (1.17)
whih willbe,then, an estimative for hfi. The essential point of the method
resides in oneivingan algorithmthat generates states with a given a priori
probability (fromrandom numbers generated uniformlyina given interval).
Contudo, oponto de partidapara odesenvolvimentodateoria dos proessosestoastios
foi a abordagem do problema do movimento Browniano. Essa teoria desenvolveu-se em
torno da equa~ao de Langevin e das adeias de Markov e serve para estudar a evolu~ao
temporalde fen^omenosques~aoaleatorios(deOliveira,1996). Pode-seinferirdasanalises
anteriores para os proessos estoastios reversveis, que no aso de modelos de n~
ao-equilbrio, para os quais asregras mirosopias n~ao podem ser assoiadas a uma
hamil-toniana,osmetodosestoastiosfazemuso dessasregrasmirosopiasouprobabilidades
de transi~ao para onduzir o sistema para estados estaionarios om respeito aos quais
n~ao se onhee a distribui~ao de probabilidade das ongura~oes. Portanto, o alulo
dos observaveis deve ser onsiderado, domesmo modoque foi feitoanteriormentepara a
Me^ania Estatstia de Equilbrio, omo valores medios das grandezas fsias ujas
me-didas s~ao feitas para ada das ongura~oes do estadoestaionario. A garantia de que a
evolu~ao dosistema alanou esse estado depende de alguns riterios.
O tema desta tese onsiste na aplia~ao desses metodos estoastios para estudar
fen^omenos rtios e transi~oes de fase tanto para modelos de equilbrio quanto de n~
ao-equilbrio. Noentanto,essa aplia~aodepende daintermedia~aoaindade outrosreursos
desenvolvidosno^ambitodaMe^aniaEstatstiadeEquilbriomasujaaplia~aotambem
vaipara alemdessasfronteiraseseajustam bastantebemaaplia~oesemfen^omenosfora
de equilbrio. Esses reursos, omo universalidade e hipoteses de esala, ontam om
justia~oes enontradas e sustentadas nas analises de grupo de renormaliza~ao 2
.
Tanto estudos teorios quanto experimentais das transi~oes de fase entre os estados
estaionarios de equilbrio onduzirama formula~aode dois oneitos fundamentais para
a ompreens~ao doomportamentortio, o dahipotese de esala (Stanley, 1999), se
ini-iandoomotrabalhode Widom(Widom,1965),eooneitode lassede universalidade,
introduzido iniialmentepor Kadano (Kadano, 1967). Com o oneito de hipotese de
esala 3
enontraram-seesustentaram-seteoriamenterela~oesuniversaisdenominadasde
2
(Thompson,1988),pg.180;(Wilson,1979).
3
leis de esala entre os expoentes rtios desrevendo o omportamento do sistema nas
proximidades do ponto rtio, assim omo enontrou-se o olapso dos dados, que
on-siste naonstru~aode urvasinvariantes portransforma~aode esala. Com ooneitode
lasse de universalidade, o omportamento rtio do sistema e lassiado segundo um
onjuntodepropriedadesuniversaisqueenvolvemassimetrias,asquaispodemser
enon-tradasnahamiltoniana,adimensionalidadedosistema,denidapeladimensionalidadeda
intera~ao,eadimensionalidadedopar^ametrode ordem. A relev^ania deste oneitoesta
no fato de que se pode a partir dele lassiar a imensa variedade dos sistemas naturais
agrupando-os em um numero pequeno de lasses. Como dizStanley:
Empirially, one nds that all systems in nature belong to one of a
om-parativelysmallnumberof suh universality lasses. Twospeimirosopi
interation Hamiltonians 5
appear almost suÆient to enompass the
univer-sality lasses neessary for stati ritialphenomena 6
.
A rela~ao entre esses oneitos de hipotese de esala, expoentes rtios e lasse de
universalidadefornee umriteriooperaionalqueeoriterio dosexpoentes rtios para
disriminar as lasses de universalidades dos diversos sistemas. Comoarma Stanley:
Two systems with the same values of ritial-pointexponents and saling
funtions are said tobelong to the same universality lass 7
.
ou omo armaLandau, parafraseando Fisher,
Those systems whih have the same set of ritial exponents are said to
belong the same universality lass 8
As leis de esala foram desenvolvidas, de maneira mais lara, a partir das tentativas
de expliarosfen^omenos rtios. Gibbs onstruiua Termodin^amianoestilo eformada
Me^ania Analtia de Lagrange, pormeio de poteniaistermodin^amios,os quais, entre
outraspropriedades, apresentamapropriedadedeseremfun~oes homog^eneasde grauum.
Comaresenteinvestiga~aoparaexpliareompatibilizarosfen^omenosdetransi~ao
de faseom osfundamentos daTermodin^amia,perebeu-se que,por meiodos trabalhos
de Widom (Widom, 1965), a fun~aopotenialtermodin^amio por exemplo, a daenergia
livre de Gibbs, deveria ser esrita omo
G(T;H)=G
r
(T;H)+G
s
(T;H); (1.18)
4
(Stanley,1971);(Thompson,1988);pg.180181;(Salinas,1996);(Callen,1985);pg.272-273.
5
EssasduaslassesaqueStanleysereferes~aoadomodelodePottsQ-estadoseadomodelon-vetores,
araterizadoporspinsapazesdevariarsobreestadosontnuos.
6
(Stanley,1999),pg.S361.
7
(Stanley,1999),pg. S359.
8
r
G
s
(T;H), e uma fun~ao termodin^amia singular. Como essa ultima fun~ao domina o
omportamentodosistemanas vizinhanas dopontortioeapropriada reesrev^e-laem
termos de uma variavelreduzida "=(T T
)=T
quese anulanoponto rtio. Do
om-portamento dessa fun~ao potenial termodin^amio singular que desreve os fen^omenos
rtios segue uma outra lei de esala que a dene, agora, omo uma fun~ao homog^enea
generalizada(Salinas, 1996; Stanley, 1971; Wilson, 1979) das variaveis envolvidas. A
hipotese de esala pode ser formulada, ent~ao, armando-se primeiramente que a parte
singular da fun~ao potenial termodin^amio, no aso aquela da energia livre de Gibbs,
G
s
(t;H), para todo positivo,obedee aequa~aofunional,
G
s (
a
; b
H)=G
s
(;H); (1.19)
ou seja, que ela e uma fun~ao homog^enea generalizada. Como o par^ametro ou esala
e arbitrariotem-se, ent~ao, a liberdadede estipular, emprinpio om objetivos
simpli-adores, que a
=1 (Salinas,1996), oque faz om que = 1=a
.
Desta forma,e possvel esrever a transforma~ao de esala que governa a fun~ao
po-tenial de Gibbs singularomo
1=a
G
s
(;H)=G
s (1;
H
b=a
): (1.20)
A fun~ao potenial termodin^amio ontem toda a informa~ao termodin^amia do
sis-tema. Pormeiodasprimeirasesegundasderivadaspodem-seobter,ent~ao,outrasvariaveis
termodin^amias, as equa~oes de estado, assim omo toda uma serie de outras rela~oes
que, por sua vez, est~ao relaionadas om os par^ametros e onstantes relevantes obtidas,
naoutrapontadatermodin^amia(n~aoteoria),ouseja,porinvestiga~oesexperimentaise
emprias. Dentreessasonstantes,destaam-seamagnetiza~ao,asusetibilidade,oalor
espeo, a onstante de expans~ao termia ea ompressibilidade isotermia. Neste
on-texto pode-se denir o fen^omeno de transi~ao de fase apartir do omportamento dessas
grandezas termodin^amias. Por meio das rela~oes da Termodin^amia e da hipotese de
esala aima pode-se deduzir uma famlia de igualdades denominadas de leis de esala
envolvendo emgeral tr^esexpoentes.
A segunda etapa da hipotese de esala e dar origem, por meio de restri~oes, ao
omportamento da fun~ao potenial termodin^amia proximo do ponto rtio, o que
onsiste em proporionar leis de pot^enias desrevendo o omportamento das
quanti-dades termodin^amiasnasproximidadesdopontortio,e,nalmente, onduzir ano~ao
de olapso dos dados por meio da onstru~ao de urvas, fun~oes esala, das
quanti-dades termodin^amias que s~ao invariantes por transforma~ao de esala. Por exemplo,
rtio(Stanley,1999; Salinas, 1996).
M( a
; b
H)= 1 b
M(;H); (1.21)
para =H 1=b
obtem-se
M
H
=M(
H
;1)=F(
H
); (1.22)
em que
H =
H a=b
M
H =
M
H (1 b)=b
; (1.23)
ujos termos denominam-se de magnetiza~ao reesalada e temperaturareesalada ou
re-duzida, eujafun~aoF(
H
)eafun~aoesala. Ograoonstrudoom estasduas
quan-tidadestermodin^amiasproporionaumolapsodeurvasemumauniafun~ao. Comoja
foi menionado,os expoentes rtios servem omo riterios operaionais para identiar
a lassedeuniversalidadedos sistemasnaturais. No entanto,haoutroriterioqueedado
pelogrupo de simetrias enontrados nahamiltoniana para sistemas emequilbrio ounas
din^amiasdenindo aevolu~aodosistema. Ambososriteriospodemsertambem
utiliza-dosparaoasodeproessosestoastiosmarkovianosirreversveis. Umpontoaobservare
queosexpoentesrtioss~aoindependentesdosistemaespeo. Noentanto,elespodem
n~ao ser os mesmos para diferentes sistemas naturais mas, quando os fen^omenos rtios
exibidos poressessistemasnaturais,apresentam omesmoonjuntode expoentes rtios,
ent~ao,neste aso,eles formamuma lassede universalidade. Noontexto destatese duas
lasses dentre as lasses de universalidade s~ao relevantes: a lasse de universalidade de
Ising e a lasse de universalidade da perola~ao direionada (de Oliveira e T^ania Tome,
2001) ou de estados absorventes. Cada uma dessas duas lasses tem um riterio
funda-mental desenvolvido teoriamenteque a dene. A lasse de universalidade domodelo de
IsingedeterminadapeloriteriodenaturezateoriaestabeleidoporGrinstein(Grinstein
etal.,1985): osmodelosquesatisfazemoun~aooprinpiodareversibilidademirosopia
equepossuemapropriedadedenominadade simetriade invers~aodosspins,
i
!
i s~ao
lassiados omopertenentes alasse deuniversalidadedomodelo de Ising. Segundo o
argumento de Grinstein (Grinstein etal.,1985)
Continuous transitions into stationaryferromagnetistates of PCAwhih
do not have assoiated Hamiltonians (i.e., are \irreversible") but whih do
have the \up-down" symmetry familiarfromIsing models, are argued tofall,
forbothstatis anddynamis,inthesame universality lassesaskinetiIsing
models 9
.
9
reionada. Essa lasse de universalidade e araterizada pelo argumento de Janssen
(Janssen, 1981) e Grassberger (Grassberger, 1982) os quais armam que, se um
mod-elo de uma unia omponenteexibeuma transi~aode faseontnuaporum unio estado
absorvente, este modelo pertene a lasse de universalidade da perola~ao direionada
(Brunstein,1999). Essasduas lassesde universalidadeonstituemum dosreursos pelos
quaisoomportamentodamaioriadosmodelostratadosnestatese-modelosde redeom
din^amiasquen~aosatisfazemoprinpiodobalaneamentodetalhado,portanto,modelos
de n~ao-equilbrio - pode ser expliado, pois s~ao tambemompreendidos pelos dois
argu-mentos aima menionados. Assim um dos objetivos desta tese e o de fazer simula~oes
omputaionais por meio de metodos estoastios de varios modelos tanto da lasse dos
modelosdovotantemajoritarioedominoritarioquantodalassedemodelosomestados
absorventes om o proposito de enontrar evid^enias sustentando os argumentos aima.
O outro objetivoede apliara oneitua~aode Yeomans de que
Classes de universalidades s~ao frequentemente lassiadas pelo modelo
mais simples pertenente aelas, 10
para enontrar o que viria a ser o modelo mais simples para a lasse dos modelos do
votantemajoritario.
Como ja foi menionado, os argumentos aima s~ao onjeturas teorias e, portanto,
eles dependemde evid^eniaspara seremsustentados. Havarios metodospara abordaros
fen^omenosrtioseextrairdelesospar^ametrosrtiosomoodovalorrtiodoindutor
da transi~ao de fase e dos expoentes rtios das leis de omportamento do sistema em
torno do ponto rtio. Contudo, pode-se reduzi-los a dois: o metodo denominado de
metodo onvenional, quee aquele de expans~ao emseries, o metodo de expans~ao-, e de
teniasde grupode renormaliza~ao(Barber, 1983),eosegundo metodoeaqueleda
sim-ula~aoomputaional, queonsisteemfazeruso de umasequ^enia denumerosaleatorios,
denominado de metodos estoastios numerios,para simular, de maneiraartiial, uma
situa~aoexperimental. Comessesmetodosreolhemos,porexemplo,evid^enias,que
on-sistem noalulo dos valores dos pontos rtios e dos expoentes rtios, para sustentar
que os modelos tratados satisfazem os argumentos ou onjeturas que os lassiam em
uma ououtralassede universalidade. Poressa raz~ao,ointeresseaquifoaliza-sesobreo
metodo de simula~ao omputaional, empartiular sobre ometodode Monte Carlo om
proessos estoastios markovianos. Este metodo onsiste de dois omponentes
funda-mentais:
1. a gera~ao das medidase osalulos das grandezas relevantes do sistema.
10
Contudo,a ado~aodesses metodos n~aoesem diuldades, poistodas as medidaseos
alulos das grandezas relevantes, que s~ao produzidos por meio de simula~oes
omputa-ionais, s~ao obtidosa partir de sistemasde tamanhos nitos. No entanto, todaa analise
teoria desenvolvida sobre fen^omenos rtios e transi~oes de fase foi feita no limite
ter-modin^amio, portanto, para sistemas innitos. Um papel fundamentale desempenhado,
ent~ao, por teorias que fazem a onex~ao entre esses dois domnios. Este proesso, por
meio do qual geramos e alulamos as grandezas relevantes, e desrito por meio de uma
equa~aode evolu~ao
P
l +1 ()=
X
0
W(j 0
)P
l (
0
); (1.24)
em que a matriz de probabilidade de transi~ao, W(j 0
), pode ser reesrita em termos
de um onjunto de regras mirosopias ouloais araterizando a din^amiado sistema.
Essas regrasdenem amudanade uma ongura~ao paraoutra, segundo, porexemplo,
o metodo\single-spin ip" que sera adotadonessa tese.
Um proesso estoastio markoviano pode ser reversvel ou irreversvel. Ambos s~ao
desritos pelamesmaequa~aodeevolu~ao. Noentanto,seadin^amiadoproessodesrito
pelamatriz de probabilidade de transi~ao n~ao satisfaz o prinpio do balaneamento
de-talhado, ent~ao trata-se de um proesso estoastio irreversvel ou de n~ao-equilbrio. Isto
signia que n~ao sepode assoiar uma hamiltoniana a esse proesso, e, portanto, n~ao se
pode falar aqui de equilbrio, ainda que se possa falar de estaionariedade. A din^amia
egovernada por um onjuntode regras loais ou mirosopias quedepois de um tempo
bastante longo levam o sistema para um estado estaionario. Caso ontrario, se essas
regras satisfazemo prinpio do balaneamento detalhado, ent~ao,pode-se onstruir uma
hamiltoniana assoiadaaosistema e,por aqui,pode-se falarde estadode equilbrio alem
do estado estaionario e para este fen^omeno temos os reursos da Me^ania Estatstia
de Equilbrio. N~ao se pode dizer o mesmo dos proessos estoastios markovianos uja
din^amia n~ao satisfaz o prinpiodobalaneamento detalhado,portanto,lassiando-se
omo fen^omenos de n~ao-equilbrio. Para este aso n~ao ha nenhuma Me^ania Estatstia
de n~ao-Equilbrio (Tome,1996), ainda assim pode-se ontarom uma serie de resultados
teoriosrelevantes, entre osquaisaqueles referentes alassede universalidade. Por
exem-plo, observou-se queas transi~oes de fasesinetiasou sejaemmodelos de n~ao-equilbrio
apresentam omportamento universal desrito por um onjunto de expoentes rtios 11
.
Mas ha mesmo muitos resultados referentes aos fen^omenos rtios e transi~oes de fase
juntamenteomateoria deesala detamanhonito,sustentados pelateoriadogrupode
renormaliza~ao(Thompson, 1988). Empartiular, oresultado que fazom queo modelo
de Isingapresente aqueles expoentes rtiosque o araterizame asimetria\up-down",
11
dade. Essa mesma simetria pode ser enontrada na din^amia assoiada a esse modelo:
a din^amia de Glauber. Desta forma, tambem pode oorrer, omo oorre que modelos
om din^amias ouregras loais ainda que n~ao satisfaam o balaneamentodetalhado, ao
possuirem simetrias, por exemplo, a simetria \up-down", omo e o aso dos modelos da
lasse do votante majoritario, passam a ser lassiados, pelo argumento de Grinstein
(Grinstein et al., 1985), na lasse de universalidade do modelo de Ising. Por meio do
metodode simula~aoomputaionalproura-seent~aoalularos expoentes rtios e
en-ontrar a lasse de universalidade ompatvelom o modelo emquest~ao. Esse e um dos
prinipaistopios desta tese parao aso domodelo dovotante majoritario, minoritarioe
do modelo om estados absorventes. Neste ontexto, de gerar medidase alular ovalor
das grandezasfsiasparaessesmodelospormeiodometododesimula~aoomputaional,
e absolutamente relevante disutir o desenvolvimento do metodo de esala de tamanho
nito. Pois,esseeometodoquepermiteestabeleeraponteentreosresultadosobtidosa
partirdossistemasnitos,omoaquelesproporionadospelos metodosdesimula~ao
om-putaional, om os resultados teorios que s~ao fundamentados no limite termodin^amio,
portanto para sistemasinnitos. Como dizBinder, domesmo modoque Landau 12
,
nite-sizesalingtehniqueshavebeomeaverypowerfultoolforanalysing
ritial phenomena by omputer simulations. 13
Ometododeesalade tamanhonito,Finite SizeSaling,eumproedimento
desen-volvido, iniialmente, por Fisher (Fisher, 1967). O metodo de esala de tamanho nito
estabaseadoemumonjuntodehipotesesdentreasquaisumasedestaaomoahipotese
entral. Eladesreve o omportamento dosistema em torno do ponto rtio atraves de
uma unia variavel,a variavel de esala, denominada de (x) assoiada ao omprimento
de orrela~ao do sistema. A hipotese entral pode ser formulada omo: nas vizinhanas
dopontortiooomportamentode umsistemanitodedimens~aoLedeterminadopela
variavelde esala
y= L
(x)
; (1.25)
emque(x)eoomprimentodeorrela~aodosistemadependente. Considera-sequeesse
omprimento, e fun~ao de um par^ametro, um par^ametro indutor, um ontrole externo,
x, para se adotar um idioma neutro, que diverge para o valor rtio x
, para sistemas
innitos. Aarma~aodeBarberquesustentaessahipoteseentral,noasoemquex=T,
diz que
12
\theunderstandingofnitesizesalingwhihisabasitoolintheanalysisofsimulationaldatanear
phasetransitions"...(Landau,2000)pg. 19.
13
of the bulk ritial temperature T
the behaviour of a system with at least
one large but nite dimension isdetermined by a saled variable y=L=(T)
where (T) is the bulk orrelation lenght and is a harateristi lenght sale
of the system 14
.
SegundoBinder(Binder,1976)eexatamentesobreestahipoteseentralqueedesenvolvida
a teoria daesala de tamanho nito. Como elemesmo diz,
One agrees that near a ritial point there is only one important
hara-teristi length, the orrelation length of order parameter utuations: then
itisplausiblethat nitesize eetsare ontrolledby aomparisonoflengths,
the lineardimension L and this orrelationlength 15
.
Como menionado no texto aima, a variavel (x) e o omprimentode orrela~aodo
sistema. Esseomprimentodeorrela~aoedependentedopar^ametroindutordatransi~ao,
x, que,omoseadmite,para amaioriados asoseT,ou, omonesta tese, opar^ametrop
de probabilidade. Se foremonsiderados,omoilustra~ao,ossistemasmagnetios,ent~ao,
serapossvelinterpretaroomprimentodeorrela~aoomoforneendootamanhotpio(o
tamanho mediode todos osaglomerados)de aglomeradosde spinsorrelaionados. T^
em-se duas situa~oes: em primeiro lugar, esse par^ametro ou variavel de esala diverge para
sistemasinnitos,ouseja,(x)!1,tendovalornitopara sistemasnitos, forneendo,
omo visto, o tamanho araterstio para aquele tamanho e temperatura do sistema,
enquanto,emsegundolugar,parasistemasnitos,essavariavelsopodeatingirnomaximo
a dimens~ao linear, L, do sistema. Como arma a hipotese aima, e a diverg^enia dessa
variavel de esala, , a responsavel pelo omportamento rtio do sistema, e, portanto,
pela singularidade das fun~oes ou grandezas fsias na depend^enia de x
= (x x
)=x
que e o par^ametroindutor de transi~aoreduzido.
Nodesdobramentodaarma~aodeBinder,pode-semenionarquehaevid^eniastanto
experimentaisquantoteoriaspara searmarumasegunda hipoteseque pode ser
formu-lada da seguinte maneira: para sistemas innitos, nas proximidades do valor rtio do
par^ametrox,x
,avaria~aodealgumasquantidadesfsias,Q,omopar^ametroreduzido,
x
=(x x
)=x
,egovernada poruma lei de pot^enia, naforma
Qjx
j
; (1.26)
em que, essa express~ao pode tambem signiar a propria deni~ao do expoente rtio
(Thompson, 1988),
lim
x
!0 h
ln(Q)
ln(x
) i
=: (1.27)
14
(Barber,1983),pg.158-159.
15
Comesta deni~ao,seQ=Q
a
jx j , emqueQ
a
eumaonstante, ent~ao,segue-se 1.27.
Entre as varias quantidades fsias, tambem o omprimentode orrela~ao, , segue a lei
de pot^enia. Pode-se, portanto,expressar daseguinteforma
_jx
xj
; (1.28)
em que e um expoentertio.
Na teoria da esala de tamanho nito, essa mesma quantidade, Q, omporta-se, em
sistemas nitos, de aordo om alei
Q
L
(x)_L z
~
Q( L
): (1.29)
Afun~ao ~
Q(x) euma fun~aode esalasuave, sem singularidadeedesreve umaurva
arredondada e desloada do ponto rtio (Binder, 1976). Por exemplo, as quantidades
fsias magnetiza~ao, M
L
, e susetibilidade,
L
, aluladas para sistemas de tamanhos
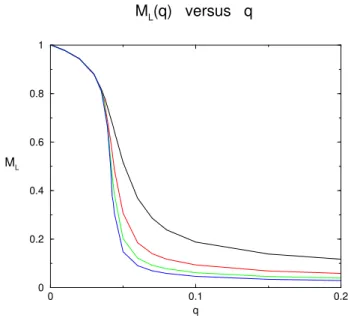
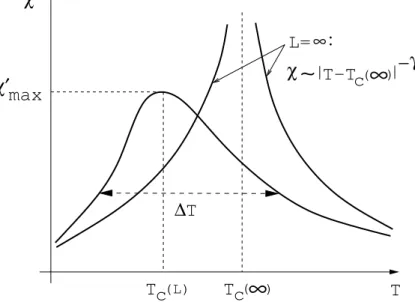
nitos temaformas orrespondentes apresentadas nasguras1.1e1.2naproximase~ao.
Deaordoomahipoteseentralnasproximidadesdopontortio,portanto,noaso
em que
lim L
!0; (1.30)
tem-se, ent~ao,que o omportamento de ~
Q(w)e talque
~
Q ( L
)(
L
)
z
: (1.31)
Pois om isso tem-se a express~ao da exig^enia do omportamentodo sistema omo uma
leide pot^eniadado queseesperaquenolimitetermodin^amioadepend^enia emL deve
sumir, o sistema e (virtualmente) innito. Portanto, om as rela~oes 1.29, 1.31 e 1.26
obtem-se,poronseguinte, oomportamentodaquantidade Q
L
(x)noasodosistemano
limite termodin^amio ousistema innito,ou seja,
Q
L
(x)_ z
_jx x
j
z
: (1.32)
Comparando1.32 om 1.26 tem-se, ent~ao,que
z =
: (1.33)
Com esta rela~aopode-se reesrever 1.29 naforma
Q
L
(x)=L =
~
Q( L
): (1.34)
Para sistemas nitos, mas om x=x
, o omprimentode orrela~ao n~ao pode passar de
L, portanto, L,e
Q
L (x
)L
=
magnetio, tomado omo ilustra~ao da teoria dos fen^omenos, o objetivo de estudar o
fe^omeno de transi~ao de fase faz uso das varia~oes que oorrem nas propriedades fsias
desritaspelasquantidadesfsiasomofun~aodatemperatura,porexemplo,opar^ametro
de ordem M, quee a magnetiza~ao espont^anea, da susetibilidade , que e a
susetibil-idade magnetia, e do umulante de quarta ordem. Esse objetivo e abordado em tr^es
etapas. Na primeira etapa, proura-se alular o valor rtio do par^ametro indutor da
transi~ao. O reurso entral usado e o umulante de quarta ordem 16
denido pela
ex-press~ao,
U
L =1
hm 4
i
L
3hm 2
i 2
L
: (1.36)
Na segunda, proura-se identiar a natureza da transi~aode fase. Aqui os reursos s~ao
os omportamentosaraterstios da grandeza magnetiza~ao,M
L
, esusetibilidade,
L ,
om o tamanho do sistema L. Na tereira etapa, segue-se a hipotese de esala, e, por
aqui, pretende-seidentiar alasse de universalidade do modelodo sistema. Istoefeito
pormeio da aplia~aodaanalise de esala de tamanho nito,ou aabordagem de esala,
que segundo Stanley (Stanley, 1999) onsiste de duas ategorias de predi~oes, em suas
proprias palavras,
The saling hypothesis has two ategories of preditions, both of whih
havebeenremarkablywellveriedbyawealthofexperimentaldataondiverse
systems. The rst ategoryisaset of relations,alledsalinglaws, that serve
to relate the various ritial-point exponents....[mais abaixo℄. The seond
ategory isa sort ofdata ollapse, whihis perhapsbest explained interms
of our simpleexample of a uniaxial ferromagnet.... 17
Destaforma,segundo esseroteiro,atereiraetapadivide-seemduaspartes. Naprimeira
parte, proura-seobterosvalores dosexpoentes rtios menionadosaimaomosquais
pode-seidentiaralassedeuniversalidade. Oreursoqueonstituiaprimeiraategoria
dahipotesede esalas~aoasleisde esalamenionadasaima,quesigniamtantoasleis
de pot^eniasquantoasrela~oesentre osexpoentes rtios. Pormeiodasleisdepot^enias
edosdadosdasimula~aoomputaionalobt^em-seosexpoentesrtios. Comosexpoentes
rtios identia-se alasse de universalidade domodelo emquest~ao. Na segunda parte,
da tereiraetapa,proura-seanalisar aonsist^enia dessesresultados envolvendo tantoo
valorrtio do par^ametro indutor da transi~ao quanto os valores dos expoentes rtios
om o reurso do olapso dos dados. Nessa parte, utiliza-se a segunda ategoria da
hipotese de esala, que esta relaionada om a onstru~ao de uma fun~ao de esala para
16
(Plishke,1994),pg.289;(deOliveira,1996),pg.1322;(deOliveiraandChiappin,1997),pg.311-312;
(Binder,1997),pg.523.
17
sistema, omo armadopor Stanley,
The saling hypothesis predits that all the urves of this family an be
\ollapsed" onto a single urve provided one plots not M versus " but rather
a saledM (M dividedbyH tosomepower) vs asaled" ("divided by H
to some dierent power) 18
.
Essas rela~oes podem ser desritas 19
, omo,
M
L
(q)=L =
~
M(L 1=
") (1.37)
L
(q)=L =
~ (L
1=
") (1.38)
U
L (q)=
~
U(L 1=
") (1.39)
em que " = (q q
)=q
. Por sua vez essas rela~oes de esala mostram que as grandezas
menionadas omportam-se, no ponto rtio q
, ou exibem um omportamentodesrito
porleis de pot^enia 20
, pois ~
M(0), (0),~ e ~
U(0) tornam-se onstantes, forneendo, para a
magnetiza~ao, M, a leide pot^enia,
M(q =q
)/L
=
~
M(0); (1.40)
enquanto para asusetibilidade magnetia,
(q=q
)/L
=
~
(0): (1.41)
Restringe-se aqui apenas a essas grandezas, pois elas s~ao reorrentes. Destas leis de
pot^enias podem-se obter os expoentes rtios por meio dos dados da simula~ao
om-putaional e de um grao log-log relaionando
lnM(q=q
)=
lnL+ln ~
M(0); (1.42)
e
ln(q =q
)=
lnL+ln(0);~ (1.43)
que desempenham papel fundamental omo riterios para resolver o problema de qual e
a lasse de universalidade dos modelos emquest~ao.
Trabalhostantoexperimentaisquantoteoriosrevelaramvaloresnumeriospara esses
expoentes rtios para modelos espeos dando origem a lasses de universalidades
18
verpg. S358-S359(Stanley,1999).
19
(Stanley,1999),pg.S358;(Landau, 2000),pg.77-78; (deOliveira, 1996),pg.1322;(Binderand
Heer-mann,1988),pg.105-109;(deOliveiraandChiappin,1997),pg. 311-312.
20