EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 1

EQUAÇÕES DI FEREN CI AI S

ORDI N ÁRI AS DE 1

a

_ORDEM

1 1 – M ÉTODOS N UM ÉRI COS P/ EDOS de 1

a

_ORDEM

•

Quando um a fórm ula explícit a não puder ser obt ida para a solução de um a EDO, ou quando a m esm a é m uit o com plicada, em pregam -se m ét odos num éricos para o cálculo aproxim ado da solução.

•

O m ét odo de it eração de Picard é capaz de fornecer soluções aproxim adas para EDOs, no ent ant o, não é int eressant e um a vez que o procedim ent o it erat ivo deve ser repet ido para cada pont o

x

em que se desej ar a solução.

A - MÉTODOS PASSO A PASSO

•

Por exem plo, para um problem a unidim ensional, a m alha espacial pode ser obt ida em pregando- se um passo uniform e

_h

( conform e figura) , de form a que:

1 0

;

2 0

2 ;

3 0

3

- MÉTODO DE EULER

•

A idéia de obt enção da solução é obt ida a part ir da definição da expansão de um a função em t orno de um pont o (Série de Taylor) :

2

(

)

( )

'( )

''( )

2

h

y x

+

h

=

y x

+

hy x

+

y x

+

"

( 1 )

•

Para pequenos valores de

h

, as pot ências

h

2_,

_h

3_{, …, são m uito} pequenas. Logo sugere- se que a expansão sej a:

(

)

( )

'( )

y x

+

h

≅

y x

+

h y x

( 2 )

'( )

( , )

y x

=

f x y

•

Da equação diferencial:

(

)

( )

( , )

•

A expressão ant erior sugere o seguint e procedim ent o de m archa

a) No prim eiro passo, a partir da inform ação em

x = x

₀:

1 0

(

0

,

0

)

y

=

y

+

h f x y

( 4 )

1 0

( )

(

)

y x

=

y x

+

h

- Que é um a aproxim ação para:

b) No segundo passo, a partir da aproxim ação anterior:

2 1

( ,

1 1

)

y

=

y

+

h f x y

( 5 )

2 0

(

)

(

2 )

c) De um a m aneira gera, o m ét odo é escrit o com o:

1

(

,

)

n n n n

y

₊

=

y

+

h f x y

( 6 )

•

Geom et ricam ent e, o m ét odo é um a aproxim ação da curva

y(x)

por um polígono cuj o 1o _{lado é t angent e à curva em}

_x

Observações:

•

Obviam ent e, est e m ét odo não é usado na prát ica, pois o erro int roduzido ao longo do procedim ento de m archa cresce com o acréscim o da coordenada de m archa.

•

No ent ant o, ele explana claram ent e o princípio dos m ét odos baseados em Série de Taylor.

•

O m ét odo de Euler pert ence à classe de m ét odos num éricos denom inados de m ét odos de 1a _{ordem, pois a expansão foi}

t runcada no t erm o cont endo apenas a prim eira pot ência de

h

.

•

A om issão dos out ros t erm os causa um erro, o qual é denom inado de erro de t runcam ent o.

Exem plo 1 : M ét odo de Euler

Aplique o Mét odo de Euler para o seguint e PVI escolhendo um a m alha com

h = 0.2

.

'

; (0)

0

y

= +

x

y

y

=

Solução:

( , )

;

0.2

f x y

= +

x

y

h

=

- Para est e problem a:

- Logo, a Eq. ( 3) torna- se:

y

_n+1

=

y

_n

+

0.2(

x

_n

+

y

_n

)

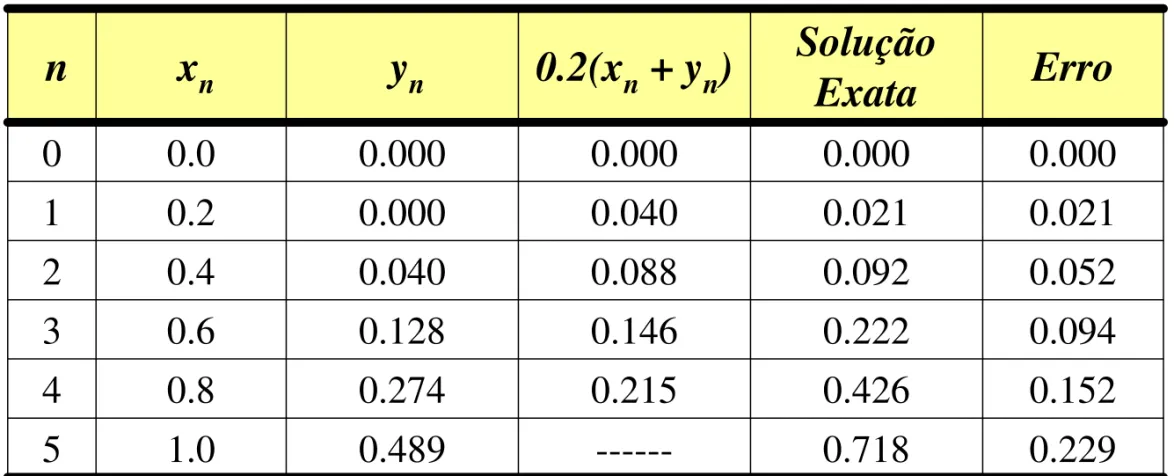
- A aproxim ação acim a é com parada com a solução exat a ( com o?) e os result ados são m ost rados na t abela a seguir:

( )

x

1

Tabela 1 - M ét odo de Euler

'

; (0)

0

y

= +

x

y

y

=

n

x

_n

y

_n

0.2(x

_n

+ y

_n

)

Solução

Exata

Erro

0

0.0

0.000

0.000

0.000

0.000

1

0.2

0.000

0.040

0.021

0.021

2

0.4

0.040

0.088

0.092

0.052

3

0.6

0.128

0.146

0.222

0.094

4

0.8

0.274

0.215

0.426

0.152

- MÉTODO DE EULER MELHORADO ( Heun)

•

A ret enção de m ais t erm os na série, para gerar m ét odos m ais precisos, leva no ent ant o a alguns problem as prát icos.

•

A subst it uiçao de

y’ = f(x,y)

na expansão produz:

2 3

(

)

( )

'

''

2

6

h

h

y x

+

h

=

y x

+

hf

+

f

+

f

+

"

( 7 )

•

Observe, porém , que

y

em

f

é função de

x

. Logo:

'

_{x y}

'

_{x y}

f

=

f

+

f y

=

f

+

f f

( 8 )

•

A est rat égia é evit ar a avaliação de t ais derivadas e subst it uí- la pela avaliação de

f

apenas, em valores “ apropriados” de

(x,y)

. “ Apropriados” no sent ido de t ornar a ordem do m ét odo a m ais elevada possível.

•

O prim eiro m ét odo a ut ilizar est a est rat égia é o denom inado M ét odo de Euler M elhorado ( M ét odo de H eun) .

•

Em cada passo avalia- se inicialm ent e um valor auxiliar:

*

1

(

,

)

n n n n

y

₊

=

y

+

h f x y

Mét odo de Eu ler

( 9 )

•

Em seguida, avalia- se a aproxim ação final:

* 1

(

,

)

(

1

,

1

)

2

n n n n n n

h

•

O Mét odo de Euler Melhorado tem um a int erpret ação física sim ples:

- No int ervalo

x

_n para

x

_n

+ h/2

, a solução

y

é aproxim ada pela linha ret a que passa por

_(x

_n

_{, y}

_n

₎

com inclinação

_f(x

_n

_{, y}

_n

₎

, e ent ão cont inua- se ao longo de um a linha ret a com inclinação

f(x

_n+1

, y

*

Observações:

•

É um M ét odo Predit or- Corret or, pois em cada passo da m alha, prim eiro se prever um valor com a Eq. ( 9 ) , post eriorm ent e se corrige pela Eq. ( 1 0 ) .

•

É um M ét odo de Segunda Ordem, pois o erro de t runcam ent o é da ordem de

h

3_.

Algorít m o do Mét odo de Euler Melhorado

•

EN TRADA: Valores iniciais de

x

₀,

y

₀,

h

e núm ero de passos

N

.

•

SAI DA: Aproxim ação

y

_n+1 para a solução

y(x

_n+1

)

em

x

_n+1

= x

₀

+

(n+1)

h

, onde

n = 0, …, N-1

.

x

_n

= x

₀

y

_n

= y

₀

LOOP:

n = 0, 1, …, N-1

x

_n+1

= x

_n

+ h

k

₁

= h f

(

x

_n

, y

_n

)

k

₂

= h f

(

x

_n+1

, y

_n

+ k

₁

)

y

_n+1

= y

_n

+

(

k

₁

+ k

₂

)/

2

I m prim e

x

_n+1 e

y

_n+1

x

_n

= x

_n+1

y

_n

= y

_n+1

Exem plo 2 : M ét odo de Euler M elhorado

Aplique o Mét odo de Euler Melhorado para o PVI do exem plo ant erior sob as m esm as condições de m alha.

Solução:

( , )

;

0.2

f x y

= +

x

y

h

=

- Para est e problem a:

- Logo, do algorítm o:

1

0.2(

n n

)

k

=

x

+

y

[

]

2

0.2

n

0.2

n

0.2(

n n

)

k

=

x

+

+

y

+

x

+

y

[

]

1

0.2

2.2

2.2

0.2

2

n n n n

y

₊

=

y

+

x

+

y

+

1

0.22(

)

0.02

n n n n

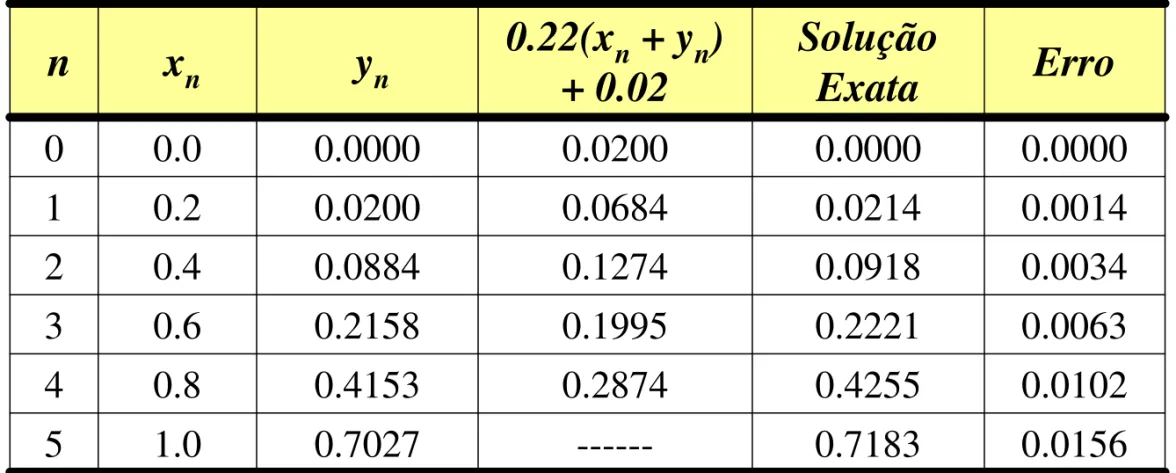
Tabela 2 - M ét odo de Euler M elhorado

'

; (0)

0

y

= +

x

y

y

=

n

x

_n

y

_n

0.22(x

n

+ y

n

)

+ 0.02

Solução

Exata

Erro

0

0.0

0.0000

0.0200

0.0000

0.0000

1

0.2

0.0200

0.0684

0.0214

0.0014

2

0.4

0.0884

0.1274

0.0918

0.0034

3

0.6

0.2158

0.1995

0.2221

0.0063

4

0.8

0.4153

0.2874

0.4255

0.0102

- MÉTODO DE RUN GE- KUTTA

•

Um dos m ét odos de m aior aplicação prát ica.

•

Em cada passo deve- se prim eiro calcular quat ro quant idades auxiliares

_k

₁,

_k

₂,

_k

₃ e

_k

₄, para a partir de então um novo valor

_y

_n+1.

•

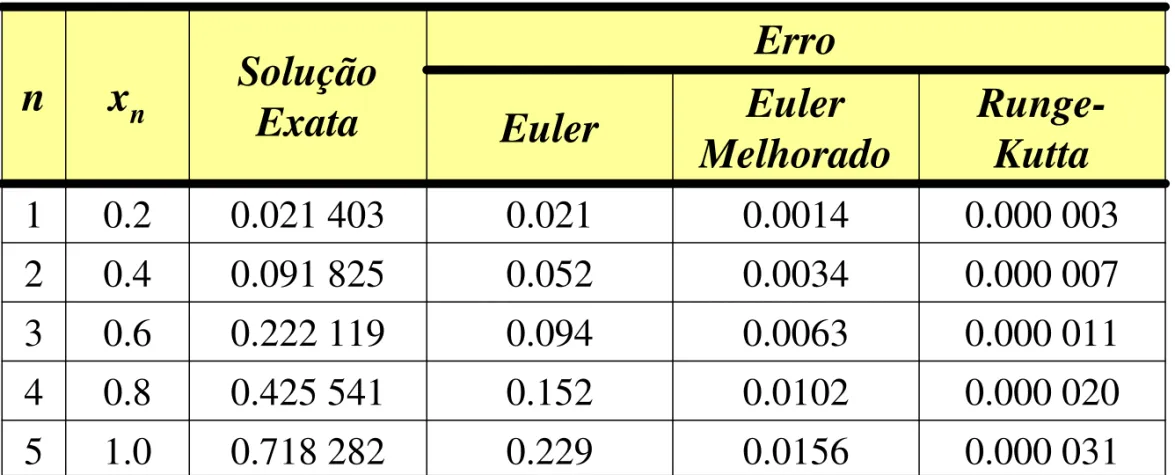
Pode ser m ost rado que o erro de t runcam ent o é da ordem de

h

5_, logo o é um m ét odo de quart a ordem.

Algorít m o do M ét odo de Runge- Kut t a

0 0

•

SAI DA: Aproxim ação

_y

_n+1 para a solução

_y

(

x

_n+1

)

em

x

_n+1

= x

₀

+

(

n+1

)

h

, onde

n = 0, …, N-1

.

LOOP:

n = 0, 1, …, N-1

k

₁

= h f

(

x

_n

, y

_n

)

k

₂

= h f

(

x

_n

+ h/2, y

_n

+ k

₁

/2

)

k

₃

= h f(x

_n

+ h/2, y

_n

+ k

₂

/2)

k

₄

= h f(x

_n

+ h, y

_n

+ k

₃

)

x

_n+1

= x

_n

+ h

y

_n+1

= y

_n

+

(

k

₁

+ 2k

₂

+ 2k

₃

+ k

₄

)/

6

I m prim e

x

_n+1 e

y

_n+1

FIM LOOP

Exem plo 3 : M ét odo de Runge- Kut t a

Aplique o Mét odo de Runge Kut t a de 4a _{Ordem para o PVI do exem plo}

ant erior sob as m esm as condições de m alha.

Solução:

( , )

;

0.2

f x y

= +

x

y

h

=

- Para est e problem a:

- Logo, do algorítm o:

1

0.2(

n n

)

k

=

x

+

y

[

]

2

0.2

n

0.1

n

0.5

1

k

=

x

+

+

y

+

k

[

]

3

0.2

n

0.1

n

0.5

2

k

=

x

+

+

y

+

k

[

]

4

0.2

n

0.2

n 3

k

=

x

+

+

y

+

k

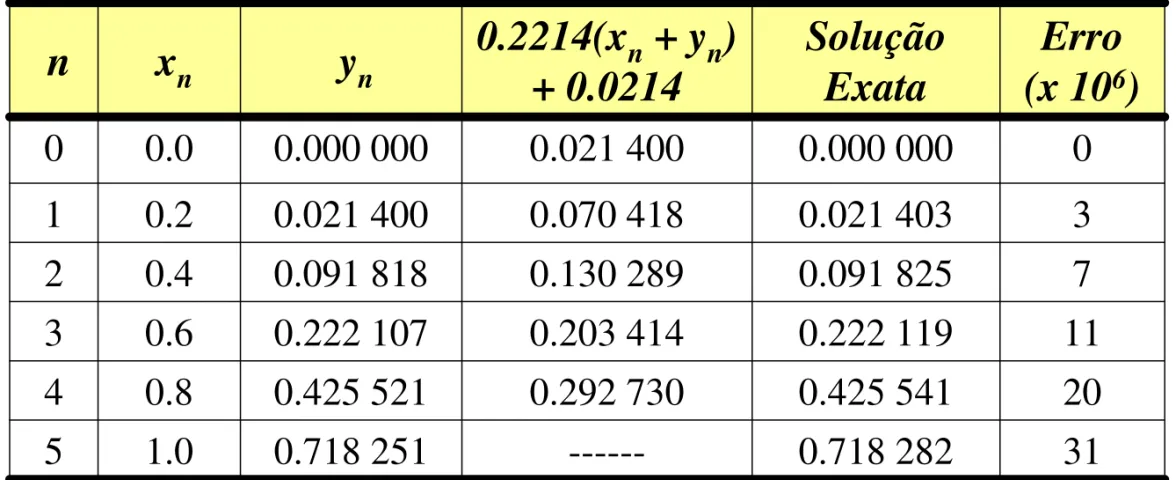
- Fazendo as subst it uições ( não recom endadas ! ) :

1

0.2214(

)

0.0214

n n n n

Tabela 3 - M ét odo de Runge- Kut t a

'

; (0)

0

y

= +

x

y

y

=

n

x

_n

y

_n

0.2214(x

n

+ y

n

)

+ 0.0214

Solução

Exata

Erro

(x 10

6

₎

0

0.0

0.000 000

0.021 400

0.000 000

0

Tabela 4 - Erro Produzido pelos 3 M ét odos

'

; (0)

0

y

= +

x

y

y

=

Erro

n

x

_n

Solução

Exata

_Euler

Euler

Melhorado

Runge-Kutta