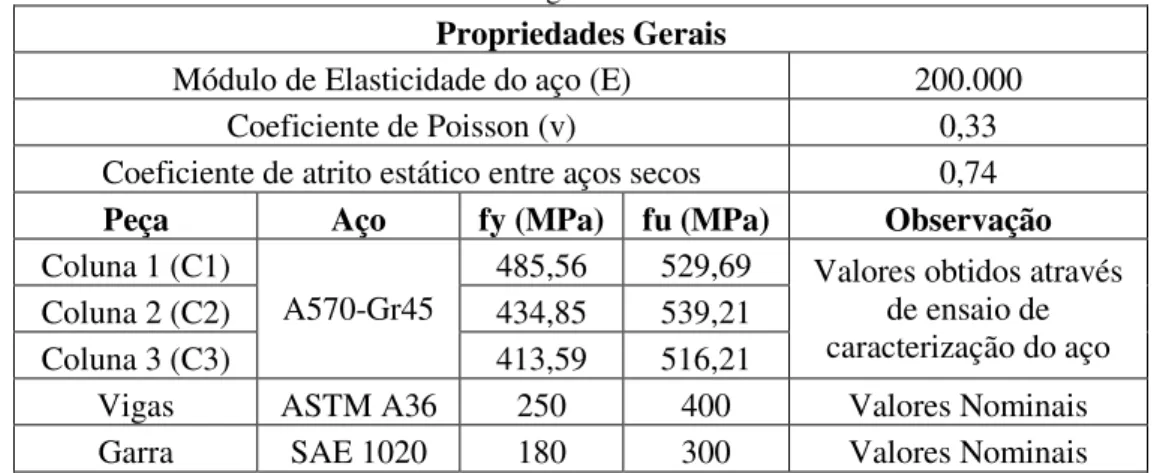
ANÁLISE DE LIGAÇÕES DE SISTEMAS DE ARMAZENAGEM INDUSTRIAL TIPO PORTA-PALLETS
Texto
Imagem


Documentos relacionados
A ligação analítica flexível (chapa de topo com pino) conforme demonstrada no trabalho é representada como o modelo simplificado, mas na prática utiliza-se
Este estudo apresenta como tema central a análise sobre os processos de inclusão social de jovens e adultos com deficiência, alunos da APAE , assim, percorrendo
O presente estudo objetivou demarcar a idade de segregação, por meio da variação radial da massa espe- cífica básica, caracterizar o comportamento de propriedades físicas no
No entanto, maiores lucros com publicidade e um crescimento no uso da plataforma em smartphones e tablets não serão suficientes para o mercado se a maior rede social do mundo
O valor da reputação dos pseudônimos é igual a 0,8 devido aos fal- sos positivos do mecanismo auxiliar, que acabam por fazer com que a reputação mesmo dos usuários que enviam
No acórdão Oosthoek’s Uitgeversmaatschappij ( 70 ), que o Governo austríaco refere nas suas observações, o Tribunal de Justiça concluiu, relativamente à compatibilidade de
Taking into account the theoretical framework we have presented as relevant for understanding the organization, expression and social impact of these civic movements, grounded on
Os dados referentes aos sentimentos dos acadêmicos de enfermagem durante a realização do banho de leito, a preparação destes para a realização, a atribuição