RECONHECIMENTO DE PADRÕES GRÁFICOS COM O APOIO
DO SOFTWARE GEOGEBRA: OS CASOS DA CONVERGÊNCIA
PONTUAL E UNIFORME
Francisco Regis Vieira Alves* Resumo: De modo particular, quando nos atemos ao caso da convergência de uma família ou sequência de funções
fn n IN , registramos nos livros de História da Matemática, o tortuoso esforço de figuras emblemáticas, tais como: Cauchy, Bolzano, Weierstrass; no sentido de indicar bases sólidas e consistentes para tal noção. Hodiernamente, verificamos a descrição de várias formas de convergência, segundo os autores de livros de Análise Real, dentre elas, sublinhamos a convergência simples (ou pontual) . . C S n f f e a convergência uniforme . . C U nf f . De modo específico, destacamos as recomendações de Lima (2010), com o intuito da identificação, distinção e compreensão dessas duas formas de convergência. Suas indicações, de natureza heurística, são significadas a partir da exploração de situações com o uso do software
Geogebra. Com tal expediente, estruturamos situações que proporcionam: (i) o
entendimento topológico do comportamento da família de funções (de modo local e global); (ii) a possibilidade de visualização de gráficos complexos e inexequiveis no ambiente lápis/papel; (iii) identificação visual da função candidata ao limite, em cada tipo de convergência; (iv) visualização da região do plano aonde ocorre a convergência uniforme. Com a presente discussão, questionamos a abordagem standard em Análise Real que restringe a atividade do aprendiz ao domínio e aplicação de definições formais, negligenciando o caráter intuitivo e heurístico desse conteúdo.
Palavras-chave: Convergência Pontual e Uniforme. Visualização. Geogebra. Ensino
1 Introdução
Análise Real é, reconhecidamente, um ramo de estudo em Matemática, que fornece vários exemplos de entraves ao entendimento, dada sua natureza intrínseca. Com efeito, deparamos um variado repertório de conceitos e definições formais que exigiram séculos, até mesmo de matemáticos profissionais, para não apenas sua descoberta, mas também, seu completo domínio e descrição consistente, do ponto de vista dos padrões de uma teoria formal.
Neste âmbito, uma noção que constituiu o “fio de Ariadne” em Matemática, na transição dos séculos XIX para o século XX, diz respeito à noção de convergência
* Doutor em Educação com ênfase no ensino de Matemática e Mestre em Matemática (UFC). Professor
(BOTTAZZINI, 1980). Neste sentido, vale recordar que no século XVIII, “mesmo os fundamentos do Cálculo permaneceram pouco esclarecidos (KLINE, 1980, p. 140)”. Em nossa discussão, diante das várias possibilidades e tipos de convergência, discutimos, em termos matemáticos simbólicos, a convergência simples (ou pontual), que se denota por
. . C S n
f f e a convergência uniforme, descrita por . . C U n
f f .
Colocaremos em destaque, sobretudo, alguns critérios e descrições comentadas por Lima (2010), em seu livro intitulado Curso de Análise. Mostraremos que, alguns desses critérios propostos, em determinados aspectos, acentuam o caráter intuitivo e metafórico para sua interpretação, entretanto, podem ser tornar inviáveis e pouco operacionalizáveis, no caso de exemplos variados e diferentes, dos quais, encontramos em sua obra.
Outro elemento facilmente explorado com o software Geogebra diz respeito ao entendimento de propriedades topológicas, na medida em que podemos visualizar e manipular a família das funções, de modo local e global, na condição de determinação para a variação de certas funções do programa. A potencialidade do software permite a aquisição de um significado dinâmico e intuitivo, antes que o lógico-formal que, de modo standard, finda por ser priorizado nos rituais indefectíveis de ensino que deparamos no locus acadêmico (ARTIGUE, 2003).
Por fim, o desafio que delineamos e apresentamos ao leitor, a partir do objeto de nossa discussão, refere-se ao fato da condução de um ensino, dos conteúdos de Análise Real, não apenas amparado em modelos lógico-formais ordinários. Mas, também, na condução de uma mediação de ensino afetada e modificada pela tecnologia.
2 Convergência pontual e uniforme e um pouco de sua história
O período histórico em que evidenciamos a grande influência de Cauchy e Bolzano ficou marcado por duas lacunas: o primeiro atinente ao conceito de convergência uniforme; enquanto que o segundo diz respeito ao conceito de continuidade uniforme. Hairer & Wanner (2008, p. 213) completam que “ambas as lacunas foram preenchidas por Weierstrass (na segunda metade do século XIX)”.
Hodiernamente, em alguns dos livros de Análise Real (AKSOY & KAMSHI. 2010; BRUCKNER, BRUCKNER & THOMSOM, 2001; DAVIDSON & DONSIG, 2010; LIMA, 2006; KRANTZ, 1951; ROSS, 1980; TRENCH, 2003) que consultamos, deparamos as seguintes definições.
Definição 1: Diz-se que a sequência de funções fn:X IR converge simplesmente (pontualmente) para a função f X: IR quando, para cada xX a sequência de números
f x f x f x f x1( ), 2( ), 3( ), 4( ),...., f xn( ),...
converge para o número( )
f x . Ou seja, para todo xX fixado, tem-se que lim n( ) ( )
n f x f x . De modo resumido, escreveremos . . c p n f f ou . . c s n f f .
Definição 2: Diz-se que a sequência de funções fn:X IR converge uniformemente para f X: IR quando, para todo 0, existe n0IN tal que
0 n( ) ( )
nn f x f x , seja qual for xX .
Esta última definição descrita em Lima (2010, p. 365) é devida ao matemático Weierstrass que, segundo Hairer & Wanner (2008, p. 215), foi fornecida em 1841. Ademais, podemos denotar n0( ) 0 para evidenciar que este índice não depende do ponto xX . Diferentemente do caso da definição 1, em que escrever
lim n( ) ( )
n f x f x , equivale a se tomar 0, para cada xX (fixo, todavia, arbitrário), obtemos n x( , ) 0, tal que f xn( ) f x( ) para todo nn x( , ) .
Por outro lado, ainda em relação à definição de convergência pontual, destacamos a seguinte descrição heurística fornecida por Lima (2010) quando indica que:
Dizer que fn f simplesmente em X significa que, fixado arbitrariamente um ponto xX , os gráficos das funções fn
intersectam a vertical levantada pelo ponto ( , 0)x numa sequência de pontos cujas coordenadas convergem para f x( ). Coletivamente, porém, os gráficos das fn podem ser bem diferentes do gráfico de f
e mesmo nunca se aproximarem dele. (LIMA, 2010, p. 364).
Um entrave que apontamos nessa orientação, fornecida por Lima, refere-se ao repertório limitado de situações, nas quais, conseguimos empregar, de modo prático, tal procedimento. Todavia, vamos ilustrar essa ultima recomendação no âmbito do entendimento de um problema com um viés histórico relevante. Nesse sentido, Hairer & Wanner (2008, p. 215-216) discutem o seguinte problema: existe uma sequência de funções contínuas f xn( ) que convergem para uma função contínua f x( ), ou seja,
A história deste problema mereceu atenção dos matemáticos no período entre 1850 até 1880, mesmo diante de numerosas tentativas e provas inconsistentes, como no caso de uma fornecida por figuras emblemáticas, como G. Cantor, em 1880 (HAIRER & WANNER, 2008, p. 216). Neste sentido, temos o caso da seguinte família de funções
2 2
( ) 2 1
n
f x nx n x . Como no jargão matemático, os autores Hairer & Wanner (2008, p. 216) comentam que “pode ser verificado facilmente que lim n( ) 0
n f x , para todo x0.”. Reparemos que para x 0 fn(0)0 e para x0, escrevemos
2 2 2 lim 1 n nx n x 2 2 2 2 lim 0 (0 ) 0 1 n x n x n x
, para cada xIR
0 (ver fig. 1-I).Todavia, com base nessa argumentação, não evidenciamos uma relação explicita, que indique as relações de dependência n( , ) x , em conformidade com a definição 1. Mas,
desejamos verificar 2 2 2 0 2 2 2 2 2 2 ( 2) 2 2 0 1 1 nx nx nx e n x x n x n n x n x .
Podemos ainda inferir as seguintes condições n1( , ) x x 2x 12 2 e 2
1( , ) 2 1 2
n x x x , quando tomamos xIR
0 . Agora, evidenciamos as relações de dependência do ponto xIR e do 0 fornecido de modo inicial.Cabe ainda observar a inexistência do apelo a qualquer caráter perceptual, com origem em seu comportamento gráfico-geométrico, seguindo apenas a definição formal 1. Todas as nossas ilações são originadas, de modo restrito, a partir do raciocínio lógico dedutivo, de natureza linear (ALVES, 2012, p. 152).
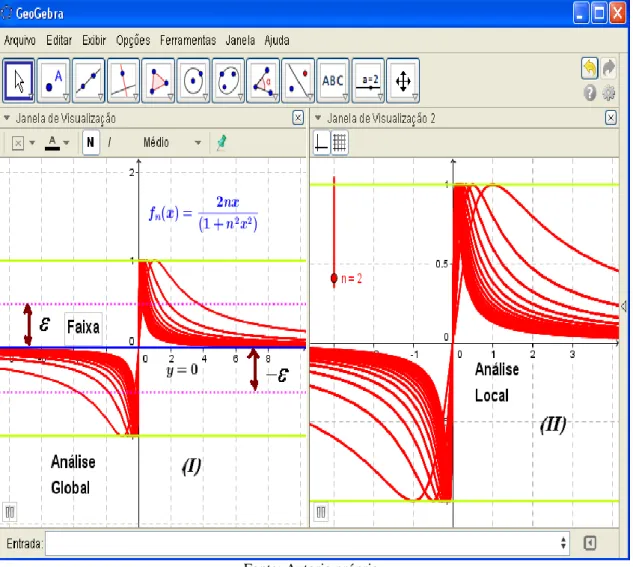
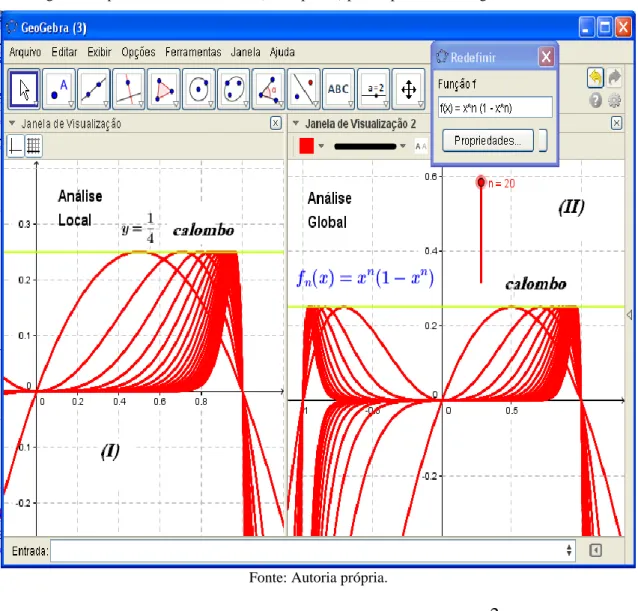
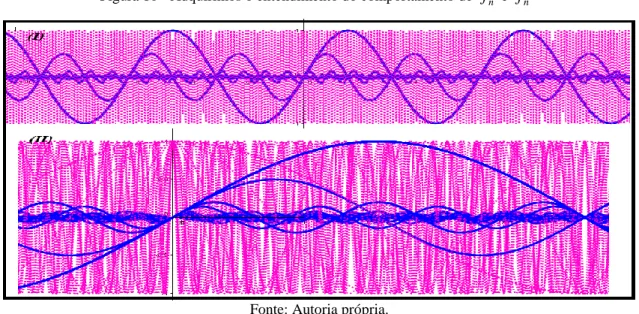
Deste modo, segundo a definição 1, mostramos a convergência sugerida pelos autores Hairer & Wanner (2008, p. 216), apesar de que, por meio deste expediente, apoiamos toda nossa argumentação, somente em inferências de ordem lógico-matemáticas. Neste caso deparamos uma primeira dificuldade de apoiarmos nosso raciocínio no expediente descritivo e qualitativo indicado por Lima (2010, p. 364). Por outro lado, com base no comportamento gráfico das funções dessa família (obtido com o software Geogebra), podemos imaginar, para valores grandes xIR e n as funções tendem a se aproximar, a se “acumular” como um “cabo” de diâmetro 0
(fig. 1-I). Não obstante, para valores x0, divisamos que há uma dispersão (afastamento), para determinadas funções componentes dessa família de funções (fig.
I-II). Observamos que o efeito gráfico do comportamento dos membros da família f n
pode ser obtido por intermédio da função (habilitar) rastro do Geogebra. Na figura 1-I, divisamos que a família ( ) 2 2 2
(1 ) n nx f x n x
admite a reta assíntota
horizontal y0, quando desenvolvemos um parecer global de seu comportamento.
Figura 1 - Identificação visual da C.S. e C.U. segundo o critério de Lima (2010, p. 364).
Fonte: Autoria própria.
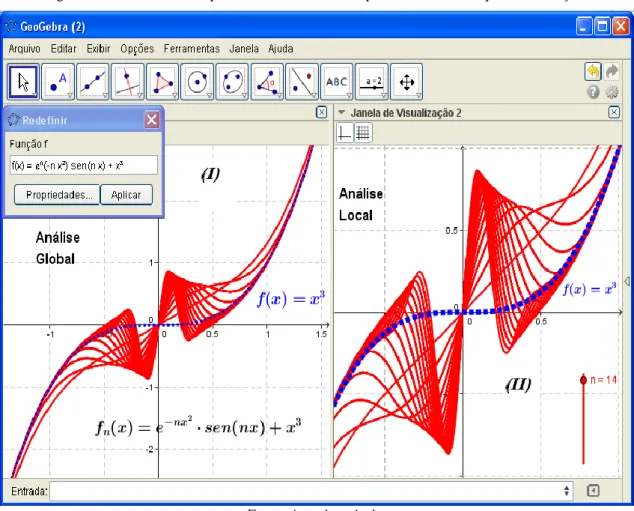
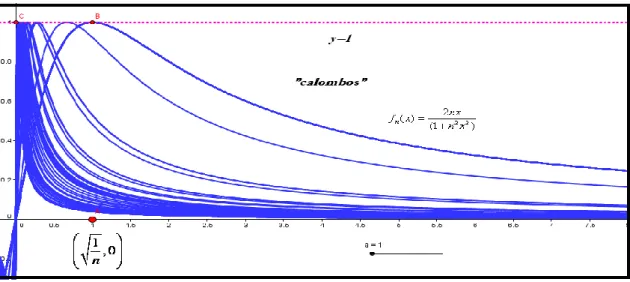
Em vários casos, lidamos com funções complexas, cuja descrição do gráfico se torna inexequível, sem o modelo computacional. Por exemplo, consideremos a família definida por f xn( )enx2sen nx( )x3, tomando valores no intervalo [ 1,1] . Por outro lado, considerando a restrição [ ,1]c , com c0, podemos escrever
2 2 2 2 3 ( ) 1 1 ( ) nx ( ) n nx n x n c sen nx f x x e sen nx e e e (ver figura 2).
Reparemos que se 2 2 2 2
0 0 nx nc 0
x c nx nc e e . Mas agora, podemos avaliar o limite da expressão 1 en c2, quando n , e agora, não levamos mais em consideração aos pontos do conjunto x[ ,1]c . Com base apenas numa argumentação formal, podemos elaborar a ilação relativa à qual, a família
2 3
( ) nx ( )
n
f x e sen nx x converge uniformemente para a função f x( )x3 (fig. 2-II). Uma das vantagens do software consiste no fato de que, escolhendo, por exemplo, n100, podemos descrever o comportamento de uma boa quantidade de funções componentes dessa família
n( )
n IN
f x . Indicamos tal fato na figura 2. A identificação visual da candidata à convergência é imediata (fig. 2-I).
Figura 2 - Com o software, podemos descrever o comportamento de uma parte das funções
Fonte: Autoria própria.
Outra característica que indica de que modo a convergência simples intervêm, é verificada na condição em que verificamos se os limites podem comutar. Com efeito, podemos admitir o caso da família f xn( )arctg x n
. Hauchecorne (2000, p. 235)evidencia que lim lim n( ) lim lim n( )
n x f x x n f x
(*). Mas, reparemos ainda que
lim lim arct lim 2 2
n x g x n n
, enquanto que lim lim arctx n g x n
lim 0x
0
.
Portanto, nesse caso, não contamos com a comutatividade dos limites indicados há pouco.
Vale observar ainda que Krantz (1951, p. 242) descreve um teorema que fornece condições suficientes para que possamos contar com a comutatividade dos limites que calculamos acima. Neste caso, a necessidade da convergência uniforme é imprescindível para garantir a igualdade em (*). Bruckner; Bruckner & Thomson (2000, p. 388-389) advertem ainda que “no cálculo de limite na convergência pontual, as operações de mudança de limites não podem ser efetuadas”. Temos, pois, um prático critério operacional, que nos permite inferir, de modo rápido, sobre o comportamento de uma família f , e que não é discutido em Lima (2010). No próximo segmento, n
destacaremos as potencialidades de uso do software.
3 Discussão de situações com o uso do software Geogebra
Para iniciar nossa discussão evidenciando o uso e exploração do software
Geogebra com vistas à interpretação e distinção do significado gráfico-geométrico da
convergência pontual e uniforme, começamos com o caso da seguinte sequência
( )
n
x f x
n
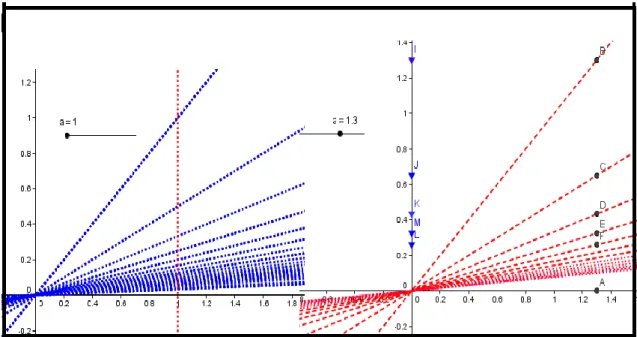
. Observando a figura 1 (lado direito) depreendemos que é possível executar uma construção básica com o software e notar que, a partir da identificação e escolha de alguns pontos no eixo das ordenas, quando tomamos uma reta xa, ao acompanhar o comportamento dinâmico dos pontos indicados nesta figura (lado direito), adquirimos o entendimento do modelo indicado por Lima (2010, p. 364).
Figura 3 - Descrição do comportamento geométrico da convergência pontual
Fonte: Autoria própria.
Encontramos em Lima (2010, p. 363) a família fn:[0,1]IR, definida por
( ) n
n
f x x . Neste caso, com base na seguinte verificação
1 1 1 1
lim lim n lim lim1 1 0 lim lim 0 lim lim n
n x x n x x n x nx
. Tal comportamento nos
informa que não lidamos com a convergência uniforme. Daí, com base no gráfico, a função ( ) 0 se 0 x<1
1 se x=1
f x
é a candidata natural ao limite que buscamos ( fn f ).
Outrossim, com apelo à percepção, depreendemos que para intervalos do tipo
[ , ]a b IR, com a1, o comportamento dos membros dessa família é de “dispersão”
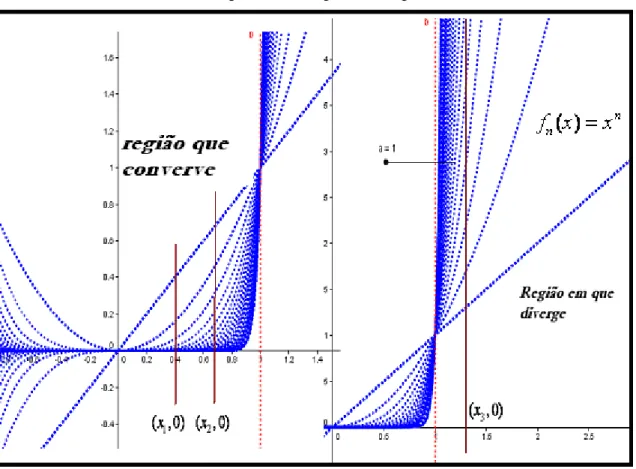
ou “afastamento”. Daí, adquirimos o entendimento da conveniência da escolha adequada da região [0,1] na reta real. Com apoio do gráfico da figura 4, podemos explorar uma região maior do plano e apreender uma visão local e global de seu comportamento. De acordo com a descrição de Lima (2010, p. 364), podemos tomar os pontos ( , 0)x1 e ( , 0)x2 , notando que as imagens devem manifestar o comportamento previsto na convergência pontual (definição 1). Todavia, se considerarmos o ponto
3
( , 0)x , depreendemos, de modo tácito, que o comportamento esperado é o da divergência de fn:[1, ) IR, uma vez que, não podemos indicar uma faixa que contenha todas as funções, a partir de um certo índice n0IN.
Figura 4 - Identificação visual da região no plano, onde temos a possibilidade de contar com a convergência e uma região de divergência
Fonte: Autoria própria.
No caso da figura 4, vale ressaltar que Bruckner; Bruckner & Thomson (2000, p. 392) comentam que no século XIX, os matemáticos interpretavam a convergência da família ( ) n
n
f x x no intervalo (0,1) como “infinitely slowly” (convergência infinitamente lenta). Hodiernamente, sabemos que nesse intervalo, não contamos com a convergência uniforme em (0,1) . Apesar de que, para todo [0, ]c [0,1) tenhamos a convergência uniforme. Com efeito
0 1 0 ( ) 0 0 n n n n c f x x c , para todo [0, ] [0,1) x c .
Outro exemplo discutido em Lima (2010, p. 364) é a seguinte função :[0,1]
n
f IR definida por f xn( )xn (1 xn) que “converge simplesmente para a função identicamente nula em [0,1].”. O autor evidencia um expediente de interpretação
metafórica do comportamento dos gráficos desta família de funções. Neste sentido, comenta que “como se vê, cada gráfico apresenta um calombo, cuja altura se mantém constante, igual a 1 4 , de modo que quando n , a forma do gráfico de f não se n aproxima da forma do gráfico da função limite” (LIMA, 2010, p. 364).
A proficuidade de seu argumento não encontra ulteriores aplicações, na medida em que não exploramos, de modo didático, sua indicação. Ademais, com base no gráfico que exibimos na figura 5, temos a possibilidade de discutir o comportamento das funções
( ) n (1 n)
n
f x x x , inclusive para valores xIR. Diferentemente da análise estruturada por Lima (2010, p. 364), divisamos a existência de dois “calombos”, quando visualizamos seu comportamento ao longo da reta real, se aproximando, neste caso, das retas x 1 e x1, respectivamente (figura 5-II, lado direito).
Figura 5 - Apelo metafórico de Lima (2010, p. 364) para explicar a convergência não uniforme
Fonte: Autoria própria.
Consideremos a seguinte sequência de funções ( ) 2 2 2
(1 ) n nx f x n x tomadas em
[0,). Fixado x0, podemos escrever lim ( ) lim 2 2 2 lim 2 2 0
(1 ) (1 ) n n n n nx x f x n x n nx .
de y1 para valores nas abcissas do tipo 1( , 0)
x . Pela via analítica, podemos obter a
seguinte derivada 3 2 2 2 2 2 2 2 2 1 '( ) 0 1 0 (1 ) n n n x f x n x x n x n
. Isto nos informa
que nos pontos do tipo
1 , 0n
, registramos que fn'( )x 0. O mesmo argumento pode ser aplicado a outras situações. De fato, na figura 6, observamos o comportamento da família de funções ( ) 2 2 2 (1 ) n nx f x n x . Mais uma vez, notamos a presença
“calombos”, todavia, eles se aproximam agora da reta x0. Segundo as indicações de Ross (1980, p. 181) podemos avaliar a imagem da função nos valores assumidos em seus pontos de máximo
1 , 0n
, por intermédio do o seguinte limitelim sup n( ) ( ) | (0, ]
n f x f x x . Ademais, escreveremos ainda que
2 22 1
1
lim sup ( , 0 ) lim sup 1
(1 1 ) n n n n n f n n n . Comprovamos tal
comportamento com base na figura 7. Seus valores máximos assumidos são 1.
Figura 6 -. Identificação visual dos valores extremos assumidos por família de funções
Fonte: Autoria própria.
Por outro lado, com base no gráfico da figura 7, compreendemos que seus pontos de mínimo (de -1) são assumidos em pontos do tipo
1 , 0n
.Figura 7 - Visualização dos pontos de mínimo e máximo da família de funções
Fonte: Autoria própria.
Podemos verificar que, no caso da família de funções f xn( )
1 x
n para(0,1)
x , de acordo com seu comportamento global e local da mesma, a candidata imediata à convergência é a função ( ) 1 se x=0
0 se x ( 1,1) e x 0
f x
. A visualização de
“lombadas” ou “calombos”, diferentemente dos casos anteriores, não é indicada nesse caso. Notamos também que não há convergência no intervalo (2, 2)(fig. 8-II).
Figura 8 - Identificação visual do comportamento de convergência simples de modo local e global
Outrossim, podemos notar que
1 1 1
lim lim 1 n lim lim 1 1 n lim lim 0n 0
n x n x n x x
. E no caso do outro limite,
verificamos que
1 lim lim 1 n n x x , com 0 x 1. Mas, se tem que 0 (1 x) 1 e
1 1
lim lim 1 n lim 0 0
n x x x
. Aqui, verificamos em (0,1) (fig. 8-II) que vale a
comutatividade dos limites, entretanto, tal condição é apenas necessária, mas não suficiente para se produzir qualquer ilação atinente ao tipo de convergência.
A outra maneira é observar seu comportamento no intervalo ( 1,1) e, para valores próximos dos pontos x 1 e x1, as funções tendem a se distanciar (na medida em que nos aproximamos da origem), uma das outras (figura 8). Mas, admitindo-se que ocorra
. . C U n
f f teríamos que dado 0, ocorre f xn( ) f x( ) , para todo x ( 1,1). Daí, se x(0,1) teremos
1x
n , para todo nn( ) .Mas, se tomarmos um ponto x(0,1) suficientemente pequeno, como 1 ( ( ) 1) ( ) 1 1 1 1 2 2 n n x x . Segue que
( ) 1 1 ( ) 1 ( ( ) 1) 1 1 2 2 n n n x o que éuma contradição, caso 1 4
, por exemplo. Conclusão, em (0,1) e, consequentemente,
em ( 1, 0) não temos convergência uniforme.
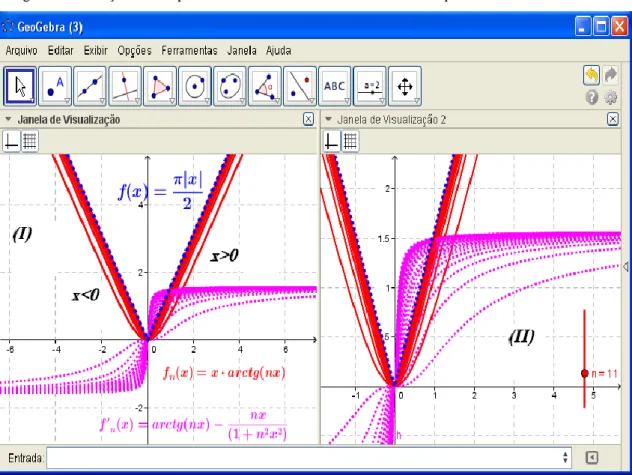
Vamos considerar a seguinte família de funções f xn( ) x arctg n x( ).
Reparemos que lim ( ) lim ( )
2 n n f x n x arctg n x x , se x0 e lim n( ) lim ( ) 2
n f x nx arctg n x x se x0. Daí, ainda com base no gráfico abaixo, vemos que
. . C S n
f f , com ( ) 2
f x x . Vamos tomar ainda a derivada
2 2 '( ) ( ) 1 n nx f x arctg nx n x .
Ademais, vemos que para x 0 fn' 0 e a família f é decrescente. Enquanto n que para x 0 fn' 0 e a família f é crescente. Tais informações podem ser n
extraídas com origem na figura 10. Reparemos que as relações analíticas do comportamento de f e n fn' estão em sintonia com o gráfico que apresentamos abaixo.
Figura 9- Descrição do comportamento de crescimento/decrescimento a partir da família de derivadas
Fonte: Autoria própria.
Em Davidson & Donsig (2010, p. 145) deparamos o seguinte exemplo de família de funções definidas por f xn( )sen nx n( ) . Com facilidade, obtemos também
que f ' ( )n x cos(nx). Os autores explicam que “a convergência uniforme não fornece
um controle para suas derivadas”. A conclusão dos autores é que em fn:[0, ] IR elas convergem uniformente, entretanto, “esta sequência não se comporta bem, no que diz respeito às suas derivadas.” (DAVIDSON & DONSIG, 2010, p. 146).
Figura 10 - Adquirimos o entendimento do comportamento de fn e fn'
Fonte: Autoria própria.
Pela via analítica, se tem que lim n'(0) lim1 1 0 '(0) n f n f e
'
lim n( ) lim 1 n
n f n se quer existe. Na figura 10-I, exibimos uma visão global de seu comportamento. Na figura 10-II, destacamos o trecho intervalo [0, ] . Notamos o comportamento suave de todas as funções (em azul) f xn( )sen nx n( ) , cujas oscilações tendem a diminuir. De outro modo, as oscilações de sua família de derivadas
' ( )n cos( )
f x nx , de modo global e local, tendem a aumentar sua freqüência. Nesse caso, um elemento de natureza cognitiva indica que nossa intuição foi contrariada. Com efeito, “a intuição é que para qualquer função suave, existem outras que oscilam de cima para baixo, bastante rápido, e permanecem próximas desta função suave.” (DAVIDSON & DONSIG, 2010, p. 146). E é exatamente isso que não ocorre na figura 10, visto que, o comportamento oscilatório impede o caráter de convergência de suas derivadas, além de que não há nenhum tipo de monotonicidade de ambas as famílias.
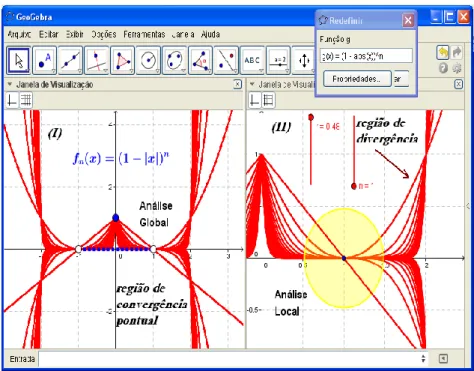
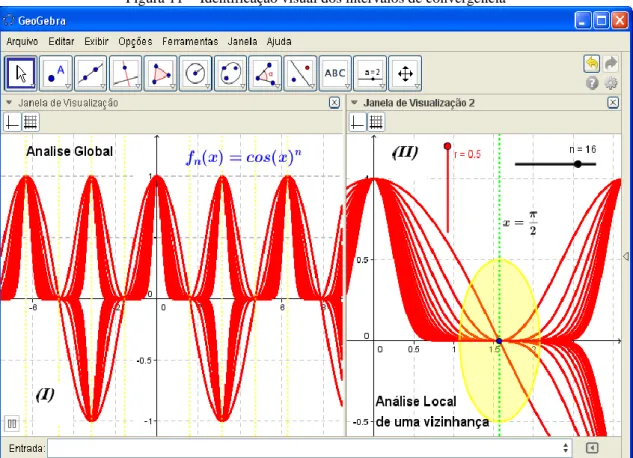
Consideremos a família de funções f xn( )cos ( )n x , com fn:IRIR. Nesse caso, com origem nos gráficos que apresentamos na figura 11, podemos adquirir o entendimento do olhar pormenorizado (global e local) que indica determinadas vizinhanças (intervalos) na reta, nas quais contamos com a convergência pontual e, noutros em que temos, de fato, a convergência uniforme.
Figura 11 - Identificação visual dos intervalos de convergência
Fonte: Autoria própria.
Todavia, tal conclusão precisa ser confirmada analiticamente. Com efeito, e consideramos um intervalo (0, 2), daí x (0, 2), podemos escrever
0 0 0
lim lim cos ( )n lim lim 1 1 0 lim 0 lim lim cos ( )n
n x n x n x n x x , pois 0cos ( ) 1n x em
(0, 2). Tal fato nos fornece um indício que não ocorre a convergência uniforme, de modo global. Divisamos várias regiões de dispersão dos gráficos e destacamos uma vizinhança, centrada no ponto ( 2, 0) (fig. 11-II) aonde se observa um comportamento semelhante ao de convergência uniforme.
Por fim, consideremos a família de funções
1
( ) n sin 1 n n f x x x . Trench (2000, p. 243) verifica que . . 0 C U n
f f , para todo [ , ]a b (0,1). Por outro lado, apesar de que, de modo intuitivo, tenhamos a esperança de alguma forma de convergência possamos identificar em relação às funções derivadas descritas por
1 1 1
'( ) n sin 1 n ( 1) cos 1 n
n
f x n x x n x , a figura 12 nos informa exatamente o contrário. Outrossim, fn' não convergem para nenhuma função na mesma região.
Figura 12 - Comportamento de divergência da família das derivadas
Fonte: Autoria própria.
Considerações finais
Neste trabalho discutimos a noção de convergência pontual e convergência uniforme. O caráter compulsório do estudo deste assunto pode ser verificado em qualquer curso de Análise Real, obrigatório nos cursos de graduação (em Matemática) no Brasil. De outro modo, buscamos descrever possibilidades de explorarmos, de modo intuitivo e heurístico, algumas das propriedades, eleitas pelos autores dos livros, que funcionam como uma alavanca para impulsionar o entendimento de um conceito historicamente importante, tendo em vista que a maioria dos estudantes manifesta dificuldade com o trato de uma linguagem formal (BRIDOUX, 2011, p. 11-12).
Deste modo, com o amparo das potencialidades gráficas do software Geogebra, mostramos e indicamos que: (i) com a função rastro do programa, podemos descobrir, sem apelos analíticos, a candidata à função limite f , de modo que fn f ; (ii) com a percepção e visualização do comportamento gráfico, conseguimos divisar as regiões (intervalos IIR) na reta, nas quais, suspeitamos (conjecturamos) algum tipo de convergência; (iii) o critério de Lima (2010, p. 364) poderá ser aplicado a uma quantidade vasta e diversificada de exemplos; (iv) determinados teoremas e critérios de convergência podem ser, rapidamente, analisados, com apoio na visualização, em momentos que antecedem o formalismo; (v) contamos a possibilidade da análise, a partir da visualização da faixa no plano em que se tem a convergência uniforme.
Na figura 13 exibimos um expediente recorrente registrado nos livros de Análise Real. Nessa figura, Bloch (2011, p. 493-495) transmite ao leitor o entendimento e a
descrição qualitativa atinente à convergência uniforme (figura 13-I) e da convergência pontual (figura 13-II). Neste escrito, mostramos que é possível veicular as mesmas ideias, com o acréscimo e vantagem da mobilidade e o caráter manipulatório dos gráficos que apresentamos neste artigo, que se contrapõe ao modelo estático que divisamos abaixo. Deste modo, suavizamos o caráter eminentemente algébrico deste conteúdo, o qual á criticado por certos autores (OTERO-GARCIA, 2011, p. 2019).
Figura 13 - Descrição gráfico-geométrica indicada pelos autores de livros de Análise Real
Fonte: Autoria própria.
Para concluir, colocamos em destaque o pensamento de Kline (1964, p. 4)) que se coaduna, com naturalidade, ao objeto de nossa discussão. Nesse sentido, ele esclarecia que “[...] primariamente, a Matemática é um método de investigação tomado como um pensamento postulacional. O processo consiste na formulação cuidadosa de definições de conceitos para serem discutidos de modo explicito pelo estabelecimento de suposições que fundamentarão a base do raciocínio.”
Ora, a descrição indicada acima por Morris Kline é o caminho mais natural para o
expert, entretanto, no que concerne ao aprendiz, ao recém-introduzido ao contexto da
Análise Real, prevemos alguns entraves, na condição em que exigimos, de imediato, uma atividade intelectiva fundamentada de modo prioritário na lógica e nos modelos das definições formais (pensamento postulacional). Vale observar ainda que a descrição de Kline lança um alerta sobre o modus operandi do matemático que, em seu contexto de investigação, antes da preponderância do formalismo e o olhar peculiar estrutural. Na etapa inicial, no momento de criação de demonstrações e a descoberta de propriedades, “a imaginação e a intuição são indispensáveis” (KLINE, 1964, p. 6).
PATTERN RECOGNITION GRAPH WITH SUPPORT OF
SOFTWARE GEOGEBRA: THE CASE OF POINTWISE
CONVERGENCE AND UNIFORM
Abstract: In particular, when we turn to the case of the convergence of a sequence or a family of functions
fn n IN , we registered in the history´ books of Mathematics, the tortuous effort of the emblematic figures such as Cauchy, Bolzano and Weierstrass, in order to indicate a solid and consistent for this notion. Currently, we check out the description of various forms of the convergence, according to the authors of books of Real Analysis, among them, we underline the simples convergence (or pointwise). . C S n
f f and the uniform convergence . . C U n
f f . In the specific way, we highlight the recommendations of Lima (2010), with the aim of identifying, understanding and distinction of these two forms of convergence. Its indications in the heuristic nature, are meant from the exploration of situations using the software Geogebra. With such object, we estructured situations that provide: (i) the understanding of the topological behavior of the family of functions (so local and global); (ii) the possibility of visualizing complex graphics and unenforceable environmental pencil / paper, (iii) visual identification of candidate function to the limit in each type of convergence, (iv) the plan view of the region where the convergence is uniform. With this discussion, we question the standard approach in Real Analysis that restricts the activity of the learner to the domain and application of formal definitions, neglecting the character and intuitive heuristic that content.
Keywords: Pointwise and Uniform convergence. Visualization. Geogebra. Teaching.
Referências
ALVES, Francisco Régis Vieira. INSIGHT: descrição e possibilidades de seu uso no ensino do Cálculo. In: Vidya (Santa Maria. Online), v. 32, 2012. p. 149-161. Disponível em: <http://sites.unifra.br/Portals/35/2012/10.pdf>. Acesso em: 26 jul. 2013.
AKSOY, Asuman; KAMSHI. Mohamed. A problem book in Real Analysis. New York: Springer. 265f.
ARTIGUE, Michelle. (2003). O que se puede aprender de la Investigación Educativa en el Nível Universitário. In: Boletín de la Asociation Matemática Venezolana. v. 10. nº 2. p. 117-134.
BOTTAZZINI, Humberto. (1986). The Higher Calculus: A History of Real and Complex Analysis from Euler to Weierstrass. New York: Springer-Verlag. 339f.
BLOCH, Ethan. The Real numbers and Real Analysis. New York: Springer. 577f. Bridoux, Stephanie. (2011). Enseignement des premières notions de topologie à l’université. Une étude de cas. Grenoble> Université Joseph Fourier. Paris 7.
Disponível em: http://tel.archives-ouvertes.fr/docs/00/66/02/49/PDF/these.pdf. Acesso em: ?
BRUCKNER, Andrew; BRUCKNER; JUDITH; THOMSON. Brian. Elementary Real Analysis. London: Prentice Hall. 752f.
DAVIDSON, Kenneth, ALLAN, R. & Donsig. (2010). Real Analysis and Applications. New York: Springer. 520f.
HAIRER, E. & WANNER, G.. Analysis by its History. 2008. New York: Springer. HAUCHECORNE, Bertrand. Les contre-exemple en Mathématiques. (2000). Paris: Edition Ellipse. 383f.
LIMA, Elon. L.. Um curso de Análise. (2010). Rio de Janeiro: SBM. 431f.
OBTER-GARCIA, Silvio. C. Uma trajetória da disciplina de Análise e um estado do conhecimento sobre seu ensino. (tese de doutorado). (2011). Rio Claro: UNESP. 528F. Disponível em:
http://www.athena.biblioteca.unesp.br/exlibris/bd/brc/33004137031P7/2011/oterogarcia _sc_me_rcla.pdf. Acesso em: ?
KLINE, Morris. (1964). Mathematics in Wetern Culture. London: Oxford University Press.
KLINE, Morris. (1980). Mathematics: the loss of certainty. Oxford: Oxford University Press. 374f.
KRANTZ, Steven. G. Real (1951). Analysis and Foundations. Second Edition. Chappman and Hall. 472f.
ROSS, Kenneth. A. (1980). Elementary Analysis: the theory of Calculus. New York: Springer. 366f.
TRENCH, William. (2003). Introduction to Real Analysis. San Antonio: Pearson Education. 613f.