Perturbações de sistemas gravitacionais: a métrica de vaidya, mini buracos negros...

Instituto de Físia

Perturbações de Sistemas Gravitaionais: a Métria de

Vaidya, Mini Buraos Negros e Gravastares

Ceilia Bertoni Martha Hadler Chirenti

Orientador: Prof. Dr. ElioAbdalla

Tese de doutorado apresentada no Instituto

deFísiaparaaobtençãodotítulodeDoutor

emCiênias.

Comissão Examinadora:

Prof. Dr. Elio Abdalla (IFUSP)

Prof. Dr. Luís RaulWeberAbramo (IFUSP)

Prof. Dr. Reuven Opher (IAG/USP)

Prof. Dr. George E. Avraam Matsas (IFT)

Prof. Dr. Carlos Alexandre Wuenshe de Souza (INPE)

São Paulo

Em primeiro lugar, gostaria de agradeer ao meu orientador, Prof. Dr. Elio Abdalla,

pela sua atenção, ajuda e orientação durante os anos do doutorado, e também desde a

iniiaçãoientía. Foium prazer euma honratrabalhar aoseu lado. Agradeçotambém

ao Prof. Dr. Alberto Saa, da Uniamp, uja ajuda em todas as etapas do trabalho se

mostrousempre providenial.

Agradeço aoProf. Dr. LuianoRezzolla, om quem trabalheina Alemanhadurante três

meses, pelafrutíferaolaboração,eaogrupode RelatividadeNumériadoInstitutoMax

Plank de Potsdam,pela hospitalidadee amizade.

Agradeço à FAPESP pelo apoio naneiro durante todo o doutorado, e ao Serviço

Ale-mão deInterâmbioAadêmio(DAAD) eà SoiedadeMax Plankpeloapoionaneiro

durante a minhaestadia naAlemanha.

Agradeço à Amélia, à Simone e à Bethe, sem as quais o Departamento de Físia

Mate-mátia não poderia existirtal omo oonheemos.

Agradeço aos olegas do grupo, Alan Maiel, Alan Pavan, Alexander, Carlos Eduardo,

Carlos Molina, Flávio, Jeferson, Karluio, Rodrigo, Roman e Sandro, pela ompanhia e

amizade,além das onstantes disussões sobre físiae outrosassuntos.

Mereem um agradeimento espeial os que foram, e são, meus ompanheiros de sala.

Agradeço à Bertha, agora no Chile, e à Mihele, agora na Alemanha, pela ompanhia

femininanasala341dodepartamento. AgradeçoespeialmenteaoamigoDavi, porestar

sempre presente e pronto a me ajudar quando preisei. Agradeço também ao Brenno,

novointegrantedo grupo, amigo novo, pelaompanhia.

Agradeço à amiga e professora Gladys Chalom do IME, pela amizade e onselhos desde

Agradeço aos amigos Bel, Adriana e Laerte, uma físia e dois astrnomos, pela amizade

duradoura.

Agradeço aos meus amigos Ader, Camila, Carla, Filipe, Maros, Mogar e Oliver, que

aompanharam de longeos meus estudos de Físia,e tiveram paiênia para esperar até

agora. Todos zeram a minhavida muito mais felize me ajudaram sempre quepossível.

Agradeço aoRubens, pelo amor,amizade epaiênia durantetodos os anos.

Agradeço aos meus pais, que semprerespeitaram as minhase deisões eme apoiaram,e

me proporionaram a liberdade para seguir a arreira que esolhi. Agradeço pelo amor

e arinho, sempre. Agradeço à minha família e em partiular à minha avó Sirley, que

sempreteve amais altaopiniãoa meurespeito, justiadaounão. Finalmente, agradeço

in memoriam ao meu av Geraldo, engenheiro, que om erteza estaria orgulhoso se

has to wander through all the outer worlds to reah the innermost shrine at the end.

RESUMO vii

ABSTRACT ix

1 Introdução: Perturbações em Relatividade Geral 1

2 Modos Quasi-Normais da Métria de Vaidya 5

2.1 A métriade Vaidya emoordenadas de one de luz . . . 5

2.2 Soluções das equações de ampo . . . 11

2.3 Perturbaçõese MQN's damétriade Vaidya . . . 16

3 Caraterização de Mini Buraos Negros através de seus Modos

Quasi-Normais 27

3.1 Miniburaos negrosem aeleradoresde partíulas . . . 27

3.2 Modelo utilizado . . . 31

4.1 Gravastar (GravitationalVauumCondensate Star) . . . 41

4.2 Vínulosnos parâmetros domodelo original . . . 43

4.3 Omodelo alternativoom pressões anistrópias . . . 46

4.4 Equações de Perturbação eResultados Numérios . . . 53

5 Conlusão 61

REFERÊNCIAS BIBLIOGRÁFICAS 63

APÊNDICE A 67

APÊNDICE B 69

APÊNDICE C 71

APÊNDICE D 73

2.1 Exemplos de urvas

r(u

=

const, v)

obtidasom a eq. (2.39),om

M

= 1

.. 12

2.2 Comportamento das urvas

r(u

=

const, v)

obtidas om aeq. (2.39) para

r(u, v

0

) =

−

u/2

→

2M

. . . 13

2.3 Curvas de

r

e

t

onstante. . . 14

2.4 Curvas de

u

onstante ediagramaonforme. . . 15

2.5 Diagrama da grade utilizada para a integração numéria da equação de

perturbação damétria de Vaidya. . . 18

2.6 Perturbaçãoeletromagnétiaom

ℓ

= 2

paraumburaonegrode Shwarzs-hilde amétria de Vaidya om afunção de massa hiperbólia. . . 19

2.7 Perturbação esalarom

ℓ

= 2

para um buraonegrode Shwarzshilde a métriade Vaidya om massa linear resentee deresente. . . 20

2.8 Perturbaçãoeletromagnétiaom

ℓ

= 2

paraumburaonegrode Shwarzs-hilde amétria de Vaidya om massa linearresente e deresente. . . . 20

2.9 A parte real (

ω

R

) da freqüênia de perturbações esalares om

ℓ

= 2

em função de

v

para funções de massa linear ehiperbólia deresentes. . . 22

2.11 Evoluçãode

ω

R

paraperturbaçõesesalares om

ℓ

= 2

ediferentes funções de massa hiperbólias,em omparaçãoom uma função de massa linear. . 24

2.12 Evolução de

ω

R

para perturbações esalares, om diferentes valores de

ℓ

para diferentes funçõesde massa linares. . . 25

3.1 Freqüênias instantâneas dos MQN's para mini buraos negros em

pro-esso de evaporação (

ℓ

= 2

). . . 35

3.2 Freqüênias instantâneas dos MQN's para mini buraos negros em

pro-esso de evaporação (

ℓ

= 3

). . . 36

3.3 Osespetros de potênias

|

Ψ(f)

|

e

|

Ψ(f)

˜

|

. . . 38

3.4 Soluçãográa para afreqüênia de máximode

|

Ψ(f

)

|

. . . 39

4.1 Limite para a ompaidade

µ

do gravastar em função da espessura

δ

c

da asa de matéria . . . 46

4.2 Exemplo típio das funções

ρ(r)

,

p

r

(r)

e

p

t

(r)

para

M

= 1

,

r

1

= 1.8

e

r

2

= 2.2

. . . 50

4.3 Comportamento de

(1

−

2m/r)

para

M

= 1

e diferentes valores de

r

1

e

r

2

= 2.2

. . . 51

4.4 Variação de

(1

−

2m/r)

min

om

δ

, para

M

= 1

e diferentes valores de

r

2

. . 51

4.5 Limitenaompaidade

µ

dogravastarom aespessura

δ

daasa, ompa-rando os resultados apresentados na gura 4.1 om os resultados obtidos

para omodelo om pressõesanisotrópias, naurvasuperior. . . 52

4.6 Diagramada grade de integração numériautilizadapara o gravastar . . . 55

4.8 Potenial

V

(r)

(

ℓ

= 2

) para gravastares om a mesma espessura

δ

e om-paidade

µ

resente. . . 56

4.9 Evolução das perturbaçõesaxiaisom

n

= 0

,

1

e

2

paraum gravastarom

M

= 1

,

r

1

= 1.85

e

r

2

= 2.2

. . . 58

4.10 Comportamento das freqüênias quasi-normais do gravastar em função de

4.1 Alguns valores típios obtidos para as freqüênias quasi-normais do modo

Estudos de perturbações em sistemas gravitaionais no âmbito da Relatividade Geral

vêm sofrendo grandes desenvolvimentos nos últimos anos, espeialmente emfae da

evo-lução dos modernos detetores de ondas gravitaionais. Abordamos neste trabalho as

perturbações de diferentes enários. Prinipiamos om a métria de Vaidya, utilizada

para desrever espaços-tempos esferiamentesimétriose dependentes do tempo. Nossas

simulaçõesmostraram queas freqüênias dos modos quasi-normais (MQN's) apresentam

um novo efeito inerial para variações rápidas da função de massa, retornando depois

aoomportamentoadiabátio. Emseguida, apresentamos um modelo para aevaporação

de mini buraos negros por radiação de Hawking inspiradono enário de riação destes

objetos emaeleradores de partíulas,previsto pelas novasteoriasom dimensõesextras.

Nosso modelo, baseado na métriade Vaidya

n

-dimensional,tornou possível aanálise de MQN'sresultandonapossibilidadede seobterosparâmetrosrelevantes doburaonegro,

omoasuamassainiialeonúmerodedimensõesextras,apartirdemedições

experimen-tais. Finalmente, realizamos um estudo sobre uma nova solução denominada gravastar,

proposta omoum modelo alternativo para oestágio nalde estrelasom grandemassa.

Obtivemoslimitespara osparâmetrosdasoluçãoeveriamos asuaestabilidadefrentea

perturbaçõesaxiais,onluindopositivamentearespeito dapossibilidadede sedistinguir

Perturbative studiesof gravitationalsystems inGeneralRelativityhavegonethrough big

developmentsinthelastyears,espeiallyduetotheevolutionofthemoderngravitational

wave detetors. We onsider in this work dierent perturbations in dierent senarios.

Firstlyweonsider theVaidyametri,mainlyusedtodesribetime-dependentspherially

symmetri spaetimes. Our simulations show that the frequenies of the quasinormal

modes(QNM's) presentanewinertialeet forrapidly varyingmassfuntions,returning

afterwards to the adiabati behavior. Next we present a model for evaporating mini

blak holes in partile aelerators, in the ontext of the new gravity models with extra

dimensions. With our model, based on the

n

-dimensional Vaidya metri, we are able to perform a QNM analysis whih results in the possibility of obtainingthe parameters of

the blak hole, suh as its initial mass and the number of extra dimensions, from the

experimentalmeasurements. Finally,wepresenta studyof anew solution,the gravastar,

proposed as an alternative model for the end state of massive stars. We obtain bounds

fortheparametersof thesolutionandverifyitsstabilityagainstaxialperturbations. Our

results indiate that the gravastar's QNM spetrum an indeed be used to distinguish a

Introdução: Perturbações em

Relatividade Geral

O estudo de perturbações emrelatividade geral tem se mostrado um ampo de pesquisa

muito ativo,desde otrabalhopioneirode Reggee Wheelerde 1957 [1℄. A análiseda

evo-lução de pequenas perturbações em um ampo gravitaional de fundo onheido fornee

informações sobre a estabilidade das soluções das equações de Einstein, e nos permite

obter um onheimentomais aprofundado aera danatureza das equaçõesde ampo da

gravitação. A estabilidade das soluções é uma de suas araterístias mais importantes.

Soluçõesinstáveisdevemdeairrapidamenteemumobjetoestável,queémaisfailmente

detetáveldevido ao seu tempode vidamaior.

Além disso, a propagação de pequenas perturbações pode ser usada para desrever

si-nais de ondas gravitaionais geradosporfontes astrofísias distantes, quando detetados

na Terra. A deteção de ondas gravitaionais, apesar de ser um projeto extremamente

desaador e experimentalmente omplexo, se torna aos pouos mais viável, om a nova

geração de projetos: detetores de massas ressonantes, interfermetros laser, ou ainda

om odetetor LISA, que onsistiráde um onjunto de três satélitesemórbita daTerra.

Adiuldade dedeteção reside,entre outrosfatores, narazãosinal/ruídoextremamente

baixaesperada.

Umdossuessos dateoriadeperturbaçãoapliadaàRelatividadeGeralfoiobtero

espe-trode freqüêniasdos modosquasi-normais de buraosnegros. Umburaonegro espalha

ondas gravitaionaisinidentes omo emum problema de espalhamentode ondasplanas

por uma barreira de potenial na Meânia Quântia. Mas, na Relatividade Geral, as

ons-dependemdas ondiçõesiniiaisdaperturbação. Portanto,asondasespalhadasarregam

informaçõessobre o burao negro, omo se fossem as suas impressões digitais ou o seu

som araterístio.

Este fatogerouumaexpetativadeque,aoseatingiremasondiçõesténias neessárias

para adeteção das ondas gravitaionais,teríamosuma nova janelaobservaional para o

universo. Informações sobre objetos astrofísios, que de outra maneira seriam invisíveis

paranós,poderiamserobtidasprourando-sepelassuasassinaturasnossinaisdetetados.

Desta forma poderíamos obter informações sobre buraos negros e estrelas ompatas, e

talvez até sobre outros tipos de objetos astrofísios ainda desonheidos. Detetores de

ondas gravitaionais seriam utilizados para se obter informações sobre o osmos, omo

as informações obtidas em raios X, miroondas ou no espetro vísivel pelos modernos

telesópios e satélitesde pesquisa.

Paree, porém, um pouo otimista demais pensar que sinais reais poderiam reetir os

resultados obtidosporuma investigação teóriaextremamenteidealizada, omoa análise

doespalhamentode ondas gravitaionaispela barreirade potenialde um buraonegro.

Estima-se que as maiores fontes astrofísias de emissão de ondas gravitaionais sejam

eventos atalísmiosextremamente violentos,tais omoa explosão de super novas,ou a

olisão de buraos negros.

A fonte mais promissora para deteção e estudo de ondas gravitaionais é o sistema

binário ompato espiralando nas últimas fases de sua vida. Este é um sistema binário

formadoporduasestrelasdenêutronsoudoisburaosnegros(ouumdeada),espiralando

para um entro omum, altura em que nalmente oalesem violentamente. Tal é o

destino, por exemplo, do famoso sistema de Hulse-Taylor, o Pulsar PSR 1913+16 [2℄,

daquiaerade240milhõesdeanos,oudeumsistemabináriodeburaosnegrosmassivos

noentro de uma galáxia.

Simulações numérias reentes (ver [3℄ e referênias) realizadas no regime não linear,

envolvendo aintegração numériadas equaçõesde Einsteinom ondiçõesiniiaisdadas,

obtiveramalgunsresultadosparaasondasgravitaionaisemitidasemproessosdestetipo.

Veriou-sequeosinal emitidoéomposto detrês fasesdistintas: movimentoemespiral,

fusão e ringdown ou deaimento. Como resultado, foi veriado que o deaimento das

ondas em modos quasi-normais é reuperado no último estágio da evolução das ondas

gravitaionais! Pelovisto, não era otimista demais pensar que aanálise de modos

quasi-normaispoderia ser efetivamenteútilpara a análise de sinais reais.

Cada vez mais tem sido observado que os métodos perturbativos fazem previsões que

dos perturbativos ompatíveis om os resultados obtidospor simulações numérias mais

omplexasnão linearesaté mesmo paraproblemas envolvendo olisõesde buraosnegros

[4℄, situaçãoque ertamente, àprimeiravista,não deveria ser bemresolvidapor ténias

destinadas a tratar de pequenas perturbações. Se a olisão de buraos negros for

estu-dada de maneiraque noinstanteiniial os dois buraos negros estejam obertos por um

horizonte omum, o problema pode ser visto omo a perturbação de um únio burao

negro. Além disso, om o passar do tempo os métodos perturbativos têm se tornado

ada vez mais úteis, e têm sido ada vez mais utilizados, mesmo om o amadureimento

dos métodos não lineares [3℄, que, por sua vez, envolvemténias de programação muito

mais avançadas, além de exigiremum maior poder omputaional. Finalmente, métodos

perturbativos baseados em tratamentos invariantes de gauge das perturbações estão na

basede grandepartedostrabalhos realizadosemrelatividadenumériaommétodosnão

lineares.

NotratamentoperturbativodaevoluçãodepequenasperturbaçõesemRelatividadeGeral,

temos duas abordagens distintas. Umaonsiste emsomar uma pequena perturbação aos

oeientes damétria,oquelevaaperturbaçõesgravitaionaisaxiaisepolares,desritas

noasodeumburaonegrodeShwarzshildpelasequaçõesdeRegge-Wheeler[1℄eZerilli

[5℄. Estas são as perturbações que podem ser identiadas om as ondas gravitaionais

emitidasporalgumproesso físioreal. Outraabordagemdiferenteonsisteemanalisara

propagaçãode um ampode teste noespaço-tempodesritopelamétria,semonsiderar

a reação do ampo sobre a métria (análise linear). Costumeiramente este método é

apliadopara amposesalares e eletromagnétios,podendoporémser apliadotambém

para ampos de spin semi-inteiro, ou mais elevado. Isto orresponde à situação físia

de espalhamento de partíulas pela barreira de potenial do burao negro ou qualquer

outroobjetoonsiderado. Emambososasos,para oburaonegrode Shwarzshild, por

exemplo, aperturbação segue uma equação de onda que pode ser esrita omo

∂

2

_ψ

ℓm

∂r

∗

₂

−

∂

2

_ψ

ℓm

∂t

2

+

V

ℓ

(r)ψ

ℓm

= 0

,

(1.1)

onde

r

∗

é a oordenada tartaruga dada por

r

∗

=

r

+ 2M

ln(r/2M

₋

1)

, e o potenial

V

ℓ

(r)

é uma função de

r

e

M

que ontém toda a físia do problema. Para perturbações

gravitaionaisaxiais,porexemplo,

V

ℓ

(r) =

1

₋

2M

r

ℓ(ℓ

+ 1)

r

2

+

2σM

r

3

,

(1.2)

é o potenial efetivo, ou potenial de Regge-Wheeler, formado por uma barreira de

po-tenial om um pio loalizado próximo de

r

= 3M

. A forma(1.2) se mantém mesmo se onsideramosamposde teste esalares oueletromagnétiosomo perturbações. O

parâ-metro

σ

é igual a 1 para perturbaçõesesalares, 0 para perturbações eletromagnétias e -3 para perturbações gravitaionais, podendo ser expresso omo

σ

= 1

−

s

2

sabe atualmentesobre buraos negrosem nosso universo. As soluções dessa equação são

esritas geralmentenaforma[6℄

Ψ(r, t, θ, φ) =

X

ℓ,m

ψ

ℓm

(r, t)

r

Y

ℓm

(θ, φ)

,

(1.3)

om

ψ(r, t) =

e

i

(

ω

R

+

iω

I

)

t

→

e

−

_ω

I

t

sin(ω

R

t

+

δ)

.

(1.4)

A estabilidade do burao negro é dada pelo sinal da exponenial naeq. (1.4). O burao

negro é onsiderado estável quando a perturbação deai exponenialmente, e instável

quando aperturbação reseexponenialmente.

Pode-seargumentarqueseriaextremamentedifíilmedirexperimentalmenteaspartíulas

espalhadas por um burao negro real, o que é verdade para buraos negros astrofísios,

porém não é assim tão erto para miniburaos negros que podem ser formados em

ae-leradores de partíulas[7℄. Apesar disso, aanálisede perturbaçõesesalares e

eletromag-nétias servemuitobemomo uma análisepreliminaremais simples daestabilidade das

soluçõesdas equações de Einstein. Alémdisso, já foi mostrado que para valores grandes

de

ℓ

, os valores das freqüênias dos modos quasi-normais para todos os tipos de pertur-bações, esalares, eletromagnétias ou gravitaionais, tornam-se iguais, dando mais uma

justiativa para o estudo da evolução de ampos de teste em sistemas gravitaionais.

Podemos ver da eq. (1.2) que para

ℓ

grande o termo proporional a

ℓ

do potenial do-mina sobre o segundo termo, de modo que o potenial torna-se igual para as diferentes

perturbações.

O estudo de perturbações em buraos negros de Shwarzshild já foi em grande parte

exauridonopassado,esuasaraterístiassãohojebemonheidas. Atualmente,odesao

seenontranoestudodeperturbaçõesemnovassoluções,motivadaspordesenvolvimentos

da teoria e novos modelos fenomenológios, ou ainda em antigas soluções onheidas já

há bastante tempo, mas que onseguiram até hoje frustrar os estudos perturbativospor

diuldades ténias. Faz parte do segundo aso a métria de Vaidya, dependente do

tempo, da qual nos oupamos no apítulo 2 deste trabalho. Do primeiro aso fazem

parte os estudos de mini buraos negros e gravastares, desenvolvidos nos apítulos 3 e

4. Veremos a seguir neste trabalhoomo osmétodos perturbativos podem ser utilizados

para estudar estes problemas, omo os resultados novos obtidos se relaionam om os

resultados já onheidos,e quaisas novasontribuiçõesquesurgem parao entendimento

Modos Quasi-Normais da Métria de

Vaidya

Neste apítulo apresentamos os resultados obtidos para os modos quasi-normais da

mé-tria de Vaidya. Nas seções 2.1 e 2.2 apresentamos um tratamento desta métria em

oordenadas de one de luz

(u, v)

, mais adequadas à análise perturbativa realizada na seção 2.3. Osresultados obtidosna seção 2.3para os modos quasi-normais (MQN's) são

omparadosomosresultadosde [8℄,enovosefeitossão identiados[9℄, devidoàmelhor

preisãodos resultados nosistema de oordenadas de one de luzutilizado.

2.1 A métria de Vaidya em oordenadas de one de

luz

Em um trabalho de 1951, P. C. Vaidya apresentou pela primeira vez uma métria para

desrever oespaço-tempoexterior a uma estrela esferiamentesimétria, onsiderando o

uxo de radiaçãoemitido pelaestrela [10℄. Neste aso, a massa daestrela não é

onside-rada onstante, omo no aso de Shwarzshild, ea métrianão deve ser estátia. Como

ponto de partida foi tomada aseguinte desrição do problema: uma massa esféria

radi-antedeveestarprovavelmenteenvolvidaporumenvelopenitoenãoestátiode radiação

om simetria radial. Tudo deve estar envolvido por um ampo gravitaional radial que

se torna ada vez mais frao om a distâniaaté o orpo entral, até o espaço se tornar

de ampo são obtidas om a suposição de que uma estrela de massa

M

eraio

r

0

omeça aemitirradiaçãoemum tempo

t

0

. À medidaqueaestrelaontinuaaemitir,aespessura da zona de radiação aumenta e a sua superfíie exterior emum instante posterior

t

=

t

1

está em

r

=

r

1

. Para

r

0

≤

r

≤

r

1

e

t

0

≤

t

≤

t

1

,seja o elementode linha daforma

ds

2

=

₋

e

ν

dt

2

+

e

λ

dr

2

+

r

2

dΩ

2

,

(2.1)

onde

λ

e

ν

são funções de

r

e

t

. Para que a energia total seja onservada, o elemento de linha obtido ao se resolver as equações de ampo para (2.6) e (2.1) deve se reduzir à

formaestátia

ds

2

=

₋

1

₋

2M

r

dt

2

+

1

₋

2M

r

−

1

dr

2

+

r

2

dΩ

2

,

(2.2)

para

r

=

r

0

,

t

=

t

0

e para

r

≥

r

1

em

t

=

t

1

.

Otensor de energia-momentodoampoeletromagnétio é dadopor

T

µν

=

F

µ

_α

F

να

₋

1

4

g

µν

_F

αβ

F

αβ

.

(2.3)

Para um uxo isotrópiode radiação, aexpressão(2.3) pode ser esrita omootensor de

energia-momentode um uidoperfeito,

T

µν

= (ρ

+

p)U

µ

U

ν

+

pg

µν

,

(2.4)

onde

U

µ

é aquadriveloidadedo uido,e

p

=

ρ/3

. Emnosso aso, porém, onsideramos um uxo de radição direionado, e não isotrópio: em ada ponto da região do espaço

onsiderada, um observador vê um uxo de energiaemapenas uma direção.

Utilizamosoordenadasnaturaisnopontodeinteresse, epodemostomarasomponentes

do tensor de energia-momento em termos das intensidades dos ampos elétrio e

mag-nétio

E

e

H

. Considerando, sem perda de generalidade, que os eixos do nosso sistema natural de oordenadas estejam orientados de tal maneira que o uxo de radiação no

ponto de interesse esteja na direção

x

e que a radiação esteja polarizada om o vetor ampo elétrio paralelo à direção

y

, as omponentes não-nulas de

T

µν

(no sistema de

oordenadas naturais) são

T

11

=

T

44

=

T

14

=

1

2

(E

2

y

+

H

z

2

) =

ρ .

(2.5)

Emum sistemade oordenadas arbitrário,

T

µν

será dado por

onde

v

µ

é um vetor nulo eradial,

v

µ

v

µ

= 0

⇒ −

e

λ

(v

1

)

2

+

e

ν

(v

4

)

2

= 0

,

v

2

=

v

3

= 0

.

(2.7)

Com a expressão usual para as omponentes de

T

µν

em termos de

g

µν

e suas derivadas, dada pelas equações de Einstein,

R

µν

−

1

2

g

µν

R

= 8πT

µν

,

(2.8)

e asequações (2.6)e (2.7), temos astrês equações de ampo:

T

₁

4

e

(

ν

−

λ

)

/

2

−

T

₄

4

= 0

_→

e

−

λ

λ

′

r

−

1

r

2

+

1

r

2

+

˙

λ

r

e

−

(

λ

+

ν

)

/

2

= 0

,

(2.9)

T

₁

1

+

T

₄

4

= 0

_→

e

−

λ

λ

′

−

ν

′

r

−

2

r

2

+

2

r

2

= 0

,

(2.10)

T

2

2

= 0

→ −

e

−

_λ

ν

′′

2

+

ν

′

2

4

−

λ

′

ν

′

4

+

ν

′

−

λ

′

2r

+

e

−

_ν

λ

¨

2

+

˙

λ

2

4

−

˙

λ

ν

˙

4

!

= 0

.

(2.11)

Tomando

e

−

_λ

= 1

₋

2m

r

,

m

=

m(r, t)

,

(2.12)

naequação de ampo (2.9),obtemos

e

ν/

2

=

₋

m

˙

m

′

1

₋

2m

r

−

₁

_/

₂

.

(2.13)

Substituindo

λ

e

ν

das equações(2.12 e (2.13))na equação de ampo(2.10), temos

˙

m

′

˙

m

−

m

′′

m

′

1

−

2m

r

=

2m

r

2

.

(2.14)

Integrando aeq. aima emrelação a

r

,obtemos

m

′

1

₋

2m

r

=

f

(m)

,

om

df

dm

=

˙

m

′

˙

m

1

₋

2m

r

−

2m

′

r

.

(2.15)

A métriaassim obtida é dada por

ds

2

=

₋

m

˙

2

f

2

1

₋

2m

r

dt

2

+

1

₋

2m

r

−

₁

dr

2

+

r

2

dΩ

2

,

(2.16)

m

′

1

₋

2m

r

A eq.(2.17) é a equação diferenial a ser resolvida para

m

, dada uma função

f

(m)

arbi-trária. A ontinuidade damétria nafronteira

r

=

R(t)

(obviamente,

R(t

1

) =

r

1

) édada por

m

=

M ,

(2.18)

˙

m

=

₋

f

(M

)

.

(2.19)

Podemosnotaraindaque,aoimporaontinuidadedamétriaem

r

=

R

,garantimos que em

r

=

r

0

,

t

=

t

0

o elemento de linha é novamente igual a(2.2).

Em 1953 a métria de Vaidya foi reapresentada em oordenadas radiativas [11℄, fazendo

uso de uma mudançade oordenadas dada impliitamentepor [12℄

(r, θ, φ, t)

_−→

(r, θ, φ, ω)

,

(2.20)

dt

=

dω

₋

c

1

₋

2m

r

−

₁

dr ,

(2.21)

onde supusemos

m

=

m(ω)

. Em oordenadas radiativas a métria pode ser reesrita de maneiramais simples omo

ds

2

=

₋

1

₋

2m

r

dω

2

+ 2cdωdr

+

r

2

dΩ

2

.

(2.22)

Para

c

= 1

, temos um uxo de radiação para dentro da estrela, e

m(ω)

é uma função de massa monótona resente do tempo avançado

ω

dado por

dω

=

dt

+

dr

∗

, om

dr

∗

=

(1

₋

2m/r)

−

₁

dr

. Para

c

=

−

1

,temos um uxo de radiaçãoparafora daestrela,e

m(ω)

é

uma função monótona deresente do tempo retardado

ω

dado por

dω

=

dt

−

dr

∗

. Esta

é aformamais onheida egeralmenteutilizada damétriade Vaidya.

Neste trabalho vamos onsiderar a métria em oordenadas de one de luz, mais

ade-quadas para problemas de evoluçãotemporal, omo a análise de MQN's. No entanto, as

diuldadesdeseobteroordenadasdeonede luzparaespaços-temposnãoestaionários

são bemonheidas. Sabe-sequeoproblema deseobteroordenadas de onede luzpara

a métria de Vaidya, onsiderando uma função de massa genéria, não é solúvel para a

maioria dos asos [13℄. Nós seguimos aqui a abordagemsemi-analítiaproposta em[14℄,

baseada noestudorealizadoem[13℄. Consideramosasequaçõesde Einsteinom simetria

esferiamente simétria ab initio em oordenadas de one de luz

(u, θ, φ, v)

. O elemento de linha esferiamente simétrionessas oordenadas é

ds

2

=

₋

2f(u, v)du dv

+

r

2

(u, v)dΩ

2

,

(2.23)

onde

f

(u, v

)

e

r(u, v)

são funções suaves e não nulas. O tensor de energia-momento de um uxo unidireionalde radiação não polarizadaé dado por

T

µν

=

1

onde

k

µ

é um vetor radial do tipo nulo (

k

µ

k

µ

_{= 0}

e

k

2

=

k

3

= 0

). Considerando, sem perda de generalidade, o aso em que o uxo de radiação se dá na direção de

v

, temos

k

µ

= (0,

0,

0,

1)

. As equações de ampo, dadas pelas equações de Einstein (2.8), om a

métria(2.23) eotensor de energia-momento(2.24),se reduzem aoseguinte onjunto de

equações:

f(u, v

) = 2B

(v

)

∂r(u, v)

∂u

,

(2.25)

∂r(u, v

)

∂v

=

−

B

(v

)

1

₋

2m(v)

r(u, v)

,

(2.26)

h(u, v) =

₋

4

B(v)m

′

(v)

r

2

_{(u, v)}

,

(2.27)

onde

B(v)

e

m(v)

são funções arbitrárias, obedeendo à ondição de energia fraa, isto é, para todovetor tipo tempo

X

µ

_(X

µ

X

µ

<

0)

, a densidade de matéria observada pelos observadoresujalinha demundo étangentea

X

µ

deveser sempremaiorouigualazero:

ρ

=

T

µν

X

µ

X

ν

≥

0

.

(2.28)

Para otensor de energia-momento(2.24), essa ondição fornee

ρ

=

T

µν

X

µ

X

ν

=

T

vv

(X

v

)

2

≥

0

⇒

T

vv

≥

0,

(2.29)

ouseja,

B(v)m

′

≤

0

.

(2.30)

A soluçãodosistema(2.25)-(2.27) orrespondeà métriade Vaidya,omo pode ser visto

de (2.23) e (2.24), que estabeleem que a métria é esferiamente simétria e possui um

uxo radial de radiação, respetivamente.

Vamosmostraragoraqueamassadeumadistribuiçãoesferiamentesimétriade matéria

pode ser desrita por

m

=

1

2

r

3

_R

23

23

,

(2.31)

seguindoaargumentaçãoexposta em[15℄. Sejaumespaço-tempoesferiamentesimétrio

arbitrário, om a métriadada por

dS

2

=

e

2

γ

(dx

4

)

2

₋

c

−

2

[e

2

α

(dx

1

)

2

+

r

2

dΩ

2

]

,

(2.32)

onde

γ

,

α

e

r

são funções de

x

1

e

x

4

e o entro de simetria é denido por

x

1

_{= 0}

, de

modo que

r(0, x

4

_{) = 0}

. Além disso, supõe-se que

r(x

1

_{, x}

4

₎

_>

₀

para todo

x

1

₆

_{= 0}

, que

e

2

γ

_>

₀

e

e

2

α

_>

₀

para todo

x

1

e

x

4

A omponente

R

3

232

do tensor de Riemannpara esta métria pode ser failmente alu-lada,

R

3

₂₃₂

= 1 +

e

−

₂

_γ

c

−

₂

r

_,

2

₄

₋

e

−

₂

_α

r

2

_,

₁

.

(2.33)

Esta omponente dotensor de Riemanné interessante porenvolver apenas primeiras

de-rivadas eporser invariantepor transformaçõesdaforma

x

¯

1

_{= ¯}

_x

1

_(x

1

_{, x}

4

₎

,

x

¯

4

_{= ¯}

_x

4

_(x

1

_{, x}

4

₎

.

Examinando a eq. (2.33), veriamos que, se

r

for usado omo uma oordenada, e

t

for usado omo uma oordenada ortogonal onjugada a

r

, ou seja,

dr/dt

= 0

, então neste sistema de oordenadas a métriaassume aforma

dS

2

=

e

2

ψ

dt

2

₋

1

c

2

dr

2

1

₋

R

3

232

+

r

2

dΩ

2

.

(2.34)

A oordenada

r

possuiaráterespaialpara

R

3

232

<

1

,mas possui arátertemporalpara

R

3

232

>

1

. Logo, neste sistema de oordenadas,

e

2

α

pode divergir. Se estas oordenadas

foremutilizadasemuma regiãovaziade umespaço-tempoesferiamentesimétrio,temos

os resultados damétriade Shwarzshild

dS

2

= (1

₋

2M/r)dt

2

₋

1

c

2

dr

2

1

₋

2M/r

+

r

2

_dΩ

2

,

(2.35)

e

M

é uma onstante. Se onsiderarmos a seguir uma distribuição esféria arbitrária de matéria envolvida pelo espaço vazio, a fronteira da matéria será uma superfíie de

desontinuidade. Deaordoom[16,17℄,amétriadeveser ontínuasobreumasuperfíie

de desontinuidade. Comparandoentão (2.34) e(2.35) temos

(R

3

₂₃₂

)

f

= 2M/r

f

,

(2.36)

onde o índie

f

india o valor na fronteira. Este resultado sugere que uma função

m(x

1

_{, x}

4

₎

pode ser denida por

m

=

1

2

rR

3

232

=

1

2

r

3

_R

23

23

.

(2.37)

Em [15℄ são apresentados mais argumentos, que não reproduziremos aqui, para mostrar

que esta identiaçãoérazoável.

Utilizandoagora adenição de massa(2.37) para amétriade Vaidyaemoordenadas

de onedeluz,podemosveriarqueafunção

m(v)

quesurgedaintegraçãodas equações de ampo,nas equações (2.26) e(2.27), é efetivamentea massa dasolução.

Para

m

′

(v)

₆

= 0

, a esolha

2B(v) =

₋

m

′

|

m

′

|

,

(2.38)

uxo radial é dirigido para o interior do burao negro se

m

′

(v)

>

0

, e é dirigido para o

exterior se

m

′

(v)

<

0

. Podemos notar que, para que a ondição de energia (2.29) seja

satisfeita,afunção

m(v)

deveser monótona,impliandoqueouxoradialdeveterapenas umadireção,paratodo

v

. Nãoépossível,portanto,terfunçõesdemassa

m(v)

osilantes.

2.2 Soluções das equações de ampo

Ométodosemi-analítiopropostoem[14℄onsisteemonstruirnumeriamenteasfunções

f

(u, v

)

,

r(u, v)

e

h(u, v)

a partir das eqs. (2.25)-(2.27). A eq. (2.26) ao longo de

u

onstante é uma equação diferenial ordinária de primeira ordem em

v

. Pode-se obter

r(u, v)

em qualquer ponto resolvendo o problema de valor iniial em

v

, onheendo-se

r(u, v

0

)

.

Vamos exempliar emdetalhe este método para a métria de Shwarzshild, que admite

soluçãoanalítia. Podemosesolher

m(v)

,

B

(v)

e

r(u, v

0

)

nas eqs. (2.25)-(2.27)de modo aobter diferentes soluções. Para

m(v) =

M

,

B(v) =

−

1/2

e

r(u, v

0

) =

−

u/2

, temosuma parametrização da métria de Shwarzshild, e a eq. (2.26) pode ser resolvida

analitia-mente,

r

+ 2M

ln(r

₋

2M

) =

1

2

(v

−

v

0

)

−

1

2

u

+ 2M

ln

−

u

₂

−

2M

.

(2.39)

Com uma outra esolha de parâmetros, obtemos a solução de Shwarzshild em termos

das oordenadas de Kruskal-Szekeres [13℄. A solução

r(u

k

, v

k

)

(o índie

k

india aqui as oordenadas de Kruskal-Szekeres) édada por

r

+ 2M

ln(r

₋

2M

) = 2M

ln

v

k

v

k0

+ 2M

ln

u

k

u

k0

.

(2.40)

Comparando as duas soluções (2.39) e (2.40), é possível enontrar uma transformação

entre os dois sistemas de oordenadas:

v

k

v

k

0

=

e

v

−

v

0

4

M

,

(2.41)

u

k

u

k0

=

e

−

u

−

u

0

4

M

u

+ 4M

u

0

+ 4M

,

(2.42)

de modoque,a partir dadenição de tempo para asoordenadas de Kruskal,

t

= 2M

ln

v

k

u

k

,

(2.43)

é possível obter

t

₋

t

0

=

v

₋

v

0

2

+

u

₋

u

0

2

−

2M

ln

u

+ 4M

u

0

+ 4M

de maneira que, se

r

=

R

F

(xo), então

t

=

v

+

onst . Esse resultado mostra que, efetivamente,

v

pode seronsideradoomootempoprópriodeum observadoremrepouso noinnito, oque não aontee om

v

k

.

Nas guras 2.1-2.3 temos alguns exemplos do omportamento de

r(u, v)

e

t(u, v)

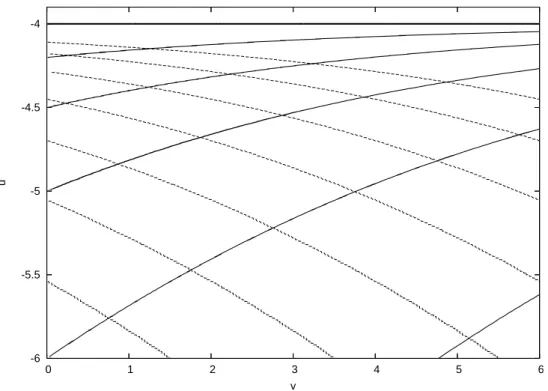
om a parametrização (2.39). Na g. 2.1 temos alguns exemplos de urvas

r(u

=

const, v)

. As urvas om valor iniial

r(u, v

0

)

<

2M

aem na singularidade

r

= 0

, enquanto as urvas om valor iniial

r(u, v

0

)

>

2M

esapam para o innito. Na g. 2.2 temos em detalhe oomportamentodestas urvas quando a ondição iniial

r(u, v

0

) =

−

u/2

tende a

2M

. Asurvasseaproximamde

r

= 2M

(tantosuperiorquantoinferiormente)durante mais tempo quanto mais próxima a ondição iniial estiver de

r

= 2M

, antes de aírem na singularidade ou esaparem. Na g. 2.3 temos um mapeamento das linhas de

r

e

t

onstantes no plano

u

×

v

.

0

1

2

3

4

5

0

1

2

3

4

5

r

v

r = 2M

Figura2.1: Exemplosde urvas

r(u

=

const, v)

obtidasom a eq. (2.39), om

M

= 1

.

Vamos nos basear nestes resultados para esolher a parametrização que será utilizada

para os asos de interesse, om

m

′

6

= 0

. Para

m

′

>

0

, por exemplo, tomamos

B

=

−

1/2

e

r(u, v

0

) =

−

u/2

. Esta esolha garante que a ondição de energia fraa (2.29) seja satisfeita.

As urvas

r(u

=

onst

, v)

obtidas pela integração da eq. (2.26) são geodésias nulas do espaço-tempo. A urva

r

= 2m(v)

é ohorizonteaparentedoburaonegro,denido omo a fronteira entre a região na qual raios de luz se afastam da singularidade (

r

′

0

0.5

1

1.5

2

2.5

3

0

2

4

6

8

10

12

14

r

v

Figura 2.2: Comportamento das urvas

r(u

=

const, v)

obtidas om a eq. (2.39) para

r(u, v

0

) =

−

u/2

→

2M

.

a região na qual raios de luz se aproximam da singularidade (

r

′

<

0

). O horizonte de

eventos é denido omo a fronteira entre as geodésias que esapam e as que aem na

singularidade[18, 19℄. Osdois horizontes podem ser vistosna gura2.4.

Com o método utilizado, o horizonte de eventos pode ser enontrado apenas

numeria-mente, por inspeção, variando-se os valores da ondição iniial

r(u, v

0

) =

−

u/2

. Uma vez enontrada,dentrodapreisãonumériadisponível,aondiçãoiniial

r(¯

u, v

0

)

talque a geodésia gerada seja a primeira a esapar da singularidade, denimos o horizonte de

eventos omo

r

HE

=

r(¯

u, v)

,e uma massa assintótia dadapor

m

ass

(¯

u) =

r(¯

u, v

0

)

2

,

(2.45)

que será utilizada na seção 2.3, no tratamento numério de perturbações na métria de

Vaidya.

Consideramosaqui afunção de massa suave

m(v) =

m

1

+

m

2

−

m

1

2

[1 + tanh

κ(v

−

v

1

)]

,

(2.46)

-6

-5.5

-5

-4.5

-4

0

1

2

3

4

5

6

u

v

Figura 2.3: Curvas de

r

onstante (linhas heias) e

t

onstante (linhas pontilhadas). O raio aumenta om

|

u

|

e

v

resentes e o tempo aumenta om

|

u

|

e

v

deresentes. Para

r

_→

2M

e

t

→ ∞

,asurvastendemassintotiamenteàreta

u

=

−

4M

, queoinideom

m(v) =







m

1

v < v

1

,

m

1

(1 +

λcv)

v

1

< v < v

2

,

m

2

=

m

1

(1 +

λcv

1

)

v > v

2

.

(2.47)

Na g. 2.4 temosaestrutura ausal orrespondenteà funçãode massahiperbólia(2.46)

obtida através do método semi-analítio. Para

κ

positivo e

m

2

> m

1

temos um burao negro om massa iniial

m

1

reebendo um uxo radial de radiação e aumentando sua massa ontinuamenteaté atingir

m

2

.

r

H

v

+

I

u

−

I

r = 2m(v)

r´<0

r´>0

r(v)

v

r=0

v=constant

Figura 2.4: Curvas de

u

onstante para a solução da eq. (2.26) om a função de massa (2.46), om

m

2

> m

1

e

κ >

0

. Todas as soluções na região abaixo da linha

r

= 2m(v

)

(horizonte aparente) possuem

r

′

<

0

. Toda solução que penetrar nesta região atingirá

a singularidade

r

= 0

em um tempo nito. Soluções onnadas à região

r

′

>

0

sempre

esaparão da singularidade e atingirão

I

+

. Neste aso existe um horizonte de eventos

(linha pontilhadano diagramaonforme apresentado) próximo àsolução

r

H

(v)

.

Devemos notar que omodelolinear, para o qual é possível obter expliitamente uma

o-ordenada tartaruga generalizada,diilmentepoderiaorresponder a umasituação físia

realista. Afunçãodemassa(2.47)édelasse

C

0

,impliandoaexistêniade asas

inni-tesimaisde distribuiçãode matériaem

v

=

v

1

e

v

=

v

2

,ondeotensordeenergia-momento é desontínuo,

T

vv

=







0

v < v

1

,

m

1

λ

4

πr

2

v

1

< v < v

2

,

0

v > v

2

.

(2.48)

2.3 Perturbações e MQN's da métria de Vaidya

As equações para perturbações esalares e eletromagnétias podem ser esritas omo [6,

20, 21, 22℄(ver demonstração nos ApêndiesA e B)

∂

2

_ψ

∂u∂v

+

V

(u, v

)f

(u, v)ψ

= 0

,

(2.49)

onde o potenial

V

(u, v)

édado por

V

(u, v) =

ℓ(ℓ

+ 1)

2r

2

_{(u, v)}

+

σ

m(v)

r

3

_{(u, v)}

,

(2.50)

onde

σ

= 1

e

σ

= 0

orrespondem, respetivamente, ao potenial para perturbações esalares eeletromagnétias(

σ

= 1

−

s

2

,onde

s

éospindaperturbação). Para umadada função de massa

m(v)

,é neessário primeiroobter as funções

f

(u, v)

e

r(u, v)

através do método semi-analítio de [14℄, para então resolver a equação (2.49) om o algoritmo de

integração araterístia de segunda ordemproposto em[23℄.

As ondições iniiais do problema são espeiadas nas duas superfíies nulas

u

=

u

0

e

v

=

v

0

omo

ψ(u

=

u

0

, v) = exp

−

(v

−

v

c

)

2

2σ

2

,

(2.51)

ψ(u, v

=

v

0

) = 0

.

(2.52)

A eq.(2.49) éintegradanumeriamente om adisretização

Ψ(N

) = Ψ(W

) + Ψ(E)

₋

Ψ(S)

₋

∆u∆vV

(X)

Ψ(W

) + Ψ(E)

2

+

O(∆

4

₎

_,

(2.53)

ondeusamosasseguintes deniçõesparaospontos

X

,

N

,

S

,

E

e

W

:

X

= (u

+ ∆u/2, v

+

∆v/2)

,

N

= (u

+ ∆u, v

+ ∆v)

,

W

= (u

+ ∆u, v)

,

E

= (u, v

+ ∆v)

e

S

= (u, v)

. Na

gura 2.5 temos uma representação da grade de integração utilizada. Devemos notar

que uma mudança de oordenadas se faz neessária para a integração numéria, para

limitarmos de maneira eiente a região de integração à região externa ao horizonte de

eventos(dependentedotempo)doburaonegro. Paratanto,denimosumanovavariável

U

U

2

≡

u

2

−

2m

ass

ln

−

u

₂

−

2m

ass

érealizadanagrade

U

×

v

. Comoresultado,avariável

U

dagradepodeassumirvaloresde

+

_∞

a

−∞

,semqueohorizontede eventosdoburaonegrosejaultrapassado. Emoutras

palavras,restringimosonossoespaçodeintegraçãopara

r(u, v)

estritamentemaiordoque

r

HE

=

r(¯

u, v)

, ouseja,

u <

u

¯

=

−

4m

ass

). Durante a integração numéria, utilizamosum

algoritmobaseado no métodode Newton para se obter raízes de funções para inverter a

eq. (2.54)eobter

u(U

)

emadapontodagrade

U

×

v

. Este artifíioé similaràdenição da oordenada tartaruga

r∗

normalmente utilizada no tratamento de perturbações na métria de Shwarzshild. A formade (2.54) é inspirada pelo desenvolvimento analítio

dopotenial

V

(u, v)

para perturbações esalares namétria de Shwarzshildno sistema de oordenadas2.39, noqualamudançade oordenadas(2.54)éneessária paraseobter

a equaçãode perturbação orrespondente à eq. (2.49) nas oordenadas usuais.

Após a integração da eq. (2.49) ser ompletada, extraímos os valores

ψ(U

max

, v)

. Para

U

max

suientementegrande,temos umaboaaproximação parao amponohorizontede

eventos. Nagura2.6temosumexemplotípiodosresultadosobtidosparaumafunçãode

massahiperbóliaemomparaçãoom oaso de umburaonegro de Shwarzshild. Nas

guras2.7e2.8temos maisalguns exemplostípios,omparandoa métriade

Shwarzs-hild om resultados obtidos para funções de massa lineares. Resultados similares são

obtidos se extrairmos os dados em outros valores de

U

. Todas as análises apresentadas aquiorrespondemadadosextraídosnohorizonte

U

max

,apenasporumaquestãode on-veniênianuméria. Como osMQN's orrespondemaos auto-estadosde uma equação de

Shrödingerefetiva[6℄, osauto-valoresomplexosassoiadospodemser lidosemqualquer

ponto, uma vez que oregime assintótio seja obtido.

As guras 2.9 e 2.10 apresentam as partes real

ω

R

e imaginária

ω

I

das perturbações em funçãode

v

. Estesresultados orrespondemafunçõesde massaderesentes eresentes, respetivamente, e são típiospara todos os valores de

ℓ

, todos ostipos de perturbaçãoe diferentes ondiçõesiniiais. Os valores daparteimagináriasão obtidostipiamenteom

uma preisão menor, apesar de exibirem o mesmo tipo de omportamento, o que pode

ser visto nas irregularidades de

ω

I

apresentadas na gura (2.10). Nas guras 2.11 e 2.12 temos mais alguns exemplos típios obtidos, para diferentes funções de massa e valores

de

ℓ

.

Esta menor preisão não é resultado de erros numérios no proedimento de integração.

De fato, asdiferenças entre asfreqüênias obtidas om passos de integração

∆u

= ∆v

=

0.2,

0.1

e

0.5

são menores do que o tamanho dos pontosutilizados nas guras 2.9e 2.10.

Areditamos que as irregularidade em

ω

I

se devem ao modo omo as freqüênias são obtidas,fazendo-seumajustedemínimosquadradosloalmente,emintervalosompouos

v

U

U

max

N

W

E

S

X

Figura 2.5: Diagrama da grade utilizada para a integração numériada eq. (2.49) . Os

pontospretosindiamospontosondeovalordoampoéonheido,apartirdasondições

iniiais (2.51) e (2.52). Os pontos vermelhos indiam os pontos onde o ampo deve ser

Figura2.6: Valoresdaperturbaçãoeletromagnétia

ψ(u

max

, v)

om

ℓ

= 2

paraum burao negro de Shwarzshild om massa

m

= 0.5

e para a métriade Vaidya om a função de massa hiperbólia (2.46), onde

v

1

= 75

,

κ

= 0.08

,

m

1

= 0.5

,e

m

2

= 0.65

(Hyperboli 3). Pode-se ver laramente, no aso dependente dotempo, a desaeleração da freqüênia de

1e-10

1e-09

1e-08

1e-07

1e-06

1e-05

1e-04

0.001

0.01

40

45

50

55

60

65

70

75

80

|

ψ

(u,v)|

v

m = 0.5 + 0.001v

m = 0.5

m = 0.5 - 0.001v

Figura 2.7: Perturbação esalar om

ℓ

= 2

para um burao negro de Shwarzshild e a métriade Vaidyaom massa linear resente ederesente.

1e-08

1e-07

1e-06

1e-05

1e-04

0.001

0.01

0.1

1

10

20

30

40

50

60

70

|

ψ

(u,v)|

v

m = 0.5 + 0.001v

m = 0.5

m = 0.5 - 0.001v

valor instantâneo. Por isso, esolhemos tomar o menor número possível de ilos para o

ajuste, apesar de issoausar irregularidadesem

ω

I

.

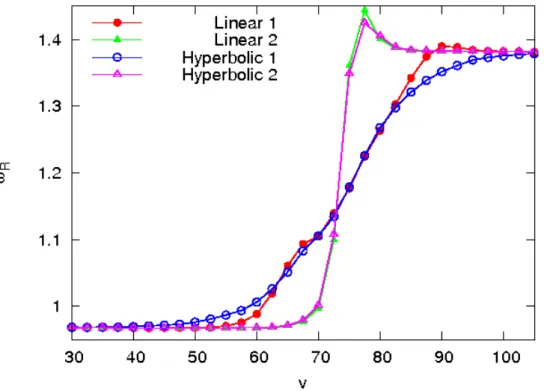
Analisemos mais detalhadamente, por exemplo, o aso de

m(v)

deresente (gura 2.9). Para osasosomvariaçãoaentuada(Linear2eHyperboli2),pode-severlaramenteo

efeitoinerial em

ω

R

próximo de

v

= 75

. A função

ω

R

(v)

não seomporta omo

m

−

₁

(v)

,

omo seria de seesperar para um regime estaionário adiabátio, omorealmenteoorre

para o aso Hyperboli 1. Após a fase de resimento aelerado,

ω

R

se omporta omo setivesse umainériaintrínsea, atingindoum valormáximo queémaiordo que

ω

R

(

∞

)

, impliando emum relaxamento orrespondente àregião om

ω

′

R

(v)

<

0

para

v >

75

.

Analisandoaindaagura2.9, pode-senotar tambémque,parao asoom variação

aen-tuada,não épossíveldetetardiferenças entre osasos om funçãode massasuavee tipo

C

0

. No entanto, vemos queoaso linearomvariaçãomaislenta(Linear1)exibealguns

efeitos ineriaispróximosa

v

=

v

2

. Emtodas asoutrasregiõesasfreqüênias seguemum omportamentoproporionala

m

−

₁

(v

)

. Não foramdetetadas diferenças apreiáveis

en-tre ostransientes dasperturbaçõesesalares eeletromagnétias. Comojáfoi menionado

anteriormenteeste omportamentoinerialtransientenãopdeser detetadopelaanálise

de MQN's realizadaem oordenadas radiativasapresentada em[8℄. Conlusões análogas

se apliamtambémaos asos om massa resente (gura 2.10).

A partir de nossas simulaçõesnumérias podemosinferir qual a situaçãoorrespondente

ao apareimento do omportamento inerial não estaionário dos MQN's. O desvio do

regimeestaionárioémedidopelasegunda derivada dafunçãodemassa,

m

′′

(v)

,quemede

a veloidade om a qual a massa varia. Heuristiamente, podemos esperar o

aparei-mentodoomportamentonãoestaionárioquando

|

1/m

′′

|

(que possuiamesmadimensão

que o tempo no sistema de unidades geométrias utilizado) for menor do que um erto

tempo araterístiode relaxamento dosistema, impedindoque o sistema relaxe e entre

emum regimeadiabátio. Existem dois tempos araterístiosassoiados omos MQN's

de buraos negros: o período de osilação

2π/ω

R

e o tempo de deaimento

|

1/ω

I

|

. O apareimento doomportamentoinerialestá assoiadoao tempo de deaimento.

Veri-amos desvios apreiáveisdo regimeestaionário sempreque

m

′′

(v)

for damesma ordem

(ou maior) doque

|

ω

I

|

, omo mostraremosa seguir

Podemosalular,porexemplo,arazão

|

m

′′

max

/ω

I

final

|

paraosdadosHyperboli4dagura 2.10 (orrespondentes ao omportamento inerial apresentado na gura 2.10). Para a

função de massa(2.46), temos

m

′′

tanh

κ(v

₋

v

1

) =

1

√

3

,

(2.56)

de modoque

m

′′

(v

)

max

=

2

3

√

3

(m

2

−

m

1

)κ

2

_.

(2.57)

Para osparâmetrosde Hyperboli4,

v

1

= 75

e

κ

= 0.8

,e

ω

final

I

≈ −

0.145

(lido dográo), temos

|

m

′′

max

/ω

I

final

| ≈

25%

. ParaosdadosHyperboli3dagura2.10(orrespondentes ao

omportamentoestaionário apresentado nagura), temos

v

1

= 75

e

κ

= 0.08

, portanto a razãoserá 100 vezes menor.

Estimar a magnitude do omportamento inerial a partir de nossas simulações sem um

modelo analítio aproximado paree ser bem mais difíil. Mais uma vez de maneira

heurístia, podemosesperar que amagnitude doefeitoseja proporionala

|

m

′′

|

τ

, onde

τ

é ointervalode tempo durante oqual

|

m

′′

|

&

_|

ω

I

|

.

Figura 2.9: A parte real (

ω

R

) da freqüênia de perturbações esalares om

ℓ

= 2

em função de

v

para funçõesde massalinear ehiperbóliaderesentes. Para todos osasos,

m

1

= 0.5

e

m

2

= 0.35

. Linear 1:

v

1

= 60

,

v

2

= 90

. Linear 2:

v

1

= 74.5

,

v

2

= 75.5

.

Hyperboli 1:

v

1

= 75

,

κ

= 0.08

. Hyperboli2:

v

1

= 75

,

κ

= 0.8

.

Todas as situações onsideradas aqui envolvem funções de massa orrespondentes a um

Figura 2.10: As partes real (

ω

R

) e imaginária(

ω

I

) da freqüênia para perturbações ele-tromagnétias om

ℓ

= 2

em função de

v

para funções de massa linear e hiperbólia resentes. Para todos os asos,

m

1

= 0.5

e

m

2

= 0.65

. Linear 3:

v

1

= 60

,

v

2

= 90

. Linear 4:

v

1

= 74.5

,

v

2

= 75.5

. Hyperboli 3:

v

1

= 75

,

κ

= 0.08

. Hyperboli 4:

v

1

= 75

,

0.95

1

1.05

1.1

1.15

1.2

1.25

1.3

1.35

1.4

30

40

50

60

70

80

90

100

ω

R

v

Linear

κ

= 0.04

κ

= 0.08

κ

= 0.12

Figura 2.11: Evolução de

ω

R

para perturbações esalares om

ℓ

= 2

e diferentes funções de massa hiperbólias, emomparação om uma função de massa linear.

nos garantequeoespaço-tempopossui aestruturaausal de umburaonegro usualpara

v

_{→ ±∞}

e, onseqüentemente, que os MQN's podem ser denidos da maneira usual e

as freqüênias orrespondentes podem ser apropriadamente omparadas. Em todos os

asos onsiderados, os transientes iniiais se dissipam e

ω(v)

passa a ser proporional a

m

−

₁

(v)

bastante rapidamente, onrmando a solidez da análise numéria de MQN's. A

integração emoordenadas nulas semostroumuito mais eientedoque aintegração em

oordenadas radiativas [8℄, permitindo-nos atingir a preisão neessária para veriar o

omportamentonão estaionário om reursos omputaionais bastante modestos.

Umaextensãointeressantedestetrabalhoseria aanálisedosMQN'srapidamente

amorte-idos (

n >

0

). Para estesmodossuperioresarazão

|

ω

I

/ω

R

|

ésempre maiordoquepara o MQNfundamentalom

n

= 0

onsideradoaqui,inluindo,para

n

suientementegrande, asos em que

|

ω

I

/ω

R

|

>

1

. Portanto, seria interessante veriar seo omportamentonão estaionário poderia ser atenuado de alguma maneira para

n >

0

. A análise numéria apresentada aqui não pode ser estendida diretamente para o aso

n >

0

, uma vez que não é possível identiarestas freqüêniasom preisãosuiente. Areditamos que este

resultado poderia ser obtido, emprinípio, através dométodoWKB, que já foi utilizado

om suesso para a obtenção dos modos superiores de perturbações do burao negro de

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

30

40

50

60

70

80

90

100

ω

R

v

m(v) = 0.5 + 0.001v

L = 1

L = 2

L = 3

L = 4

L = 5

2.5

2

1.5

1

0.5

30

40

50

60

70

80

ω

R

v

m(v) = 0.5 - 0.001v

L = 1

L = 2

L = 3

L = 4

L = 5

ilmentemantenhamasimetriaesféria intataduranteosestágiosintermediários,nossos

resultados podem ser utilizados omo uma primeira aproximação para o espalhamento

de ampos fraos por estas fontes. É fato bem onheido que, após as fases transientes,

o sistema deve se aomodar em uma onguração esferiamente simétria estaionária.

Entretanto, não devemos esqueer que o omportamento inerial não estaionário das

freqüênias dos MQN's devesurgir sempre que

|

m

′′

|

&

_|

ω

I

|

. Isto torna aanálise de

situa-ções om variaçõesrápidasuma tarefa deliada.

A evaporação por radiação de Hawking [25℄ poderia ser onsiderada omo um proesso

físio real onde a massa do burao negroderese e a simetriaesféria émantida. Nosso

métodopode ser apliadoa esse aso (ver apítulo3).

Finalmente,notamosqueasosilaçõesamorteidasorrespondemauma fase

intermediá-riadoespalhamentode ondas porburaos negrosassintotiamenteplanos. A últimafase

orrespondeaumdeaimentoquesegueumaleidepotênia. Nosproblemasonsiderados

aqui,odeaimentoemleide potêniaaparee tipiamenteparavaloresgrandesde

v

,nos quais os MQN's já atingiram a fase estaionária, sem vestígios dos transientes: a massa

doburaonegroatingiuoseuvalornalonstanteeoomportamentodosMQN'sémais

uma vez estaionário, ou seja, tudo se passa omo se tivéssemos um burao negro de

Shwarzshild. Nãodetetamos,neste aso, qualquerinuênia dadependênia temporal

dopotenialnafasenaldedeaimentoemleidepotênia. Este resultadoéonseqüênia