Teorema Central do Limite para o modelo O(N) de Heisenberg hierárquico na criticalidade...

(1)

Teorema Central do Limite para o Modelo

O(N

)

de Heisenberg Hier´

arquico na Criticalidade e o

Papel do Limite

N

_{→ ∞}

na Dinˆ

amica dos Zeros de

Lee-Yang

William Remo Pedroso Conti

Orientador: Prof. Dr. Domingos Humberto Urbano Marchetti

Disserta¸c˜ao de Mestrado submetida ao Instituto de F´ısica

da Universidade de S˜ao Paulo para a obten¸c˜ao do t´ıtulo de

Mestre em Ciˆencias.

Banca Examinadora:

Prof. Dr. Walter Felipe Wreszinski (IFUSP) Prof. Dr. Paulo Domingos Cordaro (IMEUSP) Prof. Dr. Domingos Humberto Urbano Marchetti (IFUSP)

(2)

(3)

`

A minha amada fam´ılia - Sra. Maria Cristina Pedroso Conti, Sr. Leonildo Remo Conti, Thiago Vin´ıcius Pedroso Conti e Mayara Cristina Pedroso Conti - pelo apoio e incentivo. Ao meu orientador, Prof. Dr. Domingos Humberto Urbano Marchetti, por ter-me aceito como seu aluno; pela conﬁan¸ca em mim depositada; pelo modo como tem conduzido

meus passos; por toda sua aten¸c˜ao, em todos os momentos deste projeto.

Aos meus amigos de gradua¸cão - Alex, Bruno, Eduardo, Elisa, Fábio, Felipe, Pedro, Silas, Simão Pedro, Thiago, Walter e Wilson - por todas as ajudas e incentivos.

Aos meus amigos do Grupo de Mecˆanica Estat´ıstica, meus atuais companheiros de

caminhada. `

As secret´arias e funcion´arios do Departamento de F´ısica Geral, pelo suporte e prestivi-dade.

`

A Funda¸cão de Amparo à Pesquisa do Estado de São Paulo (FAPESP), pelo apoio

(4)

(5)

Neste trabalho estabelecemos o Teorema Central do Limite para o modelo O(N) de Heisenberg hierárquico na criticalidade (sistema à temperatura inversa cr´ıtica βc) via equa¸cão a derivadas parciais (obtida na aproxima¸cão de potencial local (L _↓ 1) da transforma¸cão de grupo de renormaliza¸cão)

u(tN) = 2 Nxu

(N)

xx +u(xN)−2x u(xN)

2

−γxu(_xN)+du(N)₋u(_xN)(t,0)

com condi¸c˜ao inicial

u(N)_{(0, x) =} ₋1

N ln

"

Γ(N/2)

i√βxN/2N/2−1JN/2−1

ipβxN

#

,

no limite N _{→ ∞} (modelo esférico (N = _∞) hierárquico cont´ınuo (L _↓ 1)). Por simplicidade consideramos apenas o caso d = 4, sendo o teorema também válido para d > 4. Pelo estudo de uma dada equa¸cão a derivadas parciais (EDP) determinamos

a temperatura inversa cr´ıtica βc(d) do modelo esférico hierárquico cont´ınuo para um d > 2 qualquer, havendo conexão entre criticalidade e o ponto fixo da EDP. Por meio de uma análise geométrica da trajetória cr´ıtica _{u(x∞)(t, x), β = βc, t ≥ 0} obtemos informa¸cões sobre a dinâmica e distribui¸cão dos zeros de Lee-Yang. Mostramos que

u(x∞)(0, x) pertence à classe Pick P de fun¸cões; e verificamos indiretamente que o fluxo u(xt∞)(t, x) preserva essa classe, isto é,u

(∞)

(6)

(7)

In this work we establish the Central Limit Theorem for the hierarchical O(N) Heisen-berg model at criticality (system at inverse critical temperature βc) via partial diﬀeren-tial equation (obtained in the local potendiﬀeren-tial approximation (L_↓1) of renormalization group transformation)

u(tN) = 2 Nxu

(N)

2

−γxu(_xN)+du(N)₋u(_xN)(t,0)

with initial condition

u(N)_{(0, x) =} ₋1

N ln

"

Γ(N/2)

i√βxN/2N/2−1JN/2−1

ipβxN

#

,

in the limit N _{→ ∞} (continuum (L _↓ 1) hierarchical spherical (N = _∞) model). For simplicity we only treat the d = 4 case but the theorem is still valid for d > 4. By studying a given partial diﬀerential equation (PDE) we determine for any d > 2 the

critical inverse temperature βc(d) of the continuum hierarchical spherical model, and we show a connection between criticality and the ﬁxed point of PDE. By means of a geometric analysis of the critical trajectory _{u(x∞)(t, x), β = βc, t ≥ 0} we obtain some informations about Lee-Yang zeros’s dynamics and distribution. Finally, we show

(8)

(9)

1 Introdu¸c˜ao: Motiva¸c˜oes e Resultados 11

2 Trajet´oria Discreta: Resumo 18

2.1 O Modelo O(N) de Heisenberg Hier´arquico . . . 18

2.2 Transforma¸c˜ao do Grupo de Renormaliza¸c˜ao . . . 26

2.3 A Aproxima¸c˜ao de Potencial Local (L_↓1) . . . 40

3 Trajetória Cont´ınua: Caso N =_∞ 44 3.1 O Modelo Esférico Hierárquico . . . 44

3.2 O Teorema Central do Limite . . . 54

3.3 A Criticalidade . . . 71

3.4 O Fluxo do Ponto de Vista Geom´etrico . . . 78

3.4.1 Demonstra¸c˜ao da Proposi¸c˜ao 3.2.1 . . . 78

3.4.2 A Condi¸c˜ao Inicial u′ 0(x) e a Classe Pick de Fun¸c˜oes . . . 83

3.4.3 A Fun¸c˜ao ux(t, x) para t >0 e a Classe Pick de Fun¸c˜oes . . . 90

3.5 Conclus˜oes e Problemas em Aberto . . . 99

A Apêndices 105 A.1 Demonstra¸cão do Teorema da Fun¸cão Inversa . . . 105

A.2 Demonstra¸c˜ao do Teorema de Worpitzky . . . 108

A.3 A Classe Pick de Fun¸c˜oes . . . 116

(10)

(11)

Introdu¸c˜

ao: Motiva¸c˜

oes e

Resultados

Dados os inteiros L,K e d, com L, K >1 ed_≥1, seja

ΛK =_{0,1, . . . , LK₋1_}d_⊂Zd

uma rede ﬁnita hiperc´ubicad-dimensional de cardinalidade_|ΛK|=LKd =n. Pormodelo

O(N) de Heisenberg hierárquico entende-se o modelo que associa a cada vértice de ΛK uma variável de spin clássica yque assume valores sobre a esfera unitária emRN_{; essas}

variáveis sãodependentes segundo uma matriz de acoplamento ferromagnética chamada

matriz de intera¸cão hierárquica. Trata-se de uma matriz que não obedece invariância por transla¸cão nem alcance finito; as variáveis de spin interagem segundo uma estrutura de blocos - a cada hierarquia são formados blocos de Ld _{variáveis de spin da hierarquia} anterior, de tal maneira que na hierarquiaktem-se a rede ΛK−kde cardinalidadeL(K−k)d.

Sejaσ_k(N)(y) a distribui¸c˜ao “a priori” da vari´avel soma

X_k,Nγ = _√ 1 mγ/d

X

i∈Λk

yi, (1.0.1)

com m = Lkd_{, e} _γ _{um parâmetro que pode assumir o valor} _d _ou _d_{+ 2. Se} _M _denota o espa¸co das distribui¸cões “a priori” em RN _{invariantes por transforma¸cões ortogonais}

(12)

σ_k(N)(y) = _Rσ_k(N₋)₁(y). (1.0.2)

Sendo _{σ(_kN)(y;β), k _≥ 0_} uma fam´ılia de trajetórias parametrizada pelo inverso da temperaturaβ, eβc atemperatura inversa cr´ıtica, o propósito deste trabalho é investigar

a convergˆencia

lim k→∞σ

(N)

k (y;βc) =σgauss(y) (1.0.3)

da trajetória cr´ıtica _{σ(_kN)(y;βc), k ≥0}para a distribui¸cão gaussianaσgauss(y) quando N é muito grande. Mais especificamente, pretendemos estabelecer o Teorema Central do Limite para o modelo O(N) de Heisenberg hierárquico na criticalidade para N su-ficientemente grande. Para dar conta das flutua¸cões anormais da criticalidade, γ neste caso tem de ser escolhido igual a d+ 2.

Teorema de Lee-Yang. Sejadνn(y) a medida de Gibbs (medida de equil´ıbrio) de um sistema ferromagn´etico cl´assico de nspins, comy= (y1, . . . , yn) um elemento do espa¸co

de configura¸cão Ωn, e consideremos a fun¸cão caracter´ıstica (transformada de Fourier) dessa medida

Φn(z) =

Z

Ωn

exp_{i(z,y)Ωn}dνn(y), (1.0.4)

com (.,.)Ωn o produto interno sobre Ωnez = (z1, . . . , zn) a vari´avel conjugada. Segundo

Lee e Yang, as propriedades de equil´ıbrio termodinˆamico do sistema s˜ao regidas pela

distribui¸c˜ao dos zeros (zeros de Lee-Yang) de

ϕn(_−|z_|2) := Φn(z, . . . , z). (1.0.5)

(13)

cálculo ilustra o adensamento dos zeros, pelo limite termodinâmico n_{→ ∞}, sobre uma curva no plano complexo e explicita a maneira como as propriedades macroscópicas de equil´ıbrio do modelo são determinadas a partir da densidade (distribui¸cão emp´ırica) dos

zeros de (1.0.5).

Em 1974 Newman [24] formulou esse problema da determina¸c˜ao dos zeros de

Lee-Yang da seguinte maneira: se ϕ1(−|z|2) possui zeros sobre a reta real, ent˜ao ϕn(−|z|2)

mant´em os zeros sobre R _para _{β >} _{0 e todo}_{n, e esses zeros possivelmente se adensam}

no limite n _{→ ∞}(o adensamento somente foi levado em considera¸c˜ao por De Coninck [7]).

Teorema de Lee-Yang e o Modelo O(N) de Heisenberg Hierárquico. As fun¸cões termodinâmicas do modelo O(N) de Heisenberg hierárquico dependem das variáveis macroscópicas X_k,Nγ (1.0.1). Para esse modelo temos a seguinte rela¸cão

Φ(_mN)

z

√

mγ/d, . . . , z

√

mγ/d

=

Z

Ωm

exp_{iz_·X_k,Nγ _}dν_m(N)(y)

=

Z

RN

exp_{iz_·y_}dσ_k(N)(y) =φ(_kN)(z), (1.0.6)

comdνm(N)(y) a medida de Gibbs para um bloco dem=Lkdspins,σ(_kN)(y) a distribui¸c˜ao “a priori” da vari´avel soma X_k,Nγ , e z _·y o produto interno em RN_{. Para um estudo}

do modelo à luz do Teorema de Lee-Yang é portanto suficiente que se conhe¸ca os zeros das fun¸cões caracter´ısticas _{φ(_kN)(z)_} como fun¸cões de_−|z_|2_{. Define-se nesse contexto a}

chamada propriedade de Lee-Yang (vide Defini¸cão 2.2.7): diz-se que uma medida σ(y) em RN _{invariante por transforma¸cões ortogonais} _O(N_{) possui a propriedade de}

Lee-Yang se os zeros de sua fun¸c˜ao caracter´ıstica φ(z) = RRNexp{iz·y}dσ(y) := ϕ(−|z|2)

encontram-se na reta real e ϕ(_−|z_|2_{) pertence `a classe das fun¸c˜oes inteiras de Laguerre,}

as quais possuem a representa¸c˜ao (2.2.27).

(14)

σ_k(N)(y;βc). As fun¸cões φ(_kN)(z) também satisfazem uma rela¸cão de recorrência (mapa discreto)

φ(_kN)(z) =_Fφ(_kN₋)₁(z) (1.0.7)

- vide Proposi¸c˜ao 2.2.4.

Em [15], Kozitsky estabelece o Teorema Central do Limite para o modelo O(N) de

Heisenberg hierárquico para os casos β = βc e β < βc partindo de uma vizinhan¸ca do ponto fixo gaussiano, sendo que o tamanho de bloco é Ld _≥ _{2 e} _{d >} _{4. Nesse} estudo Kozitsky mostra que se Ld _{é um inteiro, o mapa} _F _{preserva a propriedade de} Lee-Yang. Assim, se φ(₀N)(z) = ϕ₀(N)(_−|z_|2_{) é uma fun¸cão da classe de Laguerre, então}

{ϕ(_kN)(_−|z_|2_{), k >} ₀_}_{é uma seq¨}_{uência de fun¸cões da classe de Laguerre. Para essa classe}

de fun¸cões há dispon´ıvel [24] algumas desigualdades para os momentos da distribui¸cão dos zeros, e é com o aux´ılio dessas que se mostra a convergência para o ponto fixo gaussiano.

Já em [27], Watanabe estabelece o Teorema Central do Limite para o modelo O(N) de Heisenberg hierárquico para N suficientemente grande e β =βc, partindo da fun¸cão

caracter´ıstica

φ(₀N)(z) = _√ Γ(N/2)

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_| (1.0.8)

da distribui¸cão “a priori” uniforme suportada sobre a esferaN-dimensional de raio√βN (por conveniência, considera-se esse raio ao unitário), com Ld _{= 2 e} _d _{= 4. Para} con-trolar a trajetória O(N), que parte de muito longe do ponto fixo gaussiano, Watanabe

utiliza a trajetória exatamente solúvel O(_∞) juntamente com dois ingredientes válidos para Ld _{inteiro: o fato de o mapa} _F _{preservar a propriedade de Lee-Yang, e}

positivi-dade por reflex˜ao. A propriedade de Lee-Yang ´e utilizada da mesma maneira que por

Kozitsky (desigualdades para os momentos da distribui¸cão dos zeros), e a propriedade de positividade por reflexão garante a convergência uniforme das trajetórias O(N) para as trajetórias O(_∞).

(15)

diferencia-se desdiferencia-ses dois pela utiliza¸cão da chamada aproxima¸cão de potencial local: definindo o potencial

U(t, z) =₋lnφ(_kN)(z) (1.0.9)

com parˆametro de escala

t =klnL , (1.0.10)

toma-se conjuntamente os limites k _{→ ∞} e L _↓ 1 de tal maneira que klnL per-mane¸ca fixo em um número real positivo t. Com tal procedimento, a órbita discreta

{−lnφ(_kN)(z;β), k _≥0_}torna-se cont´ınua, e a dinâmica completa se reduz a uma equa¸cão a derivadas parciais. A nossa condi¸cão inicial é dada por U(0, z) = ₋lnφ(₀N)(z), com φ(₀N)(z) dada por (1.0.8) (a condi¸cão inicial de Watanabe). Como veremos, a equa¸cão diferencial satisfeita porU(t, z) preserva simetria esférica, de tal maneira que é suficiente

considerar apenas a variável radial _|z_|. Com a finalidade de se poder tomar o limite de N para infinito, definimos o potencial adequadamente escalado em N

u(N)(t, x) = 1 NU(t,

√

N z), (1.0.11)

com x = _−|z_|2_{, e determinamos a equa¸c˜ao diferencial parcial correspondente, aqui}

denominada EDPu(N) _{(vide problema de valor inicial (2.3.16)-(2.3.17)). Trata-se de}

uma equa¸cão não-linear que apresenta o termo 1/N na frente do termo de derivada segunda. A equa¸cão com N finito é, por conseguinte, uma perturba¸cão singular da equa¸cão com N =_∞: com o limite N _{→ ∞}a ordem da equa¸cão é reduzida de segunda

para primeira (compare (2.3.16) com (3.2.1)). Devemos enfatizar que em decorrência do fato que no limite L _↓ 1 os ingredientes positividade por reflexão e propriedade de Lee-Yang deixam de valer, um método inteiramente novo foi desenvolvido em nossas análises.

Uma das motiva¸c˜oes do presente estudo ´e justamente o entendimento da EDPu(N)

como uma perturba¸c˜ao singular da EDPu(∞)_{: conhecendo a trajet´oria exatamente sol´}_uvel

(16)

um espa¸co funcional adequado. Pretende-se, além disso, estender as solu¸cões dos dois problemasnão lineares ao plano complexo de maneira tal que seja poss´ıvel compreender o que ocorre com suas singularidades.

Isso nos leva a uma outra motiva¸c˜ao: descrever o problema da convergˆencia do

ponto de vista da dinâmica doszeros de Lee-Yang. Já dissemos que o mapa _F preserva a propriedade de Lee-Yang. Partindo da fun¸cão inteira (1.0.8) que possui zeros sobre o eixo real, a seqüência de fun¸cões caracter´ısticas _{φ(_kN)(z) = ϕ_k(N)(_−|z_|2_{), k} _≥ ₀_} _induz

uma dinâmica sobre os zeros de Lee-Yang, cuja distribui¸cão no limite termodinâmico

é determinada pelos zeros da fun¸cão limite dessa seqüência. No caso de se mostrar convergência para uma fun¸cão gaussiana (Teorema Central do Limite), fun¸cão essa que

não possui zeros, deve-se mostrar que os zeros são expelidos para o infinito. Os métodos empregados por Kozitsky e por Watanabe não permitem o estudo da dinâmica dos zeros

com o aumento da hierarquia k. Na aproxima¸cão de potencial local por nós adotada, a propriedade de Lee-Yang definida pelos autores [15] e [23] não é preservada; todavia, a citada dinâmica pode ser estudada pela evolu¸cão da fun¸cão u(xN)(0, x), para a qual os zeros de φ(₀N)(z) =ϕ₀(N)(_−|z_|2_{) passam a ser pólos -}_u(N)

x (0, x) ´e uma fun¸c˜ao meromorfa.

Deste ponto de vista, a questão passa a ser: aclasseP de Pick das fun¸cões holomorfas no semi-plano superior, que inclui fun¸cões meromorfas e fun¸cões que possuem cortes no eixo real, é preservada pela dinâmica de u(xN)(t, x)? Mostraremos que com o limite N → ∞ os pólos deu(xN)(0, x) se adensam, dando origem a um corte; mas tantou(xN)(0, x) quanto a fun¸cão limite u(x∞)(0, x) pertencem à classe das fun¸cões de Pick. Além disso, para o casoN =_∞, vamos verificar que a classe de fun¸cões de Pick é preservada (u(x∞)(t, x)∈P para todo t _≥ 0) pela EDPu(x∞), e uma descri¸cão da dinâmica dos zeros de Lee-Yang será dada.

Esta disserta¸c˜ao est´a dividida em dois cap´ıtulos:

O primeiro cap´ıtulo é formado por três se¸cões. Na Se¸cão 2.1 apresentamos o modelo

(17)

local derivamos uma equa¸cão a derivadas parciais para o potencialU(t, z) =₋lnφ(_kN)(z). O segundo cap´ıtulo trata do caso N =_∞, e é formado por quatro se¸cões. Na Se¸cão

3.1 apresentamos o modelo esférico (N =_∞) hierárquico e sua versão cont´ınua (L_↓1), mostrando alguns resultados a esses associados - questão de existência de ordem de longo alcance, bem como a obten¸cão da temperatura inversa cr´ıtica. Encontra-se na Se¸cão 3.2 nosso principal resultado: o Teorema Central do Limite. Mostramos para

d = 4 que a trajet´oria cr´ıtica (β =βc(d= 4) = 4) _{u(∞)_{(t, x), t}_≥ ₀_} _{converge, quando}

t _{→ ∞}, para a fun¸c˜ao u∗_{(x) =} ₋_{x. Um ponto importante de nosso estudo ´e que esse}

teorema pode ser adaptado para d > 4, casos em que também se observa convergência para o ponto fixo gaussiano; mas as técnicas desenvolvidas também são aplicáveis para

2< d < 4, casos em que o ponto fixo é não-gaussiano - a dimensãod= 4 é o valor cr´ıtico superior para modelos hierárquicos, dimensão a partir da qual os expoentes cr´ıticos são os mesmos da teoria de campo médio com flutua¸cões gaussianas. Na Se¸cão 3.3 a questão da criticalidade é retomada, mas agora do ponto de vista exclusivamente de uma dada

equa¸cão a derivadas parciais. A Se¸cão 3.4 é dividida em três subse¸cões, e tem por propósito fazer um estudo geométrico, no plano complexo, da trajetória cr´ıtica estudada na Se¸cão 3.2. Mais especificamente, estendemos a fun¸cão u(x∞)(t, x) para o semi-plano superior do plano complexo e utilizamos o Teorema do Mapeamento de Riemann para

prover informa¸c˜oes qualitativas sobre a trajet´oria cr´ıtica.

Ao final do trabalho estão os Apêndices. Degrandeimportância são as três primeiras se¸cões, em especial a que expomos alguns fatos sobre a classe Pick de fun¸cões. Quanto à se¸cão sobrereflexão de Schwarz, esta foi colocada apenas por uma questão de completeza

- esse conceito aparece apenas na demonstra¸cão de uma proposi¸cão, e não é algo de

(18)

Trajet´

oria Discreta: Resumo

2.1 O Modelo

O

(

N

)

de Heisenberg Hier´

arquico

Por um postulado devido a Gibbs, a termodinˆamica de um sistema de spins ´e derivada de

uma distribui¸cão de probabilidade definida sobre o espa¸co de configura¸cão, denominada

medida de equil´ıbrio ou medida de Gibbs.

Para o modeloO(N) de Heisenbergferromagnéticoconsiderado sobre uma rede finita ΛK ⊂Zd de cardinalidade|ΛK|=n essa medida é dada por

dν_n(N)(y) = 1 Zn(N)

exp

−1

2 (y, Ay)Ωn

Y

i∈ΛK

dσ₀(N)(yi). (2.1.1)

Nesta express˜ao,

Z_n(N) =

Z

Ωn

exp

−1₂ (y, Ay)Ωn

Y

i∈ΛK

dσ₀(N)(yi) (2.1.2)

é a chamada fun¸cão de parti¸cão, uma normaliza¸cão necessária para que dνn(N)(y) seja uma medida de probabilidade; y denota um elemento do espa¸co de configura¸cão Ωn =

RN _{× · · · ×}RN ₌RN.n_{; (x,}_y)_Ω

n ´e o produto interno sobre Ωn

(x,y)Ωn =

X

i∈ΛK

(19)

dσ₀(N)(y) = 1 SN βN

δ_|y_{| −}pβN dNy (2.1.4)

´e a medida “a priori” uniforme sobre a esfera N-dimensional

ΣN_βN =

(

y_∈RN _: _|_y_|2₌

N

X

l=1

(yl)2 =βN

)

(2.1.5)

de raio √βN, com β o inverso da temperatura e

SN βN =

Z

RN

δ_|y_{| −}pβN dN_y₌ 2π

N/2 √_βNN−1

Γ(N/2) (2.1.6)

a ´area da superf´ıcie da esfera ΣN

βN. No modelo O(N) de Heisenberg associamos a cada vérticei_∈ΛK umavariável de spin clássica yique assume valores sobre a esfera unitária

em RN_{. Entretanto, para os prop´ositos de nosso estudo, ´e conveniente que se tenha}

yi ∈RN. Assim sendo introduzimos, na medida “a priori”, o v´ınculo (2.1.5). Tamb´em

por conveniˆencia escolhemos o raio √βN1 _{ao raio unit´ario. Quanto ao acoplamento}

entre as vari´aveis de spin yi, este ´e expresso pela matriz A= [Aij] presente na energia

Un(y) = (y, Ay)Ωn (2.1.7)

associada à configura¸cão y, sendo A = ₋J_⊗IN com IN a matriz identidade de ordem N e J = [Jij] uma matriz n×n de intera¸cão ferromagnética:

Jij ≥0 ∀i, j . (2.1.8)

O nosso interesse está na chamada intera¸cão hierárquica, que será definida a seguir. Por uma questão de completeza, fa¸camos:

1

Note que pela mudan¸ca de vari´avely′₌√_β_y_{o parˆ}_ametro_β_{passa a ser escrito no termo exponencial}

(20)

C´alculo da ´Area da Superf´ıcie de uma Esfera N-dimensional

(a) de Raio Unitário: é conveniente que se passe para coordenadas esféricas

generali-zadas; o jacobiano ´e dado por

dNy =rN−1(sinθ1)N−2(sinθ2)N−3· · · sinθN−2dr dθ1dθ2· · ·dθN−1 , (2.1.9)

com 0_≤r=_|y_|<_∞,

0_≤θ1, θ2, . . . , θN−2 ≤π

e

0_≤θN−1≤2π .

Para se chegar `a igualdade

S₁N =

Z π

0

(sinθ1)N−2dθ1

Z π

0

(sinθ2)N−3dθ2· · ·

Z π

0

sinθN−2 dθN−2

Z 2π

0

dθN−1

= 2π

N/2

Γ(N/2) , (2.1.10)

pode-se utilizar a integral gaussiana

Z

RN

e−|y|2 dNy=

Z

R

e−y2 dy

N

=πN/2 , (2.1.11)

pois essa tamb´em ´e igual a

Z

RN

e−|y|2 dNy = S₁N

Z ∞

0

rN−1e−r2 dr

= S₁N 1 2

Z ∞

0

tN/2−1e−tdt

= S₁N Γ(N/2)

(21)

(b) de Raio R: de (2.1.9) temos que

S_RN2 =RN−1S₁N , (2.1.13)

de onde se conclui, juntamente com (2.1.10), a equa¸c˜ao (2.1.6).

A Matriz de Intera¸c˜ao Hier´arquica. Dados os inteirosL,K ed,L, K >1 ed _≥1, seja para cada m = 1,2, . . . , K

Λm =_{0,1, . . . , Lm₋1_}d_⊂Zd _(2.1.14)

a rede ﬁnita hiperc´ubica d-dimensional de cardinalidade _|Λm_| = Lmd_{. Seja} _u _∈ _R|Λm|

um vetor que associa a cada v´ertice i = (i1, . . . , id) de Λm uma vari´avel real ui, e

v _∈ R|Λm−1| _{um vetor que associa a cada v´ertice} _r _{= (r}

1, . . . , rd) de Λm−1 uma vari´avel

real vr. Deﬁnimos o operador de bloco B :R|Λm| →R|Λm−1| por

Bu=v (2.1.15)

tal que a componente r desse vetor ´e dada por

vr = (Bu)r =

1 Ld/2

X

j∈Λ1

uLr+j . (2.1.16)

Seu adjunto B∗ _:_R|Λm−1|_→R|Λm|

(w, Bu)R|Λm−1| = (B

∗_{w, u)}

R|Λm| (2.1.17)

com respeito ao produto interno (w, u)R|Λm| =P_i_∈_Λ

mwiui´e

B∗v =u (2.1.18)

(22)

uLr+j = (B∗v)Lr+j =

1

Ld/2 vr ∀j ∈Λ1 . (2.1.19)

Introduzimos assim as no¸cões de bloco e hierarquia à rede ΛK: a cada vértice r de ΛK−k−1 associamos um bloco deLd vértices de ΛK−k, a saber, todos os elementos de

{Lr1, . . . , Lr1+L−1} × · · · × {Lrd, . . . , Lrd+L−1}; (2.1.20)

os vértices i_∈ΛK−k são denominadosvértices da hierarquia k e os r ∈ΛK−k−1 vértices

da k+ 1-ésima hierarquia; i_∈ΛK são vértices da hierarquia zero, e na K-ésima hierar-quia há somente um único vértice Λ0 ={0}. Se u e v denotam configura¸cões de spins,

dado um vértice r dak+ 1-ésima hierarquia, a opera¸cão realizada pelo operadorB é a

de somar todas as vari´aveis de spinui da hierarquia k associadas ar, e normalizar pela

raiz quadrada do tamanho do bloco (Ld_{). Quanto a}_B∗_{, transforma a vari´avel de spin de}

bloco vr da k+ 1-´esima hierarquia em Ld vari´aveis de spin da hierarquia k, atribuindo

a cada uma delas o mesmo valor.

Utilizando os operadores B e B∗ _{deﬁnimos, sobre} _R|ΛK|_{, a} _{matriz de intera¸c˜ao}

hier´arquica JH:

JH = K

X

k=1

L−2k(B∗)kBk. (2.1.21)

Bk ₌_{B B}_{· · ·}_B

| {z }

k−vezes

´e a aplica¸c˜ao sucessiva deB, e portantoBk_:_R|ΛK|_→_R|ΛK−k|; o ´ındice

k indica a hierarquia. Assim, o número máximo de hierarquias que se tem em ΛK éK.

Defini¸c˜ao 2.1.1 (Matriz Positiva e Positiva Definida) Uma matriz M = [Mij] n_×n real ´e dita ser positiva se

Mij >0 _∀i, j , (2.1.22)

(23)

(u, Mu)Rn >0 (2.1.23)

para todo vetor n˜ao nulo u_∈Rn_.

Proposi¸cão 2.1.2 JH é uma matrizLKd_×_LKd _{real simétrica positiva e positiva definida.}

Para demonstrarmos esta proposi¸cão é necessária a defini¸cão de distância hierárquica:

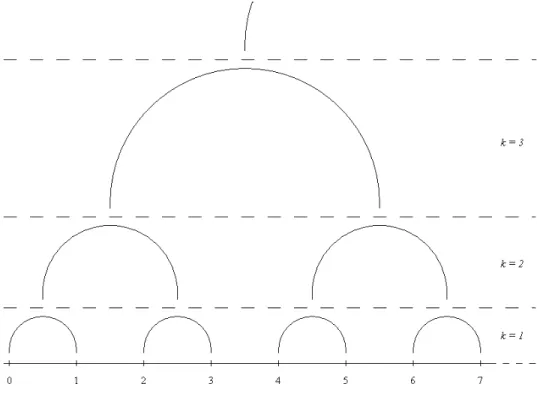
consideremos uma seqüência (θ₁, . . . ,θK) de vetoresθ_k_{∈ {}0,1, . . . , L₋1_}d_{tal que, para} cada vértice i= (i1, . . . , id)∈ΛK, temos uma única expansão na base Ld-nária

i = K

X

k=1

θ_kLk−1 . (2.1.24)

O vetor θ_k indica a posi¸cão do vértice i dentro do bloco, ao qual pertence, da k-ésima hierarquia. A t´ıtulo de esclarecimento, consideremos o exemplo mostrado pela Figura

2.1, em que L= 2 e d= 1.

(24)

O vértice i= 3 possui a expansão binária (1,1,0,0, . . . ,0): dentro do bloco da primeira hierarquia ele ocupa a posi¸cão θ1 = 1; dentro do bloco da segunda hierarquia, a posi¸cão

θ2 = 1; dentro do bloco da terceira hierarquia, a posi¸c˜aoθ3 = 0; e assim sucessivamente.

Ao vértice i= 4 está associada a expansão (0,0,1,0,0, . . . ,0).

Defini¸cão 2.1.3 (Distância Hierárquica) Seja (θ1, . . . ,θK)a expansãoLd-nária do

vértice i _∈ΛK, e (θ′1, . . . ,θ′K) a do vértice j ∈ΛK. A distância hierárquica entrei e j

´e definida por

distL(i,j) =

(

Lk(i,j) _se _i₆₌_j

0 se i=j , (2.1.25)

sendo k(i,j) =m´ax_{l _{∈ {}0,1, . . . , K_}:θl6=θ′l} a menor hierarquia k que faz com que i e j sejam cobertos por um mesmo bloco de tamanho Lkd.

Peguemos como exemplo os s´ıtios 3 e 4 da Figura 2.1, cujas expansões binárias já conhe-cemos: k(3,4) = 3; logo dist2(3,4) = 23 = 8, apesar de serem vizinhos próximos.

Observa¸cão 2.1.4 Note que a distância hierárquica não é estacionária com respeito a qualquer transla¸cão a _∈ Zd_{, isto é, em geral} _distL(i₊_a,_j ₊_a)₆_=distL(i,_j)_{. Além}

disso, a desigualdade distL(i,j)>_|i₋j_| ´e sempre satisfeita, com _|i₋j_| a distˆancia euclidiana entre os s´ıtios.

Estamos agora em posi¸c˜ao de demonstrar a Proposi¸c˜ao 2.1.2:

Demonstra¸c˜ao. Seja δi∈R|ΛK| um vetor cujas componentes ul s˜ao nulas exceto para

l =i, l,i_∈ΛK:

(δi)l=

(

0 se l₆=i

1 se l=i . (2.1.26)

(25)

(JH)ij = (δi, JHδj)R|ΛK|

= K

X

k=1

L−2k(δi,(B∗)kBkδj)R|ΛK|

= K

X

k=1

L−2k(Bkδi, Bkδj)R|ΛK−k| . (2.1.27)

Para i₆=j

(Bkδi, Bkδj)R|ΛK−k| =

(

0 se k < k(i,j)

L−dk _se _k_≥_k(i,_j) , (2.1.28)

e para i =j temos que (Bk_δ

i, Bkδj)R|ΛK−k| =L−dk para todo k. Desta maneira

(JH)ij =

(

L−(d+2)k(i,j)₋_L−(d+2)(K+1) ₁₋_L−(d+2)−1 _se _i₆₌_j

L−(d+2)₋_L−(d+2)(K+1) ₁₋_L−(d+2)−1 _se _i₌_j . (2.1.29)

Uma vez que k(i,j) = k(j,i), e (JH)ij > 0 e real para quaisquer i e j da rede ΛK,

temos que JH ´e uma matriz real sim´etrica positiva.

Seja agora s _∈ R|ΛK| um vetor qualquer n˜ao nulo e que associa a cada v´ertice _i de

ΛK uma variável real si, e r = (r1, . . . , rd). Então a forma quadrática associada a JH é

(s, JHs)R|ΛK| =

K

X

k=1

L−2k(s,(B∗)kBks)R|ΛK|

= K

X

k=1

L−2k(Bks, Bks)R|ΛK−k|

= K

X

k=1

L−2k X

r∈ΛK−k

(26)

(Bks)r =

1 Ldk/2

X

j∈Λk

sLk_r₊_j . (2.1.31)

Assim, JH ´e uma matriz positiva deﬁnida.

Pela Proposi¸cão 2.1.2 a matriz de intera¸cão hierárquica JH, definida por (2.1.21), é uma matriz de intera¸cão ferromagnética (vide (2.1.8)). Em vista desse fato, temos:

Defini¸cão 2.1.5 O modelo O(N) de Heisenberg hierárquico é definido pela medida de Gibbs (2.1.1) com energia de intera¸cão ferromagnética

Un(y) = (y, Ay)Ωn =−(L−1)(y, JH⊗INy), (2.1.32)

sendo n=_|ΛK|=LKd. O fator (L−1)´e acrescentado para garantir, no limite em que

L_↓1, a convergência do laplaceano hierárquico para o laplaceano hierárquico cont´ınuo, como será visto na Se¸cão 3.1.

2.2 Transforma¸c˜

ao do Grupo de Renormaliza¸c˜

ao

Comecemos esta se¸c˜ao por notar a estrutura da energia hier´arquica _ULKd(y):

ULKd(y) = −(L−1)

K

X

m=1

L−2m((Bm_⊗IN)y,(Bm⊗IN)y)Ω_L(K−m)d

= L−2_UL(K−1)d(y(1))−(L−1)L−2

X

r∈ΛK−1

yr(1)

2 , (2.2.1)

que é a energia hierárquica normalizada porL−2 _{de uma configura¸cão de spins de bloco}

y(1) _{= (B}_⊗_IN₎_y _{da primeira hierarquia sobre a rede ΛK}

−1, somada `a energia de

in-tera¸c˜ao das L(K−1)d _{vari´aveis de spin de bloco} _y(1)

r = ((B⊗IN)y)r da primeira

(27)

ULKd(y) =L−2kU_L(K−k)d(y(k))−(L−1)L−2k

X

r∈ΛK−k

y(_rk)2 , (2.2.2) com y(k) = (Bk_⊗_IN₎_y _{a configura¸cão de spins de bloco da} _{k-ésima hierarquia. ´}_E justamente esta caracter´ıstica da energia hierárquica que permite a implementa¸cão do

grupo de renormaliza¸c˜ao mais facilmente.

Rela¸cão de Recorrência. O nosso interesse está na evolu¸cão, com o aumento da hierarquia k, da distribui¸cão da variável soma

X_k,Nγ = _√ 1 mγ/d

X

i∈Λk

yi, (2.2.3)

com m=_|Λk|=Lkzd. Definimos com essa finalidade a medida “a priori”σ(kN) associada à escala k pela seguinte equa¸cão:

Z

Ω_LKd

δL−(γ−2d)k(Bk⊗IN)_y′−_y

dν_L(NKd)(y′) =

= 1

Z_L(N(K)−k)d

expn₋cγ,k

2 UL(K−k)d(y)

o Y

i∈ΛK−k

dσ_k(N)(yi) ; (2.2.4)

integramos a medida (2.1.1) sobre o espa¸co de configura¸cão mantendo a configura¸cão de spins de bloco da k-ésima hierarquia fixa - (2.2.4) é uma medida marginal sobre Ω_L(K−k)d. O fator γ pode assumir o valor d+ 2 ou d, introduzido a fim de se incluir ou

não a normaliza¸cão L−k_{, presente em (2.2.2), à variável de bloco; assim,}

cγ,k =

(

1 se γ =d+ 2

L−2k se γ =d . (2.2.5)

(28)

Estabeleceremos agora uma rela¸c˜ao recursiva para as medidas “a priori”:

Proposi¸c˜ao 2.2.1 As medidas “a priori” associadas a escalas consecutivas relacionam-se por

σ(_kN)(y) = 1 Ck e

cγ,k(L−1)|y|2/2 _σ(N)

k−1∗ · · · ∗σ (N)

k−1(Lγ/2y)

| {z }

Ld₋_termos

(2.2.6)

com condi¸c˜ao inicial

σ0(N)(y) =

(

0 se _|y_|<√βN

1 se _|y_{| ≥}√βN , (2.2.7)

sendo que _∗ denota o produto de convolu¸c˜ao

ρ_∗η(y) =

Z

RN

ρ(y₋y′)dη(y′), (2.2.8)

e Ck uma normaliza¸c˜ao que garante que σ_k(N) ´e uma medida de probabilidade.

Demonstra¸cão. Sendo (2.2.4) uma medida marginal, podemos obtê-la pela integra¸cão da medida de Gibbs

1 Z_L(N(K)−(k−1))d

expn₋cγ,k−1

2 UL(K−(k−1))d(y

′₎o Y

i∈ΛK−(k−1)

dσ_k(N₋)₁(y_i′) (2.2.9) sobre o espa¸co de configura¸cão Ω_L(K−(k−1))d mantendo-se fixa a configura¸cão de spins de

bloco normalizada L−(γ−2d)(B⊗IN)y′ ∈Ω

L(K−k)d. Para isso precisamos de uma rela¸c˜ao

entre as energias _UL(K−(k−1))d(y′) e U_L(K−k)d((B⊗IN)y′) an´aloga `a (2.2.1); trocando K

por K₋(k₋1) em (2.2.1):

UL(K−(k−1))d(y′) = L−2U_L(K−k)d((B⊗IN)y′)

−(L₋1)L−2 X

r∈ΛK−k

((B_⊗IN)y′₎

r

(29)

Note que

L−(γ−2d)((B⊗IN)_y′)

r =

1

L(γ−2d)

1 Ld/2

X

j∈Λ1

y′_Lr+j

= 1

Lγ/2

X

j∈Λ1

y_L′_r₊_j . (2.2.11)

Utilizando a seguinte decomposi¸c˜ao e nota¸c˜ao

δL−(γ−2d)(B⊗IN)_y′−_y

= Y

r∈ΛK−k

δL−(γ−2d)((B⊗IN)_y′)

r−yr

= Y

r∈ΛK−k

δ(.r), (2.2.12)

temos ent˜ao

Z

Ω_L(K−(k−1))d

δL−(γ−2d)(B⊗IN)y′−y

(2.2.9) =

=

Z

Ω_L(K−k)d

Z

Ω_Ld

Y

r∈ΛK−k

(

ecγ,k−1(L−1)L−2|((B⊗IN)y′)r|2/2_δ(.

r)

Y

j∈Λ1

dσ_k(N₋)₁(y′

Lr+j)

)

×

× 1

Z_L(N(K)−(k−1))d

exp

−cγ,k−1L

−2

2 UL(K−k)d((B⊗IN)y ′₎

= 1

Z_L(N(K)−k)d

expn₋cγ,k

2 UL(K−k)d(y)

o Y

r∈ΛK−k

1 Ck e

cγ,k(L−1)|yr|2/2_d(σ(N)

k−1∗ · · · ∗σ (N)

k−1

| {z }

Ld₋_termos

)(Lγ/2_y

r) ;

(2.2.13)

Ld _{termos porque a cardinalidade de Λ}

1 ´eLd. Para concluirmos (2.2.6) devemos

(30)

Quanto à condi¸cão inicial (2.2.7), essa é a fun¸cão distribui¸cão

Z y1

−∞· · · Z yN

−∞

dσ₀(N)(y′₎ _y′ _∈_RN _(2.2.14)

associada `a medida “a priori” inicial (2.1.4).

Observa¸c˜ao 2.2.2 Pela mudan¸ca de vari´avel y_→√βy, (2.2.6) passa a ser escrita

σ(_kN)(y) = 1 Ck e

β cγ,k(L−1)|y|2/2 _σ(N)

k−1∗ · · · ∗σ (N)

k−1(Lγ/2y)

| {z }

Ld₋_termos

σ₀(N)(y) =

(

0 se _|y_|<√N 1 se _|y_{| ≥}√N .

No limite de altas temperaturas (β _→ 0+_{) temos apenas a convolu¸c˜ao de} _Ld _medidas

“a priori”. Isto está em pleno acordo com o fato que nesse limite as variáveis de spin comportam-se como variáveis aleatórias independentes (não há acoplamento).

Observa¸c˜ao 2.2.3 Se_Mdenota o espa¸co das medidas “a priori” emRN_,_(2.2.6)_define

um mapa _R:_{M → M}

σ_k(N) =_Rσ(_kN₋)₁ , (2.2.15)

e a cole¸c˜ao nσ(_kN)(y)oK

(31)

Rela¸cão de Recorrência Dual. Consideremos agora a fun¸cão caracter´ıstica da me-dida “a priori” associada à escala k

φ(_kN)(z) =

Z

RN

exp_{iz_·y_}dσ_k(N)(y). (2.2.16)

Proposi¸cão 2.2.4 A medida “a priori” φ(_kN)(z) obedece a rela¸cão de recorrência

φ(_kN)(z) = 1 Nkexp

−cγ,k(L₂−1)∆ φ_k(N₋)₁(L−γ/2z)L

d

(2.2.17)

com

φ(₀N)(z) = _√ Γ(N/2)

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_| , (2.2.18)

sendo ∆ = ∂2_/∂z2

1+· · ·+∂2/∂zN2 o operador laplaceanoN-dimensional, Jν(ξ) a fun¸c˜ao

de Bessel de ordem ν, Γ(n) a fun¸c˜ao gama de Euler, e Nk uma normaliza¸c˜ao tal que

φ(_kN)(0) = 1 para todo k = 1,2, . . . , K e todo L.

Demonstra¸c˜ao. Por (2.2.6), ignorando o fator Ck, temos que

φ(_kN)(z) =

Z

RN

exp_{iz_·y_}ecγ,k(L−1)|y|2/2 _d(σ(N)

k−1∗ · · · ∗σ (N)

k−1

| {z }

Ld₋_termos

)(Lγ/2y). (2.2.19)

Uma vez que o laplaceano atua somente na vari´avel z

eiz·yecγ,k(L−1)|y|2/2 ₌

∞ X n=0 1 n!

cγ,k(L₋1) 2

n

(_|y_|)2neiz·y

= ∞ X n=0 1 n!

cγ,k(L₋1) 2

n (∆)n (i2₎n e

iz·y

= exp

−cγ,k(L₂−1)∆

(32)

e (2.2.19) ﬁca

φ(_kN)(z) = exp

−cγ,k(L₂−1) ∆

Z

RN

exp_{iz_·y_}d(σ_k(N₋)₁_{∗ · · · ∗}σ_k(N₋)₁

| {z }

Ld₋_termos

)(Lγ/2y)

= exp

−cγ,k(L₂−1) ∆

Z

RN

exp_{iL−γ/2z_·y_}d(σ_k(N₋)₁_{∗ · · · ∗}σ_k(N₋)₁

| {z }

Ld₋_termos

)(y).

(2.2.21)

Pelo Teorema da Convolu¸cão e pela defini¸cão (2.2.16), temos então que

φ(_kN)(z) = exp

−cγ,k(L−1)

2 ∆ φ

(N)

k−1(L

−γ/2_z)L

d

. (2.2.22)

De (2.2.16) e do fato que σ_k(N)(y) ´e uma medida de probabilidade, vˆe-se a necessidade de que φ(_kN)(0) = 1 para todok e todo L. Normalizamos assim (2.2.22) por

Nk= exp

−cγ,k(L₂−1)∆ φ_k(N₋)₁(L−γ/2 z)L

d

z=0

. (2.2.23)

Para finalizarmos esta demonstra¸cão temos de fazer a transformada de Fourier da me-dida “a priori” inicial (2.2.7). Utilizando coordenadas esféricas generalizadas (lembrando que o jacobiano é dado por (2.1.9)), efetuando a mudan¸ca de variável θ = θ1 −π/2, e

fazendo uso da igualdade (2.1.10) com N trocado por N ₋1, temos:

φ(₀N)(z) = 1 SN βN

Z

RN

exp_{iz_·y_}δ_|y_{| −}pβN dNy

= S

N−1 1

SN βN

Z ∞

0

rN−1δr₋pβN Z π/2

−π/2

ei|z|rsinθ(cosθ)N−2dθ dr

= (2π) N/2 SN βN Z ∞ 0

rN−1δr₋pβN JN/2−1(|z|r) (_|z_|r)N/2−1 dr

= _√ Γ(N/2)

βN_|z_|/2N/2−1JN/2−1

p

(33)

sendo

Jν(ξ) = _√ 1 πΓ(ν+1₂)

ξ 2

νZ π/2

−π/2

cos (ξsinθ)(cosθ)2ν dθ , (2.2.25)

com _ℜe(ν) > ₋1/2, a representa¸cão integral da fun¸cão de Bessel de ordem ν (vide equa¸cão (20) do Cap´ıtulo V II de [2]). Note que

φ(₀N)(0) = 1 SβN

Z

RN

δ_|y_{| −}pβN dNy= 1 , (2.2.26)

n˜ao havendo necessidade de uma normaliza¸c˜ao.

Coment´ario 2.2.5 As rela¸c˜oes recursivas (2.2.6)e (2.2.17) recebem o nome de

Trans-forma¸c˜ao de Grupo de Renormaliza¸c˜ao.

Observa¸c˜ao 2.2.6 Uma vez que φ(0N)(z) depende apenas do m´odulo |z| =

√

z_·z da variável e o operador laplaceano preserva simetria esférica, segue que φ(_kN)(z) é uma fun¸cão de _|z_| para todo k = 1,2, . . . , K.

Teorema de Lee-Yang. Devemos ressaltar que o fato de termos feito a transformada

de Fourier2 _{da medida “a priori” é de extrema importância, pois é através dessa que se}

estabelece a rela¸c˜ao com o teorema de Lee-Yang.

Defini¸c˜ao 2.2.7 (Propriedade de Lee-Yang) Uma medidaρde Borel emRN _possui

a propriedade de Lee-Yang se sua fun¸c˜ao caracter´ıstica φ(z) = RRNexp{iz·y}dρ(y)

pertence à classe das fun¸cões inteiras _L de Laguerre, as quais possuem a representa¸cão

f(ζ) = exp (λζ)

∞ Y

n=1

1 + ζ α2

n

(2.2.27)

com ζ =_−|z_|2 _∈_C_, _λ_≥₀ _e _α

1, α2, . . . n´umeros reais satisfazendo P∞_n₌₁α−n2 <∞. 2

(34)

Para a fun¸c˜ao caracter´ıstica φ(₀N)(z) temos que

φ(₀N)(z) = _√ Γ(N/2)

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_|

= Γ(N/2)

i√βNx/2N/2−1JN/2−1

ipβNx:=ϕ(₀N)(x), (2.2.28)

x=_−|z_|2 _∈_R_{. Se} _{_α

n,ν, n≥1} denotam os zeros de Jν(ξ),

(

−α

2

n,N/2−1

βN , n ≥1

)

(2.2.29)

s˜ao os zeros da medida “a priori” ϕ(₀N)(x), chamados de zeros de Lee-Yang. Desta maneira,

ϕ(₀N)(x) =

∞ Y k=1    1 +

x α2

n,N/2−1

βN

  

. (2.2.30)

Note que ϕ(₀N)(0) = 1 e que JN/2−1 i√βNx

= IN/2−1 √βNx

´e uma fun¸c˜ao inteira

de x, e portanto a condi¸cão P∞_n₌₁α_n,N/−2 ₂₋₁ < _∞ é satisfeita. Para n grande vale o comportamento assintótico

αn,N/2−1 ∼(N −1)

π

4 + (2n−1) π

2 ; (2.2.31)

para N grande tem-se que

Γ(N/2)IN/2−1

p

βNx_∼

√

βNx 2

N/2−1

. (2.2.32)

Espa¸co de Fun¸c˜oes Inteiras e a Trajet´orianφ(_kN)(z)o∞

k=1. Finalizaremos esta se¸c˜ao

(35)

de valor inicial relacionado à órbita discreta induzida pelo mapa (2.2.17). Tomaremos a liberdade de modificar algumas nota¸cões utilizadas nos citados artigos.

Seja_E o conjunto de todas as fun¸c˜oes inteiras de C _em C_{, e}

kf_kb := sup k∈N

1 bk

dk_f₍₀₎ dζk

. (2.2.33)

Para a_≥0, seja

Aa ={f ∈ E : (∀b > a) kfkb <∞}. (2.2.34)

Por ﬁm, denotando por _L a classe das fun¸c˜oes inteiras de Laguerre, sejam

L+ =_{f _{∈ L}:f(0)>0_}, _L(1) =_{f _{∈ L}:f(0) = 1_}, (2.2.35)

La=L ∩ Aa , L+a =L+∩ Aa , L(1)a =L(1)∩ Aa. (2.2.36)

Dado θ _≥0, o mapa ∆θ :_{E → E} ´e deﬁnido por

(∆θf)(ζ) =θ df(ζ)

dζ +ζ

d2_f_(ζ)

dζ2 . (2.2.37)

Consideremos agora o seguinte problema de Cauchy

∂f(t, ζ)

∂t = (∆θf)(t, ζ), t∈R+, ζ ∈C, (2.2.38)

f(0, ζ) = g(ζ),

e que a condi¸c˜ao inicial tenha a forma

g(ζ) = exp (₋εζ)h(ζ), h_{∈ A}0, ε≥0. (2.2.39)

(36)

Proposi¸c˜ao 2.2.8 (i) Para todo θ _≥ 0 e g _{∈ E} tendo a forma (2.2.39), o problema

(2.2.38) tem uma única solu¸cão em _Aε, a qual possui a seguinte representa¸cão

integral

f(t, ζ) = exp

−ζ_t

Z +∞

0

sθ−1wθ

ζs t

e−sg(ts)ds , (2.2.40)

sendo t >0 e

wθ =

∞ X

k=0

ζk

k! Γ(θ+k) . (2.2.41)

(ii) Se em (2.2.39)ε >0, a solu¸c˜ao (2.2.40)converge em_Aε para zero quandot → ∞.

(iii) Se em (2.2.39) h _{∈ L}0 e ε = 0, a solu¸c˜ao (2.2.40) tamb´em pertence a L0. Ela

diverge quando t_{→ ∞}, o que significa que Mf(t, r)_{→ ∞} para todo r _∈R₊_{. Aqui}

Mf(t, r) = sup

|ζ|≤r|

f(t, ζ)_|. (2.2.42)

A evolu¸cão descrita pela equa¸cão (2.2.38) é modificada como segue. Dividamos o semi-eixo do tempo R₊ _{em intervalos} _I_k _{= ((k}₋_{1)β, kβ],}_k _∈N_{, com} _{β >}_{0 e}

R₊₌ ∞ [

k=1

Ik. (2.2.43)

Em cada intervalo a evolu¸cão é descrita por (2.2.38), mas nos tempos t =kβ, k ₆= 0, a fun¸cão do dado inicial do problema é modificada da seguinte maneira

f(kβ, ζ)_→[f(kβ, δ−1−νζ)]δ , (2.2.44)

(37)

variando sobre uma seqüência de intervalos. No que segue, considera-se a seqüência de fun¸cões _{fk(ζ)_}∞

k=1, cada uma dessas sendo a solu¸c˜ao do seguinte problema de Cauchy

∂fk(t, ζ)

∂t =β(∆θfk)(t, ζ), β≥0, t∈(0,1], (2.2.45)

com condi¸c˜ao inicial

fk(0, ζ) = [fk−1(1, δ−1−νζ)]δ, k∈N

f0(1, ζ) = g(ζ), g∈ L+. (2.2.46)

Qualquer g _{∈ L}+ _{é descrita pelos parâmetros} _λ _e _{_{αn, n} _≥ ₁_} _{- vide representa¸cão}

(2.2.27). Dados g _{∈ L}+ _e _j _∈_N_{, deﬁnimos os momentos da distribui¸c˜ao dos zeros}

mj(g) =

∞ X

n=1

α−_n2j . (2.2.47)

e

I(g) =

(

[0,(δν ₋_{1)/λ] se} _{λ >}₀

[0,_∞) se λ= 0 . (2.2.48)

A Proposi¸cão (2.2.8) implica a existência de solu¸cões de (2.2.45)-(2.2.46) ao menos para g _{∈ L}0. O teorema a seguir estabelece a existência de solu¸cões desse problema em

uma situa¸c˜ao mais geral.

Teorema 2.2.9 Sejam g _{∈ L}+ e β_∈I(g) dados. Ent˜ao para todo k _∈ N _e _θ _≥ ₀_{, o}

problema (2.2.45)-(2.2.46) tem uma ´unica solu¸c˜ao fk, a qual pertence a _L+_λ.

Para β = 0, a seq¨uˆencia_{fk(ζ)_}∞

k=1 pode ser encontrada explicitamente

(38)

Se g _{∈ L}(1)_{, tal seq¨}_{uˆencia converge em} _A

λ para a fun¸cão f(t, ζ) ≡ 1. Podemos assim esperar que a mesma convergência, ou similar, seja válida também para valores pe-quenos de β. Por outro lado, para valores grandes deβ, a afirma¸cão (iii) da Proposi¸cão

2.2.8 sugere que há divergência. O objetivo dos autores nesse trabalho foi estudar as seguintes questões: (a) existe um valor intermediário de β, digamos β∗_{, que separa}

valores “grandes” e “pequenos” desse parâmetro?; (b) qual seria a convergência da seqüência _{fk(ζ)}∞k=1 para β = β∗? A resposta foi encontrada para ν ∈ (0,1/2) e g

escolhida em um subconjunto de _L+ _{deﬁnido por} _ν _{como segue. Seja}

ϑ(ν) := 1−δ

−ǫ

δν ₋_δ−ǫ , ǫ=

1₋2ν

4 . (2.2.49)

Defini¸cão 2.2.10 A fam´ılia_L(ν) consiste das fun¸cões g _{∈ L}(1) _{que não são constantes}

e s˜ao tais que

m2(g)

(λ+m1(g))2 ≤

δ1/2

θ+ 1 ϑ(ν),

m2(g)

(m1(g))2 ≥

δ1/2

θ+ 1 . (2.2.50)

Denotando por N₀ _{o conjunto dos n´}_{umeros naturais com exclus˜ao do 0, os autores}

enunciam seu principal teorema:

Teorema 2.2.11 Para todo θ _≥ 0 e g _{∈ L}(ν), existe β∗_∈_I(g) _{positivo e uma fun¸c˜ao}

C : [0, β∗_]_→_R

+ tal que

(i) para β < β∗_{, a seq¨}_{uˆencia de solu¸c˜oes de} _(2.2.45)_-_(2.2.46)

{fk(t, ζ) :k _∈N₀_{, f}₀_{(1, ζ) =}_C(β)g(ζ)_}

converge em _Aκ−1, com κ=β∗/(δν −1), para a fun¸c˜ao f(t, ζ)≡1;

(ii) para β =β∗_{, a seq¨}_uˆencia

{fk(t, ζ) : k _∈N₀_{, f}₀_{(1, ζ) =}_C(β∗_)g_(ζ₎_}

converge em _Aκ−1 para

f∗(t, ζ) = δ

−θνδ/(δ−1)

(1₋t(1₋δ−ν₎₎θ exp

1 β∗

1₋δ−ν 1₋t(1₋δ−ν₎ ζ

(39)

A conex˜ao entre as trajet´orias_{fk(ζ)_}∞

k=1 e φ (N)

k (z)

k=1é feita pelas identifica¸cões:

δ=Ld_; _(2.2.52)

θ =N/2 ; (2.2.53)

∆N/2 ´e o laplaceano N-dimensional

1

2(∆N/2f)(ζ) = N

2 f

′_(ζ_{) +}_xf′′_(ζ) _(2.2.54)

escrito em coordenadas esf´ericas atuando sobre fun¸c˜oes φ : RN _→ R _{O(N) invariantes}

(φ(Uz) =φ(z) _∀U _∈O(N)) deﬁnidas porf(ζ) =φ(z) com ζ =_−|z_|2_;

ν = γ−d

d ; (2.2.55)

do fato que ζ =_−|z_|2, h´a uma mudan¸ca na escala do argumento feita em (2.2.46), que passa a ser

φ(_kN)(0, z) = [φ(_kN₋)₁(1, δ−(1+ν)/2z)]δ. (2.2.56)

Além disso, o parâmetro β deve ganhar a interpreta¸cão de inverso da temperatura, e deve ser efetuada uma mudan¸ca de variável de modo que β seja escrito na condi¸cão inicial e não mais na equa¸cão de evolu¸cão (2.2.45). O problema de valor inicial estudado por Kozitsky e Wo lowiski, reescrito dessa maneira, foi estudado por Watanabe no caso

(40)

2.3 A Aproxima¸c˜

ao de Potencial Local (L

_↓

1 )

Deﬁnindo o potencial

U(t, z) =₋lnφ(_kN)(z) (2.3.1)

com parˆametro de escala

t=klnL , (2.3.2)

tomaremos conjuntamente os limitesk _{→ ∞}eL_↓1 de tal maneira queklnLpermane¸ca fixo em um número real positivo t. Com esse procedimento, como veremos na próxima proposi¸cão, a órbita discretan₋lnφ(_kN)(z)o∞

k=0torna-se cont´ınua, e a dinˆamica completa

se reduz a uma equa¸cão a derivadas parciais. O limite da dimensão do bloco L para 1 é a chamada aproxima¸cão de potencial local.

Proposi¸cão 2.3.1 O potencialU(t, z) definido por (2.3.1) e (2.3.2) satisfaz, no limite conjunto k _{→ ∞} e L_↓1, a equa¸cão diferencial parcial não-linear

Ut=₋cγ(t)

2 ∆U − |Uz|

2

−γ₂ z_·Uz+dU +cγ(t)

2 ∆U(t,0) (2.3.3)

U(0, z) =₋ln

"

Γ(N/2)

√

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_|

#

. (2.3.4)

O termo ∆U(t,0) é um multiplicador de Lagrange necessário para garantir que U(t,0) = 0 para todot_≥0, haja vista queφ_k(N)(0) = 1para todok = 0,1, . . .e todoLe a defini¸cão

(2.3.1) do potencial U(t, z); Uz =∂U/∂z com ∂/∂z = (∂/∂z1, . . . , ∂/∂zN); e

cγ(t) =

(

1 se γ =d+ 2

(41)

´e cγ,k (2.2.5) escrito em termos de t, considerando-se (2.3.2).

Demonstra¸cão. Da defini¸cão de derivada, pela defini¸cão (2.3.1) do potencial U(t, z), pela rela¸cão (2.2.17), e da observa¸cão que t₋lnL= (k₋1) lnL, temos

Ut = lim

L↓1

U(t, z)₋U(t₋lnL, z)

lnL (2.3.6)

= lim L↓1

1 lnL −ln 1 Nk exp

−cγ,k(L₂−1) ∆ φ(_kN₋)₁(L−γ/2z)L

d

+ lnφ(_kN₋)₁(z)

= lim k→∞ k t −ln 1 Nk exp −cγ(t)(e

t/k ₋₁₎

2 ∆ φ

(N)

k−1(e

−γt/2k_z)e

dt/k

+ lnφ(_kN₋)₁(z)

,

com Nk dado por (2.2.23).

Notemos agora que para k grande valem as seguintes expans˜oes:

exp

−cγ(t)(e

t/k ₋₁₎

2 ∆

= 1₋ k t

cγ(t)

2 ∆ +O (k/t)

2 _(2.3.7)

e

φ(_kN₋)₁(e−γt/2kz)e

dt/k

=

=φ(_kN₋)₁(z) +φ(_kN₋)₁(z) ₋γ 2 z·

∂lnφ(_kN₋)₁(z)

∂z +dlnφ

(N)

k−1(z)

!

k

t +O (k/t)

2 _. _(2.3.8)

Substituindo tais expressões na última igualdade de (2.3.6), e utilizando a expansão

ln (a0+a1x+O(x2)) = lna0+

a1

a0

x+O(x2) (2.3.9)

para xpequeno e a0 >0, obtemos

Ut = lim k→∞

(

cγ(t) 2

∆φ(_kN₋)₁(z) φ(_kN₋)₁(z) +

γ 2 z·

∂z −dlnφ

(N)

k−1(z)−

cγ(t)

2 ∆φ

(N)

k−1(0) +O((t/k))

)

.

(42)

Note que o ´ultimo termo ´e justamente

−cγ(t)₂ ∆φ

(N)

k−1(z)

φ(_kN₋)₁(z) − γ 2 z·

∂z +dlnφ

(N)

k−1(z)

z=0 , (2.3.11)

proveniente da expans˜ao de lnNk. Por ﬁm, pelas igualdades

∆φ(_kN₋)₁(z)

φ(_kN₋)₁(z) = ∆ lnφ

(N)

k−1(z) +

∂lnφ(_kN₋)₁(z) ∂z 2 , (2.3.12)

∆φ(_kN₋)₁(0) = ∆ lnφ(_kN₋)₁(0) (2.3.13)

e lnφ(_kN₋)₁(z) =₋U(t₋t/k, z), obtemos (2.3.3).

Quanto `a condi¸c˜ao inicial (2.3.4), esta segue imediatamente do fato que

U(0, z) =₋lnφ(₀N)(z) (2.3.14)

e de (2.2.18).

Como já observado na se¸cão anterior, a condi¸cão inicial para a fun¸cão caracter´ıstica depende de r = _|z_| = √z_·z, de modo que a condi¸cão inicial (2.3.4) também. Uma vez

que a equa¸cão de evolu¸cão (2.3.3) preserva a simetria esférica, é conveniente e suficiente que trabalhemos com a parte radial da variável z, do termo z _·Uz, e de ∆, dados respectivamente por r,r d/dr, e

1 rN−1

∂ ∂r

rN−1 ∂ ∂r

= ∂

2

∂r2 + (N −1)

1 r

∂ ∂r .

Deﬁnindo o potencial escalado

u(N)(t, x) = 1 NU(t,

√

(43)

com x=_−|z_|2 ₌₋_r2_{, o problema de valor inicial (2.3.3)-(2.3.4) torna-se}

u(_tN) =cγ(t)

2 Nxu

(N)

2

−γxu(_xN)+du(N)₋cγ(t)u(_xN)(t,0) (2.3.16)

com

u(N)(0, x) =₋ 1 N ln

"

Γ(N/2)

i√βxN/2N/2−1JN/2−1

ipβxN

#

. (2.3.17)

O termo u(xN)(t,0) em (2.3.16) é um multiplicador de Lagrange necessário para garantir que u(N)_(t,_{0) = 0 para todo} _t_≥_{0. O problema de valor inicial (2.3.16)-(2.3.17) será o}

(44)

Trajet´

oria Cont´ınua: Caso

N

=

_∞

3.1 O Modelo Esf´

erico Hier´

arquico

Um resultado clássico devido a Kac e Thompson [18] diz que a energia livre do modelo de Heisenberg O(N) é igual à correspondente energia livre do modelo esférico quando são tomados os limites termodinâmico eN _{→ ∞}, independentemente da ordem em que

tais limites são tomados. Para estabelecer o resultado, a hipótese de invariância por transla¸cão

Jxy =f(_|x₋y_|) (3.1.1)

da matriz de intera¸cão J = [Jxy] foi assumida pelos autores. Anos mais tarde, Kunz e Zumbach [19] encontraram falhas sérias na demonstra¸cão envolvendo a troca do limite

N _{→ ∞}com o limite termodinâmico, e foram capazes de confirmar o resultado de Kac-Thompson apenas para intera¸cão entre vizinhos mais próximos (Jxy = 0 se _|x₋y_|>1). A necessidade da invariância por transla¸cão foi também posta em questão por estes ´

ultimos visto que h´a exemplos cuja troca dos limites pode ser realizada mesmo quando

esta propriedade n˜ao ´e satisfeita.

Como parte de um estudo preliminar a este projeto foram estendidos e

(45)

modelo de Heisenberg O(N) hierárquico para as do modelo esférico hierárquico quando os limites n _{→ ∞} (limite termodinâmico K _{→ ∞}) e N _{→ ∞} são tomados, indepen-dentemente da ordem de tais limites. Para tanto, utilizamos uma adapta¸cão do método

empregado por Kac e Thompson [18], além do já citado artigo de Kunz e Zumbach [19], e uma generaliza¸cão (L > 1 e d _≥ 1) da defini¸cão de positividade por reflexão para o laplaceano hierárquico, encontrada em [27]. Um ponto importante a ser dito é que sendo L um inteiro estritamente maior que um na defini¸cão do último ingrediente, a

demonstra¸c˜ao da convergˆencia falha no limite L_↓1.

Também em [4] mostramos que o modelo esférico hierárquico exibe ordem de longo

alcance (vide Deﬁni¸c˜ao 4.2.1 em [21]), desde que d _≥ 3 e β > βc. Pelo chamado

critério de ordem de longo alcance (vide Defini¸cão 4.2.2 em [21]) isso implica existência de transi¸cão de fase. Essa, como exporemos nas próximas páginas deste trabalho, é do tipo condensa¸cão de Bose-Einstein no modo de energia zero. A saber, para esta parte

de [4] tomamos por base o artigo [25] de Perez, que é iniciado com a seguinte afirma¸cão:

“Uma classe ampla de sistemas clássicos e qüânticos exibe transi¸cão de fase de mesma natureza daquela observada no gás de Bose livre e no modelo esférico.”

No que se segue desta se¸cão, definiremos o operador laplaceano hierárquico (seguindo

o trabalho [27] de Watanabe, mas generalizando paraL >1 ed_≥1 quaisquer), o modelo esférico hierárquico, e mostraremos o resultado mencionado no último parágrafo.

Projetores. Seja ΛK a rede hipercúbica (2.1.14), _|ΛK_|=LKd ₌_n _{sua cardinalidade,} e JH a matriz de intera¸cão hierárquica (2.1.21). Denotamos por w ∈ R|ΛK| um vetor que associa a cada vértice i de ΛK uma componente wi∈R, e por

(w,u)R|ΛK| =

X

i∈ΛK

wiui (3.1.2)

o produto interno em R|ΛK|_{. Deﬁnimos o operador} _{laplaceano hier´arquico} _por

−∆H =−JH +µ0In, (3.1.3)

(46)

hier´arquico, sendo um gerador estoc´astico de um semi-grupo, deve satisfazer

−∆H1= 0 . (3.1.4)

Deste fato, e de (2.1.21) e (2.1.16), temos

µ0 = (1, JH1)R|Λ_K| =

1 LKd

K

X

k=1

L−2k(Bk1, Bk1)R|ΛK−k|

= K

X

k=1

L−2k . (3.1.5)

Assim,

−∆H = K

X

k=1

L−2k(₋(B∗)kBk+In). (3.1.6)

Com o operador de blocoB e seu adjuntoB∗_{, deﬁnidos respectivamente por (2.1.16)}

e (2.1.19), introduzimos uma matriz de proje¸c˜ao Pk =P2

k ortogonal, Pk =Pk∗, sobre o subespa¸co de vetores em R|ΛK| _{que assumem valor constante sobre blocos de tamanho}

Ldk_:

Pk= (B∗)kBk . (3.1.7)

Da observa¸c˜ao que Bk_(B∗₎k ₌ _BB∗ ₌ _In _{para todo} _k _{= 1,}_{2, . . . , K, mostra-se que de}

fato

P_k2 = (B∗)kBk(B∗)kBk= (B∗)kInBk =Pk, (3.1.8)

e que para j > k qualquer

PjPk = (B∗)jBj(B∗)kBk= (B∗)jBj−kBk=Pj

(47)

Para essas matrizes de proje¸cão a seguinte inclusão é verificada

PK < PK−1 <· · ·< P1 < P0≡In, (3.1.10)

no sentido que M < N se, e somente se, (u, Mu)R|ΛK| < (u, Nu)R|ΛK| para todo u ∈

R|ΛK|_.

Seja

Qk=Pk₋Pk+1 (3.1.11)

para k= 0,1, . . . , K ₋1 e

QK =PK (3.1.12)

o operador de flutua¸c˜ao de bloco.

Teorema Espectral. Enunciamos o seguinte teorema:

Teorema 3.1.1 (Teorema Espectral) A cole¸c˜ao _{Qk_}K

k=0 de matrizes n×n de

proje-¸c˜ao ortogonais

QjQk =δjkQk (3.1.13)

´e uma parti¸c˜ao espectral da unidade

In= K

X

k=0

Qk ,

e

f(₋∆H) = K

X

k=0

f(λk)Qk (3.1.14)

vale com

λk = L

−2k₋_L−2K

(48)

para qualquer fun¸c˜ao cont´ınua f : [0,1/(L2 ₋_1)]_→_R_{. Segue que} ₋_∆H _{´e uma matriz}

positiva comλk, para k= 0, . . . , K₋1, um auto-valor de multiplicidadeLd(K−k)₍₁₋_L−d₎

e λK = 0 um auto-valor simples.

Demonstra¸c˜ao. Por (3.1.11) e (3.1.9)

QjQk = (Pj ₋Pj+1)(Pk−Pk+1)

= Pj(Pk₋Pk+1)−Pj+1(Pk−Pk+1)

= (Pj ₋Pj)₋(Pj+1−Pj+1) = 0 (3.1.16)

para todo k < j < K, e o mesmo vale para j < k < K. Para j < k =K

QjQK = (Pj ₋Pj+1)PK =PK−PK = 0, (3.1.17)

e para j =k

QkQk= (Pk₋Pk+1)(Pk−Pk+1) =Pk+Pk+1−2Pk+1 =Qk. (3.1.18)

Fica assim demonstrada (3.1.13). Por deﬁni¸c˜ao,

K

X

k=0

Qk = K_X−1

k=0

(Pk₋Pk+1) +PK =P0−PK+PK =In. (3.1.19)

De (3.1.6), (3.1.7) e (3.1.11), temos

−∆H =

K

X

j=1

L−2k(₋Pj +In)

= K

X

j=1

L−2j j−1

X

k=0

Qk

= K_X−1

k=0

K

X

j=k+1

L−2j

!

(49)

o qual nos dá (3.1.14) com f(x) = x. Segue por (3.1.13) que (3.1.14) vale para qual-quer polinômio e, pelo Teorema da Aproxima¸cão de Weiertrass, para qualqual-quer fun¸cão uniformemente cont´ınua.

Por fim, uma vez quePkprojeta qualquer vetor deR|ΛK|em um vetor que é constante sobre blocos disjuntos de tamanho Ldk_{, o posto (}_rank_{) de} _Pk _é

posto Pk =Ld(K−k) ; (3.1.21)

esse é o número de blocos existentes na k-ésima hierarquia. Pela defini¸cão (3.1.11), juntamente com as inclusões (3.1.10), o posto do operador de flutua¸cão de bloco Qk é

posto Qk=Ld(K−k)₋Ld(K−k−1) , (3.1.22)

para k= 1,2, . . . , K ₋1 e

posto QK = 1, (3.1.23)

o que conclui a demonstra¸c˜ao do teorema.

Modelo Esférico Hierárquico. Sendo β _≥ 0 o inverso da temperatura, o modelo esférico hierárquico (ferromagnético) é definido pela medida de Gibbs

dν(n)(y) = 1 Qn exp

−β

2 (y,−∆Hy)Rn

dσ(n)(y). (3.1.24)

Nesta express˜ao,

Qn =

Z

Rn

exp

−β₂ (y,₋∆Hy)Rn