Anéis quânticos em superfícies não-orientáveis

UNIVERSIDADE FEDERAL DA PARAÍBA

CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA

PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA

Dissertação de Mestrado

ANÉIS QUÂNTICOS EM SUPERFÍCIES

NÃO-ORIENTÁVEIS

ANÉIS QUÂNTICOS EM SUPERFÍCIES

NÃO-ORIENTÁVEIS

por

José Fernando Oliveira de Souza

sob a orientação de

Claudio Benedito Silva Furtado

Dissertação apresentada ao Programa de

Pós-Graduação em Física da Universidade

Federal da Paraíba, em 22 de dezembro

de 2010, como requisito obrigatório para a

obtenção do título de mestre.

João Pessoa,

ANÉIS QUÂNTICOS EM SUPERFÍCIES

NÃO-ORIENTÁVEIS

por

José Fernando Oliveira de Souza

Dissertação aprovada, em 22 de dezembro de 2010, pela seguinte Banca Examinadora:

————————————————————————————

Prof. Dr. Claudio Benedito Silva Furtado - UFPB

————————————————————————————

Prof. Dr. Sérgio André Fontes Azevedo - UFPB

————————————————————————————

Prof. Dr. Tiago Homero Mariz - UFAL

João Pessoa,

* * *

Agradecimentos

- Agradeço a Fernando José e Maria Marluce, meus pais, a Tâmara Louize, minha irmã, e a Thiara Carvalho, minha namorada, por representarem mais do que, muitas vezes, consigo expressar, por

estarem presentes diariamente e por suportarem alguns de meus momentos socialmente pouco inspi-rados;

- Em especial, a Ivonete Liz, minha avó, por demonstrar, na prática, que os termos “avó” e “mãe”

realmente se confundem;

- A todos os outros membros da minha família, incluindo, também, aqueles que não compartilham de elo sanguíneo, por sempre me apoiarem e por darem, de alguma maneira, parcelas de contribuição a

minha formação e ao meu amadurecimento como pessoa;

- Aos meus verdadeiros amigos, por sempre me acrescentarem algo;

- A Claudio Furtado, meu orientador, por todo o tempo a mim dedicado e por todas as suas con-tribuições;

- A todos os professores que, de alguma forma, contribuiram para a minha formação acadêmica;

- Aos professores Tiago Mariz e Sérgio Azevedo, por suas sugestões;

* * *

“ Pauca, sed matura. ”

Resumo

Neste trabalho, exploramos o elo entre geometria e propriedades físicas no caso de anéis quânticos

bidimensionais. Com o foco nas estruturas mesoscópicas não-orientáveis, resolvemos o problema da faixa de Möbius quântica, um anel quântico cuja superfície de confinamento é uma faixa de Möbius, e

investigamos de que maneira as propriedades físicas de tais estruturas respondem à variação geométrica característica dessa particular configuração de confinamento. Mais precisamente, investigamos o modo

pelo qual a adoção de condições de contorno associadas a essa configuração geométrica específica, em particular, pode interferir nas propriedades gerais dos anéis quânticos bidimensionais. Além disso,

ainda estudamos a versão generalizada do problema, em que a faixa de Möbius apresenta um número finito n de torções.

Abstract

In this work, we explore the link between geometry and physical properties in 2D quantum rings.

With focus on the non-orientable mesoscopic structures, we solve the quantum Möbius strip problem, a quantum ring whose lockdown surface is a Möbius strip, and investigate how the physical properties of

those structures answer to the geometric variation of this particular configuration. More precisely, we investigate how the adoption of boundary conditions associated to this specific geometric configuration,

in particular, can change the general properties of the 2D quantum rings. In addition, we still study the generalized version of the problem, where the Möbius strip has a finite number n of torsions.

Sumário

1 Introdução 10

2 Anéis Quânticos 2D: Uma Visão Geral 12

2.1 Confinamento Bidimensional . . . 12

2.1.1 O Anel Comum . . . 14

2.1.2 A Faixa de Möbius . . . 15

2.2 Confinamento via Potencial Não-Trivial: O Modelo de Tan e Inkson . . . 17

2.3 Introduzindo o Fluxo Magnético Φ . . . 21

2.3.1 O Efeito Aharonov-Bohm . . . 22

2.3.2 O Potencial Vetor A~ . . . 25

2.3.3 A Fase Aharonov-Bohm . . . 28

2.3.4 Correntes Persistentes em Anéis 2D . . . 33

3 A Faixa de Möbius Quântica 36 3.1 Uma Breve Descrição do Problema . . . 36

3.2 Solução do Problema . . . 38

3.2.1 A Solução Geral ψ(ϕ, z) . . . 38

3.2.2 As Autofunções e o Espectro de Energia . . . 39

3.3 Correntes Persistentes em Faixas de Möbius . . . 46

4 A Faixa de Möbius Generalizada 52

5 Considerações Finais 55

Capítulo 1

Introdução

Nos últimos anos, os trabalhos na área de estruturas mesoscópicas vêm se multiplicando, tomando um papel de destaque no cenário da pesquisa científica de ponta. Em particular, por proporcionarem

boas oportunidades de estudar e explorar uma gama de fenômenos de natureza quântica e por apre-sentarem algumas propriedades bem peculiares, os anéis quânticos têm se tornado figuras cada vez mais

presentes nos artigos relacionados à Física Mesoscópica, sejam de natureza teórica ou experimental. Tradicionalmente, o rótulo “anel quântico” denota qualquer sistema físico onde elétrons são

con-finados em um lugar geométrico cujo traçado corresponde ao de um anel, na presença de um fluxo magnético paralelo ao eixo normal da estrutura, denominado fluxo de Aharonov-Bohm, e que passa

exatamente num círculo cujo raio r é sempre menor do que o raio internori desse anel (r < ri).

No final da década de 50, foi dado o pontapé inicial na Física dos anéis mesoscópicos, ou quânticos,

na ocasião da descoberta daquilo que viria a ser a principal motivação para as primeiras investigações teóricas e realizações experimentais nessa área: o efeito Aharonov-Bohm [1]. Os primeiros modelos

teóricos e construções experimentais surgiram impulsionados pelo interesse em observar e estudar as correntes persistentes e suas características, já previstas como consequência direta do efeito

Aharonov-Bohm. Com o passar do tempo, pensar novos sistemas com o objetivo de obter novas propriedades, especialmente em correntes persistentes, passou a ser uma ação mais que natural, quase uma regra, o

que propiciou o surgimento de uma numerosa coleção de novos modelos, estabelecendo, dessa maneira, uma vasta mesodiversidade. Em pouco tempo, essa diversidade passou a nutrir, com abundância, a

bidimensionais, com um enfoque especial em variantes do problema mais tradicional, em que tais

anéis se apresentam sob a forma de superfícies não-orientáveis, como, por exemplo, a faixa de Möbius. Na primeira parte, com uma abordagem em que percorremos desde a construção dos tais anéis

quânticos até a apresentação de algumas de suas características, estabelecemos as bases necessárias para a introdução da variação desejada na topologia do anel. Apresentamos, inicialmente, duas formas

distintas de produzir o confinamento dos elétrons em anéis, sendo eles orientáveis ou não. Logo em seguida, introduzimos o fluxo Aharonov-Bohm na configuração e, ao longo de praticamente todo o

capítulo, procuramos responder, dentre outras questões, sobre como esse fluxo afeta, especialmente, a função de onda, as condições de contorno e, consequentemente, as energias. Anteriormente a isso,

no entanto, é realizada uma breve discussão a respeito de algumas peculiaridades relativas a essa introdução, em particular.

Na segunda parte, desenvolvemos um tratamento do problema da faixa de Möbius quântica inspi-rado no trabalho de Ferreira et al. [2], de 2003. Apresentamos e resolvemos o problema da faixa

de Möbius propriamente dito, como uma espécie de variante do anel quântico tradicional, mostrando suas propriedades e observando de que forma a topologia da faixa de Möbius exerce influência nas

propriedades físicas dos anéis quânticos, de forma geral. Em complemento, para finalizar, fazemos uma análise de alguns resultados obtidos no caso em questão, em comparação, sempre que necessário,

com o caso do anel comum.

Finalmente, na última parte, também com um tratamento inspirado em [2], efetuamos uma

gene-ralização imediata do problema da faixa de Möbius quântica apresentado no capítulo 3. Dedicamos nossa atenção a uma pequena análise das características do problema da faixa de Möbius generalizada,

Capítulo 2

Anéis Quânticos 2D: Uma Visão Geral

Neste capítulo, abordamos, de forma detalhada, o problema geral dos anéis quânticos 2D sob uma perspectiva construtiva, onde, gradualmente, caracterizamos tais sistemas por meio da introdução de

um por um dos elementos que os compõem, até que sejam inteiramente identificados como a simples justaposição desses elementos.

Como ponto de partida, descrevemos como se dá o processo teórico de confinamento em um anel, destacando duas vias distintas para realizá-lo: o potencial trivial e o potencial de Tan e Inkson. Na

segunda parte, passamos a investigar o anel na presença do fluxo Aharonov-Bohm, discutindo o efeito Aharonov-Bohm, na qualidade de fenômeno quântico, e seus eventuais efeitos nas autofunções e nas

propriedades gerais dos anéis quânticos. Por fim, damos uma pequena pincelada acerca das correntes persistentes em anéis quânticos bidimensionais.

2.1

Confinamento Bidimensional

Como já antecipado, para construir tais sistemas, primeiramente, é necessário confinar os elétrons

em regiões bidimensionais de forma a definir a geometria das estruturas. Teoricamente, esse processo de confinamento pode ser realizado de inúmeras formas distintas, por meio da definição dos mais

variados potenciais confinantes. Mais largamente utilizado, entretanto, o método mais tradicional, que, exceto quando for dito o contrário, adotaremos no decorrer do presente texto, é aquele que configura

a situação física mais simples possível do ponto de vista da dinâmica do elétron: o confinamento via barreiras infinitas.

de barreiras infinitas, o potencial confinante é definido de modo a proporcionar, também, uma total

liberdade aos elétrons, no que diz respeito ao movimento. Assim, ao adotar este tipo de confinamento específico, introduzimos a identidade geométrica do sistema ao mesmo tempo que garantimos que os

elétrons, no isolamento, sejam totalmente livres.

Como primeiro passo para a construção da estrutura em questão, via tal potencial, selecionamos

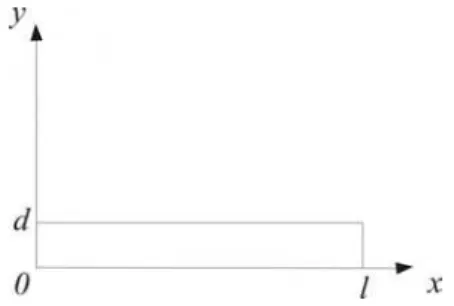
uma região quadrilátera do plano para ser ocupada pelos elétrons, pelo menosa priori. Consideremos, então, uma faixa bidimensional de comprimento l e largura d, como mostrado na figura abaixo:

Figura 2.1: Faixa de comprimento l e largura d

Para caracterizá-la como uma região física de confinamento, um determinado potencial deve ser in-troduzido. Para fins específicos, definimos, convenientemente, o seguinte potencial:

V (x, y) =

  

∞, x > l ex <0;y <0 e y > d

0, 0< x < l; 0< y < d

.

Dessa forma, permitimos a ocupação apenas da região R : _{(x, y) ;_∀x_∈[0, l],_∀y_∈[0, d]_}, uma vez que a probabilidade de encontrar um elétron em uma região com potencial infinito é nula. Além disso, em virtude da ausência de potencial, os elétrons, na região de ocupação R, possuem apenas o termo da energia correspondente à energia cinética, comportando-se, tecnicamente, como partículas livres. Em benefício de referências futuras, a este tipo de potencial que delimita regiões por meio de

descontinuidades infinitas, onde um elétron, quando confinado em um determinado lugar do espaço, é inteiramente livre, daremos o nome de potencial trivial.

Para especificar a geometria do anel, por fim, realizamos um processo de colagem das extremidades

x = 0 e x = l, processo este que, do ponto de vista prático, traduz-se como uma modificação nas condições de contorno para a função de onda, na resolução da equação de Schrödinger. É exatamente essa colagem a responsável por definir o tipo de anel que será estudado, como destacado nas duas

À primeira vista, pode parecer estranho, mas existe uma boa justificativa para tomar um caminho

aparentemente mais longo para realizar o confinamento. Em vez de simplesmente usar um potencial que defina, diretamente, um anel 2D, partir da definição de uma faixa bidimensional é uma boa

alternativa por chamar a atenção para a questão das condições de contorno, estabelecendo um vínculo de fácil visualização entre o modo de executar a colagem e a obtenção das mesmas. Isso poderá ser

melhor compreendido mais adiante, nas próximas subseções.

2.1.1

O Anel Comum

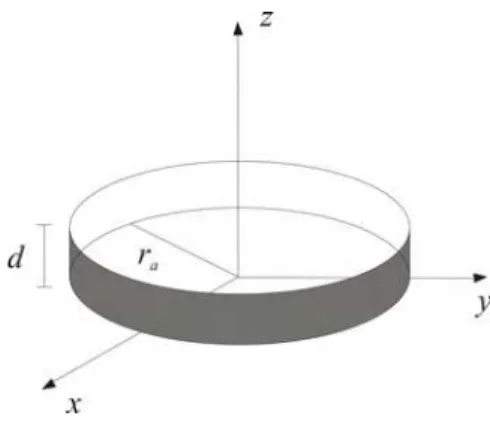
Para esta configuração, a colagem das extremidades é executada da forma mais trivial possível, identificando-as de tal maneira que, sem quaisquer novidades em relação à forma tradicional de um

anel, todos os pontos da faixa estejam, rigorosamente, sobre um raio constante ra =l/2π, de acordo

com a Figura 2.2.

Figura 2.2: Anel Comum de raio ra e largura d

Na prática, para descrever o confinamento nessa classe de anéis, redefinimos o potencialV(x, y, z)

responsável pelo confinamento na faixa bidimensional da Figura 2.1. Entretanto, como é possível ver pela Figura 2.2, o uso de coordenadas cilíndricas passa a ser mais conveniente para expressar matematicamente esse novo potencial. De forma que, temos, então:

V (r, ϕ, z) =

        

∞, _∀z _∈[0, d],_∀ϕ _∈[0,2π], _∀r_∈[0,_∞);r ₆=ra ∞, _∀z _∈(_−∞,0]_∪[d,_∞), _∀ϕ _∈[0,2π]; r=ra

0, _∀z _∈[0, d], _∀ϕ _∈[0,2π]; r=ra

Esse confinamento produzido pelo potencial acima implica, necessariamente, uma troca nas condições

de contorno. Neste caso, em especial, passamos das condições de contorno triviais, onde as funções de onda devem ser nulas nas bordas da faixa, para as condições de contorno ditas periódicas.

Em coordenadas cilíndricas, portanto, as novas condições de contorno para a função de onda, obtidas após efetuar esse tipo de procedimento descrito acima, escrevem-se como:

  

ψ(ϕ,0) = ψ(ϕ, d) = 0, _∀ϕ_∈[0,2π]

ψ(ϕ+ 2π, z) = ψ(ϕ, z), _∀z _∈[0, d] .

Com isso, vemos que a escolha dessa configuração equivale apenas a impor novas condições de contorno à solução geral da equação de Schrödinger. Na realidade, veremos que, de modo geral, o

confinamento em qualquer tipo de anel se caracteriza inteiramente apenas por modificações particu-lares nas condições de contorno.

2.1.2

A Faixa de Möbius

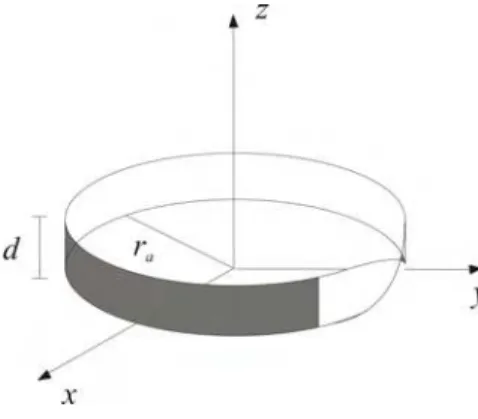
Neste tipo de anel, a colagem é efetuada logo após um giro de π, de uma extremidade da faixa, em torno do eixo que passa por x=d/2. Dessa forma, obtemos uma superfície denominada faixa de Möbius, que, dentre outras propriedades, goza da peculiaridade de não apresentar a possibilidade de se introduzir a noção de orientabilidade. Grosso modo, tal característica consiste na impossibilidade

de se identificar, por meio da definição de vetores normais a planos que tangenciam os pontos da superfície, dois lados em uma dada superfície. Isso equivale a dizer, em termos práticos, que, se um

objeto se desloca numa faixa de Möbius, ele só retornará ao seu ponto de partida após duas voltas, pois, o giro-π que antecede a colagem estabelece um contato entre os dois lados da faixa original e, ao contrário do caso de um anel comum, desconsiderando, obviamente, um movimento transversal suficiente para ultrapassar a borda, o objeto pode passar de um desses lados para o outro, livremente,

por um movimento longitudinal contínuo. Em outras palavras, forçosamente, podemos dizer que o objeto permanece em um único “lado” de comprimento maior do que seria no caso trivial.

Rigorosamente, a faixa de Möbius se caracteriza por não permitir a definição de uma orientação, que consiste basicamente, na definição de um campo vetorial normal, em toda a superfície, que seja

diferenciável. No caso específico da faixa de Möbius, se você tentar definir esse campo como no caso de uma esfera, por exemplo, perceberá que ele será necessariamente descontínuo e, portanto,

Figura 2.3: Faixa de Möbius de raio ra e largura d

simples fato de que, ao longo da faixa, os vetores perpendiculares e seus opostos “compartilham” dos

mesmos pontos. Por exemplo, no caso de uma esfera, ao percorrermos, continuamente, toda a área da superfície com um vetor normal nˆ, vemos que, no final, cada ponto só admitirá, em seu plano tangente, que esse vetor se apresente apenas em seu sentido original nˆ, e nunca em ₋nˆ. Numa faixa de Möbius, intuitivamente, é fácil ver que isso não ocorre, levando em conta a continuidade do nosso

movimento.

Não nos estenderemos, no entanto, nessa direção, porque uma descrição mais formal acerca da

questão da orientabilidade e das superfícies não-orientáveis, de modo geral, exigiria a introdução de uma série de conceitos e definições rigorosas e, consequentemente, implicaria uma distanciamento mais

agudo do ponto central deste trabalho. De fato, como nosso problema consiste em resolver a equação de Schrödinger com as condições de contorno apropriadas, independentemente do aspecto geométrico

da estrutura, é nas condições de contorno que deve residir toda a nossa atenção.

Para esta situação, em particular, as condições de contorno triviais, relativas à faixa antes da

colagem de suas extremidades, são substituídas por um outro tipo de condições de contorno, que, ainda, são periódicas, mas invertidas com relação à linha média z =d/2. Sendo assim, são chamadas adequadamente de antiperiódicas. Elas são escritas como:

  

ψ(ϕ,0) =ψ(ϕ, d) = 0

ψ(ϕ+ 2π, z) =ψ(ϕ, d₋z) .

2.2

Confinamento via Potencial Não-Trivial: O Modelo de Tan

e Inkson

Alternativamente, uma outra forma de isolar os elétrons em determinadas regiões do espaço é

introduzir um determinado potencial de confinamento que não apenas consista na alternância de barreiras infinitas de potencial e de poços infinitos, como o proposto, recentemente, por Tan e Inkson

em [6]. Neste artigo, para produzir o confinamento, é tomado como modelo o seguinte potencial:

V(r) = a1

r2 +a2r 2

−V0, (2.1)

onde V0 = 2√a1a2, sendo a1 e a2 constantes arbitrárias.

Antes de analisar o modelo propriamente dito, é interessante mostrar que este potencial, de fato,

delimita uma região de ocupação permitida aos elétrons correspondente a um anel. Para isso,

desmem-bramos o potencial V(r) e analisamos cada termo separadamente. Sendo assim, é natural que, por questão de organização, novos potenciais sejam definidos para facilitar o desenvolvimento e clareza

dessa análise.

Sejam, portanto, V1 e V2 de tal forma que podemos escrever:

V(r) =V1+V2−V0.

Ou seja, temos, por definição, que

V1 =

a1

r2 e V2 =a2r 2_.

Analisando os casos limites, podemos facilmente visualizar de que forma os potenciaisV1 eV2, em

conjunto, produzem um modelo satisfatório.

Quando r _→ 0, temos que V2 → 0, ou seja, nas proximidades de r = 0 os elétrons estariam

aproximadamente livres, tornando-se totalmente livres apenas em r = 0, quando V2 = 0. Por outro

lado, para o potencial V1, quando tomamos o mesmo limite, devemos ter V1 → ∞, o que demonstra

o que garante, por uma análise análoga, a não ocupação de regiões com r muito grande. Esses fatos são ilustrados, não rigorosamente, é claro, nas figuras abaixo.

Figura 2.4: Representação do confinamento produzido por V2.

Figura 2.5: Representação do confinamento produzido por V1.

Nessas ilustrações, quanto mais escuras são as regiões, menor é a facilidade de ocupá-las, de forma que as regiões em preto representam aquelas onde a ocupação não é permitida, ou seja, onde o potencial é

infinito. Contrariamente, quanto mais claras as regiões, mais facilmente elas são ocupadas. Portanto, as partes totalmente brancas representam as regiões onde os elétrons, quando confinados, estariam

totalmente livres.

Toda essa pequena e ingênua análise significa, basicamente, que, quando tomados conjuntamente,

Figura 2.6: Representação do confinamento produzido por V =V1+V2.

No entanto, vale a pena destacar que, apesar dessa região de confinamento apresentar uma típica

geometria de anel, o aspecto geométrico dessa estrutura difere daquela produzida a partir da faixa da Figura 2.1, via colagem das extremidades. Como é possível ver pela dependência emrdo potencialV, o anel via Tan e Inkson, ao contrário do anel descrito na seção anterior, apresenta um comprimento que varia com r, l(r) = 2πr, o que torna mais complicada a produção de faixas de Möbius. Essa dificuldade aparece em um eventual processo de colagem após o giro-π característico da fabricação de uma faixa de Möbius e, por consequência, na obtenção das condições de contorno antiperiódicas. E

é exatamente essa diferença a principal razão para a não adoção do potencial de Tan e Inkson, como potencial confinante, neste trabalho.

Uma vez demonstrada a consistência do modelo, focamos, agora, nas características do potencial e no tipo de confinamento produzido por ele.

Como primeiro ponto, deve ser destacada a versatilidade do potencial, que, sem sombra de dúvida, é uma das principais vantagens do modelo. Partindo da expressão original de V(r), é possível obter outras formas de confinamento e, consequentemente, outras mesoestruturas, como casos particulares, por meio de simples manipulações das constantes a1 ea2. Temos os seguintes casos:

1. Ponto Quântico

Fazendo a1 = 0, obtemos o seguinte potencial:

V(r)_−→VP(r) = a2r2,

2. Antiponto Quântico

Neste caso, tomando a2 = 0, temos que:

V(r)_−→VA(r) =

a1

r2.

Obtemos, dessa forma, o potencial responsável pelo confinamento em um antiponto quântico.

3. Fio Infinito 2D

Aqui, tal estrutura é obtida fazendo r0 → ∞, onde r0, como mostrado mais adiante, é o raio

médio do anel. Isso vem do fato de que uma reta pode ser vista como uma circunferência de

raio infinito.

4. Anel Quântico 1D

Fazendoa2 −→ ∞, temos queω −→ ∞, por definição. A justificativa para este limite será dada

só mais à frente.

Um outro aspecto da função V(r) que merece ser mencionado é o tipo de restrição que ela impõe ao movimento radial do elétron, já que uma das primeiras preocupações que surge, ao se escolher

usar tal potencial como uma alternativa ao potencial trivial, é sobre como o elétron se comporta na região onde a ocupação é permitida. O caminho tomado para responder esta questão é o de encontrar

o mínimo da função V e verificar como ela se comporta em torno desse mínimo. Para chegar às expressões desejadas, como primeiro passo, derivamos a expressão (2.1) com relação a r:

dV dr =−

2a1

r3 + 2a2r (2.2)

Igualando a expressão (2) a zero, obtemos

r=r0 =

a1

a2

1₄ ,

o ponto de mínimo da função V(r), que coincide com o raio médio do anel. Para finalmente obter o comportamento de V(r) nas proximidades de r = r0, expandimos a função, em série de Taylor, em

Substituindo a função V e suas primeiras derivadas, calculadas em r0, e considerando apenas os três

primeiros termos da série, encontramos:

V (r)_≈ 1

28a2(r−r0)

2

,

a expressão aproximada para o potencial de Tan e Inkson na vizinhança do mínimo, ou raio médio

do anel. Tal expressão é basicamente o potencial de um oscilador harmônico de massam e frequência

ω = q8a2

m , cuja posição de equilíbrio é r0. Vemos, então, que, no anel criado por um confinamento

via potencial de Tan e Inkson, um elétron se comporta, radialmente, como um oscilador harmônico, ou seja, um elétron aprisionado no anel executa um movimento radial harmônico simples em torno do

raio médio; não estando, portanto, livre como no caso anterior.

Para finalizar, com tudo já explicado, podemos justificar o limite, citado anteriormente, que

con-verte o anel 2D em um 1D. Como ω é a frequência com que o elétron oscila em torno do raio médio, temos que, com o limite sendo tomado, o período, consequentemente, vai a zero, caracterizando um

deslocamento desprezível do raio médio. Sendo assim, a região de confinamento passa a ser unidimen-sional, definindo, portanto, um anel 1D.

2.3

Introduzindo o Fluxo Magnético

_Φ

Além do já descrito, um anel quântico é inteiramente caracterizado quando se introduz um campo

magnético constante B~ atravessando, paralelamente ao eixo normal do anel, a região interior do anel, não incluindo, entretanto, o próprio. Tal configuração pode ser vista na figura abaixo:

Naturalmente, a partir de agora, o principal objetivo passa a ser o de encontrar o efeito da

in-trodução do campo magnético B~ nas autofunções e nas autoenergias do sistema em questão, isto é, em saber de que forma a presença desse fluxo magnético pode modificar as autofunções e as energias.

Não apenas as energias, mas também algumas outras propriedades físicas, de uma forma geral. À primeira vista, podemos pensar que nada é alterado, já que o campo é nulo no anel, ou seja,

~

B = 0 para r=ra. Entretanto, como veremos, o potencial vetor é não-nulo na região ondeB~ = 0, o

que já é suficiente para que o Hamiltoniano do sistema seja automaticamente modificado. Além disso,

um fato surpreendente emerge desta configuração em particular: o potencial vetor pode ser “sentido”, literalmente, pelos elétrons. Toda esta seção é dedicada, seja direta ou indiretamente, a este fato.

Na primeira parte desta seção, apresentamos um tratamento qualitativo do efeito Aharonov-Bohm, situando-o historicamente e descrevendo alguns pontos importantes que dizem respeito ao efeito, sem

caráter matemático. Em seguida, voltamo-nos para um tratamento predominantemente matemático, onde, primeiramente, tratamos de encontrar o potencial vetor _A~ _{e, logo após, obtemos e analisamos,}

detalhadamente, a fase Aharonov-Bohm, culminando com a determinação de novas condições de con-torno.

2.3.1

O Efeito Aharonov-Bohm

Em 1959, Aharonov e Bohm publicaram o artigo [1], que constitui um marco na Física das

es-truturas mesoscópicas, em que lançavam mão, como sugerido pelo próprio título, de uma nova inter-pretação para o potencial vetor, simplesmente para explicar um efeito antes inexplicável do ponto de

vista clássico e que, mais adiante, uma vez admitida e consolidada essa hipótese, viria a ser conhecido como Efeito Aharonov-Bohm.

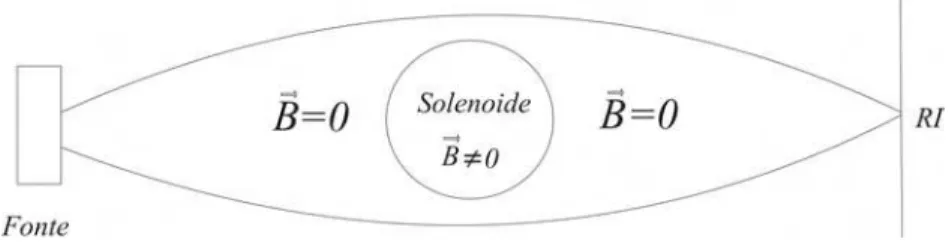
Para ilustrar, vamos considerar um dos mais tradicionais dentre os inúmeros arranjos experimentais onde o efeito Aharonov-Bohm pode ser observado. Basicamente, o objetivo de tal experimento consiste

em verificar o padrão de interferência de dois feixes de elétrons que viajam de um ponto a outro, por caminhos distintos, nas vizinhanças de uma solenoide infinito, como ilustrado na Figura 2.8.

Figura 2.8: Esquema do arranjo experimental

é até óbvio que os elétrons, em qualquer região que não seja no interior do solenoide, não sofram

qualquer tipo de influência na passagem da fonte à região RI, pois o campo magnético B~ é nulo na região externa ao solenoide e, consequentemente, não há com o que interagir. Entretanto, para

grande surpresa, observa-se que, na região de interferência, os feixes apresentam uma diferença de fase proporcional à integral R

CA~·d~l, onde C é o caminho fechado correspondente aos dois caminhos

percorridos pelos feixes, ou seja, C =Csuperior+Cinf erior.

Segundo a interpretação de Aharonov e Bohm, o que acontece é que os elétrons, de alguma forma,

interagem com o potencial vetor que, mesmoB~ sendo nulo na região externa ao solenoide, neste caso é não-nulo. Ou seja, contrariamente à noção clássica a respeito do seu papel na teoria eletromagnética,

onde não passava de um mero ente matemático, o potencial vetor passa a ter um novo significado, bem mais físico, aos olhos da Física Quântica. Ele é, para a Física Quântica, um campo capaz de

interagir, no real sentido da palavra, com partículas como os elétrons. E, como consequência desta capacidade de interagir com os elétrons, ele passa a ser o responsável por alterar a fase de um feixe

que viaje na sua presença e, consequentemente, adicionar uma fase à função de onda.

Após a publicação do artigo de 1959, uma chuva de novos trabalhos envolvendo o efeito

Aharonov-Bohm começou a aparecer. Aos poucos, foram surgindo as primeiras contestações à validade da ideia original do efeito, questionando se a explicação inicial era falaciosa ou não. Uma das hipóteses

sugeridas para explicar o efeito foi a de que, abolindo qualquer tipo de influência do campo A~ nos elétrons, a diferença de fase observada surgia como consequência da interação dos elétrons com o

campo magnético proveniente de um “vazamento de fluxo magnético”, pelas extremidades do solenoide. Ou seja, o efeito não seria nada mais que um simples fenômeno clássico. Essa ideia surgiu devido à

impossibilidade de, experimentalmente, utilizar um solenoide infinito para eliminar qualquer influência de um eventual campo vazado dos pontos inicial e final. Portanto, não era nenhum absurdo que tal

explicação fosse admitida.

Quase que simultaneamente a esses trabalhos, alguns experimentos eram realizados com o objetivo

experimentais foram escritos buscando maneiras de eliminar esse tipo de dificuldade, construindo

novas configurações alternativas para eliminar um possível efeito de um “vazamento de fluxo”, de forma a provar, de uma vez por todas, a influência real do potencial vetor, assim como proposto desde

o começo.

Um bom exemplo disso foi a sugestão da adoção de um arranjo experimental consistindo de um

toroide em substituição ao solenoide descrito no experimento original, como proposto, por exemplo, nos artigos [7], por Akira Tonomura, e [8], por Osakabeet al, em 1986. Essa modificação é interessante

devido à ausência do “vazamento” inerente ao caso do solenoide, uma vez que o campo magnético, a priori, permanece confinado no interior do toro, não havendo, portanto, “fuga” de campo magnético

por meio das extremidades. Além disso, o experimento é, ainda, montado para evitar um possível vazamento através das próprias paredes do toro. Para isso, toda a superfície do toro é coberta por

um material supercondutor, de forma a impedir, graças ao efeito Meissner, a passagem de qualquer campo magnético para a região exterior.

Com esse tipo de experimento, é possível observar o efeito Aharonov-Bohm e confirmar a existência de uma origem aparentemente incomum, pelo menos no que diz respeito ao eletromagnetismo clássico.

Mais que isso, esse experimento confirma o já estabelecido e começa a dar indícios reais da natureza quântica do efeito Aharonov-Bohm.

Uma outra tentativa de dar uma nova explicação ao efeito foi feita por Timothy H. Boyer [9]. Baseada na interação usual entre campo eletromagnético e elétrons, a nova interpretação proposta

por ele também abandona uma origem puramente quântica para o efeito. A idéia consiste basica-mente em considerar o efeito do campo eletromagnético dos elétrons do solenoide gerado a partir da

sensibilidade desses mesmos elétrons ao campo carregado pelos elétrons dos feixes. De acordo com a teoria clássica do eletromagnetismo, os elétrons dos feixes, no experimento descrito anteriormente,

carregam um campo eletromagnético. Segundo Boyer, os elétrons no solenoide sentem esse campo e, como consequência dessa interação, criam um outro campo eletromagnético que, por sua vez, será

sentido pelos elétrons dos feixes, provocando, assim, a diferença de fase verificada na região de inter-ferência RI. Em suma, segundo ele, a diferença de fase encontrada é fruto da interação dos elétrons com um campo real, via força de Lorentz, e não devido a uma possível influência do potencial vetor.

Como se vê, inúmeras foram, e são, as tentativas de invalidar a interpretação original do efeito.

2.3.2

O Potencial Vetor

A

~

Considere a situação descrita no início desta seção, onde:

~ B =

  

Bz, r < rˆ a

0, r_≥ra

Para encontrar o potencial vetor _A~_{, primeiramente, lembramos que} ~

B =_{∇ ×}~ A,~

que, convenientemente, escrevemos como:

Z

S

~

B _·d~a=

Z

S

(_{∇ ×}~ A~)_·d~a.

Utilizando o teorema de Stokes, temos:

Z

S

~

B_·d~a =

Z

C

~

A_·d~l, (2.3)

onde C é o contorno da superfícieS.

Identificando o lado esquerdo da equação (2.3) como o fluxo magnéticoΦatravés do anel,

escreve-mos:

Φ =

Z

C

~ A_·d~l,

onde Φ =Ba, sendo a=πr2

a a área da região delimitada pelo anel.

Para encontrar A~, devemos calcular a integral no lado direito da expressão (2.3) para um circuito amperiano C1 com r < ra e para outro C2 com r > ra, mostrados nas figuras 2.9 e 2.10,

respectiva-mente. No primeiro caso, temos:

Z

C

~

Figura 2.9: Circuito amperiano de raio r < ra

pois a área delimitada por C1 é a1 = πr2, onde r ≤ ra. Com isso, escrevemos para A~, para um raio

menor que o raio do anel:

~ A= rB

2 ϕ.ˆ (2.4)

No segundo caso, entretanto, o fluxo através da área delimitada por circuitos amperianos do tipo

C2 é sempre o mesmo, pois, para r ≥ ra, o campo magnético é nulo. Assim, com Φ = πra2B, temos

que, para um raio maior que o do anel:

~ A= r

2

aB

2r ϕ.ˆ (2.5)

Portanto, reunindo as expressões (2.4) e (2.5), vemos que, resumidamente, o potencial vetor, para esta situação particular, é expresso como:

~ A=

  

rB

2 ϕ,ˆ r≤ra

r2

aB

2r ϕ, rˆ ≥ra

.

Em particular, quandor =ra, que é o caso de nosso interesse, já que o anel, e consequentemente

os elétrons, encontra-se apenas nesse raio, o potencial vetor é:

~

Figura 2.10: Circuito amperiano de raio r > ra

~ A= Φ

2πra

ˆ

ϕ.

Vemos, então, que o potencial vetorA~ é diferente de zero até mesmo na região onde não há campo magnético, como já mencionado.

Além disso, por razões que residem mais adiante no texto, vale a pena observar que, quandoB~ = 0, devemos ter

~

∇ ×A~ = 0,

o que implica

~

A=_∇~χ,

ondeχé uma função escalar. Para o caso em questão, no entanto, emr=ra, sabemos queA~ = _2πrΦ

aϕˆ.

Comparando com o gradiente de χ que, em coordenadas cilíndricas, escreve-se como:

~

∇χ= ˆϕ 1 ra

∂χ ∂ϕ + ˆz

∂χ ∂z,

encontramos:

χ=ra

Φϕ

2πra

= Φϕ 2π.

2.3.3

A Fase Aharonov-Bohm

Como já foi dito no início desta seção, o Hamiltoniano do sistema é alterado quando se introduz o campo magnético. Para um elétron na presença de um potencial vetor _A~_{, como bem se sabe, o}

Hamiltoniano é:

H = 1 2m

ˆ

P ₋ e cA~

2

, (2.6)

No caso em questão, em que o elétron se encontra aprisionado à superfíce do anel, em r = ra, o

potencial vetor a ser introduzido é o já encontrado _A~ ₌ Φ 2πraϕˆ.

Para responder a questão sobre como a presença do fluxo magnético Φ pode modificar as auto-funções e as autoenergias, devemos partir para resolver a equação de Schrödinger independente do

tempo para o Hamiltoniano mostrado acima:

Hψ =Eψ.

No entanto, aqui, com relação às autofunções especificamente, usamos de um atalho para responder

tal questão, sem que seja necessário, pelo menos para esse fim, resolver a equação de Schrödinger acima, de fato.

Primeiramente, abrimos o Hamiltoniano (2.6) termo a termo:

H = 1 2m

ˆ

P ₋e cA~

2

= 1 2m

P2₋e

cPˆ·A~− e

cA~·Pˆ+ e2

c2A 2

.

Após isso, introduzimos o operador momento _Pˆ_=−i~_∇:

H = 1 2m

−~2_∇2₊ ie~

c ∇ ·~ A~+ ie~

c A~·∇~ + e2

c2A 2

.

Com isso, reescrevemos a equação de Schrödinger como:

1 2m

−~2_∇2₊ie~

c ∇ ·~ A~+ ie~

c A~·∇~ + e2

c2A 2

Com o intuito de simplificar o problema, no entanto, efetuamos, convenientemente, a seguinte

trans-formação:

  

ψ _−→ψ′ _=ψe−ie ~cχ

H _−→H′ _=e−ie ~cχHei

e ~cχ

.

Com essa mudança, a equação de Schrödinger, como apresentada na expressão (2.7), passa a ser escrita da seguinte maneira:

H′_ψ′ _=e−ie ~cχ

1 2m

−~2_∇2₊ie~

c ∇ ·~ A~+ ie~

c A~·∇~ + e2

c2A 2

ei~ecχψ′ =Eψ′. (2.8)

Notando que

H′ =e−i~ecχHei e

~cχ=−

~2

2m∇

2_,

passamos da equação (2.7) para a seguinte:

−~

2

2m∇

2_ψ′ _=Eψ′_{, (2.9)}

que é uma problema bem mais simples de tratar. Essa passagem simplificadora, num certo sentido,

justifica essa transformação efetuada. No entanto, fica faltando uma outra justificativa, num outro sentido, para a utilização dessa transformação. Falta mostrar, na realidade, que, para o problema em

questão, não faz diferença resolver a equação (2.7) ou a (2.9), isto é, falta mostrar que, independente de qual seja a equação resolvida, os resultados obtidos são equivalentes. Na sequência, buscamos tal

justificativa.

É fácil perceber que tal passagem se dá, na realidade, por meio da seguinte transformação:

  

ψ _−→ψ′ _{=U ψ}

H _−→H′ _{=U HU}−1 ,

implementada pelo operador unitário U =e−ie

~cχ. De forma geral, a transformação efetuada é:

  

ψ _−→ψ′ _{=U ψ}

onde A é um operador Hermitiano qualquer.

O operador unitárioU implementa, na verdade, uma transformação de gauge, ou seja, uma trans-formação do tipo:

  

~

A0 −→A~0+∇~χ

φ_−→φ₋1_c∂χ_∂t .

Para tornar este fato facilmente perceptível, consideramos a transformação inversa, que produz a

passagem inversa, do par (H′_{, ψ}′_{) para o par (H, ψ), ou, equivalentemente:}

1 2m

−i~_∇~

2

ψ′ =Eψ′ _−→ 1

2m

−i~_{∇ −}~ e

c

Φ 2πra

2

ψ =Eψ

Neste caso, em especial, a transformação de gauge correspondente é identificada como:

  

~ A′

0 = 0 −→A~0 =A~′0+∇~χ=∇~χ

φ′ _{= 0−→φ=φ}′₋ 1

c ∂χ

∂t = 0

,

onde _∇~_{χé o nosso potencial vetor A}~_{, cuja expressãoA}~ ₌ Φ

2πra já foi encontrada anteriormente. Aqui,

percebemos que efetuar esta transformação de gauge é equivalente a fazer a seguinte transformação

unitária:

  

H′ _{−→H =U}−1_H′_U

ψ′

−→ψ =U−1_ψ′

implementada, agora, por U−1_{, o operador inverso. Analogamente, vemos, portanto, que a passagem}

(H, ψ) _−→ (H′_{, ψ}′_{), que se dá por meio da transformação unitária implementada por U, é, de fato,}

uma transformação de Gauge.

O importante, que deve ser salientado, é que, sob transformação de gauge, ou sob qualquer outra

transformação unitária, as quantidades físicas mensuráveis são invariantes, ou seja, elas são preservadas quando um sistema evolui para outro por meio de uma transformação de gauge. Isso acontece porque

tais quantidades são representadas, em mecânica quântica, por produtos internos, que, de forma geral, são preservados por transformações unitárias.

ˆ A ab = D ψa Aˆ ψb E .

Fazendo ψa −→U ψa, ψb −→U ψb eAˆ−→UAUˆ −1, escrevemos:

ˆ

A′

ab = D ψa U

†_UAUˆ −1_U ψb

E .

Como U−1_{U =U U}−1 _{= 1, a identidade, escrevemos, ainda:}

ˆ

A′

ab = D ψa U †

UAˆ ψb

E .

Sabendo que U† _=U−1_{, pois U é unitário, temos, então, que:}

ˆ

A′

ab = D ψa Aˆ ψb E

=Aˆ

ab,

mostrando que o produto interno é, de fato, preservado, por uma transformação unitária. Portanto, como a transformação não produz diferenças nas quantidades físicas, é preferível, por questões práticas,

resolver a equação (2.9) em vez da (2.7), o que justifica, naturalmente, a escolha do início desta subseção de efetuar tal transformação para simplificar o problema.

Posto tudo isso, resta, por fim, um último ponto que deve ser revisto: as condições de contorno. Na realidade, o que deve ser observado é de que maneira as condições de contorno sofrem influência

da modificação na função de onda, que, via tal transformação, adquire uma fase. As perguntas que naturalmente surgem são: Devemos rever as condições de contorno? De que forma elas devem ser

revistas?

Esse ponto é de extrema importância, já que, como será visto mais adiante, o problema-chave

desta dissertação só se caracteriza inteiramente apenas por meio do emprego de novas condições de contorno.

Como vimos ainda no primeiro capítulo, as condições de contorno diferenciam-se de acordo com o tipo de anel a ser construído, dependendo, portanto, do tipo de processo executado antes da colagem

das extremidades da faixa. Desconsiderando esse aspecto, ou mais precisamente, desconsiderando o número de giros-π, já devidamente definidos na primeira seção, podemos eliminar a dependência em

  

ψ(ϕ,0) =ψ(ϕ, d) = 0

ψ(ϕ+ 2π) =ψ(ϕ)

. (2.10)

Na verdade, a segunda condição deveria ser escrita como ψ(ϕ+ 2π, z) = ψ(ϕ, z/d₋z), sendo a escolha entre “z” e “d₋ z” vinculada ao tipo de anel escolhido. Mas, para tornar mais fluido o desenvolvimento que segue, é interessante manter como acima.

Antes de tudo, uma observação importante que deve ser feita é que, para ψ′_{, não há mudança}

na primeira condição, uma vez que U = e−ie

~cχ(ϕ) é só função de ϕ. Portanto, vale, agora para ψ′,

exatamente a mesma condição:

ψ′(ϕ,0) =ψ′(ϕ, d) = 0. (2.11) Olhando, a partir de agora, especificamente para a segunda condição, buscamos obter uma análoga para a função ψ′_{. Para isso, partimos de ψ}′_{(ϕ+ 2π). Comoψ}′ _=ψe−ie

~cχ, temos:

ψ′(ϕ+ 2π) = ψ(ϕ+ 2π)e−i~e_c

Φ

2π(ϕ+2π).

Usando a segunda condição de (2.10) para ψ, escrevemos:

ψ′(ϕ+ 2π) =ψ(ϕ) e−i~e_cχ e−i e ~_cΦ.

Mais uma vez invocando a definição de ψ′_{, notamos, ainda, que:}

ψ′(ϕ+ 2π) = ψ′(ϕ) e−i~e_cΦ, (2.12)

que é a condição procurada. Uma vez que Φ0 = 2~πe_c , o quantum de fluxo magnético, reescrevemos a

equação (2.12) e chegamos, por fim, à condição definitiva:

ψ′_{(ϕ+ 2π) =ψ}′_{(ϕ) e}−i2π_Φ0Φ

. (2.13)

  

ψ′_{(ϕ,0) =ψ}′_{(ϕ, d) = 0}

ψ′_{(ϕ+ 2π, z) = ψ}′_{(ϕ, z/d}

−z) e−i2πΦ0Φ

,

onde a escolha fica por conta do caso a ser estudado.

Assim, fica determinado que, quando é introduzido o fluxo Aharonov-Bohm numa estrutura de

confinamento de anel, as condições de contorno se alteram, permanentemente, devido à fase Aharonov-Bohm acrescentada à função de onda, de modo a apresentar a forma mostrada logo acima.

2.3.4

Correntes Persistentes em Anéis 2D

Como consequência dessa “sensibilidade” dos elétrons ao potencial vetor, comentada anteriormente, os anéis quânticos apresentam uma outra característica bastante incomum sob a ótica da Física

Clás-sica: a existência de correntes persistentes. Ao contrário das correntes comuns, a origem das correntes persistentes não possui sustentação na teoria do eletromagnetismo clássico. Não havendo um campo

eletromagnético na região de ocupação dos elétrons, é o potencial vetor o único possível responsável direto por “interagir” com os elétrons, possibilitando a criação de correntes no anel.

Para um anel quântico bidimensional qualquer construído como na seção 2.1, contendo muitos elétrons, ondenz rotula os níveis transversais, ou canais, enϕ rotula os níveis longitudinais, a corrente

persistente, em uma dada temperatura T finita, pode ser definida, de modo geral, pela seguinte expressão:

I =₋c

∂F ∂Φ

T

,

onde F é a energia livre de Helmholtz. Esta definição faz sentido quando se leva em consideração o fato de que a energia interna E do sistema pode ser variada através de uma variação do fluxo Aharonov-Bohm Φ. Isso pode ser visualizado escrevendo a primeira lei da Termodinâmica:

dE =T dS₋IdΦ.

Com isso, teríamos que:

I =₋

∂E ∂Φ

S

Para tomar a corrente como função de Φe T, torna-se conveniente definir em termos da energia livre de Helmholtz:

I =₋

∂F ∂Φ

T

,

pois, como F = E ₋T S, temos que dF = ₋IdΦ₋SdT e, consequentemente, I = ₋∂F/∂Φ, a T

constante. A constante c fica por conta do sistema de unidades adotado.

Para o caso em que T = 0, no entanto, temos que F _−→ E, pois F = E ₋T S. Dessa forma, podemos escrever a corrente persistente como:

I =₋c

∂E0

∂Φ

T=0

,

onde E0 é a energia do estado fundamental.

A energia totalE do sistema é:

E = X

nz,nϕ

P Enϕnz

Enznϕ.

Vemos, portanto, que a energia total é a soma sobre todos os níveis nϕ e todos os canais nz, levando

em conta as suas devidas probabilidades de ocupaçãoP. Considerando um único canalnz, no entanto,

a expressão passa a ser:

E =X

nϕ

P Enϕ

Enznϕ,

uma vez que não faz mais sentido somar sobre todos os canais.

No limite completamente degenerado, quando T = 0, particularmente, a função P Enϕ

toma

apenas dois valores:

P Enϕ

=

  

0, Enϕ > εF 1, Enϕ < εF

.

Assim, para um único canal nz, temos que a corrente persistente, em T = 0, é:

onde a soma P

P Enϕ

Enznϕ, sobre todos os sítios nϕ, deve ser mínima, retratando a distribuição

compacta dos elétrons característica do estado fundamental.

Já quando a temperatura T é diferente de zero, a função P Enϕ

é uma função um pouco mais

Capítulo 3

A Faixa de Möbius Quântica

A partir de agora, focamos no problema da faixa de Möbius sob o rótulo de anel quântico. Mais precisamente, concentramo-nos na apresentação e na resolução do problema, além de introduzir uma

pequena discussão, com base nos resultados obtidos, a respeito de algumas propriedades físicas do sistema. Na primeira parte, fazemos uma breve, mas precisa, descrição formal do problema.

De-pois, obtemos, detalhadamente, a solução, para, por fim, na última parte do capítulo, fazermos uma apresentação e análise das propriedades físicas dessa classe de anéis quânticos, ditos não-orientáveis,

comparativamente às características do anéis quânticos triviais.

3.1

Uma Breve Descrição do Problema

Antes de mais nada, é necessário apresentar detalhadamente o sistema que devemos investigar.

Nosso sistema consiste basicamente em um elétron de massa m confinado em uma faixa de Möbius de largura d, comprimentol e raio ra, cuja região central, r < ra, é atravessada por um fluxo magnético

Φ paralelo ao eixo normal da faixa. No anel, o elétron, por sua vez, encontra-se inteiramente livre, já

que o potencial é nulo na faixa.

Matematicamente, o nosso problema resume-se à resolução da equação de Schrödinger para o Hamiltoniano desse sistema. Do ponto de vista prático, como já sabemos, essa imposição no

confi-namento em uma faixa de Möbius revela-se por meio de uma alteração nas condições de contorno do problema.

Figura 3.1: Aspecto geométrico da faixa de Möbius quântica

onde H é o Hamiltoniano associado ao sistema descrito logo acima, que é:

H = 1 2m

ˆ

P ₋ e c

Φ 2πra

2 ,

com as seguintes condições de contorno:

  

ψ(ϕ,0) =ψ(ϕ, d) = 0

ψ(ϕ+ 2π, z) =ψ(ϕ, d₋z) .

Efetuando a transformação já mencionada anteriormente, porém, o problema pode ser reduzido, às

custas da introdução de uma fase na função de onda, a um problema matematicamente semelhante ao de uma partícula livre, desde que, obviamente, as condições de contorno sejam desconsideradas.

Neste caso, como descrito no capítulo anterior, a solução procurada ψ(ϕ, z) é aquela que satisfaz à equação

−~

2

2m∇

2_{ψ(ϕ, z) =Eψ(ϕ, z), (3.1)}

sujeita às novas condições de contorno, mostradas abaixo:

  

ψ(ϕ,0) =ψ(ϕ, d)

ψ(ϕ+ 2π, z) =ψ(ϕ, d₋z)e−i2πΦ0Φ

.

Tais condições correspondem às condições de contorno antiperiódicas, ou de Möbius, incrementadas com um termo oriundo da fase de Aharonov-Bohm adicionada à função de onda, graças a presença

3.2

Solução do Problema

Nesta seção, buscamos resolver o problema matemático associado à faixa de Möbius quântica. Como primeiro passo, obtemos, nesta seção, de forma bem detalhada, a solução geral da equação

diferencial (3.1). Após isso, na sequência, encontramos as autofunçõesψnϕnz(ϕ, z)e as energiasEnϕnz

do problema por meio da imposição das condições de contorno antiperiódicas de Aharonov-Bohm.

3.2.1

A Solução Geral

ψ

(

ϕ, z

)

Antes de mais nada, devemos escrever o Laplaciano presente no Hamiltoniano da equação (3.1)

em coordenadas cilíndricas, uma vez que o problema tem simetria cilíndrica. Como a função de onda só é não-nula em r=ra, isto é, a função ψ é função apenas de ϕ ez, a equação de Schrödinger, neste

caso, é escrita como:

−~

2

2m

1

r2

a

∂2

∂ϕ2 +

∂2

∂z2

ψ(ϕ, z) =Eψ(ϕ, z). (3.2) Para resolver a equação diferencial (3.2), usamos o método de separação de variáveis, onde supomos que a função de onda ψ(ϕ, z) pode ser escrita como o produto de duas outras funções, sendo uma função apenas de ϕ e a outra só de z. A principal vantagem desse método, também conhecido como método de Fourier, é a de poder trocar a equação diferencial parcial por duas equações difereciais

ordinárias que, pelo menos em princípio, são mais simples de resolver e cujos métodos diretos de resolução são mais tradicionais.

Supomos, então, que:

ψ(ϕ, z) = Γ (ϕ)Z(z). (3.3) Na sequência, substituimos a função (3.3) na equação (3.2):

−~

2

2m

1

ra

∂2

∂ϕ2 +

∂2

∂z2

Γ (ϕ)Z(z) =E Γ (ϕ)Z(z),

Multiplicando os dois lados por1/ψ = 1/Γ (ϕ)Z(z), separamos a equação em uma paraΓ (ϕ)e outra para Z(z), observando que E =Eϕ+Ez:

−~ 2 2m 1 ra 1 Γ (ϕ)

d2_{Γ (ϕ)}

dϕ2 +

1

Z(z)

d2_Z(z)

dz2

=Eϕ+Ez.

Daí, então, obtemos:

− ~

2

2mr2

a

d2_{Γ (ϕ)}

dϕ2 =EϕΓ (ϕ) (3.4)

e

−~

2

2m

d2_Z(z)

∂z2 =EzZ(z), (3.5)

duas equações ordinárias, uma para Γ e outra para Z, cujas soluções gerais são, respectivamente:

  

Γ (ϕ) =Asinkϕ+Bcoskϕ Z(z) =Csink′_z+Dcosk′_z ,

onde k =

q

2mr2

aEϕ

~2 e k′ =

q

2mEz

~2 . Com isso, a solução geral, sem a imposição das condições de contorno, é:

ψ(ϕ, z) = Γ (ϕ)Z(z) = (Asinkϕ+Bcoskϕ) (Csink′_z+Dcosk′_{z). (3.6)}

3.2.2

As Autofunções e o Espectro de Energia

Finalmente, como último passo, impomos à solução geral ψ(ϕ, z) as já citadas condições de con-torno:

  

(a) ψ(ϕ,0) =ψ(ϕ, d) = 0

(b) ψ(ϕ+ 2π, z) = ψ(ϕ, d₋z)e−i2πΦ0Φ

,

Condições relativas a Z(z)

Introduzindo a função de onda (3.6) obtida logo atrás, a primeira condição escreve-se como:

ψ(ϕ,0) = (Asinkϕ+Bcoskϕ) (Csink′0 +Dcosk′0) = 0, _∀ϕ_∈[0,2π],

de onde segue, como implicação imediata, que:

D=Z(0) = 0. (3.7)

De forma análoga, da segunda condição, escrevendo-a como:

ψ(ϕ, d) = (Asinkϕ+Bcoskϕ)Csink′d= 0,

extraimos o seguinte:

Z(d) = Csink′d= 0 _⇒ k′ = nzπ

d . (3.8)

Resumindo as duas restrições (3.7) e (3.8), obtemos a forma completa, a menos de constantes, da parte dependente de z da função de onda, Z(z), e o espectro de energiaEz:

(a)

        

Znz (z) = Anzsin

nzπz

d

Enz =

n2

zπ

2_~2

2md2 , nz = 1,2,3...

Cada valor de nz corresponde a um canal no anel. Cada canal, por sua vez, pode ser visto como uma

subdivisão da faixa relativamente à energia associada ao movimento tranversal do elétron, ou seja,

um canal é um nível energético rotulado de acordo com a intensidade do momento linear na direção

z.

Aeik(ϕ+2π)+Be−ik(ϕ+2π)

Csinnzπz

d

= Aeikϕ+Be−ikϕ Csin

nzπ(d−z)

d

e−i2πΦ0Φ , onde, por conveniência, escrevemos a solução oscilanteΓ (ϕ), parte integrante da solução geralψ(ϕ, z), na forma de exponenciais complexas, em vez de senos e cossenos. Utilizando, da trigonometria, a fórmula para o seno da soma, vemos que:

sin

nzπ(d−z)

d

= sin (nzπ) cos

nzπ(−z)

d

+ sin

nzπ(−z)

d

cos (nzπ).

Observando que, para os ângulos θnz = nzπ, o seno é sempre zero e o cosseno fica alternando entre

−1 (nz ímpar) e 1 (nz par), podemos escrever a condição (b) como:

Aeik(ϕ+2π)+Be−ik(ϕ+2π)

sinnzπz

d

= Aeikϕ+Be−ikϕ

(₋1)nz sin

nzπ(−z)

d

e−i2πΦ0Φ _. Usando o fato da função seno ser ímpar e cancelando os devidos termos, podemos reescrever a

igualdade acima como:

Aeik(ϕ+2π)+Be−ik(ϕ+2π)

=₋(₋1)nz

Aeikϕ+Be−ikϕ

e−i2πΦ0Φ_. De tal igualdade, comparando os dois lados, chegamos às seguintes condições:

  

ei2πk ₌₋₍₋₁₎nz

e−i2πΦ0Φ

e−i2πk ₌₋₍₋₁₎nz

e−i2πΦ0Φ

=_⇒

=_⇒

  

ei2π

k+Φ Φ0

=₋(₋1)nz

e−i2π

k−Φ

Φ0

=₋(₋1)nz =_⇒

  

ei2π

k+Φ Φ0

= (₋1)nz+1

e−i2π

k−Φ

Φ0

= (₋1)nz+1

,

que são equivalentes à:

  

cos2πk+ 2π_ΦΦ₀+isin2πk+ 2π_ΦΦ₀= (₋1)nz+1 cos2πk₋2π Φ

Φ0

−isin2πk₋2π Φ Φ0

= (₋1)nz+1

Considerando, primeiramente, o caso em que nz é par, é fácil ver que as condições acima fornecem a

seguinte imposição:

2πk_±2π Φ

Φ0

=_±niπ,

sendo ni um número ímpar. Fazendo, portanto, ±n= 2nϕ+ 1, com nϕ inteiro, temos que:

2πk_±2π Φ

Φ0

= (2nϕ+ 1)π,

de onde, finalmente, tiramos a condição para k:

k =nϕ+

1 2 ±

Φ Φ0

.

Quando nz é ímpar, no entanto, uma outra imposição é fornecida pelas mesmas condições:

2πk_±2π Φ

Φ0

=_±npπ,

com np, neste caso, sendo um número par. De forma análoga, mas desta vez fazendo np = 2nϕ, pois

trata-se agora de um número par, obtemos:

k =nϕ±

Φ Φ0

.

Reunindo as duas restrições, portanto, vemos que, de forma geral, para um valor arbitrário de nz, a

condição para k passa a ser escrita da seguinte maneira:

k =nϕ+

1 2δnz ±

Φ Φ0

,

onde definimos δnz como:

δn =



Sendo assim, com essa restrição em mãos, podemos, por fim, chegar às expressões para as

auto-funções Γnϕ(ϕ), a menos de constantes, e para as autoenergias Enϕ:

        

Γnϕ(ϕ) =Anϕe

∓inϕ+

1 2δnz±

Φ Φ0

ϕ

Enϕ =

~2

2mr2

a

nϕ+1₂δnz ±

Φ Φ0

2 .

Aqui, para encerrar, observamos que, para um dado canal nz, o índice nϕ rotula um sítio ou nível

energético, correspondendo a um determinado valor do momento angular.

Finalmente, temos que a expressão geral da energia donϕ-ésimo sítio do nz-ésimo canal é:

Enznϕ =

n2

zπ2~2

2md2 + ~2

2mr2

a

nϕ+

1 2δnz ±

Φ Φ0

2 .

Como primeira observação, notamos que, assim como no caso do anel comum, a energia é função

do fluxo magnético Φ que atravessa o centro do anel, paralelamente ao eixo de simetria do mesmo. Entretanto, apesar da dependência quadrática em Φ, em ambos os casos, a função E =E(Φ), em si, difere por alguns termos. De fato, num anel quântico comum, o termo com o delta se faz ausente na condição para k, uma vez que a condição relativa a Γ (ϕ) é, para este caso, apenas periódica, isto é:

ψ(ϕ+ 2π, z) =ψ(ϕ, z)e−i2πΦ0Φ.

Considerando este fato, portanto, o espectro de energia, no caso do anel comum, é:

E_nAC_znϕ = n

2

zπ2~2

2md2 + ~2

2mr2

a

nϕ±

Φ Φ0

2 ,

como já antecipado. Essa diferença se manifesta, também, em algumas caracteristicas da função

E =E(Φ), como, por exemplo, nos mínimos das funções EM _eEAC_{. Aqui, E}M _{designa a expressão}

para energia no caso da faixa de Möbius e EAC _{no caso do anel comum. Com o intuito de traçar,}

graficamente, um comparativo entre os dois casos, esboçamos, primeiramente, uma comparação entre esses mínimos da energia como função deΦpara os dois casos em questão. Para tal tarefa, calculamos

Para o caso primeiro, o da faixa de Möbius, temos o seguinte:

dEM

dΦ =

~2

mr2

a

nϕ+

1 2δnz ±

Φ Φ0 ±

1 Φ0

,

a derivada de EM _{com relação a Φ. Fazendo-a igual a zero, obtemos os mínimos:}

ΦM_min =_∓

nϕ+

1 2δnz

Φ0. (3.9)

No caso do anel comum, entretanto, derivando a expressão deEAC _{com relação aΦ e igualando a}

zero, podemos obter:

ΦAC_min =_∓nϕΦ0, (3.10)

como mínimos.

Com esses resultados, é possível estabelecer uma regra com relação à disposição das parábolas de ambos os casos, em um dado canal nz e em um dado nível nϕ. O que as expressões para os mínimos

(3.9) e (3.10) nos mostram é que, paranz par, o vértice das parábolas deEM =EM(Φ)são deslocados,

horizontalmente, de Φ0/2em relação ao das parábolasEAC =EAC(Φ), enquanto, que, paranz ímpar,

os vértices coincidem. Como exemplo, consideremos o caso mais trivial, onde nϕ = 0. Para um dado

canal nz, quando nϕ = 0, temos que ΦMmin =−12δnzΦ0 e Φ

AC

min = 0, de forma que, se este determinado

canal for par, ΦM

min =−12Φ0 e, consequentemente, Φ

M

min = ΦACmin− 12Φ0. Na Figura 3.2, há um esboço

simples ilustrando esta situação para nz = 1 e nz = 2.

Além dessa observação a respeito da função E(Φ) e seus mínimos, uma outro aspecto dessa função merece uma atenção especial: a periodicidade emΦ. Como será mostrado logo em seguida, já

destacamos que EM_{(Φ) é uma função periódica de período Φ}

0, ou seja, é uma função Φ0-periódica

em Φ. Para enxergar tal propriedade, escrevamos a função E calculada em Φ′ _{= Φ + Φ}

0:

E_nM

znϕ(Φ + Φ0) =

n2

zπ2~2

2md2 + ~2

2mr2

a

nϕ+

1 2δnz ±

Φ + Φ0

Φ0

2 ,

Figura 3.2: Gráfico de x= Φ/Φ0 por y=E/Enz=1, paraE =E

M_{(A) e E =E}AC_(B).

ou seja, trata-se da mesma função E = E(Φ), mas para um sítio à frente n′

ϕ, onde n′ϕ −→ nϕ + 1.

Portanto, temos o seguinte:

E_nM

znϕ(Φ + Φ0) =E

M

nznϕ+1(Φ), condição necessária e suficiente para que a função EM_{(Φ) seja Φ}

0-periódica. Analogamente, esta

propriedade também é compartilhada com a função energia no caso do anel comum, já que a análise

apresentada logo acima é indiferente à presença ou à ausência do termo que contém o deltaδnz. Assim,

as funções EM _eEAC _{são ambas funçõesΦ}

0-periódicas. Abaixo, traçamos um esboço comparando as

funções EM_{(Φ) e E}AC_(Φ).

A periodicidade de E(Φ) reflete diretamente nas correntes persistentes, uma vez que a expressão para a corrente é proporcional a taxa com que a energia varia com o fluxo Φ. De fato, como vimos no capítulo primeiro, a corrente persistente, em T = 0 por exemplo, é, em um dado canal,

I =₋c

∂EM

0

∂Φ

,

onde EM

0 é a soma das energias relativas aos níveis nϕ ocupados de forma que a energia total seja

mínima, ou seja, a energia do estado fundamental do sistema. Vemos, portanto, como já dito, que a corrente persistente é proporcional à derivada da energia com relação ao fluxo magnético. Assim,

levando em conta que se uma determinada função é ditaΦ0-periódica, então a sua derivada também é,

automaticamente,Φ0-periódica, temos que a corrente persistente também é periódica com um período

Φ0. Este fato é facilmente visualizado quando se olha para o quociente de Newton

QN =

E(Φ +h)₋E(Φ)

h ,

uma vez que a derivada é o limite do quociente de Newton quando h _−→ 0. Fazendo Φ_−→ Φ + Φ0

em QN, é fácil ver queQN(Φ + Φ0) = QN(Φ) e, portanto, é periódico.

Para que essa e outras propriedades não sejam destacadas apenas de forma genérica e, principal-mente, para mostrar e entender de que forma a escolha da geometria da faixa de Möbius pode ter

influência direta nelas, nada mais adequado do que calcular a corrente persistente de forma explícita.

3.3

Correntes Persistentes em Faixas de Möbius

Considere uma faixa de Möbius quântica composta por N elétrons livres. Para achar a corrente persistente, para um único canal, em T = 0, devemos considerar a seguinte expressão:

I =₋c

∂EM

0

∂Φ

T=0

,

onde

Primeiramente, vamos analisar o caso em que nz é um número ímpar. Neste caso, em especial, o

termo delta δnz é nulo e, consequentemente, o espectro E

M _{passa a ser:}

E_nM_znϕ = n

2

zπ2~2

2md2 + ~2

2mr2

a

nϕ±

Φ Φ0

2 ,

o espectro do caso de um anel comum. Assim, antecipadamente, já sabemos que a expressão para a

corrente persistente, neste caso, recairá na expressão para o caso de um anel comum.

Aqui, comonϕ pode ser qualquer número inteiro, devemos distinguir dois casos ao efetuar a soma

à direita, na expressão (3.11): 1) N par e 2) N ímpar. Isso se deve ao fato de que, para N ímpar, os níveis são ocupados simetricamente com relação ao nível nϕ = 0 e, para N par, a ocupação não

apresenta essa simetria, pois, necessariamente, o último nível ocupado terá o seu oposto simétrico desocupado. Como exemplo, considere os casos em que N = 3 e N = 4. Quando N = 3, o conjunto dos níveis ocupados é[₋1,0,1], de modo que a ocupação é simétrica com relação ao nível0. Já quando

N = 4, temos duas possibilidades: [₋2,₋1,0,1] ou[₋1,0,1,2], ambas antisimétricas com relação ao

0. Essa distinção deve ser feita, pois, dependendo da paridade de N, o momento angular total pode ser nulo ou não. Consequentemente, a energia total se modifica dependendo do caso.

Assim, para N ímpar, a soma P

nϕ deve ser tomada de nϕ =−(N −1)/2 a nϕ = (N−1)/2:

E₀M =

(N−1)/2

X

−(N−1)/2

E_nM_znϕ

Já paraN par, a soma pode ser efetuada de duas formas distintas, levando em consideração o conjunto

[₋N/2, ...,0, ..., N/2₋1]ou o conjunto [₋N/2 + 1, ...,0, ..., N/2]:

         EM 0 =

PN/2−1

−N/2 EnMznϕ

EM

0 =

PN/2

−N/2+1EnMznϕ

.

No entanto, ambas as somas devem produzir a mesma energia mínima. Para isso, há uma exigência que deve ser imposta com relação ao sinal de Φ. Portanto, para o caso onde N é par, deve ser feita, ainda, mais uma distinção, de acordo com o sinal de Φ. Se Φ > 0, a soma deve ser efetuada de