Conversor c.c./c.c. para central fotovoltaica com armazenamento de energia
Texto
Imagem
![Figura 2.12 - Conversor CC/CC dual active bridge trifásico com fonte de corrente [1]](https://thumb-eu.123doks.com/thumbv2/123dok_br/15484578.1039296/28.892.141.761.113.333/figura-conversor-dual-active-bridge-trifásico-fonte-corrente.webp)
![Figura 3.4 - Principais formas de onda do conversor Dual Active Bridge [8]](https://thumb-eu.123doks.com/thumbv2/123dok_br/15484578.1039296/33.892.188.722.121.615/figura-principais-formas-onda-conversor-dual-active-bridge.webp)
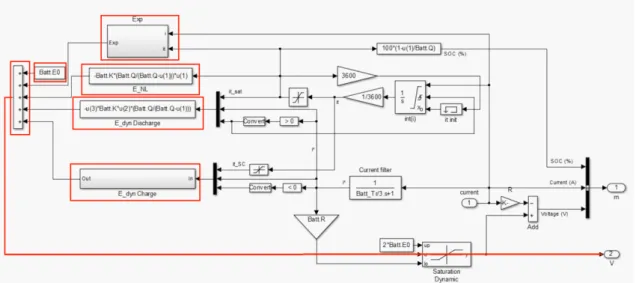
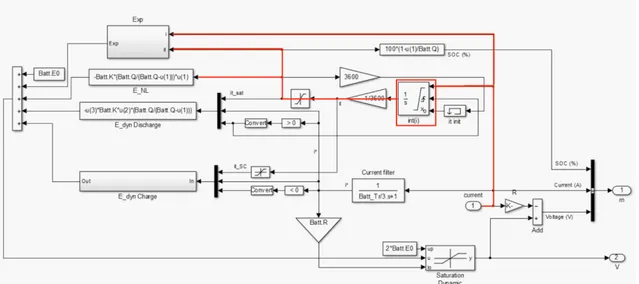
![Figura 3.7 - Cicuito equivalente do modelo de baterias existente no MATLAB [9]](https://thumb-eu.123doks.com/thumbv2/123dok_br/15484578.1039296/38.892.141.764.341.722/figura-cicuito-equivalente-do-modelo-baterias-existente-matlab.webp)
Documentos relacionados
Chora Peito Chora Joao Bosco e Vinicius 000 / 001.. Chão De Giz Camila e
Como condição de recebimento do objeto pelo órgão/entidade contratante, e posterior pagamento, o fornecedor deverá comprovar, no ato da entrega do material, a origem da mercadoria
gás é EMPREGO o setor de óleo e gás é responsável por 521.265 vagas, o correspondente a 1,3% de todos os empregos do Brasil (CAGED, jul2019) gás é INVESTIMENTO.. a cada R$
b) no âmbito da Secretaria da Receita Federal, pela liquidação do saldo consolidado, com a utilização de créditos de prejuízo fiscal e de base de cálculo negativa
O Workshop de Sensibilização foi realizado nos dias 22 e 23 de Agosto de 2003, no hotel Pergamont com representantes da Secretaria de Governo Municipal - SGM e a Secretaria
Análise: Permite a comparação numérica separadas por departamento de suporte com objetivo de determinar o comportamento, em relação ao tempo em que as OS dos
Taxas reais interessantes, apesar de ainda precificarem inflação muito alta.. Chance de ganho no carrego (HtM) e no
3259 21 Animação e dinamização de actividades lúdico-expressivas - expressão musical 50 3260 22 Animação e dinamização de actividades lúdico-expressivas -