Aula Estrutura Molecular e Ligação PARTE 5

Disciplina Ligações Químicas

Prof. Dalmo Mandelli

Ligações em Moléculas Poliatômicas

Parte 5

Teoria do orbital molecular: a abordagem dos orbitais de grupo ligantes (OGL) e a aplicação a moléculas triatômicas

Apesar de seu sucesso, a aplicação da teoria da ligação de valência à ligação em

moléculas poliatômicas leva a dificuldades conceituais.

O método indica que as ligações são localizadas.

Como consequência, conjuntos de estruturas de ressonância e a visão de ligações

envolvendo esquemas de hibridização se tornam difíceis de se estabelecer, mesmo para moléculas relativamente pequenas

Assim, vamos voltar nossa atenção para a teoria do orbital molecular (OM).

Diagramas de OM: partindo das espécies diatômicas para as poliatômicas

No tratamento da ligação em espécies diatômicas, construímos diagramas OM como abaixo

Os OAs dos dois átomos eram representados à esquerda e à direita do diagrama, com os OM no meio.

Foram construídas linhas de correlação ligando os AO aos

OM para produzir um

diagrama facilmente interpretável.

Molécula triatômica como o CO

Considere agora a situação para uma molécula triatômica como o CO₂ .

Os OM contêm contribuições de OA dos três átomos.

Temos o problema de tentar esquematizar um diagrama OM envolvendo quatro conjuntos

de orbitais (três conjuntos de OA e um conjunto de OM) .

Uma descrição da ligação no CF₄ envolve cinco conjuntos de OA e um conjunto de OM, ou seja, é um problema de seis componentes.

Da mesma forma, o SF₆ é um problema de oito componentes.

É claro que esses diagramas OM são complicados e, provavelmente, difíceis de serem construídos e interpretados.

A fim de superar essa dificuldade, é comum tratar a descrição de uma molécula poliatômica

como um problema de três componentes, um método conhecido como abordagem dos

orbitais de grupo ligantes (OGL) (Ligand Group Orbital Approach – LGO).

Abordagem OM à ligação no XH₂ linear: combinação das simetrias por inspeção

Na molécula triatômica linear XH₂ os orbitais de valência de X são os orbitais atômicos

2s e 2p.

Vamos orientar o esqueleto H-X-H de modo a coincidir com o eixo z, como mostrado na figura abaixo.

Molécula triatômica XH

Abordagem do orbital de grupo ligante (OGL) para construir um

diagrama OM para uma molécula linear XH₂ a partir das interações entre os orbitais de valência de X (orbitais atômicos 2s e 2p) e um fragmento H---H.

Para maior clareza, as linhas que marcam as energias dos orbitais 2p

são traçadas separadas, embora esses orbitais sejam, na verdade, degenerados.

Cada orbital atômico l s tem duas fases

possíveis e, quando os dois orbitais ls são tratados como um grupo, há duas combinações de fase possíveis.

Estes são

denominados orbitais de grupo ligantes (OLG) e são mostrados no

lado direito.

Estamos

transformando a descrição da ligação no XH₂ de uma base formada pelos OA dos átomos de X e H

em outra na qual a

base é formada pelos

O número de

orbitais de grupo ligantes formados é

igual ao número de

orbitais atômicos usados.

OA=OGL

Ao construirmos um diagrama OM para o XH₂ consideramos as interações entre os OA de valência de X com os

orbitais de grupo ligantes do

fragmento H---H.

Os diagramas superiores são representações mais realistas dos OM e foram obtidos computacionalmente usando Spartan '04, © Wavefunction Inc., 2003.

Orbital de grupo ligante OLG (1) tem a

simetria correta para interagir com o

orbital 2s de X, dando um OM com caráter ligante  H-X-H.

A simetria do OLG (2) coincide com a do OA 2p_z de X.

O orbital ligante resultante e sua contraparte antiligante e o diagrama OM são mostrados abaixo.

₁ 2 ₃ ₄ 

5 6

Pode-se ver as interações

correspondentes entre os orbitais.

Os OAs 2p_x e 2p_y de X se tornam orbitais

não ligantes em XH₂.

A etapa final na construção do

diagrama OM é alocar os elétrons disponíveis nos OM conforme o

princípio do aufbau

Resultado importante no tratamento OM da ligação no XH₂ é que o caráter ligante  nos orbitais ₁ e ₂ é espalhado sobre todos os três átomos,

indicando que o caráter ligante é

delocalizado ao longo do esqueleto H- X- H.

A ligação

delocalizada é um

Abordagem OM à ligação no XH

:

partindo da simetria molecular

O método mostrado anteriormente

para obter uma descrição da ligação no

XH₂ linear não pode ser facilmente estendido a moléculas maiores.

Um método mais rigoroso é identificar o grupo de pontos do XH₂ como D_h.

A tabela de caracteres é usada para

atribuir simetrias aos orbitais sobre um átomo X e aos orbitais de grupo ligantes. O diagrama OM é então construído permitindo-se as

interações entre orbitais de mesma

simetria.

Infelizmente, embora uma molécula linear XH₂ seja estruturalmente simples, a tabela de caracteres D_h não o é.

Portanto, este é um primeiro exemplo ruim do uso da teoria de grupos na análise dos orbitais.

Podemos fazer uma analogia entre as

simetrias dos orbitais em XH₂ linear e

daqueles em moléculas diatômicas

(também D_h )

No diagrama de OM ao lado são dadas as

simetrias dos orbitais no átomo X e dos orbitais de grupo ligantes.

Compare os símbolos de simetria abaixo com os das figuras ao lado.

A construção do diagrama OM abaixo é feita permitindo-se as interações (ligantes ou

Uma molécula triatômica angular - H

O

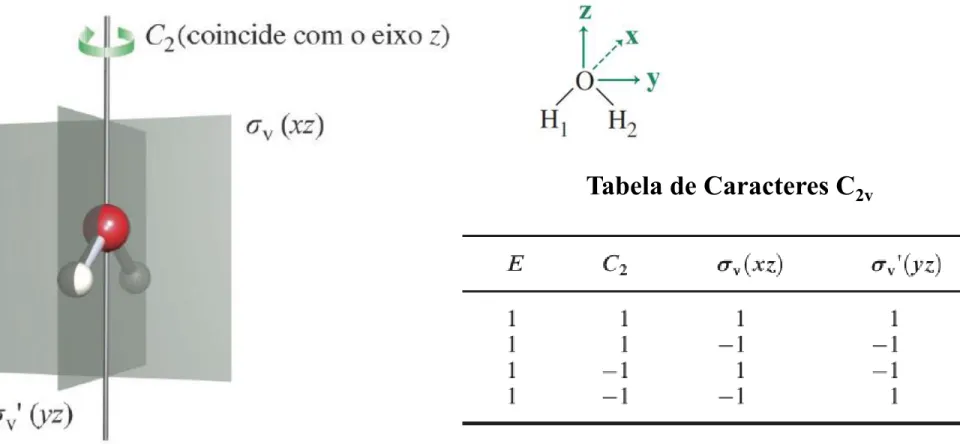
A molécula de H₂O tem simetria C_2v

Vamos usar essa informação para desenvolver um esquema OM para a ligação na H₂O.

Tabela de Caracteres C_2v

Os símbolos na primeira coluna (abaixo do símbolo do grupo de pontos) indicam os tipos de simetria dos orbitais que são permitidos para o grupo de pontos especificado.

Os números na coluna encabeçada por E (o operador identidade) indicam a degenerescência de cada tipo de orbital.

No grupo de pontos C_2v todos os orbitais têm degenerescência igual a 1 (não são degenerados).

Os símbolos na primeira coluna (abaixo do símbolo do grupo de pontos) indicam os tipos de simetria dos orbitais que são permitidos para o grupo de pontos especificado.

Os números na coluna encabeçada por E (o operador identidade) indicam a degenerescência de cada tipo de orbital.

No grupo de pontos C_2v todos os orbitais têm degenerescência igual a 1 (não são degenerados).

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Os símbolos na primeira coluna (abaixo do símbolo do grupo de pontos) indicam os tipos de simetria dos orbitais que são permitidos para o grupo de pontos especificado.

Os números na coluna encabeçada por E (o operador identidade) indicam a degenerescência de cada tipo de orbital.

No grupo de pontos C_2v todos os orbitais têm degenerescência igual a 1 (não são degenerados).

Cada linha de números que se segue ao símbolo de simetria indica como um determinado orbital se comporta sob cada operação de simetria.

Um número 1 significa que o orbital não se altera pela operação, um -1 indica que o orbital troca de sinal e um zero significa que o orbital muda de outra maneira

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Cada linha de números que se segue ao símbolo de simetria indica como um determinado orbital se comporta sob cada operação de simetria.

Um número 1 significa que o orbital não se altera pela operação,

Um número -1 indica que o orbital troca de sinal e um zero significa que o orbital muda de outra maneira

Operador E deixa o orbital atômico 2s inalterado.

Rotação em torno do eixo C₂ deixa 2s inalterado.

Reflexões através dos plano _v (xz) e _v (yz) deixam 2s inalterado.

Esses resultados correspondem à seguinte linha de caracteres

orbital atômico

2s do oxigênio

e ela coincide com o tipo de simetria A₁ na tabela de caracteres de C_2v

Assim identificamos o orbital atômico 2s no átomo de oxigênio na água como um orbital a₁

São usadas letras minúsculas para o símbolo do orbital, letras maiúsculas para o tipo de simetria na tabela de caracteres.

Operador E e a reflexão através do plano _v (xz) deixam o orbital atômico 2p_x inalterado.

Rotação em torno do eixo C₂ e reflexão através do plano _v (yz) invertem a fase de 2p_x.

Esses resultados correspondem à seguinte linha de caracteres

Esta linha coincide com o tipo de simetria B₁ na tabela de caracteres de C_2v

Portanto o orbital atômico 2p_x no átomo de oxigênio possui simetria b₁

Orbital p

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Operador E e a reflexão através do do plano _v (yz) deixam o orbital atômico 2p_y inalterado.

Rotação em torno do eixo C₂ e reflexão através do plano _v (xz)

invertem a fase de 2p_y.

Esses resultados correspondem à seguinte linha de caracteres

Esta linha coincide com o tipo de simetria B₂ na tabela de caracteres de C_2v

Portanto o orbital atômico 2p_y no átomo de oxigênio possui simetria b₂

Operador E deixa o orbital atômico 2p_z inalterado.

Rotação em torno do eixo C₂ deixa 2p_z inalterado.

Reflexões através dos plano _v (xz) e _v (yz) deixam 2p_z inalterado.

Esses resultados correspondem à seguinte linha de caracteres

Da mesma forma que para 2s, esta linha coincide com o tipo de simetria A₁ na tabela de caracteres de C_2v

Assim identificamos o orbital atômico 2p_z no átomo de oxigênio na água como um orbital a₁

São usadas letras minúsculas para o símbolo do orbital, mas letras maiúsculas para o tipo de simetria na tabela de caracteres.

Natureza dos OGL (Orbitais de Grupo Ligantes) H---H

A etapa seguinte é definir a

natureza dos orbitais de

grupo ligantes H---H que são

permitidos dentro do grupo de pontos C_2v

Como iniciamos com dois

orbitais 1s do H, só podem ser construídos dois OGL.

As simetrias desses OGL são deduzidas como segue.

Vamos ver o que ocorre com

cada um dos dois orbitais 1s do H quando é realizada cada operação de simetria.

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Ambos os orbitais 1s são deixados inalterados por

E e pela reflexão através do plano _v (yz)

Mas ambos são afetados pela rotação em torno do eixo C₂ e pela reflexão

através do plano _v (xz).

Essas informações são resumidas na seguinte linha de caracteres:

"2" mostra que “2 orbitais ficam inalterados pela operação" “0" significa que "nenhum orbital é inalterado pela operação".

Ambos os orbitais 1s são deixados inalterados por

E e pela reflexão através do plano _v (yz)

Mas ambos são afetados pela rotação em torno do eixo C₂ e pela reflexão

através do plano _v (xz).

Essas informações são resumidas na seguinte linha de caracteres:

Em seguida, observamos dois fatos:

(i) podemos construir apenas dois OGL

(ii) a simetria de cada OGL deve

corresponder a um dos tipos de simetria na tabela de caracteres.

Agora, comparamos a linha de caracteres vista anteriormente com os somatórios de duas linhas de caracteres na tabela de caracteres de C_2v

É encontrada uma combinação com o somatório dos caracteres para as representações A₁ e B₂.

Assim podemos deduzir que os dois OGL possuem simetrias a₁ e b₂, respectivamente.

OM a₁ de menor E OM a₁ de maior E

OM b₂ OM b₁

Nesse caso, é relativamente simples usar os símbolos de simetria a₁ e b₂ para esquematizar os OGL mostrados

O orbital a₁ corresponde a uma combinação em fase de orbitais 1s do H, enquanto o orbital b₂ é a combinação fora de fase de orbitais l s do H.

No entanto, uma vez conhecidas suas simetrias, o método rigoroso de determinar a natureza dos orbitais é o que segue

Agora, olhamos o efeito que cada operação de simetria do grupo de pontos C_2v tem sobre ₁.

O operador E e a reflexão através do plano _v (yz) deixam ₁ inalterado

Mas uma rotação de C₂ e uma reflexão através do plano _v(xz)

transformam, cada uma delas, ₁ em ₂

Os resultados são anotados na forma de uma linha de caracteres:



_

Representemos os orbitais 1s dos dois átomos de H como ₁ e ₂.

Para determinar a composição do OGL a₁ do fragmento H---H na H₂O, multiplicamos cada caractere da linha vista anteriormente pelo caractere correspondente para a

representação A₁ na tabela de caracteres de C_2v isto é,

O resultado da multiplicação dá a função de onda não normalizada para o orbital a₁

Isso pode ser simplificado dividindo-se por 2 e, após a normalização tem-se a equação final para a função de onda

combinação em fase

De modo semelhante, pelo uso da representação B₂ na tabela de caracteres de C_2v

podemos escrever a equação não normalizada

combinação fora de fase

e em seguida sua versão normalizada

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

OM a₁ de menor E OM a₁ de maior E

OM b₂ OM b₁

Como construir o diagrama abaixo via simetria?

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Cada um dos orbitais 2s e 2p_z,

do átomo de oxigênio possui a

simetria correta (a₁) para interagir com o orbital a₁ do fragmento H---H.

Essas interações de orbitais devem levar a três OM: dois OM ligantes com simetria a₁

e um OM antiligante (a₁)

Em termos de simetria, o OM

a₁ de menor E também

poderia incluir o caráter 2p_z,

mas o caráter 2s domina por causa da separação de E entre os orbitais atômicos 2s e 2p_z

Como construir o diagrama abaixo via simetria?

_H

A interação entre o orbital atômico 2p_y e o OGL com

simetria b₂ leva a dois OM que possuem caráter ligante e

antiligante H-O-H, respectivamente.

O orbital 2p_x do oxigênio tem

simetria b₁ e não há nenhuma

combinação de simetria com um OGL.

Dessa forma, o orbital 2p_x do oxigênio é não ligante na H₂O.

Como construir o diagrama abaixo via simetria?

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Os oito elétrons de valência na

H₂O ocupam os OM de acordo

com o princípio de aufbau

Formam-se dois OM ligantes

H-O-H ocupados e outros dois

(também OM ocupados) com caráter principalmente de oxigênio.

Como construir o diagrama abaixo via simetria?

_H

2

O

Teoria do OM aplicada às moléculas poliatômicas BH₃, NH₃ e CH₄



_

v



C

NH

Consideremos as ligações no BH₃ e no NH₃.

Em ambas as moléculas envolvem interações , mas enquanto o BH₃ tem simetria D_3h, o NH₃ pertence ao grupo de pontos C_3v.









C

, S

C

_C

2

C

BH

A existência do BH₃ em fase gasosa foi estabelecida ainda que a molécula

dimerize facilmente para B₂H₆

BH₃ pertence ao grupo de pontos D_3h

Considerando as interações de orbitais

entre os orbitais atômicos do átomo de B

e os OGL de um fragmento H₃

apropriado, podemos estabelecer um

esquema de ligação molecular.

BH









C

, S

C

_C

2

C

Começamos escolhendo um conjunto apropriado de eixos.

O eixo z coincide com o eixo C₃ do BH₃, e todos os átomos localizam-se no plano xy.

BH









C

_C

2

C

-o orbital 2s tem simetria a₁

-o orbital 2p_z tem simetria a₂

-os orbitais 2p_x, e 2p_y são degenerados e o conjunto de orbitais tem simetria e

Apóstrofos únicos são simétricos para _h e

apóstrofos duplos são assimétricos quando é necessária uma distinção entre representações (C_3h, C_5h, D_3h, D_5h).

Consideramos a natureza dos três OGL que são formados a partir de combinações lineares dos três orbitais 1s do H.

Por referência ao fragmento H, no BH₃, calculamos quantos orbitais 1s do H são deixados inalterados por operação de simetria no grupo de pontos D_3h

O resultado é representado pela seguinte linha de caracteres:

3 = 3 orbitais ficam inalterados pela operação

1 = 1 orbital ficou inalterado pela operação

0 = nenhum orbital é inalterado pela operação

Essa mesma linha de caracteres pode ser obtida pelo somatório das linhas de

caracteres para as representações A₁' e

E' na tabela de caracteres de D_3h

Assim, os três OGL têm simetrias a₁' ou e'

Identificador e designa um conjunto de orbitais duplamente degenerados.

Agora temos que determinar a função de onda para cada OGL.

Sejam os três orbitais 1s do H no fragmento H₃ do BH₃: ₁ ₂ ₃

₃ ₂

₁









C

_C

2

C

Devemos avaliar como ₁ é afetado por cada

operação de simetria do grupo de pontos D_3h

A operação C₃ transforma ₁ em ₂

C₃2 _transforma 

1 em 3

As três operações C₂

-deixam ₁ inalterado

-transformam ₁ em ₂

-transformam ₁ em ₃

OGL (1)

_BH

Devemos avaliar como ₁ é afetado por cada

operação de simetria do grupo de pontos D_3h

A operação C₃ transforma ₁ em ₂

C₃2 _transforma 

1 em 3

As três operações C₂

-deixam ₁ inalterado

-transformam ₁ em ₂

-transformam ₁ em ₃

A linha de caracteres a seguir fornece o resultado completo:

continua em OGL (1)









C

_C

2

C

OGL (1)

_BH

A função de onda não normalizada para o OGL (1) é determinada multiplicando-se

cada caractere na linha vista anteriormente pelo caractere correspondente para a representação A₁' na tabela de caracteres de D_3h

BH

A função de onda não normalizada para o OGL (1) é determinada multiplicando-se cada caractere na linha vista anteriormente pelo caractere correspondente para a representação A₁' na tabela de caracteres de D_3h

Após simplificação (dividindo por 4) e normalização, a função de onda pode ser escrita como abaixo.

BH

D_3h

E

Esta função e pode ser descrita esquematicamente como uma

combinação em fase de orbitais

1s apresentada como o OGL(1)

BH

E

BH

https://chem.libretexts.org/Textbook_Maps/Inorganic_Chemistry_Textbook_Maps/Map%3A_Inorganic_Chemistry_(Housecroft)/05%3A_Bonding_in_polyatomic_mol ecules/5.5%3A_MO_Theory_Applied_to_Polyatomic_Molecules_%5C(BH_3%5C)%2C_%5C(NH_3%5C)%2C_and_%5C(CH_4%5C)/5.5A%3A_%5C(BH_3%5C)

How to determine the shapes of the LGO_S?

-LGO's symmetry labels are a₁' + e'. There are 3 LGOs that can be made out of these symmetry labels - One LGO is from a₁' and two LGOs are from e' due to doubly degenerate. In order to determine the shape of each LGO, we would use the wavefunctions.

-Three H in BH₃ are assigned with Ψ₁, Ψ₂, Ψ₃. Now lets look at how each Ψ is affected by the symmetry operations of the D_3h and their results are completed in the following table:

LGO(1)

₃ ₂

₁

OGL (2)

Vamos usar um procedimento semelhante para deduzir que a

equação ao lado

descreve a

função de onda normalizada para um dos orbitais e' degenerados.

De modo

esquemático, isto é representado como o OGL(2)

Este orbital

contém um plano nodal.

BH

Vê-se que as operações do grupo de pontos

D_3h transformam ₁ da seguinte maneira:

Deduzindo a função de onda para os orbitais e_´

A função de onda não

normalizada para o OGL(2) é determinada multiplicando-se

cada caractere na linha obtida acima pelo caractere

correspondente para a

representação E' na tabela de caracteres de D_3h

₃ ₂

₁

OGL (2)

(e) = 2₁ - 1₂ - 1₃ + 0₁ + 0₃ + 0₂ + 2₁ - ₂ - ₃ + 0₁ + 0₃ + 0₂

(e) = 4₁ - 2₂ - 2₃

(e) = 2(2₁ - ₂ - ₃)

Simplificando (divide-se por 2)

Normalizando

(e) = (21 ₁ - ₂ - ₃)

√6

Multiplicando pela linha correspondente

E´ obtém-se...

OGL (2)

BH

https://chem.libretexts.org/Textbook_Maps/Inorganic_Chemistry_Textbook_Maps/Map%3A_Inorganic_Chemistry_(Housecroft)/05%3A_Bonding_in_polyatomic_mol ecules/5.5%3A_MO_Theory_Applied_to_Polyatomic_Molecules_%5C(BH_3%5C)%2C_%5C(NH_3%5C)%2C_and_%5C(CH_4%5C)/5.5A%3A_%5C(BH_3%5C)

LGO (2)

Cada orbital e' deve conter um plano nodal, e os planos nos dois orbitais são ortogonais um ao outro.

De modo similar, podemos escrever a equação abaixo para descrever o segundo

orbital e‘

O plano nodal passa pelo átomo H(1) e o orbital 1s desse átomo não faz nenhuma contribuição para o OGL.

Isso está representado como o OGL(3)

OGL (3)

BH

-Noticed that in the LGO2, we have 1 nodal plane which is the horizontal line between the positive charge and negative charge.

-Therefore, the LGO3 (doubly degenerate with e') would also 1 nodal plane and its wavefunction would be Ψ(e') = 1/√2 (Ψ2-Ψ3). The shape of the LGO3 is

https://chem.libretexts.org/Textbook_Maps/Inorganic_Chemistry_Textbook_Maps/Map%3A_Inorganic_Chemistry_(Housecroft)/05%3A_Bonding_in_polyatomic_mol ecules/5.5%3A_MO_Theory_Applied_to_Polyatomic_Molecules_%5C(BH_3%5C)%2C_%5C(NH_3%5C)%2C_and_%5C(CH_4%5C)/5.5A%3A_%5C(BH_3%5C)

LGO (3)

OGL (3)

OGL (2)

O orbital 2p_z, no átomo de B tem simetria a₂"

e não se pode encontrar qualquer

combinação de simetria com um OGL do fragmento H₃

Assim, o orbital 2p_z, é não ligante no BH₃.

A abordagem OM descreve a ligação no BH₃

em termos de três OM de simetrias a₁' e e'.

O orbital a₁' possui caráter ligante  e está

delocalizado sobre todos os quatro átomos.

Os orbitais e' também exibem caráter delocalizado, e a ligação no BH₃ é descrita

considerando-se uma combinação de todos os três OM ligantes.

O diagrama OM para o BH₃, pode agora ser construído

permitindo-se que os orbitais de mesma simetria interajam. _

3

₂

BH

A molécula de NH₃ tem simetria C_3v e pode ser derivado um esquema de ligação considerando-se a interação entre os OA do átomo de N e os OGL de um fragmento H₃ apropriado.

Um conjunto apropriado de eixos tem o eixo z coincidente com o eixo C₃ do NH₃

Os eixos x e y são direcionados conforme mostrado

ao lado

_

v





C

NH

NH

NH

Olhando-se como cada operação de simetria afeta cada orbital do átomo de N do NH₃, as simetrias dos orbitais são identificadas da seguinte maneira:

-cada um dos orbitais 2s e 2p_z tem simetria a₁; -os orbitais 2p_x e 2p_y são degenerados e o conjunto de orbitais tem simetria e.



_

v



C

NH

Para determinar a natureza dos orbitais de grupo ligantes, consideramos quantos orbitais 1s do H são deixados inalterados por cada operação de simetria no grupo C_3v.

O resultado é representado pela linha de caracteres:



_

v



C

NH

NH

Os três OGL têm simetrias a₁ e e.

Embora os símbolos de simetria dos OGL dos fragmentos H₃ no NH₃ e BH₃ difiram (as moléculas pertencem a diferentes grupos de pontos), as funções de onda

Os três OGL têm simetrias a₁ e e.

Embora os símbolos de simetria dos OGL dos fragmentos H₃ no NH₃ e BH₃ difiram (as moléculas pertencem a diferentes grupos de pontos), as funções de onda

ERRO: invertidos aqui na 2ª Ed. do Inorg. Chem, C. Housecroft

Os três OGL têm simetrias a₁ e e.

Embora os símbolos de simetria dos OGL dos fragmentos H₃ no NH₃ e BH₃ difiram (as moléculas pertencem a diferentes grupos de pontos), as funções de onda

normalizadas para os OGL são as mesmas.

Um dos OM e

HOMO (a₁)

OM a₁ de E mais baixa

OM gerados com Spartan 04©Wavefunction Inc. 2003

NH

O diagrama OM é qualitativo

e construído permitindo-se

interações entre orbitais com as mesmas simetrias.

Como os orbitais 2s e 2p_z do nitrogênio têm simetria a₁ eles podem interagir com o OGL a₁, formando três OM a₁.

Em termos de simetria, o OM

a₁ de mais baixa E também poderia conter o caráter 2pz

do N, mas a separação de E dos OA 2s e 2p é tal que o caráter 2s predomina. Isto é

análogo ao caso para a H₂O

descrito anteriormente.

NH

NH

Após construir o

diagrama OM, os oito elétrons de valência são colocados nos OM em conformidade com o

princípio de aufbau.

Os caracteres de três dos orbitais ocupados são

mostrados no lado direito.

O orbital (a₁) de mais baixa E tem caráter

ligante N- H

deslocalizado.

O OM de mais alta E

ocupado (HOMO) tem

algum caráter ligante N- H, mas retém um lóbulo de orbital apontando

A molécula de CH₄ tem simetria T_d

A relação entre um tetraedro e um cubo é vista

formalmente pelo fato de o grupo de pontos Td pertencer a uma família de grupo de pontos cúbico.

Tal família inclui os grupos de pontos T_d e O_h.

A tabela mostra parte da tabela de caracteres de T_d.

Os eixos C₃ no CH₄ coincidem com as ligações C-H e os eixos C₂ e S₄ coincidem com os eixos x, y e z definidos ao lado.

CH

Segundo a simetria T_d , os orbitais do átomo de C do CH₄ são classificados como segue:

-o orbital 2s tem simetria a₁

-os orbitais 2p_x, 2p_y e 2_p, são degenerados e o conjunto de orbitais tem simetria t₂.

Para construir os OGL do fragmento H₄ no CH₄ , começamos calculando o

número de orbitais ls do H deixados inalterados por cada operação de simetria do grupo de pontos .

O resultado é resumido na linha de caracteres:

2 = duas ligações inalteradas

0 = sem ligações inalteradas (todas se alteraram)

Para GLO =em C_2v vimos

Resulta esta mesma linha de caracteres quando é feito o somatório das linhas de caracteres para as representações A₁ e T₂ na tabela de caracteres de T_d.

Portanto, os quatro orbitais de grupo ligantes têm simetrias a₁ e t₂; o símbolo t

designa um conjunto triplamente degenerado de orbitais.

As funções de onda normalizadas para esses OGL são dadas abaixo

OA 2s, 2p_x 2p_ye 2p_z do C

4 OA 1s do H

OA 2s, 2p_x 2p_ye 2p_z do C

4 OA 1s do H

combinam-se gerando 4 OGL

Por comparação as simetrias dos OA 2s, 2p_x, 2p_y e 2p_z do C podem ser combinadas facilmente com as simetrias dos 4 OGL do H

T_d

OM ligantes triplamente degenerados (t₂)

OM ligante (a₁)

T_d

OM ligantes triplamente degenerados (t₂)

OM ligante (a₁)

BH₃

CH₄

NH₃

Uma comparação dos modelos de ligação OM e LV

Teoria da Ligação de Valência: para descrever a ligação usa esquemas de hibridização adequados de forma que as ligações conhecidas como

estruturalmente equivalentes fiquem equivalentes no esquema de ligação. Portanto, pela TLV todas as ligações são equivalentes

Um orbital híbrido contribui para cada ligação X-H localizada (X = B, C ou N).

BH₃

CH₄

NH₃

Teoria do Orbital Molecular indica que o caráter ligante é delocalizado.

Além disso, existem no BH₃, NH₃ e no CH₄ dois tipos

diferentes de OM ligante: um OM único envolvendo o orbital atômico 2s do átomo central, e um conjunto

degenerado de dois (no BH₃ e NH₃) ou três (no CH₄) OM envolvendo os orbitais 2p do átomo central.

Como as ligações podem ser idênticas (mostrado por RMN 1_{H, IV ?}

BH₃

CH₄

NH₃

A evidência para esses ordenamentos dos OM vem da

espectroscopia de fotoelétrons

Como os resultados da teoria OM podem responder pela equivalência experimentalmente observada das ligações

X- H em uma dada molécula?

Vamos usar o CH₄ para explicar...

Uma comparação dos modelos de ligação OM e LV

CH₄

Espectro fotoeletrônico do CH₄

Brundle, C.R.; Robin, M.B.

J. Chem. Phys. 1970 , 53, 2196.

a₁

t₂

Na teoria OM, a ligação em uma molécula é

descrita pela combinação dos caracteres de todos

os OM ocupados que têm caráter ligante.

O orbital a₁ é esfericamente simétrico e oferece igual caráter ligante em todas as quatro interações C-H.

Os orbitais t₂ devem ser considerados um conjunto e não orbitais individuais.

Tomados juntos, esse conjunto de orbitais oferece uma imagem de quatro interações ligantes C- H equivalentes e, portanto, o quadro global é de equivalência de ligação C-H.

March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, 7th Edition (2013), Localized Chemical Bonding, Photoelectron Spectroscopy, em

CH₄

a₁

t₂

Na teoria OM, a ligação em uma molécula é

descrita pela combinação dos caracteres de todos os OM ocupados que têm caráter ligante.

O orbital a₁ é esfericamente simétrico e oferece igual caráter ligante em todas as quatro interações C-H.

Os orbitais t₂ devem ser considerados um conjunto e não orbitais individuais.

Tomados juntos, esse conjunto de orbitais oferece uma imagem de quatro interações ligantes C- H equivalentes e, portanto, o quadro global é de equivalência de ligação C-H.

(

t

)

(

a

)

a₁

CH₄

a₁

t₂

O espectro fotoelétrico de CH₄ mostra duas bandas (20-23 eV e 14 eV), e não a única banda esperada da equivalência das quatro ligações C-H.

Na verdade o espectro fotoeletrônico e a TOM apenas sugerem que o C usa os orbitais disponíveis para formar quatro ligações e os elétrons nas

ligações são distribuídos entre o carbono e os quatro átomos envolvidos nas ligações

(

t

)

(

a

)

Teoria do orbital molecular: as análises das ligações logo se tornam complicadas

Embora o BF₃ seja uma molécula bastante simples, a discussão a seguir

demonstra a complexidade do tratamento quando a base de OA de cada átomo contém orbitais s e p.

A molécula de BF₃ tem simetria D_3h

O eixo z é definido para coincidir com o eixo C₃ e a molécula localiza-se no plano xy

Assim como no BH₃, aos OA do B no BF₃ são atribuídas as seguintes simetrias:

BF

complexidade quando comparado ao BH₃

-orbital 2s tem simetria a₁'

-o orbital 2p_z tem simetria a₂"

-os orbitais 2p_x e 2p_y são degenerados com simetria e'

Acima estão as representações dos OGL para um fragmento D_3h de F₃ cuja geometria é análoga à do BF₃.

Triângulo de F₃ localiza-se no plano xy.

OGL(5), OGL(8) e OGL(9) contêm contribuições dos OA 2p_z dirigidos perpendicularmente ao triângulo de F₃.

Os tamanhos relativos dos lóbulos de cada representam as contribuições relativas dos OA de cada F aos respectivos OGL. _{C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.}

OGL envolvendo os orbitais 2s do F no BF₃ e que têm simetrias a₁ e e' podem ser derivados da mesma maneira que para o fragmento H₃ no BH₃.

Eles são mostrados como OGL(1)-OGL(3)

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Os orbitais p nos átomos de F podem ser divididos em dois tipos: os que se localizam no plano da molécula (2p_x e 2p_y) e os perpendiculares ao plano (2p_z).

Os OGL podem ser formados de combinações de orbitais 2p_z e de combinações dos

orbitais 2p no plano.

Em primeiro lugar, vamos considerar os orbitais 2p_z.

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

O procedimento para derivar as funções de onda que descrevem os OGL permitidos dentro do grupo de pontos D_3h é o mesmo que utilizamos antes, mas há uma

importante diferença:

Quando consideramos como um orbital 2p_z é alterado por uma operação de

simetria, temos que procurar não apenas pelo orbital sendo transformado para outra posição, mas também por uma mudança da fase.

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

Se um orbital p_z, é

perpendicular a um

plano _h, a reflexão

através do plano mudará sua fase, mas sua

posição permanecerá a

mesma.



p

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

BF

Isto é exemplificado quando calculamos

quantos orbitais 2p_z do F ficam inalterados por cada operação de

simetria no grupo de pontos D_3h.

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

BF



A linha de caracteres vista a seguir resume o resultado.

Um sinal negativo significa que o orbital está na mesma posição, mas sua fase mudou.



p

C₃ 3 = 3 orbitais ficam inalterados pela operação

1 = 1 orbital ficou inalterado pela operação

1 = 1 orbital ficou inalterado pela operação, mas mudou o sinal 0 = nenhum orbital é inalterado pela operação (todos se alteram)

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

3 - 3 orbitais ficam inalterados pela operação 1 - 1 orbital ficou inalterado pela operação

-1 - 1 orbital ficou inalterado pela operação, mas mudou o sinal 0 - nenhum orbital é inalterado pela operação (todos se alteram)

 0 - uma entrada diferente de zero somente se o orbital(is) não muda(m) de posição. 0 - qualquer orbital que mude de posição durante a operação de simetria

1 - qualquer orbital que permaneça na posição original (como um orbital p que mantém sua

G. Miesler, P. Fischer, D. Tarr, Química Inorgânica, 5ª Ed.

C. Housecroft e A. G. Sharpe, Quimica Inorgâanica, 4ª Ed.

posição e direção (sinais de seus lóbulos)

-1 - qualquer orbital que permaneça na posição original com os sinais de seus lóbulos invertidos

Esta linha de caracteres também é produzida pela soma das linhas de caracteres para as representações A₂" e E" na tabela de caracteres de D_3h

Portanto, os OGL são de simetrias a₂" e e".

Considerando os efeitos de cada operação em um dos orbitais 2px_z, do F no fragmento F₃, podemos (como anteriormente) chegar a uma equação da função de onda não

normalizada de cada OGL.

Considere que os três orbitais 2p_z do F sejam ₁ ₂ ₃ e geramos a seguinte linha de caracteres

Considere que os três orbitais 2p, do F sejam







de fase orbital

p

C₃



_

3











A multiplicação de cada caractere dessa linha pelo caractere correspondente na linha para a representação A₂" na tabela de caracteres de D_3h dá a forma não normalizada da função de onda para o OGL a₂"

A simplificação e a normalização fornecem a equação:

Assim, o OGL a₂" pode ser descrito como uma

combinação em fase de orbitais 2p_z, e é

mostrado na forma do OGL(5).

De modo semelhante, podem ser deduzidas as equações para os orbitais e

OGL(8)

BF

Pode ser utilizado o mesmo procedimento para derivar o fato de os orbitais 2p do F no

plano se combinarem dando OGL(4) e OGL(10) com simetrias a₁ e a₂ respectivamente...

...e dois conjuntos de OGL e, indicados como OGL(6), OGL(7) e OGL(11) e OGL (12).

D_3h

Agora estamos em posição de

construir um diagrama OM

qualitativo para descrever a ligação no BF₃.

As simetrias dos orbitais do B

pertencentes ao grupo D_3h são dadas do lado esquerdo da figura e as dos

OGL foram7 são mostradas

anteriormente.

O problema é considerado em três etapas:

• procure interações de orbitais que deem origem a OM 

• procure interações de orbitais que deem origem a orbitais 

• procure qualquer orbital que tenha uma simetria que impede interações

de orbitais entre fragmentos.

A ligação  no BF₃ surge das

interações que envolvem os orbitais a₁' e e' do fragmento.

Existem dois OGL do fragmento F₃

com simetria a₁ e três conjuntos

de orbitais e'.

A extensão da mistura entre orbitais

do fragmento de mesma simetria

depende das suas energias relativas, e é impossível prever com qualquer grau de confiabilidade.

D_3h

BH

BF

BH

BF

Podemos supor uma imagem da ligação  que imita a do BH₃.

O OM do BH₃ (direita) envolve o OGL(1) na formação dos OM a₁' e a₁'* simbolizados na

figura da direita (BF₃), mas deixa o OGL(4) como um orbital não ligante.

Esse modelo pode ser refinado permitindo-se de que parte do caráter do OGL(4) seja misturado nos OM a₁' e a₁'* com caráter ligante ou antiligante B- F.

BH

BF

De modo semelhante, poderíamos permitir que

contribuições vindas dos OM e' do fragmento

contendo caráter 2p_x e 2p_y do F se misturassem nos

OM e' e e'* com caráter ligante ou antiligante B- F.

No mais simples dos quadros de ligação, esses OM contêm caráter 2s do F, e os OGL (6), (7), (11) e (12)

BH

BF

Avaliar a extensão da mistura de orbitais é difícil, se não impossível, em um nível qualitativo.

BH

BF

A simetria a₂" do orbital 2p_z do B combina-se com a do

BH

BF

Os únicos orbitais no fragmento F₃ para os quais não há nenhuma combinação de simetria no

átomo de B são aqueles com simetrias e" e a₂'

(ou seja, OGL 8, 9 e 10).

OM a₁

OM a₂

OM e D_3h

Segue acima a imagem global de ligação para o BF₃

Há quatro OM ligantes, quatro OM antiligantes e oito OM não ligantes.

OM a₁

OM a₂

OM e D_3h

Trata-se de uma imagem simples da ligação que não permite mistura de orbitais.

No entanto, ela oferece uma descrição que inclui o caráter  parcial em cada ligação B-F, sendo, portanto, consistente com o tratamento LV

OA 2p ocupado no F

D_3h

Trata-se de uma imagem simples da ligação que não permite mistura de orbitais.

No entanto, ela oferece uma descrição que inclui o caráter  parcial em cada ligação B-F, sendo, portanto, consistente com o tratamento LV

OA 2p ocupado no F

Teoria do orbital molecular: aprendendo a usar a teoria objetivamente

Vamos mostrar maneiras objetivas de utilizar o modelo OM para explicar aspectos particulares a respeito de

uma molécula.

Isto frequentemente envolve o desenho de um diagrama OM parcial para a molécula em questão.

Temos que considerar as implicações desse tratamento parcial: pode ser perigoso porque os aspectos de ligação, a não ser aqueles sobre os quais se está concentrado, são

ignorados.

Ligação



no CO

Para desenvolver uma descrição OM da ligação  no CO₂ temos que considerar que orbitais de valência não podem ser usados após a ligação .

A molécula de CO₂ pertence ao grupo de pontos D_h.

O eixo z é definido para coincidir com o eixo C_.

eixo z

Ligação



no CO

Pode ser desenvolvida uma imagem semelhante a

molécula XH₂ para a ligação 

no CO₂,

A diferença é que os orbitais 1s do H

em XH₂ são substituídos pelos orbitais

2s e 2p_z do O no CO₂.

A sobreposição deles com os orbitais

2s e 2p_z, do C leva à formação de seis OM com simetria _g ou _u, quatro ocupados e dois desocupados.

Ligação



no CO

Uma combinação em fase de orbitais 2p é não centrossimétrica e tem simetria _u ,

enquanto uma combinação fora de fase é centrossimétrica e tem simetria _g.

Somente os OGL _u têm a simetria correta para interagir com os orbitais 2p_x e 2p_y do C, deixando os OGL _g como OM não ligantes no CO₂.

Após a formação de interações  C O, os

orbitais restantes são os orbitais 2p_x e 2p_y

do C e do O.

Agora usamos a abordagem

dos OGL para descrever a

ligação  em termos das

interações entre os orbitais

2p_x e 2p_y do C e os OGL

(derivados dos orbitais 2p_x e

2p_y do O) de um fragmento

O----O.

Ligação



no CO

Após preencher os OM ligantes  de mais baixa E, há oito elétrons

restantes que ocupam os OM _u e  _g.

Para cada conjunto degenerado de OM, o caráter do segundo OM _u é o mesmo que o primeiro, mas é ortogonal em relação a ele.

Cada OM _u tem caráter de ligação  O- C-O delocalizada, e o resultado líquido de ter ambos os orbitais _u ocupados é uma ordem de ligação _u de 1 por interação CO.

[NO₃]

Pela Teoria de Ligação de Valência (TLV) são necessárias três estruturas

de ressonância para levar em conta a equivalência das ligações N-O

A ordem de ligação líquida por ligação N-O é 1,33.

A teoria do OM nos permite

representar o sistema  N-O em termos de interações delocalizadas.

Interação ligante  NO

Orbital híbrido sp2 _no

[NO₃]

Tem simetria D_3h e o eixo z é definido para coincidir com o eixo C₃.

Os orbitais de valência de cada átomo de N e O são orbitais 2s e 2p.

A ligação  pode ser descrita em termos das interações do orbital 2p_z do N com os OGL apropriados do fragmento O₃

Interação ligante  NO

Orbital híbrido sp2 _no

[NO

]

No grupo pontual D_3h o orbital 2p_z do N tem uma simetria a₂“

Os OGL que podem ser construídos a partir dos

orbitais 2p_z do O são mostrados ao lado juntamente com suas simetrias

O método de derivação é

idêntico àquele para os

OGL correspondentes

para o fragmento F₃ no BF₃

D_3h

x y

[NO

]

O diagrama parcial de

OM pode ser construído por coincidência de

simetrias dos orbitais.

Os OM resultantes têm caráter ligante  (a₂"), não ligante (e") e anti-ligante  (a₂"*)

OM a₂"*

OM a₂" mostrando a deslocalização do caráter 