O número de ouro e a proporção áurea: harmonia e beleza na matemática da vida / The gold number and golden ratio: harmony and beauty in the mathematics of life

(1)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761

O número de ouro e a proporção áurea: harmonia e beleza na matemática

da vida

The gold number and golden ratio: harmony and beauty in the

mathematics of life

DOI:10.34117/bjdv6n5-517

Recebimento dos originais: 29/04/2020 Aceitação para publicação: 26/05/2020

Deborah Alves Horta

Me. em Pesquisa Operacional e Inteligência computacional pela UCAM Campos Licencianda em Matemática - IF Fluminense campus Campos Centro Instituição: Instituto Federal Fluminense (IFF) campus Campos Centro Endereço: Rua Dr. Siqueira, 273 - Parque Dom Bosco, Campos dos Goytacazes, RJ

E-mail: dhorta@iff.edu.br

Thiago Fragoso Gonçalves

Licenciado em Matemática

Instituição: Instituto Federal Fluminense (IFF) campus Campos Centro Endereço: Rua Dr. Siqueira, 273 - Parque Dom Bosco, Campos dos Goytacazes, RJ

E-mail: thiagobarramares@gmail.com

Igor Cardoso de Abreu

Licenciado em Matemática

E-mail: igorabreu10@gmail.com

Bruna Beraldo de Souza

Licencianda em Matemática

E-mail: brunabsouzamatiff@gmail.com

RESUMO

O foco do estudo é o número phi (ϕ), também conhecido como número de ouro ou número áureo e tem por finalidade mostrar a presença da matemática, especialmente do número de ouro ou da razão áurea, em nossas vidas. Estudiosos e matemáticos afirmam que este “misterioso número”, adotado como símbolo da harmonia e perfeição, está presente em diferentes áreas da vida humana, tais como arquitetura, artes, e biologia. Na matemática este número está relacionado a figuras geométricas como triângulos, retângulos, pentágonos e decágonos. É possível, ainda, estabelecer uma relação com a sequência de Fibonacci. Partindo da origem do nome, seguindo com a demonstração de seu desenvolvimento matemático e representação geométrica, chegaremos à constatação de sua aplicação nas diversas áreas da vida humana. Vale destacar que o estudo da presença do número de ouro em nosso cotidiano pode ser muito útil em sala de aula, já que pode ajudar a despertar o interesse dos alunos para a importância e presença da matemática em nossas vidas. A pesquisa mostrou que o número de ouro está presente nas relações de proporção em obras de arte, nas dimensões do corpo de certos peixes

(2)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 e em algumas obras arquitetônicas, por exemplo. Os resultados mostram, ainda, que por volta de 1500, Leonardo da Vinci descobriu que o corpo humano obedece à proporção áurea e decidiu fazer uso do número em suas obras, das quais podemos citar o Homem Vitruviano a Mona Lisa e que o número também está presente em obras arquitetônicas como o Taj Mahal e a Capela Notre Dame du Haut, entre outras. Por fim, pode-se perceber, também, que a utilização da natureza e do cotidiano na contextualização do ensino de matemática, torna mais fácil sua visualização e compreensão.

Palavras-chave: Número de ouro, número phi, razão áurea, matemática. ABSTRACT

The focus of the study is the phi number (ϕ), also known as the golden number or golden number, and its purpose is to show the presence of mathematics, especially the golden number or golden ratio, in our lives. Scholars and mathematicians say that this "mysterious number", adopted as a symbol of harmony and perfection, is present in different areas of human life, such as architecture, arts, and biology. In mathematics, this number is related to geometric figures such as triangles, rectangles, pentagons and decagons. It is also possible to establish a relationship with the Fibonacci sequence. Starting from the origin of the name, following with the demonstration of its mathematical development and geometric representation, we will arrive at the verification of its application in the different areas of human life. It is worth mentioning that the study of the presence of the gold number in our daily lives can be very useful in the classroom, since it can help to arouse the interest of students to the importance and presence of mathematics in our lives. Research has shown that the gold number is present in the proportion ratios in works of art, in the dimensions of the body of certain fish and in some architectural works, for example. The results also show that around 1500, Leonardo da Vinci discovered that the human body obeys the golden ratio and decided to make use of the number in his works, of which we can quote the Vitruvian Man to Mona Lisa and that the number is also present in architectural works such as the Taj Mahal and the Notre Dame du Haut Chapel, among others. Finally, it can also be seen that the use of nature and everyday life in the context of teaching mathematics, makes it easier to visualize and understand.

Keywords: Gold number, phi number, golden ratio, mathematics. 1 INTRODUÇÃO

O homem sempre buscou a perfeição e a matemática é um importante instrumento nessa busca. Martins (2008) destaca que existe um número que desde a antiguidade desperta a curiosidade de estudiosos, um número “mágico” que organiza o universo em uma mesma proporção: o número phi, que tem o valor (arredondado com três casas decimais) ϕ = 1,618.

“Séculos antes de Cristo os pitagóricos estudaram as relações entre os segmentos de um pentagrama [figura obtida traçando-se as diagonais de um pentágono regular] e descobriram um número que tem muita importância na geometria, estética, arquitetura e biologia”. (BELUSSI et al., 2005).

(3)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Este número, que organiza o universo em uma mesma proporção – a “divina proporção”, mais tarde foi denominado número de ouro e pode ser desenvolvido matematicamente mediante a divisão de um segmento em duas partes.

Sabe-se que, geometricamente, um segmento pode ser divido em dois de infinitas formas, mas existe uma que parece mais harmoniosa aos olhos e que define uma razão específica, denominada razão áurea. Vamos analisar a presença desse misterioso número na matemática da vida, isto é, identificar sua presença em áreas como arquitetura, artes, geometria e biologia.

2 O NÚMERO DE OURO (PHI)

A história do número de ouro é tão antiga que não se sabe ao certo quando nem onde ele surgiu. O primeiro registro escrito sobre um número sagrado, que acredita-se ser o número de ouro está no Papiro de Rhind, também conhecido como Papiro de Ahmes, nome do escriba que o grafou, que data de cerca de 1650 a.C.

Segundo Lima et al. (2012), o número de ouro, frequentemente chamado número áureo, número Phi ou razão de Phidias é uma constante real algébrica irracional denotada pela letra grega ϕ (phi), em homenagem ao escultor Phidias (Fídias), que sempre preocupado com a beleza e harmonia de suas obras, o teria utilizado para conceber o Partenon.

3 O NÚMERO ÁUREO E A MATEMÁTICA

Boaventura (2011) destaca que o número áureo está por traz de construções arquitetônicas, obras de arte e processos que envolvem crescimento biológico, principalmente no corpo humano, mas que o fato de poder ser encontrado através de desenvolvimento matemático é que o torna ainda mais fascinante.

Na matemática este número está relacionado a figuras geométricas como triângulos, retângulos, pentágonos e decágonos. É possível, ainda, estabelecer uma relação com a sequência de Fibonacci.

3.1 SEGMENTO ÁUREO: DIVISÃO ÁUREA DE UM SEGMENTO

A primeira definição do que mais tarde ficou conhecido como Segmento Áureo, foi dada por volta de 300 a.C. por Euclides de Alexandria (LÍVIO, 2006, apud ALMEIDA et al., 2010, p. 3) que assim definiu: “Diz-se que uma linha reta é cortada na razão extrema e média quando, assim como a linha toda está para o maior segmento, o maior segmento está para o menor” (LÍVIO, 2006, p.14, apud ALMEIDA et al., p. 3).

(4)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Pode-se dizer, então, que o desenvolvimento do número de ouro feito por meio da divisão de um segmento dá-se de acordo com a seguinte definição: “um segmento [AB] está dividido por um ponto [P] na razão áurea quando uma das partes por ele determinada é a média geométrica entre o segmento e a outra parte” (QUEIROGA; VITOR, 2007, p. 39). Portanto, AP² = AB.PB e o segmento AP é chamado áureo de AB.

Considere AB um segmento e P um ponto pertencente à reta-suporte desse segmento. Geometricamente temos duas possibilidades:

i) P é interior

ii) P é exterior

3.1.1 Segmento Áureo Interno e Segmento Áureo Externo

Segundo Garcia (2006), podemos definir matematicamente um segmento áureo (figura 1) da seguinte forma:

(5)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Fonte: Os autores. AB AC= AC CB ⇔ 𝑥 𝑎= 𝑎 𝑥−𝑎 ⇔ 𝑎 2 _{= 𝑥}2_{− 𝑥𝑎 ⇔ 𝑥}2_{− 𝑎𝑥 − 𝑎}2 _{= 0}

Resolvendo esta equação do segundo grau, teremos as seguintes raízes:

𝑥′ = 𝑎 (1+√5)

2 e 𝑥

′′_{= 𝑎}(1−√5)

2

A segunda será descartada por conveniência, já que a Geometria não admite medidas negativas.

O número (1+√5)

2 = 1,6180339887 … é o número de ouro que é irracional.

Então, temos a seguinte relação:

𝑥

𝑎=

1+√5 2 ⇔

𝑥

𝑎= 𝜙, e como, por definição 𝑥 𝑎= 𝑎 𝑥−𝑎, então 𝑎 𝑥−𝑎= 𝜙

Assim, dado um segmento, tanto podemos obter seu segmento áureo interno, quanto o seu segmento áureo externo.

Observando novamente a Figura 1, o entendimento é imediato: se AC̅̅̅̅ foi o segmento dado, temos como construir CB̅̅̅̅, seu segmento áureo externo. Da mesma forma, poderíamos obter um ponto P entre A e C tal que:

AC AP= AP PC = 𝜙, ou AC PC = PC

AP= 𝜙, dependendo de como tiver sido feita a construção

geométrica.

O problema também tem resolução aritmética, como no exemplo de Tahan:

Achar o segmento áureo de um segmento que mede 40 cm. Solução:

O segmento áureo interno será: 40 x 0,618 ou 24,72 cm. O segmento áureo externo será: 40 x 1,618 ou 64,72 cm. (TAHAN, 1973, p. 241)

(6)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 O processo mais conhecido para a construção dos segmentos áureos é o exibido no exemplo a seguir (figura 2):

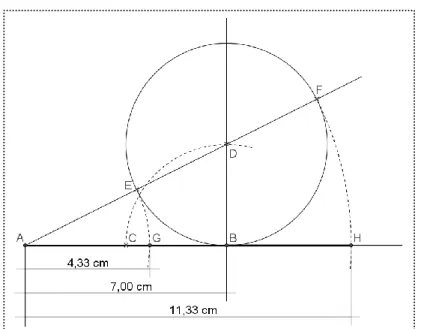
Figura 2: Construção do Segmento Áureo Interno e Externo de AB = 7cm. Fonte: Os autores.

Pelo processo da Figura 2, podemos traçar tanto o segmento áureo interno quanto o externo de AB = 7cm. Consiste em:

1- Traçar o segmento AB = 7cm; 2- Achar C, ponto médio de AB̅̅̅̅;

3- Traçar uma reta perpendicular a AB̅̅̅̅ passando pelo ponto B;

4- Ponta-seca em B, raio BC̅̅̅̅, determinar D na intersecção com a perpendicular; 5- Traçar a semirreta AD;

6- Ponta-seca em D, raio BC̅̅̅̅, determinar E e F na intersecção com AD⃗⃗⃗⃗⃗ ; 7- Ponta-seca em A, raio AE̅̅̅̅, determinar G na intersecção com AB̅̅̅̅; 8- Traçar a semirreta AB;

9- Ponta-seca em A, raio AF̅̅̅̅, determinar H na intersecção com AB̅̅̅̅.

Os pontos G e H são pontos de ouro do segmento, e conforme Tahan, estando o ponto de ouro no segmento diremos que o ponto de ouro é interno (...) o ponto de ouro externo fica no prolongamento do segmento (TAHAN, 1973, p. 233).

(7)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Sendo G, portanto, o ponto de ouro interno, ele divide o segmento AB em duas partes desiguais. E, nesse caso, o maior segmento (...) é chamado segmento áureo interno ou, apenas, segmento áureo (TAHAN, 1973, p. 233), ou seja, o segmento AG = 4,33 cm, que torna válida

a proporção áurea AB

AG =

AG

GB = 𝜙, ou segundo a interpretação aritmética, AB x 0,618 = AG.

O ponto H também divide o segmento AB em média e extrema razão, tornando válida a

proporção áurea AH

AB =

AB

BH = 𝜙 , ou segundo a interpretação aritmética, AB x 1,618 = AH .

Assim, AH = 11,33 cm é o segmento áureo externo de AB.

3.2 TRIÂNGULO ÁUREO

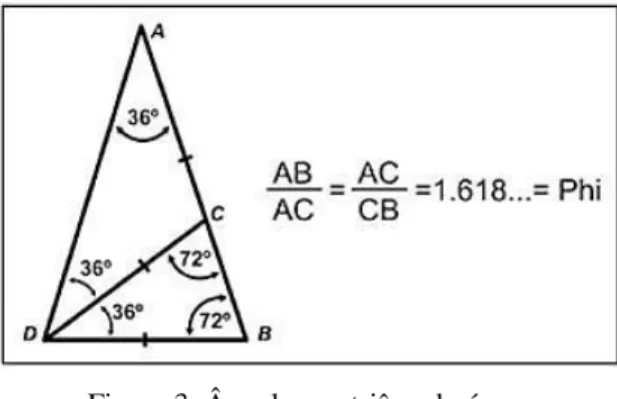
Um triângulo de ouro é um triângulo isósceles no qual a divisão do comprimento de um dos lados pelo comprimento da base é o número de ouro. De acordo com Oliveira (2010) um triângulo áureo caracteriza-se por ser um triângulo com ângulos de base medindo 72° e ângulo do ápice medindo 36º, como mostra a figura 3.

Traçando-se uma bissetriz num de seus dois ângulos de 72º, surge um novo triângulo, semelhante ao maior, e repetindo a operação, isso acontece infinitas vezes.

Figura 3: Ângulos no triângulo áureo Fonte: BOZOLA, LONGATO, BOZOLA (2011)

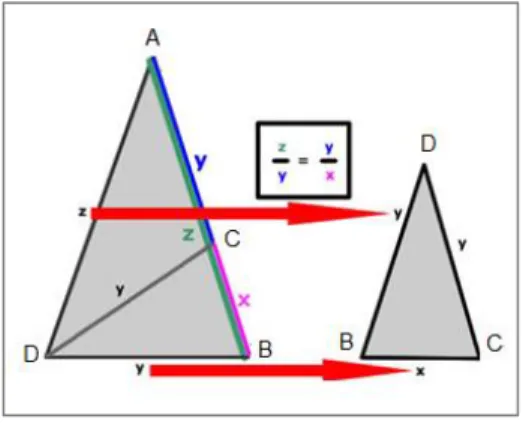
Todos os triângulos isósceles que possuam dois ângulos de 72º e um de 36º com uma relação áurea entre seus lados, serão denominados triângulos áureos. Analisando o triângulo DAB e o triângulo CDB separadamente, teremos (figura 4):

(8)

Figura 4: Razão áurea no triângulo PIROPO (2009)

Estabelecemos, então, a razão áurea entre o comprimento de um dos lados (z) e a base (y) do triângulo áureo DAB, da seguinte forma: 𝑧

𝑦=

𝑦

𝑥 ; onde z = x + y .

Logo, y² = x² + xy  y² – xy – x² = 0 e, para x = 1, as raízes são:

y′ = 1− √5

2 = − 0,618 … y” = 1+√5

2 = 𝟏, 𝟔𝟏𝟖 … = ϕ

3.3 SEQUÊNCIA DE FIBONACCI E O NÚMERO DE OURO

A sequência de Fibonacci é dada por: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... e seus termos são denominados números de Fibonacci. Para todo número natural n, os termos t da sequência podem ser definidos da seguinte forma:

t(1) = 1 ; t(2) = 1 ; t(3) = 2 ,

então, a sequência é dada por: t(n+1) = t(n-1) + t(n). Para n = 3, temos:

t(3+1) = t(3-1) + t(3) => t(4) = t(2) + t(3) => 3 = 1 + 2 Para n = 8, temos:

t(8+1) = t(8-1) + t(8) => t(9) = t(7) + t(8) => 34 = 13 + 21

Esta sequência não tem limite superior, mas quando se divide um termo pelo seu antecessor, é possível perceber que a razão encontrada convergirá para o número de ouro. Vamos demonstrar essa convergência desenvolvendo os cálculos com os onzes termos iniciais da sequência. Adote a série {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89}:

(9)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 2 1= 2 ; 3 2= 1,5 ; 5 3= 1,666 … ; 8 5= 1,6 ; 13 8 = 1,625 ; 21 13= 1,615 … ; 34 21= 1, 619 … ; 55 341,617 … ; 89 55= 1,61818 …

Podemos visualizar, de forma mais clara, o comportamento dessas razões no gráfico a seguir (figura 5), onde é possível notar que a razão r vai se aproximando do número ϕ = 1,618.

Figura 5: Comportamento das razões entre os termos da sequência de Fibonacci e a aproximação com o número de ouro

Fonte: SODRÉ; TOFFOLI (2005)

3.4 RETÂNGULO ÁUREO

Oliveira (2010) diz que a construção do retângulo áureo (figura 6) é simples, bastando, apenas, seguir o esquema abaixo:

Construa um quadrado de lado unitário; Divida um dos lados do quadrado ao meio; Estenda a base do quadrado e marque o ponto G. Trace uma diagonal do vértice F ao vértice oposto B.

Usando a diagonal (FB) como raio, trace um arco do vértice B do retângulo até o ponto G da base que foi estendida;

Pelo ponto de interseção do arco com o segmento da base trace um segmento perpendicular à base (marque o ponto H).

Ligue os pontos B e H do lado superior do retângulo; O retângulo AHGD formado é o retângulo áureo.

(10)

Figura 6: Retângulo de ouro Fonte: Os autores.

Analisando o triângulo retângulo FCB, teremos: BF² = FC² + CB² e, como o quadrado ABCD é unitário, CD = 1 e FC = 0,5.

Então, BF² = 1² + 0,5²  BF = √1,25 = 1,118033988… e, portanto, FG - FC = CG  1,118033988... – 0,5 = 0,618033988...

O retângulo AHGD tem, portanto, lado AD = 1 e lado DG = 1 + 0,618033988... = ϕ, sendo por isso, denominado retângulo áureo.

O retângulo de ouro também pode ser formado com base na sequência de Fibonacci (vista anteriormente), já que “o quociente entre o sucessor e o antecessor se aproxima, gradativamente, do número de ouro.” (FERRER, 2005). Assim, teríamos um retângulo como o da figura 7.

Figura 7: Retângulo áureo construído usando-se a sequência da Fibonacci Fonte: Os autores

Como vimos anteriormente, é possível perceber que a razão entre os lados convergirá para o número de ouro.

(11)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 2 1= 2 ; 3 2= 1,5 ; 5 3= 1,666 … ; 8 5= 1,6 ; 13 8 = 1,625 ; 21 13= 1,615 …

Se continuarmos o processo, obedecendo aos números da sequência de Fibonacci, chegaremos aos lados de valor 1597 e 987 e obteremos o retângulo cuja razão entre é igual a 1,61803... . Esse processo mostra que a razão entre os números da sequência, isto é, os lados do retângulo, se aproximará cada vez mais do número áureo. Portanto, qualquer retângulo que tenha a razão entre o lado maior e o lado menor igual a phi será um retângulo dourado.

3.5 O RETÂNGULO ÁUREO E A ESPIRAL ÁUREA

Já sabemos que o retângulo de ouro pode ser construído com a sequência de Fibonacci. Vamos ver agora que relação esse retângulo tem com a Espiral áurea.

“Se utilizarmos um compasso e traçarmos o quarto de circunferência inscrito em cada quadrado, encontraremos uma espiral formada pela concordância de arcos cujos raios são os elementos da sequência de Fibonacci.” (BOAVENTURA, 2011)

Ao fazermos o traçado dos arcos, como sugere Boaventura, eis que surge a espiral áurea, como mostra a figura 8.

Figura 8: Espiral dourada sobre sequência de retângulos áureos Fonte: LAURO (2005, p. 40).

Uma espiral áurea (também conhecida como espiral dourada ou espiral de ouro) é uma espiral logarítmica com um valor específico para o fator de crescimento. É importante

ressaltar que toda espiral áurea é uma espiral logarítmica, mas nem toda espiral logarítmica é uma espiral áurea.

Peck (2007) afirma que ao contrário do que dizem a maior parte dos autores, a concha do Nautilus (molusco marinho) não tem a forma de uma espiral dourada e sim de uma espiral logarítmica, pois ela não se expande com a mesma taxa de crescimento que a concha do referido molusco.

(12)

“A concha do molusco Nautilus é, talvez, o exemplo mais famoso nesse assunto, mas hoje sabemos que ela não é uma espiral áurea, como já mostrado por Clemente Falbo no artigo ‘Espirais da concha do mar’ publicado na Science. A confusão ocorre porque ela se encaixa na categoria de espiral logarítmica, na qual a espiral áurea também se encontra”. (PECK, 2007)

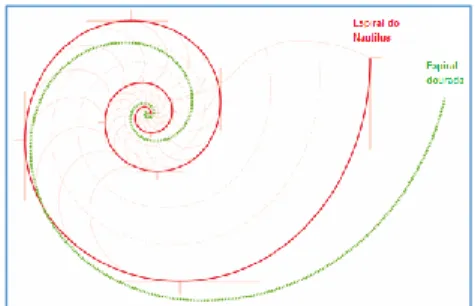
As imagens a seguir (figuras 9 e 10) ilustram a situação. Note que as espirais não coincidem, pois apresentam diferentes taxas de crescimento (isso pode ser facilmente verificado com o auxílio de um software de geometria dinâmica).

Figura 9: Concha do Nautilus Figura 10: Relação entre a espiral do Nautilus Fonte: PECK (2007) marinho e a espiral áurea

Fonte: MORI (2010)

Bortolossi (2009) afirma que esse equívoco é bastante comum em muitos livros e documentos sobre o assunto e mostra em seu trabalho (disponível no site de UFF – Universidade Federal Fluminense) que não há como a concha do Nautilus obedecer à taxa de crescimento da espiral dourada.

3.6 DIVISÃO DA CIRCUNFERÊNCIA: PENTÁGONO REGULAR

Devemos aproveitar a oportunidade para esclarecer como se dá o processo de divisão da circunferência em 5 partes iguais (formando um pentágono regular inscrito), e demonstrar porque este é um processo de construção exato. Na figura 11 temos uma circunferência que passou por este processo de divisão.

Com o auxílio de um compasso desenhe uma circunferência e marque o centro O; Trace o diâmetro e marque, em uma de suas extremidades, o ponto P;

Trace um perpendicular ao diâmetro passando por O e marque o ponto A em uma das extremidades;

(13)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Divida o segmento OP ao meio e marque o ponto M;

Com a ponta seca do compasso em M, e amplitude AM, trace o arco de circunferência que sai de A e vai até o lado oposto do segmento OP;

Marque o ponto G;

Transfira a medido GA, a partir do ponto A, para os dois lados e marque os demais pontos de divisão da circunferência.

Figura 11: pentágono regular Fonte: Os autores

Ferrer (2005) destaca que as diagonais de um pentágono dividem uma à outra em média e extrema razão. Pela figura anterior podemos notar que a razão entre a diagonal AD do pentágono e um de seus lados DC aproxima-se do número de ouro (ϕ) e que o triângulo DAC é um triângulo áureo.

Partindo do pentágono podemos obter o pentagrama, como mostra a figura 12.

(14)

Fonte: Os autores

O pentágono menor (ABCDE) está em proporção com o pentágono maior (FGHIJ). “A razão entre as medidas dos lados dos dois pentágonos é igual ao quadrado do número de ouro.” (OLIVEIRA, 2010)

Podemos notar que razão entre o lado FG (do pentágono maior) e o lado ED (do pentágono menor) corresponde ao quadrado da razão áurea. Algebricamente podemos escrever:

FG ED=

4

1,528 = 2,617 … = ϕ

2

3.7 DIVISÃO DA CIRCUNFERÊNCIA: DECÁGONO REGULAR

A figura 13 mostra um decágono regular, polígono cuja inscrição na circunferência tem profunda conexão com o pentagrama e o pentágono regular inscrito. A seguir, a divisão da circunferência em dez partes iguais e a construção do decágono regular inscrito seguido de passo-a-passo:

Figura 13: Divisão da Circunferência em 10 Partes Iguais e Construção do Decágono Regular Inscrito. Fonte: Os autores.

1- Traçar uma reta qualquer que intersecte a circunferência em dois pontos de seu hemisfério inferior;

2- Traçar uma reta perpendicular à anterior passando por O, que determina A e B na circunferência;

3- Traçar uma perpendicular à reta AB passando por O , que determina C e D na circunferência;

(15)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 4- Achar M, ponto médio de OD̅̅̅̅;

5- Ponta-seca em M, raio MA̅̅̅̅̅, determinar E em CD̅̅̅̅;

6- Traçar o segmento OE, que é o nosso 𝑙₁₀, isto é, o lado do nosso decágono regular inscrito;

7- Ponta-seca em A, raio OE̅̅̅̅, determinar F e G na circunferência;

8- Para minimizar os erros de traçado, passemos ao outro pólo do diâmetro AB̅̅̅̅: ponta-seca em B, raio OE̅̅̅̅, determinar H e I na circunferência;

9- Ponta-seca em F, raio OE̅̅̅̅, determinar J na circunferência; 10- Ponta-seca em G, raio OE̅̅̅̅, determinar K na circunferência; 11- Ponta-seca em H, raio OE̅̅̅̅, determinar L na circunferência; 12- Ponta-seca em I, raio OE̅̅̅̅, determinar N na circunferência;

13- Ponta-seca em J, raio OE̅̅̅̅, conferir se o ponto encontrado coincide com L; 14- Ponta-seca em K, raio OE̅̅̅̅, conferir se o ponto encontrado coincide com N;

15- Traçar os segmentos AF, FJ, JL, LH, HB, BI, IN, NK, KG e GA, completando assim, a figura pretendida.

Mas o quê garante que o processo de construção é exato e o 𝑙₁₀ é realmente o lado do decágono regular inscrito?

Antes de prosseguirmos com a demonstração, faz-se mister uma explanação sobre a relação entre a base e os lados do triângulo isósceles (figura 14) cujos ângulos da base medem 72º, também chamado de triângulo áureo.

Figura 14: Relação entre os Lados e a Base do Triângulo Áureo. Fonte: ALHANATI (S.D.).

Os lados do pentágono marcam sobre a circunferência arcos de 72º (360º/5). Os triângulos amarelo e azul são isósceles com ângulos de 72º nas bases (ALHANATI, S.D.).

Isso se explica porque tanto no triângulo amarelo quanto no azul, os ângulos da base estão inscritos na circunferência, o que faz com que eles sejam a metade do arco que eles

(16)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 determinam. Como todos eles abrangem dois arcos de 72º, ou seja, arcos de 2 . 72º = 144º, então cada um deles vale 72º.

A diagonal AC̅̅̅̅ e todas as demais estão divididas em dois segmentos L e 𝑎. Como os referidos triângulos são semelhantes, os seus lados são proporcionais 𝐿

𝑎 =

a+L

L ,

consequentemente o lado L é o segmento áureo da diagonal 𝑎 + 𝐿. (ALHANATI, S.D.)

Quer isto dizer que, nos triângulos isósceles com esta configuração angular, ou seja, ângulos de 72º na base e ângulo de 36º oposto a ela (e também aqueles, em que os ângulos se invertem, ou seja, ângulos de 36º na base e ângulo de 72º oposto a ela) a razão entre lado e

base é áurea. Com este conhecimento em mente, podemos avançar à demonstração (figura 15):

Figura 15: Demonstração do Processo de Divisão da Circunferência em 10 Partes Iguais. Fonte: Os autores.

Hipótese: Um decágono regular de lado 𝑙₁₀ está inscrito numa circunferência de raio 𝑅. A razão deste raio para um segmento 𝑥 é áurea (por construção). Não se pode deixar de considerar a figura 12.

Tese: 𝑥 = 𝑙₁₀.

Demonstração: A partir de um quadrado de lado 𝑅 foi traçado um retângulo áureo de comprimento (𝑅 + 𝑥) e largura 𝑅, de forma que 𝑅+𝑥

𝑅 =

𝑅

𝑥 = 𝜙 (𝟏).

O processo de divisão da circunferência em dez partes iguais, para a obtenção do decágono regular inscrito, a divide em dez arcos de medida 360º

10 = 36º. Igual medida têm os

ângulos centrais que os determinam. Considerando dois vértices consecutivos do decágono regular e os raios da circunferência que os contém, forma-se um triângulo isósceles de base 𝑙₁₀

(17)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 e lados 𝑅 , com ângulos da base de 72º e ângulo oposto à base de 36º, tal qual vimos anteriormente, sendo, portanto, um triângulo áureo. Assim, temos que 𝑅

𝑙10 = 𝜙 (𝟐). Pela unicidade da igualdade entre (𝟏) e (𝟐), temos que:

𝑅 𝑙10 =

𝑅

𝑥 = 𝜙 ⟺ 𝒍𝟏𝟎 = 𝒙 (c.q.d)

4 A PRESENÇA DO NÚMERO ÁUREO EM DIFERENTES ÁREAS DA VIDA HUMANA

Embora não se saiba ao certo sua origem, uma coisa é unânime: todos concordam que a razão áurea está presente em grande número de animais e plantas, inclusive nas dimensões do corpo humano, fato pelo qual ficou conhecida também como “proporção divina”.

A descoberta da razão áurea no seio da natureza, foi como ter encontrado um padrão no caos, ou melhor, ter conseguido ver algum tipo de afinidade entre espécimes de seres vivos muito antagônicos, sem contar que sempre havia alguma finalidade em ser do jeito que era.

Isto gerou certo encantamento nos homens, que passaram a adotá-la como padrão de beleza, como nas palavras de Oliveira:

A razão áurea, além de um conceito matemático, é uma expressão de harmonia e beleza. Os antigos gregos avaliavam essa harmonia nos seres vivos e não-vivos, buscando em suas dimensões uma proporção que se aproximasse da razão áurea. (OLIVEIRA, 2010, p. 19)

Segundo Ferreira e Oliveira, para os gregos, o número de ouro representava harmonia, equilíbrio e beleza (FERREIRA; OLIVEIRA, 2010, p. 80).

Então, o número de ouro passou a ser visto como ideal de perfeição, e desde os tempos mais antigos foi, e continua sendo usado na pintura, na escultura, música, arquitetura, teatro, enfim, nas artes de maneira geral.

4.1 O NÚMERO DE OURO NA NATUREZA

Podemos ver a proporção divina presente nas dimensões de folhas de plantas (figura 16), que são dispostas de forma a evitar que as folhas de cima façam sombra nas de baixo num certo ângulo que pode ser calculado em função de 𝜙. Trata-se de uma circunferência completa (360º ) dividida pelo quadrado de 𝜙 , que resultará num ângulo de aproximadamente 137º30’28’’.

(18)

Figura 16: Disposição das Folhas das Plantas (Vista Superior). Fonte: TAHAN (1973, p. 248).

Algumas flores apresentam o número de ouro na distribuição de seus espirais, como mostra a figura 17, que tem 34 espirais para a direta e 21 para a esquerda. Note que esses números pertencem à sequência de Fibonacci que, como já vimos, tende ao número dourado.

Figura 17: Sequência de Fibonacci e a distribuição das espirais de uma flor Fonte: VENTURA (2005)

A Natureza "arrumou" as sementes do girassol sem intervalos, na forma mais eficiente possível, formando espirais logarítmicas que tanto curvam para a esquerda como para a direita. O curioso é que os números de espirais em cada direção são (quase sempre) números vizinhos na sequência de Fibonacci (...).

(19)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 4.2 O NÚMERO ÁUREO E O CORPO HUMANO

Martins (2008) afirma que pesquisas estatísticas como a da Revista Odonto Ciência (2006) revelam a presença da proporção divina em nosso corpo. Podemos destacar a razão entre: 1) a altura de uma pessoa e a distância de seu umbigo até o chão; 2) o comprimento do braço e o comprimento do cotovelo até o dedo; 3) o comprimento da perna inteira e a distância do joelho até o chão; entre outras.

O umbigo, por exemplo, é o ponto áureo de nossa altura, assim como o comprimento dos dedos que está relacionado de maneira áurea com suas falanges, como mostra a figura 18.

Figura 18: Proporções Divinas do Corpo Humano Fonte: GUIMARÃES (1997, p. 65) apud LAURO (2005, p. 45).

4.3 O NÚMERO ÁUREO NAS ARTES

Renomados pintores como Piet Mondrian (1872-1944) e Leonardo da Vinci (1452-1519) usaram o número de ouro em algumas de suas obras. A partir de 1917 Mondrian inicia sua fase neoplástica e trabalha com linhas paralelas que formam retângulos que se relacionam entre si na razão áurea. Obras como a “Composição com vermelho, amarelo, azul e preto” de 1921 e “Nova York” de 1942 (figuras 19 e 20) são exemplos da preocupação do artista com a harmonia, beleza e perfeição.

Figura 19: Composição com vermelho, Figura 20: Nova York (Mondrian - 1942) amarelo, azul e preto (Mondrian - 1921)

(20)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Martins (2008) afirma que, por volta de 1500, Leonardo da Vinci descobriu que o corpo humano obedece à proporção áurea e mediante tal descoberta decidiu fazer uso do número áureo em suas obras. A busca pela perfeição e harmonia está claramente presente em duas de suas mais famosas criações, o Homem Vitruviano (1490) – figura 13 e a Mona Lisa (1507) – figura 22.

A excelência dos desenhos de Leonardo da Vinci revela os seus conhecimentos matemáticos bem como a utilização da razão áurea como garante de uma perfeição, beleza e harmonia únicas. (...) Um exemplo é a tradicional representação do homem em forma de estrela de cinco pontas de Leonardo, a qual foi inspirada no pentágono regular e estrelado inscrito na circunferência. (BARISON, S.D., p.4).

Figura 22: Monalisa e os “Retângulos Mágicos” Fonte: LAURO (2005, p. 64)

Figura 21: Homem Vitruviano de Leonardo da Vinci. Fonte: BARISON, (S.D., p.4).

(21)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 Outro que foi adepto do uso dos retângulos de ouro foi Salvador Dali. A exemplo disso, uma de suas mais famosas telas – A Última Ceia (figura 23):

Figura 23: A Última Ceia, de Salvador Dali. Fonte: OLIVEIRA (2010, p. 33).

Oliveira explica o quadro: Salvador Dali pintou “O Sacramento da Ultima Ceia” em um quadro com dimensões áureas, 270 cm x 167 cm, o quociente entre eles gera 1,6180339..., e o foco da foto está em João Batista, o discípulo preferido de Jesus (OLIVEIRA 2010, p. 33).

4.4 O NÚMERO ÁUREO NA MÚSICA

O número áureo está presente na fabricação de instrumentos, no compasso de algumas músicas e até em tons e semitons. A perfeição associada a esse número não iria passar incólume pelos músicos.

Alguns garantem que os grandes Mestres da música valiam-se e valem-se da razão áurea em suas composições. E segundo Oliveira, na música, existem artigos que relacionam as composições de Mozart, Bethoveen (Quinta Sinfonia), Schubert e outros com a razão áurea (OLIVEIRA, 2010, p. 37).

Instrumentos como o teclado (figura 24) também levam esse número consigo:

A quantidade de teclas de uma oitava é igual a 13, sendo 8 teclas brancas e 5 teclas pretas e mais a divisão entre teclas brancas e pretas e de grupos de 3 e 2, coincidência ou não podemos visualizar que ali tem a sequência de Fibonacci ( 2, 3, 5, 8, 13). (OLIVEIRA, 2010, p. 39).

(22)

Figura 24: O Teclado e sua relação com a Sequência de Fibonacci. Fonte: OLIVEIRA, (2010, p. 38).

4.5 O NÚMERO DE OURO NA ARQUITETURA

“Arquitetos famosos também adotaram a razão áurea como parâmetro para a construção de suas obras.” (FERRER, 2005)

A arquitetura talvez tenha sido a primeira forma de arte a utilizar o número de ouro. Além das pirâmides de Gizé, que talvez deixe dúvidas quanto à intencionalidade, temos o Parthenon (figura 25), construído por volta de 447 a.C. e 433 a.C. na Grécia, e que devido à quantidade de retângulos áureos utilizados, não deixa sombra de dúvidas.

Outro belo exemplar de arquitetura baseada nas proporções áureas é o Taj Mahal, maior mausoléu do mundo, terminado em 1652 e localizado na Índia. Recentemente eleito uma das novas Sete Maravilhas do Mundo, o Taj Mahal (figura 26) foi dado pelo imperador Shah Jahan como prova de amor à sua esposa favorita que morrera dando à luz um filho.

Figura 25: Retângulos aúreos no Parthenon Figura 26: Retângulos aúreos no Taj Mahal Fonte: OLIVEIRA (2010, p. 28). Fonte: OLIVEIRA (2010, p. 29).

5 CONSIDERAÇÕES FINAIS

Estudar o número de ouro, apesar de muito interessante, é muito complexo, uma vez que exige certo conhecimento matemático para a compreensão de seu conceito inicial. Mas, o estudo de suas

(23)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 aplicações em nosso cotidiano pode ser muito útil em sala de aula, já que pode ajudar a despertar o interesse dos alunos para a importância e presença da matemática em nossas vidas.

Este artigo foi desenvolvido com o objetivo de mostrar como a harmonia de nosso corpo, a perfeição de obras de arte e a beleza de flores podem se relacionar com a matemática.

A pesquisa procurou abordar, de forma sucinta, o conceito algébrico e geométrico do número áureo e sua relação com diferentes áreas da vida humana. E, ainda, buscar argumentos científicos para a abordagem do tema em sala de aula.

Representações artísticas de Leonardo da Vinci e Piet Mondrian e obras arquitetônicas de Fídias e Le Corbusier foram base para comprovação da importância desse estudo, assim como construções realizadas pelos autores com auxílio de régua e compasso e software de geometria dinâmica (Geogebra).

Espera-se que este trabalho contribua para despertar o interesse em novas pesquisas sobre o assunto e que seja ferramenta para se trabalhar conceitos geométricos no ensino médio.

REFERÊNCIAS

ALHANATI, Lucien Silvano. Matemática Geometria GEO Polígonos GEO08 Decágono

GEO0803. Disponível em: <http://alfaconnection.net/pag_avsm/geo0803.htm>. Acesso em: 22 jan.

2014.

ALHANATI, Lucien Silvano. Matemática Geometria GEO Polígonos GEO08 Pentágono

GEO0801. Disponível em: <http://alfaconnection.net/pag_avsm/geo0801.htm#GEO080101>. Acesso em: 22 jan. 2014.

ALMEIDA, Ana Mary Fonseca Barreto de et al. Razão Áurea: um elemento motivador para o

estudo de razões e sequências na educação básica. In: Encontro Nacional de Educação

Matemática, 10, 2010, Salvador – Ba. Anais do X Encontro Nacional de Educação Matemática. Salvador - Ba: Sbem, 2010. p. 1 - 10. Disponível em: < http://goo.gl/6cCTAF>. Acesso em: 22 jan. 2014.

BARISON, Maria Bernadete et al. Número de Ouro. Disponível em: <http://www.mat.uel.br/geometrica/artigos/st-15-tc.pdf>. Acesso em: 22 jan. 2014.

(24)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 BELUSSI, Giuliano Miyaishi et al. Número de Ouro. Londrina, 2005. Disponível em: <http://www.mat.uel.br/geometrica/artigos/ST-15-TC.pdf>. Acessa em 07 jan. 2014.

BOAVENTURA, Luana Lima. História da Matemática. São Carlos, 2011. Disponível em: < http://goo.gl/LVk3ZG>. Acesso em: 05 jan. 2014.

BORTOLOSSI, Humberto José. O número de ouro. 2009. Disponível em: < http://www.uff.br/cdme/rza/rza-html/rza-spirals-br.html>. Acesso em 12 jan. 2014.

BOZOLA, Antonio Roberto; LONGATO, Franco Marcelo; BOZOLA, Adriana Parro. Análise

geométrica da forma da beleza da mama e da forma de prótese baseado na proporção Phi: aplicação prática. 2011. Revista Brasileira de Cirurgia Plástica, v. 26 n. 1 – jan/fev/mar 2011.

Disponível em: <http://www.rbcp.org.br/detalhe_artigo.asp?id=797>. Acesso em: 20 jan. 2014.

FERRER, Joseane Vieira. O Número de Ouro na Arte, Arquitetura e Natureza: beleza e harmonia. Brasília, 2005. Disponível em: <http://goo.gl/yS2vEL>. Acesso em: 10 jan. 2014.

LAURO, Maira Mendias. A Razão Áurea e os Padrões Harmônicos na Natureza, Artes e Arquitetura. Exacta, São Paulo, v. 3, p.35-48, jul. 2005. Disponível em: < http://www.redalyc.org/articulo.oa?id=81000304>. Acesso em: 15 jan. 2014.

LIMA, Ingrid Mariana Rodrigues de et al. Oficina: O Número de Ouro, Seus Mistérios e

sua Presença em Nossas Vidas. Paraná, 2012. Disponível em: <http://w3.ufsm.br/ceem/eiemat/Anais/arquivos/RE/RE_Lima_Ingrid.pdf>. Acesso em: 10 jan. 2014.

MORI, Kentaro. “Nature by Numbers”: Fibonacci e a matemática como descrição do mundo. 2010. Disponível em: <http://scienceblogs.com.br/100nexos/2010/03/nature_by_numbers_fibonacci_e/>. Acesso em 14 jan. 2014

(25)

Braz. J. of Develop.,Curitiba, v. 6, n.5, p.30834-30858 may. 2020. ISSN 2525-8761 OLIVEIRA, Edson de; FERREIRA, Thiago Emanuel. O Número de Ouro e suas manifestaçoes na

natureza e na arte. Revista Complexus: Instituto Superior de Engenharia Arquitetura e

Design, CEUNSP, Salto-SP, p.64-81, 1 set. 2010.

OLIVEIRA, Cristiano Barreto. Razão Áurea: Suas aplicações e importância no Ensino de Matemática. Aparecida de Goiânia, 2010. Disponível em: <http://goo.gl/FFXUiH>. Acesso em: 05 jan. 2014.

PECK, Akkana. The Fibonacci Spiral and the Nautilus. 2007. Disponível em: < http://www.shallowsky.com/blog/science/fibonautilus.html>. Acesso em 12 jan. 2014.

PIROPO, B. Um número muito especial IV: o pentagrama. 2009. Disponível em: < http://www.bpiropo.com.br/fpc20070122.htm>. Acesso 20 jan. 2014.

QUEIROGA, Alberto Luiz Fernandes; VITOR, Cláudio Barros. Desenho Geométrico: licenciatura em matemática 2º período. Manaus, 2007. Disponível em: <http://pt.slideshare.net/cursoraizes/desenho-geomtrico>. Acesso em: 05 jan. 2014.

SODRÉ, U.; TOFFOLI, Sônia F.L. Alegria Matemática: Sequências de Fibonacci: Propriedades

matemáticas. 2005. Disponível em: <http://goo.gl/fCrBy>. Acesso em: 17 jan. 2014.

TAHAN, Malba. As Maravilhas da Matemática. 2. ed. Rio de Janeiro: Bloch, 1973. 804 p.

VERA CLOTILDE GARCIA. Universidade Federal do Rio Grande do Sul Instituto de Matemática. O Número de Ouro como instrumento de aprendizagem significativa no estudo dos

números irracionais. Disponível em: <http://goo.gl/4VA2gZ>. Acesso em: 22 jan. 2014.