4 Estabilidad de Sistemas Lineales

UNIVERSIDAD AUTÓNOMA DE BAJA CALIFORNIA FACULTAD DE INGENIERÍA MEXICALI

SISTEMAS LINEALES 1

Dr. Lars Lindner

Contenido

1 Introducción 4

Control en bucle abierto y en bucle cerrado ... 4

1.1 Términos de control ... 7

1.2 Ejemplos de aplicaciones de sistemas de control ... 9

1.3 2 Medios para Representación 11 Elementos del diagrama funcional o diagrama de flujo de señales ... 11

2.1 2.1.1 Bloque de transferencia y línea de acción ... 11

2.1.2 Elementos de interconexión ... 14

Estructuras del diagrama funcional y simplificaciones ... 17

2.2 2.2.1 Estructura en serie ... 17

2.2.2 Estructura en paralela ... 17

2.2.3 Estructura en bucle ... 21

2.2.4 Ecuación diferencial con bloques de transferencia ... 25

Cálculo de bucles de control con elementos proporcional ... 27

2.3 Conversión de diagramas funcionales ... 30

2.4 2.4.1 Reglas para la conversión ... 30

2.4.2 Tabla de las reglas de conversión... 31

2.4.3 Ejemplos de aplicación ... 34

3 Métodos Matemáticos 36 Normalización de ecuaciones (estandarización) ... 36

3.1 Linealización de elementos del bucle de control ... 39

3.3.3 Sistema de segundo orden (Elemento PT2) ... 55

La transformación de Laplace ... 66

3.4 3.4.1 Transformaciones matemáticas ... 66

3.4.2 Dominio original y dominio de imagen ... 67

3.4.3 Transformación y transformación inversa de Laplace ... 69

Funciones de prueba ... 72

3.5 3.5.1 El impulso unitario δ(t) ... 72

3.5.2 El escalón unitario σ(t) ... 73

3.5.3 La rampa unitaria ρ(t) ... 76

3.5.4 Función armónica ... 79

Aplicación de la transformación de Laplace ... 80

3.6 3.6.1 Linealidad ... 80

3.6.2 Teoremas de desplazamiento ... 81

3.6.3 Teorema de similitud ... 86

3.6.4 Teorema de convolución ... 87

3.6.5 Teorema de diferenciación e integración ... 89

3.6.6 Teoremas de valor limite... 91

Función de transferencia ... 95

3.7 3.7.1 Descomposición en fracciones parciales ... 96

3.7.2 Ecuación característica y diagrama polo-raíces ... 97

3.7.3 Solución de ecuaciones diferenciales lineales con coeficientes constantes con la transformación de Laplace ... 100

Respuesta en frecuencia de elementos de transferencia ... 103

3.8 3.8.1 Respuesta en frecuencia ... 103

3.8.2 Respuesta en frecuencia y función de transferencia ... 108

3.8.3 Respuesta en frecuencia y diagrama de Bode ... 109

3.8.4 Respuesta en frecuencia y diagrama de Nyquist ... 119

3.8.5 Respuesta en frecuencia y respuesta al escalón ... 121

1

Introducción

Control en bucle abierto y en bucle cerrado

1.1

Frecuentemente se deben implementar técnicas de bucle cerrado o abierto en sistemas de

control, en las cuales ciertas magnitudes del sistema tienen un comportamiento ordenado. En

casos simples se supone que las magnitudes son constantes, aunque afectan perturbaciones al

sistema. Estas tareas generalmente se resuelven con un sistema de control en bucle abierto o en

bucle cerrado. A continuación se explicaran y compararan dichos métodos.

El control en bucle cerrado es un proceso, en donde se mide en forma continua una magnitud, la

variable controlada, y se compara con otra magnitud, la variable de referencia. Con el resultado

de la comparación se influye la variable controlada, tal que esta se adapta a la variable de

referencia. El sistema completo es conocido como bucle de control.

Ejemplo 1.1: Control en bucle abierto

El control en bucle abierto (lazo abierto) de la temperatura interior 𝑇_𝑖 de una habitación es

dependiente de la temperatura exterior 𝑇_𝑎. Un elemento de control regula el flujo de energía para

la habitación en función de la temperatura exterior actual 𝑇_𝑎.

Fuente de calor o electricidad

Válvula, Tiristor, Disruptor

Habitación para calentar con

calefacción

i

T

Elemento de

control M

Transformador de medida Medidor de temperatura

exterior

a

El sistema es un control en bucle abierto, debido a que no se está midiendo la variable controlada

(temperatura interior 𝑇_𝑖). Se controla la temperatura de la habitación 𝑇_𝑖 en función de la

temperatura exterior 𝑇_𝑎, la magnitud más importante en un sistema de calefacción. La

característica más importante en un bucle de control abierto es el modo de acción abierto, la

temperatura interior no influye al flujo de energía.

Ejemplo 1.2: Control en bucle cerrado

El control en bucle cerrado (lazo cerrado) de la temperatura interior 𝑇_𝑖 fijo a una temperatura

prescrita 𝑇_𝑠. Se regula el flujo de energía en función de la diferencia entre la temperatura interior

𝑇𝑖 y la temperatura prescrita 𝑇𝑠. Por lo tanto la cadena de acción está cerrada.

Fuente de calor o electricidad

Válvula, Tiristor, Disruptor

Habitación para calentar con

calefacción

Comparador y

controlador M

Medidor de temperatura

interior

i

T

Transformador de medida

Valor prescrito

s

T

Figura 2: Esquema tecnológico de un control cerrado de temperatura

Los controles en bucle abierto no consideran todas las perturbaciones. El Ejemplo 1.1 solo

considera cambios en la temperatura exterior, pero no perturbaciones en el flujo de energía. Sin

embargo controles en bucle abierto generalmente reaccionan más rápido a perturbaciones. Si se

disminuye la temperatura exterior, el control interviene antes que la perturbación baje la

Tabla 1: Características de controles en bucle abierto y cerrado

Característica Control en bucle abierto Control en bucle cerrado

Cadena de acción: Abierta Cerrada

Medición y comparación de la

magnitud regulada: No Si

Reacción a perturbaciones en

general:

Solo se reacciona a

perturbaciones, que se están

midiendo.

Impide todas las

perturbaciones, que actúan

sobre el sistema.

Reacción a perturbaciones en el

tiempo:

Reacciona rápido, porque se

miden directo las

perturbaciones.

Solo reacciona cuando se

cambia la diferencia entre valor

prescrito e instantáneo.

Esfuerzo técnico:

Alto esfuerzo, si se debe

considerar muchas

perturbaciones. Bajo esfuerzo,

si no aparece ninguna

perturbación.

Bajo esfuerzo: Medición de la

variable controlada,

comparación del prescrito e

instantáneo, amplificación de la

potencia.

Comportamiento en sistemas

inestables:

Control en bucle abierto con

sistemas inestables es

inutilizable.

Sistemas inestables requieren

control en bucle cerrado.

Tabla 2: Ventajas y desventajas de controles en bucle abierto y cerrado

Control en bucle abierto Control en bucle cerrado

Ventajas

 Construcción más simple

 Si el sistema controlado es estable, no hay problema de estabilidad  Conveniente cuando la medición de

salidas es complicado o costoso  En general menos costoso

 Compensa perturbaciones o cambios de los parámetros del sistema continuamente

 Exactitud en la igualación de los valores reales y prescritos

Desventajas

 No compensa perturbaciones o cambios de los parámetros del sistema, la salida puede ser diferente a la deseada

 Requiere recalibración periódica del sistema

 Un sistema estable se puede hacer inestable por cerrar el bucle  Construcción más compleja

Términos de control

1.2

La meta de controles técnicos es la mejora del comportamiento de magnitudes físicas en el

tiempo, por ejemplo la tensión eléctrica, la potencia, la velocidad de giro, la presión y la

temperatura.

El sistema controlado es la parte en un sistema técnico, que se quiere influir. En el Ejemplo 1.1 el

sistema controlado consiste en la calefacción y la habitación para calentar. La variable de entrada

del sistema controlado es la variable de control 𝑦 (flujo de calor), la magnitud para controlar se

denomina variable controlada 𝑥 y en este caso corresponde a la temperatura interior 𝑇_𝑖.

Sistema controlado

Variable de control Variable controlada

Variable de perturbación

y x

z

Figura 1: Sistema controlado con entrada y salida

Se registra la variable controlada 𝑥 en el punto de medición y se compara con la variable de

referencia 𝑤 calculando la diferencia. Se define la variable de referencia al control desde fuera, la

variable controlada debe seguir la variable de referencia. La diferencia:

𝑥𝑑= 𝑤 − 𝑥 ( 1 )

se denomina variable de error. Las perturbaciones se nombran con 𝑧, ellasactúan en puntos de

perturbaciones e influyen la variable controlada 𝑥. Una meta importante del control es suprimir la

influencia de las perturbaciones a la variable controlada. Si ocurre una disminución de la variable

equipo final de control, la variable de control 𝑦 , actúa en el punto de control del sistema

controlado. El sistema controlado se encuentra entre el punto de control y el equipo de medición.

El sistema de control consiste del equipo de medición, el comparador, el controlador y el equipo

final de control; es decir todos los equipos, excepto el sistema controlado, forman parte del

sistema de control.

Se recomienda incluir en el análisis del sistema controlado todas las partes del sistema de control

que están predeterminados el proceso de producción. Los cálculos y estudios de control se dirigen

entonces a las características del controlador, que son modificables por el usuario (estructura y

parámetros) y que se tienen que determinar en la síntesis del controlador.

Punto de medición Sistema controlado Lugar de control Lugar de perturbación

Comparador Controlador Equipo final de control Equipo de medición r y d x w y z x

Sistema de control

Figura 2: Elementos y términos de control

En el Ejemplo 1.2 el sistema controlado consiste de la calefacción y la habitación que se desea

calentar, la variable controlada es la temperatura interior 𝑇_𝑖. La salida del controlador determina

el comportamiento del equipo final de control. Generalmente los equipos finales de control son

amplificadores de potencia, controladores de potencia con tiristores, conmutadores para influir la

potencia eléctrica o válvulas para regular el flujo de calor.

Se mide la variable controlada con el equipo de medición, por ejemplo un puente de medición de

temperatura y se lleva al comparador. La variable de referencia (temperatura prescrita) se puede

Ejemplos de aplicaciones de sistemas de control

1.3

Sistema de control de velocidad: El principio básico del regulador de velocidad de Watt para una

máquina se ilustra en el diagrama esquemático de la Figura 3. La cantidad de combustible que se

admite para la máquina se ajusta de acuerdo con la diferencia entre la velocidad de la máquina

que se pretende y la velocidad real.

Figura 3: Regulador de velocidad de Watt

La secuencia de acciones puede describirse del modo siguiente: el regulador de velocidad se ajusta

de modo que, a la velocidad deseada, no fluya aceite a presión en ningún lado del cilindro de

potencia. Si la velocidad real cae abajo del valor deseado debido a una perturbación, la

disminución de la fuerza centrífuga del regulador de velocidad provoca que la válvula de control se

mueva hacia abajo, aportando más combustible y la velocidad del motor aumenta hasta alcanzar

el valor deseado. En cambio, si la velocidad del motor aumenta sobre el valor deseado, el

incremento en la fuerza centrífuga del controlador provoca que la válvula de control se mueva

hacia arriba. Esto disminuye la provisión de combustible y la velocidad del motor se reduce hasta

Asimismo, puede trabajar en un ambiente intolerable para operadores humanos. Por ejemplo,

puede funcionar en temperaturas extremas, en un ambiente de presión alta o baja, bajo el agua o

en el espacio. Hay robots especiales para la extinción de incendios, las exploraciones submarinas y

espaciales, por mencionar algunos. El robot industrial debe manejar partes mecánicas que tengan

una forma y un peso determinado.

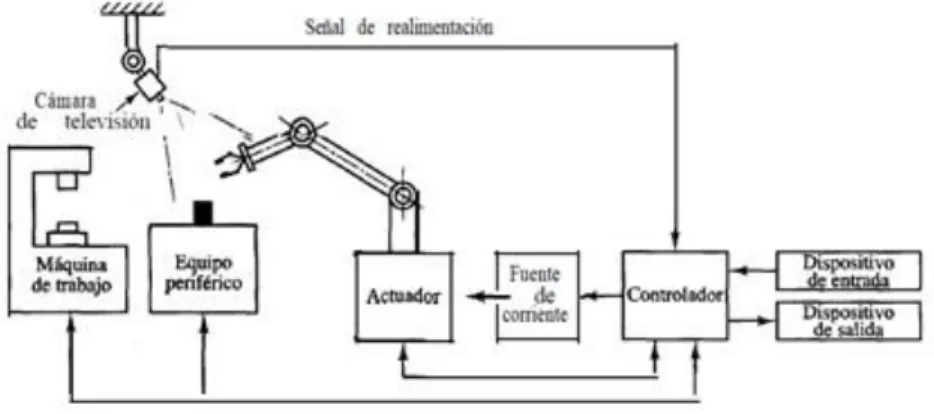
Figura 4: Control de un robot industrial

Por lo tanto, debe tener al menos un brazo, una muñeca y una mano. Debe tener la fuerza

suficiente para realizar la tarea y la capacidad para al menos una movilidad limitada. De hecho,

algunos robots actuales son capaces de moverse libremente por sí mismos en un espacio limitado

en una fábrica. El robot industrial debe tener algunos sensores. A los robots de nivel bajo, se les

instalan microinterruptores en los brazos como un tipo de sensor. El robot toca primero un objeto

y después, mediante los microinterruptores, confirma la existencia del objeto en el espacio y

avanza al paso siguiente programado. En un robot de nivel alto se usa un medio óptico para

rastrear el fondo del objeto. El robot reconoce el patrón y determina la presencia y orientación del

objeto. Se requiere de una computadora para procesar las señales del proceso de reconocimiento

de patrones (véase Figura 4). En algunas aplicaciones, el robot computarizado reconoce la

presencia y orientación de cada parte mecánica mediante un proceso de reconocimiento de

patrones que consiste en la lectura de los números de código que se fijan a cada parte. A

continuación el robot levanta la parte. La mueve a un lugar conveniente para su ensamble, y

después ensambla varias partes para formar un componente. Una computadora digital bien

2

Medios para Representación

Elementos del diagrama funcional o diagrama de flujo

2.1

de señales

2.1.1

Bloque de transferencia y línea de acción

( )

d

X s

( )

W s X s( )

( )

Z s

( )

Y s

( )

S

G s

( )

C

G s

_

Ilustración 5: Bucle de control cerrado estándar

El diagrama funcional Ilustración 5 muestra un bucle de control cerrado en su forma estándar. La

función de transferencia del controlador 𝐺_𝐶(𝑠) y del sistema controlado 𝐺_𝑆(𝑠) se expresa con

bloques de transferencia. Cada bloque contiene mínimo una entrada, mínimo una salida y un

comportamiento de transferencia:

Comportamiento de Transferencia

Entrada Salida

II. Respuesta al escalón, que es la reacción del sistema a un escalón en la entrada

III. Respuesta en frecuencia, que es la reacción del sistema a un señal armónica en la entrada

IV. Función de transferencia para señales de entrada transformadas en Laplace

La ecuación diferencial, la respuesta al escalón, la respuesta en frecuencia y la función de

transferencia (I-IV) representan el mismo comportamiento y por lo tanto tienen la misma

estructura:

Ecuación diferencial

( )

x t y t( )

1 dy

T y x

dt

  

Respuesta al escalón

( )

x t y t( )

1 T1

𝑜𝑟𝑑𝑒𝑛𝑎𝑑𝑎 𝑦(𝑡) 𝑎𝑏𝑠𝑐𝑖𝑠𝑎 𝑡

Respuesta en

frecuencia

( )

X j





1 1 1 j



Función de

transferencia

( )

X s Y s( )

Ejemplo 2.1: Elemento de retardo eléctrico y mecánico (Elemento _𝑷𝑻𝟏)

R

C

( ) _e( )

x t u t y t( ) u t_s( )

( )

i t

Ilustración 7: Circuito RC

k

r

f

c

( ) e( )

x t s t

( ) s( )

y t s t

Ilustración 8: Sistema resorte amortiguación

Se cambia la voltaje de 𝑢_𝑒= 0 a

𝑢𝑒0 = 𝑥0.

Se cambia la posición de 𝑠_𝑒= 0 a

𝑠𝑒0 = 𝑥0.

𝑖 = 𝐶 ∙𝑑𝑢_{𝑑𝑡 = 𝐶 ∙ 𝑢}𝑠 𝑠̇

𝑢𝑒= 𝑖 ∙ 𝑅 + 𝑢𝑠

𝑢𝑒= 𝑅𝐶 ∙ 𝑢̇𝑠+ 𝑢𝑠

𝑥 = 𝑇1𝑦̇ + 𝑦

𝑟𝑘∙𝑑𝑠_{𝑑𝑡 = 𝑐}𝑠 𝑓(𝑠𝑒− 𝑠𝑠)

𝑟𝑘∙ 𝑠̇𝑠+ 𝑐𝑓∙ 𝑠𝑠= 𝑐𝑓∙ 𝑠𝑒

𝑠𝑒=𝑟_𝑐𝑘

𝑓∙ 𝑠̇𝑠+ 𝑠𝑠

𝑥 = 𝑇1𝑦̇ + 𝑦

con 𝑇₁= 𝑅𝐶 con 𝑇1=𝑟_𝑐𝑘_𝑓

La ecuación diferencial de las dos sistemas es idéntica y resulta tienen la misma solución en el

tiempo. La ecuación diferencial se convierte a la función de transferencia mediante

Sistemas no-lineales también se pueden representar con bloques de transferencia:

Ecuación de control

( )

u t

i t

( )

2

I

 

k

U

Curva característica

estacionaria

( )

x t

y t

( )

x

y

La curva característica describe el comportamiento estacionario de un amplificador con limitación.

2.1.2

Elementos de interconexión

Con elementos de interconexión se conectan los bloques de transferencia. Los siguientes

elementos son usuales:

 Ramificación  Adición, Inversión  Multiplicación, División

Elemento de ramificación: El señal se ramifica. Cada magnitud de salida es igual la magnitud de

entrada 𝑦(𝑡) = 𝑥(𝑡).

( )

x t

( )

y t

( )

y t

Elemento de adición: Los magnitudes que entran se suman según su signo a una magnitud que

sale. Los signos positivos se pueden omitir, los signos negativos se tienen que indicar.

1

( )

x t

1 2 3

( )

( )

( )

( )

y t

 

x t



x t



x t

2

( )

x t

3

( )

x t

_

Elemento de inversión:

( )

( )

y t

 

x t

( )

x t

Elemento de multiplicación:

1

( )

x t

2

( )

x t

1 2

( )

( )

( )

y t



x t



x t

Elemento de división:

1

( )

x t

2

( )

x t

1 2

( )

( ) /

( )

y t



x t

x t

Las líneas de acción siempre son unidireccionales. No hay retroacciones sobre las líneas de acción

y también se asume sin retroacción los bloques de transferencia. Si hay retroacciones, se tienen

que describir con líneas de acción.

Ejemplo 2.2: Diagramas funcionales

a) Ecuación de un bucle de control con dos perturbaciones 𝑧₁ y 𝑧₂:

b) Elementos diferenciales e integrales:

𝑦(𝑡) =_𝑇1

𝐼∙ ∫ 𝑥(𝑡) 𝑑𝑡

1 I T



( )

y t

( )

x t

𝑦(𝑡) = 𝑇𝐷∙𝑑𝑥(𝑡)_𝑑𝑡

D

T

d

dt

( )

y t

( )

x t

c) Ecuación de la potencia eléctrica 𝑃:

𝑃 = 𝑈 ∙ 𝐼

U

I

P

d) Relación entre fuerza 𝐹, aceleración 𝑎, y distancia 𝑠 de una masa 𝑚:

𝑎(𝑡) =𝐹(𝑡)_𝑚 𝑣(𝑡) = ∫ 𝑎(𝑡) 𝑑𝑡 𝑠(𝑡) = ∫ 𝑣(𝑡) 𝑑𝑡

1

m

( )

v t

( )

F t

s t

( )





( )

a t

e) Ecuación de un bucle cerrado con elementos proporcionales:

𝑥𝑑 = 𝑤 − 𝑥 𝑦 = 𝐾𝑅∙ 𝑥𝑑 𝑥 = 𝐾𝑠∙ 𝑦

d

x

w y x

S

K

R

K

Estructuras del diagrama funcional y simplificaciones

2.2

Las siguientes reglas de simplificación y transformación para estructuras del flujo de señales son

válidas para bucles de control que se describen mediante:

 Elementos proporcionales

 Funciones de respuesta en frecuencia  Funciones de transferencia en Laplace  Funciones de transferencia en z

Con esto la ventaja más importante es que las magnitudes de salida resultan por multiplicación

con la entrada. En los siguientes ejemplos se aplican las reglas de simplificación a elementos

proporcionales sin retardo.

2.2.1

Estructura en serie

La conexión en serie de varios bloques de transferencia se puede juntar a un bloque de

transferencia.

e

x

1

K K₂ K₃

a

x

1 e

K x K K₁ ₂x_e K K₁ ₂K₃x_e

El factor de transferencia de una estructura en serie resulta por la multiplicación de los factores

de transferencias individuales:

1 K 2 K 3 K 1 e

K x

-+

+ 2 e

K x

3 e

K x

e x e x e x e

x x_a

El factor de transferencia de una estructura en paralela resulta de la adición de los factores de

transferencia individuales, teniendo en cuenta los signos de cada factor.

𝑥𝑎= (𝐾1− 𝐾2+ 𝐾3) ∙ 𝑥𝑒= 𝐾 ∙ 𝑥𝑒

Ejemplo 2.3: Un ejemplo de electrotécnica

Se calcula la respuesta en frecuencia de una conexión en serie de dos elementos de retardo sin

efecto retroactivo, que están desacoplados. Sin efecto retroactivo aquí significa, que si se cambia

la carga en la salida de un elemento de transferencia, que no hay un efecto hacia su elemento

anterior. En el siguiente ejemplo no se cambiaría el voltaje 𝑢_𝑠1(𝑡) , cuando haya un cortocircuito

en la salida 𝑢_𝑠2(𝑡). Este comportamiento solo existe en teoría, la tercera ley de Newton enseña

que siempre hay efectos retroactivos.

1

( )

e

u

t

u

( )

t

( ) 0

i t 

1

R

C

1

R

C

2

( )

e

u

t

u

( )

t

Ilustración 9: Filtro de paso-bajo de segundo orden desacoplado

El amplificador debe ser ideal: Resistencia de entrada 𝑅_𝑖 → ∞ , Resistencia de salida 𝑅_𝑠→ 0 ,

Amplificación 𝐾 = 1. Para cada voltaje existe una función de transferencia hacia el próximo

1

(

)

F j



u

(

j



)

(

)

e

u

j



u

(

j



)

u

(

j



)

(

)

K

F

j



F j

(



)

Ilustración 10: Diagrama de flujo de señales del filtro de paso-bajo desacoplado

La respuesta en frecuencia es el cociente entre la salida y la entrada con una señal armónica en la

entrada. Con la ley del divisor de tensión resulta:

𝐹1(𝑗𝜔) =𝑢_𝑢𝑠1(𝑗𝜔)

𝑒1(𝑗𝜔) =

1 𝑗𝜔𝐶⁄ 1

𝑅1+ 1 𝑗𝜔𝐶⁄ 1=

1

1 + 𝑗𝜔𝑅1𝐶1=

1

1 + 𝑗𝜔𝑇1

𝐹2(𝑗𝜔) =𝑢_𝑢𝑠2(𝑗𝜔)

𝑒2(𝑗𝜔) =

1 𝑗𝜔𝐶⁄ 2

𝑅2+ 1 𝑗𝜔𝐶⁄ 2=

1

1 + 𝑗𝜔𝑅2𝐶2=

1

1 + 𝑗𝜔𝑇2

, con las constantes de tiempo 𝑇₁ = 𝑅₁𝐶₁ y 𝑇₂= 𝑅₂𝐶₂. Para el amplificador vale:

𝐹𝐾=𝑢_𝑢𝑒2(𝑗𝜔)

𝑠1(𝑗𝜔) = 1

La conexión en serie de varios bloques de transferencia se puede representar mediante un solo

bloque:

𝐹(𝑗𝜔) =_𝑢𝑢𝑠2(𝑗𝜔)

𝑒1(𝑗𝜔) = 𝐹1(𝑗𝜔) ∙ 𝐹𝐾(𝑗𝜔) ∙ 𝐹2(𝑗𝜔)

=_{1 + 𝑗𝜔𝑇}1

1∙

1

1 + 𝑗𝜔𝑇2 =

1

1 + 𝑗𝜔 ∙ (𝑇1+ 𝑇2) + (𝑗𝜔)2∙ 𝑇1∙ 𝑇2 ( 2 )

En lo siguiente se elimina el amplificador del filtro de paso-bajo (Ilustración 9) y así la corriente

( )

u t

u

( )

t

( ) e i t 1

R

C

R

C

u

( )

t

2( ) i t

1( ) i t

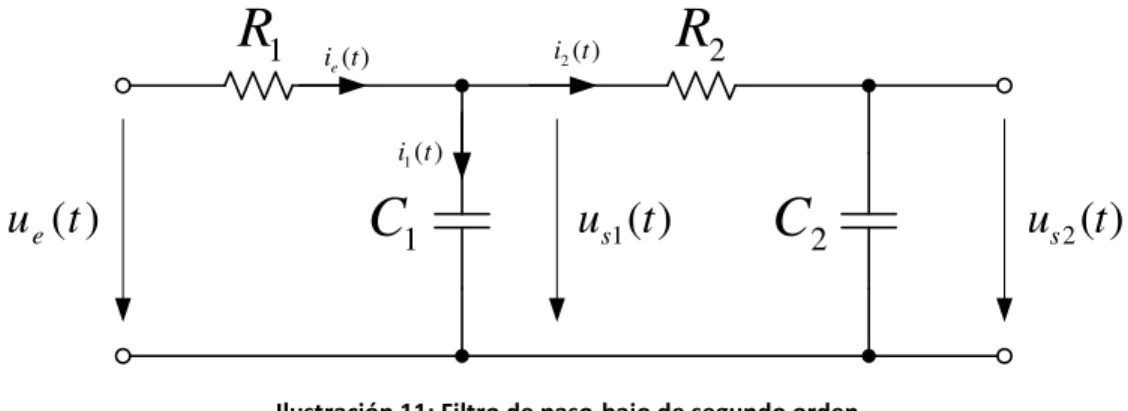
Ilustración 11: Filtro de paso-bajo de segundo orden

El nuevo diagrama de flujo de señales que contiene el efecto retroactivo por la corriente

𝑖2(𝑡) ≠ 0 se puede determinar aplicando las leyes de Kirchhoff:

e

u

i

i

u

i

u

1

1

R

1

C

1

R

1

C

Ilustración 12: Bloques de transferencia del filtro de paso-bajo

Con un análisis de red y usando la ley del divisor de tensión resulta en:

𝐹(𝑗𝜔) =𝑢_𝑢𝑠2(𝑗𝜔)

𝑒(𝑗𝜔) =

𝑢𝑠2

𝑢𝑠1∙

𝑢𝑠1

𝑢𝑒

=_{1 + 𝑗𝜔𝑅}1

2𝐶2∙

1

𝑗𝜔𝐶1‖ (𝑅2+ 1𝑗𝜔𝐶2)

𝑅1+ 1_{𝑗𝜔𝐶1}‖ (𝑅2+ 1_{𝑗𝜔𝐶2})

=_{1 + 𝑗𝜔𝑅}1

2𝐶2∙

1 + 𝑗𝜔𝑅2𝐶2

1 + 𝑗𝜔(𝑅1𝐶2+ 𝑅2𝐶2+ 𝑅1𝐶2) + (𝑗𝜔)2𝑅1𝐶1𝑅2𝐶2

=_{1 + 𝑗𝜔 ∙ (𝑇} 1

1+ 𝑇2+ 𝑇12) + (𝑗𝜔)2∙ 𝑇1∙ 𝑇2 ( 3 )

2.2.3

Estructura en bucle

2.2.3.1

Estructura con realimentación negativa indirecta

En la rama de realimentación del diagrama de flujo de señales hay un bloque de transferencia con

el factor 𝐾_𝑀, se compara la variable de referencia 𝑤 con la señal 𝑥 ∙ 𝐾_𝑀. Los registradores de

voltaje por ejemplo tienen una estructura así. La variable de referencia 𝑤 (tensión eléctrica) y la

variable controlada 𝑥 (posición del lápiz) no tienen la misma dimensión.

S

K

M

K

C

K

M

x K



_

w

y

x

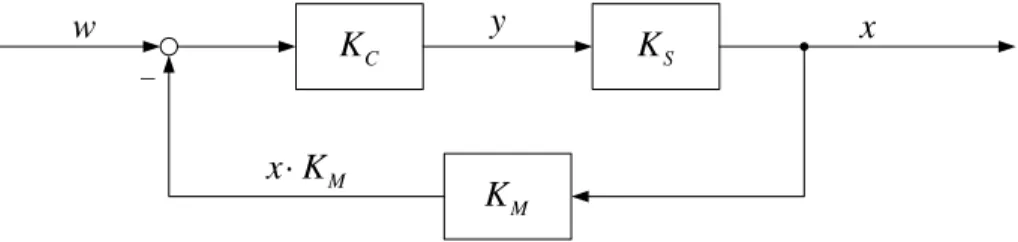
Ilustración 13: Estructura de bucle de control con realimentación negativa indirecta

Los factores de transferencia 𝐾_𝐶, 𝐾_𝑆, 𝐾_𝑀 son del controlador, del sistema controlado y del equipo

de medición. La ecuación del bucle de control se crea, tomando una vuelta en el bucle y después

separando los variables. Con la ecuación de bucle de control se puede determinar la función de

transferencia y de respuesta en frecuencia.

𝑥 = 𝐾𝐶∙ 𝐾𝑆∙ (𝑤 − 𝑥 ∙ 𝐾𝑀)

𝑥 ∙ (1 + 𝐾𝑀∙ 𝐾𝐶∙ 𝐾𝑆) = 𝑤 ∙ 𝐾𝐶∙ 𝐾𝑆

𝑥 =_{1 + 𝐾}𝐾𝐶∙ 𝐾𝑆

𝑀∙ 𝐾𝐶∙ 𝐾𝑆∙ 𝑤 = 𝐾 ∙ 𝑤

( 4 )

𝐾=_𝑤𝑥 =_{1 +𝐾}𝐾𝐶∙𝐾𝑆

2.2.3.2

Estructura con realimentación negativa directa

La mayoría de los bucles de control con sola una realimentación se pueden expresar con

realimentación negativa directa. Los factores de transferencia 𝐾_𝐶, 𝐾_𝑆 son del controlador y del

sistema controlado. S K C K _

w y x

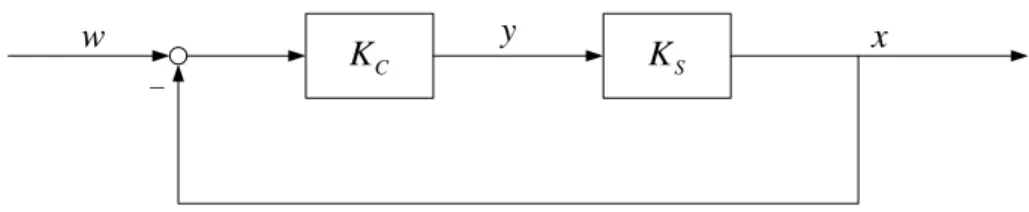
Ilustración 14: Estructura de bucle de control con realimentación negativa directa

La ecuación del bucle de control se determina tomando la formula ( 4 ) y sustituyendo 𝐾_𝑀= 1:

( 5 )

1 C S C S K K K K    x w

Se plantea el siguiente bucle de control con las funciones de transferencia:

2( )

G s

1( )

G s

_ ( )

W s Y s( ) X s( )

, con:

𝐺1(𝑠) =𝑁_𝐷1(𝑠)

1(𝑠) 𝐺2(𝑠) =

𝑁2(𝑠)

𝐷2(𝑠)

Aplicando formula ( 5 ) se recibe la función de transferencia del bucle de control:

𝐾=_𝑤𝑥 =_{1 +}𝐾𝐶_𝐾∙𝐾𝑆

En general se define la siguiente formula:

( 6 )

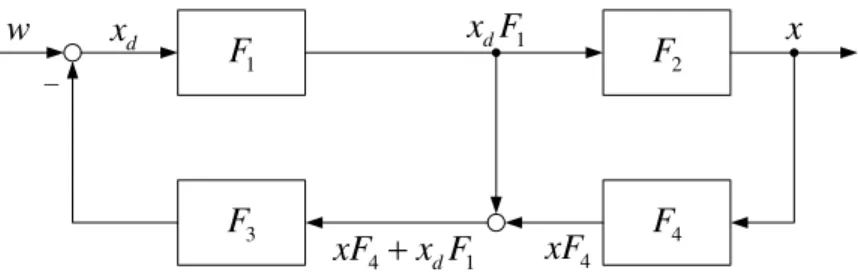
Ejemplo 2.4: Comportamiento de transferencia

de un bucle de control con realimentación de una variable intermedia. Las funciones 𝐹₁… 𝐹₄

representan aquí cualquier comportamiento de transferencia.

2

F

1

F

_

w x

4

F

3

F

d

x x Fd 1

4

xF

4 d 1

xF x F

Ilustración 15: Bucle de control con variable intermedia

La salida 𝑥 es una función de la variable de error, pues 𝑥 = 𝑥_𝑑𝐹₁𝐹₂. En seguida se calcula la

variable de error 𝑥_𝑑 en función de la salida sobre las realimentaciones:

𝑥𝑑= 𝑤 − 𝐹3(𝑥𝐹4+ 𝑥𝑑𝐹1)

= 𝑤 − 𝑥𝑑𝐹1𝐹2𝐹3𝐹4− 𝑥𝑑𝐹1𝐹3

𝑤 =_𝐹𝑥

1𝐹2[1 + 𝐹1𝐹2𝐹3𝐹4+ 𝐹1𝐹3]

Resulta la función de transferencia completa:

𝐹 = 𝑥

𝑤 =

𝐹1𝐹2

1 + 𝐹1𝐹3+ 𝐹1𝐹2𝐹3𝐹4

𝐺(𝑠) =_{1 +}𝐺1_𝐺𝐺2

1𝐺2=

𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑜𝑓𝑢𝑛𝑐𝑖𝑜𝑛𝑒𝑠𝑟𝑎𝑚𝑎𝑑𝑒𝑖𝑑𝑎

Tomando en cuenta el resulta del Ejemplo 2.4 se define la siguiente fórmula para varios bucles en

cascada:

( 7 )

Ejemplo 2.5: Bucle cerrado en cascada I

3( )

G s

1( )

G s

_ ( )

W s X s( )

2( )

G s

_

Se calcula la función de transferencia con formula ( 7 ):

𝐺(𝑠) =_𝑊(𝑠)𝑋(𝑠) =_{1 + 𝐺}𝐺1𝐺2𝐺3

2𝐺3+ 𝐺1𝐺2𝐺3

Ejemplo 2.6: Bucle cerrado en cascada II

3( )

G s

1( )

G s

_ ( )

W s X s( )

2( )

G s G s₄( )

_

5( )

G s

Se calcula la función de transferencia con formula ( 7 ):

𝐺(𝑠) =_{𝑊(𝑠) =}𝑋(𝑠) _{1 + 𝐺} 𝐺1𝐺2𝐺3𝐺4

4− 𝐺2𝐺3𝐺4𝐺5+ 𝐺1𝐺2𝐺3𝐺4

2.2.4

Ecuación diferencial con bloques de transferencia

Para representar una ED de orden 𝑛 con bloques de transferencia se tienen que introducir

variables de estado e integradores. Se requieren 𝑛 + 1 variables de estados e 𝑛 integradores.

Las 𝑛 condiciones iniciales de la ED se definen en los parámetros de los integradores, puesto que

cada integrador necesita un valor donde empieza a integrar.

a) Ecuación diferencial de primer orden

𝑥(𝑡) = 𝑦̇(𝑡) + 𝑦(𝑡)

Se definen variables de estado

𝑦1 = 𝑦

𝑦2 = 𝑦̇1= 𝑦̇

, que se sustituyen en la ED y se despeja la mayor variable de estado:

𝑥 = 𝑦2+ 𝑦1

𝑦2= 𝑥 − 𝑦1

Esta ecuación se modela con bloques de transferencia como un bucle de control, cuando existen

dos representaciones del integrador:

_

2

y



y

x

_

2

y

1

s

1

y

x

b) Sistema de segundo orden

𝑦̈(𝑡) + 16𝑦(𝑡) = 𝑥(𝑡)

𝑦1 = 𝑦

𝑦2 = 𝑦̇1

𝑦3 = 𝑦̇2 = 𝑥 − 16𝑦1

_ 3

y

y

x

y

16

1

16

s



y

x

Las condiciones iniciales se definen en los parámetros de los integradores.

c) Sistema de segundo orden

𝑦̈(𝑡) + 6𝑦̇(𝑡) + 5𝑦(𝑡) = 𝑥(𝑡) = 0

𝑦1= 𝑦

𝑦2= 𝑦̇1

𝑦3= 𝑦̇2= −6𝑦2− 5𝑦1

_ 3

y

y

y

6

5

1

6

5

s



s



y

x

Como la ED es homogénea (entrada 𝑥(𝑡) = 0), el sistema es libre y su movimiento solo depende

Cálculo de bucles de control con elementos

2.3

proporcional

Se estudia un bucle de control sin retardos. Controlador y sistema controlado son elementos

proporcionales. Con el comportamiento de transferencia se quiere determinar el factor de

control. El comportamiento de transferencia para un bucle de control sin retardos es la relación

entre la variable de entrada con la variable de salida en el dominio de tiempo.

d

x

1

z

z

S

K

C

K

w

y

x

Ilustración 16: Bucle de control con elementos ideales

𝐾𝐶 y 𝐾𝑆 son factores de transferencia del controlador (ganancia del controlador) y del sistema controlado (ganancia del sistema). Hay que distinguir entre dos variables de perturbación: 𝑧₁ en

la entrada (suministro) y 𝑧₂ en la salida (carga) del sistema controlado. En sistemas técnicos la

variable de control 𝑦 equivale a la potencia suministrada al sistema. La variable de perturbación

de suministro disminuye esta potencia, si actúa negativa. La variable de perturbación de carga

influye la variable controlada directa. Si una perturbación actúa dentro del sistema controlado, se

transforma a la entrada o salida del sistema usando las reglas del párrafo 2.4. Usualmente se

estudian separados los efectos de la variable de referencia y las perturbaciones a la variable

controlada.

Función de transferencia de la perturbación de suministro: 𝑤 = 0, 𝑧₁≠ 0, 𝑧₂= 0

(−𝑥 ∙ 𝐾𝐶 + 𝑧1) ∙ 𝐾𝑆 = 𝑥 𝑥 ∙ (1 + 𝐾𝐶 ∙ 𝐾𝑆) = 𝐾𝑆∙ 𝑧1

Sin control, cuando 𝐾_𝐶 = 0, resulta 𝐾_𝑧1 = 𝐾_𝑆.

Función de transferencia de la perturbación de carga: 𝑤 = 0, 𝑧₁= 0, 𝑧₂≠ 0

−𝑥 ∙ 𝐾𝐶∙ 𝐾𝑆+ 𝑧2= 𝑥 𝑥 ∙ (1 + 𝐾𝐶∙ 𝐾𝑆) = 𝑧2

Sin control, cuando 𝐾_𝐶 = 0, resulta 𝐾_𝑧2 = 1.

Por el controlador se disminuye el efecto de las perturbaciones a la variable controlada. El factor

de control 𝑟 es una medida de la supresión de perturbaciones. La relación entre la función de

transferencia de perturbación con control y sin control resulta el factor de control:

Con el factor de control se puede calcular el comportamiento de bucles de control sin retardos. Si

los bucles tienen retardos, el factor de control solo es válido para el comportamiento estacionario.

Un control en bucle cerrado es mejor, cuando menor es el factor de control.

𝐾𝑧1 =

𝑥 𝑧1=

𝐾𝑆

1 +𝐾𝐶∙𝐾𝑆

𝐾𝑧2 =

𝑥 𝑧2 =

1

1 +𝐾𝐶∙𝐾𝑆

𝑟=_{1 +𝐾}1

𝐶∙𝐾𝑆 =

𝐾𝑧 (𝑐𝑜𝑛𝑐𝑜𝑛𝑡𝑟𝑜𝑙)

Ejemplo 2.7: Factor de control con elementos proporcionales

Controlador y sistema controlado son elementos proporcionales con 𝐾_𝐶 = 12 y 𝐾_𝑆= 2. Variable

de referencia 𝑤 y variable de perturbación de suministro se cambian de cero a uno. Se calculan

los resultados de la variable controlada 𝑥.

d

x

z

S

K

K

w

y

x

Respuesta a la variable de referencia:

𝑤(𝑡) = {0 para 𝑡 ≤ 0_{1 para 𝑡 > 0} 𝑧(𝑡) = 0

𝑥 = 𝐾𝐶∙ 𝐾𝑆

1 + 𝐾𝐶∙ 𝐾𝑆∙ 𝑤 = 0.96 < 𝑤

Respuesta a la perturbación:

𝑧(𝑡) = {0 para 𝑡 ≤ 0_{1 para 𝑡 > 0} 𝑤(𝑡) = 0

𝑥𝑧 =_{1 + 𝐾}𝐾𝑆

𝐶∙ 𝐾𝑆∙ 𝑧 = 0.08 > 0

𝑟 =_{1 + 𝐾}1

Conversión de diagramas funcionales

2.4

2.4.1

Reglas para la conversión

En diagramas funcionales más complejos, las reglas de conversión simples ya no son suficientes,

para llevar a cabo más estudios sobre sistemas de control. Eso también es el caso, cuando se

intersectan lazos separados entre ellos. Esto se llama enlazamiento.

Para transformar estructuras de control se necesitan las siguientes operaciones:

 Juntar bloques de transferencia en seria o en paralela  Simplificar estructuras realimentadas

 Trasladar bloques de transferencia y lugares de adición o elementos de ramificación  Trasladar y juntar lugares de adición

 Trasladar lugares de adición y de ramificación

A continuación se presentan reglas, con las que se puede convertir un diagrama funcional mallado

así, que en consecuencia se puede determinar la respuesta en frecuencia o la función de

transferencia. El comportamiento de transferencia de las estructuras en una regla es equivalente.

Las reglas de conversión están especificadas para la respuesta en frecuencia 𝐹(𝑗𝜔) y funciones

armónicas 𝑥_𝑒(𝑗𝜔) y 𝑥_𝑎(𝑗𝜔). Las reglas también valen para funciones de transferencia 𝐺(𝑠) o si

2.4.2

Tabla de las reglas de conversión

1. Unión de bloques de transferencia paralelas

𝑥𝑎 = (𝐹1± 𝐹2) ∙ 𝑥𝑒

1

F

2

F

e

x x_a



1 2

F



F

e

x

x

2. Unión de bloques de transferencia en serie

𝑥𝑎 = 𝐹1∙ 𝐹2∙ 𝑥𝑒

1

F F₂

e

x x_a

1 2

F F



e

x

x

3. Estructura en bucle con realimentación negativa indirecta

𝑥𝑎= 𝐹1∙ (𝑥𝑒∓ 𝐹2∙ 𝑥𝑎)

1

F

2

F

e

x x_a

1 1 2 1 F F F   e

x x_a

4. Estructura en bucle con realimentación negativa directa

𝑥𝑎= 𝐹1∙ (𝑥𝑒∓ 𝑥𝑎)

1

F

e

x xa

1 1 1 F F  e

5. Traslado del lugar de adición y bloque de transferencia

𝑥𝑎= 𝐹 ∙ (𝑥𝑒1± 𝑥𝑒2)

F

1

e

x x_a





6. Traslado del lugar de adición y bloque de transferencia

𝑥𝑎= 𝐹 ∙ 𝑥𝑒1± 𝑥𝑒2

F 1 e x



x x_a



2

e

x

1 F

7. Traslado del elemento de ramificación y bloque de transferencia

𝑥𝑎 = 𝐹 ∙ 𝑥𝑒

F e x a x a

x xe

a x a x F F

8. Traslado del elemento de ramificación y bloque de transferencia

𝑥𝑎1= 𝐹 ∙ 𝑥𝑒, 𝑥𝑎2= 𝑥𝑒

e x 1 a x 2 a x F F e x

1 /F

9. Traslado del lugar de adición

𝑥𝑎= 𝑥𝑒1± 𝑥𝑒2± 𝑥𝑒3

1 e x





x x_e1



3 e x



10. Unión de lugares de adición

𝑥𝑎= 𝑥𝑒1± 𝑥𝑒2± 𝑥𝑒3

1 e x









11. Traslado del lugar de adición y elemento de ramificación

𝑥𝑎= 𝑥𝑒1± 𝑥𝑒2

2.4.3

Ejemplos de aplicación

Ejemplo 2.8: Control de velocidad de giro:

En control se necesita mucho la regla no. 5. Se presenta el control de velocidad de giro con la

suposición que el sistema controlado, el controlador y el equipo de medición no contienen

retardos o elementos no linéales.

S

K

T

K

C

K

x

U

_

w

n

U

n

T

K

U

U

𝑛𝑤= 2000 𝑚𝑖𝑛−1 Variable de referencia (velocidad de giro)

𝑛𝑥 Variable controlada (velocidad de giro)

𝑈𝑦 Variable de control (Tensión eléctrica de inducido)

𝐾𝐶 = 20 Factor de ganancia del controlador

𝐾𝑆= 500 𝑚𝑖𝑛−1/𝑉 Factor de ganancia del sistema controlada

𝐾𝑇 = 1 𝑚𝑉/𝑚𝑖𝑛−1 Constante tacométrica

La variable de referencia 𝑛_𝑤 se tiene que convertir a una voltaje 𝑈_𝑤 mediante el elemento de

transferencia 𝐾_𝑇. Se quiere calcular la variable controlada 𝑛_𝑥 para un valor de referencia de

𝑛𝑤 = 2000 𝑚𝑖𝑛−1. Con regla no. 5 se puede trasladar el bloque de transferencia 𝐾𝑇:

S

K

C

K

_

w

n

U

U

n

T

K

Los bloques 𝐾_𝑇 y 𝐾_𝐶 se unen a un solo bloque:

S

K

C T

K



K

_

w

n

U

n

De la formula ( 8 ) se determina el valor estacionario de la variable controlada 𝑛_𝑥:

𝑛𝑥∙ (1 + 𝐾𝑇 ∙ 𝐾𝐶∙ 𝐾𝑆) = 𝐾𝑇∙ 𝐾𝐶∙ 𝐾𝑆∙ 𝑛𝑤

𝑛𝑥 =_{1 + 𝐾}𝐾𝑇∙ 𝐾𝐶∙ 𝐾𝑆

𝑇∙ 𝐾𝐶∙ 𝐾𝑆∙ 𝑛𝑤= 1818.2 𝑚𝑖𝑛

−1

El bucle de control tiene un valor de error estacionario de:

𝑛𝑥𝑑 = 𝑛𝑤− 𝑛𝑥 = 181.8 𝑚𝑖𝑛−1

y alcanza solo cerca 91% del valor de referencia. Este error se puede disminuir a través del

aumento del factor de ganancia del controlador. Sin embargo eso puede hacer inestable el bucle

de control, si existen elementos de retardo en el mismo.

Ejemplo 2.9 Diagrama funcional:

El siguiente diagrama funcional queda para estudios en la casa:

22

F

21

F

_

e

x x_a

1

F

_

31

F

32

3

Métodos Matemáticos

Normalización de ecuaciones (estandarización)

3.1

Con valores sin dimensiones se simplifican la aplicación de métodos de control. Las magnitudes del

sistema de control se relacionan a valores característicos con la estandarización. Estas magnitudes

se dividen con los valores característicos y resultan adimensional. Valores característicos en

general son valores operativos (valores nominales) o valores del punto de operación 𝑂. Se

considera la siguiente ecuación lineal de un sistema controlado:

𝑥 = 𝐾𝑆∙ 𝑓(𝑦)

Si la variable controlada 𝑥 tiene otra dimensión que la variable de control 𝑦, entonces la

dimensión del factor 𝐾_𝑆 no es [1]. Se relacionan las variables 𝑥 y 𝑦 a sus valores nominales 𝑥_𝑁

y 𝑦_𝑁, resulta en:

𝑥

𝑥𝑁= 𝐾𝑆∙

1

𝑥𝑁∙ 𝑓 (𝑦𝑁∙

𝑦

𝑦𝑁)

𝑥′_{= 𝐾}

𝑆∙𝑦_𝑥𝑁

𝑁∙ 𝑓(𝑦

′₎

𝑥′_{= 𝐾}

𝑆′∙ 𝑓(𝑦′)

Las magnitudes normalizadas 𝑥′, 𝑦′ y 𝐾_𝑆′ son adimensional. Las ventajas son:

 Resultan ecuaciones adimensionales más simples  Diagramas funcionales serán más simples

 Sistemas normalizadas se pueden comparar (mejor)

El voltaje 𝑈_𝑥 del alternador de un vehículo depende de la velocidad de giro 𝑛_𝑦. El factor 𝐾_𝑆

representa la constante de motor, que depende de la construcción del mismo:

𝑈𝑥 = 𝐾𝑆∙ 𝑛𝑦 [𝑉] = [_{𝑟𝑝𝑚] ∙}𝑉 [𝑟𝑝𝑚]

El voltaje nominal resulta por la velocidad nominal 𝑈_𝑥𝑁 = 𝐾_𝑆∙ 𝑛_𝑦𝑁, entonces:

𝑈𝑥

𝑈𝑥𝑁 =

𝐾𝑆∙ 𝑛𝑦

𝐾𝑆∙ 𝑛𝑦𝑁 [1] = [1]

Entonces el valor nominal del voltaje es igual al valor nominal de la velocidad: 𝑈_𝑥′ = 𝑛_𝑦′. El voltaje

𝑈𝑥 se convierte a un valor fraccionado adimensional.

Por ejemplo:

𝑈𝑥𝑁 = 24 𝑉𝐷𝐶

𝑛𝑦𝑁= 236 𝑟𝑝𝑚

𝑛𝑦= 59 𝑟𝑝𝑚

Ilustración 17: Pittman GM9236S021

La constante de motor es 𝐾_𝑆=𝑈𝑥𝑁 𝑛𝑦𝑁=

24 𝑉

236 𝑟𝑝𝑚≈ 0.102 𝑉

𝑟𝑝𝑚. La velocidad nominal resulta:

Hay que normalizar la ecuación del desplazamiento 𝑥(𝑡) = ∫ 𝑣 𝑑𝑡 con los valores nominales

𝑥𝑁= 1 𝑚 y 𝑣𝑁 = 0.2 𝑚𝑠−1:

𝑥(𝑡)

𝑥𝑁 =

𝑣𝑁

𝑥𝑁∙ ∫

𝑣(𝑡)

𝑣𝑁 𝑑𝑡

𝑥′₌ 1

𝑇𝐼∙ ∫ 𝑣

′_𝑑𝑡

[1] = [1_{𝑠] ∙}[1] ∙ [𝑠]

La constante de tiempo de integración 𝑇_𝐼= 5 𝑠 es el tiempo que necesita un objeto para llegar a

𝑥𝑁= 1 𝑚, si se mueve constante con 𝑣𝑁= 0.2 𝑚𝑠−1.

Ejemplo 3.3:

Hay que normalizar la ecuación de velocidad 𝑣(𝑡) =𝑑𝑥

𝑑𝑡 con los valores nominales 𝑣𝑁= 2 𝑚𝑠−1

y 𝑥_𝑁 = 0.5 𝑚:

𝑣(𝑡)

𝑣𝑁 =

𝑥𝑁

𝑣𝑁∙

𝑑 (𝑥(𝑡)_𝑥

𝑁 )

𝑑𝑡

𝑣′_{(𝑡) = 𝑇}

𝐷∙𝑑𝑥 ′_(𝑡)

𝑑𝑡

[1] = [𝑠] ∙ [1_𝑠]

La constante de tiempo de diferenciación 𝑇_𝐷= 0.25 𝑠 es el tiempo que necesita un objeto para

Linealización de elementos del bucle de control

3.2

3.2.1

Definición de linealidad

Elementos del sistema de control son lineales, si cumplen el principio de amplificación y el

principio de superposición.

Principio de amplificación:

La amplificación del argumento de una función lineal 𝑥 = 𝑓(𝑦) con un factor 𝐾, amplifica igual el

valor de la función:

𝐾 ∙ 𝑥 = 𝑓(𝐾 ∙ 𝑦) = 𝐾 ∙ 𝑓(𝑦) ( 9 )

Ilustración 18: Principio de amplificación

Principio de superposición:

Ilustración 19: Principio de superposición

Ejemplo 3.4: Elemento proporcional

Hay que investigar, si un elemento proporcional 𝑥 = 𝐾_𝑃∙ 𝑦 = 𝑓(𝑦) es lineal. Se le aplica el

principio de amplificación:

𝐾 ∙ 𝑥 = 𝐾 ∙ 𝐾𝑃𝑦 = 𝐾𝑃∙ 𝐾𝑦 = 𝑓(𝐾𝑦)

, y el principio de superposición:

𝑥1= 𝐾𝑃𝑦1

𝑥2= 𝐾𝑃𝑦2

𝑥1± 𝑥2= 𝐾𝑃𝑦1± 𝐾𝑃𝑦2= 𝐾𝑃(𝑦1± 𝑦2)

𝑥1± 𝑥2= 𝑓(𝑦1) ± 𝑓(𝑦2) = 𝑓(𝑦1± 𝑦2)

Como el elemento proporcional cumple con los dos teoremas, es lineal.

Muchos métodos eficientes de teoría de control solamente se pueden aplicar a elementos

lineales. Elementos no-lineales se tienen que linealizar entonces, para que se puedan aplicar esos

métodos. Las perturbaciones en control de referencia fija solo causan desviaciones pequeñas

alrededor del punto de operación. Por lo tanto las curvas características no-lineales se linealizan

con precisión alta en el punto de operación. El arranque del sistema de control no se toma en

3.2.2

Linealización de una entrada

Curvas características, que se determinaron mediante mediciones experimentales, se linealizan en

un punto de operación 𝑂 aplicando la tangente en este punto. Un punto de operación 𝑂 es un

punto (valores constantes) específico del sistema de control, donde se quiere mantener el sistema

estable alrededor de este punto.

Ilustración 20: Linealización de una curva característica experimental

La constante de proporcionalidad 𝐾_𝑃 es la ganancia del elemento del bucle de control en el

estado estable para pequeños cambios en la variable de entrada. La dimensión de 𝐾_𝑃 se define

con la dimensión de la variable de salida dividida con la dimensión de la variable de entrada:

dim [𝐾𝑃] =dim [𝑥]_{dim [𝑦]} ( 11 )

Si se puede representar la curva característica analítica (con ecuaciones), entonces la constante de

, se consideran las siguientes magnitudes:

𝑦 = 𝑓(𝑡) Variable de entrada 𝑥 = 𝑓(𝑦(𝑡)) Variable de salida

𝑦𝑂 = 𝑐𝑜𝑛𝑠𝑡. Punto de operación 𝑂 𝑥𝑂= 𝑐𝑜𝑛𝑠𝑡. Punto de operación 𝑂

∆𝑦(𝑡) Pequeña desviación de 𝑦_𝑂 ∆𝑥(𝑡) Pequeña desviación de 𝑥_𝑂

La salida 𝑥(𝑡) es una función de la entrada y por eso también una función del tiempo. El punto de

operación 𝑂 se define por las constantes 𝑦_𝑂 y 𝑥_𝑂 y será el punto alrededor se linealiza la

función no-lineal 𝑓(𝑦). El valor de esta función en el punto de operación se puede aproximar con:

𝑥 = 𝑓(𝑦) = 𝑓(𝑦𝑂+ ∆𝑦(𝑡)) ≈ 𝑥𝑂+ ∆𝑥(𝑡) ( 12 )

Formula ( 12 ) corresponde al Teorema de Taylor de una función racional que se termina tras del

primer término. La fórmula muestra el cambio que haya en la variable de salida, si hay un cambio

en la variable de entrada. Ilustración 21 muestra la linealización gráficamente. El punto 𝐴 se

aproxima mediante el punto 𝐵:

Ilustración 21: Linealización de una curva característica analítica

La pequeña desviación ∆𝑥(𝑡) se define entonces con la pendiente de la función 𝑓(𝑦) en el

punto de operación:

Restando la parte constante 𝑥_𝑂 = 𝑓(𝑦_𝑂) resulta en:

∆𝑥(𝑡) =𝑑𝑓(𝑦)

𝑑𝑦 |_𝑂∙ ∆𝑦(𝑡) =

!

𝐾𝑃∙ ∆𝑦(𝑡) ( 14 )

La linealización resulta en un elemento proporcional, cuya constante de proporcionalidad 𝐾_𝑃

depende del punto de operación seleccionado. Solo es válida para pequeñas desviaciones

alrededor del punto de operación.

( )

y t x t( )

( )

f y

K

El error de la aproximación ( 12 ) se llama error absoluto de linealización y representa la distancia

entre el punto 𝐵 y el punto 𝐴:

𝑒𝑎𝑏𝑠= |𝑓(𝑦𝑂+ ∆𝑦(𝑡)) − (𝑥𝑂+ ∆𝑥(𝑡))|

𝑒𝑎𝑏𝑠= |𝑓(𝑦𝑂+ ∆𝑦(𝑡)) − 𝑓(𝑦𝑂) − 𝐾𝑃∙ ∆𝑦(𝑡)| ( 15 )

Este error es más grande, lo más grande es la curvatura de la función 𝑥 = 𝑓(𝑦), que depende

directo de la segunda derivada 𝑓′′(𝑦). El cociente diferencial de la segunda derivada se define

mediante:

∆2_𝑥

∆𝑦2=

𝑓(𝑦 + ∆𝑦) + 𝑓(𝑦 − ∆𝑦) − 2𝑓(𝑦)

∆𝑦2 ( 16 )

Ejemplo 3.5: Linealización de una función con una entrada

Se necesita linealizar un elemento no-lineal 𝑥(𝑡) = 2 ∙ 𝑦2(𝑡) en el punto de operación 𝑦_𝑂 = 5.

Primero se calcula la componente faltante del punto de operación 𝑥_𝑂 = 𝑓(𝑦_𝑂) = 2 ∙ 𝑦_𝑂2 = 50 ,

después se aplica el teorema de Taylor y se calcula la constante de proporcionalidad:

𝐾𝑃=𝑑𝑓(𝑦)_{𝑑𝑦 |}

𝑦𝑂=5

= 4 ∙ 𝑦𝑂 = 20

El elemento no-lineal se aproxima entonces con una función lineal en el punto de operación ( 12 )

:

𝑥(𝑡) ≈ 𝑥𝑂+ ∆𝑥(𝑡) = 𝑥𝑂+ 𝐾𝑃∙ ∆𝑦(𝑡) = 50 + 20 ∙ ∆𝑦(𝑡)

Un cambio ∆𝑦(𝑡) de la variable de control en el punto de operación 𝑦_𝑂 = 5 se amplifica con

𝐾𝑃= 20. Lo más grande es este cambio, más grande será el error absoluto de linealización 𝑒𝑎𝑏𝑠, porque se aumentará la distancia entre punto 𝐴 y punto 𝐵 en la linealización (Ilustración 21).

Por ejemplo con un cambio de la variable de control ∆𝑦(𝑡) = 0.1 , la variable controlada valdrá

𝑥 = 50 + 20 ∙ 0.1 = 52. Sin linealización la variable controlada será 𝑥 = 𝑓(𝑦_𝑂+ ∆𝑦(𝑡)) = 2 ∙

(5 + 0.1)2_{= 52.02. La diferencia entre los dos valores representa el error absoluto de}

linealización:

𝑒𝑎𝑏𝑠= |𝑓(𝑦𝑂+ ∆𝑦(𝑡)) − 𝑓(𝑦𝑂) − 𝐾𝑃∙ ∆𝑦(𝑡)| = |52.02 − 52| = 0.02

Se sustituye entonces el elemento no-lineal con un elemento proporcional, cuya constante de

proporcionalidad 𝐾_𝑃 depende del punto de operación alrededor se linealiza el elemento

no-lineal:

( )

3.2.3

Linealización de varias entradas

Elementos no-lineales pueden tener más que una entrada:

1

( )

y t

( )

x t

1 2

( ,

,...,

)

f y y

y

2

( )

y t

( )

m

y t

...

Ilustración 22: Elemento no-lineal con varias entradas

𝑥(𝑡) = 𝑓(𝑦1, 𝑦2, ⋯ , 𝑦𝑚)

Ahora se tiene que aplicar el teorema de Taylor a cada variable de entrada. Formula ( 12 ) se

convierte a:

𝑥 = 𝑓(𝑦1𝑂+ ∆𝑦1(𝑡), 𝑦2𝑂+ ∆𝑦2(𝑡), ⋯ , 𝑦𝑚𝑂+ ∆𝑦𝑚(𝑡)) ≈ 𝑥𝑂+ ∆𝑥(𝑡) ( 17 )

La pequeña desviación ∆𝑥(𝑡) ahora representa el diferencial total, que contiene las derivadas

parciales con respeto a cada variable de entrada:

𝑥𝑂+ ∆𝑥(𝑡) = 𝑓(𝑦1𝑂, 𝑦2𝑂, ⋯ , 𝑦𝑚𝑂) +_𝜕𝑦𝜕𝑓

1|_𝑂∙ ∆𝑦1(𝑡) +

𝜕𝑓

𝜕𝑦2|_𝑂∙ ∆𝑦2(𝑡) + ⋯ +

𝜕𝑓

𝜕𝑦𝑚|_𝑂∙ ∆𝑦𝑚(𝑡) ( 18 )

y que se puede expresar como suma:

∆𝑥(𝑡) = ∑_𝜕𝑦𝜕𝑓

𝑖|𝑂∙ ∆𝑦𝑖(𝑡) 𝑚

𝑖=1

( 19 )

Cada derivada parcial representa una constante de proporcionalidad y el elemento no-lineal se

aproxima con una combinación lineal de varios elementos proporcionales:

Todas las entradas ahora influyen separadas a la salida, se dice que las entradas están

desacopladas mutuamente:

1

( )

y t



( )

x t



K

2

( )

y t



K

( )

y t



K

Ilustración 23: Varios elementos proporcionales en paralelo

Ejemplo 3.6: Linealización de una función con dos entrada

Se quiere linealizar el elemento no-lineal:

𝑥(𝑡) = 𝑓(𝑦1, 𝑦2) =𝑦1

2_(𝑡)

𝑦2(𝑡)

en el punto de operación 𝑦_1𝑂 = 1 y 𝑦_2𝑂 = 2.

Primero se calcula la componente faltante del punto de operación 𝑥_𝑂 = 𝑓(𝑦_1𝑂, 𝑦_2𝑂) =𝑦1𝑂2

𝑦2𝑂= 0.5

, después se aplica el teorema de Taylor y se calculan las constantes de proporcionalidad:

𝐾𝑃1=_𝜕𝑦𝜕𝑓

1|𝑦1𝑂 𝑦2𝑂

=2 ∙ 𝑦_𝑦 1𝑂

2𝑂 = 1

𝐾𝑃2=_𝜕𝑦𝜕𝑓

2|𝑦1𝑂 𝑦2𝑂

= −𝑦1𝑂2

Calculo de ecuaciones diferenciales para bucles de

3.3

control

Usualmente la relación entre la magnitud de entrada y salida de un sistema de control se describe

con ecuaciones diferenciales no-lineales, cuyas soluciones son laboriosos por lo general. Se limita

el análisis del sistema entonces al punto de operación 𝑂, donde se puede linealizar el sistema. El

resultado es una ecuación diferencial lineal con coeficientes constantes y real:

𝑎𝑛∙𝑑

𝑛_𝑦

𝑑𝑡𝑛+ 𝑎𝑛−1∙

𝑑𝑛−1_𝑦

𝑑𝑡𝑛−1+ ⋯ + 𝑎1∙

𝑑𝑦

𝑑𝑡 + 𝑎0∙ 𝑦 =

𝑏𝑚∙𝑑

𝑚_𝑥

𝑑𝑡𝑚 + 𝑏𝑚−1∙𝑑

𝑚−1_𝑥

𝑑𝑡𝑚−1+ ⋯ + 𝑏1∙𝑑𝑥_{𝑑𝑡 + 𝑏}0∙ 𝑥 _{(𝐧 ≥ 𝐦)} ( 21 )

𝑛 representa el orden de la ecuación diferencial (ED) y depende del “la cantidad de los

acumuladores de energía” del sistema.

3.3.1

Solución de ecuaciones diferenciales lineales

Si se conoce la función de entrada 𝑥(𝑡) y los 𝑛 valores iniciales:

𝑦(0), 𝑦̇(0), 𝑦̈(0), …, 𝑦(𝑛−1)₍₀₎

, se puede determinar la solución completa 𝑦(𝑡) de la ecuación diferencial. Puesto que la ED es

lineal, la solución completa resulta por la suma de la solución homogénea y la solución particular

𝑦(𝑡) = 𝑦ℎ(𝑡) + 𝑦𝑝(𝑡). Con los valores iniciales se determinan las constantes de integración de

𝑦ℎ(𝑡). Por el tipo de la función de entrada 𝑥(𝑡) se plantea el tipo de la solución particular 𝑦𝑝(𝑡).

3.3.1.1

Solución homogénea de una ecuación diferencial homogénea

Se resuelve la ED homogénea

planteando la solución homogénea mediante 𝑦_ℎ(𝑡) = 𝐶 ∙ 𝑒𝛼𝑡 con 𝐶, 𝛼 ∈ ℝ, puesto que esta es

la solución homogénea de una ED lineal homogénea de primer orden. Sustituyendo 𝑦_ℎ(𝑡) y sus

derivadas en la ED ( 22 ):

𝑎𝑛∙ 𝐶 ∙ 𝛼𝑛𝑒𝛼𝑡+ 𝑎𝑛−1∙ 𝐶 ∙ 𝛼𝑛−1𝑒𝛼𝑡+ ⋯ + 𝑎1∙ 𝐶 ∙ 𝛼𝑒𝛼𝑡+ 𝑎0∙ 𝐶 ∙ 𝑒𝛼𝑡 = 0 ( 23 )

Factorizando 𝐶 ∙ 𝑒𝛼𝑡 lleva a la ecuación característica:

𝑎𝑛∙ 𝛼𝑛+ 𝑎𝑛−1∙ 𝛼𝑛−1+ ⋯ + 𝑎1∙ 𝛼 + 𝑎0 = 0 ( 24 )

Según el Teorema fundamental del algebra, ese polinomio tiene 𝑛 raíces 𝛼₁, 𝛼₂, … , 𝛼_𝑛 en el

conjunto de los números complejos. La ecuación característica ( 24 ) se puede factorizar en 𝑛

factores lineales:

𝑎𝑛∙ 𝛼𝑛+ 𝑎𝑛−1∙ 𝛼𝑛−1+ ⋯ + 𝑎1∙ 𝛼 + 𝑎0= 𝑎𝑛∙ (𝛼 − 𝛼1) ∙ (𝛼 − 𝛼2) ∙ … ∙ (𝛼 − 𝛼𝑛) = 0 ( 25 )

Si las 𝑛 raíces de la ecuación característica son reales y distintas, la solución homogénea 𝑦_ℎ(𝑡)

resulta en:

𝑦ℎ(𝑡) = 𝐶1∙ 𝑒𝛼1𝑡+ 𝐶2∙ 𝑒𝛼2𝑡+ ⋯ + 𝐶𝑛∙ 𝑒𝛼𝑛𝑡= ∑ 𝐶𝑖∙ 𝑒𝛼𝑖𝑡

𝑛

𝑖=1

( 26 )

Si las 𝑛 raíces de la ecuación característica son reales y repetidas, la solución homogénea 𝑦_ℎ(𝑡)

resulta en:

𝑦ℎ(𝑡) = 𝑒𝛼1𝑡∙ (𝐶1+ 𝐶2∙ 𝑡 + 𝐶3∙ 𝑡2+ ⋯ + 𝐶𝑛∙ 𝑡𝑛−1) = 𝑒𝛼1𝑡∙ ∑ 𝐶𝑖∙ 𝑡𝑖−1

𝑛

(𝛼 − 𝛼1) ∙ (𝛼 − 𝛼2) = (𝛼 − (𝛿 + 𝑗𝜔)) ∙ (𝛼 − (𝛿 − 𝑗𝜔))

= (𝛼 − 𝛿 − 𝑗𝜔) ∙ (𝛼 − 𝛿 + 𝑗𝜔)

= (𝛼 − 𝛿)2_{− (𝑗𝜔)}2

= (𝛼 − 𝛿)2_{+ 𝜔}2

Si las 𝑚 =𝑛

2 raíces de la ecuación característica son complejas conjugadas:

𝛼1,2= 𝛿1± 𝑗𝜔1, … , 𝛼𝑛−1,𝑛 = 𝛿𝑚± 𝑗𝜔𝑚

, la solución homogénea 𝑦_ℎ(𝑡) resulta en:

𝑦ℎ(𝑡) = 𝑒𝛿1𝑡∙ [𝐶11∙ 𝑒𝑗𝜔1𝑡+ 𝐶12∙ 𝑒−𝑗𝜔1𝑡] + 𝑒𝛿2𝑡∙ [𝐶21∙ 𝑒𝑗𝜔2𝑡+ 𝐶22∙ 𝑒−𝑗𝜔2𝑡] + ⋯ + 𝑒𝛿𝑚𝑡

∙ [𝐶𝑚1∙ 𝑒𝑗𝜔𝑚𝑡+ 𝐶𝑚2∙ 𝑒−𝑗𝜔𝑚𝑡]

= ∑ 𝑒𝛿𝑖𝑡_{∙ [𝐶𝑖1∙ 𝑒}𝑗𝜔𝑖𝑡_{+ 𝐶𝑖2∙ 𝑒}−𝑗𝜔𝑖𝑡_]

𝑚

𝑖=1 ( 28 )

En el caso de 𝑛 = 2 la solución homogénea 𝑦_ℎ(𝑡) = 𝑒𝛿1𝑡∙ [𝐶₁₁∙ 𝑒𝑗𝜔1𝑡+ 𝐶₁₂∙ 𝑒−𝑗𝜔1𝑡] _{se puede}

transformar con la fórmula de Euler 𝑒±𝑗𝜔𝑡= cos(𝜔𝑡) ± 𝑗sen(ωt) a la siguiente forma:

𝑦ℎ(𝑡) = 𝑒𝛿1𝑡∙ [(𝑗𝐶11− 𝑗𝐶12) ∙ 𝑠𝑒𝑛(𝜔1𝑡) + (𝐶11+ 𝐶12) ∙ 𝑐𝑜𝑠(𝜔1𝑡)]

La solución homogénea 𝑦_ℎ(𝑡) es una función real, los coeficientes del seno y coseno también

deben ser reales, por eso las constantes tienen que ser complejas conjugadas 𝐶₁= 𝑎 + 𝑗𝑏 y

𝐶2= 𝑎 − 𝑗𝑏. Así los coeficientes del seno y coseno se convierten en números reales:

𝑗𝐶11− 𝑗𝐶12 = −2𝑏 = 𝐵1

𝐶11+ 𝐶12= 2𝑎 = 𝐵2

La solución homogénea 𝑦_ℎ(𝑡) ahora se presente en su forma trigonométrica:

𝑦ℎ(𝑡) = 𝑒𝛿1𝑡∙ [𝐵1∙ sen(ω1𝑡) + 𝐵2∙ cos (𝜔1𝑡)]

𝑦ℎ(𝑡) = 𝐴𝑒𝛿𝑡sen(𝜔𝑑𝑡 + 𝜙)