U
niversidade
F
ederal da
B
ahia
-UFBA
I
nstituto de
M
atem
atica
´
-IM
Programa deP ´os-Graduac¸ao em˜ Matematica´ -PGMAT Tese deDoutorado
Pesin’s Entropy Formula for
C
1
non-uniformly expanding maps.
Felipe Fonseca dos Santos
Salvador-BA
Pesin’s Entropy Formula for
C
non-uniformly expanding maps.
Felipe Fonseca dos Santos
Tese de Doutorado apresentada ao Colegiado da Pós-Graduação em Matemática UFBA/UFAL como requisito
parcial para obtenção do título de Doutor em Matemática.
Orientador: Prof. Dr. Vitor D. Martins de Araújo
Salvador-BA
Santos, Felipe Fonseca dos.
Pesin’s Entropy Formula forC1 non-uniformly expanding maps
/Felipe Fonseca dos Santos. – Salvador, 2017.
93 f. : il.
Orientador: Vitor Domingos Martins de Araújo.
Tese (Doutorado - Doutorado em Matemática) – Universidade Federal da Bahia, Programa de Pós-graduação em Matemática, 2017.
1. Fórmula de Entropia de Pesin 2. Estados de Equilíbrio. 3. Medidas SRB\física-fraca. 4. Expansão não uniforme 5.Teoria Ergódica. I. Araújo, Vitor Domingos Martins de. II. Título.
-Pesin’s Entropy Formula for
C
1non-uniformly expanding
maps.
Tese de Doutorado submetida ao Colegiado de Pós-graduação em Ma-temática UFBA/UFAL como parte dos requisitos necessários à obtenção do
título de Doutor em Matemática.
Banca examinadora:
Prof. Dr. Vitor D. Martins de Araújo (Orientador) UFBA
Prof. Dr. Paulo César Rodrigues Pinto Varandas UFBA
Prof. Dr. Augusto Armando de Castro Jr UFBA
Profa. Dr. Maria José Pacífico UFRJ
Profa. Dr. Vanessa Ribeiro Ramos UFMA
Agradecimentos
Agradeço primeiramente à Deus por estar sempre comigo, iluminando a minha vida, por ter me capacitado e por estar sempre me protegendo e me dando força.
À Milena, que tanto amo, companheira de todas as horas, obrigado pela sua confiança e compreensão em ceder grande parte do nosso tempo a esses anos de estudos. Seu amor é fundamental na minha vida e me faz sempre acreditar que posso ir mais longe.
Ao meus pais Joel e Rosely, meus irmãos Willian e Liz, minha avó Terezinha e minha sobrinha Lara por fazerem de tudo para me ver feliz. O amor, carinho e apoio de Vocês é muito importante na minha vida.
A todos os meus tios, tias, primos e amigos, por sempre torcerem e me apoiarem em todos os momentos e por compreenderem a minha ausência em muitas ocasiões.
A toda à Família Borges, por todo apoio e carinho. Sou feliz por ter três maravilhosas Famílias.
Ao Professor Vitor Araújo, que novamente me deu a honra e a satis-fação de sua valiosa orientação, pela sua amizade, incentivo, paciência, dedicação, por ter acreditado em mim e pelas grandes oportunidades de aprendizagem a que me proporcionou. Você é um exemplo para mim.
Aos membros da banca, que muito me honraram com suas presenças, Prof. Augusto Armado de Castro Jr, Profa. Maria José Pacífico Prof.
Paulo Cesar Pinto Varandas, Profa. Vanessa Ribeiro Ramos e Prof. Vitor
Domingos Martins de Araújo agradeço pelos enriquecedores comentários e sugestões ao trabalho.
À todos os meus Professores do curso de doutorado: Luciana Salgado, Manuel Stadlbauer, Paulo Varandas, Vilton Pinheiro, Vitor Araújo e Ter-tuliano Franco, pelos valiosos conhecimentos matemáticos que comparti-lharam comigo ao longo das disciplinas, seminários e conversas informais nesse período e por estarem sempre dispostos a ajudar. Vocês são inspira-ção para minha vida profissional.
Ed, Elen, Heides, Morro, Moa, Roberto, Cattai e Vinicius. Obrigado a todos Vocês!
A todos os funcionários da pós-graduação do IM da UFBA por estarem sempre dispostos a me ajudar, em especial a Davilene, Mayara, Márcio, Kleber e Diogo.
Agradeço também aos meus professores da UFRB e da UFBA (período do mestrado) por terem me incentivado e preparado para estar aqui. O apoio e amizade de vocês foram fundamentais.
Provamos a existência de estados de equilíbrio com propriedades espe-ciais para uma classe de homeomorfismos locais positivamente expansivos e potenciais contínuos, definidos em espaço métrico compacto. Além disso, formulamos uma generalização de classeC1 da Fórmula de Entropia de
Pesin: toda medida ergódica weak-SRB-like satisfaz a Fórmula de Entropia de Pesin para transformações de classeC1não uniformemente expansoras.
Mostramos que para transformação expansora fraca, tal que Leb-q.t.px
te-nha frequência positiva de tempos hiperbólicos, medidas weak-SRB-like, existem e satisfazem a Fórmula de Entropia de Pesin e são estados de equi-líbrio para o potencialψ=−log|detD f|. Em particular, isso é válido para
qualquer transformação expansora de classeC1e neste caso o conjunto de
medidas de probabilidade invariantes que satisfazem a Fórmula de Entro-pia de Pesin é o fecho convexo na topologia fraca∗das medidas ergódicas
weak-SRB-like.
Abstract
We prove existence of equilibrium states with special properties for a class of distance expanding local homeomorphisms on compact metric spaces and continuous potentials. Moreover, we formulate a C1
genera-lization of Pesin’s Entropy Formula: all ergodic weak-SRB-like measures satisfy Pesin’s Entropy Formula for C1 non-uniformly expanding maps.
We show that for weak-expanding maps such that Leb-a.ex has positive
frequency of hyperbolic times, then all the necessarily existing ergodic weak-SRB-like measures satisfy Pesin’s Entropy Formula and are equili-brium states for the potential ψ = −log|detD f|. In particular, this holds
for any C1-expanding map and in this case the set of invariant probability
measures that satisfy Pesin’s Entropy Formula is the weak∗-closed convex
hull of the ergodic weak-SRB-like measures.
Keywords: Ergodic theory, non-uniform expansion, SRB\physical-like
Sumário
Lista de Figuras xiii
1 Introdução e descrição dos resultados 1
1.1 Comentários e Questões futuras . . . 8
1.2 Organização do trabalho . . . 11
2 Statement of the results 13 2.1 Topological pressure . . . 13
2.2 Expanding maps . . . 15
2.3 Transfer operator . . . 15
2.4 Weak-SRB-like and SRB-like probability measures . . . 15
2.5 SRB-like measures as limits of SRB measures . . . 17
2.6 Non-uniformly expanding maps . . . 18
2.7 Weak and non-uniformly expanding maps . . . 20
3 Examples of application 23 3.1 Expanding map . . . 23
3.2 C1Non uniformly expanding maps . . . 26
3.3 Weak-expanding and non-uniformly expanding maps . . . . 27
4 Preliminary definitions and results 31 4.1 Invariant andν-SRB-like measures . . . 31
4.2 Measure-theoretic entropy . . . 33
5 Continuous variation of SRB-like measures 37 5.1 Measures with prescribed Jacobian. Conformal measures . . 37
5.2 SRB measures . . . 38
5.3 Limits of SRB-measures . . . 39
6 Expanding maps on compact metric spaces 41
6.1 Basic properties of expanding open maps . . . 41
6.2 Conformal measures. Weak Gibbs property . . . 42
6.3 Initial partition . . . 44
6.4 Expansive maps and existence of equilibrium states . . . 44
6.5 Large deviations . . . 45
6.6 Proof of Theorem B . . . 49
7 Entropy Formula 53 7.1 Hyperbolic Times . . . 53
7.2 Proof of Theorem D . . . 60
8 Ergodic weak-SRB-like measure 63 8.1 Ergodic expanding invariant measures . . . 63
8.2 Ergodic expanding weak-SRB-like measures . . . 66
9 Weak-Expanding non-uniformly expanding maps 69 9.1 Weak-SRB-like, equilibrium and expanding measures . . . . 69
9.2 Expanding Case . . . 70
9.3 Proof of Corollary I . . . 71
9.4 Proof of Corollary C . . . 72
Lista de Figuras
1.1 Olho de Bowen. . . 9
1.2 Gráfico de f. . . 11
3.1 Graph of f. . . 25
7.1 Flexible covering with hyperbolic preballs . . . 56
Capítulo 1
Introdução e descrição dos
resultados
Os estados de equilíbrio, um conceito originalmente da Mecânica Esta-tística, é uma classe especial de medidas de probabilidade. Na definição clássica, dadas uma transformação contínua T : X → X definida em um
espaço métrico compacto X e uma função contínua φ : X → R chamada
de potencial, dizemos que uma medida de probabilidade T-invariante é
φ-estado de equilíbrio (ou estado de equilíbrio para o potencialφ) se
Ptop(T, φ)=hµ(T)+ Z
φdµ, onde Ptop(T, φ)= sup λ∈MT
(
hλ(T)+ Z
φdλ
)
,
e MT é o conjunto de todas as medidas de probabilidade T-invariantes.
Nesta relação,Ptop(T, φ) é chamadapressão topológicae a igualdade acima do
lado direito é conhecida porPrincípio Variacional; veja por exemplo [47, 29]
para as definições de entropiahµ(T) e pressão topológica. Postergamos as
definições formais para os próximos capítulos.
Dependendo do sistema dinâmico e potencial estudados (T, φ), os
es-tados de equilíbrio podem ter propriedades que fornecem informação útil sobre o sistema. Sinai, Ruelle e Bowen [38, 13, 12, 34] foram os pioneiros da teoria dos estados de equilíbrio para sistemas dinâmicos uniformemente hiperbólicos. Eles estabeleceram uma importante conexão entre estados de equilíbrio e medidas que são caracterizadas por fornecer informações assintóticas sobre um conjunto de trajetórias, isto é, dada uma medidaµ, esperamos que suabacia
B(µ)=
x∈X: 1 n
n−1
X
j=0
φ(Tjx)−−−−→
n→+∞
Z
φdµ, ∀φ∈C0(X,R)
seja grande do ponto de vista da medida de Lebesgue ou alguma outra medida de referência relevante. Essas medidas são chamadasmedidas SRB
em homenagem a Sinai, Ruelle e Bowen, e tambémmedidas físicasdevido
à origem de muitos conceitos na Mecânica Estatística.
Apesar do substancial progresso de vários autores em estender essa teoria, uma visão global ainda está longe de ser completa. Por exemplo, a estratégia básica utilizada por Sinai-Ruelle-Bowen foi (semi-)conjugar a dinâmica a um subshift de tipo finito, através de uma partição Markov, e usar as fortes propriedades topológicas e ergódicas das Cadeias de Mar-kov Topológicas para obter resultados para a dinâmica uniformemente hiperbólica original.
No entanto, a existência de partições de Markov é conhecida apenas em alguns casos e, muitas vezes, tais partições podem não ser finitas. Além disso, existem transformações que não admitem estados de equilíbrio ou medidas físicas/SRB (como por exemplo, a transformação identidade).
Em muitas situações com algum tipo de expansão, é possível garantir que os estados de equilíbrio sempre existam. No entanto, os estados de equilíbrio geralmente não são únicos e, pela forma como são obtidos, não fornecem informações adicionais para o estudo da dinâmica. No contexto das funções uniformemente expansoras, Ruelle mostrou em [35] que existe um único estado de equilíbrio que é uma medida física/SRB se o potencial
for Hölder contínuo e a dinâmica f for transitiva.
Neste sentido, surgem algumas questões naturais:
1. Quando um sistema dinâmico tem um estado de equilíbrio?
2. Se tais medidas existem, que propriedades estatísticas essas proba-bilidades exibem em relação à medida de referência (possivelmente não-invariante)?
3. Quando existe, o estado de equilíbrio é único?
A existência de estados de equilíbrio é uma propriedade relativamente mais simples que muitas vezes pode ser estabelecida através de argumen-tos de compacidade. Entretanto, as propriedades estatísticas e a unicidade do estado de equilíbrio são geralmente mais sutis e requerem uma melhor compreensão da dinâmica. Em nosso contexto, não esperamos ter uma unicidade de estado de equilíbrio, porque consideramos:
• sistemas dinâmicos com baixa regularidade: contínua ou de classe
C1somente; e
3
Do Formalismo Termodinâmico a resposta para a primeira questão é conhecida e afirmativa para todas as transformações expansivas (também chamadas transformações Ruelle expansiva), em um espaço métrico com-pactoXe para todo potencial contínuo; veja [37, 29].
Inspirado na definição de medida observável introduzida por Keller em [25], Catsigeras-Henrich apresentam em [18] a noção de medidas “SRB-like” ou pseudo-físicas (uma generalização da noção de medida física/SRB)
e mostram que tais medidas sempre existem para toda transformação con-tínua definida em um espaço métrico compacto. Além disto, eles mostram que a definição de medida “SRB-like” é ótima em certo sentido, se o objetivo for descrever as estatísticas assintóticas de Lebesgue quase toda órbita do sistema. Mais precisamente, dado um pontox∈Xdenotamos o conjunto
pω(x)=
µ∈ MT;∃nj −−−−→
j→+∞ +∞tal queσnj(x)=
1
nj nj−1
X
i=0
δTi(x) w∗
−−−−→
j→+∞ µ
.
Fixado uma medida de referência ν (não necessariamente a medida de
Lebesgue) para o espaço métricoX, dizemos queµ∈ MT éν-SRB-like se,
e só se,ν(Aε(µ))>0 para todoε >0, onde
Aε(µ)={x∈ X; dist(pω(x), µ)< ε}
é a baciaε-fraca de atração deµe dist é uma métrica que induz a topologia
fraca∗no espaço das medidas de probabilidades Boreliana.
Mostramos que, em nosso contexto, as medidas “ν-SRB-like” são
par-ticularmente interessantes, porque podem ser vistas como medidas que surgem naturalmente como pontos de acumulação de medidasν-SRB.
Teorema A. Seja T :X→X uma transformação aberta, expansiva e topologica-mente transitiva definida em um espaço métrico compacto X. Considere(φn)n≥1 uma sequência de potenciais Hölder contínuas, (νn)n≥1 uma sequência de medi-das conformes associados a(T, φn)e (µn)n≥1 uma sequência de medidasνn-SRB.
Assuma que:
1. φnj −−−−→
j→+∞ φna topologia da convergência uniforme;
2. νnj w∗
−−−−→
j→+∞ νna topologia fraca* de convergência de medidas;
3. µnj w∗
−−−−→
Entãoνé medida conforme para(T, φ)eµéν-SRB-like. Em particularµéφ-estado de equilíbrio. Além disso, se T é topologicamente exata então ν(X\Aε(µ)) = 0
para todoε >0.
Relacionando agora as transformações que expandem distância e as medidas “ν-SRB-like”, obtemos uma resposta positiva para a segunda pergunta.
Teorema B. Seja T : X → X uma transformação aberta, expansiva e topolo-gicamente transitiva, definida em um espaço métrico compacto X e φ : X → R
contínua. Então, para cada (necessariamente existente) medidaφ-conformeν=νφ
todas as (necessariamente existentes) medidasνφ-SRB-like sãoφ-estado de
equilí-brio.
Esse resultado, em particular, estende o principal resultado obtido por Catsigeras-Henrich em [19], onde foram estudadas apenas as medidas “SRB-like” com respeito à medida de Lebesgue para dinâmicasC1
expan-soras do círculo.
Em [17], Catsigeras, Cerminara e Henrich estendem a noção de medidas SRB-like, as medidas “weak-SRB-like” ou weak pseudo-física. Diz-se que uma medidaµ∈ MT éν-weak-SRB-like se, e só se,
lim sup
n→+∞
1
nlogν(Aε,n(µ))=0 ∀ε >0,
ondeAε,n(µ)= {x∈ X : dist(σn(x), µ)< ε}é a baciaε-fraca de µem tempo
n.
Observamos que seµé umφ-estado de equilíbrio e se “relaciona bem” com a medida de referênciaνentãoµé combinação convexa fraca∗de
medi-das ergódicas weak-SRB-like. Além disso, seµé o únicoφ-estado de
equi-líbrio entãoµpossui cota superior de grandes desvios, isto é, para qualquer vizinhança fraca∗ V de µ em M
1 (espaço das medidas de probabilidade
Boreliana), então a probabilidadeν({x∈X: σn(x) := 1nPnj=−01δTj(x) ∈ M1\V})
decresce exponencialmente com n em uma taxa que depende do
“tama-nho” deV.
Corolário C. Sejam T : X → X uma transformação aberta, expansiva e topolo-gicamente transitiva, definida em um espaço métrico compacto X,φ:X→Rum
potencial contínuo eνuma medidaφ-conforme. Seµé umφ-estado de equilíbrio tal que hν(T, µ)< ∞então quase toda componente ergódicaµxdeµé uma medida
5
superior de grandes desvios: para toda vizinhança fraca∗Vdeµtemos
lim sup
n→+∞
1
nlogν({x∈X: σn(x)∈ M1\V})≤ −I(V) onde I(V)=sup{r>0 :Kr(φ)⊂ V}.
Considere agora Muma variedade Riemanniana compacta finita sem
bordo. Na década de 1970, Pesin mostrou uma relação entre dois impor-tantes conceitos matemáticos: os expoentes de Lyapunov e a entropia para sistemas dinâmicos diferenciáveis.
Mais precisamente, em [28], Pesin mostrou que se µ é uma medida
f-invariante para um difeomorfismo de classeC2(ouC1+α,α >0) definido
em uma variedade compacta que é absolutamente contínua com respeito a medida de Lebesgue, então
hµ(f)= Z
Σ+dµ, (1.0.1)
ondeΣ+ denota a soma dos expoentes de Lyapunov positivos em pontos
regulares, contando suas multiplicidades. Dizemos que uma medida f
-invarianteµsatisfaz a Fórmula de entropia de Pesin seµsatisfaz a equação
(1.0.1).
Ledrappier e Young em [26], no mesmo contexto que Pesin, generaliza-ram a fórmula de entropia de Pesin, mostrando que uma medida invariante satisfaz a Fórmula de Entropia de Pesin se, e somente se, tiver medidas condicionais absolutamente contínuas em relação a medida de Lebesgue nas folhas instáveis.
Podemos também citar, Liu, Qian e Zhu que obtiveram em [27, 30]
generalizações da fórmula de entropia de Pesin para endomorfismos de classeC2.
Para funções de classeC1, a ausência de distorção limitada impossibilita
o uso de muitos métodos já conhecidos para obter a Fórmula de Entropia de Pesin para dinâmicas de classeC2(ouC1+α,α >0). Recentemente, Xueting
Tian mostrou em [44] a fórmula de entropia de Pesin para dinâmica entre
C1eC1+α.
Entretanto, podemos encontrar diversos resultados já obtidos para sis-temas dinâmicos de classeC1:
• Ali Tahzibi em [40] mostrou a fórmula de entropia de Pesin para
difeomorfismos C1 genéricos que preserva área em superfícies de
• Bessa-Varandas em [10] mostraram que vale o resultado anterior
para tempo contínuo (fluxos incompreensíveis) em variedades de dimensão 3;
• Hao Qiu em [31] provou que se f é Anosov transitiva então C1
-genericamente existe uma única medida SRB que satisfaz a fórmula de entropia de Pesin;
• Em 2012, Sun e Tian exibem em [39] condições para que uma medida invarianteµsatisfaça a fórmula de entropia de Pesin para
difeomor-fismos C1 com decomposição dominada ao longo da órbita para µ
quase todos os pontos. Além disso, entre outras coisas, eles esten-dem o resultado obtido em [40] para qualquer dimensão;
• Catsigeras e Enrich estabelecem relação entre as medidas “SRB-like” e
a fórmula de entropia de Pesin para funçõesC1-expansoras no círculo
em [19]. Posteriormente, Catsigeras, Cerminara e Enrich estenderam essa relação para difeomorfismos C1 com decomposição dominada
em [16]. Os mesmos autores, em [17] estendem o resultado para difeomorfismosC1Anosov para medidas “weak-SRB-like”;
• Yang e Cao, mais recentemente, mostraram em [14], que se f é um
di-feomorfismoC1que admite atratorΛcom decomposição dominada
TΛM = E⊕Ftal que para qualquer medida suportada em Λtemos
que todos os expoentes de Lyapunov ao longo deEsão não positivos
e todos os expoentes de Lyapunov ao longo de F são não
negati-vos, então existe medida suportada emΛque satisfaz a fórmula de
entropia de Pesin.
Apesar de muito progresso nessa direção, ainda há muitas questões em aberto. Nesse sentido, foi investigada a Fórmula de entropia de Pesin para difeomorfismos locais de classeC1não uniformemente expansor.
Teorema D. Seja f : M → M um difeomorfismo local de classe C1 não unifor-memente expansor. Então toda medida de probabilidade expansora weak-SRB-like satisfaz a fórmula de entropia de Pesin. Além disso, todas as medidas de probabi-lidades ergódicas SRB-like são expansoras.
7
que medida ergódica “weak-SRB-like” sempre existe para difeomorfismos Anosov de classeC1e, mais recentemente em [20], Catsigeras e Troubetzkoy
mostram que, para funções contínuas C0-genérica do intervalo, todas as
medidas ergódicas são SRB-like.
Relacionando os conceitos das medidas “weak-SRB-like”, Fórmula de Entropia de Pesin e estado de equilíbrio obtemos
Corolário E. Seja f : M → M um difeomorfismo local de classe C1 não unifor-memente expansor eψ =−log|detD f|. Se Ptop(f, ψ)=0então, toda medida de
probabilidade weak-SRB-like éψ-estado de equilíbrio e todas as (necessariamente existentes) medidas expansora ergódicas weak-SRB-like satisfazem a Fórmula de Entropia de Pesin.
Ademais, supondo propriedades de expansão mais fortes obtemos:
Corolário F. Seja f : M → M um difeomorfismo local de classe C1 expansor fraco e não uniformemente expansor. Então,
1. Todas as (necessariamente existentes) medidas de probabilidade weak-SRB-like são ψ-estados de equilíbrio e, em particular satisfazem a Fórmula de Entropia de Pesin;
2. Existe medida de probabilidade ergódica weak-SRB-like;
3. Seψ < 0não existe medida de probabilidade atômica weak-SRB-like;
4. Se D = {x ∈ M : kD f(x)−1k = 1} é finito e ψ < 0 quase todas as componentes ergódicas de um ψ-estado de equilíbrio são medidas weak-SRB-like. Além disso, toda medida de probabilidade weak-SRB-likeµ, suas componentes ergódicasµx são medidas de probabilidades expansoras
weak-SRB-like paraµ-quase todo x no subconjunto expansor.
Em particular, vemos que uma construção análoga ao resultado de existência de medida física/SRB e atômica para uma aplicação quadrática,
obtida por Keller em [23], não é possível entre transformaçõesC1
uniforme-mente expansoras, embora genericauniforme-mente tais medidas sejam singulares com respeito a qualquer forma de volume.
Corolário G. Não existe medida atômica SRB para uma transformação expansora C1de uma variedade compacta.
Pelo trabalho de Ávila e Bochi em [7], é sabido que C1-genericamente
as transformações de classe C1 de uma variedade compacta sem bordo
contínua em relação a medida de Lebesgue. Esse é um dos empecilhos que assegura que não é possível obter um análogo aos resultados obtidos por Pesin, Ledrappier e Young em [28, 26] de modo geral. Mas podemos nos perguntar se é possível estabelecer condições necessárias e suficientes para que um análogo à Fórmula de Entropia de Pesin seja satisfeita. Neste sentido, obtemos a seguinte caracterização para dinâmicaC1-expansora.
Corolário H. Seja f : M → M uma função expansora de classe C1. Então uma medida de probabilidade f -invariante µ satisfaz a Fórmula de entropia de Pesin se, e somente se, suas componentes ergódicasµx são weak-SRB-likeµ-q.t.p.
x∈ M. Além disso, todas as medidas de probabilidade weak-SRB-like satisfazem a Fórmula de entropia de Pesin e, em particular, são ψ-estados de equilíbrio. Adicionalmente, se existe uma única medida de probabilidade µ weak-SRB-like, então µé SRB, Leb(B(µ)) = 1, µ é o únicoψ-estado de equilíbrio, é ergódico e possui cota superior de grandes desvios.
Concluímos a introdução com a seguinte versão fraca de estabilidade estatística para dinâmicaC1-expansora: os pontos de acumulação de toda
sequência de medidas weak-SRB-like são combinações lineares convexas generalizadas de medidas ergódicas weak-SRB-like.
Corolário I. Sejam {fn : M → M}n≥1 uma sequência de funções expansoras de classe C1tal que fn→− f na topologia C1e f : M→M é uma função expansora de
classe C1. Considere para cada n ≥1,µnuma medida weak-SRB-like associada a
fn. Então todo ponto de acumulação da sequência(µn)n≥1é um estado de equilíbrio para o potencialψ =−log|detD f|(em particular, satisfaz a Fórmula de Entropia de Pesin) e quase todas as suas componentes ergódicas são medidas weak-SRB-like.
1.1
Comentários e Questões futuras
Nesta seção listamos algumas questões baseadas nos estudos realizados na presente tese e que serão objeto de trabalhos futuros.
Questão 1.1.1. Nas mesmas hipóteses do Corolário C será possível obter uma cota inferior de grandes desvios que tenha a mesma taxa encontrada no Corolário C? Talvez seja necessário considerar que a dinâmica é topologicamente misturadora.
Questão 1.1.2. Será possível obter uma propriedade estatística para as medidas weak-SRB-like, como no caso do Corolário C, para transformação expansora fraca não uniformimente expansora?
1.1. Comentários e Questões futuras 9
Alguns exemplos que surgiram naturalmente durante o desenvolvi-mento deste trabalho também motivaram algumas questões.
O primeiro exemplo é atribuído a Bowen, e pode ser encontrado em maior detalhe para nosso contexto no Exemplo 5.5 em [18].
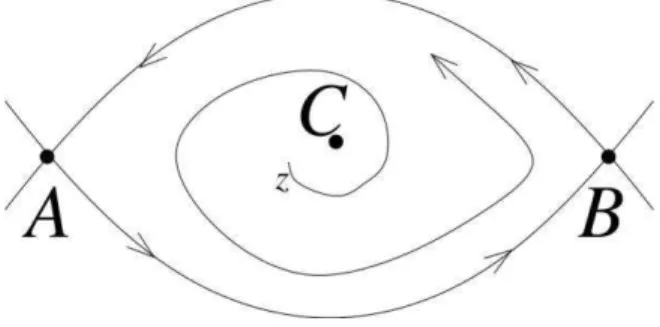
Exemplo 1.1.4. Considere um difeomorfismo f em uma bola deR2com dois pontos
de sela A e B, de modo que uma componente conexa da variedade global instável Wu(A)\{A} é um arco que coincide com uma componente conexa da variedade
global estável Ws(B)\{B} e, inversamente, a componente conexa Wu(B)\{B} =
Ws(A)\{A}. Seja f , de modo que exista uma fonte C ⊂ U onde U é o conjunto aberto com bordo Wu(A)∪Wu(B).
Figura 1.1: Olho de Bowen.
Se os autovalores da derivada de f em A e B forem adequadamente escolhidos conforme especificado em [42, 22], então a sequência{n1
Pn−1
j=0 δfj(x)}n≥0 para todos
x ∈ U\{C} não é convergente. Neste caso existe pelo menos duas subsequências convergentes para diferentes combinações convexas dos deltas de DiracδAeδB.
Assim, como observado em [18], as medidas de probabilidade SRB-like são combinações convexas de δA eδB e formam um segmento no espaço M das
me-didas de probabilidade. Este exemplo mostra que as meme-didas SRB-like não são necessariamente ergódicas.
Além disso, os autovalores de D f nos pontos de sela A e B podem ser adequada-mente modificados para obter a convergência da sequência{1nPn−1
j=0 δfj(x)}n≥0como
indicado no Lema (i) da página 457 em [41]. Na verdade, fazendo uma pequena pertubação C0de f fora de uma pequena vizinhança dos pontos de sela A e B temos que oω-limite das órbitas em U\{C}ainda contém os pontos A e B, obtendo que a sequência (2.4.1) converge para uma única medidaµ = λδA+(1−λ)δB para
todo x ∈ U\{C}, com uma constante fixa 0 < λ < 1. Então, µé a única medida SRB-like. Isso prova que o conjunto de medidas de probabilidade SRB-like não depende continuamente da função.
Questão 1.1.5. Quando podemos afirmar que um sistema dinâmico (f, φ) tem medida de probabilidade ergódicaνφ-SRB-like ouνφ-weak-SRB-like?
Questão 1.1.6. Pelo exemplo 1.1.4, sabemos que o conjunto das medidas de probabilidadeνφ-SRB-like não depende, em geral, continuamente com a função.
Será que adicionando a dinâmica propriedade de expansão forte (como nos casos do Corolário C e Corolário H) podemos ter variação contínua das medidasνφ-SRB-like
ouνφ-weak-SRB-like?
Questão 1.1.7. Existe dependência contínua entre as medidas de probabilidades
νφ-SRB-like (ouνφ-weak-SRB-like) e o potencialφ?
Uma resposta positiva nesta direção é dada no Teorema A, no entanto, não sabemos em geral se a medida limite (veja Teorema A) é ergódica.
Questão 1.1.8. No caso de uma resposta positiva na Questão 1.1.6, será que há estabilidade estocástica?
O próximo exemplo é uma adaptação da transformação Intermitente (Manneville-Pomeau) em um homeomorfismo local do círculo.
Exemplo 1.1.9. Considere I=[−1,1]e a transformação fˆ:I→I (veja a Figura 1.2) dada por
ˆ
f(x)= (
2√x−1 se x≥0,
1−2√|x| caso contrário.
Esta transformação induz um homeomorfismo local contínuo f : S1 → S1
através da identificaçãoS1=I/∼, onde−1∼1. Esta é uma transformação que só não é diferenciável no ponto 0, possui frequência positiva de tempos hiperbólicos para Lebesgue quase todos os pontos, como pode ser visto em [1, seção 5].
Este é um exemplo de transformação expansora fraca e não uniforme-mente expansora, mas não é um difeomorfismo localC1em todo ponto.
Este exemplo sugere que podemos pensar em uma generalização do Teorema B usando as mesmas ideias do Teorema D, substituindo a medida de Lebesgue por uma medida expansoraφ-conformeνparaφ ∈ C0(X,R)
1.2. Organização do trabalho 11
y=x
y=f(x)
−1 −0.5 0 0.5 1
−0.5 0.5
−1 0 1
Figura 1.2: Gráfico de f.
Pode ser necessário considerar hipóteses adicionais sobre os potenciais, como por exemplo que os potenciais contínuos sejampotenciais hiperbólicos
(veja a definição e resultados sobre o potencial hiperbólico Hölder contínuo em [33]).
Além disso, também podemos pensar em uma generalição do Teorema D para o caso de difeomorfismo local de classe C1 afastado de conjunto
crítico/singular com frequência positiva de tempos hiperbólicos (veja [2]
para definição de conjunto crítico/singular).
Questão 1.1.11. Seja f : M→ M um difeomorfismo local de classe C1 afastado de um conjunto crítico/singularCcom recorrência lenta aCe tal que para alguns
0 < σ < 1, b, δ > 0 e θ > 0 Leb−q.t.p. x tem frequência positiva ≥ θ de
(σ, δ,b)-tempos hiperbólicos para f . Todas as medidas de probabilidade expansora weak-SRB-like satisfazem a Fórmula de Entropia de Pesin?
1.2
Organização do trabalho
A tese está dividida em nove capítulos, incluindo o capítulo introdutó-rio “Introdução e descrição dos resultados”. Nos capítulos 2 e 4 denomina-dos respectivamente “Statement of the results” e “Preliminary definitions and results” serão introduzidos os principais resultados da tese, grande parte das definições básicas e notações necessárias ao longo do texto, além de alguns resultados auxiliares sobre medidas de probabilidades ν
-SRB-like,νφ-weak-SRB-like e entropia.
aplicados.
No Capítulo 5, “Continuous variation of SRB-like measures” será pro-vado o Teorema A.
No Capítulo 6, “Expanding maps on compact metric space” serão exi-bidas algumas propriedades das aplicações expansivas e a demonstração do Teorema B.
No Capítulo 7, “Entropy Formula” serão usadas as propriedades dos tempos hiperbólicos e das medidas weak-SRB-like para provar uma refor-mulação da Fórmula de Entropia para difeomorfismo local de classe C1
não uniformemente expansor (o Teorema D).
No Capítulo 8, “Ergodic weak-SRB-like measure” será estudado a exis-tência de medida ergódica weak-SRB-like, sua relação com a Fórmula de Entropia de Pesin e a prova do Corolário E.
Chapter 2
Statement of the results
Let T : X → X be a continuous transformation defined on a compact
metric space (X,d).
2.1
Topological pressure
The dynamical ball of center x ∈ X, radius δ > 0, and length n ≥ 1 is defined by
B(x,n, δ)={y∈ X:d(Tjx,Tjy)≤δ, 0≤ j≤n−1}.
Letνbe a Borel probability measure onX. We define
hν(T,x) = lim
δ→0lim supn→+∞ −
1
nlogν(B(x,n, δ)) and
hν(T, µ) = µ−ess suphν(T,x). (2.1.1)
Note thatνis not necessarilyT-invariant, and ifµ is ergodicT-invariant,
we have for µ-a.e. x ∈ X, hµ(T,x) = hµ(T), the usual metric entropy of T
with respect toµ.
Letnbe a natural number,ε >0 and letKbe a compact subset ofX. A
subsetFofXis said to (n, ε) spanKwith respect toTif∀x∈Kthere exists y∈Fwithd(Tjx,Tjy)≤εfor all 0≤ j≤n−1, that is,
K⊂[
x∈F
B(x,n, ε).
IfKis a compact subset ofX. Let
h(T;K)=lim
ε→0lim infn→+∞
1
nlogN(n, ε,K), (2.1.2)
whereN(n, ε,K) denote the smallest cardinality of any (n, ε)-spanning set
forKwith respect toT.
Definition 1. The topological entropyofT ishtop(T) = sup{h(T,K); K ⊂ X},
where the supremum is taken over the collection of all compact subset of
X.
Letφ:X →Rbe a real continuous function that we call thepotential.
Given an open coverαforX we define the pressurePT(φ, α) ofφwith
respect toαby
PT(φ, α) := lim
n→+∞
1
nlog infU⊂αn
X U∈U
eSnφ(U)
where the infimum is taken over all subcovers U of αn = ∨n−1
j=0T−j(α), Snφ(x) :=Pnj=−01φ(Tjx) andSnφ(U) :=sup{Snφ(x); x∈U}.
Definition 2. Thetopological pressure Ptop(T, φ) of the potential φwith
re-spect to the dynamicsTis defined by
Ptop(T, φ)=lim δ→0
sup
|α|≤δ
PT(φ, α)
where|α|denotes the diameter of the open coverα.
For given n > 0 andε > 0, a subset E ⊂ X is called (n, ε)-separated if
x,y∈E,x, ythen there exists 0≤ j≤n−1 such thatd(Tjx,Tjy)> ε.
An alternative way of defining topological pressure is through the no-tion of (n, ε)-separated set.
Definition 3. The topological pressure Ptop(T, φ) of the potential φ with
respect to the dynamicsTis defined by
Ptop(T, φ)=lim
ε→0lim supn→+∞
1
nlog sup
X
x∈E
eSnφ(x)
where the supremum is taken over all maximal (n, ε)-separated setsE.
2.2. Expanding maps 15
2.2
Expanding maps
A continuous mapping T : X → X is expanding (with respect to the
metric d) if there exist constants λ > 1, η > 0 andn ≥ 1, such that for all x,y∈X
if d(x,y)<2η then d(Tn(x),Tn(y))≥λd(x,y). (2.2.1)
In the sequel we will always assume (without loss of generality, see chapter 3 in [29]) thatn=1, that is
d(x,y)< 2η =⇒ d(T(x),T(y))≥λd(x,y). (2.2.2)
We refer the reader to [21, 6, 29] for more details and properties of expand-ing map.
2.3
Transfer operator
We consider the Ruelle-Perron-Fröbenius transfer operator LT,φ = Lφ
associated toT :X →Xand the continuous function (potential)φ:X→ R
as the linear operator defined on the spaceC0(X,R) of continuous functions
g:X→Rby
Lφ(g)(x)= X
T(y)=x
eφ(y)g(y).
The dual of the Ruelle-Perron-Fröbenius transfer operator is given by
L∗
φ : M1 → M1
η 7→ L∗
φη: C0(X,R) → R
ψ 7→
Z
Lφψdη.
whereM1is the set of Borel probabilities inX.
2.4
Weak-SRB-like and SRB-like probability
mea-sures
For any pointx∈Xconsider,
σn(x)=
1
n
n−1
X
j=0
δTj(x) (2.4.1)
Definition 4. For each pointx ∈ M, denotepω(x)⊂ MT the limit set with
initial statex,
pω(x) := (
µ∈ MT;∃nj −−−−→
j→+∞ +∞s.t.σnj(x)
w∗
−−−−→
j→+∞ µ
)
.
Definition 5. Fix a reference measureνfor the spaceX, we say that
prob-ability measureµ∈ MT isν-SRB (orν-physical) ifν(B(µ))>0, where
B(µ)=
x∈ X;pω(x)={µ} is the "ergodic basin" ofµ.
Letµ∈ MT andε > 0. We will consider the following measurable sets
inX:
Aε,n(µ) :={x∈X: dist(σn(x), µ)< ε}; (2.4.2)
Aε(µ) :={x∈X: dist(pω(x), µ)< ε}. (2.4.3)
We callAε,n(µ) theε-pseudo basin ofµup to time n,Aε(µ) the basin ofε-weak
statistical attractionof µand dist is a metric inM1 that induces the weak∗
topology (see definition in (4.1.1)).
Definition 6. Fix a reference probability measureνfor the spaceX. We say
that aT-invariant probability measureµis:
1. ν-SRB-like(orν-physical-like), if and only ifν(Aε(µ))>0 for allε >0;
2. ν-weak-SRB-like(orν-weak-physical-like), if and only if
lim sup
n→+∞
1
nlogν(Aε,n(µ))=0∀ε >0.
Whenν=Leb we say thatµis simply SRB-like (or weak-SRB-like).
Remark 2.4.1. It is easy to see that every ν-SRB measure is also a ν-SRB-like measure. Moreover, theν-SRB-like measures are particular case ofν -weak-SRB-like (see item B in [17]).
We denote W∗
T(ν) ⊂ MT the set of ν-weak-SRB-like probability
mea-sures. Whenν=Leb we denoteWT∗(Leb) =WT∗.
Definition 7. Given T : X → X and an arbitrary continuous function
φ : M → R, we say that a probability measure ν is conformal forT with
respect toφ(orφ-conformal) if there existsλ >0 so thatL∗
2.5. SRB-like measures as limits of SRB measures 17
2.5
SRB-like measures as limits of SRB measures
The next result shows that we can see theν-SRB-like measures as
mea-sures that naturally arise as accumulation points ofνn-SRB measures.
Theorem A. Let T : X→ X be an open expanding topologically transitive map of a compact metric space X,(φn)n≥1a sequence of Hölder continuous potentials,
(νn)n≥1a sequence of conformal measures associated to the pair(T, φn)and(µn)n≥1 a sequence ofνn-SRB measures. Assume that
1. φnj −−−−→
j→+∞ φ(in the topology of uniform convergence);
2. νnj w∗
−−−−→
j→+∞ ν(in the weak
∗topology);
3. µnj w∗
−−−−→
j→+∞ µ(in the weak
∗topology).
Thenνis a conformal measure for(T, φ)andµisν-SRB-like. In particular,µis an equilibrium state for the potentialφ. Moreover, if T is topologically exact then
ν(X\Aε(µ))=0for allε >0.
This is one of the motivations for the study of SRB-like measures as the natural extension of the notion of physical/SRB measure forC1 maps.
Additional justification is given by the results of this work.
It is worth noting that Hölder continuous potentials are only used in this work on the assumption of Theorem A and all continuous potentials can be approximated by Lipschitz potentials (and all Lipschitz continuous potential areα-Hölder continuous forα∈(0,1]) see Remark 5.2.4.
The next result extends, in particular, the main result obtained in [19, Theorem 2.3] valid only for expanding circle maps.
Theorem B. Let T : X → X be an open expanding topologically transitive map of a compact metric space X andφ : X → R a continuous potential. For each (necessarily existing) conformal measure νφ all the (necessarily existing)
νφ-SRB-like measures are equilibrium states for the potentialφ.
Definition 8. Let T : X → X be a continuous map and φ : X → R a
continuous potential. Givenr>0 we consider the set inMT
Kr(φ)={µ∈ MT : hµ(T)+ Z
φdµ≥Ptop(T, φ)−r}
Corollary C. Let T : X → X be an open expanding topologically transitive map of a compact metric space X, φ : X → R a continuous potential and ν a
φ-conformal measure. Ifµis aφ-equilibrium state such that hν(T, µ)< ∞ then
every ergodic componentµxofµis aν-weak-SRB-like measure. Moreover, ifµis
the unique φ-equilibrium state thenµ isν-SRB,ν(B(µ)) = 1 andµsatisfies the following large deviation bound: for every weak∗neighborhoodVofµwe have
lim sup
n→+∞
1
nlogν({x∈X: σn(x)∈ M1\V})≤ −I(V) where I(V)=sup{r>0 :Kr(φ)⊂ V}.
2.6
Non-uniformly expanding maps
We denote byk · k a Riemannian norm on the compactm-dimensional
boundaryless manifoldM,m≥ 1; byd(·,·) the induced distance and by Leb
a Riemannian volume form, which we callLebesgue measureorvolumeand
assume to be normalized: Leb(M) = 1. Note that Leb is not necessarily
f-invariant.
Recall that aC1-map f : M→Misuniformly expandingor justexpanding
if there is someλ >1 such for some choice of a metric inMone has
kD f(x)vk> λkvk, for allx ∈Mand allv∈TxM\{0}.
In what follows we write always f : M→ MbeC1local diffeomorphism
andψ:=−log|detD f|.
Next corollary suggests that Theorem B should be extended to weaker forms of expansion.
Recall that a Borel set in a topological space is said to have total proba-bility if it has probaproba-bility one for every f-invariant probability measure.
Corollary 2.6.1. Let f : M → M be C1 local diffeomorphism and Y be a subset with total probability. If
lim inf
n→+∞
1
n
n−1
X
j=0
logkD f(fj(x))−1k<0, ∀x∈Y,
2.6. Non-uniformly expanding maps 19
Proof. For a C1-local diffeomorphism f : M → M we have that Leb is
ψ-conformal. Moreover, we know by Theorem 1.15 in [3] that if
lim inf
n→+∞
1
n
n−1
X
j=0
logkD f(fj(x))−1k<0
forxin a total probability subset, then f is uniformly expanding. Thus, by
Theorem B we concluded the proof.
The Lyapunov exponents of a C1 local diffeomorphism f of a compact
manifoldM are defined by Oseledets Theorem which states that, for any f-invariant probability measure µ, for almost all points x ∈ M there is
κ(x) ≥ 1, a filtration TxM = F1(x) ⊃ F2(x) ⊃ · · · ⊃ Fκ(x)(x) ⊃ Fκ(x)+1(x) = {0},
and numbersλ1(x)> λ2(x)>· · ·> λk(x) suchD f(x)·Fi(x)=Fi(f(x)) and
lim
n→±∞
1
nlogkD f
n(x)vk=λ i(x)
for all v ∈ Fi(x)\Fi+1(x) and 0 ≤ i ≤ κ(x). The numbers λi(x) are called
Lyapunov exponents of f at the point x. For more details on Lyapunov
exponents and non-uniform hyperbolicity see [9].
Definition 9. Let f : M → M be C1 local diffeomorphism. We say that
µ∈ Mf satisfies the Pesin Entropy Formula if
hµ(f)= Z
Σ+dµ,
whereΣ+denotes the sum of the positive Lyapunov exponents at a regular
point, counting multiplicities.
Let 0< σ <1 we denote,
H(σ)=
x∈M; lim sup
n→+∞
1
n
n−1
X
j=0
logkD f(fj(x))−1k<logσ
(2.6.1)
Definition 10. We say that f : M → Misnon-uniformly expandingif there
existsσ∈(0,1) such that Leb(H(σ))=1.
A probability measureµ(not necessarily invariant) isexpandingif there
existsσ∈(0,1) such thatµ(H(σ))=1.
Theorem D. Let f : M → M be non-uniformly expanding. Every expanding weak-SRB-like probability measure satisfies Pesin’s Entropy Formula. In parti-cular, all ergodic SRB-like probability measures are expanding.
Now we add a condition ensuring that there exists expanding ergodic weak-SRB-like probability measure and that all weak-SRB-like measures become equilibrium states.
Corollary E. Let f : M → M be non-uniformly expanding. If Ptop(f, ψ) = 0,
then all weak-SRB-like probability measures areψ-equilibrium states and all the (necessarily existing) expanding ergodic weak-SRB-like measures satisfy Pesin’s Entropy Formula.
2.7
Weak and non-uniformly expanding maps
Now we strengthen the assumptions on non-uniform expansion to im-prove properties of weak-SRB-like measures.
Definition 11. We say that f is weak-expanding if, kD f(x)−1k ≤ 1 for all x∈M.
We say that a probability measure is atomic if it is supported on a finite set. We denote supp(µ) the support of probability measureµ.
Corollary F. Let f :M→M be weak-expanding and non-uniformly expanding. Then,
1. all the (necessarily existing) weak-SRB-like probability measures are ψ -equilibrium states and, in particular, satisfy Pesin’s Entropy Formula;
2. there exists some ergodic weak-SRB-like probability measure;
3. ifψ < 0there is no atomic weak-SRB-like probability measure;
4. if D = {x ∈ M : kD f(x)−1k = 1} is finite and ψ < 0 almost all ergodic components of aψ-equilibrium state are weak-SRB-like measures. Moreover all weak-SRB-like probability measures µ its ergodic components µx are
expanding weak-SRB-like probability measure forµ-a.e. x∈M\D.
In particular, we see that an analogous result to the existence of an atomic physical measure for a quadratic map, as obtained by Keller in [23], is not possible in theC1expanding setting, although generically such
2.7. Weak and non-uniformly expanding maps 21
Corollary G. No atomic measure is a SRB measure for a C1uniformly expanding map of a compact manifold.
We now restate the previous results in the uniformly expanding setting.
Corollary H. Let f : M → M be a C1-expanding map. Then an f -invariant probability measureµsatisfies Pesin’s Entropy Formula if and only if its ergodic components µx are weak-SRB-likeµ-a.e. x ∈ M. Moreover, all the (necessarily
existing) weak-SRB-like probability measures satisfy Pesin’s Entropy Formula, in particular, areψ-equilibrium states. In addition, ifµis the unique weak-SRB-like probability measure thenµis SRB probability measure,Leb(B(µ))=1, is ergodic,
µis the uniqueψ-equilibrium state andµsatisfies large deviation bound.
Using this we get a weak statistical stability result in the uniformly
C1-expanding setting: all weak∗ accumulation points of weak-SRB-like
measures are generalized convex linear combinations of ergodic weak-SRB-like measures, as follows.
Corollary I. Let{fn : M → M}n≥1 a sequence of C1-expanding maps such that fn→− f in the C1-topology and f :M→M be a C1-expanding map. Let(µn)n≥1 a sequence of weak-SRB-like measures associated fn. Then all accumulation points of
Chapter 3
Examples of application
Here we present some examples of applications. In the first section we show the construction of a C1 uniformly expanding map with many
different SRB-like measures which in particular satisfies the assumptions
of Theorem B and Corollary H.
In the second section we present a class of non uniformly expanding
C1local diffeomorphisms satisfying the assumptions of Theorem D. In the
third section we exhibit examples of weak-expanding and non uniformly expanding transformations which are not uniformly expanding in the set-ting of Corollary F.
3.1
Expanding map with several absolutely
con-tinuous invariant probability measures
We present the construction of a C1-expanding map f : S1 → S1 that
has several SRB-Like measures. Moreover, such measures are absolutely continuous with respect to Lebesgue measure (which in particular means that f does not belong to aC1generic subset ofC1(M,M), see [8]).
Example 3.1.1. Following [11], we first adopt some notation for Cantor sets with positive Lebesgue measure. Let I be a closed interval andαn > 0 numbers
with P∞
n=0αn < |I|, where|E| denotes the one-dimensional Lebesgue measure of
the subset E of I. Let a = a1a2. . .an denote a sequence of 0′s and 1′s of length
n=n(a); we denote the empty sequence a=∅with n(a)=0. Define I∅=I=[a,b], I∗
∅ =
h
a+b
2 −
α0
2,a+2b+
α0
2
i
and I∗
a ⊂Ia recursively as follows.
Let Ia0and Ia1be the left and right intervals remaining when the interior of Ia∗
is removed from Ia; let I∗abe the closed interval of length
αn(ak)
2n(ak) and having the same
center as Iak(k=0,1).
The Cantor set KI is given by KI =
∞
T
m=0
S
n(a)=m
Ia.
This is the standard construction of the Cantor set except that we allow our-selves some flexibility in the lengths of the removed intervals. The measure of KI
isLeb(KI)=|I| −P∞n=0αn>0.
Suppose that another interval J ⊃ I is given together with βn > 0 such that
P∞
n=0βn < |J|. One can then construct Ja, Ja∗and KJ as above. Let us assume now
that βn
αn −−−→n→∞ γ ≥ 0. Following the construction of Bowen [11], we get g: I → J
a C1orientation preserving homeomorphism so that g′(x) = γfor all x ∈ K
I and
g′(x)>1for all x∈I.
More precisely, let us take J = [−1,1] and chooseβn > 0with P∞n=0βn < 2
and βn+1
βn → 1,
e.g. βn = (n+100)1 2
. Let I= hβ20,1iandαn =
βn+1
2 . Then
P∞
n=0αn <
1− β0
2 and γ = lim
βn
αn = 2. We define a homeomorphism G : (−I)∪I → J by
G(x)= (
g(x) if x ∈I
−g(−x) if x ∈(−I) ,where KJ =
T+∞
n=0G−n(J)and G|KJ :KJ .
Consider now c1 =
3β0
2 −2 β40
3
, c2 =
9β0
4 −3 β40
2
; f1 : [−β20,−β40] →
[−1,−β0
4]given by
f1(x)=c1 x+β0
2
!3
−c2 x+ β0
2
!2
+2 x+β0
2
!
−1
and f2 : [β0
4,
β0
2]→[
β0
4,1]given by f2(x)= c1
x− β0
2
3
+c2x− β0
2
2
+2x− β0
2
+1. Then, we have
1. f1−β0
2
=−1, f1−β0
4
=−β40, f2β40= β40 and f2β20=1
2. f+
1
β0
2
= lim
h→0+
f1(β20+h)−f1(β20)
h =2, f
+
2
β0
4
=2, f−
1
β0
4
= lim
h→0−
f1(β40+h)−f1(β40)
h =
2and f−
2
β0
2
=2.
Consider now J1 = h−β40,β0
4
i
, I1 =
β20
8,
β0
4
and choose β′
n =
β0βn
4 > 0 with
P∞
n=0β′n <
β0
2 and
β′
n+1
β′
n =
βn+1
βn → 1. Let α
′
n =
β′
n+1
2 , then
P∞
n=0α′n =
P∞
n=0
β′
n+1
2 < 1
2
β0
2 −β′0
= 12
β0
2 −
β20
4
andγ=lim β′n
α′
n =lim
2βn
βn+1 =2.
Similarly to the above construction, we obtain a homeomorphism G1 : (−I1)∪
I1 →J1 given by
G1(x)= (
g1(x) if x∈I1
3.1. Expanding map 25
where KJ1 =
T+∞
n=0G−1n(J1)is a Cantor set with positive Lebesgue measure, G1|KJ1 :
KJ1 and g1 : I1 → J1 is a C1 orientation preserving homeomorphism so that
g′1(x)=2for all x∈ KJ1 and g′1(x)>1for all x∈I1. Similarly we obtain f3 : [0,β20
8] → [−1,−
β0
4]and f4 : [−
β20
8,0] → [
β0
4,1]such that f3(0) = −1, f3(β20
8) = −
β0
4, f3−(
β20
8) = 2, f3+(0) = 2, f4(
−β20
8 ) =
β0
4, f4(0) = 1, f+
4 (−
β20
8)=2and f4−(0)=2
Finally, define the function f : J → J by (see Figure 3.1 for its graph)
f(x)=
G(x) if x∈(−I)∪I f1(x) if x∈−β0
2,−
β0
4
f2(x) if x∈β40,β20
G1(x) if x∈(−I1)∪I1 f4(x) if x∈
−β20
8,0
f3(x) if x∈
0, β20
8
,
Figure 3.1: Graph of f.
Identifying−1 and1and making a linear change of coordinates we obtain a C1expanding map of the circle f : S1 .
ConsiderLebKJthe normalized Lebesgue measure of the set KJ, this is,LebKJ(A)=
Leb(A∩KJ)/Leb(KJ)for all measurable A⊂ J. DenoteΣ+2 ={0,1}Nand consider
the homeomorphism h: KJ → Σ+2 that associates each point x∈ KJ the sequence
a∈Σ+
2 describing its location in the set KJ, this is, a is such that Ia∩KJ ={x}. Let
µbe the Bernoulli measure inΣ+
Claim 3.1.2. µ=h∗LebKJ
We show that this relation holds for an algebra of subsets which generates the Borelσ-algebra ofΣ+2. For a= a1a2. . .anwe have thatµ([a]) =1/2n. Moreover,
h−1([a]) =I
a∩KJ, soLebKJ(h−
1([a]))= Leb
KJ(Ia∩KJ). By construction, at each
step all remaining intervals in the construction of KJ have the same length. Thus,
the n-th stage contains2n intervals I
a (among them) all with the same Lebesgue
measure. SinceLebKJ is a probability measure, we have
2nLeb
KJ(Ia∩KJ)=1=⇒LebKJ(Ia∩KJ)=
1 2n.
We conclude that LebKJ(Ia ∩ KJ) = LebKJ(h−
1([a])) = µ([a]) for all a = a1a2. . .an, n≥1proving the Claim.
Clearly h◦ f|KJ = σ◦h whereσis the standard left shiftσ : Σ +
2 . Sinceµ
isσ-invariant, thenLebKJ is f|KJ-invariant. Consequently(f,LebKJ) is mixing,
htop(f)=log 2=hLebKJ(f)=hµ(σ)andLebKJ ≪Leb.
Hence lim
n→+∞σn(x) = LebKJ forLebKJ−a.e, x ∈ KJ and |KJ| > 0, so it follows
thatLebKJ is a SRB-like measure. By Theorem B, LebKJ is an equilibrium state
for the potentialψ=−log|f′|.
SimilarlyLebKJ1 is also a SRB-like measure, but distinct formLebKJ.
Note that this construction allows us to obtain countably many ergodic SRB-like measures by reapplying the construction to each removed subin-terval of the first Cantor set.
Note also that, if we take a sequence of Hölder continuous potentials
φn converging toψ = −log|f′|, choose νn a φn-conformal measure and a
νn-SRB measure µnand weak∗accumulation points ν, µas in Theorem A,
since f is topologically exact thenν(Aε(µ)) =1 for allε >0. Thereforeνis
not Lebesgue measure onS1.
3.2
C
1Non uniformly expanding maps
Next we present an example that is a robust (C1 open) class of
non-uniformly expandingC1 local diffeomorphisms.
This family of maps was introduced in [2], (see also subsection 2.1 in [3, Chapter 1]) and maps in this class exhibit non-uniform expansion Lebesgue almost everywhere but are not uniformly expanding.