Análise do escoamento em duto curto de orifício (short tube orifices) e estudo dos mecanismos de queda de pressão via gitt para uso em sistemas de refrigeração

Universidade Federal da Paraíba

Centro de Tecnologia

Programa de Pós Graduação em Engenharia Mecânica

Mestrado-Doutorado

ANÁLISE DO ESCOAMENTO EM DUTO CURTO DE ORIFÍCIO (SHORT TUBE ORIFICES) E ESTUDO DOS MECANISMOS DE QUEDA DE PRESSÃO VIA GITT

PARA USO EM SISTEMAS DE REFRIGERAÇÃO

Por

Felipe Vilar da Silva

Felipe Vilar da Silva

ANÁLISE DO ESCOAMENTO EM DUTO CURTO DE ORIFÍCIO (SHORT TUBE ORIFICES) E ESTUDO DOS MECANISMOS DE QUEDA DE PRESSÃO VIA GITT

PARA USO EM SISTEMAS DE REFRIGERAÇÃO

Dissertação apresentada ao Curso de Pós- Graduação em Engenharia Mecânica da Universidade Federal da Paraíba, como requisito para a obtenção do título de Mestre em Engenharia Mecânica.

Orientador: Carlos Antônio Cabral dos Santos

ANÁLISE DO ESCOAMENTO EM DUTO CURTO DE ORIFÍCIO (SHORT TUBE ORIFICES) E ESTUDO DOS MECANISMOS DE QUEDA DE PRESSÃO VIA GITT

PARA USO EM SISTEMAS DE REFRIGERAÇÃO

Por

Felipe Vilar da Silva

Dissertação Aprovada em 01 de Novembro de 2011

Período letivo 2011.2

Examinador Interno UFPB Orientador

Examinador Interno

Examinador Externo

Examinador Externo

iii

Agradecimentos

Ao professor Carlos Cabral, orientador desta dissertação, por todo o seu esforço e a sua dedicação para que o melhor sempre fosse alcançado.

Aos professores e funcionários do Programa de Pós Graduação em Engenharia Mecânica PPGEM/UFPB, pela dedicação e contribuição à minha formação.

Ao CNPQ pelo suporte financeiro ao longo do período de cursos.

iv

ANÁLISE DO ESCOAMENTO EM DUTO CURTO DE ORIFÍCIO S(HORT TUBE ORIFICES) E ESTUDO DOS MECANISMOS DE QUEDA DE PRESSÃO VIA GITT

PARA USO EM SISTEMAS DE REFRIGERAÇÃO

RESUMO

O presente trabalho aponta para um estudo aprofundado dos mecanismos envolvidos queda de pressão e escoamento em dutos curtos de orifício. O escoamento diferentemente da grande maioria dos trabalhos disponíveis na literatura é na primeira etapa abordado através de uma formulação viscosa através de equações de camada limite. As equações na presente proposta se apresentam numa forma que dificultam ou até impossibilitam uma abordagem de soluções via técnicas matemáticas tradicionais, tais como, separação de variáveis, funções de Green entre outras. Para resolver o problema na formulação proposta é empregada a técnica da Transformada Integral Generalizada, para além das equações da continuidade de movimento, poder resolver simultaneamente a equação da energia na formulação entálpica. A formulação entálpica será utilizada para quantificar o efeito da expansão nos short tube orifices.

Os resultados obtidos serão apresentados na forma adimensionalizada para os campos Hidrodinâmico e Térmico e parâmetros de interesse práticos na engenharia.

v

ANALISYS OF THE FLOW IN SHORT TUBE ORIFICES AND

STUDY OS THE EXPANSION PROCESS BY G.I.T.T

ABSTRACT

This work points to a detailed study of the mechanisms involved in the expansion and flow in short tube orifices. The flow unlike the vast majority of available works in the literature is at the first step addressed through a viscous formulation using boundary layer equations. The equations in this proposal are presented in a way that make it difficult or impossible to approach a solution via the traditional mathematical techniques, such as separation of variables, Green's functions among others. To resolve the issue will be used in formulating the proposed Generalized Integral Transform technique, in addition to the equations of continuity and the momentum, be able to solve the energy equation in the enthalpy formulation. The enthalpy formulation is used to capture the effect of expansion in the short tube orifices.

The results will be presented as adimensionalized for hydrodynamic and thermal fields and parameters of practical interest in engineering.

vi

SUMÁRIO

1. Introdução...01

1.1 Dispositivos de Expansão...01

1.2 Revisão Bibliográfica...13

1.3 Modelos para previsão da vazão em escoamentos bifásicos ...15

1.4 Regimes de Escoamento Bifásico em tubos Horizontais...10

1.5 A Técnica da Transformada Integral...13

2 Formulação do problema. ...16

2.1 Considerações no Escoamento...16

2.2 Leis de Conservação...17

2.3 Adimensionalização do problema...20

3 Aplicação da Técnica da Transformada Integral...24

3.1 Solução do Campo Hidrodinamico...24

3.2 Solução do Campo Térmico...31

4 Resultados e Conclusões...38

vii

LISTA DE FIGURAS

Figura 1.1 Escoamento Borbulhado...09

Figura 1.2 Escoamento Tamponado ...09

Figura 1.3 Escoamento Pistonado ...10

Figura 1.4 Escoamento Anular ...10

Figura 1.5 Escoamento Disperso ...11

Figura 4.1 Variação da velocidade não desenvolvida no tubo ...39

Figura 4.2 Perfil de Velocidades no Escoamento ...40

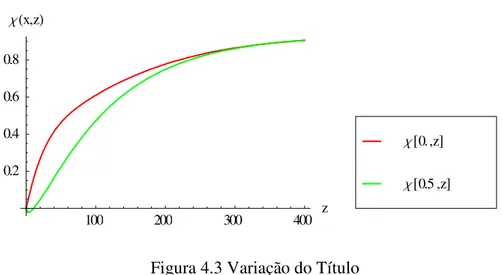
Figura 4.3 Variação do Título no Escoamento ...41

Figura 4.4 Variação do Título ao longo do tubo com o número de Ecket ...41

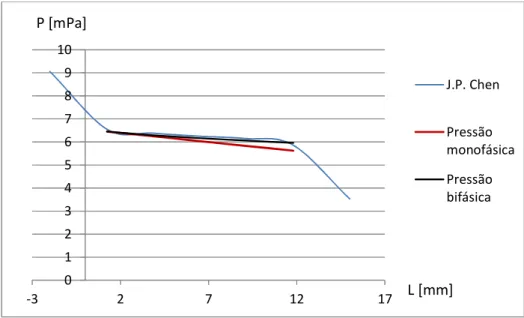
Figura 4.5 Queda de pressão ao longo do tubo ...42

Figura 4.6 Queda de pressão para modelo proposto ...43

viii

LISTA DE TABELAS

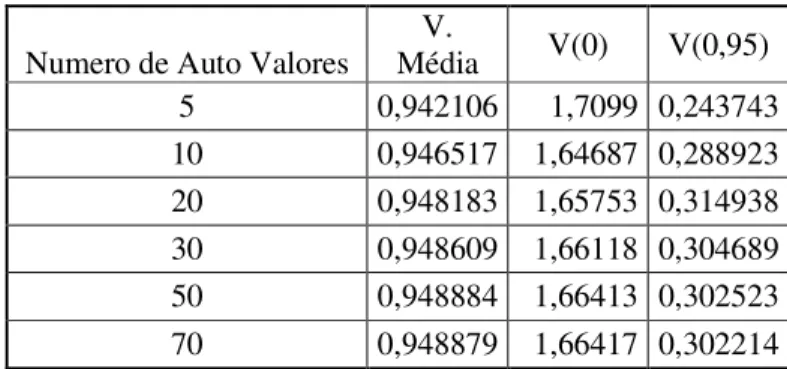
Tabela 4.1 Auto-valores do problema hidrodinâmico ...40

Tabela 4.2 Convergência do campo de Velocidade na entrada do duto ...41

Tabela 4.3 Convergência do Campo de Velocidade na saída do duto ...41

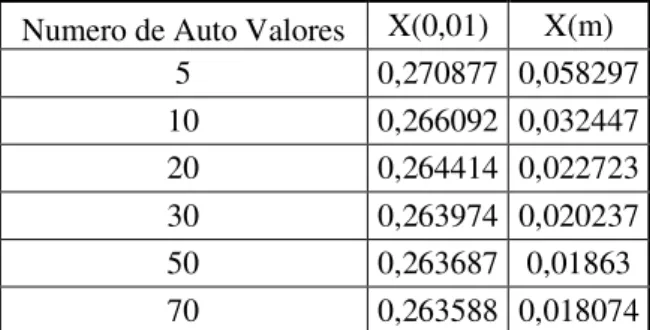
Tabela 4.4 Convergência da Entalpia Adimensional a 1% da entrada do duto ...42

ix

NOMENCLATURA

A - Área

Bi - Número de Biot

Cp - Calor específico.

CV - Coeficiente do campo de velocidades.

CT - Coeficiente do campo térmico.

Ec - Número de Ecket

f - Fator de Atrito

g - Gravidade

G - Velocidade de fluxo (definida como o produto da massa específica pela velocidade)

h - Entalpia

H - Entalpia adimensional

J0 - Função de Bessel de primeira espécie e ordem zero.

J1 - Função de Bessel de primeira espécie e ordem um.

k - Condutividade térmica

K - Condutividade térmica adimensional

x

Nu - Número de Nusselt.

p - Pressão

P - Pressão adimensional

Pe - Número de Peclet

Pr - Número de Prandtl

q - Fluxo de calor

r - Raio

R - Raio adimensional

Rdes - Razão de deslizamento.

Re - Número de Reynolds.

t - Tempo

u - Velocidade

U - Velocidade Adimensional

X - Título

z - Comprimento

Z - Comprimento adimensional.

Letras Gregas

ED - Relativo ao escoamento em desenvolvimento

α

- Difusibilidade Térmica

xi

fv - Fração de vazio.

µ - Viscosidade dinâmica

~

ψ - Autofunção normalizada do campo de velocidade.

λ - Autovalor relacionado à funçãoψ~ .

β - Autovalor relacionado à função Γ

Φ - Dissipação viscosa

Γ - Autofunção normalizada do campo térmico.

Subscritos

* - Adimensional.

bi - Bifásico

g - Gás

i - Índice para série agrupada.

j - Índice para série agrupada.

l - Líquido

o - Entrada

t - Tubo

∞ - Valor da grandeza no escoamento completamente desenvolvido.

1

CAPÍTULO 1

1. INTRODUÇÂO

1.1 Dispositivos de Expansão

O dispositivo de expansão usado em sistemas de refrigeração por compressão de vapor tem normalmente dois propósitos. Um é reduzir a pressão do refrigerante da pressão do condensador para a pressão do evaporador, e o outro é de regular a vazão mássica de refrigerante fluindo do condensador para o evaporador. Basicamente existem dois tipos de dispositivos de expansão, o de restrição variável e de restrição constante. No primeiro a área de escoamento pode ser variada dependendo do sistema de controle. Exemplos dos dispositivos mais populares deste tipo são as válvulas de expansão automáticas e termostáticas. No outro os dispositivos podem ser divididos em 3 categorias, orifício de expansão, short tube orifice e tubo capilar.

As válvulas de expansão termostáticas tem sido usada extensamente em sistemas de refrigeração sendo divididas principalmente em dois grupos, as válvulas termostáticas e as válvula elétricas, que comparada às anterior elétricas tinham um tempo de resposta menor e controle com grande precisão, entretanto seu uso é restrito às condições de operação do sistema, os fabricantes fornecem gráficos e tabelas obtidos de forma empírica que descrevem o comportamento destas válvulas para refrigerantes específicos, e correlacionam fluxo de massa densidade e queda de pressão obtida. O que acontece é que muitas vezes não existe mercado para a faixa de operação pretendida, o que em conjunto com o custo elevado limita o uso das válvulas de expansão a unidades de grande porte.

2 que um longo tubo com dimensões que vão de 1 a 6m de comprimento e diâmetro de 0,5 a 2 mm. Após a entrada do liquido refrigerando no tubo a pressão cai devido à perda de carga por fricção e pela aceleração do refrigerante devido à mudança de área da tubulação para o tubo capilar. Na maioria das vezes o liquido evapora dentro do tubo e as características do escoamento tornam-se diferentes do convencional dificultando a previsão exata da queda de pressão por isso a escolha de um tubo capilar normalmente envolve ajustes manuais por tentativa e erro reduzindo-se o tamanho do tubo até a obtenção de um comprimento que se ajuste a queda de pressão desejada. Assim a principal desvantagem do tubo capilar é que uma vez instalado e o sistema posto em funcionamento, impossibilita o controle de carga do equipamento devido a uma variação na carga térmica do espaço refrigerado. Muitos trabalhos são encontrados na literatura focados em investigação experimental para descrever o escoamento em tubos capilares e desenvolver modelos sistemáticos para prever o comportamento do escoamento e sua influência nos diferentes componentes do sistema

3 configurações bem como descrever o perfil de temperatura velocidade e pressão ao longo do dispositivo.

Através dos anos, as características de desempenho dos” short tube orifices” têm sido estudados por um grande número de pesquisadores. Os estudos mais produtivos tem sido feitos pelos seguintes pesquisadores:

(Pasqua 1953) estudou as características de liquido subresfriado e saturado em escoamento de R-12, através de um short tube de vidro. Para liquido subresfriado entrando nos tubos, ele descobriu que o liquido expandia dentro do tubo quando a pressão de saída estava próxima ou abaixo da pressão de saturação. O fluido dentro do tubo foi descrito como centro interno de líquido meta estável cercado por um anel bifásico anular. O diâmetro do centro de liquido metaestável diminuía a medida que o fluido seguia para a saída do tubo. Ele formulou uma correlação para calcular a vazão mássica para liquido saturado entrando no tubo.

(Mei 1982) investigou o escoamento de liquido sub resfriado de R-22 através de pequenos tubos com 7.5 < L/D < 11.9 em uma bomba de calor. Ele descobriu que o primeiro estágio da expansão ocorria a um grau de sub resfriamento de 22.2. ºC Entretanto, não houve indicação de segundo estagio da expansão na faixa de operação normal da bomba de calor. Ele propôs duas correlações, para grau de sub-resfriamento maior que 22.2 ºC e grau de subresfriamento menor que 22.2º, para R - 22 fluindo através de Short Tubes.

1.2 Revisão Bibliográfica

4 que o escoamento tinha uma dependência muito fraca da pressão de saída para a faixa de operação da bomba de calor, eles recomendavam que a razão L/D deveria se maior que 5 para que o escoamento expandisse na saída.

(Kim 1993) fez um estudo experimental do escoamento bifásico de um liquido subresfriado R-22 e HFC R134a através de “short tube orifices” com uma faixa de relação L/D entre 7 e 20. Os resultados mostraram que a vazão mássica era dependente da pressão e sub-resfriamento de entrada mas era insensível as condições de saída devido proximidade do estrangulamento. Para escoamento bifásico entrando no short tube, a vazão mássica diminuía com o aumento do título. Eles observavam que o ponto de expansão movia-se na direção da secção de entrada do tubo quando o grau de subresfriamento diminuía, Eles propuseram uma correlação bem como ”short tube orifices”.

(Payne e O’Neal 1998) estudaram as características do escoamento de R-407c através de “short tube orifices” com um diâmetro variando de 1.09-1.94 mm. Os efeitos do subresfriamento de entrada pressão de entrada, pressão de saída, comprimento do tubo, diâmetro do tubo e concentração de lubrificante na vazão mássica foram testados. Eles descobriram que a adição de óleo ao lubrificante aumentava a vazão mássica em mais de 12% para escoamento bifásico entrando no pequeno tubo, mas tinha baixo efeito na vazão mássica de alto grau de subresfriamento.

(Singh et al. 2001) apresentou dados experimentais sobre o escoamento do refrigerante R134a através de “short tube orifices” com e sem visualização da saída. As condições de entrada foram variadas, subresfriamento de 40 ºC à condição de saturação. Os resultados do experimento indicaram que a vazão mássica era sensível a pressão de entrada, subresfriamento de entrada e diâmetro do tubo.

5 experimento mostraram que a vazão através de um pequeno tubo flexível era fortemente dependente da pressão de condensação, subresfriamento título e módulo se elasticidade do material do tubo. Entretanto a vazão mostrou pouca dependência da pressão de evaporação. Eles concluíram que o controle na vazão com o pequeno tubo flexível não era tão bom como o de uma válvula de expansão termostática.

(Liu ET al. 2004) estudou as características do escoamento de R-744 através de “short tube orifices”. Os tubos com comprimentos entre 8.02 e 25.42 mm e diâmetros entre 0.83 e 1.53 mm foram testados. Os resultados mostraram que o escoamento bloqueado existiu sob uma larga faixa de operações. O inicio da expansão moveu-se para o plano de saída do tubo quando a pressão de entrada aumentou. Eles reportaram que a as dimensões do chanfro de entrada não tinham efeito evidente na vazão mássica.

(Kim ET al. 2005) estudaram a vazão mássica de R-410A através de “short tube orifices” com pressões de entrada aproximando-se do ponto crítico. Eles descobriram que uma diminuição na vazão mássica com redução do subresfriamento tornava-se mais significante quando a pressão de entrada aumentava além de 3604 kPa, devido a maior mudança de densidade. Uma correlação empírica através de uma lei de potencia de parâmetros adimensionais gerados pelo teorema de Pi Buckingham.

1.3 Modelos para previsão da vazão em escoamentos bifásicos

6 Hsu e Grahan apresentaram as seguintes formas gerais da equação de escoamento crítico, que a partir delas dividem-se os modelos específicos para caracterizar o escoamento.

(

)

[

− +

]

− + ∂

∂

− =

g f cr

x k x k

x xk

P G

ν ν

1 ) 1 (

1

2

(1.1)

Para escoamento unidimensional, bifásico, e três transportes interfaciais ∂k/∂P,

P

g ∂

∂ν / e ∂x/∂P devem ser considerados onde k é a proporção de vapor para a velocidade do líquido, x é o título, e ν_gé o volume específico do vapor. A mudança de volume específico

com relação a pressão ∂ν_g /∂P, é determinada pela taxa de transferência de calor interfacial.

A transferência de momento interfacial determina o quão rápido cada fase é acelerada, i.e.

P k ∂

∂ / . A taxa de evaporação ∂x/∂P, é estimada pela transferência de massa interfacial.

Modelo de equilíbrio homogêneo (Homogeneou equilibrium model)

O modelo HEM é derivado de uma extensão da análise de escoamento monofásico com as seguintes hipóteses: A composição da mistura é homogênea em cada fase, as velocidades de vapor e líquido são iguais e a mistura bifásica está em equilíbrio termodinâmico com propriedades tomadas como medias das fases liquido e vapor em cada secção. Existem três métodos diferentes para avaliar o modelo de Equilíbrio Homogêneo: (1) Modelo Isentálpico, (2) Modelo Isentrópico e (3) modelo de Sajben. A maior diferença entre estes três modelos é a avaliação do termo ∂x/∂P. Estes três modelos estimaram ∂x/∂P

usando a hipótese de precesso isentálpico, isentrópico e Linha de Fanne respectivamente.

7 Este modelo determina o termo ∂x/∂P usando a hipótese de processo em

escoamento isentálpico e a relação termodinâmica h=h_f +xh_fg

_

O modelo isentálpico é dado

por:

2 1

1

− +

−

− =

dP dh

h v

dP d x dP dh

h dP dv G

fg fg fg fg f

fg fg f

cr

ν ν

(1.2)

Modelo Isentrópico. Para o Modelo isentrópico o termo ∂x/∂P é determinado pelas

hipóteses de escoamento isentrópico e a relação termodinâmica s=s_f +xs_fg

_

. O modelo

Isentrópico é dado por

2 1

1

− +

−

− =

dP ds

h v

dP d x dP ds

h dP dv G

fg fg fg fg f

fg fg f

cr

ν ν

(1.3)

Modelo de Sajben. As hipóteses para este modelo é que o escoamento é adiabático com atrito e em área constante. Portanto o escoamento segue a linha de Fanne. A equação da linha de Fanne é derivada da equação da energia e da continuidade.

0 2

_ 2 _ 2

= −

−

+ _f

fg fg t fg

fg h

h h

G

ν ν ν

ν ν

8 onde

cte u xh h

h m

fg

f + + =

=

2

2 _

(1.5)

A expressão para volume especifico médio ν_ é obtida resolvendo a equação

quadrática. Diferenciando

_

ν _{em relação a pressão e então eliminando o termo de raiz quadrada}

usando a expressão para

_

ν _{temos a seguinte relação:}

+

+ − ∂

∂ + ∂

∂

+ ∂

∂ − = ∂ ∂

fg fg

f fg fg f fg

fg fg

fg

fg fg

h G

h h P G h

P h

h

P G

P

ν ν

ν ν ν

ν ν

ν

2 _

2

2 _

1

(1.6)

Portanto o Modelo Sajben fornece

(

)

[

]

2 1

1

1− + −

+ −

=

dP h d

x x dP

h h d

h

G

fg fg

g f fg

f fg f

fg fg

cr

ν ν

ν ν

ν

ν

(1.7)

9 Os modelos Homogêneo Resfriado foram desenvolvidos para aplicações no caso em que o escoamento é homogêneo e transferência de massa interfacial é restrita devido ao tempo insuficiente. Assim os modelos homogêneos resfriados ou modelos metaestáveis homogêneos assumem as seguintes hipóteses: As duas fases são homogenias e as velocidades das duas fases é a mesma, não ocorre transferência de massa entre as fases. Dois modelos homogêneos resfriados que podem ser encontrados na literatura são: O (1) modelo de Wallis e (2) o modelo de Smith.

Modelo de Wallis

O modelo de Wallis aplica as hipóteses acima na equação geral de Hsu e Graham e assim temos:

(

)

2 1 1

1 1

∂ ∂ − + ∂ ∂ − =

−

P x P

x

Gcr g f

ν ν

(1.8)

Modelo de Smith. Smith obteve um modelo usando a relação homogênea bifásica e a

relação pressão/volume para um processo isentrópico proposta por Tangren et al.

(

x

)

cte

P − _f − =

Γ

1

_ ν ν

(1.9)

Onde

(

)

(

)

f vg

f pg

C x xC

C x xC

− +

− + =

Γ

1 1

10 Nota-se que a equação acima foi baseada na hipótese de que a fase liquida é incompressível e a fase vapor se comporta como um gás ideal. Para o escoamento de liquido incompressível o calor específico do líquido Cf pode ser aproximado como Cpf.

Aplicando a equação geral de Hsu e Graham com a hipótese de =0

∂ ∂

P

x _{a equação}

para o modelo de Smith é dada por:

(

)

(

)

2 1

1 1

− +

− + =

g pf vg

pf pg

cr

x P C x xC

C x xC

G

ν

(1.11)

Modelo de equilíbrio não homogêneo

O modelo de equilíbrio não homogêneo é um pouco complicado por considerar todos os três transportes interfaciais sem nenhuma limitação. O modelo de equilíbrio não homogêneo difere dos outros modelos, pois ele assume velocidades diferentes para a fase liquida e vapor, portanto deve-se calcular a razão de deslizamento entre as fases. Os métodos de avaliação do modelo não homogêneo são o modelo de Fauske e o Modelo de Moody, Os dois modelos são similares exceto na forma de avaliação da razão de deslizamento.

1.4 Regimes de Escoamento Bifásico em tubos Horizontais

O escoamento nos short tubes é um escoamento bifásico, de líquido e gás e existem diversos padrões identificáveis de regimes de escoamento em tubos horizontais são eles:

Borbulhante (Bubble Flow)

11 Figura 1.1 Escoamento Borbulhado

Tamponado (Plug Flow)

Nesse tipo de regime formam-se bolsões alongados de gás que tendem a se mover na parte superior do tubo, podendo haver ou não a presença de pequenas bolhas na região imediatamente abaixo dos bolsões, conforme mostra a Figura 1.2

Figura 1.2 Escoamento Tamponado

Pistonado (Slug Flow)

Nesse tipo de regime ocorre rompimento da interface líquido-gás em alguns pontos e gotículas do líquido são suspensas na fase gasosa; cristas do líquido podem atingir a superfície superior do tubo. Esse escoamento tende a ocorrer à medida que a velocidade do gás aumenta, e é mostrado na Figura 1.3.

Figura 1.3 Escoamento Pistonado Anular (Annular Flow)

12 na parte inferior do tubo é maior que na superior. A interface é instável e apresenta bolhas no filme líquido, assim como considerável quantidade de líquido é mantida suspensa na fase gasosa na forma de filamentos, conforme mostra a Figura 1.4.

Figura 1.4 Escoamento Anular

Disperso (Spray Flow)

Nesse tipo de regime o líquido disperso na fase gasosa sob a forma de gotículas, é arrastado pelo gás, conforme mostra a Figura 1.5.

Figura 1.5 Escoamento Disperso

13 1.5 A Técnica da Transformada Integral

Devido as limitações da técnica de separação de variáveis na solução de problemas mais complexos envolvendo Equações Diferenciais Parciais surgiu a Técnica da Transformada Integral Clássica que supera a limitação de que o problema seja homogêneo, é um método analítico de soluções de problemas difusivos de calor e massa, onde a ideia básica consiste em transformar o sistema de equações diferencias parciais em um sistema de equações diferenciais ordinárias desacoplado que pode ser solucionado de maneira mais simples, uma vez que, obtida a solução do sistema aplica-se a formula da inversa pra recuperar o potencial original do sistema. Existe uma vasta literatura compilada por MIKHAILOV e ÖZISIK [1993].

Embora a técnica da Transformada Clássica obtivesse êxito na solução de problemas não homogêneos muitos problemas práticos envolviam um problemas com não-linearedades que não podiam ser resolvidos por tal método. Sentiu-se então a necessidade de aperfeiçoar o método e torna-lo capaz de resolver tais problemas.Com o trabalho ÖZISIK e MURRAY [1984] sobre a solução de problemas difusivos com condições de contorno variáveis surgiu a Técnica da Transformada Integral Generalizada capaz de resolver qualquer tipo de problema seja linear ou não linear através de uma solução híbrida analítico-numérica. O trabalho mais completo e sistemático sobre a GITT foi feito por COTTA [1993], que dividiu os problemas nas seguintes categorias:

14 - Problemas com coeficientes variáveis nas condições de contorno do problema. Nestes problemas incluem-se os problemas com coeficientes dependentes do tempo (condução com número de Biot variável) e problemas com coeficientes dependentes do espaço (convecção forçada em dutos aletados).

- Problemas com fronteiras móveis. Estes problemas são comuns na analise de solidificação e fundição de metais, soldagem e crescimento de cristais, os quais apresentam domínio irregular e consistem de matérias/fases diferentes, com propriedades de transporte e termofísicas distintas.

- Problemas que envolvem problemas auxiliares complicados. Estes problemas são muito aplicados na convecção forçada interna, periódica e transiente, na análise de trocadores de calor bitubulares e na secagem de meios porosos capilares.

- Problemas não lineares. Nesta categoria se encontra a maioria dos problemas práticos na engenharia, particularmente na mecânica dos fluidos e transferência de calor, onde pode-se citar: condução de calor com condutividade térmica variável, solução das equações de camada limite e solução das equações de Navier-Stokes.

Segundo COTTA [1993] A solução de um determinado problema através da GITT, independente da classe a qual ele pertença, pode ser resumida em 5 passo básicos:

1. Escolha do problema de Auto Valor, também conhecido como problema auxiliar deve conter o máximo de informações sobre o problema

2. Desenvolver do Par transformado- Inversa

3. Transformar o problema original e fazer uso das condições iniciais e de contorno disponíveis, transformando o problema em um sistema de equações diferenciais ordinárias

15 5. Usar a formula da inversa para recuperar o potencial original do problema

16

CAPÍTULO II

2. Formulação do problema

O objetivo deste capítulo é apresentar e desenvolver as equações unidimensionais de conservação de massa energia e quantidade de movimento para o escoamento em short tubes, trata-se de um escoamento em desenvolvimento e devido as complicações matemáticas será usado a técnica da transformada integral generalizada (GITT) para a sua solução, o objetivo da solução é obter os perfis de velocidade e gradientes de pressão ao longo do tubo, o efeito bifásico do escoamento será inserido através de uma realimentação do valor do título em cada ponto do duto para correção das propriedades termodinâmicas envolvidas no processo, as propriedades serão consideradas como média das fases em cada secção.

Para a solução serão consideradas as seguintes hipóteses simplificadoras:

2.1 Considerações no escoamento

• Regime Permanente

• Não há difusão axial

• Escoamento em desenvolvimento

• Velocidade como função da posição axial e radial V = V(r,z)

• O escoamento é estratificado, ou seja há uma separação clara das fases líquida e gasosa.

• Propriedades termofísicas constantes

• Escoamento na posição horizontal com efeitos gravitacionais desprezíveis

17 Conservação da massa:

A forma vetorial da equação da conservação da massa é

0 = ⋅ ∇ + V Dt D ρ ρ (2.1)

(

)

0 )

(.

= →

 uz

dz d dz

m d

ρ (2.2)

Com:

z u

G=ρ (2.3)

cte

G= (2.4)

Conservação do momentum:

A forma vetorial geral da Equação da quantidade de movimento é

→ → → + ∇ + ∇ −

= P V g

Dt V D

ρ µ

ρ 2 (2.5)

Com a hipótese de escoamento unidimensional e o desenvolvimento dos operadores contidos na equação temos:

∂ ∂ + ∂ ∂ + ∂ ∂ ∂ ∂ − + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 1 1 z v v r r v r r r z P g z v v r v r v v t

v _{z z z}

z z z z r z θ µ ρ θ

ρ θ _(2.6)

Dadas as condições de escoamento do problema temos a anulação de alguns termos resultando na equação que rege o problema hidrodinâmico

∂ ∂ + ∂ ∂ + ∂ ∂ ∂ ∂ − + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 1 1 z v v r r v r r P r z P g z v v v r v r v v t

v z z z

z z z z z r z θ µ ρ θ

ρ θ _(2.7)

0 0 _{0 0}

18 ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ r u r r r z P z u

u z z

z

1

µ

ρ (2.8)

Conservação da energia

Segundo Bejan [1984] a equação geral e vetorial para a equação da energia tem a seguinte forma: − − + Φ + ∇ + + ∇ − ∇ − = → → → → → → → → r g Dt D V Dt D g V Dt DP P V q Dt DT

cp .

2 . . . 2 2

ρ

ρ

µ

µ

ρ

(2.9)

Após o uso das hipóteses de escoamento unidimensional, simplificações pertinente ao problema e análise de escala para se desprezar os efeitos da dissipação viscosa temos a equação final. dt DP r T kr r r z T u

c_{p z} +

∂ ∂ ∂ ∂ = ∂ ∂ 1

ρ (2.10)

Segundo Bejan [1984] temos:

T h cp

∂ ∂

= (2.11)

Assim podemos usar

T c

h = p (2.12)

Considerando cp constante pode-se fazer

z P u y P u x P u t P r T kr r r z T c

u x y z

p z ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ 1

19 Substituindo 2.12 em 2.13 temos a eq do calor na formulação entálpica

z P u r h c kr r r z h u _z p z ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ 1

ρ (2.14)

Dividindo a eq (2.14) por

ρ

temos

z P u r h c kr r r z h u z p z ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ ρ ρ

1 _(2.15)

O termo

p

c k

ρ é reconhecido como a difusibilidade térmica do fluido substituindo temos:

z P u r h r r r z h u z z ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ ρ α

1 _(2.16)

Consideremos que na parede do tubo a transferência de calor por condução é igual a transferência por convecção assim:

[

− ∞

]

= ∂ ∂

− h T T

r T

k_{f ext p} (2.17)

Multiplicando a eq por Cp.

[

− ∞

]

= ∂ ∂

− h C T C T

r T C

k ext p p p

p

f (2.18)

[

− ∞

]

=

∂ ∂

− h h h

r h

k_{f ext p} (2.19)

Portanto para solução do problema deve-se resolver simultaneamente as eq. da continuidade da quantidade de movimento e da energia resultando no seguinte sistema de Eq. Diferenciais Parciais.

(

)

=0

∂ ∂

z

u

20 ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ r u r r r z P z u

u z z

z

1

µ

ρ (2.21)

z P u r h r r r z h u z z ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ ρ α

1 _(2.22)

2.3 Adimensionalização do problema

A adimensionalização possibilita o uso da expansão em auto funções do problema de Sturm-Liouvulle, seguindo assim o formalismo exigido para o uso da GITT

Para a adimensionalização do problema serão usados os seguintes grupos adimensionais:

0

u u U ₌ z ,

0

r r R= ,

0

r z Z = ,

0 * Gu P P = L 0 * µ µ µ = ,

L V 0 ν ν = L 0 * α α α = h h h H l ∆ − =

Adimensionalização da Eq. da Continuidade.

( )

0

(

*

)

0

0 0 _ = ∂ ∂ → = ∂ ∂ U Z r u u z l

_ρ

ρ

ρ

(2.23)

( )

* 0

* = ∂ ∂ → = G Z G U

ρ (2.24)

Adimensionalização da equação da quantidade de movimento

( )

∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ r u r r r z P z u

u z z

z

1

µ

ρ (2.25)

21

( )

∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ R U R R R r u Z P r u Z U U r

u _{l l}

l _{* *}1

2 0 0 _ 0 * 0 2 0 _ 0 2 0 _ µ µ ρ ρ

ρ _(2.26)

Dividindo tudo por

0 2 0 _ r u l ρ

( )

∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ R U R R R r u Z P Z U U l l 1 1 * 0 0 0 0 _ * * µ µ ρ

ρ (2.27)

( )

∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ R U R R R Z P Z U U 1 Re 1 * 0 * *

_µ

ρ

(2.28)

( )

∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ R U R R R Z P Z U 1 Re 1 * 0 *

µ

(2.29)

Adimensilnalização da Eq. do Calor

Substituindo os grupos adimensionais na equação da energia temos:

Z P U r u R H R R R r Z H U r u _o ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ * 0 _ 3 * 2 0 0 0

0 α 1 _{α (2.30)}

Rearrumando: Z P U H u R H R R R r u Z H U o ∂ ∂ ∆ + ∂ ∂ ∂ ∂ = ∂ ∂ * _ 2 * 0 0 0 1 1 α α (2.31)

Analizando o termo

22 Pr Re 0 0 0 0 0

0 _{→ →}

α υ υ υ υ α l l l

l u r

r u

(2.32)

O termo H u_o

∆

_ 2

é conhecido como o numero de Ecket

Substituindo os grupos adimensionais na eq. Obtemos

(

)

Z

P EcU R H R R R Z H U ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ * * 0 0 1 Pr Re 1

α

(2.33)

O produto do número de Reynolds com o número de Prandtl fornece o número de Peclet

(

)

Z

P EcU R H R R R Pe Z H U ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ * * 0 1 1

α

(2.34)

Utilizando os mesmo grupos adimensionais anteriores podemos adimensionalizar as condições de contorno da seguinte forma :

[

− ∞

]

=

∂ ∂

− h h h

r h

k_{f ext p}

(2.35)

(

)

(

)

− − − − = ∂ − − ∂ − ∞ l v l l p ext l v l f h h h h h h h R h h h h r k 0 (2.36)

[

∞

]

=

[

− ∞

]

∂ ∂ → − = ∂ ∂

− H H

23 O termo

f ext k

r

h _{0 é reconhecível como o número de Biot dessa forma a equação na forma}

adimensional tem a forma:

[

−

]

=0

+ ∂ ∂

∞

H H Bio R H

p (2.38)

Na forma adimensionalizada o sistema de EDPs. Que regem o problema tem a forma:

( )

=0

∂ ∂ →

= G

Z G U

ρ (2.39)

∂ ∂ ∂

∂ +

∂ ∂ − = ∂ ∂

R U R R R Z

P Z

U 1

Re 2 *

0 *

µ

(2.40)

(

)

Z

P EcU R

H R R R Pe Z

H

∂ ∂ + ∂ ∂ ∂

∂ =

∂

∂ *

0

2

α

24 CAPÍTULO 3

3. Aplicação da técnica da transformada integral

3.1 Solução do Campo hidrodinâmico

3.1.1 Problema auxiliar

Como escolha do problema auxiliar para solução do campo hidrodinâmico tem-se:

0 ) ( )

( ~

2 ~

= + R R dR

R Rd dR

d

i i

i _{λ ψ}

ψ

(3.1)

Com as seguintes condições de contorno :

0 ) 0 (

~

=

dR dψ_i

(3.2)

0 ) 1 (

~

=

i

ψ (3.3)

Este problema é conhecido como problema de Stourm-Liouville, e tem a seguinte solução:

(

R

)

J

R _i

i

i(λ, ) 0 λ,

ψ = (3.4)

Onde J0

(

λi,R

)

é a função de Bessel e λisão os autovalores associados ao problema, que podem ser

obtidos pela seguinte auto-condição:

( )

0

0 i =

25 Analogamente os auto valores do problema podem ser obtidos através do método da contagem de sinal, (Mikhailov e Özisik, 1984, Mikhailov e Vulchanov, 1983), o qual oferece segurança e cálculos automáticos de muitos autovalores e como desejado, com precisão controlada

Com a obtenção dos autovalores e das autofunções normalizadas podemos escrever o Par Transformada-Inversa dado por :

=

1 0

~ _

) , ( ) ( )

(Z R RU R Z dR

U ψi (3.6)

∞

=

=

1

_ ~

) ( ) ( )

( i

i i R U Z Z

U ψ (3.7)

dR R R

N N

R

R i

i i

i = =

1 0

2 ~ ~

~

) , ( ,

) , ( ) ( :

Onde ψ ψ β ψ β

3.1.2 Solução do problema Principal

(

)

∂ ∂ ∂

∂ +

∂ ∂ − = ∂ ∂

R U R R R Z

P Z

Z R

U 1

Re 2

, *

0 *

µ

(3.8)

Para acelerar a convergência da solução o seguinte passo intermediário deverá ser adotado

) ( ) , ( )

,

(R Z U R Z U R

U = _ED + _∞ (3.9)

Onde:

) 1 ( 2 )

( 2

R R

U_∞ = − que é o perfil clássico do escoamento completamente desenvolvido em

26 O procedimento é justificado pelo seguinte fato: O perfil de velocidades em desenvolvimento é composto de duas partes, uma parcela em desenvolvimento que representa os efeitos de entrada do tubo e outra parcela completamente desenvolvida que será o perfil do escoamento após passado o comprimento de entrada no tubo.

Assim tem-se:

(

)

(

)

(

(

)

)

∂ − + ∂ ∂ ∂ + ∂ ∂ − = ∂ − + ∂ R R U R R R Z P Z R

U_{ED * ED} 2

0 *

2 _{1 21}

Re 2 1

2

µ

(3.10)

(

)

− ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ R R U R R R Z P Z

U_{ED ED}

4 1 Re 2 * 0 *

µ

(3.11)

(

)

0 * * 0 * Re 16 1 Re 2

µ

µ

− ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ R U R R R Z P Z

U_{ED ED}

(3.12)

Aplicando-se o operador R _idR

~ 1 0

ψ

na Eq tem-se:

(

)

− ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ 1 0 ~ 0 * 1 0 ~ * 0 1 0 ~ * 1 0 ~ Re 16 Re 2 dR R dR R U R R dR R Z P dR Z U

R ED _i

i i ED i

ψ

µ

ψ

µ

ψ

ψ

(3.13)

Tomando-se o problema auxiliar e aplicando-se o operador

1 0 0 Re 2 dR U_ED µ resulta: 0 ) ( Re 2 Re 2 1 0 ~ 2 0 1 0 ~ 0 =

+ U R RdR

dR dR Rd

dR d

U i _{i ED i}

ED λ ψ

µ ψ

µ

27

Subtraindo a Eq. principal do problema auxiliar tem-se

= − − ∂ ∂ 1 0 1 0 1 0 ~ 2 0 ~ 0 ~ Re 2 Re 2 dR R U dR dR Rd dR d U dR Z U

R ED _ED i _{i ED i}

i λ ψ

µ ψ µ ψ

(

)

− ∂ ∂ ∂ ∂ + ∂ ∂ − 1 0 ~ 0 * 1 0 ~ * 0 1 0 ~ * Re 16 Re 2 dR R dR R U R R dR R Z P i ED i i ψ µ ψ µ

ψ (3.15)

Organizando a Equação tem-se

= − + ∂ ∂ + ∂ ∂ 1 0 ~ 2 0 1 0 ~ 0 * 1 0 ~ * 1 0 ~ Re 2 Re 16 dR R U dR R dR R Z P dR Z U

R ED _{i i i ED i}

i

λ

ψ

µ

ψ

µ

ψ

ψ

∂ ∂ ∂ ∂ − 1 0 ~ ~ 0 Re 2 dR R U R R dR Rd dR d U ED i i ED ψ ψ µ (3.16)

No termo a direita da igualdade pode ser aplicado o teorema de Green e usar a formula da Inversa no termo que contém os auto-valores assim tem-se

0 Re 2 Re 16 __ 2 0 1 0 ~ 0 * 1 0 ~ * 1 0 ~ = − + ∂ ∂ + ∂ ∂ i i i i ED

i R dR R dR U

Z P dR Z U

Rψ ψ µ ψ µ λ (3.17)

O gradiente de pressão que aparece na Equação pode ser obtido aplicando o operador

1 0

RdR

na equação da Quantidade de Movimento

28 + ∂ ∂ ∂ ∂ + ∂ ∂ − = ∂ ∂ 1 0 0 * 1 0 * 0 1 0 * 1 0 Re 16 2

Re R dR RdR

U R R R R dR Z P R dR Z U

R ED _µ ED µ _(3.18)

+ ∂ ∂ ∂ ∂ − ∂ ∂ = ∂ ∂ − 1 0 0 * 1 0 0 * 1 0 * Re 16 Re 2

2 dR RdR

R U R R dR Z U R Z

P ED µ ED µ _(3.19)

+ ∂ ∂ − ∂ = ∂ ∂ − 0 * 1 0 0 * 1 0 * Re 8 Re 2

2 µ µ

R U R dR Z U R Z

P ED ED _(3.20)

Da condição de contorno do Problema temos que o termo R U R ED

∂ ∂

se anula em 0 assim:

+ ∂ ∂ − ∂ ∂ = ∂ ∂ − 0 * 0 * 1 0 * Re 8 ) , 1 ( Re 2

2 µ µ

R Z U dR Z U R Z

P ED ED _(3.21)

Aplicando a transformada ∞

= = 1 _ ~ ) ( ) ( ) ( i i i R U Z Z

U ψ temos:

+ ∂ ∂ − ∂ ∂ = ∂ ∂ − ∞ = ∞ = 0 * 1 ____ ~ 0 * 1 0 1 ____ ~ * Re 8 ) ( ) 1 ( Re 2 ) ( ) (

2 ψ µ ψ µ

i

ED i i

EDi

i U z

R dR Z Z U R R Z P (3.22)

Utilizando das propriedades das series e integrais e rearranjando os termos tem-se:

∞ = + ∂ ∂ − ∂ ∂ = ∂ ∂ − 1 0 * ___ ~ 0 * 1 0 ____ ~ * Re 16 ) ( ) 1 ( Re 2 ) ( 2 i EDi i EDi

i U z

R Z Z U dR R Z

P µ ψ µ

ψ (3.23)

Substituindo o gradiente de Pressão na equação anterior tem-se :

+ + ∂ ∂ − ∂ ∂ − ∂ ∂ ∞ = ∞ = 1 0 ~ 0 * 1 ___ ~ 0 * 1 0 1 ____ ~ 1 0 ~ Re 8 ) ( ) 1 ( Re 2 ) (

2 U z R dR

29 0 Re 2 Re 16 __ 2 0 1 0 ~ 0 * = − _{i i}

idR U

Rψ µ λ

µ (3.24) ∞ = + ∂ ∂ − − ∂ ∂ 1 0 1 ____ 1 0 ~ ~ 1 0 ~ 0 * 1 0 ~ _{( )} 2 Re 16 i EDi i i i ED i Z Z U dR R dR R dR R dR Z U

Rψ µ ψ ψ ψ

0 Re 2 Re 16 ) ( ) 1 ( Re 4 __ 2 0 1 0 ~ 0 * 1 0 ~ 1 ___ ~ 0 * = − + ∂ ∂ ∞ = i i i i i EDi i U dR R dR R z U R λ µ ψ µ ψ ψ µ (3.25)

Substituindo a Transformada ∞

= = 1 _ ~ ) ( ) ( ) ( i i i R U Z Z

U ψ com um índice diferente tem-se:

∞ = ∞ = + ∂ ∂ − ∂ ∂ 1 0 1 ____ 1 0 ~ ~ 1 0 1 ____ ~ ~ _{( )} 2 i EDi i i j EDj j i Z Z U dR R dR R dR Z U

Rψ ψ ψ ψ

0 Re 2 ) ( ) 1 ( Re 4 __ 2 0 1 0 ~ 1 ___ ~ 0 * = − ∂ ∂ ∞ = i i i i EDi i U dR R z U R λ µ ψ ψ µ (3.26)

Reorganizando e explicitando os coeficientes tem-se:

∞ = ∂ ∂ + ∂ ∂ − ∂ ∂ 1 1 0 __ ~ ~ 1 0 0 * ____ 1 0 ~ ~ 1 0 ____ ~

~ ₍₁₎

Re 4 ) ( 2 j j j i EDi j i EDj j

i R dRU

R Z Z U dR R dR R Z U dR

Rψ ψ ψ ψ µ ψ ψ

0 Re 2 __ 2 0 =

− µ λ_iU_i (3.27)

∞ = = − + ∂ ∂ 1 __ 2 0 __ ____ 0 Re 2 2 1 j i i j ij EDj

ij CV U U

Z U

CV µ λ (3.28)

− = 1 0 1 0 ~ ~ 1 0 ~ ~ 2

1 R dR R dR R dR

CV _ij ψ_iψ _j ψ_i ψ _j (3.29)

∂ ∂ = 1 0 ~ ~ 0

* ₍₁₎

Re 4

2 R dR

R

CV i _j

ij ψ

ψ µ

30 A eq. ainda pode ser escrita de forma mais compacta na forma:

∞ = = + ∂ ∂ 1 __ 2 0 __ ____ Re 2 2 1 j i i i ij EDj

ij CV U U

Z U

CV µ λ (3.31)

A equação acima representa o potencial de velocidades do escoamento, existe solução para o problema e pode ser obtida obtendo-se uma condição inicial transformada que pode ser

determinada aplicando o operador

1 0

~

dR

Rψ_i na condição inicial original assim

= + _∞ 1 0 ~ 1 0 ~ 1 0 ~ ) ( ) ( ) ( ) 0 , ( )

(RU R dR R RU R dR R R dR

Rψi ψi ψi

(3.32)

dR R dR R

U =− _i + _i

1 0 ~ 1 0 3 ~ __ 2 ) 0

( ψ ψ

(3.33)

A Velocidade Média pode ser determinada através da integração do perfil de velocidades

assim:

[

]

= − + = + = ∞ 1 0 1 0 3 1 0 1 0 1 0 1 0 2 2 ) , ( ) ( ) , ( RdR dR R dR R dR Z R RU RdR dR R U Z R U R U_média

( ) ( )

[ ]

( )

1 2 2 2 1 1 __ 1 0 2 1 1 0 4 1 0 2 1 0 __ ~ + = − + ∞ = ∞ = i i i i i i Z U CVm R R R dR Z U R Rψ (3.34)

( )

1 2 1 __ + = ∞ = i i i

média CVmU Z

31

=

1 0

~

dR R

32 3.2 Solução do campo térmico

O problema de autovalor associado escolhido é:

( )

__

_{( )}

₀ 2

__

= Φ + Φ

R R

dR R d R dR

d

i i i

β (3.37)

( )

0 ₀

__ = Φ

dR d i

(3.38)

( )

1 __

_{( )}

₁ * __

i i

Bi dR

d

Φ − =

Φ _(3.39)

A solução analítica do problema é:

) ( ) ,

( ₀

__

R J

R _i

i β = β

Φ (3.40)

Os autovalores são obtidos através da auto-condição dada abaixo:

i i

i J

J

Bi* ₀(β ) ₁(β )β

= (3.41)

33 dR R R N N R R Z H R Z R H dR Z R H R R Z H i i i i i i i i i i Φ = Φ = Φ Φ = Φ = ∞ = 1 0 __ 2 __ __ 1 __ 1 0 __ ) , ( , ) , ( ) ( : Onde ) ( ) ( ) , ( ) , ( ) ( ) ( β β Problema principal dZ dP EcU R Z R H R R R Pe Z Z R H e + ∂ ∂ ∂ ∂ = ∂

∂ ( , ) 2

α

( , )

(3.42)

Operando-se o problema principal com Φ

( )

1

0 __

dR R

R i :

( )

( )

+ Φ

( )[

+ ∞

]

∂ ∂ ∂ ∂ Φ = ∂ ∂ Φ 1 0 __ 1 0 __ 1 0 __ ) ( ) , ( ) , ( 2 ) , ( dR R U Z R U R R dZ dP Ec dR R Z R H R R R Pe dR Z Z R H R

R i i

e

i (3.43)

Analisando-se o primeiro termo da equação e substituindo a inversa temos:

( )

( )

( ) ( )

Z H dR R R R dR H Z R R dR Z Z R H R

R i j j

j j j j i i ∂ ∂ Φ Φ → Φ ∂ ∂ Φ = ∂ ∂ Φ ∞ = ∞ = __ __ __ 1 1 0 1 0 1 __ __ __ 1 0 __ _{( , )} (3.44) Z H CT j j ∂ ∂ ∞ = __ 1

1 (3.45)

( ) ( )

R RdR R

CT i j

__ __ 1

0

1= Φ Φ (3.46)

34 ∂ ∂ ∂ ∂ Φ 1 0 __ 2 dR R H R R Pe_e i

(3.47)

Olhando para o problema auxiliar e operando-o com H R Z dR Pe_e

1

0 ( , )

2 _{, obtem-se:}

(

)

( )

R

( ) (

R H R Z

)

dR Pe dR dR R d R dR d Z R H

Pe _e i i

i e Φ = Φ 1 0 __ 2 1 0 __ , 2 , 2

β (3.48)

(

)

( )

R

( )

R H

( )

Z dR Pe dR dR R d R dR d Z R H Pe j j j i i e i e ∞ = Φ Φ = Φ 1 0 1 __ __ __ 2 1 0 __ 2 , 2

β (3.49)

(

)

( )

R

( )

R R dRH

( )

Z Pe dR dR R d R dR d Z R H

Pe j j

j i i e i e __ 1 1 0 __ __ 2 1 0 __ ) ( 2 , 2 ∞ = Φ Φ = Φ

β (3.50)

O termo R

( )

R RdR

j j i ∞ = Φ Φ 1 1 0 __ __ )

( só existe quando i = j e vale 1 assim somando o problema auxiliar

transformado com o problema principal temos:

(

)

Φ

( )

+ +

+ ∂ ∂ ∂ ∂ Φ = ∞ = 1 0 __ 2 __ 1 0 __ __ 1 2 , 2 2

1 _i j

e i e i e j j H Pe dR dR R d R dR d Z R H Pe dR R H R R Pe H CT β

´

Φ

( )

[

+

∞

]

1 0 __

)

(

)

,

(

R

Z

U

R

dR

U

R

R

dZ

dP

Ec

i (3.51)

(

)

Φ

( )

+

+ ∂ ∂ ∂ ∂ Φ = − ∞ = dR R d R dR d Z R H dR R H R R Pe H Pe H

CT i i

e j i e j j __ 1 0 __ __ 2 __ 1 , 2 2 1 β

( )

[

+

∞

]

Φ

+

1 0 __ __

2

₍

_,

₎

₍

₎

2

dR

R

U

Z

R

U

R

R

dZ

dP

Ec

H

Pe

_e

β

i j i

(3.52)

35

(

)

Φ

( )

=

+ ∂ ∂ ∂ ∂ Φ dR R d R dR d Z R H dR R H R R Pe i i e __ 1 0 __ , 2

(

)

Φ

( )

+ ∂ ∂ Φ 1 0 __ __ , ) , ( ) ( 2 dR dR R d R Z R H R Z R H R R Pe i i e (3.53)

(

)

( )

_i j

e e H Pe i i

Pe

_dR

dR

R

d

R

Z

R

H

R

H

R

2 __

1 0 2 1 0 __ __ 2

_,

β +

Φ

+

∂

∂

Φ

(3.54)

Das condições de contorno do problema:

Para R=0 0 __ = Φ

∂

∂

R

H

R

i (3.55)

(

,

)

( )

0

__ = Φ dR R d R Z R H i (3.56) Para R=1 ) 1 ( ) , 1 ( ) ( __ __ i

i Bi Z H Z

R

H

R

= Φ

Φ

∂

∂

(3.57)

(

,

)

( )

*__(1) (1, )

36

Substituindo e reorganizando a equação temos:

j i e i e

H

Pe

Z

H

Bi

Bi

Pe

__ 2 __

₂

)

,

1

(

)

1

(

)

*

(

2

β

+

Φ

−

(3.59)

Substituindo a inversa:

j i e j j i e j i e j j i e H Pe Z H Bi Bi Pe H Pe Z H Bi Bi Pe __ 2 1 __ __ __ __ 2 1 __ __ __ ₂ ) ( ) 1 ( ) 1 ( ) * ( 2 2 ) ( ) 1 ( ) 1 ( ) * ( 2 β

β → − Φ Φ +

+ Φ Φ − ∞ = ∞ = (3.60)

Como não trata-se de um problema com numero de Biot Variável o termo torna-se apenas:

j i e H Pe __ 2 2

β (3.61)

O ultimo termo da equação da energia pode ser operado substituindo o perfil de velocidades completamente desenvolvido o e aplicando a formula da inversa assim:

( )

[

+

]

→ Φ ∞ 1 0 __ ) ( ) ,

(R Z U R dR U R R dZ dP Ec i

( )

+ Φ

( )

− Φ

( )

Φ ∞ = R R R R dR Z U R R R dZ dP

Ec i i

j ED j i __ 1 0 3 __ 1 0 1 0 1 __ ~ __ 2 2 ) ( ) ( ψ (3.62)

( )

+ Φ

( )

− Φ

( )

Φ ∞ = R R R R Z U dR R R dZ dP

Ec i i

j EDj i __ 1 0 3 __ 1 0 1 1 0 __ __ 2 2 )

( (3.63)

Com a solução de todos os termos e o gradiente de pressão expresso pela equação (3.23) podemos reescrever a equação da energia na seguinte forma:

3 ) ( 2 2 1 1 __ __ 2 __ 1 CT Z U CT dZ dP Ec H Pe Z H CT j EDj j i e ij j + + − = ∂ ∂ ∞ = ∞ =

β

δ

(3.64)

37

dR R R R

CT _ij = Φ_i Φ_j 1 0 ) ( ) (

1 (3.65)

dR R R R

CT _ij = _j Φ_i

1 0 ~ ) ( ) (

2 ψ (3.66)

Φ − Φ = 1 0 3 1 0 ) ( 2 ) ( 2

3 R RdR R R dR

CT _ij δ_{ij i i} (3.67)

A equação ainda pode ser escrita mais compactamente na forma:

0 3 ) ( 2 2

1 __ __

1 2 __ = + − − ∂ ∂ ∞ = ij ij ED ij j j i e ij j

ij CT U Z CT

dZ dP Ec H Pe Z H

CT δ β δ (3.68)

Substituindo a Expressão para o Gradiente de Pressão 3.23 em 3.64 a Equação toma a forma:

) ( 3 ) ( 2 ) ( 2 ) ( 1 __ __ 1 2 Z U CT dZ Z U d CT Z H PeEc dZ Z H d

CT _ij j

j ij j j i ij j

ij − − −

∞ = β δ 0 ) ( ) ( 5 ) ( ) ( 4 1 __ __ __ __ = − − ∞ = k k j ijk k j

ijk CT U Z U Z

dZ Z U d Z U

CT (3.69)

Reescrevendo os coeficientes da Equação acima temos :

dR R R R

CT _ij = Φi Φj 1 0 __ __ ) ( ) (

1 (3.70)

dR R R dR R R dR R R Ec

CT _ij = Φi − Φi _j

1 0 1 0 __ 3 1 0 __ ) ( ) ( ) ( 4

38 Φ − Φ − Φ = dR d dR R R dR d dR R R dR R R R Ec

CT i j

j i j i AD ij ) 1 ( ) ( ) 1 ( ) ( ) ( ) ( 2 Re 8 3 1 0 __ 3 1 0 __ 1 0

__ _{ψ ψ}

ψ

µ _(3.72)

dR R R dR R R R Ec

CT _ijk = Φi Φj _k

1 0 1 0 __ __ ) ( ) ( ) ( 2

4 ψ (3.73)

dR d dR R R R Ec CT k j i AD ijk ) 1 ( ) ( ) ( Re 4 5 1 0 __ _ψ ψ µ Φ = (3.74)

A Condição inicial do problema pode ser obtida por Aplicando o operador Φ

1 0

dR R i

Assim H_i(0)=0 (3.75)

A entalpia média no escoamento é determinada pela seguinte expressão

[

]

= + = ∞ média média U dR R U Z R U Z R H H 1

0 ( , ) ( , ) ( )

Substituindo o perfil de velocidades e aplicando a inversa temos:

) ( 2 ) ( 1 1 1 1 __ Z H m CT Z U m CT U H i i i j j ij édia m média ∞ = ∞ = +

= (3.76)

dR R R R m

CT _ij = Φi _j 1 0 __ ) ( ) (

1 ψ (3.77)

Φ − Φ

= R R dR R R dR m

CT _i i i

39

CAPÍTULO IV

4.

Resultados e Conclusões

Os resultados do modelamento matemático foram implementados em uma plataforma simbólica utilizando o software Matehmatica 8.0 os resultados foram obtidos em um computador com processador Core i3 2,54GHz com 4 GB de RAM DDR3 1333 MHz

Tabela 4.1 Auto-valores do problema hidrodinâmico

Auto-valores Velocidade

Contagem de sinais Mathematica

N Auto valor Norma N Auto valor Norma

1 2,40482 0,13476 1

2,40483 0,13476

2 5,52007 0,05789 2 _{5,52008 0,05789}

3 8,65371 0,03684 3 _{8,65373 0,03684}

4 11,79.150 0,02701 4 _{11,79153 0,02702}

5 14,93.086 0,02133 5 _{14,93092 0,02133}

6 18,07.098 0,01761 6

18,07106 0,01762

7 21,21.152 0,01501 7 21,21164 0,015

8 24,35.233 0,01307 8 _{24,35247 0,01307}

9 27,49.330 0,01157 9

27,49348 0,01158

10 30,63.438 0,01038 10 _{30,63461 0,01039}

11 33,77.555 0,00942 11

33,77582 0,00943