ETODO TIGHT-BINDING APLICADO A NANOFITA DE GRAFENO COM CAMPO EL´ ETRICO

(1)

DEPARTAMENTO DE F´ISICA

LUAN VIEIRA DE CASTRO

M´

ETODO TIGHT-BINDING APLICADO

A NANOFITA DE GRAFENO COM

CAMPO EL´

ETRICO

(2)

LUAN VIEIRA DE CASTRO

M´

ETODO TIGHT-BINDING APLICADO

A NANOFITA DE GRAFENO COM

CAMPO EL´

ETRICO

Monografia submetida à Coordena¸cão do Curso de Gradua¸cão em F´ısica, da Univer-sidade Federal do Ceará, como requisito par-cial para a obten¸cão do grau de Bacharel em F´ısica

Orientador:

Prof. Dr. Jo˜ao Milton Pereira Jr.

(3)

M´

ETODO TIGHT-BINDING APLICADO

A NANOFITA DE GRAFENO COM

CAMPO EL´

ETRICO

Monografia submetida à Coordena¸cão do Curso de Gradua¸cão em F´ısica, da Univer-sidade Federal do Ceará, como requisito par-cial para a obten¸cão do grau de Bacharel em F´ısica

Aprovada em / /

BANCA EXAMINADORA

Prof. Dr. Jo˜ao Milton Pereira Junior (Orientador) Universidade Federal do Cear´a

Prof. Dr. Andrey Chaves Universidade Federal do Cear´a

(4)

Dados Internacionais de Cataloga¸c˜ao na Publica¸c˜ao

Universidade Federal do Cear´a

Biblioteca Setorial de F´ısica

C532m Castro, Luan Vieira de.

M´etodo Tight-Binding aplicado a nanofita de grafeno

com campo el´etrico / Luan Vieira de Castro. – 2014.

48 p.;il.

Monografia - Universidade Federal do Cear´a,

Departa-mento de F´ısica, Centro de Ciˆencias, Fortaleza, 2014. ´

Area de Concentra¸c˜ao: F´ısica

Orienta¸c˜ao: Prof. Dr. Jo˜ao Milton Pereira Jr.

1. F´ısica do estado s´olido. 2. Nanofita de Grafeno. 3.

Tight-Binding. 4. Rela¸cão de dispersão. 5. Campo elétrico. I.

(5)

(6)

AGRADECIMENTOS

(7)

(8)

ABSTRACT

(9)

(10)

LISTA DE FIGURAS

1 Número de publica¸cões sobre grafeno nos últimos anos. Fonte:[3] . . . . p. 13

2 C´elula unit´aria de grafeno. . . p. 13

3 Nanofita de Grafeno: armchair (Direita) e zig-zag (Esquerda) com a

c´elula unit´aria em destaque. . . p. 15

4 Rela¸cão de dispersão próxima à um dos cones de Dirac numa

monoca-mada de grafeno. Imagem adaptada de [3] . . . p. 16

5 Duas aplica¸c˜oes para grafeno: (a) Grafeno utilizando na produ¸c˜ao de

c´elulas solares[9]. (b) Grafeno utilizado em sensores de g´as [10] . . . p. 18

6 ´atomos de carbono em uma rede hexagonal de grafeno. R1, R2 e R3

denotam as distâncias aos vizinhos mais próximos de um átomo tipo B

(azul) da rede. . . p. 26

7 rela¸c˜ao de dispers˜ao para uma folha de grafeno infinita. . . p. 28

8 Na aproxima¸c˜ao de segundos vizinhos, somamos sobre os dois grupos de

´atomos mostrados na figura. . . p. 29

9 Resultado para a rela¸c˜ao de dispers˜ao para nanofita de bordas armchair

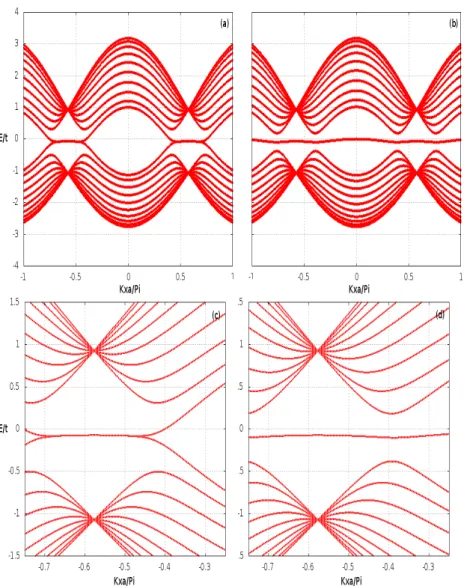
sem campo el´etrico com: (a)Ny = 20, (b)21 e (c)22 linhas. . . p. 33

10 Resultado para a rela¸c˜ao de dispers˜ao de nanofitas zigzag com (a)Ny =

20 linhas e (b)Ny = 21 linhas. As figuras (c) e (d) representam uma

amplia¸cão da região próxima aos estados de borda. Foram utilizados

valores de t0 = 2.8 eV e t1 = 0.01 eV . . . p. 35

11 Proje¸cão da rela¸cão de dispersão para folha infinita de grafeno ao longo

(11)

≈

brillouin para Nx = (a)20, (b)21 e (c)22 linhas. Em (d),(e) e (f) est´a

plotado o zoom da regi˜ao pr´oxima ao gap para cada uma das figuras.

As energias est˜ao colocadas em unidades de t0 e os vetores de onda em

unidades de π/a. . . p. 37

13 Rela¸cão de dispersão para nanofitas de bordas zigzag com aplica¸cão de campo elétrico de _≈ 1V /nm. A figura representa a primeira zona de brillouin para Nx= (a)20 e (b)21 linhas. Em (c),(d) está plotado o zoom

da regi˜ao pr´oxima aos estados de borda para cada uma das figuras.As

energias est˜ao colocadas em unidades de t0 e os vetores de onda em

unidades de π/a. . . p. 38

14 Energia em fun¸cão do campo elétrica para: (a) nanofita de 20 linhas com borda armchair e (b) nanofita de 20 linhas com borda zigzag. Na figura, plotamos energia em unidades det0 em fun¸cão dee0/t, que é proporcional

ao campo. . . p. 39

15 (a)Potêncial elétrico em fun¸cão da posi¸cão y ao longo da fita. (b) Campo

elétrico em fun¸cão da posi¸cão. Note que não há informa¸cão alguma a

respeito da região de varia¸cão de potêncial. . . p. 41

16 Resultado para nanofita armchair submetida a um po¸co de potˆencial com n´umero de linhas, da esquerda para direita: Ny = 20, 21 e 22 linhas. Os

resultados s˜ao mostrados com os seguinte valores de altura da barreira:

0.25t0(a)-(c); 0.5t0 (d)-(f); 0.75t0(g)-(i); t0(j)-(m). . . p. 43

17 Resultado para nanofita zigzag submetida a um po¸co de potˆencial com n´umero de linhas, da esquerda para direita: Ny = 20 e 21 . Os resultados

s˜ao mostrados com os seguinte valores de altura da barreira: 0.25t0(a)(b);

0.5t0 (c)(d); 0.75t0(e)(f); t0(g)(h). . . p. 44

18 densidade de probabilidade para dois auto estados arbitr´arios na nanofita. A figura de cima mostra o resultado para um estado localizado no po¸co

com altura da barreira V = (a)0, (b)0.5t0 e (c)4t0. Na figura de baixo

o mesmo resultado com a fun¸c˜ao de onda localizada na barreira e V =

(12)

SUM ´

ARIO

1 INTRODUC¸ ˜AO p. 12

1.1 Defini¸c˜oes . . . p. 12

1.2 Propriedades . . . p. 15

1.3 Aplica¸c˜oes . . . p. 17

1.4 Sum´ario . . . p. 18

2 MODELO TE ´ORICO p. 19

2.1 M´etodo Tight-binding . . . p. 19

2.2 Formalismo quˆantico de segunda quantiza¸c˜ao . . . p. 21

2.3 Modelo Tight-binding aplicado em grafeno . . . p. 24

2.3.1 Folha infinita . . . p. 24

2.3.2 Nanofita de Grafeno . . . p. 28

3 RESULTADOS p. 33

3.1 Nanofita Sem Campo el´etrico . . . p. 33

3.2 Campo el´etrico com potencial linear com a posi¸c˜ao . . . p. 36

3.3 Po¸co de potencial . . . p. 40

4 CONCLUS ˜AO p. 46

(13)

1 INTRODUC

¸ ˜

AO

1.1 Defini¸

c˜

oes

Os primeiros trabalhos te´oricos sobre grafeno datam de 1947 quando Wallace fez os primeiros calculos usando um modelo Tight-Binding para determinar as suas propriedades eletrˆonicas[1]. Neste trabalho, Wallace estava mais interessado em um estudo das

pro-priedades do grafite (um arranjo de folhas de carbono empilhadas uma sobre a outra), utilizando grafeno simplesmente como um passo intermedi´ario.

Em 5 de outubro de 2010, o prêmio Nobel de f´ısica foi dado à Konstantin Novoselov e Andre Geim pelos trabalhos pioneiros na sintetiza¸cão de monocamadas de grafite ou, como passou a ser chamado, grafeno[2]. Desde então, têm sido realizados vários estudos

para tentar entender as propriedade eletrônicas, mecânicas, ópticas, térmicas e qu´ımicas desse material, que tem grande potêncial para aplica¸cões em várias áreas da indústria e tecnologia. Para ilustrarmos a aten¸cão que tem sido dada pela comunidade cient´ıfica para conseguir controlar as propriedades desse material nos últimos anos, a figura 1[3] mostra

o número de publica¸cões realizadas sobre grafeno nos últimos anos.

De uma forma geral, grafeno pode ser definido como uma monocamada plana de átomos de carbonos arranjados numa estrutura tipo favo-de-mel, com uma distância de 0.142 nm entre os átomos. Átomos de carbono possuem estrutura de Lewis dada por

1s2_,₂_s2_,₂_p2_{. No grafeno, esses quatro orbitais atˆomicos da camada de valˆencia se}

hib-ridizam formando três liga¸cões σ fortes no plano, responsável pela forte estrutura plana do grafeno, e um orbital π perpendicular ao plano, responsáveis pelas propriedades de transporte ao longo da folha.

(14)

13

Figura 1: Número de publica¸cões sobre grafeno nos últimos anos. Fonte:[3]

e~a2.N´os definimos as subredes A e B no grafeno como as redes formadas pelos ´atomos do

tipo A (em vermelho) e as redes formadas por ´atomos do tipo B (em azul). Como podemos ver da figura, esses vetores s˜ao dados por: ~a1 = 3a/2~i+

√

3a/2~j; ~a2 = 3a/2~i−

√

3a/2~j. Qualquer átomo do tipo A pode ser alcan¸cado de outro átomo do tipo A por um vetor de transla¸cão da rede T~ = n ~a1 +m ~a2, onde n em são inteiros, o mesmo valendo para

átomos do tipo B. Os átomos A e B na figura 2 não são equivalentes e não podem ser alcan¸cados um do outro através de um vetor de transla¸cão da rede. Ambos formam redes

triangulares e n´os rotulamos as redes formadas por esses ´atomos de subrede A e subrede B, respectivamente.

Figura 2: C´elula unit´aria de grafeno.

(15)

recen-temente. Primeiro, acreditava-se que tais estruturas essencialmente bidimensionais (2D) não poderiam existir. A razão para isso é que, na natureza, crescimento de cristais exige altas temperaturas, o que torna estruturas de baixas dimensionalidade instáveis, devido a flutua¸cões térmicas [4]. Portanto, materiais bidimensionais, como o grafeno, se

decompo-riam em estruturas tridimensionais mais estáveis, como nanotubos de carbono, fulerenos, etc. O segundo motivo é que, mesmo que existissem, não haveria aparato experimental para observar tal estrutura. Essa última dificuldade foi resolvida devido ao efeito que o grafeno cria num substrato de sil´ıcio que permite a sua observa¸cão direta através de um

microsc´opio ´otico comum [4].

Antes de terminar essa se¸cão, precisamos definir uma subcategoria de materias de grafeno que será o principal objeto de estudo desse trabalho. Em estudos teóricos, nor-malmente consideramos o grafeno como uma folha infinita e, à partir da´ı, utilizamos nosso modelo para pré-dizer as propriedades desse material. Nesse trabalho, estaremos

mais interessados numa subestrutura unidimensional de grafeno, na nanofita de grafeno, que pode ser considerada como uma região entre o corte de dois planos paralelos da folha. Assim, uma nanofita é infinita em uma dire¸cão, mas discreta na outra. Vamos escolher nosso sistema de coordenadas com o eixo y na dire¸cão finita da folha e x na infinita.

Pre-cisamos além disso definir ao longo de quais planos faremos os cortes da fita, que definem as bordas. Trabalharemos aqui os dois tipos mais básicos de bordas: bordas armchair e bordas zigzag. Na figura 5 representamos essas duas geometrias. A borda armchair é obtida quando realizamos um corte ao longo da dire¸cão das arestas no grafeno e a zigzag

quando realizamos um corte ao longo dos vértices. As duas geometrias para as bordas estão defasadas de um ângulo de 30◦_{. Na figura, também está representada a célula} unitária para cada uma das geometrias. Essas estruturas podem ser obtidas através do

modo usual de produ¸cão de grafeno, a clivagem micromecânica ou através de um processo de corte de um nanotubo.

(16)

15

Figura 3: Nanofita de Grafeno: armchair (Direita) e zig-zag (Esquerda) com a c´elula unit´aria em destaque.

1.2 Propriedades

Das propriedades do grafeno, a que chama mais aten¸cão é sem dúvida o fato de que elétrons no grafeno se comportam como part´ıculas relativ´ısticas de spin 1/2, sem massa e obedecendo uma equa¸cão do tipo Dirac. Isso se deve ao fato de que sua rela¸cão de

dispersão possui uma forma linear em torno de um conjunto finito de pontos equivalentes K e K’ do espa¸co rec´ıproco, tal como a de férmion livre de Dirac. No lugar do spin, surge no grafeno o que se chama de um pseudo-spin, associado ao fato de o elétron se encontrar em um átomo da subrede A ou um átomo da subrede B no grafeno. Assim, uma de suas

primeiras aplica¸cões, pode ser vista como utilizar o grafeno para entender fenômenos as-sociados a part´ıculas relativ´ısticas, que entra no escopo da eletrodinâmica quântica. Isso levou a uma melhor compreensão de fenômenos conhecidos, como o Efeito Hall Quântico Anômalo e a predi¸cão de novos fenômenos como o tunelamento de Klein[4][3][5]. Este

´

ultimo é apresentado na eletrodinâmica quântica como o paradoxo de Klein, onde uma part´ıcula que faz uma incidência normal ao longo de uma barreira de potencial consegue tunelar, ou melhor atravessar, com probabilidade de 100 %. No grafeno, isso é poss´ıvel simplesmente mudando o estado de elétron para buraco, e vice-versa, ao atravessar a

bar-reira.

(17)

Figura 4: Rela¸cão de dispersão próxima à um dos cones de Dirac numa monocamada de grafeno. Imagem adaptada de [3]

mobilidade eletrˆonica, podendo esta ´ultima alcan¸car valores da ordem de 200.000 cm2_/Vs,

que ´e muito alto em compara¸c˜ao com os valores medidos para outros semicondutores, como

o antimoneato de ´ındio, por exemplo, que possu´ı me da ordem de 77,000 cm2_{/Vs.. Faixas}

de valores altas como essas são alcan¸cadas em uma folha de grafeno principalmente por esse material ser suave e livre de defeitos. Numa amostra, é ainda poss´ıvel modificar essa mobilidade pela introdu¸cão de defeitos, aplicando pertuba¸cões externas e/ou através de

intera¸c˜ao com outras moleculas na sua superf´ıcie.

Apesar dessas excepcionais propriedades exibidas por uma nanofita de grafeno ainda há problemas que poderiam impedir sua aplica¸cão na eletrônica. Uma delas é o fato de o espectro de energia do grafeno exibir gap zero, o que impede o uso do grafeno em

aplica¸cões lógicas. Uma forma de ser resolver isso, como ficará claro mais adiante, é uti-lizar uma nanofita de grafeno, pois, para esse sistema, é poss´ıvel a abertura de um gap. Além disso, a aplica¸cão de pertuba¸cões externas como strain[6], impurezas[7], campos externos (principal assunto discutido nesse trabalho) podem servir como mecanismo de

controle do gap na nanofita.

Grafeno também possu´ı excelentes propriedades ópticas, mecânicas e térmicas. Uma ´

unica folha de grafeno absorve 2,3% da luz que incide sobre ela. Essa absor¸cão cresce linearmente com o número de camadas de grafeno e é poss´ıvel mostrar que ela está

(18)

17

rela¸cão a suas propriedades mecânicas, grafeno possui um módulo de elasticidade grande e, portanto, pode ser muito bom em aplica¸cões de dispositivos eletrônicos, tornando-se resistente a aplica¸cão de strain. Para concluir, grafeno também exibe alta condutividade térmica devido as liga¸cões covalente C-C entre átomos de carbono. Cálculos feitos através

de espectroscopia micro-Raman confocal, determinaram valores de at´e 5300 W/mK no grafeno [3].

Resumindo, apresentamos nessa se¸cão um breve resumo de algumas das principais propriedades f´ısicas do grafeno que tem sido fonte de discussão nos estudos atuais sobre esse material. Na próxima se¸cão, veremos como algumas dessas propriedades estão sendo

utilizadas ou prometem ser utilizadas em aplica¸c˜oes futuras.

1.3 Aplica¸

c˜

oes

Devido a suas propriedades, o grafeno promete ter aplica¸cão em várias áreas como bio engenharia, no melhoramento de materiais, na optoeletrônica, etc. Além disso, as pesquisas em grafeno geraram um crescente interesse da comunidade cientifica em outros

materiais bidimensionais como nitreto de boro, sulfito de tântalo(IV), etc. Grafeno, com-binado com essas novas estruturas pode gerar materiais ainda mais interessantes, tanto do ponto de vista teórico quanto prático.

Uma propriedade do grafeno que chama aten¸c˜ao ´e sua sensibilidade qu´ımica. Quando

uma única molécula de gás é adsorvida numa folha de grafeno, ocorre uma mudan¸ca na resistividade local, o que torna poss´ıvel sua deteçcão. Assim, como consequência di-reta dessa propriedade, uma poss´ıvel aplica¸cão de grafeno é como um sensor bioelétrico, servindo para detectar n´ıveis de glicose, hemoglobina, colesterol e até sequenciamento de

DNA. Essa propriedade também permite a aplica¸cão de grafeno em dispositivos de segu-ran¸ca como um sensor de gás.

Uma segunda poss´ıvel utiliza¸cão de grafeno é na fabrica¸cão de materiais para indústria aeroespacial. Por ser um material leve, forte e resistente, grafeno é bastante indicado para substituir os materiais usados atualmente. Além disso, sua alta mobilidade eletrônica pode

(19)

Figura 5: Duas aplica¸cões para grafeno: (a) Grafeno utilizando na produ¸cão de células solares[9]. (b) Grafeno utilizado em sensores de gás [10]

Para concluir, um terceira aplica¸cão futura do grafeno pode ser na optoeletronica. Como foi dito antes, uma única monocamada de grafeno absorve 2,3% da luz que incide sobre ela. Logo 97,7% da luz é transmitida através da folha, propriedade que torna o grafeno ideal para trabalhos em optoeletrônica. Assim, é provável que veremos num futuro próximo grafeno utilizado em aparelhos de touch-screen, LCD, diodos, etc.

1.4 Sum´

ario

No pr´oximo capitulo, discutiremos as principais ferramentas matematicas utilizadas

no trabalho desenvolvido aqui. Na primeira se¸cão tentaremos dar uma idéia geral so-bre em que se baseia o modelo tight-binding e como ele é trabalhado no formalismo de primeira quantiza¸cão. Em seguida, definiremos o formalismo de segunda quantiza¸cão e mostraremos como o modelo Tight-Binding se modifica nesse nova formula¸cão.

Aplicare-mos ent˜ao, para o caso da folha infinita. Por fim, aplicareAplicare-mos o modelo Tight-binding para a nanofita de grafeno e chegaremos na equa¸c˜ao matricial que deve ser satisfeita pelos operadores no espa¸co de fase para se determinar as auto-energias. No terceiro Capitulo, discutiremos os principais resultados obtidos nesse trabalho. Come¸caremos com o caso da

(20)

19

2 MODELO TE ´

ORICO

2.1 M´

etodo Tight-binding

Nesta se¸c˜ao vamos falar sobre alguns aspectos gerais da aproxima¸c˜ao Tight-binding

que será usada posteriormente, dentro do formalismo de segunda quantiza¸cão, para deter-minar as propriedades de propaga¸cão eletrônica sobre uma nanofita de grafeno. Maiores detalhes dos cálculos apresentados aqui se encontram em [11].

Quando tentamos encontrar as fun¸c˜oes de onda que determinam a propaga¸c˜ao de

elétrons em um cristal, encontramos solu¸cões que são completamente localizadas em s´ıtios da rede (que levam a uma descri¸cão em termos de orbitais atômicos) e outras que estão espalhadas sobre o cristal (e que, portanto, não tem nenhuma semelhan¸ca alguma com os orbitais atômicos). A aproxima¸cão Tight-binding serve para descrever estados

inter-mediários entre essas duas aproxima¸cões, isto é, que são próximos das fun¸cões de onda atômica, mas não tão próximas a ponto de não ser necessário nenhuma corre¸cão.

O Hamiltoniano para um el´etron num cristal pode ser escrito da seguinte forma:

H =Hat+ ∆U, (2.1)

ondeHaté o Hamiltoniano atômico para um elétron em um átomo isolado do cristal e ∆U

contém todas as corre¸cões para reproduzir o potencial completo do cristal. Se ∆U fosse constru´ıdo de tal forma que ele fosse zero sempre que uma dada fun¸cão de onda atômica não o fosse, então, para um cristal formado por N átomos, ψn produziria N n´ıveis com

fun¸c˜oes de onda ψn(~r−R~) para cada s´ıtio R~ da rede e a solu¸c˜ao para um dado cristal

seria dada por:

Ψ_n~k(~r) =X

~ R

(21)

´

E fácil de mostrar que Ψnk satisfaz o teorema de Bloch1 e portanto é uma poss´ıvel solu¸cão

para o Hamiltoniano no cristal nessas condi¸cões. No entanto, não é verdade que ∆U(~r) vai satisfazer essa propriedade, para o Hamiltoniano contendo ∆U ₆= 0. Mesmo assim, a abordagem acima sugere que procuremos solu¸cões da seguinte forma:

Ψ_n~k =X

~ R

ei~k·R~_φ₍_~r₋_R_~₎_. _(2.3)

Em geral, no entanto, esperamos que o produto ∆U(~r)Ψn(~r) seja bastante pequeno em

rela¸cão as energias caracter´ısticas do sistema, de modo que é razoável escreverφ(~r) como um produto de fun¸cão de onda atômica:

φ(~r) = X

n

bnψn(~r) (2.4)

Substituindo essas expressões na equa¸cão de Schrödinger e fazendo o produto interno com Ψm é poss´ıvel mostrar, depois de algumas contas, que essas rela¸cões geram a seguinte

equa¸c˜ao de auto-valores:

(ǫ(~k)₋Em)bm =−(ǫ(~k)−Em)Pn(P_R~6=0

R

Ψ∗

m(~r)ψn(~r−R~)ei~k·R~d~r)bn

+P

n(

R

Ψ∗

m(~r)∆U ψn(~r)d~r)bn+Pn(P_R~₆₌₀R Ψ∗m(~r)∆U(R~)ψn(~r−R~)ei~k·R~d~r)bn.

(2.5)

O lado direito dessa equa¸cão é normalmente muito pequeno, pois envolve termos com produtos de fun¸cões de onda centradas em s´ıtios diferentes e termos em ∆U. Logo, o mesmo deve ser verdade para o lado esquerdo. Isso será verdade seǫ(~k)₋Em oubmforem

muito pequenos. Como, normalmente, ǫ(~k) _≈ Es para um dado estado, dependendo da

degenerescência do estado s, a equa¸cão acima gera um sistema de equa¸cões para se deter-minar os coeficientes da combina¸cão linear de estados que geram a fun¸cãoφ(~r).

Observe que as rela¸cões obtidas aqui partem do pressuposto inicial de que a Hamil-toniana no cristal é muito próxima de Hat e é nisso que está baseado a aproxima¸cão

tight-binding. Na próxima se¸cão, falaremos sobre o formalismo de segunda quantiza¸cão e em seguida como um Hamiltoniano Tight-Binding pode ser descrito em termo de oper-adores de cria¸cão e destrui¸cão usando esse novo formalismo.

1

O teorema de Bloch diz que a fun¸cão de onda que descrevem os estados numa região região onde

existe um potêncial periódico aplicado, isto éU(~r+T~) =U(r), são da seguinte forma: Ψ~_k(~r) =ei~k·~ruk(~r),

(22)

21

2.2 Formalismo quˆ

antico de segunda quantiza¸

c˜

ao

Essa se¸cão servirá de base para determinarmos as auto-energias de um elétron em uma nanofita de grafeno. Falaremos primeiro do formalismo de segunda quantiza¸cão para

f´ermions e, em seguida, mostraremos como se pode reescrever o Hamiltoniano Tight-Binding nesta nova base.

A primeira quantiza¸cão em f´ısica refere-se à quantiza¸cão da energia e estados de um part´ıcula submetida à um dado confinamento. Posteriormente, percebeu-se que as for¸cas

de intera¸cão entre part´ıculas eram causadas por outras part´ıculas e que essas part´ıculas eram quantizadas[12]. Aqui não entraremos em detalhes a respeito de como esse processo ocorreu. No entanto, resta-nos saber que isso, de um modo geral, levou ao formalismo de segunda quantiza¸cão que será estudado nessa se¸cão.

Agora, considere um sistema de N part´ıculas. Como nosso trabalho envolve a propaga¸c˜ao

de elétrons em uma nanofita de grafeno, nos limitaremos ao estudo de sistema de part´ıculas fermiônicas. Férmions podem ser definidos como part´ıculas de spin semi inteiro idênticas que obedecem ao princ´ıpio de exclusão de Pauli, isto é, duas part´ıculas fermiônicas não podem ocupar o mesmo estado quântico.

Como próximo passo, definimos o número de ocupa¸cãonjcomo o número de part´ıculas

que estão ocupando o estado j. Como foi dito antes, Férmions obedecem ao princ´ıpio de exclusão de Pauli. Logonj, para férmions só pode ser 0 ou 1.

No formalismo de segunda quantiza¸c˜ao, o estado de um sistema de N part´ıculas pode

ser escrito da seguinte forma, utilizando a nota¸c˜ao de Ket’s de Dirac:

|Ψ_i=_|n1, n2, n3· · ·, ni,· · ·i. (2.6)

Aqui,_|Ψ_irepresenta o estado geral do sistema de N part´ıculas enié o número de ocupa¸cão

para o estado i. Quando não há nenhuma part´ıcula ocupando qualquer estado, chamamos este de estado de vácuo e, em nota¸cão de Dirac, representamos esse estado por:

(23)

Além disso, a condi¸cão de ortonormaliza¸cão para os estados de uma part´ıcula requerem

que_|Ψ_i satisfa¸ca a seguinte rela¸c˜ao:

hΨ_|Ψ′_i= ∞

Y

i=0

δni,n′i. (2.8)

Continuando, definimos o operador n´umero Ni para o estado i com a propriedade de

que o valor esperado dáni, o número de ocupa¸cão para o estado i. Em nota¸cão de bra’s

e ket’s esse operador assume a seguinte forma:

Ni =ni| · · ·ni· · ·ih· · ·ni· · · |. (2.9)

O tratamento de um sistema de part´ıculas é enormemente facilitado com a introdu¸cão dos operadores chamados de cria¸cão e destrui¸cão. Esses operadores tem a propriedade de

que quando atuam em um estado criam ou destroem uma part´ıcula nesse estado. Isto ´e, esses operadores tem a seguinte forma para um dado estado i:

a†_i_{| · · ·}ni −1· · ·i=ci(ni)| · · ·ni· · ·i (2.10)

ai| · · ·ni· · ·i=c′i(ni)| · · ·ni−1· · ·i (2.11)

Além disso, como estamos tratando de part´ıculas fermiônicas, temos ainda que exigir, como foi dito anteriormente, que elas obede¸cam ao princ´ıpio de exclusão de Pauli. É

poss´ıvel mostrar que essas rela¸cões são estabelecidas se os operadores definidos acima satisfa¸cam as seguintes rela¸cões de anticomuta¸cão:

{ai, a†j}=aia†j +a

†

jai =δij; (2.12)

{ai, aj}= 0; (2.13)

(24)

23

Das rela¸c˜oes 2.13 e 2.14 ´e obvio que: aiai =a†ia

†

i = 0. Observe tamb´em, das equa¸c˜oes

2.10 e 2.11, que a†iai|Ψi=ci(ni)c′i(ni)|Ψi, que tem a mesma forma do operador n´umero.

Assim ´e natural tomarmosa†_iai =Ni, e, portanto, temos a seguinte rela¸c˜ao: ci(ni)c′i(ni) =

ni. Tomemos agora o operador Ni2:

N_i2 =a†_iaia†iai =a†i(1−a

†

iai)ai =a†iai−a†ia

†

iaiai =a†iai =Ni, (2.15)

portanto, N2

i =Ni, o que implica que ni(ni −1) = 0, comprovando que os valores de ni

s´o podem ser 0 ou 1. Considere os operadores abaixo:

A†_i =ni(−1)Σi| · · ·1−ni· · ·ih· · ·ni· · · | (2.16)

Ai = (1−ni)(−1)Σi| · · ·ni· · ·ih· · ·1−ni· · · | (2.17)

´

E f´acil mostrar que esses operadores satisfazem todas as rela¸c˜oes acima e, portanto,

cor-respondem aos operadores de cria¸cão e destrui¸cão associados ao estado de férmion, isto é A†_i = a†_i e Ai = ai. Em posse desses valores, podemos escrever o estado geral de uma

part´ıcula em termos de operadores de cria¸c˜ao e destrui¸c˜ao:

|Ψ_i= ∞

Y

i=0

ani

i

√

ni!|

0_i. (2.18)

Vejamos agora como fica o operador Hamiltoniano para um dado sistema na nota¸c˜ao

do formalismo de segunda quantiza¸c˜ao. Seja ǫi a energia associada ao estado i de um

sistema de part´ıculas. Considere que para cada estado i h´a ni2 part´ıculas ocupando esse

estado. Assim, para esse sistema, a energia total ´e dada por:

E = ∞

X

i=0

niǫi (2.19)

Ora, sabemos queE =_hH_ieni =ha†iaii, logo podemos escrever o Hamiltoniano total do

sistema como:

H = ∞

X

i=0

ǫia†iai. (2.20)

No entanto, essa aproxima¸cão não está completamente correta quando tentamos

determi-2

No nosso caso, como estamos trabalhando com part´ıculas fermiˆonicas,ni s´o pode ser igual a 0 ou 1.

(25)

nar a Hamiltoniana para um sistema mais geral poss´ıvel[14]. A aproxima¸cão acima supõe que não haja intera¸cão entre os estados ocupados pelas part´ıculas. Se quisermos consid-erar a situa¸cão mais geral poss´ıvel, devemos supor que existam termos correspondentes a uma intera¸cão entre as part´ıculas e os estados seguintes, bem como uma intera¸cão entre as

próprias part´ıculas que compõem o sistema. Por exemplo, se estivermos tratando de um elétron numa rede atômica, na situa¸cão mais realista, devemos incluir termos que corre-spondam a energia de intera¸cão entre os elétrons e os s´ıtios atômicos, elétrons e elétrons, elétrons e buracos, elétrons e fónons, fónons e buracos, etc, tornando o problema cada vez

mais complicado. Como foi dito na se¸cão 2.1, a aproxima¸cão Tight-Binding consiste numa visão intermediária que fornece uma pequena corre¸cão a visão de orbital atômico. Assim, considera-se que o elétron tem uma pequena chance de tunelar de um s´ıtio i para um s´ıtio j dentro do átomo. Em termos dessa nova aproxima¸cão podemos escrever a Hamiltoniana

do sistema para uma part´ıcula fermiˆonica na aproxima¸c˜ao Tigh-Binding como:

H =X

i

ǫia†iai+

X

i,j

ti,j(a†iaj +aia†j). (2.21)

Aqui, ai(a†i) e aj(a†j) são os operadores de cria¸cão (destrui¸cão) nos sit´ıos i e j,

respec-tivamente, enquantoti,j ´e o termo de hopping (ou integral de superposi¸c˜ao) entre os dois

´orbitais dados em termos da energia de intera¸c˜ao por:

ti,j =

Z

hΨ_|∆Ui,j|Ψi=

Y

l

Z

h0_| a †

l

√_n

l|

∆Uij|

al

√_n

l|

0_i= ∆Ui,j. (2.22)

Na próxima se¸cão, veremos como o modelo Tight-Binding se aplica para determinar as auto energias no grafeno. Veremos primeiro o caso da folha infinita e, em seguida, passaremos ao estudo de nanofitas com campo elétrico aplicado.

2.3 Modelo Tight-binding aplicado em grafeno

2.3.1 Folha infinita

(26)

25

que o elétron está ’fortemente ligado’ e, portanto, só pode interagir com os vizinhos mais próximos. Nesse caso tem-se o seguinte Hamiltoniano para o elétron no grafeno [5]

H =₋tX

i,j

(a†_ibj+aib†j). (2.23)

Estamos usando ai e bj para diferenciar os ´atomos das subredes A e B. N˜ao colocamos o

primeiro termo de 2.21 por que o único efeito desse termo é deslocar o zero de potencial. Como requisitado pelo teorema de Bloch e a periodicidade da rede, é conveniente escrever os operadores de cria¸cão e destrui¸cão em termos de suas transformadas para o espa¸co

rec´ıproco. Tem-se ent˜ao:

ai =

1

√

N

X

~k

ei~k·r~i_a

k (2.24)

a†i =

1

√

N

X

~k

e−i~k·r~i_a†

k (2.25)

bj =

1

√

N

X

~k′

ei~k′·r~j_b

k′ (2.26)

b†_j = √1

N

X

~k′

ei~k′·r~j_b†

k′ (2.27)

Substituindo essas express˜oes no Hamiltoniano do sistema tem-se:

H =₋ t

N

X

i,j

X

k,k′

(e−i~k·r~i_ei~k′·r~j_a†

kbk′ +ei~k·r~ie−i~k ′_·_r_~

j_a

kb†k′) (2.28)

Podemos rearranjar essas expressões para deixarmos em termos de distância relativa entre os s´ıtios atômicos:

H =₋ t

N

X

i,j

X

k,k′

(e−i~k·(r~i−r~j)_ei(~k′−~k)·r~j_a†

kbk′ +ei~k·(r~i−r~j)e−i(~k ′₋~k₎_·_r_~

j_a

kb†k′) (2.29)

Podemos simplificar essa express˜ao, usando a seguinte identidade matem´atica: P

kei(k−k

′₎_·_r

i =

δ_~k,~_k′. Substituindo isso no Hamiltoniano do sistema, encontramos:

H=₋ t

N

X

i,j

X

k

(e−i~k·(r~i−r~j)_a†

kbk+ei~k·(r~i−r~j)·r~jakb†k). (2.30)

(27)

vizin-hos mais próximos. Portanto, iremos repetir a mesma soma sobre mais próximos vizinvizin-hos, para cada s´ıtio j. A figura 6 mostra os termos que participam dessa intera¸cão de primeiros vizinhos.

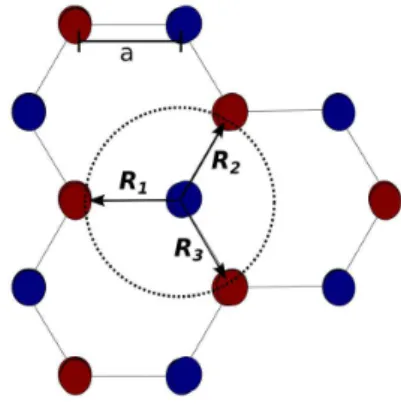
Figura 6: átomos de carbono em uma rede hexagonal de grafeno. R1, R2 e R3 denotam as distâncias aos vizinhos mais próximos de um átomo tipo B (azul) da rede.

Colocando a origem no átomo B da figura, vemos que as distâncias dadas são: R~1 =

−a~i;R~2 =a/2~i+a

√

3/2~j;R3 =a/2~i−a

√

3/2~j. Logo, para um valor de j fixado a soma sobre os mais pr´oximos vizinhos do tipo B, constitu´ıda de ´atomos do tipo A, fica:

X

i

e−i~k·(~ri−r~j)₌_e−i~k·R~1

+e−i~k·R~2

+e−i~k·R~3

=eikxa_{+ 2}_e−ikxa/2_cos₍√₃_k

ya/2) = g(~k). (2.31)

Essa expressão, que nós rotulamos de g(~k), é chamada de fator de estrutura da rede cristalina. Como dissemos, a soma em j é a mesma para cada átomo i da rede. Logo, considerando que temos N átomos na rede, o somatório em i,j fica N vezes o somatório em j. Substituindo isso mais os resultados da equa¸cão 2.31 na expressão 2.30, da Hamiltoniana do sistema, obtemos:

H =₋tX

k

(g(~k)a_~k†b_~k +g(~k)∗a_~kb_~k†) (2.32)

Esse é o Hamiltoniano para o elétron no grafeno no espa¸co de Hilbert em termos dos momentos~k. Esse Hamiltoniano pode ser escrito também como H =P

khΨk|H|Ψki,

onde_|Ψki=|ak, bkie ak,bk são as transformadas dos operadores de cria¸cão e destrui¸cão.

(28)

27

h(Ψk)i|H|(Ψk)ji. Assim temos:

Ek   ak bk  =  

0 ₋tg(~k)

−tg∗₍~k₎ ₀

    ak bk 

. (2.33)

Os auto valores dessa equa¸c˜ao d˜ao as auto energias associadas ao Ψk. Para encontrarmos

essas grandezas, o determinante da matriz H - EI tem que ser igual a zero. Assim, devemos resolver a seguinte equa¸c˜ao:

Ek tg(~k)

tg∗₍~k₎ _E

k

= 0 _↔Ek2−t2|g(~k)|2 = 0. (2.34)

Cujas raizes s˜ao dadas por:

Ek =±

q

3 + 4cos(√3kya) +cos(3kxa/2)cos(

√

3kya/2) (2.35)

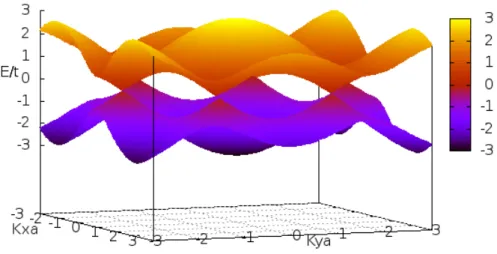
Na figura 7 representamos essas duas solu¸c˜oes em fun¸c˜ao de kxa e kya. Na figura,

vemos seis pontos de contato entre a banda de condu¸c˜ao e a banda de valˆencia3_{. Da}

figura, observa-se que a rela¸cão de dispersão tem uma aparência cônica se escolhermos valores de ~k muito próximos deles. Esses pontos são os chamados cones de Dirac e é por essa forma cônica que dissemos que elétrons propagando-se no grafeno comportam-se como part´ıculas relativ´ısticas sem massa4_.

Na próxima subse¸cão, finalmente desenvolvermos o Hamiltoniano tight-binding para uma part´ıcula em uma nanofita de grafeno. Trabalharemos na aproxima¸cão de segundo

vizinhos, isto é, incluiremos os segundos s´ıtios mais próximos para o nosso cálculo da rela¸cão de dispersão. Incluiremos o termo de intera¸cão entre o elétron e potencial na nanofita.

3

Quando determinamos as energias de um cristal e representamos essas energias no espa¸co de fase, isto

é, em fun¸cão dekxeky, para um sistema bidimensional, as bandas de condu¸cão e valência correspondem

ao n´ıvel de energia mais baixo desocupado e mais alto ocupado, respectivamente. 4_`

A luz da relatividade, uma part´ıcula de massa m, energia E e momento p satisfaz obedece a seguinte

rela¸c˜ao: E2

=p2

c2

−m2

c4

, onde c é a velocidade da luz. Se m = 0, então temos a seguinte rela¸cão entre

momento e energia: E = ±|pc|. Como, pela mecânica quântica, momento também é proporcional ao

(29)

Figura 7: rela¸c˜ao de dispers˜ao para uma folha de grafeno infinita.

2.3.2 Nanofita de Grafeno

Nesta se¸c˜ao estamos interessados em descrever uma forma de determinar as auto

en-ergias de uma nanofita de grafeno de N linhas. Existem dois tipos de geometrias a se considerar: bordas armchair e bordas zigzag. Vamos, por conven¸cão, come¸car sempre com linhas de átomos do tipo B para bordas zigzag (bordas armchair sempre possuem os dois tipos de átomos). A principal diferen¸ca introduzida agora é que o sistema só

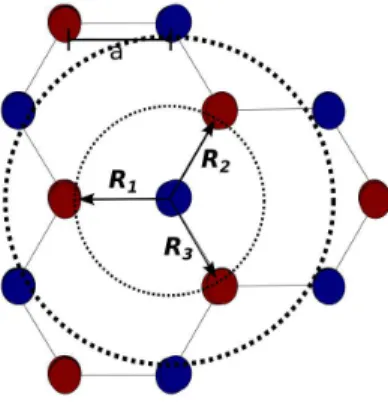
tem periodicidade em uma dire¸cão, que chamaremos a dire¸cão x. Além disso, incluire-mos nos nossos cálculos para a rela¸cão de dispersão as intera¸cões entre segundos vizinhos.

A figura 8 representa os termos que incluiremos na nossa aproxima¸cão. Agora, além de um termo de hopping entre primeiros vizinhos, que representa a energia de intera¸cão

entre o s´ıtio atual e os primeiros vizinhos, há também a possibilidade de hopping entre os segundos vizinhos. Assim nos temos: t0 ≈ 2.8 eV para representar a intera¸cão entre

primeiros vizinhos e t1 ≈ 0.1 eV para representar a intera¸c˜ao entre os segundos

vizin-hos. Além disso, temos que considerar a energia potencial elétrica devido a intera¸cão

da part´ıcula com o campo el´etrico. Chamaremos essa energia de Vi. Mais tarde

(30)

29

Figura 8: Na aproxima¸c˜ao de segundos vizinhos, somamos sobre os dois grupos de ´atomos mostrados na figura.

observa¸cões, o Hamiltoniano para o elétron na nanofita de grafeno usando aproxima¸cão tight-Binding com segundos vizinhos submetido a campo elétrico fica:

H =X

i

Vi(a†iai+b†ibi)−t0

X

(i,j)

(aib†j+a

†

ibj)−t1

X

((i,j))

(aia†j +a

†

iaj +bib†j+b

†

ibj) (2.36)

Como foi dito anteriormente, devido `a periodicidade da fita ao longo da dire¸c˜ao x,

faremos uma transformada de Fourier na dire¸cão x dos operadores de cria¸cão e destrui¸cão na nanofita de grafeno. Assim temos:

ai =

1

√

NA

X

kx,n

eikxrxi_a

kx,n; (2.37)

a†_i = √1

NA

X

kx,n

e−ikxrxi_a†

kx,n; (2.38)

bj =

1

√

NB

X

kx,n

eikxrxj_b

k′

x,n′; (2.39)

b†_j = √1

NB

X

k′

x,n′

e−ikxrxj_a†

k′

x,n′; (2.40)

NA e NB representam o n´umero de linhas de ´atomos do tipo A e do tipo B. Aqui

é preciso distinguir entre os dois casos: quando a borda é zigzag e quando a borda é armchair. Quando a borda é armchair tem-se NA =NB =N. Quando a borda é zigzag

(31)

Substituindo essas express˜oes na Hamiltoniana 2.36 e simplificando, chegamos a seguinte express˜ao para a Hamiltoniana na nanofita:

H= X

kx,n

ǫna†kx,nakx,n−

X

kx,n,n′

(τ0n,n′(k_x)a_k_x_,nb †

kx,n′+τ1n,n′(kx)(a

†

kx,nakx,n′+b

†

kx,nakx,n′) +h.c.)

(2.41)

N´os utilizamos h.c. para denotar o conjugado hermitiniano da express˜ao que aparece

no somatório. Na equa¸cão 2.41, τ0n,n′ eτ₁_n,n′ representam os termos que surgem quando se considere somente a intera¸cão entre os primeiros e segundos vizinhos, respectivamente. Esses termos vão depender da geometria da nanofita. Logo, para a nanofita de borda armchair tem-se:

τ0n,n′ =t₀(αδ_n,n′ +βδ_n,n′₋₁+γδ_n,n′₊₁); (2.42)

τ1n,n′ =−t₁(η(δ_n,n′₊₁+δ_n,n′₋₁) +θ(δ_n,n′₊₂+δ_n,n₋₂)). (2.43) E, para zigzag, tem-se:

τ0n,n′ =t₀(βδ_n,n′_∓₁+γδ_n,n′_±₁); (2.44)

τ1n.n′ =t₁(ζδ_n,n′+θ(δ_n,n′−2+δn,n′−2)). (2.45)

Aqui, os sinais de sima representam linhas do tipo B e o sinal de baixo linhas do tipo A. As constantes, α,β,γ,η,θ eζ s˜ao mostradas nas tabelas 1 e 2 abaixo.

Armchair Zigzag

α t0eikxa 0

β t0eikxa/2 2t0cos(

√

3kxa/2)

γ t0eikxa/2 t0

Tabela 1: Coeficientes de τ0n,n′.

Armchair Zigzag

ζ 0 2t1cos(

√

3kxa)

η 2t1cos(3kxa/2) 0

θ t1 2t1cos(

√

3kxa/2)

Tabela 2: Coeficientes de τ1n,n′.

Com isso, nós construimos o Hamiltoniano tight-binding completo para o elétron em termos de kx e do número de linhas com intera¸cão de primeiros e segundos vizinhos.

(32)

31

de Heinsenberg da mecânica quântica, nós descrevemos a evolu¸cão temporal de um oper-ador A e este satisfaz a seguinte equa¸cão de movimento: i¯hdA/dt = [A, H](Equa¸cão de Heinsenberg). Lembremos então que os operadores akx,n’s e bkx,n’s são auto estados do

sistema com energia E(kx) e apliquemos a equa¸c˜ao de movimento de Heinsenberg para

cada um dos operadores. Desde que o Hamiltoniano do sistema n˜ao depende explicita-mente do tempo, podemos esperar uma dependˆencia temporal dos operadores da forma

eiEt/¯h_{. Logo:}

[akx,n, H] =i¯h

dakx,n

dt =E(kx)akx,n (2.46)

[bkx,n, H] =i¯h

dbkx,n

dt =E(kxbkx,n) (2.47)

Agora, faremos uma observa¸cão que simplificará muito nossas contas. Uma vez que só aparecem termos quadráticos no Hamiltoniano, não faz diferen¸ca o tipo de estat´ıstica que utilizamos para os operadores, se é de Fermi ou de Bose5_{. No Final das contas}

obteremos os mesmos resultados. Dessa forma, vamos supor que, ao inv´es das rela¸c˜oes de

anticomuta¸cão desenvolvidas na se¸cão 2.2, os operadores satisfazem rela¸cões análogas de comuta¸cão, isto é, eles satisfazem equa¸cões 2.12, 2.13 e 2.14, substituindo o anticomutador pelo comutador entre operadores A, B arbitrários: [A, B] =AB₋BA. Assim, as equa¸cões de movimento 2.46 e 2.47 ficam:

E(kx)akx,n =Vnakx,n+

X

n

τ0n,n′(k_x)b_k_x_,n′ +

X

n

τ1n,n′a_k_x_,n′; (2.48)

E(kx)bkx,n =Vnbkx,n+

X

n

τ∗

0n,n′(kx)akx,n′ +

X

n

τ1n,n′b_k_x_,n′. (2.49)

Sendo aT

kx,n o vetor coluna que representa os operadores de cria¸c˜ao e destrui¸c˜ao para

´atomos do tipo A ebT

kx,n para o tipo B. Essa rela¸c˜ao pode ser escrita mais compactamente

na forma matricial. Logo:

Ek





akx,n

bkx,n



= 



T1+V T0

T∗

0 T1+V



 



akx,n

bkx,n



 (2.50)

5

Estat´ıstica de Fermi-Dirac trabalha com part´ıculas fermiˆonicas e a de Bose-Einstein com part´ıculas

(33)

Os autovalores dessa equa¸cão matricial dão as autoenergias permitidas para o sistema, enquanto seus autovetores dão as fun¸cões de onda no espa¸co de fase. Para uma sistema de N linhas esse problema se resume a resolver um determinante secular 2Nx2N. As submatricesT0,T1 eǫ na expressão são dadas por:

T0 =

           

α β 0 0 0 _{· · ·}

β α γ 0 0 _{· · ·} 0 γ α β 0 _{· · ·} 0 0 β α γ _{· · ·}

... ... ... ... ... ...             (2.51)

T1 =

           

ζ η θ 0 0 _{· · ·}

η ζ η θ 0 _{· · ·}

θ η ζ η θ _{· · ·}

0 θ η ζ η _{· · ·}

... ... ... ... ... ...             (2.52) V =            

V1 0 0 0 0 · · ·

0 V2 0 0 0 · · ·

0 0 V3 0 0 · · ·

0 0 0 V4 0 · · ·

... ... ... ... ... ...             (2.53)

(34)

33

3 RESULTADOS

3.1 Nanofita Sem Campo el´

etrico

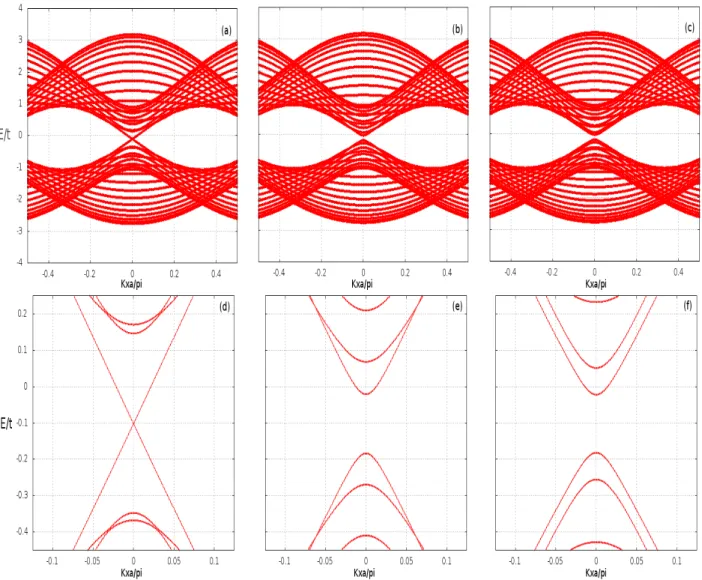
Figura 9: Resultado para a rela¸cão de dispersão para nanofita de bordas armchair sem campo elétrico com: (a)Ny = 20, (b)21 e (c)22 linhas.

(35)

da figura é que a fita é condutora (não há gap) para Ny = 20 linhas e é semicondutora

nos demais casos. Em geral, obtˆem-se uma fita condutora sempre queNy = 3M−1, onde

M é um inteiro. Qualitativamente, podemos explicar esse efeito como uma consequência da discretiza¸cão do número de linhas. No caso da folha infinita, todos os valores poss´ıveis

de kx e ky são acess´ıveis. No entanto, a discretiza¸cão das linhas na dire¸cão y gera uma

discretiza¸c˜ao nos poss´ıveis valores de ky e podemos pensar nas curvas da figura 9 como

energias correspondentes a valores fixados deky. Logo, se voltarmos para a rela¸c˜ao de

dis-pers˜ao da figura 7, esperamos qualitativamente que a fita seja condutora sempre que um

dos valores deky coincidir com um dos v´ertices dos cones de Dirac, que deve representar o

que ocorre paraNy = 3M−1. Uma explica¸cão mais matemática para essa condi¸cão pode

ser encontrada em [15], onde o Hamiltoniano do elétron no grafeno é resolvido dentro da aproxima¸cão de que ele satisfaz a equa¸cão de Dirac próximo aos pontos K e K’ do espa¸co

rec´ıproco. Condi¸cões de contorno são colocadas para que a fun¸cão de onda vá a zero nas bordas, o que leva a um valor deky = 0 e, consequentemente um poss´ıvel estado condutor,

sempre que a condi¸c˜ao acima ´e satisfeita.

Vejamos agora o que acontece para nanofitas de bordas zigzag. Antes de discutir-mos os resultados apresentados na figura 10, precisadiscutir-mos fazer uma pequena digress˜ao a

respeito do resultado obtido para 21 linhas e, de um modo geral, para um estado cor-respondente a um n´umero impar de linhas. Uma nanofita zigzag com n´umero impar de linhas apresenta uma linha zigzag incompleta em uma das bordas. Apesar de artifi-cial, nosso modelo computacional permite que fa¸camos essa escolha. Analisaremos esse

caso para ver quais mudan¸cas na rela¸cão de dispersão decorrem desse fato. Para todos os fins, estamos considerando que o elétron na borda não tem probabilidade de sair da fita.

Os cálculos foram feitos considerando que a fita sempre come¸ca com uma linha de átomos do tipo B. A figura 10 mostra a rela¸cão de dispersão para nanofitas com 20 e

21 linhas. Uma primeira diferen¸ca que se nota, em rela¸cão ao caso armchair, é que aqui as fitas são sempre condutoras. No entanto, diferente do caso armchair, o contato entre a banda de valência e a banda de condu¸cão não ocorre só nos pontos K(K’) e sim num intervalo de valores dekx. Esse efeito não é originado das propriedades da folha 2D. Como

(36)

35

estados.

Figura 10: Resultado para a rela¸c˜ao de dispers˜ao de nanofitas zigzag com (a)Ny = 20

linhas e (b)Ny = 21 linhas. As figuras (c) e (d) representam uma amplia¸c˜ao da regi˜ao

pr´oxima aos estados de borda. Foram utilizados valores det0 = 2.8 eV e t1 = 0.01 eV

Para concluir essa se¸cão, a figura 11 mostra a proje¸cão da rela¸cão de dispersão da folha infinita nos eixos armchair e zigzag. A compara¸cão com os resultados das figuras 9(b) e

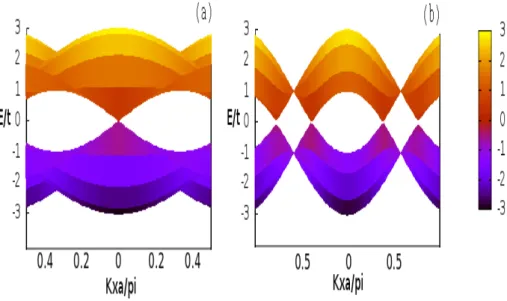
??(c), reflete a tendência que os resultados para fita tem de se aproximar dos resultados da folha quando o número de linhas tender a infinito. Além disso a figura 11(b), deixa claro que o estado central nas nanofitas zigzag é um estado de borda, já que o mesmo não surge quando tomamos a folha infinita.

(37)

Figura 11: Proje¸cão da rela¸cão de dispersão para folha infinita de grafeno ao longo do plano formado pelo eixo E e: (a) eixo da borda armchair e (b)zigzag.

nanofitas.

3.2 Campo el´

etrico com potencial linear com a posi¸

c˜

ao

Nesta se¸cão trabalharemos o efeito da aplica¸cão de um potencial que cresce linear-mente com a posi¸cão na nanofita, ou seja, trabalharemos com um campo uniforme aplicado ao longo da dire¸cão y na nanofita. Assim, a energia potencial elétrica como fun¸cão da

posi¸c˜ao y na nanofita ´e dada por:

V(y) = e0

y

a, (3.1)

ondee0 é uma constante que tem unidade de energia e aé a distância entre os átomos de

carbono.

Vamos escolher a origem na primeira linha d´ımera da nanofita armchair e na primeira

linha da nanofita zigzag. O campo el´etrico pode ser obtido facilmente do gradiente do potˆencial eletrico, C~ele. = −∇V = −e0/a~j. Estamos interessados em valores de campo

que sejam da ordem das constantes caracter´ısticas da rede, ou seja, da ordem det0/a. Um

campo dessa magnitude é da ordem de_≈1 V/nm. Por isso, para as rela¸cões de dispersão

apresentadas a seguir escolhemose0 = 0.05t0, para nanofita armchair ee0 = 0.044t0, para

nanofita zigzag. Para nanofita armchair a posi¸c˜ao das linhas ´e dada poryn = (

√

(38)

37

Para a fita de borda zigzag tem-seyn= 3a(n−1)/2 se n ´e impar eyn = 2a+ 3a(n/2−1)

se n é par. Aqui, é claro, na posi¸cão das fitas tomaremosVn=V(yn).

A figuras 12 e 13 mostram os resultados obtidos para nanofita de bordas armchair com Ny = 20, 21 e 22 linhas e zigzag com Ny = 20 e 21 linhas, respectivamente.

Com-Figura 12: Rela¸cão de dispersão para nanofitas de bordas armchair com aplica¸cão de campo elétrico de_≈1V /nm. A figura representa a primeira zona de brillouin paraNx =

(a)20, (b)21 e (c)22 linhas. Em (d),(e) e (f) está plotado o zoom da região próxima ao gap para cada uma das figuras. As energias estão colocadas em unidades det0 e os vetores de

onda em unidades deπ/a.

(39)

Figura 13: Rela¸cão de dispersão para nanofitas de bordas zigzag com aplica¸cão de campo elétrico de_≈ 1V /nm. A figura representa a primeira zona de brillouin para Nx = (a)20

e (b)21 linhas. Em (c),(d) está plotado o zoom da região próxima aos estados de borda para cada uma das figuras.As energias estão colocadas em unidades det0 e os vetores de

onda em unidades deπ/a.

um deslocamento das bandas de energia na dire¸cão de crescimento do campo, resultado que pode ser mostrado utilizando teoria da pertuba¸cão. Esse efeito pode ser visto mais claramente na figura 14, onde plotamos a energia, em unidades de E/t, em fun¸cão dee0/t,

que é proporcional ao valor do campo para nanofita com 20 linhas com bordas armchair e zigzag e valor dekx = 0. Na figura, é clara a dependência crescente das energias com os

valores do campo. Um outro efeito que se observa nos resultados apresentados nas figuras 12, 13 e 14 ´e que algumas algumas curvas de energias se tornam mais energeticas que as

(40)

39

Figura 14: Energia em fun¸cão do campo elétrica para: (a) nanofita de 20 linhas com borda armchair e (b) nanofita de 20 linhas com borda zigzag. Na figura, plotamos energia em unidades de t0 em fun¸cão de e0/t, que é proporcional ao campo.

de que algumas distribi¸cões são mais favoraveis ao campo do que outras, isto é, são mais

densas nas regi˜oes de maiores energias.

As figuras 12 (c), (d) e (e), mostram um zoom da região próxima ao n´ıvel de fermi das nanofitas de borda armchair. As figuras mostram a abertura de um pequeno gap na fita de 20 linhas, bem como uma diminui¸cão do gap para as demais fitas numa região

de valores de kx pr´oxima `a π/20a. Esses gaps se assemelham a anticrossings (ou

non-crossing), que surgem quando há um acoplamento entre os estados. Uma das implica¸cões desse efeito é que, sob determinadas condi¸cões, um elétron pode tunelar de um banda para outra mudando, é claro, seu estado de elétron para buraco.

As figuras 13 (c), (d) e (e), mostram um zoom da regi˜ao pr´oxima aos estados de borda

numa nanofita zigzag. Os resultados mostram que o efeito do campo elétrico aplicado de 1 V/nm é deformar os estados de borda apresentados pela nanofita. Para fita de 20 linhas, vemos que a aplica¸cão do campo elétrico muda suas propriedades eletrônicas, passando de condutora para semicondutora, com o intervalo na região de pequeno gap

assemelhando-se a um anticrossing. Para 21 linhas, vemos que a fita continua condutora com o estado de borda tornando-se mais assimétrico em torno da banda de valência-banda de condu¸cão.

(41)

submetida a um po¸co de potˆencial.

3.3 Po¸

co de potencial

A figura 15 representa o perfil de uma nanofita com um po¸co de potencial ao longo da dire¸cão y da fita. Em duas linhas vizinhas, na borda do po¸co, há uma varia¸cão abrupta de energia, de V = 0 paraV =V0 e vice-versa. Em nosso modelo, só estamos interessados no

campo nas linhas da nanofita. Assim, como a varia¸c˜ao de energia potencial s´o acontece na

região entre as linhas, não trabalharemos com o campo nessa região, ou seja, como V varia na borda do po¸co. basta para nós saber C~ele =~0 nas regiões de interesse. Assumiremos,

como est´a ilustrado na figura 15, que a regi˜ao de V = V0 abrange seis linhas a direita

e seis linhas a esquerda da fita, de modo que o po¸co tem largura L = N ₋12. Nossos c´alculos foram feitos para ambas geometrias, armchair e zigzag.

Na figura 16 est´a representado o resultado para nanofitas armchair comNy = 20, 21 e 22

linhas. Na figura 17 plotamos o mesmo resultado para nanofitas zigzag com Ny = 20 e

21 linhas.

Na figura 16, plotamos resultados para alturas da po¸co, da esquerda para a direita, de 0.25t0, 0.5t0, 0.75t0 e 1.0t0. Vemos, de um modo geral, que as energias aumentam a

medida que tomamos valores cada vez maiores de altura dos po¸cos de potencial. Esse aumento se deve ao fato de que, com valores pequenos de altura de barreira, todas as

regiões são acess´ıveis. Logo, devido ao aumento da energia na região fora do po¸co, há um aumento resultante das energias. Assim, apesar de estarmos aumentado as alturas, os estados ainda estão espalhados ao longo da fita. Logo, aumentando as energias de deter-minados s´ıtios da rede, aumenta-se as energias dos estados como um todo. Os resultados

também mostram que a presen¸ca do po¸co gera deforma¸cões nas curvas de energia que podem gerar grandes modifica¸cões nas propriedades eletrônicas da fita, como velocidade de grupo, massa efetiva, etc. Além disso, um efeito interessante ascende no caso armchair, quando consideramos a aplica¸cão de um po¸co de potencial. A medida que a altura da

po¸co vai se tornando maior, surgem, no limite entre a banda de valência e a banda de condu¸cão, estados que tornam-se cada vez mais planos. Eles, portanto, assemelham-se a estados de bordas como os apresentados na fita zig-zag sem a presen¸ca do campo. Um outro efeito observado nos resultados apresentados na figura 16 é a abertura de um gap

(42)

41

Figura 15: (a)Potêncial elétrico em fun¸cão da posi¸cão y ao longo da fita. (b) Campo elétrico em fun¸cão da posi¸cão. Note que não há informa¸cão alguma a respeito da região de varia¸cão de potêncial.

Na figura 17, plotamos resultados para alturas do po¸co, da esquerda para a direita, de 0.0, 0.25t0, 0.5t0 e 0.75t0. Vemos, assim como no caso das fitas armchair, um aumento

sucessivo das energias das fitas. Os resultados mostram também que as fitas continuam condutoras mesmo após a aplica¸cão do po¸co de potencial. No entanto, como pode ser

visto na figura 17(h), a fita de 21 linhas torna-se semicondutora com um valor apropriado para a altura da barreira, desde que o estado passa a ficar acima da banda de condu¸cão. De um modo geral, assim como no caso da fita de borda armchair, podemos ver que a aplica¸cão do po¸co de potencial gera modifica¸cões na rela¸cão de dispersão que tem como

(43)

Como foi dito anteriormente, quando a altura da barreira é pequena ainda há uma grande probabilidade para que o elétron localizado dentro do po¸co salte para fora e, portanto, nessa situa¸cão, a fun¸cão de onda ao longo da dire¸cão y continua espalhada ao longo da fita. No entanto, a medida que aumentarmos a diferen¸ca de potencial entre

o po¸co e a barreira é esperado que surjam estados completamente localizados no po¸co e estados completamente localizados nas barreiras. A figura 18 mostra ilustra esse resultado. Plotamos as probabilidades em fun¸cão da linha numa fita armchair de 20 linhas para dois estados arbitrários com kx = 0. Observa-se claramente dos resultados que, um dos

(44)

43

Figura 16: Resultado para nanofita armchair submetida a um po¸co de potˆencial com n´umero de linhas, da esquerda para direita: Ny = 20, 21 e 22 linhas. Os resultados

s˜ao mostrados com os seguinte valores de altura da barreira: 0.25t0(a)-(c); 0.5t0 (d)-(f);

(45)

Figura 17: Resultado para nanofita zigzag submetida a um po¸co de potêncial com número de linhas, da esquerda para direita: Ny = 20 e 21 . Os resultados são mostrados com os

(46)

45

Figura 18: densidade de probabilidade para dois auto estados arbitr´arios na nanofita. A figura de cima mostra o resultado para um estado localizado no po¸co com altura da barreira V = (a)0, (b)0.5t0 e (c)4t0. Na figura de baixo o mesmo resultado com a fun¸c˜ao

(47)

4 CONCLUS ˜

AO

Neste trabalho, foi apresentado um estudo das propriedades eletrˆonicas numa nanofita de grafeno utilizando o modelo tight-binding. Para tal fim, utilizamos uma aproxima¸c˜ao

que inclu´ıa possibilidade de ”salto”para primeiros e segundos vizinhos na rede.

Inicialmente, foi apresentada uma abordagem para esse modelo dentro do formalismo de primeira quantiza¸cão e, logo em seguida, introduzimos o formalismo de segunda quan-tiza¸cão para que pudéssemos tratar a aproxima¸cão Tight-binding nesse novo formalismo,

que ´e mais adequado ao tratamento de problemas que envolvam muitas part´ıculas.

O modelo Tight-binding foi então aplicado a uma nanofita de grafeno com duas geome-trias para as bordas, armchair e zigzag, e, através das propriedades de simetria satisfeitas pelo sistema, chegamos a uma rela¸cão matricial. Baseados nisso, fizemos um cálculo da rela¸cão de dispersão para a nanofita. Assim, conseguimos determinar várias propriedades

da nanofita de grafeno, como o fato de nanofitas armchair serem condutoras somente quando o número de linhas for múltiplo de 3M ₋1 e que nanofitas zigzag são sempre condutoras e apresentam estados localizados nas bordas.

Deixamos para discutir aqui um erro cometido durante a elabora¸c˜ao do modelo para

inclusão de intera¸cões entre segundos vizinhos. Vale salientar, que apesar de termos cometido esse erro na elabora¸cão dos nossos cálculos, as modifica¸cões geradas nos nossos resultados são bastante pequenas devido ao valor pequeno escolhido para o parâmetro de hopping entre segundos vizinhos, t1 = 0,01 eV. Além disso, esse termo não modifica

(48)

47

com a exponencial da energia. Não poder´ıamos admitir isso, à principio, devido ao fato de que a inclusão da intera¸cão entre segundos vizinhos gera termos acoplados entre oper-adores nos s´ıtios A e B. Logo, essa aproxima¸cão não está necessariamente corrente. No entanto, vale salientar novamente que, como a acoplagem é pequena (t1 é pequeno), esse

efeito n˜ao altera a parte dos resultados que estamos interessados, isto ´e, o efeito do campo.

Nosso próximo e último passo, foi aplicar um potencial eletroestático na nanofita, cálcular as novas rela¸cões de dispersão e tentar explicar alguns efeitos gerados por essa modifica¸cão.

Em primeiro lugar, para o caso do campo el´etrico uniforme, verificamos a presen¸ca

do efeito Stark que, como já dissemos, aumenta as energias com o aumento do campo. Em segundo lugar, de um modo geral, o efeito do campo, fragmenta as bandas de ener-gia, passando acoplagem entre estados e modificando as propriedades eletrônicas da fita. Esse efeito é importante por que, como também já falamos, a possibilidade de modificar

reversivelmente as propriedades eletrônicas pode possibilitar a utiliza¸cão de grafeno em dispositivos eletrônicos.

No caso do po¸co de potencial também verificamos uma grande modifica¸cão nas ban-das de energia e também verificamos a possibilidade de mudar reversivelmente as pro-priedades da fita de condutora para semicondutora. Além, como também já foi explicado,

a aplica¸cão do po¸co gera estados de borda na nanofita armchair que, talvez, um estudo mais minuncioso da solu¸cão para fun¸cão de onda na fita revele a natureza desses resultados.

Conclu´ımos que o grafeno ´e um material com propriedades muito interessantes, tanto do ponto de vista teorico como experimental. Quanto mais estudarmos essas propriedades

(49)

REFERˆ

ENCIAS

[1] P. R. Wallace, The Band Theory of Graphite Phys. Rev. 71, 622, 1947.

[2] K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 306, 666-669 2004.

[3] Virendra Singh, Daeha Joung, Lei Zhai, Soumen Das, Saiful I. Khondaker, Sudipta Seal, Graphene based materials: Past, present and future Elsevier, 2011.

[4] Andr´e K. Geim Graphene: Status and prospectus Science, 324, 5934 2009.

[5] Silvia Helena Roberto de Sena Tese:transporte e Estados Confinados de Portadores de Carga em Nanoestruturas de Grafeno Universidade Federal do Cear´a 2010. [6] Silvia Helena Roberto de Sena Propriedades eletrˆonicas de tricamada de grafeno

e nanofitas de carbono tensionadas Universidade Federal do Cear´a, Universiteit Antwerpen 2012.

[7] R.N. Costa Filho Graphene Ribbon with a line of impurities: Opening a gap, Phys. Rev. B 76, 193409 (2007).

[8] V. G. Kravets, A. N. Grigorenko, R. R. Nair, P. Blake, S. Anissimova, K. S. Novoselov, and A. K. Geim Spectroscopic ellipsometry of graphene and an exciton-shifted van Hove peak in absorption Phys. Rev. 81, 155413, 2010

[9] Gary Tomas. Graphene and Silicon Work Together For Solar Applications. Azom.

2013. Dispon´ıvel em : ¡http://www.azom.com/article.aspx?ArticleID=10120¿.

Acesso em 29/11/2013

[10] Belle dum´e.DNA helps turn graphene into a chemical sensor. Physics World. 2010. Dispon´ıvel em : ¡http://physicsworld.com/cws/article/news/2010/aug/31/dna-helps-turn-graphene-into-a-chemical-sensor¿ Acesso em 29/11/2013.

[11] Neil W. Ascroft and N. David Mermim, F´ısica do Estado S´olido. Cengage learning 2013.

[12] Gerald D. MahanMany-Particles Physics Plenum press 1990.

[13] Bipin R. Desai, Quantum Mechanics with Basic field Theory. Cambridge University press 2010.

[14] Jung Hoon HanSolid State Physics 2010.