1 REnCiMa, v. 10, n.2, p. 01-14, 2019
AS CONEXÕES TRABALHADAS ATRAVÉS
DA RESOLUÇÃO DE PROBLEMAS
NA FORMAÇÃO INICIAL DE PROFESSORES DE MATEMÁTICA
1CONNECTIONS WORKED THROUGH PROBLEM SOLVING IN INITIAL TEACHER TRAINING IN MATHEMATICS
Norma Suely Gomes Allevato
Universidade Cruzeiro do Sul, normallev@gmail.com
Lourdes de la Rosa Onuchic
Universidade Estadual Paulista Júlio de Mesquita Filho, lronuchic@gmail.com
Resumo
Orientações curriculares atuais e pesquisas consideram que a aprendizagem deve ocorrer por um processo ativo e construtivo em que os estudantes realizam as atividades de sala de aula à luz de suas crenças e assimilam as informações dentro de suas estruturas de conhecimento pré-existentes. Guiado por essas orientações, o presente trabalho aborda as Conexões no âmbito da Educação Matemática. O objetivo é apresentar reflexões acerca das possibilidades do trabalho com conexões através da resolução de problemas na aprendizagem e na formação inicial de professores de Matemática. Trata-se de um estudo teórico-bibliográfico, apoiado em trabalhos de diversos autores que tratam desse tema. Os estudos realizados permitiram identificar diversas formas de estabelecer conexões em benefício da aprendizagem matemática e da compreensão da Matemática como um corpo de conhecimentos em que conceitos e procedimentos são relacionados; ratificar que a resolução de problemas é um relevante e eficiente recurso na criação de contextos de ensino via conexões; e, finalmente, que os professores devem vivenciar, na formação inicial, situações de resolução de problemas que envolvam conexões matemáticas, a fim de incorporá-las em sua prática profissional futura.
Palavras-chave: Educação Matemática, Ensino Superior, Formação Inicial de
Professores, Resolução de Problemas, Conexões.
Abstract
Current curriculum guidelines and researches consider that learning must occur through an active and constructive process for students to carry out classroom activities supported by their beliefs, and to be able to understand the information within their a priori knowledge structures. The present work approaches the concept of Connections in a way guided by these considerations, in the scope of Mathematics Education. The aim of this article is to come out some reflections on the possibilities of working with connections through
1
Trabalho constituído a partir da versão publicada nos anais do VII Seminário Internacional de Pesquisa em Educação Matemática, realizado em 2018, em Foz do Iguaçu – PR/Brasil.
2 REnCiMa, v. 10, n.2, p. 01-14, 2019 problem solving in learning and in Initial Teacher Training in Mathematics. This is a theoretical-bibliographic study supported by the works of several authors that deal with this topic. The studies carried out allowed us to identify several ways of establishing connections for the development of mathematical learning, and the understanding of Mathematics as a body of knowledge that relates concepts and procedures; ratifying that problem solving is a relevant and efficient resource to make contexts of teaching up via connections; and, finally, teachers should experience problem solving situations involving mathematical connections in their Initial Teacher Training in order to incorporate these practices into their future professional performance.
Keywords: Mathematics Education, Higher Education, Initial Teacher Training, Problem
Solving, Connections.
Introdução
Atualmente, há consenso quanto à orientação de que a aprendizagem matemática deve ocorrer por um processo ativo e construtivo em que os estudantes realizam as atividades de sala de aula à luz de suas crenças e assimilam as informações dentro de suas estruturas de conhecimento pré-existentes. Resulta que cada estudante constrói um tipo de matemática “personalizada”. Para alguns, a Matemática é um conjunto de regras e fatos isolados; para outros, é uma rede de ideias na qual cada ideia é conectada a várias outras (HODGSON, 1995). Esta segunda é a perspectiva que sustenta as atuais orientações de ensino, e sobre a qual nos debruçamos no presente trabalho: a das conexões. Mas como os professores podem possibilitar aos alunos experiências que lhes permitam perceber e estabelecer essas conexões? Como capacitar ou preparar os professores para realizar este trabalho com seus alunos em sala de aula de Matemática?
Orientado por essas questões, o presente trabalho ratifica e dá continuidade a trabalhos apresentados por nós nos IV e VI SIPEM – Seminário Internacional de Pesquisa e Educação Matemática, realizados em 2009 e 2015, respectivamente. Esses trabalhos, explicitando propostas de mudança nas Licenciaturas, tiveram como eixo norteador a concepção de que os professores apenas incorporarão à sua prática docente as abordagens que efetivamente vivenciarem ao aprender Matemática durante sua formação inicial.
Em Onuchic e Allevato (2009), apresentado no IV SIPEM, foi defendida a perspectiva de que, através da resolução de problemas, se pode explorar as “grandes ideias” da Matemática Escolar; e no VI SIPEM, em Onuchic e Allevato (2015) esteve em destaque o conceito de proporcionalidade como conceito unificador, no sentido de que possibilita um trabalho no qual outros conceitos podem ser abordados de forma integrada. Em ambos os trabalhos foram analisados contextos de ensino e aprendizagem constituídos a partir de problemas geradores, no âmbito da Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas. (ALLEVATO; ONUCHIC, 2014)
Dando continuidade a essa trajetória e, ao mesmo tempo, ampliando e aprofundando tais perspectivas, o presente trabalho tem o objetivo de apresentar
3 REnCiMa, v. 10, n.2, p. 01-14, 2019 reflexões acerca das possibilidades do trabalho com conexões através da resolução de problemas na aprendizagem e na formação inicial de professores de Matemática. Ele está organizado em cinco seções, além desta introdução e das considerações finais. A primeira seção retoma as ideias basilares discutidas nos trabalhos de 2009 e 2015, quais sejam, as de possibilitar a construção de conhecimento das grandes ideias e dos conceitos unificadores da Matemática através da resolução de problemas. Na segunda seção, é abordado o significado de “conexões”, bem como sua importância relativamente à visão dos alunos sobre a Matemática, aos conhecimentos e aos processos matemáticos que podem desenvolver. Em seguida, uma seção discute as possibilidades de se trabalhar com conexões através da resolução de problemas. Então, um exemplo é apresentado, na terceira seção, de um problema que pode ser desenvolvido junto à Licenciatura, pois envolve conteúdos abordados no Ensino Superior, cuja resolução desencadeia várias situações de conexões matemáticas. Na quinta seção, situamos as reflexões no âmbito da Licenciatura, em que se realiza a formação inicial de professores de Matemática.
As grandes ideias, os conceitos unificadores e a aprendizagem matemática
Desde a Antiguidade até os dias atuais, a resolução de problemas tem sido o mote da construção de conhecimento, matemático e ligado a outras ciências, e um tópico sempre presente nos currículos de Matemática. No entanto, num processo dinâmico de se constituir pela constante reconstrução, ela, a resolução de problemas, vivencia um processo permanente de (res)significação, de geração de novas formas de concebê-la e de incorporá-la no trabalho de sala de aula. Uma concepção a que temos dedicado nossas práticas e pesquisas refere-se à Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas, que se constitui num caminho para ensinar Matemática e não apenas para ensinar a resolver problemas. Tem como princípio que o problema é um ponto de partida e orientação para a aprendizagem de novos conceitos e novos conteúdos matemáticos.
A palavra composta ensino-aprendizagem-avaliação tem sido empregada para expressar a concepção de que ensino, aprendizagem e avaliação devem ocorrer simultaneamente durante as atividades de sala de aula. O professor é o guia, o orientador dos processos de construção do conhecimento e os alunos são co-construtores desse conhecimento; e a avaliação deve estar integrada ao processo de ensino-aprendizagem, com vistas a acompanhar o crescimento dos alunos e reorientar as práticas de sala de aula, quando necessário.
Não há formas rígidas de programar e implementar o trabalho com o Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas, mas, após algumas revisões e aprimoramentos, ele apresenta as seguintes etapas, sugeridas para a implementação dessa prática em sala de aula: (1) proposição do problema; (2) alunos em grupo são desafiados a utilizar seus conhecimentos prévios; (3) os alunos nos grupos discutem e aprimoram sua compreensão; (4) o professor observa, incentiva e os auxilia em problemas secundários; (5) os alunos resolvem o problema; (6) os alunos registram as resoluções na lousa; (7) em plenária, discutem as resoluções obtidas; (8) professor e
4 REnCiMa, v. 10, n.2, p. 01-14, 2019 alunos chegam a um consenso sobre a resolução; (9) o professor formaliza o “novo” conteúdo; e (10)ocorre a proposição de novos problemas.2
O estudo desenvolvido em Onuchic e Allevato (2009) ressalta que essa concepção de resolução de problemas pode ser bastante profícua na construção do conhecimento das grandes ideias presentes na Matemática. Tratam-se daquelas que são estruturais na Matemática, na constituição de conceitos e na estruturação teórico-formal dos seus diversos ramos, como a Geometria, a Álgebra, a Aritmética... Uma delas é a de operação matemática e sua relação com a ideia de dimensão. Uma sequência de atividades utilizando o material manipulativo Linking Cubs é apresentada e discutida, possibilitando o desenvolvimento de compreensões sobre as relações entre operações e dimensão. Também é desenvolvida uma discussão sobre a importância, a potencialidade da resolução de problemas como atividade desencadeadora de aprendizagem sobre o que é uma teoria matemática e sobre como ela é constituída: por conceitos (primitivos ou definidos) e proposições decorrentes deles (postulados ou teoremas – na forma de lemas, teoremas ou corolários); e de qual é o papel de cada um deles dentro de uma teoria.
Avançando nesse sentido, num trabalho com foco nos conceitos unificadores, Onuchic e Allevato (2015) destacam que algumas ideias são catalizadoras de conexões matemáticas, especialmente se trabalhadas através da resolução de problemas. No artigo, é tomado como referência o conceito de proporcionalidade, destacando-se que relações proporcionais, como uma ideia unificadora desempenham um papel chave em outros assuntos matemáticos importantes como: razões, proporções, porcentagem, taxa, escala, semelhança de figuras geométricas, declividade, funções lineares, divisão em partes direta e inversamente proporcionais, regras de três, probabilidade e chance, sequências, distribuições de frequências e estatística, razões trigonométricas, movimento em velocidade constante, juros simples, entre outros. São apresentados dois problemas, foram desenvolvidos com professores em formação inicial, como geradores de reflexões e aprendizagem acerca do significado do conceito de proporcionalidade e de suas relações com diversos outros conceitos e objetos matemáticos, como as diferentes representações e as aplicações em outras áreas do conhecimento e/ou no cotidiano. São exemplos de conceitos unificadores, ainda, o conceito de razão, de função, entre outros.
Dando continuidade a essa construção intelectual e, ao mesmo tempo, ampliando e aprofundando compreensões nesse sentido, o presente trabalho constitui-se numa reapresentação de Onuchic e Allevato (2018), em que se pretendeu ressaltar essa mesma forma de trabalho – o Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas – possibilitando que professores e alunos, ao longo da resolução de problemas, estabeleçam conexões de diversas naturezas, e não só entre os diversos ramos da Matemática, como no trabalho de 2009. Vale reafirmar que, em todos os 3 (três) trabalhos, sempre esteve em evidência a defesa da importância de que os futuros professores de Matemática vivenciem essas práticas na formação inicial, a fim de que venham a incorporá-las em sua atividade docente futura.
2
O leitor interessado em um detalhamento de como são realizadas essas etapas pode consultar Allevato e Onuchic (2014)
5 REnCiMa, v. 10, n.2, p. 01-14, 2019 Desse modo, as próximas seções têm as conexões no centro das discussões e reflexões.
As conexões e a aprendizagem matemática
Muitas são as ideias que se encontram na literatura relativas a conexões e que têm a ver com ligar, relacionar, ancorar, articular, associar... O conceito de conexões projetou-se significativamente a partir da publicação dos Standards 2000, oficialmente Principles
and Standards for School Mathematics (NCTM, 2000), que indicou Conexões entre os
cinco Padrões de Procedimento essenciais a serem desenvolvidos no trabalho com alunos desde a Educação Infantil até o Ensino Médio.
Mas a que se referem as conexões? Há, ressalte-se, uma diversidade de perspectivas a considerar. Em geral, a literatura especifica conexões entre a Matemática e outras disciplinas ou domínios do saber, como a Física, a Medicina ou as Artes, e entre a Matemática e a vida real, incluindo as práticas culturais diárias como tomar banho ou ir ao supermercado. No Ensino Superior, ganham destaque as relações entre a Matemática e as profissões ou o mundo do trabalho. São também frequentes as referências às conexões dentro da própria Matemática; entre conteúdos de domínios distintos, como a Aritmética e a Geometria; e entre conceitos e procedimentos, como entre o conceito de área e o(s) procedimento(s) adotado(s) para determinar o seu valor.
Essas perspectivas são registradas na Base Nacional Comum Curricular – BNCC (BRASIL, 2017), apoiada no pressuposto de que a aprendizagem em Matemática está relacionada à apreensão de significados dos objetos matemáticos resultantes das conexões que os alunos estabelecem entre eles e os demais componentes, entre eles e seu cotidiano e entre os diferentes temas matemáticos.
Com menor frequência se consideram conexões entre os diferentes estágios de desenvolvimento das ideias e conceitos matemáticos. Elas deveriam ter as concepções e conhecimentos prévios dos alunos como ponto de partida para novas aprendizagens. (CANAVARRO, 2017)
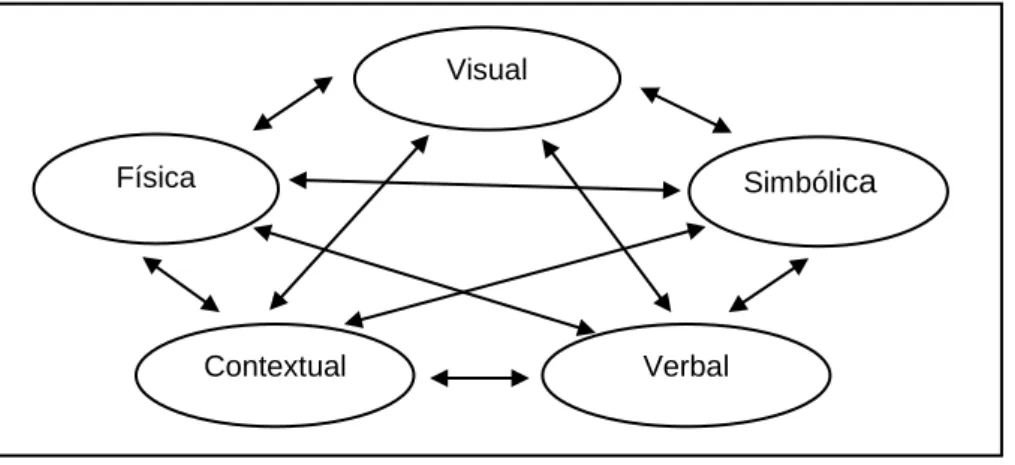
Apoiando-se em Lesh, Post e Behr (1987), Canavarro destaca, ainda, as representações múltiplas e suas conexões, que podem ser consideradas para cada conceito.
Visual
Física Simbólica
Contextual Verbal
Figura 1: Representações matemáticas e suas conexões
6 REnCiMa, v. 10, n.2, p. 01-14, 2019 Destaca que a representação simbólica, em particular, é uma representação por excelência da Matemática, porque simplifica a forma de referenciar algo e permite a manipulação e a construção de resoluções. Também indica, certamente, o uso da expressão, oral e escrita, e de outras formas de representação e suas conexões, conforme ilustrado na Figura 1.
Nesse sentido, Van de Walle (2009), apoiando-se no diagrama a seguir (Figura 2), explica que “nós usamos as ideias que já temos (pontos azuis) para construir uma nova ideia (ponto vermelho), construindo uma rede de conexões entre elas. Quanto mais ideias houver e mais conexões se formarem, melhor será a compreensão.
Mas o objetivo fundamental das conexões não se basta em proporcionar conhecimento sobre os objetos matemáticos e suas relações. Ampliando a compreensão das ideias e dos conceitos matemáticos, consequentemente as conexões permitem aos alunos dar sentido à Matemática e entendê-la como um corpo coerente, articulado e poderoso.
Com relação aos estágios de desenvolvimento das ideias, as conexões poderão ser constituídas baseando-se em conhecimentos prévios. Alguns conteúdos matemáticos, por exemplo para os 6º a 9º anos de escolaridade – como números racionais, proporcionalidade e relações lineares – estão intimamente ligados. A aprendizagem deve ser construída de modo que, à medida que os alunos vão se deparando com conteúdos matemáticos novos e diversificados, vão encontrando muitas oportunidades de utilizar e estabelecer conexões com conteúdos já aprendidos. Ou seja, quando os alunos se baseiam nos conhecimentos matemáticos que já possuem para aprender novos conceitos, utilizando uma gama de representações matemáticas, e até quando seu acesso a tecnologias sofisticadas aumenta, as conexões que se estabelecem proporcionam-lhes um maior poder matemático. (NCTM, 2000)
Portanto, há que se desenvolver reflexões e implementar ações que possibilitem tirar partido das conexões para ampliar a compreensão da Matemática pelos alunos. Canavarro (2017, p. 39) assevera: “Naturalmente, não basta enunciar a sua existência ou apresentar exemplos esporádicos. As conexões precisam integrar a experiência matemática dos alunos, de forma intencional e continuada.” Para apoiar a abordagem
Figura 2: Relações entre ideias
Fonte: Van de Walle (2009, p. 43)
7 REnCiMa, v. 10, n.2, p. 01-14, 2019 com conexões, a autora sugere o trabalho com representações múltiplas e com modelagem. No presente trabalho, nós indicamos a Resolução de Problemas.
As conexões e a resolução de problemas
Conforme já destacado neste artigo, as conexões passaram a ter mais destaque quando os Standards (NCTM, 2000) forneceram os princípios e os padrões a serem considerados na Matemática Escolar, apontando, em particular, 5 (cinco) padrões de processo: Resolução de Problemas, Raciocínio e Prova, Comunicação, Conexões e Representação. Ressalte-se, aí, a atribuição de igual estatuto à Resolução de Problemas e às Conexões como processos relevantes para a aprendizagem da Matemática Escolar.
Na associação desses dois processos, o usual nos contextos de ensino é que sejam considerados os contextos de aplicação fora da Matemática. Certamente, a resolução de problemas “reais” envolve os estudantes e promove o estabelecimento e o uso de conexões. Esses problemas ilustram como as conexões podem contribuir para uma maior compreensão de padrões e regularidades em situações problemáticas. Claramente, os problemas com contextos ricos implicam a existência de conexões com outras disciplinas (p. ex., as ciências naturais, os estudos sociais, as artes), bem como com o mundo real e com as experiências da vida quotidiana dos alunos.
Mas isso não é suficiente para torná-los proficientes em seu uso. Os estudantes precisam refletir sobre seus próprios esforços de envolver-se no estabelecimento e na identificação das conexões e de seu papel na resolução dos problemas, e explorar o uso de variadas conexões. Concordando com Hodgson (1995), consideramos que estudantes capazes de aplicar e transitar entre diferentes representações de uma situação-problema ou de um conceito matemático, possuem um conjunto de ferramentas flexíveis e poderosas para a resolução de problemas. É importante que eles construam um repertório de conexões, como um “kit de ferramentas”, que lhes ofereça caminhos alternativos e criativos de resolução para os problemas propostos. E, ainda, embora não seja condição suficiente para o sucesso na resolução de um problema, a habilidade de estabelecer conexões é necessária para o desenvolvimento da autonomia do estudante nessa atividade.
Ademais, pela via das conexões matemáticas, os alunos desenvolvem uma predisposição para utilizarem essas relações na resolução de problemas, que pode ser estimulada por questões que o professor apresenta, como: Como podemos utilizar, hoje, neste trabalho com triângulos semelhantes, o que discutimos na semana passada sobre desenhos em escala? “É necessário que os alunos se tornem explicitamente conscientes da existência de conexões matemáticas.” (NCTM, 2000, p. 71)
Entretanto, o conhecimento é pessoal e emerge de nossas ativas tentativas de interpretar o mundo que nos cerca, de modo que as conexões entre processos e conceitos matemáticos sejam objetos abstratos. Ponte (2010) assevera que o sentido de uma ideia matemática depende das conexões estabelecidas entre ela e aquelas que já possuímos, havendo, assim, uma natureza pessoal em qualquer conceito matemático. Sendo construtos da mente, as conexões conduzem a uma intrigante questão: os conceitos matemáticos (tais como gráficos e equações) são inerentemente conectados
8 REnCiMa, v. 10, n.2, p. 01-14, 2019 ou, de fato, as conexões existem somente na mente dos aprendizes? Hodgson (1995) considera que, independente da resposta a esta questão filosófica:
Se os estudantes não são capazes de estabelecer conexões, então as conexões não podem ser utilizadas em situações problema, independentemente de se elas existem ou não. No entanto, uma vez que elas estão estabelecidas na mente do aprendiz, as conexões são “coisas” que podem ser recuperadas da memória e, se necessário, aplicadas nos problemas. É por esta razão que as conexões são consideradas ferramentas para a resolução de problemas. (HODGSON, 1995, p. 15)
Ainda, alunos com um repertório maior de conhecimentos, como os de Ensino Médio e Superior, devem desenvolver uma maior capacidade de relacionar ideias matemáticas a partir da compreensão de que várias abordagens de um problema poderão conduzir a resultados equivalentes, mesmo que pareçam diferentes. (NCTM, 2000)
Decorre, portanto, que uma vez que as conexões são ferramentas para a resolução de problemas, as tarefas propostas pelos professores, aos alunos, devem promover o uso de conexões nas resoluções. Mas, reciprocamente e, para além da concepção de ferramenta, como qualquer recurso ou objeto utilizado por alguém ou alguma coisa para atingir um objetivo específico, nós defendemos que a resolução de problemas se constitui em uma atividade que promove a percepção e a compreensão das conexões – com situações de fora da ou com elementos internos à Matemática -, pelo estudante. O exemplo que apresentamos a seguir, ilustra este segundo caso.
Um exemplo
Este exemplo ilustra, conforme já explicitamos, que, em geral, a investigação que se realiza no decurso da resolução de um problema conduz naturalmente à necessidade de utilização de conexões. Por sua vez, o uso de conexões para resolver problemas, conduz à necessidade de seu estabelecimento.
Como Vc = x3 e Vp= 3x, de Vc = Vp + 1 tem-se . Portanto
. Sendo uma função contínua e uma
equação do 3o grau sem o termo quadrado, em sua resolução pode ser empregada a Fórmula de Cardano-Tartaglia.
Em uma publicação de 1545, Cardano (1501 – 1576) mostra que, sob certas condições, uma das raízes da equação de 3o grau, desprovida do termo em
é dada por
Seja Vc o volume de um cubo de aresta x, e seja Vp o volume de um
paralelepípedo com área da base 3 e altura igual à aresta do cubo. Determine x. de modo que Vc = Vp + 1.
Fonte: Trotta, Imenes e Jakubovic (1980)
9 REnCiMa, v. 10, n.2, p. 01-14, 2019 Sabe-se que, na realidade, essa fórmula foi deduzida por Tartaglia, embora tenha sido publicada primeiramente por Cardano e, por isso sua denominação como fórmula de Cardano-Tartaglia.
Para o caso do problema aqui proposto, em que q = -3 e p = -1, usando-se essa fórmula tem-se que:
logo:
Vê-se, então, que tal resolução depende do cálculo de . Como não existe número real que ao quadrado seja negativo, essa equação do 3o grau não tem raízes reais.
Sendo tem-se que p(1) = -3 e p(2) = 1, de modo que a equação tem uma raiz real compreendida entre 1 e 2, mais precisamente entre 1,8 e 1,9 pois p(1,8).p(1,9)<0 e, desse modo, conclui-se que o problema tem solução.
Ainda, vendo de outro modo, quando a aresta x do cubo é pequena, o volume Vc
será menor que Vp+ 1(por exemplo, para x = 1, Vc=1, Vp+ 1 = 4 e Vc< Vp+1).
Mas, à medida que x aumenta, todas as arestas do cubo aumentam, o que não ocorre com o paralelepípedo. Então, o volume Vc se aproxima de Vp+1, chegando até a
ultrapassá-lo (por exemplo, para x=2, Vc=8, Vp+ 1 = 7 e Vc> Vp+1). Assim, se x for
aumentando lentamente de 1 até 2, haverá um momento em que Vc=Vp+1 e, então, o
valor de x será uma raiz real da equação .
Ou seja, tem-se uma equação polinomial do 3o grau, sabe-se que ela possui uma raiz real, mas não se conseguiu obtê-la pela fórmula de Cardano-Tartaglia, pois ela conduz à raiz quadrada de um número negativo. Como sair desse impasse?
Uma possibilidade de encontrar a saída consiste em:
1. perceber que a impossibilidade de extração de raízes quadradas de números negativos não é definitiva, mas está relacionada com nossa situação presente, em que só conhecemos os números reais;
2. criar números que, elevados ao quadrado, possam resultar em números negativos, para poder prosseguir com a resolução da equação através da fórmula de Cardano-Tartaglia (esta é maneira de “negar”, de não aceitar tal impossibilidade; é o modo de libertarmo-nos da situação presente para poder avançar);
3. operar (adicionar, multiplicar, radiciar, etc) com estes novos números; se possível, inclusive, serão mantidas nestas operações as propriedades operatórias dos números
10 REnCiMa, v. 10, n.2, p. 01-14, 2019 reais (como a comutativa da adição e da multiplicação, como a distributiva da multiplicação em relação à adição, etc.);
4. retomar o problema dado e verificar se, operando com os novos números, é possível resolvê-lo; e resolvê-lo é obter um número real!
A certeza de que essa equação tem uma raiz real, nos levou a extrair a raiz quadrada de números negativos, o que levou à criação da unidade imaginária e aos números complexos, em que i2 = –1. Prosseguindo na resolução da equação
, onde
, recaímos em:
Agora, procuramos calcular . Se x+yi for uma raiz cúbica de , então . A resolução desta equação leva a um sistema de equações do 3o grau, gerando um círculo vicioso. Tem-se, aqui, a necessidade da radiciação de números complexos, que é possível com o apoio da representação geométrica desses números, e pode ser expressa na forma trigonométrica, onde ) com
, e , com 0 ≤ θ < 2π. Daí se pode deduzir que ,
que produz n raízes distintas, quando a k se atribuem os valores de k=0, 1, ... , n – 1. Completando a resolução do problema, temos:
e
Assim, • e
• os argumentos formam a P.A.: , de razão As raízes cúbicas de são:
11 REnCiMa, v. 10, n.2, p. 01-14, 2019 Da mesma forma tem-se que , ou seja, as raízes cúbicas de
são .
Substituindo esses valores na expressão a que chegamos através da fórmula de Cardano-Tartaglia, tem-se:
x1 = w0+ =
x2 = w1+ =
x3 = w2+ =
Portanto, a equação possui 3(três) raízes reais, que são: x1 =
x2 =
x3 =
Porém, x2 e x3, por serem negativos, não convêm ao problema proposto, uma vez
que a solicitação do problema é a determinação de uma medida, a da aresta do cubo. Assim, a aresta do cubo mede x1 = .
A resolução deste problema possibilita estabelecer diversos tipos de conexões, a começar por aquelas entre diversos ramos da Matemática: a Teoria dos Números, a Álgebra e a Geometria. Também são contemplados diversos tipos de representação – a algébrica (nas resoluções e manipulações desenvolvidas no decurso da resolução), a gráfica (por exemplo: na compreensão da necessidade e na visualização do módulo e argumento de números complexos) e a pictórica (na representação inicial do cubo e do paralelepípedo). O problema é efetivamente gerador de situações em que há necessidade de o resolvedor, dependendo da série em que se encontra, resgatar conteúdos diversos anteriormente estudados fazendo conexões para aprender novos conteúdos. O problema envolve conexões entre conceitos e procedimentos de cálculo relativos a área e volume, conjuntos numéricos, raízes de polinômios, potenciação, números complexos – unidade imaginária, definição, operações (em particular a radiciação), representação geométrica, conjugado –, ângulos, trigonometria. Na Licenciatura, constitui-se como um problema útil para que os futuros professores vivenciem a construção de conhecimentos sobre novos conceitos e conteúdos, percebendo a necessidade de resgatar e/ou estabelecer conexões entre conteúdos previamente aprendidos, retomando-os e compreendendo-os de forma mais aprofundada dentro de uma perspectiva de aprendizagem em espiral.
As conexões na formação inicial
Ensinar é um empreendimento bastante complexo. Sabe-se que o conhecimento básico que sustenta o ensino de Matemática deve incluir o conhecimento do que é Matemática, do que constitui cada um dos seus ramos, das conexões feitas entre as ideias matemáticas dos estudantes, da forma como os estudantes aprendem, da cultura
12 REnCiMa, v. 10, n.2, p. 01-14, 2019 escolar onde o trabalho está sendo feito, além de outros fatores pertinentes ao contexto escolar. É um processo intrincado, complexo e delicado, que envolve a criação de uma comunidade de aprendizagem e o desafio aos estudantes em dar sentido às ideias matemáticas, promovendo o desenvolvimento de sua compreensão. O processo de ensino envolve a tomada de muitas decisões importantes como, por exemplo, “quando se deve falar?”, “quando se deve levantar mais questões?” e “quando se deve, simplesmente, encorajar os alunos a pensar”. Consequentemente, não é surpreendente que aprender a ensinar bem é um empreendimento de longa carreira. (NÓVOA; 2001)
O trabalho de ensinar tem raízes na formação inicial dos professores e é mantido, ao longo de toda a sua carreira, num processo contínuo de aprender o que os estudantes entendem, como eles entendem e quais atividades de aprendizagem contribuem eficientemente para que haja uma compreensão efetiva, significativa e útil.
Concordando com Canavarro (2017, p. 38), consideramos que “não basta convocar a unânime bondade das conexões, é preciso saber como as promover, na teoria e na prática.” Essa afirmação nos remete às questões ligadas à formação do professor, adequada e necessária para que práticas docentes eficientes se concretizem. É preciso coerência entre a formação oferecida e a prática esperada do futuro professor. Os professores precisam aprender para também ensinar. E, nesse sentido, é preciso considerar uma peculiaridade muito especial na preparação do professor: ele aprende a profissão num lugar similar àquele em que vai atuar, porém numa situação invertida.
Das discussões promovidas no presente artigo, resulta que os professores devem promover atividades de sala de aula que desempenhem dupla função: elas devem preparar os estudantes tanto para o estabelecimento de novas conexões como para o uso de conexões já conhecidas na resolução de um conjunto de problemas. “Como professores, nós devemos ser conscientes de tais conexões e sermos capazes de delineá-las para resolver problemas.” (HODGSON, 1995, p. 18)
Entra em cena, com isso, um conjunto de conhecimentos de que o professor deve dispor como conhecimento curricular, conhecimento do conteúdo, conhecimento didático do conteúdo, entre outros (TARDIF, 2002). Para realçar essas conexões, os professores deverão conhecer as necessidades dos seus alunos, bem como a Matemática que estudaram nos anos anteriores e a que irão estudar nos anos seguintes. Assumindo que a compreensão envolve o estabelecimento de conexões, os professores deverão basear-se nas experiências prévias dos alunos e não as repetir, desenvolvendo práticas em espiral que, ao mesmo tempo, retomam e avançam, em direção à construção de novos conhecimentos e ideias. Novas ideias surgem naturalmente como extensões de aprendizagens matemáticas anteriores.
Considerações finais
Neste artigo, desenvolvemos reflexões acerca das possibilidades do trabalho com conexões através da resolução de problemas na aprendizagem e na formação inicial de professores de Matemática, fazendo uso da Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas (ALLEVATO; ONUCHIC, 2014). Apoiadas em diversos autores que abordam essa temática, ratificamos nossa
13 REnCiMa, v. 10, n.2, p. 01-14, 2019 posição de que os alunos desenvolvem uma atitude mais favorável relativamente à Matemática, apreciando o seu valor como explicação das situações de fora da Matemática e possibilidade de predição/intervenção sobre essas situações, reconhecendo a utilidade da Matemática. Além disso, os alunos aprendem não somente conteúdos matemáticos como também assuntos extra matemáticos. Ainda, por meio de um ensino que enfatize a interrelação das diversas ideias matemáticas, os alunos não só aprendem Matemática, mas superam visões e percepções estreitas de compartimentalização, mecanização e falta de significação das aprendizagens. (CARREIRA, 2010)
Ademais, ficou notório que as conexões não devem ser vistas meramente como interessantes fatos matemáticos, mas como componentes essenciais para o sucesso na resolução de problemas, assim como a resolução de problemas é atividade essencial para construção de conhecimento matemático pelas conexões.
É preciso que, em sua formação inicial, os futuros professores vivenciem intensamente práticas que os coloquem nesse contexto das conexões, enquanto aprendem a Matemática da Educação Superior e se preparam para sua atuação profissional futura. Esperamos que este trabalho contribua para as reflexões e mudanças nesse sentido.
Referências
ALLEVATO, N. S. G; ONUCHIC, L. R. Ensino-aprendizagem-avaliação de Matemática: por que através da resolução de problemas. In: ONUCHIC, L. R. et al. (Org.). Resolução
de problemas: teoria e prática. Jundiaí: Paco, 2014.
BRASIL. Conselho Nacional de Educação. Base Nacional Comum Curricular. Brasília, 2017.
CANAVARRO, A. P. O que a investigação nos diz acerca da aprendizagem da matemática com conexões – ideias da teoria ilustradas com exemplos. Educação e
Matemática. Lisboa, n. 144-145, p. 38-42, out, nov, dez. 2017.
CARREIRA, S. Conexões Matemáticas – Ligar o que se foi desligando. Educação e
Matemática. Lisboa, n. 110, p. 13-18, out, nov, dez. 2010.
HODGSON, T. R. Connections as Problem-Solving Tools. In: HOUSE, P. A.; COXFORD, A. F. (Ed.). Connecting Mathematics across the Curriculum. Yearbook 1995. Reston: NCTM, 1995. p. 13 - 21.
LESH, R.; POST, T.; BEHR, M. Representations and Translations among Representations in Mathematics Learning and Problem Solving. In: JANVIER, C. Problems of
Representations in the Teaching and Learning of Mathematics. Hillsdale, NJ:
Lawrence Erlbaum, 1987.
NCTM-National Council of Teachers of Mathematics. Principles and Standards for
School Mathematics. Reston,VA: NCTM, 2000.
NÓVOA, A. O professor pesquisador e reflexivo. 2001. Disponível em http://www.tvebrasil.com.br/SALTO/entrevistas/antonio_novoa.htm. Acesso em: 25 mai. 2009.
14 REnCiMa, v. 10, n.2, p. 01-14, 2019 ONUCHIC, L. R.; ALLEVATO, N. S. G. Proporcionalidade através da Resolução de Problemas no Curso Superior de Licenciatura em Matemática. In: SIPEM – Seminário Internacional de Pesquisa em Educação Matemática, 6. 2015, Pirenópolis. Anais... 2015. Disponível em: <http://www.sbembrasil.org.br/visipem/anais/story_html5.html> Acesso em: 01. jun. 2018
ONUCHIC, L. R.; ALLEVATO, N. S. G. Resolução de Problemas na Licenciatura em Matemática – Rumo à compreensão e à aquisição das grandes ideias contidas na Matemática Escolar. In: SIPEM – Seminário Internacional de Pesquisa em Educação Matemática, 4. 2009, Brasília. Anais... 2009. v. 1.
PONTE, J. P. Conexões no Programa de Matemática do Ensino Básico. Educação e
Matemática. Lisboa, n. 110, p. 3-6, out, nov, dez. 2010.
TARDIF, M. Saberes docentes e formação profissional. Petrópolis: Vozes, 2002.
TROTTA, F.; IMENES, L. M. P.; JAKUBOVIC, J. Matemática Aplicada. Vol. 3, São Paulo: Moderna, 1980.
VAN de WALLE, J. A. Matemática no Ensino Fundamental: formação de professores e aplicação em sala de aula. Tradução: Paulo Henrique Colonese. 6. ed. Porto Alegre: Artmed, 2009.