Dinâmica de redes neurais e formação de agregados em redes complexas

Dinâmia de Redes Neurais e Formação de

Agregados em Redes Complexas.

Fortaleza CE

Dinâmia de Redes Neurais e Formação de

Agregados em Redes Complexas.

Dissertaçãoapresentada aoCursode

Pós-Graduação emFísiadaUniversidade F

e-deral do Ceará omo parte dos requisitos

para a obtenção do título de Mestre em

Físia.

Orientador:

Prof. Dr. José Soares de Andrade Júnior

Departamento de Físia

Centro de Ciênias

Universidade Federal do Ceará

Fortaleza CE

•

Ao professor e amigo José Soares de Andrade Júnior pela orientação e

on-ança;

•

Ao professor AsânioDias Araújo;

•

Ao professor eamigo André AutoMoreira, pelos ensinamentose disussões;

•

Aos professores Gil de Aquino Farias e Raimundo Nogueira da Costa Filho,

pelos onselhos e inentivos;

•

Aosprofessores doDepartamentode Físia,emespeial Murilo,Evangelistae

Eloneide;

•

Ao amigoTony eao Ramos, quepossibilitaram o trabalhonos laboratórios;

•

Aos funionáriosdoDepartamentode Físia,Ana Cleide,Rejane eElias;

•

Aos amigos do departamento Teldo, Daniela, Luís Araripe, José Filho,

Mar-elo, Emerson, Talita, Munarim, Marília, Marilza, Fabríio, Danyel, Tayroni,

Geová,Hiroshe, Assis,Jeanlex, King, Franiné, José Alves;

•

Aos amigos pessoais, Adriana Ribeiro,Sérgio Bastos, Ari, Reinalde,Rodrigo,

Fátima,Grazi, Eveline, Gledson,Cialdini,Silvana, Flávio,Mithele, Lia,

Nei-ara, Adriana, AnaCláudia,Carolina,Moreira, Cláudio,Luis José, Erasmo;

Na primeira parte deste trabalho, propomos um modelo de resimento

om-petitivo de agregados em redes omplexas para simular a propagação de idéias ou

opiniõesemomunidades. Investigamosomoasdistribuiçõesde tamanhosde

agre-gados variam om a topologia de onstrução da rede e om o número de sementes

aleatoriamentedispersas naestrutura. Para tal,analisamosredesdotipode

Erdös-Rényi, redes de ontato preferenial e a hamada rede Apoloniana. Esta última

apresenta distribuições de tamanho de agregado em forma de uma lei de potênia

P

(n)

_∼

n

−

α

omumexpoente

α

≈

1.0

,onde

n

éotamanhodoagregado. Resultados similares são observados om as distribuições obtidas para as frações de votos por

andidato às eleições proporionais para deputados no Brasil. Na segunda parte,

analisamos o omportamento temporal da atividade neural em redes om

arate-rístias de mundo pequeno e em redes onstruídas segundo o modelo do ontato

preferenial. Nesta primeira topologia, estudamos omo a série temporal se

om-portaomavariaçãodoalanedasonexões. Emambas astopologias,observamos

Theproess bywhihnew trendsand ideaspropagateinsoialommunitiesan

have a profound impat in the life of individuals. To understand this proess, we

introdue a ompetitive luster growth model in omplex networks. In our model,

eahlusterrepresentsthesetofindividualswithaertainopinionorpreferene. We

investigatehowthe lustersizedistributiondepends onthe topologyof thenetwork

and howit isaeted by the numberof initialseeds dispersedin the struture. We

study ourmodelusingdierentnetworkmodels,namely,theErdos-Renyigeometry,

the preferential attahment model, and the so-alled Apollonian network. This

last omplex geometry displays a luster size distribution that follows a power-law

P

(n)

_∼

n

−

α

with an exponent

α

≈

1.0

, where

n

is the luster size. Similar results have been obtained for the distributions of number of votes per andidate in the

proportional eletions for federal representation in Brazil. In the seond part of

this work,weinvestigatethetemporalbehaviorofneuralnetworkswithsmallworld

topology and in networks built aording to the preferentialattahment model. In

the rst ase we study the eet of the range of onnetions onthe behavior of the

time series. Inbothtopologies,wedetettheexisteneofylesandinvestigatehow

Resumo . . . p.i

Abstrat . . . p.ii

Lista de Figuras p.v

Introdução p.2

1 Redes Complexas p.5

1.1 Introdução . . . p.5

1.2 Teoria dos grafose omodelo de Erdös-Rényi . . . p.5

1.2.1 Distribuição de Conetividade . . . p.6

1.2.2 Distânia Média . . . p.7

1.3 Redes de Mundo Pequeno: uma nova topologia. . . p.7

1.4 O Modelo de Watts-Strogatz . . . p.9

1.5 O modelo doontato preferenial . . . p.12

1.5.1 A equação mestra daevoluçãoda rede . . . p.14

1.5.2 O tratamentoontínuo . . . p.15

1.6 O trunamento exponenialda distribuiçãode onetividade . . . p.16

1.7 Rede Apoloniana . . . p.19

1.8 Propriedades observadas em redes reais . . . p.22

1.8.1 Internet . . . p.22

1.8.4 Outros sistemas . . . p.23

1.9 Redes Neurais . . . p.24

2 Cresimento de Agregados em Redes Complexas p.34

2.1 Introdução . . . p.34

2.2 Eleições . . . p.37

2.3 Modelo . . . p.40

2.4 Conlusões. . . p.47

3 Dinâmia de Redes Neurais Complexas p.48

3.1 Introdução . . . p.48

3.2 O érebro humano . . . p.49

3.3 Eletroenefalograma- EEG . . . p.55

3.4 Modelo daatividade neural . . . p.57

3.5 Resultados e Disussões . . . p.60

3.5.1 Topologiade Watts-Strogatz (WS) . . . p.60

3.5.2 Topologiado Contato Preferenial. . . p.68

3.6 Conlusões. . . p.71

4 Conlusões p.72

Referênias p.74

1 Representação de um grafo om o onjunto

V

=

{

1

,

2

,

3

,

4

,

5

,

6

,

7

}

e o

onjunto

E

=

{{

1

,

2

}

,

{

1

,

5

}

,

{

2

,

5

}

,

{

3

,

4

}

,

{

5

,

7

}}

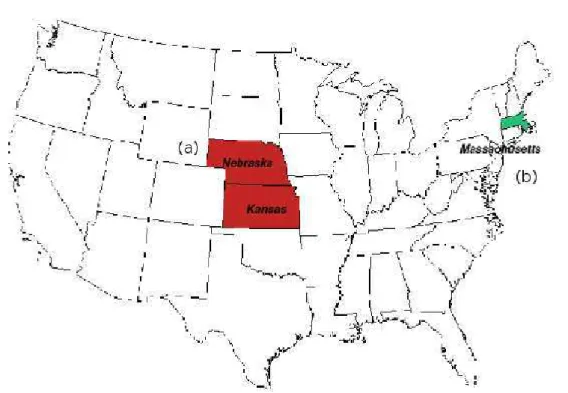
. . . p.6

2 Mapa dos Estados Unidos mostrando (a) origem das artas e (b) loal

onde a pessoa-alvoseenontrava. . . p.8

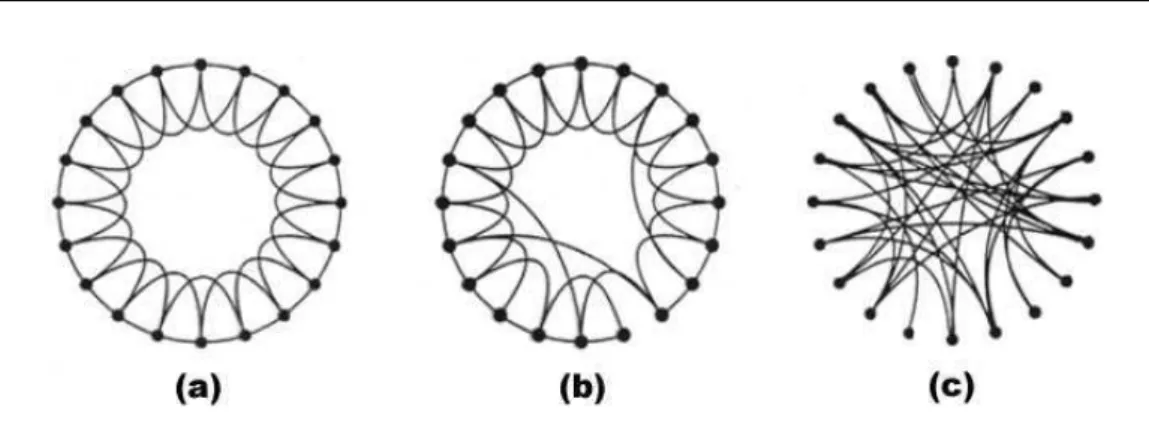
3 ModeloderedeWatts-Strongatz: a)Iniialmentetemosumarederegular

om 20 nós, sendo ada nó ligado aos seus 4 primeiros vizinhos. b)

Alteramos o valor de

p

,entre 0 e 1,) atéhegarmos em

p

= 1

,onde a

troa dasligaçõesé feita deforma aleatória. . . p.10

4 TroadeumaligaçãodeumarededotipoWS.Onó

v

estáligado

iniial-mente ao nó

v

′

. Com atroaaleatória daligação

v

é ligadodiretamente

ao nó

v

′′

. . . p.10

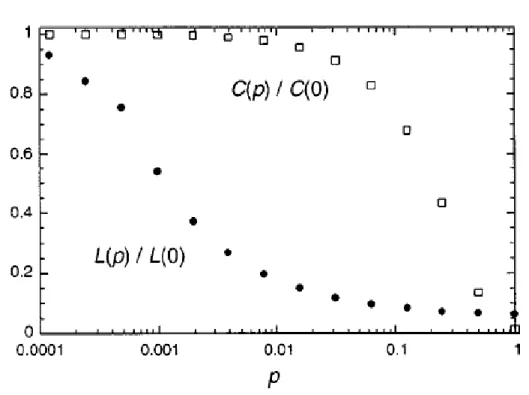
5 Menoraminho médio e Coeiente de agregação paramodelos de rede

WS om

N

= 10

4

. Os dados são normalizados pelos valores de

L

(0)

e

C

(0)

paraumarederegular. Observeaquedaaentuadadomenor

ami-nho médioparapequenosvaloresde

p

,orrespondendo aum

omporta-mento araterístiodalassederedesdemundopequeno. Duranteesta

queda,

C

permanee quase onstante, indiando que a transição para

a rede de mundo pequeno é quase impereptível a nível loal. Figura

retirada de(ALBERT;BARABÁSI,2002) . . . p.11

6 Distribuição de onetividade do modelo WS om

N

= 10

4

e

h

k

i

= 6

para

p

= 0

.

0

(írulo),

p

= 0

.

1

(quadrado)e

p

= 0

.

3

(triâgulo).. . . p.12

7 Uma rede gerada pelo modelo do ontato preferenial. Ilustração

de rede. Observamos que as distribuições seguem um

omporta-mento em lei de potênia,

P

∝

k

−

α

, seguido de um trunamento

exponenial. A posição do trunamento depende do tamanho da

rede. . . p.17

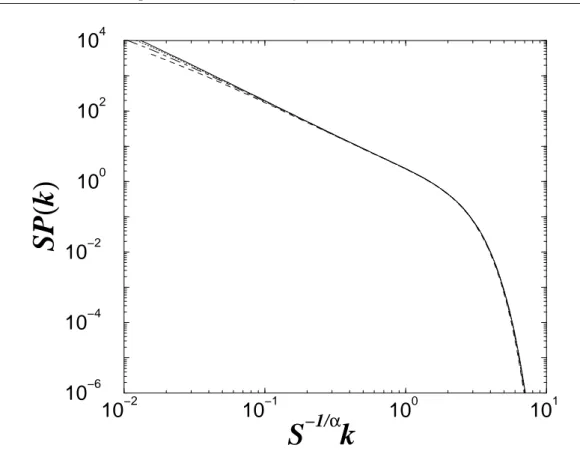
9 As mesmas distribuições aumuladas da Fig. 8 reesalonadas

se-gundo

S

1/α

de formaaolapsar aregião de deaimento exponenial. p.18

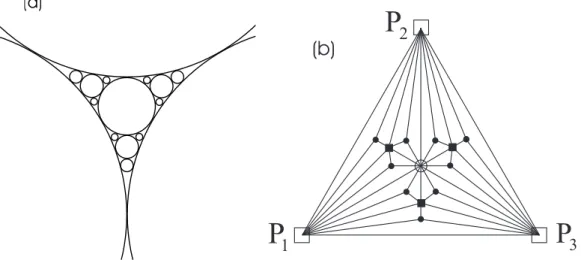
10 (a) Formato Apoloniano lássio, (b) Rede Apoloniana, primeira,

segundaetereirageraçãorepresentadasrespetivamentepelos

sím-bolos

,

e

•

(ANDRADEetal., 2004). . . p.20

11 Distânia média entre dois nós

L

omo função do numero de nós

N

. A linha sólida é um guia para os olhos e tem uma inlinação

3/4. Odetalhemostraempapelsemilogo oeientede agregação

C

omo função de

N

. A linha traejada mostra ovalorobservado

para grandes redes

C

= 0.828

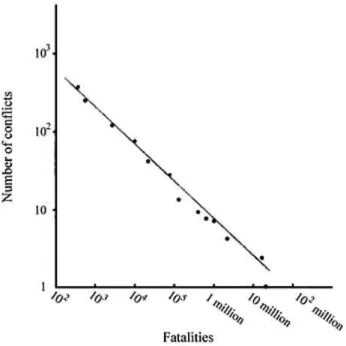
. . . p.21

12 Lei de potênia para guerras(BUCHANAN, 2000). . . p.36

13 Distribuiçõesde números de votos porandidato nas eleições

pro-porionaispara (a) DeputadosEstaduaise(b) DeputadosFederais

ompetitivo de agregados. Nesta gura usamos a tereira geração

daredeApoloniana,Seção1.7doCapítulo1,omosubstratoparao

resimento. Esseesolhasedeveaaraterístiaplanardestarede

que afaz partiularmenteapropriada para uma representação

grá-a. No primeiropasso doproesso de resimento (a), algunsnós

(marados pelo quadrado, triângulo, estrela e pelo irulo maior)

são esolhidos para servirem de sementes para o resimento de

agregados narede. Todos osdemaisnós (marados pelos pequenos

pontos) não são assoiados a nenhum dos agregados neste passo;

esses nósserãoosúniosaessíveisaoresimento. Aslinhas

trae-jadasligam ouum par de nós que já pertenem aalgum agregado,

ou um par de nós aessíveis. Nesse passo, essas onexões não

in-ueniam o resimento. As linhas mais largas ligam um nó que

já foi inorporado a um agregado a algum nó ainda aessível. São

essas linhaquemediamoresimentodosagregados. Aada passo

qualquerumadessaslinhaspode seresolhidaomamesma

proba-bilidade,eonóaessíveléinorporadoaomesmoagregadoqueseu

vizinho. Desta forma, a veloidade om que um agregado rese é

proporionala seu perímetro, istoé, ao número de de onexões de

um nó no agregado para um nó aessível. No segundo passo (b)

um novonóé inorporado aoagregado maradopelos quadrados e

novaslinhaslargassãoadiionadasaoperímetrodesseagregado. O

proesso ontinuaaté quetodos osnóstenhamsido inorporadosa

algum dos agregados (). Nesse pontoo tamanho dos agregados é

omputado. Esse meanismode resimento éuma espéie de

pro-esso gananioso, ouseja, quantomaior o perímetrodo agregado

de resimento ompetitivo aontee sobre uma rede do tipo ER.

Essas distribuiçõesforamobtidasomredesontento

10

5

nós. Para

garantiruma boaamostragemestatístia, foramobtidos

10

5

amos-tras de agregados para ada urva. Isso implia que foram feitas

mais realizações para os asos om menos sementes de forma a

manter o número de amostras de agregados onstante. As

distri-buiçõesobtidas om essa topologiaseguem aproximadamenteuma

formaexponenialomumomprimentoaraterístiodependendo

do número de sementes

n

s

. As linhas traejadas orrespondem as funções

P

(n) =

n

s

e

−

n

s

n

. As linhas ontínuas são as funções

p(n) =

Cn

1

−

γ

s

n

−

γ

exp(

−

n

s

n)

,om osparâmetros

C

= 0.85

±

0.003

,

e

γ

= 0.2

±

0.05

,obtidosapartirde umajustelinearparaosdados olapsadosmostradosnodetalhe. Aguramostraqueparaasredes

do tipo ER a formada distribuição é ompletamentedeterminada

peladensidade de sementes para o proesso de resimento.. . . . p.43

16 Distribuiçõesde tamanhos normalizadosobtidas quando o modelo

é realizado sobre uma rede onstruída om o esquema do ontato

preferenial (BARABÁSI; ALBERT, 1999). Foram usados

10

7

nós e

obtidos

10

5

amostras para ada valor de

n

s

. Diferente do obser-vadoomasredesERnãoépossívelolapsarasdistribuiçõesnesse

aso. Noentanto,nota-sequeparaqualquervalorde

n

s

sãoobtidas distribuições altamente dispersas om tamanhos de agregado indo

de apenas alguns nós até quase toda a rede. A linha ontínua é

um ajuste em lei de potênia,

P

(n)

∼

n

−

α

, om expoente

α

= 1.2

, obtida para a região em esala da distribuição om

n

s

= 10

2

. A

inlinação das urvas paree reser a medida que o número de

doresimentosobrearedeApoloniana(ANDRADEetal.,2004). As

distribuiçõesforamobtidasparaa15

a

geraçãodaredeApoloniana,

oqueorrespondea

N

= 7174456

nós. Cadaurvaéobtidadeuma amostra de

10

5

agregados. Neste aso as distribuições apresentam

a forma de uma lei de potênia,

P

(n)

∼

n

−

α

om um expoente

α

_≈

1.0

, independente do número de sementes. A linha ontinuaé

um ajuste linear para a região em esala para os dados om

n

s

=

10

2

sementes. A forma em degraus periódios das distribuições é

remanesente da estrutura auto similar resultante da onstrução

hierárquiada rede Apoloniana. . . p.46

18 Representação emdiagramaem bloos dosistema nervoso. . . p.49

19 Ilustração de uma élula nervosa. Esta élula é formada por: (1)

O orpo de neurnio ou Somma, (2) Dendritos, (3) Axnio e (4)

Terminais Sináptios. . . p.51

20 Organização estrutural dos níveis noérebro . . . p.53

21 Mapa itoarquiteturaldo órtex erebral. As diferentes áreas são

identiadaspelaespessuradesuasamadasetiposdeélulasnelas

ontidas. Algumasdasáreasespeíasmaisimportantessãoomo

segue. Córtex motor: bandamotora, área4; áreapré-motora, área

6;amposoularesfrontais, área8. Córtex somestésio: áreas3,1,

2. Córtex visual: áreas 17, 18, 19. Córtex auditivo: áreas 41 e 42

(BRODAL, 1981). . . p.54

22 Registro eletroenefalográo real típio. . . p.56

23 Parte daevolução temporaldaatividadeneural

A(t)

emuma rede WS ontendo2048nós,omaprobabilidadesderealoação(rewire)

igual a zero,

p

= 0

, naurvado topo,e om

p

= 1

, naurvaabaixo. p.61

24 Visualização da formação de períodos, em que (a), (b) e ()

es-tão em intervalos de tempo distintos e onseutivos exibindo um

peloperíodo, T. . . p.63

26 Fraçãode redes periódias,

φ

, pelonúmerode nós,N,para

diferen-tes valores de probabilidadede realoação

p

ou

rewire

. . . p.64

27 Fraçãode redesperiódias

φ

pelaprobabilidadederealoação

p

,ou

rewire, para vários tamanhos de rede. . . p.65

28 Representação gráa dos parâmetros

a

0

,

a

1

e

a

2

om função de

N

. p.66

29 Renormalização da fração de redes periódias

φ

′

omo função da

tanh de renormalizaçãoda probabilidadede realoação

p

′

. . . p.67

30 PeriodoMédio para ada tamanhode rede, emesala logarítmia,

1000 diferentes gerações de rede, epara um valorde probabilidade

de realoação igual para todos,

p

= 0.9

. A linha traejada orres-pondea

T

∼

√

N

. . . p.68

31 Evoluçãotemporaldaatividadeneuralemredeonstruídasegundo

o modelo doontato preferenial ontendo 2048 nós. . . p.69

32 A urva do topo (a), mostra a fração de redes periódia

φ

pelo tamanho darede

N

, eaurvaabaixo(b) mostraotamanhomédio

Introdução

Sistemas om interações simples entre seus elementos onstituintes, mas om

muitosgrausde liberdade, podemexibirmorfologiasompliadaseapresentar

om-portamentos dinâmios intrinados, tais omo fenomenologias emergentes,

avalan-hes,ritialidadeeleisdeesala(BAK,1996). Quandotratamosomestessistemas,

usualmentedenominadossistemas omplexos,hásempreaexpetativadequeexista

um númeropequeno de leisbásias governando aessênia doomportamento

glo-baldofenmenoem estudo. Énesteontexto quealgunssistemasomplexospodem

ser ompreendidos emtermos de leis de esala (STANLEY, 1999). Neste aso, diz-se

que osistemaéinvariantede esala,ouseja,háadependêniade uma determinada

grandeza om algumparâmetro relevantena formade uma lei de potênia.

Nestas iruntânias, o oneito de universalidade implia que diferentes

fen-menos invariantes de esala oorrendo nanatureza, podem ser lassiados em um

númeroomparativamentepequenodelasses,usualmentedenidaspelosexpoentes

de suas leisde esala. Esse oneito permitequesistemasmais ompliadospossam

ser desritos por modelos simples, desde que os ingredientes mínimos neessários

para denirem a sua lasse de universalidade estejam presentes naformulação.

Umdosdesaosnoestudodesistemasomplexosonsisteemmodelaranatureza

diversa dos seus onstituintes e a intrinada estrutura das suas interações. Entre

as ténias usadas om maior suesso para estudar os sistemas omplexos estão os

modelos disretos baseados em agentes. Nesses modelos, os agentes podem oupar

umnúmeronitodeestadoseosistemaevoluiempassosdisretosdetempo. Aada

passo, todos osagentes usam alguma regrapara deidir queestado irãoassumir no

próximo passo. Cadaagenteestá onetado a um pequeno grupode outros agentes

nosistema,osvizinhos. Aregradeevoluçãodeumdeterminadoagenteédesritapor

uma função, que toma omo parâmetro os estados de seus vizinhos. Tipiamente,

mesmo tempo.

A simpliidade e liberdade na denição das regras de interação zeram desses

modelos disretos uma ferramenta ideal para o estudo de diversos sistemas

om-plexos. Nessa linha de abordagem, um dos modelos mais estudados é o hamado

autmato elular. Tipiamente, nesse tipo de modelo os agentes são dispostos em

uma rede regular e todos usam a mesma regra de evolução. Autmatos elulares

foram empregadosnopassadoomo um modelopara oestudo de sistemasaótios,

auto-organizaçãoeomputaçãoemergente. Apesardosuessodosautmatos

elula-res omo um modelopara sistemasdesentralizados, aestrutura regular,om todos

os agentes exeutando a mesma função e om as interações denidas em uma rede

periódia, é propriedadeque por si sóinduz uma ordemglobal e que não se espera

observar em sistemasreais. No universo dos modelos disretos, oextremo oposto à

estrutura regulardosautmatoselulareséoupadopelohamadomodelodasredes

Booleanas. NasredesBooleanasaestruturadasinteraçõesédenidaaleatoriamente

e ada agente usa uma regrade evoluçãodiferente. Redes Booleanasforam

propos-tas iniialmente omo um modelo para redes de regulação genétia, mas já foram

usadasemsistemastãovariadosomointeraçõesemgrupossoiais,evoluçãoeredes

neurais. Esse modelo exibe várias propriedades observadas em sistemas reais, uma

das mais intrigantes provavelmentesendo uma transição entre uma fase ordenadae

uma aótia. Na fase ordenada, o sistema evolui para atratores que onsistem de

estados xosoupequenos ilos. Nafaseaótia, osatratores onsistem de grandes

ilos, ujo omprimentovariaexponenialmenteom tamanhodo sistema.

Neste trabalho utilizaremos uma lasse de modelos para sistemas omplexos

onde asleis de esala e ooneito de universalidade pratiamenteditam a

sistemá-tia de sua abordagem. Como veremos, as denominadas redes omplexas servem

omo paradigma para os mais diferentes sistemas. Uma vez que essas redes são

modelos plausíveis para araterizar a natureza das interações que regem alguns

sistemas omplexos(STROGATZ,2001),oestudo eaaraterização de suas

proprie-dades éfundamentalpara a desrição de taissistemas. Por exemplo,sabe-se que a

onetividade de vários sistemas omplexos é notadamente anmala,seguindo uma

distribuição deprobabilidadenaformadeuma leide potênia. Esse tipode sistema

pode, então, ser modeladopela regra do ontato preferenial (BARABÁSI; ALBERT,

one-tividade global da estrutura (ALBERT; JEONG;BARABÁSI, 2000) e ontrolam uma

série de proessos dinâmios. Uma outra propriedade observada, é a araterístia

de mundo pequeno. As redes de mundo pequeno têm a propriedade de que a

dis-tânia média entre qualquer par de nós da rede, medida pelo número mínimo de

onexões que separam osnós, é proporionalao logaritmodo número total de nós.

Outrapropriedadedegrandeinteresseemredesomplexaséumvalorrelativamente

alto para ohamadooeiente de agregação.

Esta dissertação está organizada da seguinte forma. No Capítulo 1,

apresen-tamos uma revisão sobre alguns dos prinipais oneitos da estatístia de redes

omplexas. São desritos osmodelosde redede Erdös eRényi, de mundo pequeno,

de ontato preferenial e de Apolnio. Mostramos então algumas das propriedades

observadas empiriamenteem redes reais e um breve histório sobre redes neurais.

No Capítulo 2, introduzimos um modelo de resimento ompetitivo de agregados

em redes omplexas utilizandomodelos de rede de Erdös e Rényi, de ontato

pre-ferenial e de Apolnio. Mostramos omo a topologia om que a rede é onstruída

interfere na formação dos agregados. Constatamos que as distribuições obtidas

se-gundo o modelo de Apolnio são similares às distribuições obtidas para as frações

de votos porandidato observada nas eleiçõesproporionaisnoBrasil(COSTAetal.,

2002). No Capítulo 3, abordamos um problema dinâmio envolvendo a evolução

temporal da atividade neural em redes om estruturas regulares e desordenadas.

Observamos, emalguns asos, aexistênia de formação de períodos nas séries

tem-porais desta atividade,e investigamosomo atransição da estrutura de onstrução

da redeinuenia naformaçãodestes períodos. Para talanálise,porexemplo,

vari-amos a probabilidadede realoaçãono modelo de rede de Watts-Strogatz (WATTS;

STROGATZ, 1998), que também dene a aleatoriedade das onexões entre os seus

nós. Outro aspeto abordado, diz respeito à forma omo o tamanho da rede

in-terfere na formação dos períodos. Adiionalmente, um estudo similar é feito para

redes onstruídas segundo o modelo doontato preferenial. Finalmente, no

Capí-tulo 4,apresentamos nossasonlusõessobre todososresultadosobtidos,bemomo

1 Redes Complexas

1.1 Introdução

A modelagemde redes omplexastem sido o foo de muitos trabalhos reentes

em meânia estatístia para a representação de sistemas físios, químios,

biológi-os eatémesmosoiais. Nesteapítulo,estudaremosaspropriedadesestatístiasde

algumas redesomplexas,introduzindo osoneitos neessáriospara aonstruçãoe

entendimentodestas,omoateoriadosgrafos,adistribuiçãodeonetividade,a

dis-tânia médiaeooeientede agregação. Emseguida,desreveremosa experiênia

de Stanley Milgram, que propõe o famoso seis graus de separação. Disutiremos

também, a topologia de algumas redes reais, omo por exemplo, WWW e redes

metabólias. Porm, faremos um brevehistório sobre redes neurais.

1.2 Teoria dos grafos e o modelo de Erdös-Rényi

Podemos denir um grafo

G

= (V, E)

(DIESTEL, 2000) omo um par de on-juntos

V

e

E

que satisfaz

E

⊆

[V

]

2

, onde ada elemento de

E

é formado por dois elementos de

V

. Graamente, os elementos do onjunto

V

representam os sítios, e os elementos do onjunto

E

representam as ligações entre os sítios. Podemos visualizar um exemplo de um grafo naFig. 1.

Com o onheimento da teoria dos grafos e om o surgimento do interesse no

estudoderedesomtopologiaomplexas,PaulErdöseAlfrédRényi(ERDÖS;RÉNYI,

1959) propõemum modelo, noqual,um sistemaom

N

nós, onde ada nó pode se onetar aoutro randomiamenteom uma probabilidade

ξ

, riandoum grafoom

Figura 1: Representação de umgrafoom oonjunto

V

=

{

1

,

2

,

3

,

4

,

5

,

6

,

7

}

e o onjunto

E

=

_{{

1

,

2

_}

,

_{

1

,

5

_}

,

_{

2

,

5

_}

,

_{

3

,

4

_}

,

_{

5

,

7

_}}

.

Para o melhor entendimento de problemas que envolvem sistemas om um

nú-mero elevado de elementos, é neessário a introduçãode algumasdenições:

1.2.1 Distribuição de Conetividade

A distribuição de onetividade,

p(k)

, representa a probabilidade de um nó ter uma onetividade

k

. Aprobabilidadede

p

i

(k

i

)

,de queum determinadonó

i

tenha um número

k

i

de onexõesé dada pelobinomial,

p

i

(k

i

) =

C

N

k

i

−

1

ξ

k

i

(1

₋

ξ)

N

−

1

−

k

i

(1.1)

poisonó

i

podeestabeleeraté

N

−

1

onexões,sendoqueaprobabilidadedeque

k

i

dessas onexõesexistamé

ξ

k

i

,aprobabilidadede queasdemais

N

−

1

−

k

i

onexões estejam ausentes é

(1

−

ξ)

N

−

1

−

k

i

, e

C

k

i

N

−

1

é onúmero de diferentes ombinaçõesem

que asonexõespodemser distribuídas. Nolimite emque

N

vaia innito,aforma binomial seaproximada distribuiçãode Poisson,

p(k)

_≈

e

−h

k

i

h

k

i

k

k!

,

(1.2)

onde

h

k

i

=

ξN

é a onetividade média. Isso mostra que, apesar da distribuição aleatóriadeonexões, aredeéhomogênea,ouseja,osnóstêm,aproximadamente, o

a onetividade dos nós não são variáveisindependentes.

1.2.2 Distânia Média

A distâniaentre dois nósédenida omoonúmeromínimode onexõesqueos

separam. A distâniamédia

l

é amédia das distânias entre todos os pares de nós. Eventualmente, sea probabilidade

ξ

de onexão for suientemente pequeno, pode aonteer de não existir um aminho onetando dois nós; neste aso, a distânia

entre eles éinnita. Quando istooorre,a distâniamédiatoma apenasospares de

nós emummesmoagregado ompletamenteonetado. Emmédia,adanótem

h

k

i

primeiros vizinhos. Cada um desses tem

h

k

i

vizinhos, resultando em

h

k

i

2

segundos

vizinhos,

h

k

i

3

tereiros vizinhos,e assim pordiante. Se onúmero

N

de nós de uma rede for suientemente grande,

ln(N

)

≫ h

k

i

, o número de nós a uma distânia

l

ontinuaresendo exponenialmenteaté que,eventualmente, onúmerode vizinhos

aumadistânia

l

adaordemdotamanhodarede,

N

. Nestaondição,adistânia média deve reser logaritmiamenteom o tamanhodarede,

l

_∼

lnN

ln

_h

k

_i

.

(1.3)

1.3 Redes de Mundo Pequeno: uma nova topologia

Em1967,osoiólogoepsiólogoameriano,StanleyMilgram (MILGRAM,1967)

realizou uma experiênia om o intuito de veriar o grau de ligação entre as

pes-soas. A experiênia onsistiaem esolher 150 pessoas em Wihita, Kansas, Omaha

e Nebraska, eada uma delas reebiauma artaontendo instruçõesespeías

ex-pliando o experimento. Basiamente teriam que fazer hegar um envelope a uma

pessoa, que deveria ser desonheida, hamada de pessoa-alvo, loalizada em

Bos-ton. Na Fig. 2 mostramos o mapa norte ameriano para ilustrar a distânia entre

Figura 2: Mapa dosEstados Unidos mostrando (a) origemdas artas e (b) loal onde a

pessoa-alvo seenontrava.

O onteúdo de ada envelope era:

1. O nome, ea informaçãoque apessoa-alvo era orretor em Boston.

2. Algumasregras,omoporexemplo: sevoênãoonheediretamentea

pessoa-alvo,repasseodoumentoparaumamigoquetenhaumapossívelrelaçãoom

o alvo.

3. Para registrar o perurso, ada intermediário deve assinar seu nome. Isto é

importante, pois evita que oenvelope volte para a mesma pessoa, e podemos

rastrear de quem partiu o envelope.

Várias artas foram perdidas, e nuna hegaram, mas as que hegaram não

tiveram mais que 6 amigos intermediários. Tal resultado, onheido omo seis

graus de separação, nos revelaque pessoas aparentementedesonheidas têm uma

grande probabilidade de possuírem, em um erto grau, amigos em omum que as

1.4 O Modelo de Watts-Strogatz

As primeirastentativasde expliaros seis graus de separação onsistiam

exa-tamenteem suporum aráteraleatóriopara osgrafos de olaboração(RAPOPORT,

1957), não levando em onta o fato das pessoas possuírem um núleo de amizades

loais, onde vários amigos são amigos emomum, aresidos de alguns amigos

dis-tantes, queneste aso, seomportamomo onexõesaleatórias. Assim, deveríamos

esperar que os grafos possuíssem um erto grau de regularidade loal, isto é, uma

região onde o grafo se assemelha a uma rede regular. Para tal situação,

reente-menteDunan Watts eSteven Strogatz (WATTS;STROGATZ,1998) propuseramum

modelode rede que nada mais é doque uma interpolaçãoentre uma rede regulare

um grafoaleatório.

A onstruçãodaredeWatts-Strongatz (WS)érealizadademaneirasimplesatravés

do seguinte algoritmo:

1. Construirumgraforegular,porexemplo,umanelunidimensionalomligações

entre primeiros e segundos vizinhos, de modo que o número de onexões seja

igual a

k

= 4

.

2. Com probabilidade

p

, probabilidade de realoação, troar a ligação,

L

vv

′

por uma ligaçãoaleatória

L

vv

′′

,onde

v

′′

éumsítiosorteado aleatoriamente, Fig.4.

Assim, a probabilidade de realoação nos diz qual é a probabilidade de fazer

umatroade ligação. Para

p

= 0

,nenhumatroaéfeita,jápara

p

= 1

,haverá troa.

3. Repetir oitem anterior (passo 2)para todas asligaçõesda rede.

Atavésdestealgoritmo,alaraapossibilidadedeinterpolaçãoentreumaestrutura

regular, ou seja, om valorda probabilidade

p

= 0

, e uma estrutura aleatória,om

p

= 1

. Para pequenos valores de

p

temos uma estrutura om vizinhança bem

denida, om exeção de alguns defeitos, que são regiõesonde existem sítios om

ligações de longo alane. Para quantiar esses defeitos, torna-se neessária a

Figura 3: Modelo de rede Watts-Strongatz: a)Iniialmentetemos uma rede regular om

20 nós, sendo ada nó ligado aos seus 4 primeiros vizinhos. b) Alteramos o valor de

p

, entre0e1,)atéhegarmosem

p

= 1

,ondeatroadasligaçõeséfeitadeformaaleatória.

menos um vizinho emomum,

C

a

é a probabilidadede que

i

e

j

sejamonetados. Em redes de relações soiais, por exemplo, as onexões entre pessoas se iniiam,

normalmente, através de onheidos em omum. Se tomarmos omo parâmetro a

onetividade média, temos que o oeiente de agregação vai a zero para grandes

redes,

C

a

=

ξ

=

h

k

i

/N

.

Figura4: Troa deumaligaçãodeumarededotipoWS.Onó

v

estáligado iniialmente ao nó

v

′

. Com a troa aleatória daligação

v

é ligado diretamenteao nó

v

′′

Mostramos na Fig. 5 que a distânia média

l

deai rapidamente om a adição de pouas ligaçõesde longo alane, enquanto

C

permanee om valoraltopor um amplo intervalode

p

.

Figura 5: Menor aminho médio e Coeiente de agregação para modelos de rede WS

om

N

= 10

4

. Os dados são normalizados pelos valores de

L

(0)

e

C

(0)

para uma rede regular. Observeaquedaaentuadadomenoraminho médioparapequenosvaloresde

p

, orrespondendoaumomportamento araterístiodalassede redesdemundopequeno.

Durante estaqueda,

C

permanee quaseonstante, indiando queatransição para a rede de mundo pequeno é quase impereptível a nível loal. Figura retirada de (ALBERT;

BARABÁSI, 2002)

em torno da onetividade média,

h

k

i

, mas que deai rapidamentepara valores de k afastadosde

h

k

i

.

AFig.6mostraadistribuiçãodeonetividadeparaumarede

W S

om

N

= 10

4

e

< k >= 6

. Como resimento daprobabilidadede realoação,a larguradaurva aumenta, onvergindo para uma distribuição de onetividade obtida pelo modelo

3

5

7

9

k

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

1.1

P(k)

Figura 6: Distribuição de onetividade do modelo WS om

N

= 10

4

e

h

k

i

= 6

para

p

= 0

.

0

(írulo),

p

= 0

.

1

(quadrado)e

p

= 0

.

3

(triâgulo).

1.5 O modelo do ontato preferenial

Asredesaleatóriastêmdistribuiçãode onetividadePoissoniana,omumvalor

araterístioparaaonetividade. Noasode umadistribuiçãoemleide potênia,

não há valor araterístio. Na prátia, a onetividade dos nós só é limitada pelo

númeronitodeonexões. Poressarazão,asredesquetêmessetipode distribuição

são hamadas redes sem esala(sale-free networks).

Como diferentes redes reais apresentam distribuições em lei de potênia, pode

existir um meanismo universal queleva asredes a tomaremesta forma. Omodelo

doontato preferenial(BARABÁSI;ALBERT,1999)propõequeesseomportamento

emerge da dinâmiade evolução da rede. As seguintes regras onstituem este

mo-delo:

(i) A rede deve ser onstruída em um proesso de resimento. Neste aso, a rede

Figura7: Umarede geradapelomodelodoontatopreferenial. Ilustraçãoretirada

de Strogatz (STROGATZ, 2001)

nós já presentes narede.

(ii)Aoestabeleeremnovasonexões,osnósbusam,preferenialmente,osnósmais

onetados. Mais preisamente, a probabilidade

Π

i

de uma onexão ser dirigida a

um nó

i

é proporionalà sua onetividade

k

i

,

Π(k

i

) =

k

i

P

j

k

j

,

(1.4)

introduzido para normalizar a probabilidade. Como ada onexão liga dois nós, o

termo de normalizaçãoé identio ao dobro donúmero de onexões.

1.5.1 A equação mestra da evolução da rede

Parademonstrarqueessemodelosimplesleva,naturalmente,aumadistribuição

de onetividadeemleide potênia,vamos estudaraevoluçãodapopulação

S

k

(N)

de nós omonetividade

k

,numaredeomum número

S

de nós. Quandoum novo nó entra na rede, o valor de

S

k

deve mudar segundo (DOROGOVTSEV; MENDES; SAMUKHIN, 2000; KRAPIVSKY;REDNER;LEYVRAZ, 2000)

S

k

(N

+ 1) =

S

k

(N

) +

m

k

₋

1

P

k

′

k

′

S

k

′

(N

)

S

k

−

1

(N

)

−

m

k

P

k

′

k

′

S

k

′

(N

)

S

k

(N

) +

δ

k,m

.

(1.5)

A primeira pareladaEq. (1.5) dáontados nós quejá tinham onetividade

k

na rede de tamanho

N

−

1

. A segunda parela é referente à probabilidadede que um nóom onetividade

k

−

1

reebauma onexãoeseja promovidopara apopulação

S

k

. O tereiro termo subtrai os nós om onetividade

k

que reebem mais uma

onexão. O últimotermo aresentao novonó que entra narede om

m

onexões.

A probabilidade de um nó ter onetividade

k

é, simplesmente,

p(k, N

) =

S

k

(N

)/N

. Vamos, agora, determinar a forma de

p(k)

no limite em que

N

vai a

innito. Neste limite, o número total de onexões no sistema pode ser aproximado

por

mN

, e o termode normalização,portanto,a

2mN

.

Temos, então,

p(k) =

k

−

1

2

p(k

−

1)

−

k

2

p(k) +

δ

k,m

,

(1.6)

que leva a

p(k) =

k

−

1

k

+ 2

p(k

−

1)

(1.7)

e

p(m) =

2

resultando, nalmente, em

p(k) =

2m(m

+ 1)

k(k

+ 1)(k

+ 2)

.

(1.9)

No limite em que

k

vai ao innito, essa solução é levada a uma lei de potênia

p(k)

_∼

k

−

γ

om o expoente

γ

= 3

.

1.5.2 O tratamento ontínuo

Um outro meio de determinar a formada distribuiçãode onetividade no

mo-delo doontato preferenial éatravés dotratamentoontínuo(BARABÁSI; ALBERT,

1999). Neste tratamento, relaiona-se a onetividade média dos nós,

h

k

i

i

, om o instante

i

emque o nó é introduzidona rede. Para isso, podemos expressar a taxa om quea onetividade médiado nórese om o tamanhodarede na forma

∂

_h

k

i

i

∂S

=

mΠ(

h

k

i

i

).

(1.10)

Usando a formado ontato preferenial (1.4), obtemos

∂

_h

k

i

i

∂S

=

h

k

i

i

P

j

k

j

.

(1.11)

A solução de (1.11) deve satisfazer à ondição iniial de que o nó entrou na rede

no instante

i

om onetividade

m

. Como ada nó introduz

m

onexões à rede, no limite assintótio aonstante de normalização pode ser tomadaomo

X

j

k

j

∼

2mN.

(1.12)

Dessa forma,a solução de (1.11) deveser

h

k

i

i

=

m

N

i

β

,

(1.13)

Neste ponto, vamos determinar a probabilidade

P

(k)

para que um nó tenha onetividade maior que

k

. Podemos esperar que os nós que atingirama onetivi-dade

k

sejam aqueles que entraram primeirona rede. Usando a Eq. 1.13, podemos determinar que, numa rede de tamanho

N

, os nós ujas onetividades superem

k

devem ser aqueles introduzidos antes do instante

i

=

m

1/β

_N/k

1/β

. Fazemos, então,

a assoiaçãode

P

(k)

om afração da redeformada pelos nós introduzidosantes do instante

i

,

P

(k)

_∝

m

k

1/β

.

(1.14)

A função

P

(k)

é uma distribuição aumulada e pode ser relaionada om a distri-buição de onetividade,

ρ(k) =

₋

∂P

(k)

∂k

∝

m

1/β

β

k

−

1

−

1/β

_.

(1.15)

Chegamos, assim, a uma distribuição em lei de potênia om expoente

γ

=

1 + 1/β

= 3

, em onordânia om o resultado enontrado através da equação

mestra na Seção1.5.1.

1.6 O trunamento exponenial da distribuição de

onetividade

AsoluçãodaEq.1.9éexatanolimiteemqueotamanhodarede

S

vaiainnito. Soluçõespara tamanhos de rede nitospodem ser obtidas iterandoaequação (1.5)

numeriamente. A Fig. 8 mostra a distribuição de probabilidade aumulada para

diferentes tamanhos de rede. A distribuição aumulada é denida omo

P

(k) =

∞

X

k

′

_=k

p(k

′

)

(1.16)

e devederesersegundo umaleide potêniaom expoente

α

=

γ

−

1 = 2

. AFig. 8 mostra que,mesmo emtamanhos nitos, adistribuiçãosegue oomportamentoem

1

10

100

1000

10000

k

10

−8

10

−6

10

−4

10

−2

10

0

P

(

k

)

S=2

12

S=2

14

S=2

16

S=2

18

Figura 8: Distribuição aumulada de onetividade para diferentes tamanhos de

rede. Observamos queas distribuiçõesseguem umomportamentoemleide

potên-ia,

P

∝

k

−

α

,seguido de um trunamento exponenial. A posição dotrunamento

depende do tamanho darede.

de onexões. Aima deum erto valor, adistribuiçãomuda paraum deaimentodo

tipo exponenial 1

. Nota-se, na Fig. 8, que a posição do trunamento exponenial

move-se para maiores valores de

k

quando a rede rese.

A partir do resultado do tratamento ontínuo, pode-se ompreender omo o

trunamento depende do tamanho da rede. Vimos que a onetividade de um nó

resesegundo

(i/S)

β

. Osnósmaisonetados,portanto,estãoprovavelmenteentre

aqueles presentes nosprimeirosmomentosdarede,

i

≈

1

. Portanto,aprobabilidade deenontrarumnóommaisque

S

β

onexões, deveirrapidamenteazero,ouseja,o

expoente

β

= 1/α

ontrola aposiçãodo trunamentoexponenial. AFig. 9mostra que, de fato, aposiçãodo trunamentoolapsa quando asurvassão reesalonadas

1

De fato,pode-semostrarqueadistribuiçãoapresenta umtrunamento dotipo

e

−

k

2

(DORO-10

−2

10

−1

10

0

10

1

S

−1/

α

k

10

−6

10

−4

10

−2

10

0

10

2

10

4

SP

(

k

)

Figura9: AsmesmasdistribuiçõesaumuladasdaFig.8reesalonadassegundo

S

1/α

de formaa olapsara regiãode deaimentoexponenial.

segundo (DOROGOVTSEV; MENDES; SAMUKHIN, 2001; KRAPIVSKY; REDNER;

LEY-VRAZ, 2000)

P

(k)

_≡

SP

k

S

1/α

(1.17)

Aposiçãodotrunamentoexponenialdeterminaonúmeromáximodeonexões

que um nó pode atingir em uma rede gerada pelo modelo do ontato preferenial.

Essa informação é relevante porque esses nós mais fortemente ligados formam um

esqueleto que aessa toda arede. Foi mostrado que a onetividade global darede

é fortemente sensível à eliminação dos maiores nós (ALBERT; JEONG; BARABÁSI,

2000).

Diferentes efeitos observados em redes reais podem afetar a posição do

as onexões são estabeleidas pelos vos, apresenta um trunamento relativamente

pequeno. É evidenteque um aeroporto tem um limite nonúmero de vosque

on-segue reeber por dia e esse limite estabelee o valor máximo para a onetividade

independente do tamanho da rede. O trunamento é afetado, também, se os nós

que entram narede, aoestabeleerem suas onexões, aessamapenasuma parte da

rede. Roteadores, por exemplo, devem, mais provavelmente, estabeleer onexões

om os outros roteadores siamente mais próximos; uma página da internet deve

ter linkspara páginas om assuntos emomum. Pode-se mostrarque, neste aso, a

onetividade emqueaontee otrunamentodeve reser logaritmiamenteom o

tamanho darede (MOSSA;AMARAL, 2002).

1.7 Rede Apoloniana

Modelosdeterminístiosderedesomplexaspodemser partiularmente

adequa-dosparaonstruirredesompropriedadestopológiaspredeterminadas,porexemplo

altograu de agregação, ompatação,et. Algunsexemplos de modelos

determinís-tios de redes sem esala foram propostos e usados om suesso para desrever o

resimento de redes aleatórias (JUNG; KAHNG, 2001; DOROGOVTSEV; GOLTSEV;

MENDES, 2002),mas estes modelosnão apresentam apropriedade de serem

aomo-dados emespaços Eulidianos. Reentemente (ANDRADEet al., 2004) introduziram

uma nova lasse de redes, hamadas redes Apolonianas,ujaspropriedades são:

•

podem ser tanto determinístiasomo aleatórias;

•

são sem esala;

•

possuemaraterístia de pequeno mundo;

•

podem ser aomodadas emespaçoseulidianos.

Nasuaversãodeterminístia,aredeApolonianapodeserrelaionadaomo

pro-blemadoempaotamentode esferasde aordoomomatemátiogregoApolniode

Perga(BOYD;MATH,1973). Nasuasoluçãolássia,iniialmentetemostrêsírulos

então preenhidosda mesmaforma,omomostrado na Fig.10a . Adistribuição de

tamanhos deírulossegueumaleide potêniaomexpoentepróximoa1.3(BOYD;

MATH, 1973). De fato, existem muitas outras topologias om diferentes dimensões

fratais (HERRMANN; MANTICA; BESSIS, 1990). Esse proedimento pode também

ser generalizadopara dimensõesmais altas (BARAM;HERRMANN;RIVIER, 2004).

(b)

2

P

3

P

1

P

Figura10: (a)FormatoApolonianolássio,(b)RedeApoloniana,primeira,segunda

etereirageraçãorepresentadasrespetivamentepelossímbolos

,

e

•

(ANDRADE et al.,2004).

O empaotamentoApolonianopode ser utilizadopara desrever

empaotamen-tos densosde grão efoi tambémusadoomo ummodelosimples paraturbulêniae

fragmentação. Conetandoosentros das esferas quesetoamporlinhas,obtém-se

a rede que no aso lássio da Fig. 10.a, resulta na triangulação orrespondente à

rede de forças no empaotamentode Apolnio. A rede resultanteé o quese hama

uma rede Apoloniana(ANDRADE etal.,2004).

E possívelnotar quearedeApolonianaé de fatosemesala. AFig. 10bmostra

queaadageração

n

onúmerodesítios

N

resedeumfatordetrêseaoordenação de ada sítio por um fator de dois. Mais preisamente, a ada geração

n(n

=

0,

1,

2, ...)

existem

m(k, n) = 3

n

_,

₃

n

−

1

_,

₃

n

−

2

_{, ...,}

₃

2

_,

_3,

_1,

e3vértiesomonetividade

k

= 3,

3

_×

2,

3

_×

2

2

_{, ...,}

₃

_×

₂

n

−

1

_,

₃

_×

₂

n

_,

e

2

n+1

, respetivamente, onde o último

númerode vérties eonetividadeorrespondeaos três antos, P1,P2,P3. Devido

à araterístiadisreta desse espetro, é onveniente trabalhar om a distribuição

umulativa

P

(k) =

P

k

′≥

k

m(k

′

, n)/N

n

, onde

N

n

= 3 + (3

n+1

₋

_1)/2

sitions na geração

n

. Ésimples mostrar que:

P

(k)

∝

k

1

−

γ

om

γ

= 1 + ln 3/

ln 2

≈

2.585

. AaraterístiadepequenomundodaredeApolonianaémostradanaFig.11.

0.5

1.0

1.5

2.0

ln(lnN)

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

ln

(l

)

10

0

10

1

10

2

10

3

10

4

10

5

10

6

N

0.76

0.80

0.84

C

0.75

Figura 11: Distânia média entre dois nós

L

omo função do numero de nós

N

. A linha sólida é um guia para os olhos e tem uma inlinação 3/4. O detalhe mostra

em papelsemilogooeientedeagregação

C

omofunção de

N

. A linhatraejada mostra o valorobservado para grandesredes

C

= 0.828

.

É observado que

l

∝

(ln

N)

β

,om

β

≈

3/4

. Este éum novoomportamenteentre o mundo pequeno,

l

∼

ln

N

, e ultra pequeno,

l

∼

ln(ln

N

)

(ADLER, 1985; AMARAL, 2000a). Uma segunda propriedade araterizando uma rede de mundopequeno é o

oeiente de agregação. Foi mostrado por Andrade et. al.(ANDRADE etal., 2004)

que no limite de grandes redes o oeiente onverge para 0.828 (ver detalhe na

Fig. 11). Esse é um valorrelativamente alto, quando omparado por exemplo om

o observado para as redes de olaboração de atores

C

= 0.79

(WATTS; STROGATZ, 1998). Oomportamentodestasduaspropriedadesaraterizaoenáriodepequeno

1.8 Propriedades observadas em redes reais

Várias redes omplexas podem ser onstruídas a partir de dados obtidos de

sistemas reais. Umarevisão sobre as propriedades das redes de diferentes sistemas

pode serenontradaem(ALBERT;BARABÁSI,2002). Nesta seção,vamosapresentar

algumas propriedadesobservadas emredes de sistemas naturaise artiiais.

1.8.1 Internet

As informaçõesquetrafegam narede mundialde omputadores, ainternet, são

distribuídas por roteadores que determinam para onde ada paote de informação

deveir. Umestudodaredede roteadores(PASTOR-SATORRAS;VESPIGNANI, 2001a)

mostrouque ainternetnão obedeeuma distribuiçãode onetividadePoissoniana.

De fato,a distribuiçãode onetividade tema formade uma leide potênia

p(k)

∼

k

−

γ

, om

γ

= 2.23

(PASTOR-SATORRAS; VESPIGNANI, 2001a). O oeiente de agregação,

C

a

, medido em diferentes momentos entre 1997 e 1999, por exemplo, variouentre 0.18 a0.3(PASTOR-SATORRAS;VESPIGNANI, 2001a),sendobemmaior

que o esperado em uma rede aleatória om os mesmos parâmetros,

C

a

= 0.0001

. Mostrou-se, também, que adistâniamédia é daordem de

l

∼

9

.

1.8.2 WWW

Umaoutravisãopossíveldainternetonsisteemdeterminaraspropriedadesda

redeformadapelaspáginasdehipertexto(ALBERT;JEONG;BARABÁSI,1999). Neste

tipo de rede, as onexões têm direção, ou seja, é possível determinar o número de

itaçõesemumapágina eonúmerodeitaçõespara umapágina. Analisandoarede

formadapormaisde300.000páginas,veriou-seque,nesteaso,tambémseobtém

uma distribuição de onetividade em leide potênia, om expoente

γ

= 2.45

para o númerode itaçõesporpágina,e

γ

= 2.1

paraonúmerode vezes queada página é itada. A distânia média observada na rede de páginas da internet é de era

de 16 onexões (ALBERT;JEONG;BARABÁSI, 1999). O oeiente de agregação foi

1.8.3 Redes metabólias

Em um trabalho reente (JEONG et al., 2000) estudou-se a rede orrespondente

ao metabolismo de 43 diferentes organismos. Os nós da rede são os substratos e

as onexões são estabeleidas quando esses substratos partiipam em uma mesma

reação químia noorganismo. Essa rede tem umadistribuição de onetividade em

leidepotêniaomexpoente

γ

entre2.0e2.4,dependendodoorganismo,edistânia média

l

daordem de 3.3.

1.8.4 Outros sistemas

Muitos outros sistemas estudados apresentam propriedades semelhantes. O

pe-queno valorobservadoparaadistâniamédiaemrelaçãoaotamanhodos sistemasé

onsistenteom oprevistopelomodeloER.Noentanto,asredesreaisnormalmente

apresentam oeientes de agregação bem mais altos que os previstos por esse

mo-delo. Outro ponto em que o modelo ER falha é na distribuição de onetividade.

Osexemplosmostrados aimatêm distribuiçãode onetividadeemleide potênia.

Esse tipo de distribuição não aontee em todos os sistemas. As redes eológias

formadas pelas onexões predador-presa, por exemplo, obedeem uma distribuição

exponenial (CAMACHO; GUIMERA; AMARAL, 2002). Entretanto, distribuições em

lei de potênia são observadas em vários sistemas distintos, indiando um proesso

universal de formaçãopara esse tipo de rede. Também foramobservadas

distribui-ções em lei de potênia nas redes formadas pelas olaborações de atores em lmes

de inema (BARABÁSI; ALBERT,1999), na rede de olaborações emartigos

ientí-os (NEWMAN, 2001), enarede de relaçõessexuais naSuéia (LIJEROSetal.,2001),

dentre outras.

Um exemplo dentro do ampo da Físia foi observado no mapa de

onforma-çõesemagregados de partíulasqueinteragemvia potenialLennard-Jones(DOYE,

2002). Esse resultado foiobtido onstruindo-se o mapa de onformaçõesde um

sis-tema de 14 átomos. Omapa apresentamilharesde estadosque são mínimosloais.

Cada umdesses estadosétratadoomoumnónaredeeasonexõessão

estabelei-das seexiste apossibilidadedosistema seguirdiretamentede um mínimoaooutro.

de potênia om expoente

γ

= 2.78

.

1.9 Redes Neurais

Conluímos este apítulo introdutório om algumas notas histórias sobre

re-des neurais. A era moderna das redes neurais omeçou om o trabalho pioneiro

de MCulloh e Pitts (MCCULLOCH; PITTS, 1943). MCulloh foi um psiquiatra e

neuroanatomista por treinamento; passou era de 20 anos reetindo sobre a

re-presentação de um evento no sistema nervoso. Pitts foi um prodígio matemátio

que se assoiou a MCulloh em 1942. De aordo om Rall (1990), o artigo de

1943 de MCulloh e Pitts surgiu dentro de uma omunidade de modelagem

neu-ral em atividade na Universidade de Chiago por pelo menos ino anos antes de

1943, sob a liderança de Rashevsky. No seu artigo, MCulloh e Pitts desrevem

um álulo lógiodas redes neurais queuniava osestudos de neurosiologiae da

lógia matemátia. Eles supuseram que o modelo formal de um neurnio deveria

seguir umaleitudoounada. Comum númerosuientedessasunidades simplese

om onexões sináptias ajustadas apropriadamentee operandode formasínrona,

MCulloh e Pitts mostraram que uma rede assim onstituída realizaria, a

priní-pio, a omputação de qualquer função omputável. Este foi um resultado muito

signiativo, sendo reonheido omo o nasimento das disiplinas de redes

neu-rais e inteligênia artiial. Este trabalho inueniou von Neumann a usar haves

de atraso idealizadas, derivadas do neurnio de MCulloh-Pitts na onstrução do

EDVAC(Eletroni Disrete VariableAutomatiComputer)que foidesenvolvido a

partirdoENIAC(EletroniNumerialIntegratorandComputer)(AsprayeBurks,

1986). O ENIAC foi o primeiro omputador eletrnio de propósito geral, que foi

onstruído na Esola de Engenharia Elétria Moore da University of Pennsylvania

de 1943a1946. Ateoriade MCulloh-Pittssobreredesneuraisformaissedestaou

de formaproeminentenasegundadas quatropalestrasproferidasporvonNeumann

na University of Illinois em 1949. Em 1948, foi publiado o livro Cybernetis

de Wiener, desrevendo alguns oneitos importantes sobre ontrole, omuniação

e proessamento estatístio de sinais. A segunda edição do livro foi publiada em

1961, adiionando material novo sobre aprendizagem e auto-organização. Neste

desse assunto, mas foi om Hopeld (mais de 30 anos depois) que se onseguiu

onsumar aligação entre a meânia estatístia e ossistemas de aprendizagem.

O próximodesenvolvimentosigniativo das redes neurais veio em1949,om a

publiaçãodolivrode HebbTheOrganizationofBehavior,noqualfoiapresentada

pelaprimeiravezumaformulaçãoexplíitadeumaregradeaprendizagemsiológia

para amodiaçãosináptia. Espeiamente,Hebb propsqueaonetividadedo

érebro éontinuamentemodiadaonformeumorganismovaiaprendendotarefas

funionais diferentes e que agrupamentosneurais são riados por taismodiações.

Hebb deu seguimento a uma sugestão anterior de Ramón y Cajál e apresentou o

seu agora famoso postulado de aprendizagem, que arma que a eiênia de uma

sinapse variável entre dois neurnios é aumentada pela ativação repetida de um

neurnio ausadapelooutroneurnio, atravésdaquelasinapse. Oartigode

Rohes-ter, Holland,HaibteDuda(1956)talvez sejaaprimeiratentativadeusar simulação

omputaionalpara testar uma teoria sobre redesneurais bemformuladaom base

no postulado de aprendizagem de Hebb; os resultados de simulação relatados

na-quele artigo mostram laramente que se deve adiionar inibição para que a teoria

realmente funione. Naquele mesmo ano, Uttley (1956) demonstrou que uma rede

neural om sinapses modiáveis pode aprender a lassiar onjuntos simples de

padrões binários em lasses orrespondentes. Uttley introduziu o assim hamado

neurnio integra e disparaom fuga,o qualfoi mais tardeanalisado formalmente

porCaianiello(1961). Emumtrabalhoposterior,Uttley(1979)formulouahipótese

de que a eiênia de uma sinapse variável do sistema nervoso depende da relação

estatístia entre os estados utuantes em ambos os lados daquela sinapse, fazendo

assim umaassoiação om a teoriada informaçãode Shannon. Em 1952, foi

publi-ado o livro de Ashby, DesignforaBrain: The Origin of Adaptive Behavior. Este

livro trata da noção básia de que o omportamento adaptativo não é inato mas

sim é aprendido, e que através da aprendizagem o omportamento de um sistema

normalmenteevolui. Olivroenfatizaosaspetosdinâmiosdoorganismovivoomo

uma máquinae ooneito orrelaionadode estabilidade.

Em1954,Minskyesreveuumatesededoutoramentoemredesneurais na

Uni-versidade dePrineton,intituladaTheoryof Neural-Analog ReinforementSystems

and ItsAppliation to theBrain-ModelProblem. Em1961,foi publiadoumartigo

Intelli-gene, este artigo ontém uma grande seção sobre otema queagora é denominado

redes neurais. Em 1967, foi publiado o livro de Minsky, Computation: Finite and

InniteMahines. Estelivro,estendeu osresultadosde 1943deMCullohePittse

osoloounoontextodateoriadosautmatosedateoriadaomputação. Também

em 1954,a idéiade um ltroadaptativo não-linearfoi propostaporGabor,um dos

pioneiros da teoria da omuniação e o inventor da holograa. Ele onstruiu essa

máquina om a ajuda de olaboradores, e os detalhes estão desritos em Gabor et

al. (1960). A aprendizagem era realizada alimentando-se a máquina om amostras

de um proesso estoástio, juntamente om a função-alvo que a máquina deveria

produzir.

Nosanos50,iniiou-seotrabalhosobreamemóriaassoiativaporTaylor(1956).

ElefoiseguidoporSteinbruh(1961)queintroduziuamatriz de aprendizagem,esta

matrizonsistedeumaredeplanardehavesinterpostasentrearranjosdereeptores

sensoriais eatuadores motores. Em 1969,foi publiado porWillshaw, Buneman

e Longuet-Higgins um elegante artigo sobre a memóriaassoiativanão-holográa.

Este artigo apresenta dois modelos engenhosos de rede: um sistema ótio simples

realizando uma memória de orrelação e uma rede neural intimamenterelaionada

om ele, inspiradanamemóriaóptia. Outrasontribuiçõessigniativasao

desen-volvimento iniial da memória assoiativa inluem os artigos de Anderson (1972),

Kohonen (1972) e Nakano (1972), que de maneira independente e no mesmo ano

introduziram a idéia de uma memória por matriz de orrelação, baseada na regra

de aprendizagem ao produto externo.

Von Neumann foi uma das grandes guras da iênia na primeira metade do

séulo vinte. A arquitetura de vonNeumann, básiapara oprojetode um

omputa-dor digital, é assim denominada emsua homenagem. Em 1955, foi onvidado pela

Universidade de Yale para proferir as Palestras Silliman durante 1956. Ele morreu

em 1957, e omanusrito inaabado das Palestras Sillimanfoi publiado mais tarde

omo um livro,The Computer and the Brain (1958).

Umaquestãopartiularmenteinteressantenoontextodasredesneuraiséaquela

do projeto de uma rede onável om neurnios que podem ser vistos omo

om-ponentes não-onáveis. Este problema importante foi resolvidoporvon Neumann

a sugerir a utilização de uma representação redundante distribuída para as redes

neurais. WinogradeCowanmostraramomoumnúmerograndede elementospode

oletivamente representar um oneito individual, om o aumento orrespondente

em robustez e paralelismo.

Cera de 15 anos após a publiação do lássio artigo de MCulloh e Pitts,

uma nova abordagem para o problema de reonheimento de padrões foi

introdu-zida porRosenblatt(1958)emseu trabalhosobreopereptron,ummétodoinovador

de aprendizagem supervisionada. O oroamento do trabalho de Rosenblatt foi o

hamado teorema da onvergênia do pereptron, uja primeira demonstração foi

delineada por Rosenblatt (l960b); outras provas do teorema também apareeram

em Noviko (1963) e outros. Em 1960, Widrow e Hof introduziram o algoritmo

do mínimoquadradomédio(LMS, Least Mean-Square) eo usarampara formular o

Adaline (adaptive linear element, elemento linear adaptativo). A diferença entre o

pereptron e oAdaline está noproedimento de aprendizagem. Uma das primeiras

redesneuraisemamadastreináveisommúltiploselementosadaptativosfoia

estru-tura Madaline (multiple-adaline)proposta porWidrowe seus estudantes (Widrow,

1962). Em1967,Amariutilizouométododogradienteestoástioparalassiação

adaptativa de padrões. Em 1965, foi publiado o livrode Nilsson, Learning

Mahi-nes queainda é aexposição mais bemesrita sobre padrõeslinearmente separáveis

por hipersuperfíies. Durante o período lássio do pereptron nos anos 1960,

pa-reia que asredes neuraispoderiam realizarqualquer oisa. Mas então veio o livro

de Minsky e Papert (1969), que utilizarammétodos matemátios para demonstrar

que existem limites fundamentaispara aquilo que os pereptrons de amada únia

podem alular. Eles armavamque não havia razãopara supor quequalquer uma

das limitações do pereptron de amada únia poderia ser superada na versão de

múltiplasamadas.

Umproblema importanteenontrado noprojetode um pereptron demúltiplas

amadas é o problema de atribuição de rédito (i.e., o problema de atribuir

ré-dito a neurnios oultos da rede). A terminologia atribuição de rédito utilizada

primeiro por Minsky (1961), sob o título de O problema de Atribuiçãode Crédito

para Sistemas de Aprendizagem por Reforço. No nal dos anos 60, já havia sido

formulada a maioria das idéias e oneitos neessários para resolver o problema de

fundamen-tam as redes (neurais de atratores) reorrentes que são agora denominadas redes

de Hopeld. Entretanto, tivemos que esperar até os anos 80 para que emergissem

as soluçõespara esses problemas básios. De aordo om Cowan (1990) houve três

razões para este atraso de mais de 10anos:

•

Uma razão foi tenológia - não havia omputadores pessoais ou estações de

trabalho para aexperimentação. Quando Gabor, porexemplo, desenvolveu o

seu ltro não-linear de aprendizagem, seu grupo de pesquisadores levou mais

seis anos para onstruir o ltro om dispositivos analógios (Gabor, 1954;

Gabor et. al.,1960).

•

A outrarazãofoi empartepsiológia eemparte naneira. A monograade

1969 de Minsky e Papert ertamentenão enorajou ninguématrabalhar om

pereptrons,tampouo asagênias aapoiartrabalhos sobre eles.

•

A analogia entre redes neurais e spins de grade foi prematura. O modelo do

vidro de spins de Sherringtone Kirkpatrik foi inventado somente em1975.

Estes fatores ontribuíram de um modo ou de outro para o esmoreimento do

interesse ontinuado em redes neurais nos anos 70. Muitos pesquisadores, om

ex-eção daqueles que trabalhavam em psiologiae em neuroiênias, abandonaram a

área durante aquela déada. De fato, somente um punhado dos pioneiros originais

mantiveram seu omprometimento om as redes neurais. De uma perspetiva de

engenharia, podemos onsiderar os anos 70 omo uma déada de adormeimento

para asredes neurais. Umaatividadeimportanteque emergiunos anos 70foramos

mapasauto-organizáveisutilizandoaprendizagemompetitiva. Otrabalhoem

simu-lação omputaionalfeitoporvonder Malsburg(1973)talvez tenhasido oprimeiro

a demonstrar a auto-organização. Em 1976, Willshaw e von der Malsburg

publi-aram o primeiro artigo sobre a formação de mapas auto-organizáveis, motivados

pelos mapas ordenados de forma topológia do érebro. Nos anos 80, foram feitas

importantes ontribuiçõesemváriasfrentes àteoriaeaoprojetode redesneurais,e

omissohouveumressurgimentodointeressepelasredesneurais. Grossberg(1980),

baseando-se no seu trabalho anterior sobre aprendizagem ompetitiva (Grossberg,

1972, 1976a,b),estabeleeuumnovoprinípiodeauto-organizaçãoonheidoomo

a teoria envolve uma amada de reonheimento de baixo para ima (bottom-up)

e uma amada generativa de ima para baixo (top-down). Se o padrão de entrada

e o padrão realimentado aprendido oinidirem, então oorre um estado dinâmio

hamado de ressonânia adaptativa (i.e., ampliação e prolongamento da

ativi-dade neural). Este prinípiodeprojeçõespara frente/paratrásfoi redesobertopor

outros pesquisadores sob diferentes aspetos. Em 1982, Hopeld utilizoua idéia de

uma função de energia para formular um novo modo de se entender a omputação

exeutada porredes reorrentes om onexõessináptias simétrias. Alémdisso, ele

estabeleeu o isomorsmo entre uma rede reorrente assim denida e o modelo de

IsingutilizadonaFísiaEstatístia. Estaanalogiadesenadeouum grandeinteresse

da físia teória (e dos físios) pela modelagem neural, transformando om isso a

área de redes neurais. Esta lasse partiular de redes neurais om realimentação

atraiu muita atenção nos anos 1980, e no deorrer do tempo tornou-se onheida

omoredesdeHopeld. ApesardeasrededeHopeldnãoseremmodelosrealístios

dos sistemas neurobiológios, o prinípio que elas inorporam, isto é, o

armazena-mentode informaçãoemredes dinamiamenteestáveis, éprofundo. A origemdeste

prinípio remonta aotrabalhopioneirode muitos outros investigadores:

•

Cragg e Tamperley (1954, 1955) observaram que assim omo os neurnios

podem serdisparados (ativados) ou não disparados (quiesentes), também

osátomosemumaredetêmseus spinsapontandoparaima ouparabaixo;

•

Cowan (1967) introduziu a araterístia de disparo sigmóide e a ondição

de disparosuave para um neurnio que era baseada na função logístia;

•

Grossberg (1967, 1968) introduziu o modelo aditivo de um neurnio,

envol-vendo equações não-lineares de diferenças/difereniais e explorou o uso do

modeloomo uma base para a memóriade urtoprazo;

•

Amari (1972) introduziu, de forma independente, o modelo aditivo de um

neurnio e o utilizou para estudar o omportamento dinâmio de elementos

semelhantes aneurnios onetados aleatoriamente;

•

WilsoneCowan(1972)derivaramequaçõesdifereniaisnão-linearesaopladas