Integração de heurísticas lagrangeanas com algoritmos exatos para a otimização de de conjuntos

Centro de Ciênias

Departamento de Computação

Pós Graduaçãoem Ciênia da Computação

Mestrado em Ciênia da Computação

Integração de Heurístias Lagrangeanas om

Algoritmos Exatos para a Otimização de

Partiionamento de Conjuntos

Alexsandro de Oliveira Alves

Centro de Ciênias

Departamento de Computação

Mestrado em Ciênia da Computação

Integração de Heurístias Lagrangeanas om

Algoritmos Exatos para a Otimização de

Partiionamento de Conjuntos

Alexsandro de Oliveira Alves

(alexsandrolia.uf.br)

Dissertação submetida ao Programa de

Mestrado e Doutorado em Ciênia da

Computação da Universidade Federal

do Ceará omo requisito parial para

obtenção de grau de Mestre em Ciênia

da Computação.

Orientador: RafaelCastro deAndrade

Aos meus pais, peloapoio morale naneiro.

E,deformaespeial,àminhaesposa FatiéliaFrotapeloarinhoompartilhadoepelos

Em primeiro lugar, agradeço a Deus, meu únio e suiente Salvador, pelo dom da

vida. Agradeço por ser meu refúgio e minha proteção e por me dar disernimento e

serenidadenos momentosdeisivos daminha vida.

Agradeço aos meus pais por proporionarem a minha eduação e formação

aadêmia. Agradeço aos meus familiares pelos inentivos e por sempre estarem

dispostos a meajudar.

AgradeçoàminhaesposaFatiéliaFrota, peloamor,arinho,respeito, ompreensão

eompanheirismoque,juntamenteom abenção egraçade Deus, me sustentam eme

inentivama sempre areditar elutar pelos meus sonhose objetivos.

Agradeço a todos os professores da Universidade Federal do Ceará UFC e da

Universidade EstadualdoCearáUECE queforamresponsáveispelaminhaformação

aadêmia, e, em espeial, ao Prof. Maros José Negreiros Gomes que além de

eduadore professor,tornou-se um amigoque sempreareditouna minhaapaidade,

perseverançae seriedade. Sempre quedele preisamos, eleestá disposto aajudar.

Agradeço aomeu orientador Prof. RafaelCastro de Andrade,porter aeitadome

orientarapartirdosegundo anodoMestrado,apósdeisõesdifíeisedesaadorasque

tive quetomar. Agradeçoporsua orientação, apoioe ompreensão.

Agradeço aos membros da bana por terem aeito prontamente o onvite para

partiiparda omissãoexaminadora desta dissertação de Mestrado.

Agradeço aos meus olegas do grupo de pesquisa ParGO (Paralelismo, Grafos e

Otimização)edoLAB2pelatroadeexperiênias, emespeial aoÍtalo,AlineePablo

om quem tive maior proximidade.

Agradeço a todos os olegas e amigos da UECE, que junto omigo onstituíram a

eTenológio pelonaniamentoda minha bolsade estudos durante o Mestrado.

Neste trabalho avaliamos métodos heurístios e exatos para o Problema de

Partiionamento de Conjuntos (PPC). Realizamos testes omputaionais om

heurístias lagrangeanas baseadas em algoritmos gulosos, busa tabu e método de

otimizaçãopelosubgradiente. Osresultadosobtidos,omparadosomosdaliteratura,

omprovam a eiênia de nossas heurístias na obtenção de limites inferiores e

superiores de boa qualidade, em tempo omputaional razoável, para instânias da

literatura. Utilizamos um esquema de Branh and Bound para tentar resolver

instânias do PPC à otimalidade e para omprovar a qualidade dos resultados

alançadospornossas heurístias.

PALAVRAS CHAVE: Partiionamento de onjuntos. Busa tabu. Heurístias

In this work we evaluate both exat and heuristi methods for the set partitioning

problem (SPP). These heuristis are based on greedy algorithms, tabu searh and

subgradient optimization. Computational experiments performed on benhmark

instanes of the problem indiate that our heuristis are ompetitive with existing

ones from the literature in obtainingboth lower and upper bounds of good quality in

reasonableexeutiontime. WeuseaBranhandBoundalgorithmthatallowstoprove

optimalityofsolutionsobtainedbyourheuristisforalargesetofbenhmarkinstanes

oftheSPP.Thus,weshowthatourheuristisareeientinobtainingfeasiblesolutions

of goodqualityfor this problem.

KEYWORDS: Set Partitioning. Tabu Searh. Lagrangian Heuristis. Subgradient

Lista de Algoritmos ix

1 Introdução 1

2 Coneitos Básios 3

2.1 Problemade Partiionamentode Conjuntos . . . 3

2.2 Problemade Reobrimentode Conjuntos . . . 4

2.3 Problemade Paking . . . 4

2.4 Apliações . . . 5

2.5 Revisão Bibliográa . . . 6

3 Estratégias de Resolução 8 3.1 Ténias de Pré-proessamento . . . 8

3.1.1 Colunas iguais. . . 9

3.1.2 Linhas dominantes e linhas iguais . . . 9

3.1.3 Clique de linha . . . 10

3.2 Heurístia GulosaConstrutiva . . . 11

3.2.1 Critério de seleção de Chvàtal . . . 11

3.2.2 Critérios de seleção de Balas eHo . . . 12

3.2.3 Critérios de seleção de Vasko e Wilson . . . 12

3.3 Busa Tabu . . . 12

3.4 Relaxação Lagrangeana. . . 15

3.5 Heurístia de Otimização peloSubgradiente . . . 16

3.5.1 Subgradiente . . . 16

3.5.2 Otimização pelo subgradiente . . . 17

3.6 Heurístia LagrangeanaPura . . . 18

3.7 Heurístia Lagrangeanade Custo Complementar . . . 18

3.8 Algoritmo de Integração . . . 18

3.9 Branh and Bound . . . 19

4 Resultados Computaionais 24 4.1 Introdução . . . 24

4.2 Pré-proessamento . . . 25

4.3 MIP Cplex. . . 28

4.4 Busa Tabu . . . 30

4.7 Resultados da Literatura . . . 38

4.7.1 Algoritmo genétio . . . 38

4.7.2 Algoritmo função dual subaditiva . . . 40

5 Considerações Finais e Trabalhos Futuros 44

3.1 Algoritmo BusaTabu . . . 14

3.2 Ténias de redução e onstrução de solução viávelpara o PPC . . . . 19

3.3 Otimização pelo subgradientee heurístias lagrangeanas . . . 20

3.4 Branh-and-Bound . . . 22

Introdução

Neste trabalho apresentamos heurístias lagrangeanas baseadas em algoritmos

onstrutivos gulosos, meta-heurístia busa tabu e otimização pelo subgradiente para

obtenção de limites inferiores e superiores para o Problema de Partiionamento de

Conjuntos (PPC). Um esquema de Branh and Bound é empregado na tentativa de

provara otimalidadede soluções enontradas por nossasheurístias.

O PPC é um problema de otimização ombinatória NP-difíil [25℄ que possui

apliações prátias tais omo esalonamento de tripulação de linhas aéreas [32℄,

roteamento de veíulos [24℄, redistribuição polítia de território [43℄, loalização de

failidades[7℄, investimento de apitais eprojetode iruitoselétrios[43℄.

As prinipaismotivaçõespara a realizaçãodeste trabalhosão desenvolver métodos

apazes de obter boas soluções viáveis para o PPC, investigando om maior

profundidadeousode algoritmosmeta-heurístiosassoiadosaalgoritmosexatospara

resolverinstânias da literatura.

A inovação destetrabalhoestá naformaomoas ténias de resolução (algoritmos

gulosos,busatabuemétododeotimizaçãopelosubgradiente)foramorganizadaspara,

em onjunto,obter limitesinferiores e superiores de boa qualidadepara instânias da

literatura. Osresultados obtidos mostramque nossas heurístias são ompetitivasem

relaçãoàsexistentes naliteratura. Utilizamosumesquemade BranhandBound para

omprovara qualidadedos limitesobtidos por nossas heurístias.

Parte dos resultados heurístios deste trabalhoestão publiados em[2℄, tendosido

para aresolução desse problema.

O trabalho está organizado omo segue. No próximo apítulo denimos o PPC e

apresentamos sua formulação lássia de programação inteira. Destaamos uma ±erie

de apliações do PPC, que omprovam a importânia do seu estudo. Em seguida,

fazemos uma revisão bibliográa dos prinipais trabalhos que abordam o PPC. No

apítulo3abordamosasestratégias de resoluçãoeosalgoritmosqueutilizamospara o

PPC.Noapítulo4desrevemos osresultados omputaionaisobtidos,omparando-os

om resultados existentes na literatura. No apítulo 5 apresentamos uma onlusão e

Coneitos Básios

Neste apítulo iniialmente denimos o Problema de Partiionamento de Conjuntos

(PPC)e apresentamossua formulaçãolássia de programaçãointeira. Nasseções2.2

e2.3abordamosproblemasdeoberturarelaionadosaoPPC.Naseção2.4destaamos

as prinipais apliações do PPC. Na seção 2.5 fazemos uma revisão bibliográa dos

prinipaistrabalhos que abordamesse problema.

2.1 Problema de Partiionamento de Conjuntos

Seja

A

= [

a

ij

]m

×

n

uma matriz de elementos 01, onde

M

e

N

representam, respetivamente, o onjuntode índies das linhas e das olunas de

A

. Cada elemento

da matriz é igual a um (

a

ij

= 1

), se a oluna

j

obrir a linha

i

, ou é igual a zero (

a

ij

= 0

),aso ontrário. A ada oluna

j

assoiamosum usto

c

j

.

Seja

J

(

i

) =

{

j

|

a

ij

= 1

, j

∈ N }

o onjuntode olunasque obre alinha

i

∈ M

e

R

(

j

) =

_{

i

_|

a

ij

= 1

, i

∈ M}

oonjuntode linhas oberto pelaoluna

j

∈ N

.

Um partiionamentoé um onjunto de olunas

N

′

_{⊆ N}

, talque todalinha de

M

éoberta exatamenteporuma das olunas de

N

′

. A soluçãodoproblema onsisteem

min

x

∈{

0

,

1

}

n

n

X

j

=1

c

j

x

j

(2.1)

sujeito a:

n

X

j

=1

a

ij

x

j

= 1

, i

= 1

, . . . , m

(2.2)

onde atribuímos o valor

x

j

= 1

, se a oluna

j

∈ N

(om usto

c

j

) estiver na solução doproblema, e

x

j

= 0

, aso ontrário.

2.2 Problema de Reobrimento de Conjuntos

OProblemadeReobrimentodeConjunto(PRC)éumarelaxaçãodoPPC.Adiferença

entre eles reside exlusivamente na natureza das restrições dos problemas. O PRC é

denido pelaseguinteformulaçãode programação inteira 01 [30℄:

min

x

∈{

0

,

1

}

n

n

X

j

=1

c

j

x

j

(2.3)

sujeito a:

n

X

j

=1

a

ij

x

j

≥

1

, i

= 1

, . . . , m

(2.4)

Garnkel e Nemhauser [26℄ abordam um modelo matemátio que leva à

transformação de um PPC em um PRC, enquanto [33℄ mostram a onversão entre

esses problemas através de métodos algébrios.

2.3 Problema de Paking

OPPC,segundo[30℄,podeseronsideradoumasopartiulardoProblemadePaking

(PP), ujafomulaçãomatemátia é denida omo segue:

max

x

∈{

0

,

1

}

n

n

X

j

=1

c

j

x

j

(2.5)

sujeito a:

n

X

j

=1

OonjuntoderestriçõesdoPPondiionamaoberturadisjuntadaslinhasdamatriz

A

porumsubonjuntos desuasolunas. OmodelodoPPpossuigrandeapliaçãoprátia

na solução do problemas de ortes geométrios, aondiionamento de embalagens e

arregamento de veíulos. Ténias de onversão de um PPC em um PP podem ser

onsultadasem [30℄.

2.4 Apliações

Muitosproblemas de otimizaçãoombinatóriapodem ser modeladosomoum PPC, o

quejustia a variedade de áreas de apliaçãodesse problema, taisomo:

•

Aloação de serviços de emergênia [43℄.

•

Aloação de tripulação emlinhas aéreas [32℄.

•

Análisede amostrasde sangue[38℄

•

Balaneamento de apaidade emlinhas de produção [43℄.

•

Caminho emGrafos[30℄.

•

Distribuiçãodotráfego de omuniaçõesemsatélites [43℄.

•

Estoagem de itens sujeitos àdeterioração [30℄

•

Gestãoestratégia [26℄.

•

Investimentode apitais[43℄.

•

Loalizaçãode failidades [43℄.

•

Lógiasimbólia[17℄.

•

Planejamentode adeia de suprimentos [30℄.

•

Planejamentode tarefas [30℄.

•

Problemade oloração de grafos[30℄.

•

Problemade orte [30℄.

•

Projeto de iruitos[30℄.

•

Reuperaçãode informaçõesembano de dados [5℄.

•

Roteamento de petroleiros[23℄.

de tripulação em linhas aéreas é provavelmente a área de apliação mais estudada do

PPC [20℄. A variedade de apliações do PPC reete a importânia do estudo desse

problema, bemomo a busapormetodologiaseientes para soluioná-lo.

2.5 Revisão Bibliográa

Com relação ao problema de esalonamento de tripulação em linhas aéreas, itamos

os seguintes trabalhos. Lavoie, Minoux e Odier [36℄ apresentam um algoritmo que

aborda a aloação de tripulação omo um problema de reobrimento de onjuntos

e utiliza geração parial de olunas para soluioná-lo. Desaulniers et al [18℄ utiliza

um modelo de uxo de redes om reursos variáveis formulado omo um problema

de programação inteira, não linear e multi-produto. O autor aplia uma extensão do

prinípio da deomposição de Dantzig-Wolfe e reduz o problema para um PPC que

é resolvido pela apliação de um esquema de Branh and Bound. EmdenWeinert

e Proksh [19℄ apresentam uma abordagem para a programação de tripulações via

reozimento simulado (Simulated Annealing). Os autores abordam omo melhorar a

performanedessaheurístianoquedizrespeitoaotempodeexeuçãoeàqualidadeda

solução nal. Ozdemire Mohan [39℄ modelam o problema de aloação de tripulações

omo um grafo, no qual os vérties são os vos e as arestas representam restrições

de dependênia entre os vos. Cada aminho no grafo é uma seqüênia fatível de

vos que pode ser assoiada a uma tripulação. O autor aplia a esse modelo um

algoritmo genétio e uma heurístia de busa loal. Pimentel [40℄ propõe uma nova

metodologia para a solução de problemas de reobrimento de onjuntos de grande

porte,om apliaçãonoproblema de aloaçãode tripulaçõesde ompanhiasaéreas. A

autora apresenta uma formulação que divide a solução do problema em duas etapas:

geraçãoderotaseotimização. Naetapadeotimizaçãoédesenvolvidaumametodologia

para resolverproblemas modeladosomo um problema de reobrimentode onjuntos,

enquanto na etapa de geração de rotas é utilizado um algoritmo paralelo, baseado

na meta-heurístia GRASP [41℄. Beasley e Cao [11℄ apliam um algoritmo baseado

emprogramaçãodinâmiapara o problema de esalonamentode tripulaçãoem linhas

aéreas.

ComoexemplosdeestratégiasderesoluçãodoPPC,itamososseguintestrabalhos.

BalasePadberg[6℄destaamasténias deenumeração implíitaemétodosde planos

deortebaseadosnosimplexparaaresoluçãodoPPC.Marsten[37℄desreveasténias

de Branh-and-Bound e de Branh-and-Cut omo sendo as ferramentas, baseadas em

programaçãolinear,maispopularesentrepesquisadoresparasoluionaroPPC.Fleuren

heurístias ao problema dual da relaxação linear para forneer limites inferiores para

um esquema de Branh-and-Bound. Homan e Padberg [32℄ propõem um algoritmo

exato, baseado em Branh-and-Cut que envolve a relaxação linear do problema e a

inorporação de ortes derivados do estudo do politopo do PPC. Atamtürk et al [4℄

apresentamum algoritmoheurístio queinorporaredução doproblema,programação

linear, planos de orte, proedimento dual lagrangeano e ténias de perturbação

dos ustos. Chu e Beasley [15℄ desenvolvem uma heurístia baseada em algoritmos

genétios. Borndörfer [12℄ desenvolve um algoritmo baseado em Branh-and-Cut que

utiliza relaxação linear. Barahona e Anbil [8℄ utilizam um algoritmo de volume para

resolverarelaxaçãolineardoPPC,utilizandoumaextensãodoalgoritmodeotimização

pelosubgradiente, paraalançarsoluçõesprimaiseduaisdeboaqualidade. Segundoos

autores,esseproedimentoérápidoesimples,requerendomenoresforçoomputaional

quandoassoiadoaométodosimplex,epode ser paralelizadode formadireta. Klabjan

[35℄ apresenta um algoritmo que omputa função dual subaditiva (FSO) ótima para

problemas de programação inteira. Oautor mostra omo gerar FSO geradora e omo

obter solução primal ótima para o PPC, utilizando pré-proessamento, desigualdades

de lique, heurístia de expansão baseada em programação linear, proedimento de

geração de linhas e um esquema de Branh-and-Cut. Desigualdades válidas para o

PPC são enontradasem Balase Padberg [6℄ eem Sheralie Lee [43℄.

No próximo apítulo, abordamos as ténias de resolução heurístias e exatas que

Estratégias de Resolução

Iniialmente, abordamos ténias de pré-proessamento para o Problema de

PartiionamentodeConjuntos(PPC).Naseção3.2apresentamosumaheurístiagulosa

onstrutiva e as estratégias de seleção de olunas que adotamos para a obtenção de

soluçõesviáveisparaoproblema. Naseção3.3apresentamosumesquemadebusatabu

paraobtenção de limitessuperiores. Nasseções3.4e3.5abordamos, respetivamente,

umesquemaderelaxaçãolagrangeanaeumaheurístiadeotimizaçãopelosubgradiente

para obtenção de limites inferiores. Nas seções 3.6 e 3.7 apresentamos heurístias

lagrangeanas, que integram as ténias de resolução anteriores om o objetivo de

melhorar os limites obtidos para o PPC. Na seção 3.8 desrevemos o algoritmo de

integração utilizado. Na seção 3.9 abordamos o esquema de Branh and Bound que

adotamos para tentar soluionar oPPC àotimalidade.

3.1 Ténias de Pré-proessamento

Esquemas de pré-proessamento são proedimentos empregados na reformulação de

modelosde programaçãomatemátia,que podem reduzir asdimensões doproblema e

otempode exeução de algoritmosutilizadosnasua resolução. São ténias baseadas

emimpliaçõeslógias derivadas de ondiçõesde viabilidadee otimalidade[4℄.

Para o PPC, proedimentos de redução podem ser apliados para tentar reduzir

as dimensões do modelo de programação inteira, de modo que a solução ótima da

instâniadoproblema original sejaa mesma dainstâniareformulada. Pelaapliação

dessas ténias, olunas redundantes do PPC que jamais poderiam fazer parte de

uma solução viável são removidas. Isso pode, inlusive, resultar na eliminação de

restrições redundantes que são automatiamente satisfeitas quando outras o são. A

reduçãodonúmerodevariáveisede restriçõesaseremonsideradasfazomquealguns

métodos de resolução trabalhem melhor [12℄. No trabalhode Eso [21℄ é mostrado que

Em Borndörfer [12℄, há uma listagem de métodos de pré-proessamento e análises

probabilístiasdausabilidadedeles. Pesquisasreentessobreoempregodessasténias

para oPPC podem ser enontradas emSavelsbergh [42℄ eKlabjan[35℄.

Aseguirapresentamosasténiasdepré-proessamentoqueutilizamosparaoPPC.

3.1.1 Colunas iguais

Seuma oluna

j

∈ N

puderser representada porumaombinaçãode

k

outrasolunas

de menorusto total, talque

k >

0

, então a oluna

j

pode ser removidadoproblema. Considerando

S

⊂ N \

j

omosendoumaoleçãode

k

olunas,essaténiaderedução

pode ser formalmentedenida omosegue, segundo [44℄. Sejam

j

e

S

taisque

R

(

j

) =

[

h

∈

S

R

(

h

)

, onde

R

(

h1

)

∩ R

(

h2

) =

∅

,

∀

h1, h2

∈

S,

Se

c

j

≥

X

h

∈

S

c

h

então aoluna

j

∈ N

pode ser removida doproblema.

Utilizamos esse método de pré-proessamento partiularmente para

k

= 1

, para eliminarmos toda oluna

j

de usto

c

j

que seja igual à oluna

p

de usto

c

p

tal que

j, p

_{∈ N}

e

c

j

≥

c

p

. Não implementamos esse proedimento para valores de

k >

1

,

devidoaograndenúmerodeombinaçõesde olunasaseremanalisadas,queimpliaria

num maior usto omputaional.

No exemplo abaixo, mostramos uma instâniado PPC onde as olunas

j1

e

j6

são

iguais. A oluna

j6

é eliminada,uma vez que

c6

> c1

.

j1

j2

j3

j4

j5

j6

i1

1 0 1 0 0 1

i2

0 1 0 1 0 0

i3

1 0 1 1 1 1

i4

0 1 0 0 0 0

i5

1 0 0 0 1 1

c1

= 1

c2

= 3

c3

= 5

c4

= 2

c5

= 4

c6

= 6

3.1.2 Linhas dominantes e linhas iguais

p

podem ser eliminadasdo problema, bem omo a linha

p

, uma vez que os onjuntos

J

(

p

)

e

J

(

q

)

passama ser iguais, após aeliminaçãodas olunas de

J

(

q

)

\ J

(

p

)

[35℄.

A seguir mostramos um exemplo da apliação desse proedimento numa instânia

do PPC. Na tabela 3.1,

J

(

i5

)

⊆ J

(

i4

)

, então podemos eliminar a oluna

j1

, pois a atribuição dela à solução,

x1

= 1

, violariaa restrição assoiada à linha

i5

. Após a eliminaçãodaoluna

j1

,aslinhas

i4

e

i5

tornam-seiguaisealinha

i5

podesereliminada.

Natabela3.2, resultanteapósaseliminaçõesnatabela3.1,

J

(

i2

)

⊆ J

(

i3

)

. Asolunas

j2

e

j5

, que obrema linha

i3

mas não obrem a linha

i2

, podem ser eliminadas, bem

omoa linha dominada

i2

, resultando nainstâniapresente na tabela3.3.

Tabela 3.1:

j1

j2

j3

j4

j5

j6

i1

0 1 1 0 0 1

i2

1 0 0 1 0 1

i3

0 1 0 1 1 1

i4

1 0 1 1 0 0

i5

0 0 1 1 0 0

Tabela 3.2:

j2

j3

j4

j5

j6

i1

1 1 0 0 1

i2

0 0 1 0 1

i3

1 0 1 1 1

i4

0 1 1 0 0

Tabela 3.3:

j3

j4

j6

i1

1 0 1

i3

0 1 1

i4

1 1 0

3.1.3 Clique de linha

O nome desse método de pré-proessamento se deve ao fato de que uma instânia do

PPCpodeser representadaporum grafoGonexonão orientado [12℄,ondeosvérties

são as olunas

j

∈ N

. Há uma aresta interligando um par de vérties de G quando

elesobrempelomenosuma linhaemomum. Portanto,ada restriçãodoPPC éuma

lique em G e somente um vértie de ada lique pode estar presente numa solução

viáveldo problema.

Este proedimentode redução é denido omo segue, onforme [35℄. Se existir no

PPC uma linha

i

e uma oluna

j

, tais que

j /

∈ J

(

i

)

e

R

(

j

)

∩ R

(

k

)

6

=

∅

, para todo

k

_{∈ J}

(

i

)

, então podemos eliminaraoluna

j

.

AinstâniadoPPCaseguirilustraaapliaçãodesseproedimentoparaeliminação

de olunas. Na tabela 3.4, om relação à linha

i1

, temos o onjunto

J

(

i1

) =

{

j1, j2, j6, j7

_}

e seu omplemento

J

(

i1

) =

{

j3, j4, j5

}

. A oluna

j5

∈ J

(

i1

)

obre

pelo menos uma linha em omum om todas as olunas que obrem a linha

i1

.

Conseqüentemente, a oluna

j5

pode ser eliminada do problema, uma vez que a

atribuiçãodelaaumasoluçãodoPPC,

x5

= 1

,violariaarestriçãoassoiadaalinha

i1

. Atabela3.5mostraainstâniaapósaeliminaçãodaoluna

j5

. Omesmoproedimento

é apliado a todas as linhas da instânia à proura de olunas para eliminação que

j1

j2

j3

j4

j5

j6

j7

i1

1 1 0 0 0 1 1

i2

0 0 1 1 0 1 0

i3

1 0 1 0 1 0 1

i4

0 1 0 1 1 1 1

j1

j2

j3

j4

j6

j7

i1

1 1 0 0 1 1

i2

0 0 1 1 1 0

i3

1 0 1 0 0 1

i4

0 1 0 1 1 1

A seguir apresentamos um algoritmo guloso e as estratégias de seleção de olunas

adotadas para a obtenção de soluções viáveis, que posteriormente são utilizadas num

proedimentode busatabuparaenontrar limitessuperioresparainstâniasdoPPC.

3.2 Heurístia Gulosa Construtiva

Utilizamosuma heurístiagulosaonstrutivaqueutilizaritériosdeseleçãode olunas

para obtenção de soluções primais viáveis para o PPC. Tais ritérios provêm de

heurístiasdesenvolvidas por[5,16,45℄parao problemade reobrimentodeonjuntos.

A heurístia gulosa funiona omo segue. Iniialmente, nenhuma variável é

representada no vetor solução,

x

j

= 0

, j

∈ N

. Ordenamos as variáveis de aordo om o ritério seleionado, dentre os apresentados em 3.2.1, 3.2.2 e 3.2.3. A ada

iteração, seleionamos uma variável

r

para ompor uma solução viável (

x

r

= 1

). Como onseqüênia, toda oluna

k

∈ J

(

i

)

\

r

tal que a linha

i

∈ R

(

r

)

é eliminada doproblema. Esse proedimento terminaquando uma solução viável é enontrada ou

quandoveriamos queo ritériode seleção de olunasadotadonão obtém suessona

determinação de uma solução viável. Cada um dos ritérios de seleção de olunas é

avaliado separadamente pela heurístia e a soluçãoviável do PPC om menor usto é

utilizada,aso sejaenontrada.

Aseguirdesrevemososritériosde seleçãodeolunasimplementadosnaheurístia

onstrutiva gulosa parao PPC.

3.2.1 Critério de seleção de Chvàtal

O ritério de seleção de olunas de [16℄ onsiste na esolha de uma oluna

j

∈ N

do

PPC por iteração, para ompor uma solução viável, de aordo om a razão entre o

ustodaoluna

j

,

c

j

, ea ardinalidadedoonjunto

R

(

j

)

. Asolunas queapresentam menor razão e não violam as restrições do problema têm preferênia na seleção para

Osritériosde seleçãode [5℄onsistemnautilizaçãodas seguintes funçõesdeavaliação

de olunas:

•

c

j

: ordenação das olunas

j

∈ N

do problema pelo usto resente, dando

preferênia àsolunas de menor usto para ompor ovetor solução.

•

c

j

log2

(

k

j)

: ordenação das olunas

j

∈ N

doproblema pelarazão entre o usto da oluna

j

e ologaritmodo número de linhas obertas nabase

2

.

•

c

j

k

j

log2

(

k

j

)

: ordenação das olunas

j

∈ N

doproblema pela razão entre ousto

daoluna

j

e onúmero de linha obertas, multipliadopelologaritmonabase

2

destevalor.

•

c

j

k

j

ln

(

k

j

)

: ordenação das olunas

j

∈ N

do problema pela razão entre o usto

da oluna

j

e o número de linhas obertas, multipliadopelologaritmo natural

destevalor.

Nasfórmulas aima,

c

j

éo usto daoluna

j

e

k

j

éa ardinalidadedoonjunto

R

(

j

)

. 3.2.3 Critérios de seleção de Vasko e Wilson

Alémdas funçõesde avaliaçãomenionadas,utilizamostambémosritériosde seleção

de olunasde [45℄:

•

c

j

k

2

j

: ordenaçãodasolunas

j

∈ N

doproblemapelarazãoentreoustodaoluna

j

eo quadradodo número de linhas obertas.

•

√

_c

j

k

2

j

: ordenaçãodas olunas

j

∈ N

doproblemapelarazãoentrearaizquadrada

dousto daoluna

j

e oquadrado donúmero de linhas obertas.

ea seleçãode olunasde aordoom o índie resenteque as identia.

A solução enontrada pela heurístia gulosa menionada é parâmetro de entrada

paraa meta-heurístiabusa tabu, apresentada a seguir,que tem omoobjetivo obter

limitessuperiores para oPPC.

3.3 Busa Tabu

A meta-heurístia busa tabu (BT) ou tabu searh foi proposta, independentemente,

por [28℄ e por [31℄ e onstitui um proedimento iterativo para resolver problemas de

otimização ombinatória. A BT possui meanismos para esapar de ótimosloais, no

De aordo om [29℄, a BT parte de uma solução viável iniial

s0

∈

S

, onde

S

onstitui o onjunto de soluções viáveis do problema analisado. Em problemas de

minimização omo o PPC, a BT, a ada iteração, explora um subonjunto

V

da vizinhança

V

(

s

)

dasolução orrente

s

, embusa de um ótimo loalatravés daseleção da solução vizinha

s

′

_{∈ V}

de menor valor, mesmo que o valor de

s

′

seja maior que o

de

s

. A transição entre as soluções

s

→

s

′

, que oorre a ada iteração, onstitui o

que denominamosde movimento. Uma função de avaliação

f

é utilizada para avaliar

aqualidadedasoluçãoorrente

s

. Amelhorsoluçãogeradaaté aiteraçãoorrente,

s

∗

,

ésempre armazenada.

Para prevenir possíveis retornos a soluções previamente geradas (ilagem), a BT

utiliza uma memóriade urto prazo ou lista tabu, que identia os movimentosmais

reentementerealizados eosimpede deserem exeutadosporum determinadonúmero

|

T

_|

de iterações.

Movimentos presentes na lista tabu podem ser realizados, aso anova solução

s

′

_∈

V

(

s

)

satisfaça oritériode aspiração,quepermitearealizaçãode um movimentotabu

seelelevaraumasoluçãoujovalorsejamenordoqueodamelhorsoluçãoenontrada

até então,

s

∗

.

Alistatabuonstituiumamemóriadeurtoprazoquepossibilitaumadiversiação

na busa por novas soluções, à medida que direiona essa busa para novas áreas do

espaço de solução, permitindo a fuga de ótimos loais. Memórias de médio e longo

prazo também são utilizadas para armazenar soluções ompletas e informações de

suas vizinhanças. O uso desses meanismos de memória possibilita estratégias de

aprendizado, que podem ser utilizadas para a realização de busas mais minuiosas

sobre uma região promissora do espaço de busa (intensiação). O armazenamento

dos movimentos e das araterístias histórias das soluções alançadas leva a uma

análise profunda da vizinhança da solução orrente e guia a busa para regiões

inexploradasdo espaço de soluções(diversiação).

Oalgoritmo3.1mostraofunionamentodabusa tabuqueadotamos paraoPPC.

Os parâmetros de entrada são denidos omo segue.

f

é uma função de avaliação de

soluções.

h

é a função de aspiração que avalia se o melhor movimento da iteração

orrente,

Iter

,está nalista tabu edeterminaa suarealização seanovasoluçãogerada

tiver usto inferior ao da melhor solução onheida.

|V|

india a ardinalidade do

onjuntodesoluçõesexistentesnavizinhança

V

(

s

)

dasoluçãoorrente

s

aadaiteração.

BT

max

india onúmeromáximo de iteraçõessem melhorianousto damelhorsolução

viávelenontrada,queonstituioritériode paradaadotadonanossabusatabu.

A

e

c

são, respetivamente, amatriz de restriçõese ovetor de ustos das olunasdoPPC.

gulosa e dos ritérios de seleção de olunas abordados na seção 3.2, enquanto

p

é um

parâmetro perentual utilizado na análise da vizinhançada solução orrente

s

(busa

loal).

Algoritmo 3.1Algoritmo BusaTabu

Entrada:

f

,

h

,

|V|

,

|

T

|

,

BT

max

,

A

= [

a

ij

]m

×

n

,

c

∈

R

+

,

s

,

p

Saída: Limitesuperior

s

1:

s

∗

_←

_s

; /*solução iniial */

2:

Iter

←

0

; /* iteraçãoorrente */ 3:

MelhorIter

←

0

;

4:

T

← ∅

; /*lista tabu */

5: enquanto Condição de parada não é satisfeitafazer

6:

Iter

←

Iter

+ 1

;

7: Realizarbusaloalpara obteromelhormovimento

s

′

davizinhançadasolução

orrente,

V

(

s

)

, talque

s

′

não seja tabu (

s

′

_∈

_/

_T

) ou

f

(

s

′

₎

_{< h}

₍

_f

₍

_s

₎₎

;

8: Atualizara listatabu;

9:

s

←

s

′

; /*realiza movimento*/

10: se

f

(

s

)

< f

(

s

∗

₎

então

11:

s

∗

_←

_s

;

12:

MelhorIter

←

Iter

;

13: m se

14: Atualizara função de aspiração

h

;

15: m enquanto

16:

s

←

s

∗

;

17: Retorne

s

;

A BT, a ada iteração, seleiona o melhor movimento

s

→

s

′

, que não seja tabu

ou que satisfaça o ritério de aspiração. Na atualização da lista tabu, os movimentos

mais reentes são armazenadose impedidosde serem realizados durante

|

T

|

iterações,

exeto seo ritériode aspiração for satisfeito,e depoissão retiradosdalistatabu.

A melhor solução

s

′

esolhida é aquela om melhor avaliação na vizinhança da

solução orrente

s

, om relação ao valorda função objetivo, à listatabu e ao ritério

de aspiração. Realizamosuma busa loalna vizinhança

V

(

s

)

omo segue. A solução orrente

s

é formada por um subonjunto de olunas de

A

que onstitui uma solução

viável para o PPC. Seja

C

(

|

s

|

,

2)

o total de ombinações de pares de olunas de

s

dois a dois. Seja

s

¯

=

N \

s

. Seleionamos aleatoriamente

p

%

dos pares de olunas da solução orrente

s

que são utilizados na busa por troas entre olunas de

s

e de

¯

s

, onde

p

é um parâmetro de entrada. Uma oluna de

s

pode ser troada por duas

de

s

¯

ou duas olunas de

s

podem ser troadas por uma ou duas olunas de

s

¯

, desde que as olunas envolvidas nas possíveis troas ubram o mesmo onjunto de linhas.

Após a oleta de todos os movimentos possíveis, a BT seleionaaquele que apresenta

troas que proporionem redução no usto da solução orrente

s

. Dessa forma, os

movimentos promovem uma transição entre soluções viáveis do PPC a ada iteração

daBT, embusa de um ótimoglobal.

A melhor solução obtida pela BT onstitui um limite superior para o usto da

solução ótima do PPC e é utilizado omo parâmetro de entrada para a heurístia de

otimizaçãopelosubgradienteeparaasheurístiaslagrangeanasdenidasnaspróximas

seções.

3.4 Relaxação Lagrangeana

Uma alternativa à utilização da Relaxação de Programação Linear para o PPC é a

Relaxação Lagrangeana (RL) que onsiste na dualização das restrições de igualdade

do modelo de programação inteira, inorporando-as à função objetivo através de

multipliadores de Lagrange. A solução ótima do problema de programação inteira

resultante(problemalagrangeano)forneeumlimiteinferiordovalordasoluçãoótima

doPPC. Combase nolimiteinferior enontrado enum limitesuperior onheidopara

o usto da soluçãodo problema podemos avaliarquão próximo dasolução ótima está

umasoluçãoviável disponível. De aordoom[27℄, experiênias prátiastêmindiado

queaRL forneemuito bons limites inferioresom ustoomputaionalrazoávelpara

problemas de otimização ombinatória.

Considereaformulaçãodeprogramaçãointeiradesritaem(2.1)(2.2). Assoiando

ao onjunto de restrições (2.2) multipliadores de Lagrange

λ

∈

R

m

e, em seguida,

inorporandoesse onjuntode restriçõesàfunção objetivo(2.1),obtemosaformulação

doproblema relaxado:

L

(

λ

) = min

x

∈{

0

,

1

}

n

n

X

j

=1

c

j

x

j

+

m

X

i

=1

λ

i

1

−

n

X

j

=1

a

ij

x

j

!

(3.1)

queé equivalentea

L

(

λ

) = min

x

∈{

0

,

1

}

n

n

X

j

=1

c

j

−

m

X

i

=1

λ

i

a

ij

!

x

j

+

m

X

i

=1

λ

i

(3.2)

Oproblemaduallagrangeano,ujasoluçãoótimaforneeovalordosmultipliadores

de lagrangeque levamaolimite inferior máximo para o PPC, é dadopor:

max

λ

∈R

m

L(

λ

) = max

_λ

_∈R

m

[ min

_x

∈{

0

,

1

}

n

{

c

t

_x

_{+ (}

_λ

₎

t

₍

_e

−

A

x

)

_}

]

(3.3)

onde

e

∈

1

m

e

c

∈

R

n

+

éo vetor ujaomponente

c

j

é ousto daoluna

j

.

C

j

=

c

j

−

m

X

i

=1

λ

i

a

ij

,

j

= 1

, . . . , n

(3.4)

A solução

x

¯

∈ {

0

,

1

}

n

doproblema lagrangeano,dado

λ

¯

∈

R

m

, para

j

= 1

, . . . , n

, é dadapor:

¯

x

j

=







1

,

se

C

j

≤

0

0

,

aso ontrário;

(3.5)

e o valor orrespondente da solução do problema lagrangeano (limite inferior para o

PPC) édado por:

Z

LB

=

n

X

j

=1

C

j

x

¯

j

+

m

X

i

=1

¯

λ

i

(3.6)

A seguir apresentamos o método de otimização pelo subgradiente, apliado para

enontrar valores numérios para osmultipliadores de Lagrange para oPPC.

3.5 Heurístia de Otimização pelo Subgradiente

Iniialmentedenimossubgradienteparaoonjuntode restriçõesdoPPC.Emseguida

abordamosomeanismo de funionamento iterativodaotimização pelo subgradiente.

3.5.1 Subgradiente

Por denição, um vetor

g

= (

g1, g2, . . . , g

m)

t

é subgradiente de L em

λ

se, para todo

λ

_∈

R

m

,temos que L

(

λ

)

≤

L

(

λ

) + (

λ

−

λ

)

t

_g

[22℄.

OonjuntodesubgradientesdeLem

λ

éumonjuntoonvexodenotadopor

∇

L

(

λ

)

ehamadode subdiferenial de Lem

λ

. Emdeorrêniadisso, seosvetores

g

1

e

g

2

são

dois subgradientes em

λ

, então qualquer ombinação onvexa deles,

θ g

1

+ (1

₋

θ

)

g

2

,

para

θ

∈

[0

,

1]

, tambémé um subgradiente.

Proposição 1 Para

λ

∈

R

m

, sejam

S

o onjunto de soluções do PPC e

H

(

λ

) =

_{

x

ˆ

_{∈ S |}

L(

λ

) =

λ

t

_e

_{+ (}

_c

t

₋

_λ

t

_A

_{) ˆ}

_x

_}

. Para todo

x

ˆ

∈

H

(

λ

)

,

(

e

− A

x

ˆ

)

∈ ∇

L(

λ

)

. Logo

(

e

− A

x

ˆ

)

é um subgradiente de

L(

λ

)

[22℄.

Demonstração:

L(

λ

) =

min

{

λ

t

_e

_{+ (}

_c

t

₋

_λ

t

_A

₎

_x

_{} ≤}

_λ

t

_e

_{+ (}

_c

t

₋

_λ

t

_A

₎

_x,

_∀

_x

_{∈ {}

₀

_,

₁

_}

n

.

Para um dado

λ

∈

R

n

, e em partiular para

x

ˆ

∈

H

(

λ

)

, temos que:

L(

λ

)

_≤

λ

t

e

+ (

c

t

₋

_λ

t

_A

_{) ˆ}

_x

. Por denição de H(

λ

),

L(

λ

) =

λ

t

_e

_{+ (}

_c

t

₋

_λ

t

_A

_{) ˆ}

_x

.

L(

λ

)

₋

L(

λ

)

_≤

(

λ

t

₋

λ

t

₎

_e

₋

₍

_λ

t

₋

_λ

t

₎

_A

_x

_ˆ

_≤

₍

_λ

t

₋

_λ

t

_{) (}

_e

_−A

_x

_ˆ

₎

_≤

₍

_λ

t

₋

_λ

t

₎

_g,

_∀

_λ

_∈

R

m

.

Logo

g

= (

e

− A

x

ˆ

)

onstitui um subgradiente de

L(

λ

)

. Portanto

g

∈ ∇

L(

λ

)

.

Logo, o subgradientepara ada restrição relaxada doPPC é dado por

g

i

= 1

−

n

X

j

=1

a

ij

x

j

,

i

= 1

, . . . , m

(3.7)

3.5.2 Otimização pelo subgradiente

A otimização pelo subgradiente é um proesso iterativo que onsiste nadeterminação

de uma seqüênia de multipliadores de Lagrange, que se espera onvergir para um

vetor ótimo

λ

∗

_∈

_R

m

, solução do problema dual lagrangeano (3.3). A heurístia de

otimizaçãopelosubgradiente para oPPC é denida omo segue, segundo [10℄.

Partimos de um onjunto de multipliadores

λ

0

∈

R

m

, tal que

λ

0

= 0

. A ada

iteração

t

≥

0

atualizamos osmultipliadores de Lagrangede aordo oma expressão:

λ

t

+1

i

=

λ

t

i

+

tp

t

_g

t

i

,

i

= 1

, ..., m

(3.8)

onde

g

t

i

, ai-ésima omponentedo subgradiente

g

naiteração

t

,é dada por:

g

i

t

= 1

−

n

X

j

=1

a

ij

x

¯

j

,

i

= 1

, . . . , m

(3.9)

sendo

x

¯

a solução do problema lagrangeano 3.1 e 3.2.

tp

t

, o tamanho do passo na

iteração

t

, é dadopor:

tp

t

₌

_π













Z

U B

−

Z

LB

t

m

X

i

=1

(

g

t

i

)

2













(3.10)

onde

0

< π

≤

2

.

Z

U B

é o melhor limite superior para o problema, obtido pela busa tabu,e

Z

t

LB

é o valorda soluçãodoproblema lagrangeano naiteração

t

.

Após um número máximo de iterações sem arésimo no valor do melhor limite

inferior onheido, o parâmetro

π

é reduzido pela metade. Os ritériosde parada são

Z

U B

−

Z

LB

t

<

1

ou

π <

0

,

005

.

A heurístia lagrangeana pura (HLP) onsiste em assoiar às olunas do PPC o

usto reduzido obtido nas iterações da otimização pelo subgradiente [3℄. Apliamos

a heurístia gulosa onstrutiva e a busa tabu às instânias do PPC om os ustos

modiados, para tentar enontrar soluções viáveis de melhor qualidade. Quando

a HLP obtém um limite superior inferior ao melhor limite superior orrente,

Z

U B

é atualizado. A HLP éexeutada nas iterações daotimizaçãopelosubgradiente emque

o valor da solução do problema lagrangeano é maior do que o melhor limite inferior

orrente.

3.7 Heurístia Lagrangeana de Custo Complementar

A diferençaentre aHLP e aheurístia lagrangeanade usto omplementar (HLCC) é

que aquela utiliza omo usto da oluna

j

o valor

C

j

(usto reduzido), enquanto esta utiliza o valor

c

j

(1

−

x

¯

j

)

, para

j

= 1

,

2

, . . . , n

, onde

c

j

é o usto original da oluna

j

e

x

¯

j

é o valor da omponente

j

na solução do problema lagrangeano [3℄. Da mesma forma que na HLP, a heurístia gulosa e a busa tabu são apliadas às instânias

do PPC om os ustos das olunas modiados. O objetivo é utilizar informações

daestrutura da solução do problema lagrangeano, para tentar enontrar bons limites

inferiores esuperiores para as instânias do PPC. A HLCC é exeutada nas iterações

daotimizaçãopelosubgradienteemque ovalordasoluçãodoproblema lagrangeanoé

maiordo queo melhorlimite inferior orrente.

A seguir apresentamos algoritmosque ombinamas ténias disutidas nas seções

anteriorespara omporas heurístias lagrangeanaspara o PPC.

3.8 Algoritmo de Integração

Asténias de reduçãoe osmétodos heurístiosde onstruçãode soluçõesviáveispara

oPPC são apliadosonforme oalgoritmo3.2.

Iniialmente as ténias de pré-proessamento são apliadas para reduzir as

dimensões do PPC. Em seguida, apliamos os métodos heurístios de onstrução

de soluções viáveis. Avaliamos ada um dos ritérios gulosos de seleção de olunas,

desritos em 3.2.1, 3.2.2 e 3.2.3, em proedimentos distintos e utilizamos a solução

de menor usto obtida,

X

inicial

, omo parâmetro de entrada para a busa tabu, que proura obter uma nova solução viável om menor usto. O usto da melhor solução

viávelobtida onstituio limitesuperior

Z

U B

que éretornado peloalgoritmo3.2. A otimização pelo subgradiente, assoiada às heurístias lagrangeanas, é desrita

Entrada: Matriz

A

= [

a

ij

]m

×

n

de elementos01, vetor de ustos

c

∈

R

n

+

Saída: Limitesuperior

Z

U B

1: /* Pré-proessamento*/

2: Apliação doproedimento paraolunas iguais

3: repetir

4: Apliaçãodos proedimentospara linhas dominantes elinhas iguais

5: Apliaçãodo proedimentopara lique de linha

6: até não haver eliminaçãode linhas ouolunas

7: /* Métodos heurístios de onstrução*/

8: Exeutar proedimentos de onstrução de soluções viáveis, a partir dos ritérios

gulosos de seleção de olunas.

X

inicial

onstitui a melhor solução enontrada om usto

c

X

9: /* BusaTabu */

10: Exeutarabusatabu quereebeasolução

X

inicial

eretornaolimitesuperior

Z

U B

obtidos, respetivamente.

t

india a iteração orrente,

cont

é um ontador para a

quantidade de iterações sem melhoriano valorde

Z

LB

. O valorde

π

é reduzido pela metade, quando

cont

atinge o valor máximo

α

, que india a quantidade limite de

iterações sem melhoria no valor do melhor limite inferior orrente. Nas iterações da

otimização pelo subgradiente em que o valor da solução do problema lagrangeano é

maior do que

Z

LB

, apliamos a HLP ou a HLCC, para tentar reduzir o GAP entre

Z

U B

e

Z

LB

doPPC.

De aordo om o algoritmo 3.3, na primeira iteração da otimização pelo

subgradiente, atribuímos ao vetor de multipliadores de Lagrange o valor

λ

= 0

. Iniialmenteo parâmetro de relaxação

π

assume ovalor

2

.

Nas iterações da otimização pelo subgradiente, quando um dos omponentes do

vetor de multipliadores de Lagrange

λ

i

, para

i

= 1

, . . . , m

, for nulo e o subgradiente orrespondente for negativo, então realizamos a projeção do valor do subgradiente

para zero. Segundo [10℄ essa projeção é neessária para que o fator do subgradiente

não interra no álulo do tamanho do passo, o que favoree a onvergênia para

λ

∗

naotimização pelosubgradiente.

Os ritérios de parada adotados foram valor de

π <

0

.

005

ou

Z

U B

−

Z

LB

<

1

. A seguirabordamos oesquema de Branh and Bound queadotamos para oPPC.

3.9 Branh and Bound

OBranhandBound(B&B)realizaumpartiionamentoiterativodoespaçodesoluções

S

do PPC em subproblemas, talque

S

é denido peloonjunto de restrições

A

x

= 1

e

x

∈ {

0

,

1

}

n

Entrada: Matriz

A

= [

a

ij

]m

×

n

, vetor de ustos

c

∈

R

n

+

, limite superior

Z

U B

,

α

. Saída: Limitesuperior

Z

U B

, limite inferior

Z

LB

.

1:

t

←

0

;

π

←

2

;

λ

t

i

←

0

;

g

t

i

←

1

,

i

= 1

, . . . , m

;

Z

U B

←

Z

U B

; 2:

C

t

j

←

c

j

,

j

= 1

, . . . , n

;

Z

t

LB

←

0

;

Z

LB

←

0

;

tp

t

é dado pela equação (3.10);

cont

←

0

; 3: repetir

4: Atualizarmultipliadores de Lagrange

λ

t

+1

i

,

i

= 1

, . . . , m

, por(3.8); 5: Calularusto reduzido

C

t

+1

j

,

j

= 1

, . . . , n

, por(3.4); 6: Obter solução

x

¯

doproblema lagrangeano por (3.5); 7: Calularsubgradiente

g

t

+1

i

,

i

= 1

, . . . , m

,por(3.9); 8: se

g

t

+1

i

<

0

e

λ

t

+1

i

= 0

então

9:

g

t

+1

i

←

0

; 10: m se

11: Calularusto do problema lagrangeano

Z

t

+1

LB

por(3.6); 12: se

Z

t

+1

LB

>

Z

LB

então 13:

Z

LB

←

Z

t

+1

LB

; 14:

cont

←

0

;

15: Exeutarheurístia lagrangeana, que retornalimite superior

Z

U B

; /*HLP ouHLCC */

16: se

Z

U B

< Z

U B

então 17:

Z

U B

←

Z

U B

;

18: m se

19: senão

20:

cont

←

cont

+ 1

; 21: se

cont

=

α

então 22:

π

←

π/

2

;

23:

cont

←

0

;

24: m se

25: m se

26: Calulartamanho do passo

tp

t

+1

por(3.10);

27:

t

←

t

+ 1

;

B&B, sendo

S

R

=

{

x

∈

R

n

_{| A}

_x

_{= 1}

_,

₀

_≤

_x

_≤

₁

_}

oonjunto de soluções doproblema

relaxado.

O funionamento do B&B para um problema de minimização é apresentado pelo

algoritmo 3.4, onde L denota a lista de subproblemas (nós) ativos

{

NO

i

}

e NO

0

é o

nó raiz, ou seja, é a relaxação linear do problema inteiro original.

z

i

denota o limite inferior orrespondente ao valor da relaxação linear do subproblema NO

i

.

z

ub

denota o valor da melhor solução inteira viável onheida do problema original.

z

lb

denota o valor do melhor limite inferior obtido através da relaxação linear dos nós gerados

naárvore de B&B.

x

i

denota a solução da relaxação linear de NO

i

. Iniialmente,

z

ub

assume o valor de

Z

U B

, melhor limite superior obtido pela exeução das heurístias lagrangeanas.

O algoritmo B&B é tipiamente visto omo uma árvore de busa. A árvore

é onstruída iterativamente através da formação de novos nós por um proesso de

ramiação(branhing)deumnó

k

existente, paraoqualasoluçãoótimadarelaxação

é fraionária. Nesse proesso dois nós lhos são formados a partir da seleção de uma

das variáveis

x

j

de valorfraionário (variável de branhing). Os nós lhos são riados a partir da xação de

x

j

em 1 e em 0, respetivamente, no intuito de assegurar que o onjunto de restrições assoiado aos nós lhos de

k

não inlua soluções nas quais a

variávelde branhing esolhida assumao mesmo valorfraionário.

A etapa denominada poda é utilizada omo ritério para avaliar se um nó da

árvore nãoneessita serexplorado. Classiamosum nóomo fathoming nas seguintes

situações:

•

Inviabilidade: quandopelomenos umadas restriçõesdomodelode programação

linearé violada.

•

Bound: quando o valor da sua relaxação linear é maior ou igual ao valor da

melhorsolução inteira viávelonheida (

z

ub

);

•

quando o valor da relaxação linear do nó é inteiro e esse valor é inferior

z

ub

.

Nesse aso, atualizamos

z

ub

para assumir o valor

z

i

e removemos de L todos os subproblemas

j

om

z

j

≥

z

ub

.

Realizamosa poda dos nós onsideradosfathoming para tentarobter a solução ótima

eprovar aotimalidade sem uma busa exaustivano espaçode soluções doproblema.

O

B

&

B

termina quando todos os nós são fathoming ou quando enontramos um nódaárvoreujasoluçãoéinteiraetemvalor(limiteinferior)igualaovalordomelhor

1: /* Iniialização*/

L

← {

NO

0

}

;

z0

←

0

;

z

lb

←

0

;

z

ub

←

Z

U B

;

opt

←

0

;

2: /* Condiçõesde parada*/

3: enquanto

L

6

=

∅

ou

opt

= 0

fazer

4: Seleionar eremoverum subproblema NO

i

de L, talque

i

≥

0

; 5: Computar arelaxação linear de NO

i

, ujovaloré

z

i

; 6: se

z

i

> z

ub

então

7: Irpara passo 3; /* poda */

8: m se

9: se

z

i

> z

lb

então 10:

z

lb

←

z

i

; 11: m se

12: se

x

i

for uma soluçãointeiraentão 13: se

z

i

< z

ub

então

14:

z

ub

←

z

i

;

15: Remover de L todos ossubproblemas

j

om

z

j

≥

z

ub

; /* poda */

16: m se

17: se

z

ub

=

z

lb

então 18:

opt

←

1

;

19: m se

20: senão

21: /*Partiionamento*/

Seja

{

S

ij

_}

j

=2

j

=1

um partiionamento do onjunto de restrições

S

i

do problema

{

NO

i

}

. Adiionaros problemas

{

NO

ij

}

j

j

=2

=1

a L,seforemviáveis, onde

{

NO

ij

}

éNO

i

om região de viabilidaderestrita a

{

S

ij

_}

;

22: m se

23: m enquanto

24: se

opt

= 1

então 25:

x

∗

, referente à melhorsolução inteira viável,é solução ótimaom valor

z

ub

; 26: senão se existir

x

,referente àmelhor soluçãointeira viável então

27: a solução

x

é retornada om valor

z

ub

; 28: senão

29: o problema éinviável;

branhing. Como ritério de seleção de nós adotamos o best bound, que onsiste em

esolher, entre todos os nós inexplorados de L, aquele que apresenta menor valor de

limiteinferior.

Para implementar a listade nós não exploradosL,utilizamosaestrutura de dados

heap na qual os nós am dispostos em um vetor e o nó de menor limite inferior a

situado na abeça do heap, tendo maior prioridade na seleção do próximo nó a ser

analisadopeloB&B.

A seguir abordamos os resultados omputaionais obtidos pelas estratégias de

Resultados Computaionais

Nesteapítuloabordamososresultadosomputaionaisalançadospelasestratégiasde

resolução apresentadas no apítulo anterior. Iniialmente, desrevemos as instânias

do PPC que utilizamos neste trabalho e o resultado da apliação das ténias de

pré-proessamentosobreelas. Naseção 4.3apresentamososresultados daexeuçãoda

rotina CPXmipopt da Cplex Callable Library para resolver instânias do PPC. Na

seção 4.4 desrevemos os resultados da meta-heurístia busa tabu. Na seção 4.5

apresentamos os limites superior e inferior alançados pelas heurístias lagrangeanas.

Na seção 4.6 abordamos os resultados alançados pelo Branh and Bound. Na seção

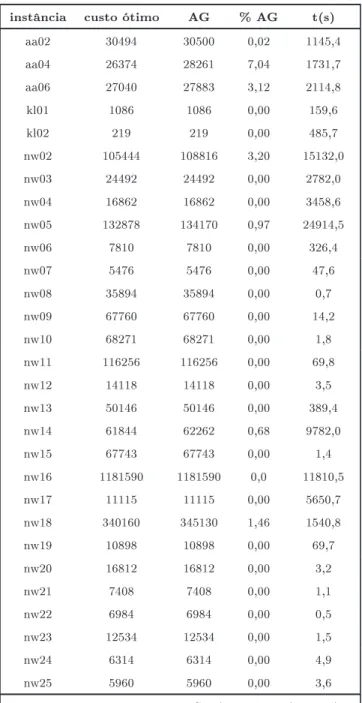
4.7 omparamos os resultados obtidos pelas heurístias lagrangeanas om resultados

existentes naliteratura.

4.1 Introdução

Asténias de pré-proessamento, asheurístias onstrutivagulosa elagrangeanase o

esquema de Branh and Bound apresentados foram implementados om a linguagem

deprogramação C++nosistemaoperaionalGNULinux. Para omputar arelaxação

linearno esquemade Branh and Bound,utilizamosoCplex [1℄. A máquinautilizada

paraarealização dostestes dosalgoritmospossui umproessador Pentium IV de3000

MHze 512 MB de memóriaRAM DDR2.

Os algoritmos implementados foram utilizados para resolver 54 instânias de

HomanePadberg[32℄paraoPPC,presentesnaOR-Library[9℄. Ovalordadensidade,

relação entre a quantidade de elementos

a

ij

= 1

e o total de elementos da matriz

A

, araterístiadoPPC,variaentre0,99%e36,90%,oquemostraoquantoasinstânias

doPPC utilizadassão espaças.

Emvirtudedelimitaçãodereursodememóriafísia,nãofomosapazesderesolver

Nas tabelas queseguem utilizamosa seguintelegenda:

instânia identiadordasinstâniasde[32℄

linhas númerodelinhasdainstâniadoPPCanterioràapliaçãodopré-proessamento

olunas númerodeolunasdainstâniadoPPCanterioràapliaçãodopré-proessamento

linhasPP númerodelinhasdainstâniadoPPCapósapliaçãodopré-proessamento

olunasPP númerodeolunasdainstâniadoPPCapósapliaçãodopré-proessamento

%linha perentualdonúmerodelinhaseliminadasnopré-proessamento

%olunas perentualdonúmerodeolunaseliminadasnopré-proessamento

pClique parâmetroutilizadonaténiadereduçãoliquedelinhas

ustoótimo ustodasoluçãoótimaobtidopeloMIPCplex

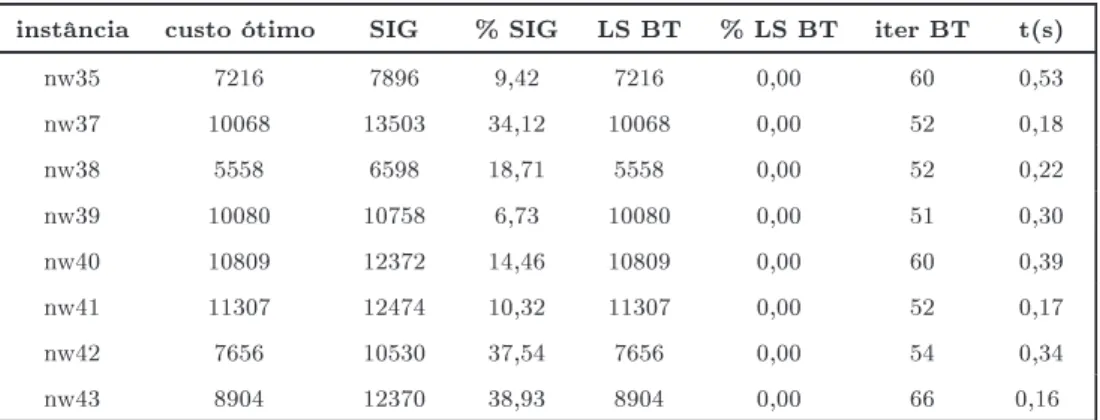
SIG valordasoluçãodaheurístiagulosaonstrutiva

%SIG diferençarelativaentreSIGeoustoótimo

LSBT limitesuperiorobtidopelabusatabu

%LSBT diferençarelativaentreLStabueoustoótimo

iterBT númerodeiteraçõesexeutadasnabusatabu

LSHL limitesuperiorobtidopelasheurístiaslagrangeanas

%LSHL diferençarelativaentreLSHLeoustoótimo

LIHL limiteinferiorobtidopelasheurístiaslagrangeanas

%LIHL diferençarelativaentreLIHLeoustoótimo

GAP diferençarelativaentreLSHLeLIHL

nIOS númerodeiteraçõesexeutadasdaotimizaçãopelosubgradiente

estimativaLS estimativadelimitesuperior

%estimativaLS diferençarelativaentreestimativaLSeoustoótimo

iterMIP númerodeiteraçõesdosimplex

nNodes númerodenósusadopararesolveroproblemainteirodoPPC

nCortes númerodeortesdeliqueadiionadosduranteaotimizaçãopeloCplex

nDesigualdades númerodedesigualdadesdeliquegeradaspeloCplex

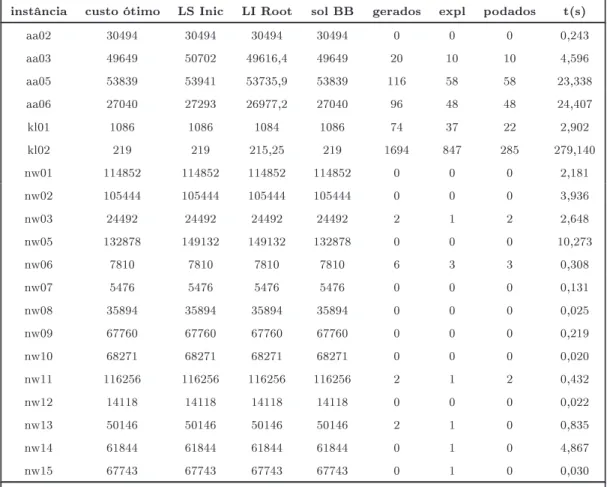
LSIni limitesuperioriniialparaoBranhandBound

LIRoot limiteinferiorobtidonaotimizaçãodonóraizdoBranhandBound

solBB soluçãoobtidapeloBranhandBound

gerados númerodenósgeradosduranteexeuçãodoBranhandBound

expl númerodenósexploradosduranteexeuçãodoBranhandBound

inexpl númerodenósinexploradosduranteexeuçãodoBranhandBound

t(s) tempodeexeução(CPU)emsegundos

4.2 Pré-proessamento

As ténias de pré-proessamento foram apliadas onforme o algoritmo 4.1.

Iniialmente,apliamosoproedimentode eliminaçãode olunasiguaise,emseguida,

de forma iterativa, apliamos os proedimentos de linhas dominantes, linhas iguais e

Entrada: Matriz

A = [

a

ij

]m

×

n

, vetor de ustos

c

∈

R

n

+

, pClique

Saída: Matriz

A = [

a

ij

]m

×

n

om quantidademenor ouigual de linhas ede olunas 1: Apliar proedimentode olunas iguais

2: repetir

3: Apliar proedimentode linhasdominantes eiguais

4: Apliar proedimentode lique de linha

5: até não haver eliminaçãode linhas ouolunas

Atabela4.1apresentaonúmero de linhasede olunasdamatriz

A

= [

a

ij

]m

×

n

das instânias do PPC antes e depois da apliação dos métodos de pré-proessamento,

bem omo a perentagem de eliminação desses elementos em relação ao total. O

parâmetro de entrada pClique é determinado empiriamente para o proedimento

lique de linha (3.1.3) e india a quantidade máxima de olunas que devem obrir

umalinhapara queestasejaonsideradanoproesso de busaporolunasquepodem

sereliminadas. Deaordoomtestesexperimentaisrealizados,aapliaçãodasténias

de pré-proessamento om valorde parâmetro pClique maior que o informado resulta

namesma quantidade de linhas e de olunas eliminadas, mas pode exigir maiorusto

omputaional. O valor de pClique igual a zero india que o proedimento lique de

linhas não eliminalinhas ou olunasnas instânias onsideradas.

Osresultados omputaionais apresentados natabela4.1mostramque aapliação

dos métodos de pré-proessamento na maioria das instânias do PPC analisadas

promovem reduções signiativas no número de variáveis (olunas) e de restrições

(linhas)doproblema. Emmédia5,91%das linhase27,35%das olunassão eliminadas

naapliaçãodas ténias de pré-proessamento. Destaamos osresultados obtidosem

us02 onde houve a eliminação de 55% das linhas e em us04, onde houve redução de

84,98%das olunas.

Tabela4.1InstâniasdeHomanePadberg[32℄

instânia linhas olunas linhasPP %linhas olunasPP % olunas pClique t(s)

aa01 823 8904 617 25,03 7544 15,27 308 6,78

aa02 531 5198 362 31,83 3848 25,97 179 1,84

aa03 825 8627 553 32,97 6707 22,26 176 6,76

aa04 426 7195 343 19,48 6123 14,90 144 1,98

aa05 801 8308 533 33,46 6246 24,82 167 4,44

aa06 646 7292 504 21,98 5902 19,06 199 5,03

kl01 55 7479 47 14,54 5915 20,91 1192 1,19

kl02 71 36699 69 2,82 16542 54,93 0 0,10

nw01 135 51975 135 0,00 49903 3,99 630 1,37

nw02 145 87879 145 0,00 85256 2,98 993 2,25