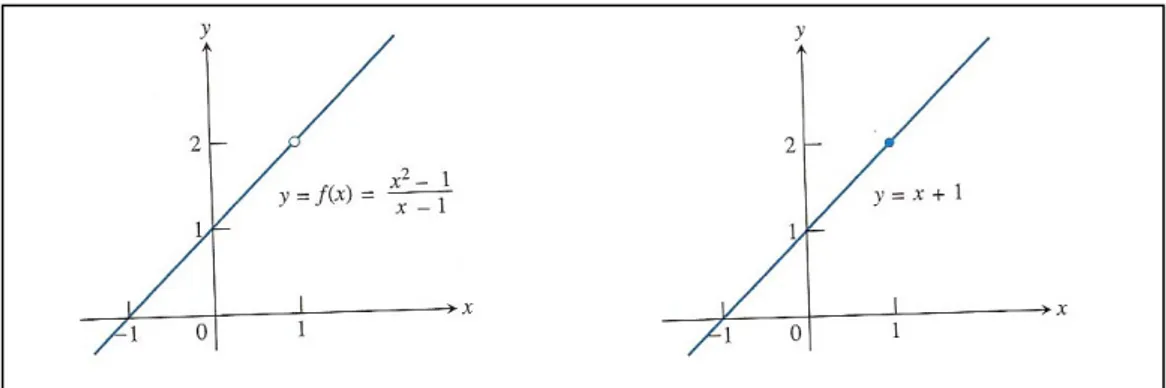Lílian Isabel Ferreira Amorim
A (RE) CONSTRUÇÃO DO CONCEITO DE LIMITE
DO CÁLCULO PARA A ANÁLISE:
UM ESTUDO COM ALUNOS DO CURSO DE
LICENCIATURA EM MATEMÁTICA
Lílian Isabel Ferreira Amorim
A (re)construção do conceito de Limite
do Cálculo para a Análise:
Um estudo com alunos do curso de
Licenciatura em Matemática
Dissertação apresentada à Banca Examinadora, como exigência parcial à obtenção do Título de Mestre em Educação Matemática pelo Mestrado Profissional em Educação Matemática da Universidade Federal de Ouro Preto, sob orientação do Prof. Dr. Frederico da Silva Reis.
OURO PRETO
Catalogação: sisbin@sisbin.ufop.br
A524r Amorim, Lílian Isabel Ferreira.
A (re)construção do conceito de limite do cálculo para a análise [manuscrito] : um estudo com alunos do curso de licenciatura em matemática / Lílian Isabel Ferreira Amorim. – 2011.
133 f.: il., color.; graf.; tabs.; quadros.
Orientador: Prof. Dr. Frederico da Silva Reis.
Dissertação (Mestrado) - Universidade Federal de Ouro Preto. Instituto de Ciências Exatas e Biológicas. Departamento de Matemática.
Área de concentração:Educação Matemática.
1. Matemática - Estudo e ensino - Teses. 2. Cálculo - Estudo e ensino - Teses. 3. Cálculo diferencial - Teses. 4. Limites - Teses. 5. Ensino superior - Teses. I. Universidade Federal de Ouro Preto. II. Título.
UNIVERSIDADE FEDERAL DE OURO PRETO
INSTITUTO DE CIÊNCIAS EXATAS E BIOLÓGICAS DEPARTAMENTO DE MATEMÁTICA
Mestrado Profissional em Educação Matemática
DISSERTAÇÃO DE MESTRADO
A (re)construção do conceito de Limite
do Cálculo para a Análise:
Um estudo com alunos do curso de
Licenciatura em Matemática
Autor: Lílian Isabel Ferreira Amorim
Orientador: Frederico da Silva Reis
Este exemplar corresponde à redação final da Dissertação defendida por Lílian Isabel Ferreira Amorim e aprovada pela Comissão Examinadora.
Data: 26 de agosto de 2011
Assinatura:...
Orientador
COMISSÃO EXAMINADORA:
______________________________________________ Prof. Dr. Carlos Alberto Santana Soares (UFJF)
_______________________________________________ Profª. Dra. Marger da Conceição Ventura Viana (UFOP)
AGRADECIMENTOS
A Deus, princípio e fim de todas as coisas, por me permitir chegar até aqui!
Aos meus pais, Vicente e Joaninha, gênese de toda a minha vida, responsáveis pela pessoa que sou hoje. Obrigada pela dedicação, pelo incentivo e pelas orações constantes.
Ao meu esposo, Jeremias, pelo companheirismo, fazendo valer a expressão do latim cum paines, aquele que divide o pão, neste caso especial, o pão saboroso da descoberta e o pão amargo da ausência. Amo você!
Aos meus irmãos: Claudenise, César e Nara, pelo apoio, pelo desejo sincero de que tudo desse certo. Obrigada!
Aos sobrinhos, cunhados, tios, primos e amigos, obrigada pela torcida!
Às babás: Dona Cleide, Benta e Dany, a quem confiei Samuel, o meu bem mais precioso. Obrigada porque foram a extensão do meu olhar, do meu braço e do meu colo...
Kelly, obrigada por tudo, pelo convívio, pelas partilhas, pelos estudos, com certeza, tudo isso fez esta caminhada mais agradável! A sua amizade foi o presente mais precioso deste percurso.
Aos amigos Daniel e Osvaldo, integrantes do “Quarteto Fantástico”, a amizade construída nessa trajetória. Aprendi muito com vocês!
A todos os colegas da minha turma e das outras turmas que tive a grata satisfação de conviver, obrigada pelo companheirismo.
Alexandre e Carmem, passageiros da mesma estrada, longa estrada! 506 km para ser mais precisa, suficiente para partilharmos risos, lágrimas, saudades, histórias, VIDA, suficiente para fazer de nós bons amigos.
Ao ISEIB, colegas e alunos, agradeço a oportunidade da realização deste trabalho e a contribuição valiosa no meu crescimento pessoal e profissional.
À coordenadora do Mestrado, Ana Cristina Ferreira, cuja dedicação e presteza são essenciais para o bom êxito do Programa e para o nosso desenvolvimento profissional. Obrigada pelo exemplo!
A todos os professores do Mestrado que contribuíram para minha formação profissional.
A Carlos Soares e Marger Viana, agradeço as importantes contribuições dadas ao meu trabalho e, de maneira geral, a valiosa contribuição à Educação Matemática.
RESUMO
Esta pesquisa discutiu, de forma geral, o ensino de Cálculo e de Análise na perspectiva da Educação Matemática Superior e, especificamente, investigou o papel das imagens conceituais e definições conceituais para a aprendizagem de Limites de Funções Reais de uma Variável. A natureza da pesquisa priorizou os aspectos qualitativos, preponderantes sobre os aspectos quantitativos. A pesquisa justifica-se já que diversos trabalhos vêm evidenciando os obstáculos epistemológicos em relação ao conceito de limite e ainda, a necessidade de se realizarem pesquisas que discutam a transição do Cálculo para a Análise. Formulamos a seguinte questão de investigação: Como uma proposta de ensino, baseada nas imagens conceituais, relacionadas ao conceito de limite de uma função, (re)construídas por alunos do curso de Licenciatura em Matemática, após cursarem Análise Real, pode contribuir para a aprendizagem desses alunos? O referencial teórico foi primordialmente baseado nos trabalhos de David Tall, Shlomo Vinner, Bernard Cornu, Márcia Pinto e Frederico Reis. As atividades foram realizadas pelos sujeitos de pesquisa, alunos do curso de Licenciatura em Matemática, dentro da disciplina Análise Real. A pesquisa teórico-bibliográfica contemplou o ensino de Cálculo e de Análise e o Pensamento Matemático Avançado. Apresentamos também a abordagem do conceito de limites em livros didáticos de Cálculo e Análise utilizados em cursos de Licenciatura em Matemática de universidades mineiras e ainda elaboramos um conjunto de atividades didáticas realizadas com alunos do curso de Licenciatura em Matemática, em uma disciplina de Fundamentos de Análise Real. As considerações finais do nosso trabalho apontam que uma proposta de ensino, baseada nas imagens conceituais dos alunos, pode contribuir para que o Professor de Análise entenda e situe o momento e a aprendizagem de seus alunos; perceba a importância de identificar e desconstruir imagens conceituais equivocadas e/ou conflitantes; reconheça a necessidade de (re)construir imagens conceituais coerentes e que explorem elementos intuitivos; trabalhe na perspectiva de se construir definições conceituais de acordo com as definições formais; repense a prática pedagógica e planeje as ações; incentive uma postura mais crítica e ativa nos alunos e, assim, contribua para desmistificar o “horror” à Análise.
ABSTRACT
This research discussed in general, the teaching of calculus and analysis in the perspective of the Mathematics Education in college and investigated the role of the conceptual images and the conceptual definitions for learning the Limits of Real Functions of one Variable. The research prioritized the qualitative aspects prevailing on the quantitative aspects. This research is justified just because many studies have evidenced the epistemological obstacles about the concept of limit and the necessity of doing researches that discuss the transition from Calculus to Analysis. We formulated the question: How can a teaching proposal based on concept images related to the concept of a function, (re) created by students of the Bachelor´s degree in Mathematics, after attending the Real analysis, can contribute to the learning of these students? The authors analyzed were David Tall, Shlomo Vinner, Bernard Cornu, Márcia Pinto and Frederico Reis. The activities were developed by the researches, students of the Bachelor´s Degree in Mathematics, in the Real Analysis subject. The theoretical and research literature has included the teaching of Calculus and Analysis, and the Advanced Mathematical Thinking. We also present the approach of the concept of limits in textbooks used in Calculus and Analysis Degree Courses in Mathematics at Universities in “Minas Gerais” and developed a set of didactic activities with students from Bachelor´s Degree in Mathematics, in the Fundamentals of Real Analysis subject. The final considerations indicate that a proposal based on teaching students the concept images can help the teacher understand and verify the time and the students learning, and realize the importance of identifying and deconstructing conceptual misguided images and/or conflictants, and recognize the necessity of (re)create conceptual consistent images and explore intuitive elements, as well as working in the perspective of creating conceptual definitions according to the formal definitions, rethink their practice and plan their actions, encourage a more critical and active in their students and thus contribute to demystify the “horror” of the Analysis.
Lista de Quadros
1. Quadro 1 – Questão 1 – item a ...92
2. Quadro 2 – Questão 1 – item b ...92
3. Quadro 3 – Questão 2 – itens a, b, c, d, e ...94
4. Quadro 4 – Questão 3 – itens a, b, c, d, e ...96
5. Quadro 5 – Questão 5.1...103
6. Quadro 6 – Questão 5.2...103
7. Quadro 7 – Questão 6 – item a ...105
8. Quadro 8 – Questão 6 – item b ...105
9. Quadro 9 – Atividade 2 – Questão 2.1...112
Lista de Figuras
1. Figura 1: Triângulos característicos ...34
2. Figura 2: Imagem conceitual ...57
3. Figura 3: Relação entre secante e tangente no ponto P...62
4. Figura 4: Relação entre secante e tangente no ponto P...62
5. Figura 5: Gráfico mostrando a relação − na definição de limite...63
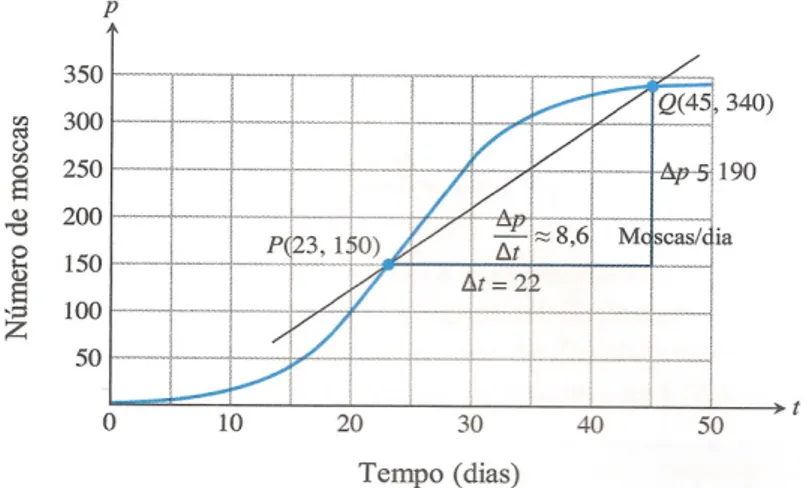
6. Figura 6: Crescimento de uma população das frutas num experimento controlado...66
7. Figura 7.1 e 7.2: Gráfico de f idêntico ao da reta y= x + 1, exceto em x = 1...67
8. Figura 8: Relação entre e na definição de limite...68
9. Figura 9: Relação entre secantes e tangentes...70
10.Figura 10.1 e 10.2: Tabela mostrando os valores de mpq para valores de x próximos de 1...70
11.Figura 11: Q tende a P pela direita e pela esquerda...70
12.Figura 12: Gráficos (a), (b) e (c), mostrando lim → ( )...71
13.Figura 13: Diagrama de Flechas...73
14.Figura 14: Diagrama de Flechas apresentando a relação − na definição de limite...73
15.Figura 15: Gráficos (a), (b) e (c) apresentando a relação − na definição de limite...74
16.Figura 16: Gráfico da questão 5.1 da Atividade I (Pós-Cálculo)...84
17.Figura 17: Gráfico da questão 5.2 da Atividade I (Pós-Cálculo)...84
18.Figura 18: Gráfico da questão 2.1 da Atividade II (Pós-Análise)...86
19.Figura 19: Gráfico da questão 2.2 da Atividade II (Pós-Análise)...86
20.Figura 20: Gráfico da questão 5 da Atividade II (Pós-Análise)...87
21.Figura 21: Gráfico do Aluno A1 – Questão 4 - Atividade I...99
22.Figura 22: Gráfico do Aluno A5 – Questão 4 - Atividade I...99
23.Figura 23: Gráfico do Aluno A2 – Questão 4 - Atividade I...99
24.Figura 24: Gráfico do Aluno A7 – Questão 4 - Atividade I...99
26.Figura 26: Gráfico do Aluno A8 – Questão 4 - Atividade I...100
27.Figura 27: Gráfico do Aluno A4 – Questão 4 - Atividade I...100
28.Figura 28: Gráfico da questão 5.1 da Atividade I (Pós-Cálculo)...101
29.Figura 29: Gráfico da questão 5.2 da Atividade I (Pós-Cálculo)...107
30.Figura 30: Resposta do Aluno A6 – Questão 6 – Atividade 1...106
31.Figura 31: Resposta do Aluno A8 – Questão 6 – Atividade 1...106
32.Figura 32: Gráfico do Aluno A7 - Questão 1 - Atividade II...109
33.Figura 33: Gráfico do Aluno A3 - Questão 1 - Atividade II...109
34.Figura 34: Gráfico do aluno A1 - Questão 1 - Atividade II ...109
35.Figura 35: Gráfico do Aluno A4 - Questão 1 - Atividade II...109
36.Figura 36: Gráfico do Aluno A1 – Questão 1 b - Atividade II ...110
37.Figura 37: Gráfico do Aluno A9 – Questão 1 b - Atividade II ...110
38.Figura 38: Gráfico da questão 2.1 da Atividade II (Pós-Análise)...111
39.Figura 39: Gráfico da questão 2.2 da Atividade II (Pós-Análise)...111
40.Figura 40: Gráfico do Aluno A3 – Questão 3a - Atividade II...114
41.Figura 41: Gráfico do Aluno A9 – Questão 3a - Atividade II...114
42.Figura 42: Gráfico do Aluno A3 – Questão 4a - Atividade II...115
43.Figura 43: Gráfico do Aluno A3 – Questão 4b - Atividade II...115
44.Figura 44: Gráfico da questão 5 da Atividade II (Pós-Análise)...116
45.Figura 45: Diagrama de Flechas elaborado pelo Aluno A9 – Questão 5 – Atividade II...119
SUMÁRIO
Introdução
ENSINO DE CÁLCULO E DE ANÁLISE: BUSCANDO MOTIVAÇÕES E
LEVANTANDO INDAGAÇÕES...15
I.1. Um breve histórico ... ...15
I.2. Iniciando a discussão ... 18
I.3. Destacando alguns trabalhos sobre o Ensino de Cálculo e Análise ... 19
I.4. Destacando os trabalhos da linha Advanced Mathematical Thinking ... 22
I.5. Mais alguns estudos de pesquisadores brasileiros ... 25
I.6. Apresentando nossa Questão de Investigação ... 27
I.7. Apresentando nosso objetivo ... 27
I.8. Apresentando nossas tarefas ... 28
I.9. Apresentando nossa Metodologia de Pesquisa ... 28
I.10. Estrutura da Dissertação ... 29
Capítulo 1 A CONSTRUÇÃO DO CONCEITO DE LIMITE: UM PERCURSO DO CÁLCULO PARA A ANÁLISE ...30
1.1. Um breve histórico sobre o desenvolvimento do conceito de limite ...30
1.2. Um pouco sobre o ensino de limites ... ...37
Capítulo 2 BUSCANDO CONEXÕES ENTRE O PENSAMENTO MATEMÁTICO AVANÇADO E AS NOÇÕES DE IMAGEM CONCEITUAL E DEFINIÇÃO CONCEITUAL ...47
2.2. Imagem conceitual e definição conceitual ... 52
Capítulo 3 APRESENTANDO A ABORDAGEM DO CONCEITO DE LIMITE EM ALGUNS LIVROS DIDÁTICOS DE CÁLCULO E ANÁLISE ...60
3.1. Apresentando os livros didáticos analisados ... 60
3.2. Apresentando os livros didáticos de Cálculo ... 61
3.3. Apresentando os livros didáticos de Análise ... 75
Capítulo 4 APRESENTANDO NOSSA PESQUISA ...80
4.1. Retomando a questão de investigação e as tarefas de pesquisa ... 80
4.2. Apresentando o contexto da pesquisa de campo ... 81
4.3. Descrevendo a metodologia de pesquisa ... 82
Capítulo 5 (RE)CONSTRUINDO O CONCEITO DE LIMITE DO CÁLCULO PARA A ANÁLISE: EVIDÊNCIAS DE UMA PESQUISA ...91
5.1. Análise da Atividade I (Pós-Cálculo) ... 92
5.2. Descrevendo o trabalho com limites em Análise ... 107
5.3. Análise da Atividade II (Pós – Análise) ... 109
5.4. Análise do Questionário de Avaliação Final ... 121
CONSIDERAÇÕES FINAIS ... 124
Introdução
ENSINO DE CÁLCULO E DE ANÁLISE:
BUSCANDO MOTIVAÇÕES E LEVANTANDO INDAGAÇÕES
O Cálculo foi a primeira conquista da Matemática moderna(...) Creio que só ele define, de modo inequívoco, o começo da Matemática moderna; e o sistema de Análise Matemática, que é o seu desenvolvimento lógico, ainda constitui o avanço técnico de maior importância no pensamento exato.
John Von Neuman
I.1. Um breve histórico
A Matemática é uma ciência, a Rainha das Ciências, segundo Gilberto Garbi (1997) e, ao entrarmos em contato com ela, dificilmente ficaremos indiferentes; assim, são gerados dois tipos de sentimento: paixão ou aversão. Isso pode ser influenciado por vários fatores, tais como: metodologia, professor, currículo e, em alguns casos, a aversão pode ser modificada, dependendo da forma como é direcionado o ensino.
Entretanto, o meu objetivo aqui não é discutir tais questões e sim me posicionar no primeiro grupo, ou seja, dos amantes da Matemática, desde o primeiro contato. A possibilidade que ela nos oferece de compreensão do mundo é fascinante, como afirmou Galileu Galilei apud GARBI, (1997, p. 209): “O universo é um grande livro que não pode ser compreendido a menos que antes se aprenda a entender a linguagem e a ler as letras nas quais ele está composto. Ele está escrito na linguagem da Matemática”.
Com esse pensamento, enveredei pelo caminho da Matemática em 1999, quando comecei a cursar Licenciatura em Matemática na Universidade Estadual de Montes Claros – UNIMONTES. Uma experiência muito proveitosa, pois exigiu de minha parte persistência, disciplina e muita dedicação.
Acreditava que somente naquele semestre do curso estava realmente estudando Matemática. A possibilidade de demonstrar, provar, por meio de uma estrutura lógica baseada nas definições, resultados simples como, por exemplo, que 2 é um número irracional, pois até então, tal ideia era aceita pelo fato de que esse número não pode ser escrito na forma
b
a , a e b ∈Z, com b ≠ 0, fez com que eu me dedicasse ao estudo desta
disciplina com mais afinco e persistência; era capaz de ficar dias inteiros lendo, buscando, fazendo e refazendo exercícios e demonstrações. Foi um trabalho árduo, mas que valeu a pena.
Também no ano de 1999, começou minha experiência docente, uma vez que fui convidada a monitorar as turmas de 8ª série do Ensino Fundamental e 1°, 2° e 3° anos do Ensino Médio do Colégio Professor Servelino Ribeiro, em Bocaiuva – MG, onde cursei os Ensinos Fundamental e Médio e onde estou, até os dias atuais, lecionando para esses níveis de ensino.
Terminei a graduação em dezembro de 2002 e, em janeiro de 2003, iniciei o curso de Especialização em Educação Matemática Superior na UNIMONTES, que muito me enriqueceu e alargou os meus horizontes no sentido de continuar a minha formação acadêmica, pois o meu objetivo, ao cursar Matemática, sempre foi lecionar para o Ensino Superior.
De uma forma particular, essa especialização me fez perceber, ainda mais, a minha paixão pela Matemática, quando cursei, pela segunda vez, as disciplinas de Análise Real e Estruturas Algébricas, pois entendi que muitas “imagens conceituais” que eu considerava não compreendidas na graduação precisavam apenas ser amadurecidas.
Especialmente na disciplina Análise Real, com a Profª. Dra. Márcia Maria Fusaro Pinto, na época professora da UFMG, é que percebi as reais possibilidades de tal conteúdo, na formação docente. Como ela tratou esta disciplina sem um excesso de rigor e formalismo e buscou um equilíbrio entre rigor e intuição, escolhi como tema de meu projeto de pesquisa o tópico Limites, tentando entender como ocorre a construção e/ou reconstrução desse conceito do Cálculo para a Análise e como se dá o processo de ensino e aprendizagem em sala de aula.
tenhamos um maior número, também, de matemáticos profissionais conscientes da importância de seu papel na formação dos estudantes.
Tudo isso foi muito importante!
Tive a oportunidade de ministrar, em janeiro de 2004, um curso na Faculdade de Ciência e Tecnologia de Montes Claros – FACIT, que foi denominado Pré-Cálculo e que consistiu em uma revisão de conteúdos do Ensino Médio, tais como números reais, funções e trigonometria, com o objetivo de “corrigir falhas” na formação matemática dos vestibulandos aprovados nos cursos de Engenharia Química, Engenharia de Computação e Engenharia de Controle e Automação, visando um melhor aproveitamento deles nas disciplinas de Cálculo. Foi uma experiência gratificante, pois tive a oportunidade de trabalhar com alunos de faixas etárias bastante diversificadas, embora isso tenha sido também muito difícil. Havia algumas pessoas que tinham parado seus estudos há dez, quinze anos. Não tive a oportunidade de comprovar se o objetivo foi alcançado, embora tivesse sido bem avaliada por parte dos alunos.
Desde o ano 1999, atuo como docente na educação básica, tanto na rede particular de ensino como na pública, em Bocaiuva – MG. De 2008 a 2010, fiz parte do corpo docente do Instituto Superior de Educação Ibituruna – ISEIB, em Montes Claros – MG, onde lecionei as disciplinas: História da Matemática, Fundamentos de Matemática I e II, Estruturas Algébricas, Cálculo I e Cálculo II para o curso de Licenciatura em Matemática.
Mesmo com pouca experiência, foi possível perceber a dificuldade dos alunos em compreender os conceitos matemáticos e a própria linguagem da Matemática formal. Especialmente na disciplina Estruturas Algébricas, na qual praticamente ao longo de todo o semestre, falamos e praticamos as provas / demonstrações formais. É importante lembrar que sempre busquei trabalhar valorizando a intuição, tentando fazer com que o percurso dos alunos por tal disciplina não fosse tão árduo, mas as dificuldades e percalços, infelizmente, tornaram-se uma realidade.
Já na disciplina Cálculo II, primeiramente, senti certo avanço na turma, em relação aos conceitos que trouxeram do Cálculo I. Nas primeiras semanas de aula, basicamente revimos e buscamos compreender algumas ideias e conceitos trabalhados no semestre anterior.
construí muitos gráficos para compreender a ideia de integral indefinida, depois integral definida e dei especial atenção às aplicações das integrais. É claro que também discuti com os alunos as técnicas de integração, mas acredito que o entendimento da importância do Cálculo passa pela compreensão da sua utilidade.
Atualmente, tenho ministrado regularmente a disciplina Cálculo I para os cursos de Matemática e Física no Instituto Federal do Norte de Minas Gerais – IFNMG, onde sou professora efetiva e estou buscando realizar um trabalho que valorize, mais uma vez, os aspectos intuitivos relacionados aos principais conceitos do Cálculo I, baseando-me em Frederico da Silva Reis (2001), pois penso que é possível um equilíbrio entre rigor e intuição ao discutir a ementa desta disciplina e, então, inicialmente, estou procurando valorizar as construções de gráficos, tabelas e mesmo as questões de onde os limites surgem, como no caso da reta tangente a uma curva e no estudo da velocidade de um objeto. É importante também destacar a importância da compreensão da linguagem que, para os alunos, pode ser algo totalmente novo.
Espero que esse caminho que estou trilhando seja produtivo para a comunidade de educadores matemáticos e que também seja longo...
I.2. Iniciando a discussão
É comum que alguns questionamentos sejam feitos, pelos alunos e professores, em relação ao Cálculo e seu ensino, como por exemplo: Qual é a sua utilidade? Qual é a importância para outras áreas do conhecimento? Qual é a melhor forma para ensinar / aprender Cálculo Diferencial e Integral?
O Cálculo não se resume a determinar tangentes, áreas e volumes com aplicações apenas dentro da Matemática. São inúmeras as suas aplicações. Para se ter uma ideia, os diversos ramos da Engenharia, bem como da Física, da Química, da Biologia, da Medicina, da Administração, da Astronomia, da Economia se utilizam do Cálculo. Segundo Elenice Zuin (2001, p. 34), até mesmo na Psicologia, na Linguística e nas Ciências Políticas, o Cálculo vem sendo empregado.
bactérias; encontrar a maximização dos lucros na fabricação de certo produto; mensurar as variações instantâneas na corrente elétrica.
Com as aplicações da integral, é possível determinar o trabalho necessário para enviar uma sonda espacial a outro planeta; determinar a quantidade de diluição de um corante em determinados testes fisiológicos; calcular o fluxo sanguíneo através de uma artéria, dentre outras aplicações contidas em Earl Swokowski (1994).
Daí, o nosso questionamento: Como conceitos tão ricos, tão importantes, em particular, os conceitos de limite, derivada e integral são ensinados nos cursos de Licenciatura em Matemática de um modo tão vazio, sem significado, como uma série de algoritmos e regras que, por si só, são apenas mecanizadas?
Dario Fiorentini (1995) sustenta que “a forma como vemos / entendemos a Matemática tem fortes implicações no modo como entendemos e praticamos o ensino da Matemática e vice-versa”, ponto de vista com o qual nos identificamos.
I.3. Destacando alguns trabalhos sobre o Ensino de Cálculo e Análise
Segundo a Sociedade Brasileira de Matemática – SBM (1995, p. 5), em um de seus boletins informativos:
O ensino de Cálculo nas universidades brasileiras tem sido objeto de questionamento em diversos fóruns em função das dificuldades apresentadas pelos alunos na sua aprendizagem, bem como pela alta evasão dos estudantes dos primeiros períodos, matriculados nesta disciplina.
Esse questionamento deve-se aos altos índices de reprovação e evasão nas universidades públicas brasileiras, desde aquela época até os dias atuais.
passiva e consiste na memorização e reprodução (imitação / repetição) precisa dos raciocínios e procedimentos ditados pelo professor ou pelo livro.
Quem é (são) o(s) responsável(is) por essa situação ou esse estado de coisas? Acreditamos que a responsabilidade de mudar esse quadro que aí se encontra é, de fato, de todos aqueles que, de alguma forma, estão envolvidos nesse processo de ensino e aprendizagem, concordando com Jonas Lachini (2001, p.146) ao afirmar que: “Na ação pedagógica, tanto o sucesso quanto o insucesso em uma disciplina específica, nascem das relações instituídas por professores e alunos, em torno do trabalho com conteúdos curriculares”.
Outra possibilidade a se pensar, quando se discutem os problemas no ensino de Cálculo, recai sobre a prática pedagógica dos professores, de acordo com Reis (2001, p. 23):
A prática pedagógica do professor de Cálculo deve se pautar, primeiramente, na reflexão e compreensão do papel fundamental do Cálculo Diferencial e Integral na formação matemática de seus alunos. Somente estabelecendo elementos que esclareçam a real função do Cálculo na formação matemática do aluno, o professor terá condições de refletir sobre que objetivos traçar, que conteúdos e metodologias estabelecer, enfim, que prática pedagógica desenvolver.
Neste ponto, temos a necessidade de questionar o ensino de Análise Real, uma vez que os tópicos fundamentais do ensino de Cálculo são os mesmos de um curso de Análise, disciplina obrigatória nos cursos de Licenciatura em Matemática e que concebemos como de fundamental importância para a formação do Professor de Matemática, por abordar formalmente, conteúdos trabalhados nos Ensinos Fundamental e Médio, como números e funções.
Uma discussão acerca daementa, da bibliografia e do papel da disciplina Análise Real, nos cursos de Licenciatura em Matemática, já foi realizada por Plínio Moreira, Helena Cury e Carlos Vianna (2005) quando enviaram questionários para 80 matemáticos, pesquisadores titulares ou professores titulares de 16 instituições universitárias e de pesquisa brasileiras, com questões envolvendo os assuntos acima citados. Destes, obtiveram 31 respostas de matemáticos que representavam 14 destas instituições.
em Matemática, que argumentos você apresentaria”? (MOREIRA, CURY e VIANNA, 2005, p.15)
A 1ª categoria de respostas descrita pelos pesquisadores apontou a importância da Análise por se constituir numa possibilidade do aluno “tomar contato” com o significado e com as formas de se pensar Matemática. Moreira, Cury e Vianna (2005, p. 21) afirmam que, por isso:
Desenvolve o raciocínio lógico e a capacidade de “pensar matematicamente”, proporcionando, também, maior maturidade intelectual ao aluno. O trabalho na disciplina abrange métodos, técnicas, estruturas, concepções e valores fundamentais da matemática, constituindo-se, assim, em uma introdução ao que se poderia chamar de “cultura matemática” (grifos dos autores).
Uma 2ª categoria levantada por Moreira, Cury e Vianna (2005, p. 22) relaciona-se ao fato de que a disciplina proporciona uma compreensão “sólida e profunda” de conceitos que são considerados básicos na Matemática escolar e assim:
[...] explica os “porquês” e dá mais segurança ao futuro professor da escola. Proporciona a construção de uma visão integrada e logicamente consistente da matemática elementar, em substituição a uma visão que a concebe como um amontoado desconexo de fórmulas e regras (grifo dos autores).
Ainda uma 3ª categoria destacada por Moreira, Cury e Vianna (2005, p. 23) descreve que: “A disciplina constitui, para o aluno, um espaço de percepção da matemática como um instrumento que permite um entendimento profundo de certos fenômenos naturais e que tem aplicações em outras ciências”.
Embora os autores da pesquisa critiquem algumas das respostas dadas, que questionam a necessidade de um professor da educação básica estudar Análise Real, acreditamos na importância dessa disciplina para a formação de Professores de Matemática, mas há que se repensar sua abordagem em sala de aula, na perspectiva de Alexandre Brito (2010, p. 25), ao pontuar:
Daí, deparamo-nos com uma série de problemas em relação ao ensino e à aprendizagem dessa disciplina. O aluno, quando tem o primeiro contato com a Análise, se vê diante dos aspectos formais da Matemática, até então desconhecidos para uma maioria dos estudantes, pois essa disciplina se encontra na grade curricular no final do curso de licenciatura, o que não deveria ser diferente, mas contrasta com o ensino da Matemática que o antecede, de um modo geral, privilegiando os aspectos computacionais e de manipulação simbólica, cujo objetivo é obter um resultado, uma resposta final, como no caso do Cálculo.
Então, o processo de ensino e aprendizagem da Análise, nos cursos de graduação, acaba não sendo muito diferente do Cálculo, embora privilegie aspectos diferentes; enquanto no Cálculo há um excesso de algoritmização e falta de compreensão e aplicação dos conteúdos, na Análise há um excesso de rigor e formalismo (REIS, 2009), o que faz com que a maioria dos alunos recorra à memorização e reprodução precisa dos principais resultados e de suas demonstrações, sem que isso lhes faça algum sentido. Essa visão é corroborada por Márcia Fusaro Pinto (1998, p.293), ao afirmar que:
O ensino de Análise Matemática tem demonstrado ser uma tarefa difícil. Estando no centro vital da transição dos estudantes do pensamento elementar para o pensamento avançado em Matemática, demandas conceituais são colocadas aos estudantes, como aquelas preocupadas com definições formais e prova formal.
Essa discussão sobre a “transição de pensamentos” é abordada pelos estudiosos do Pensamento Matemático Avançado, que passamos agora a destacar.
I.4. Destacando os trabalhos da linha Advanced Mathematical Thinking
Pensamos, então, que há muito que se pesquisar sobre o ensino de Análise Real; o aluno e suas “imagens conceituais” devem ser objeto de estudo e investigação.
Entendemos imagens conceituais, na perspectiva de David Tall e Shlomo Vinner (1981), como sendo os processos e imagens mentais relacionados à aquisição de um conceito.
Thinking tendo como seu editor, David Tall) contêm diversos artigos relacionados ao ensino de Matemática avançada e são divididos em três focos principais:
1. A natureza do pensamento avançado, cujos tópicos incluem os processos envolvidos na concepção do Pensamento Matemático Avançado, a criatividade matemática e a prova matemática;
2. A teoria cognitiva do Pensamento Matemático Avançado, cujos tópicos incluem o papel das definições, o papel dos símbolos e a abstração reflexiva;
3. A pesquisa envolvendo o ensino e a aprendizagem do Pensamento Matemático Avançado, cujos tópicos incluem o desenvolvimento cognitivo e dificuldades conceituais relacionadas a funções, limites, Análise, infinito, prova e ainda, o uso do computador.
No Capítulo 1 – The Psychology of Advanced Mathematical Thinking, Tall (1991, p. 3) caracteriza o Pensamento Matemático Avançado como aquele que dá “atitude produtiva de se considerar a contextualização de um problema, numa investigação matemática, leva à formulação produtiva de conjecturas e ao estágio de refinamento e prova” (tradução nossa).
Em relação ao Pensamento Matemático Avançado e o Pensamento Matemático Elementar, Tall (1991, p. 3) afirma que existe semelhança com os ciclos de atividades relacionados a esses pensamentos: “Muitas das atividades que ocorrem neste ciclo também ocorrem na resolução de problemas matemáticos elementares, mas a possibilidade de definição formal e dedução é um fator que distingue o Pensamento Matemático Avançado” (tradução nossa).
Mais do que a possibilidade da definição formal e dedução, acreditamos que a necessidade dessa postura formal é o que caracteriza / distingue o Pensamento Matemático Avançado, uma vez que, tal possibilidade também existe em níveis mais elementares, mas não se torna uma necessidade premente.
O movimento do pensamento matemático elementar para o avançado envolve uma transição significante: de descrever para definir, de convencer para provar de uma maneira lógica baseada nas definições. Esta transição requer uma reconstrução cognitiva, a qual é vista durante a luta inicial dos estudantes universitários com as abstrações formais, enfrentadas por eles no primeiro ano de universidade (grifos do autor; tradução nossa).
Outro aspecto interessante é destacado por Tall (1985), ao criticar os professores que, ao se questionarem “por que os alunos não aprendem Análise?”, simplesmente reorganizam a disciplina, alterando alguns tópicos do conteúdo, sem primeiro investigar como os alunos pensam: “Para compreender por que os estudantes não conseguem aprender Análise, claramente se requer um estudo dos estudantes como o sujeito-problema / objeto da pesquisa” (TALL, 1985, p. 1).
O pesquisador destaca também os conflitos causados pelas imagens conceituais nos estudantes, especialmente aqueles referentes a números reais e limites. Ainda, aponta para o problema da utilização de definições nas provas matemáticas como uma das maiores dificuldades na aprendizagem matemática de Análise, ao tratar das concepções dos estudantes sobre a teoria em que a Análise está construída.
Tais conflitos, em particular a aprendizagem dos números reais e limites, já haviam sido estudados por Tall e Schwarzenberger (1978). Os autores acreditam que as causas dos conflitos podem estar associadas a três fatores: uma “infelicidade linguística”, que se refere à utilização inadequada / inapropriada de terminologias e/ou simbologias matemáticas por parte do professor e que poderia ser eliminada por uma escolha mais cuidadosa das motivações ou definições; “distinção genuína da Matemática” ou ainda “eventuais particularidades na experiência anterior do indivíduo”, o que poderia ser sanado por um professor sensível ciente da situação. David Tall e Rolph Schwarzenberger (1978, p. 49) consideram ainda que: “Em todos os três tipos de conflito, o papel do professor em encontrar uma resolução adequada será crucial e mais decisivo do que fatores como a escolha da ementa, livro didático ou recursos audiovisuais”.
Esses autores questionam o sentido do ensino formalista de Análise, para aqueles que não serão matemáticos profissionais.
I.5. Mais alguns estudos de pesquisadores brasileiros
Em sua tese de doutorado, Reis (2001) discute como a relação tensional entre rigor e intuição acontece e se manifesta no ensino universitário de Cálculo e Análise, a partir dos estudos de manuais didáticos e de entrevistas semiestruturadas com quatro professores-pesquisadores que se destacavam nessa área à época, como autores de estudos e livros didáticos: Prof. Dr. Roberto Ribeiro Baldino – UNESP – Rio Claro; Prof. Dr. Geraldo Ávila – UFG; Prof. Dr. Djairo Guedes de Figueiredo – UNICAMP e Prof. Dr. Elon Lages Lima – IMPA – RJ.
No centro da obra, discutem-se aspectos rigorosos e intuitivos do ensino das disciplinas em questão e a relação dicotômica / não complementar entre rigor e intuição verificada no ensino atual. Reis (2001, p. 202) considera que:
Talvez a melhor metáfora, que agora se nos apresenta, seja o de uma reta com dupla seta, onde, numa extremidade pode-se representar o rigor e, na outra a intuição [...] É claro que o ponto ideal é o do equilíbrio, mas esse ponto, na verdade, é difícil de ser conseguido. O trabalho do professor pode situar-se em qualquer um dos pontos dessa reta contínua. O professor tem autonomia para deslocar-se para qualquer ponto dessa reta. Se o deslocamento tender a ser, com mais freqüência, para a esquerda (intuição), isso pode denotar uma preocupação pedagógica mais voltada à produção de sentidos e significados e à formação de conceitos. Se o deslocamento for, com mais freqüência, para a direita (rigor), isso poderá significar uma preocupação e uma ação pedagógica mais sintático-procedimental. Essas tendências, mais à direita ou à esquerda, dependem, de um lado, das concepções, valores e conhecimentos do professor e, de outro, das condições intelectuais dos alunos e materiais (aqui entrariam os livros didáticos) da instituição.
Por fim, destacamos ainda Pinto (2001), que relata uma pesquisa realizada com alunos do Departamento de Matemática e do Instituto de Educação da Universidade de Warwick – Inglaterra, que cursavam Análise ao final de seus cursos. A autora constatou que, apesar da complexidade envolvida nos problemas que os estudantes enfrentavam em seu primeiro contato com a Análise Real, é possível descrever um padrão permeando seu desenvolvimento durante este momento, daí relacionou dois tipos de aluno.
nova experiência dentro do contexto em estudo no momento; sua estratégia principal é a de “tornar rotina” o uso das novas ideias. O segundo tipo de aluno usa sua experiência para “atribuir significado” ao novo contexto em termos de seu conhecimento anterior. Sua estratégia principal é a de “explorar” o conceito novo, analogicamente, interpretando-o. A autora considera ainda que as dificuldades centrais para esses dois tipos de alunos não são as mesmas.
Para os que “extraem significado” o problema não está em trabalhar com uma nova noção de prova, que requer deduções a partir de definições. As dificuldades cognitivas ao estudar Análise Real parecem estar, de início, relacionadas à habilidade em coordenar os processos nas afirmações quantificadas apresentadas na teoria e trabalhar com a lógica proposicional. Na impossibilidade de produzir significado para o novo contexto, ou, às vezes, em decorrência de uma visão restrita da própria matemática, tais estudantes tendem a trabalhar o conteúdo de modo mecanizado, não reflexivo, sobrecarregando a memória e evocando inúmeros resultados que não sabem relacionar conceitualmente, em geral, estes estudantes não trabalham com independência.
Para os estudantes que “atribuem significado”, o vivenciar da nova experiência está íntima e invariavelmente ligado à reconstrução de experiências prévias; o que parece requerer do aprendiz um esforço cognitivo maior do que simplesmente compartimentalizar uma nova construção. Estudantes como esses podem ser derrotados por imagens conceituais restritas, não adequadas à exploração do conceito que pretendem desenvolver. Quando expostos a diferentes representações ou aspectos de um mesmo conceito, podem adicioná-los ao conhecimento que estão construindo como se fossem informações desconexas, ao invés de refinar sua imagem conceitual, focando gradualmente na definição formal.
Ainda em relação a esses dois tipos de aprendizes, Pinto (2001, p. 128) tece uma consideração que parece se encaixar perfeitamente no perfil dos estudantes de Análise, não só da Inglaterra, mas também do Brasil:
Concluindo, destacamos a perspectiva de Pinto (2001, p. 144) da qual nos valemos para justificar a relevância de nossa própria pesquisa: “Há que se investir em investigar meios de atenuar a transição dos Cálculos para a Análise. Neste sentido, esta investigação nos mostra que não há uma engenharia ou fórmula única para conduzir o ensino de Matemática avançada”.
1.6. Apresentando nossa Questão de Investigação
A partir das considerações inicias até aqui colocadas, podemos elaborar a seguinte questão passível de investigação:
Como uma proposta de ensino, baseada nas imagens conceituais, relacionadas ao conceito de limite de uma função, (re)construídas por alunos do curso de Licenciatura em Matemática, após cursarem Análise Real, pode contribuir para a aprendizagem desses alunos?
Essa questão se enquadra na linha de pesquisa de Educação Matemática no Ensino Superior: Ensino de Cálculo e de Análise desenvolvida na Linha 1: Educação Matemática Superior, Informática Educacional e Modelagem Matemática do Mestrado Profissional em Educação Matemática da Universidade Federal de Ouro Preto.
I.7. Apresentando nosso objetivo
• Desvendar a contribuição de uma proposta de ensino, baseada nas imagens conceituais, relacionadas ao conceito de limite de uma função, (re) construídas por alunos do curso de Licenciatura em Matemática, após cursarem Análise Real, para a aprendizagem desses alunos.
I.8. Apresentando nossas tarefas
• Apresentação da abordagem do conceito de Limite em alguns livros didáticos de Cálculo e Análise utilizados em cursos de Licenciatura em Matemática;
• Elaboração de um conjunto de atividades didáticas, como sugestões, a partir de uma proposta de ensino, baseada nas imagens conceituais, relacionadas ao conceito de limites de funções reais de uma variável, para disciplinas de Fundamentos de Análise Real, em cursos de Licenciatura em Matemática, como Produto Educacional do Mestrado Profissional em Educação Matemática.
I.9. Apresentando nossa Metodologia de Pesquisa
• Pesquisa teórico-bibliográfica sobre Educação Matemática no Ensino Superior, Ensino de Cálculo Diferencial e Integral e Ensino de Análise Real: leitura, síntese e discussão de artigos científicos, livros, dissertações e teses;
• Pesquisa documental, a partir da análise da apresentação e da abordagem do conceito de limites, em livros didáticos de Cálculo Diferencial e Integral e Análise Real utilizados em cursos de Licenciatura em Matemática de universidades mineiras como UFOP, UFMG, UNIMONTES, ISEIB e IFNMG;
• Pesquisa de campo com alunos do curso de Licenciatura em Matemática do Instituto Superior de Educação Ibituruna – ISEIB de Montes Claros – MG, a partir do planejamento, implementação e avaliação de duas atividades didáticas sobre limites de funções reais de uma variável.
I.10. Estrutura da Dissertação
Após a presente Introdução, na qual apresentamos as ideias iniciais da nossa pesquisa, caminhamos para o Capítulo 1, no qual tecemos algumas considerações sobre a história e o ensino de limites.
No Capítulo 3, apresentamos a abordagem do conceito de limites, em livros didáticos de Cálculo Diferencial e Integral e Análise Real utilizados em cursos de Licenciatura em Matemática de universidades mineiras.
No Capítulo 4, apresentamos nossa pesquisa em seu contexto e descrevemos o detalhamento da pesquisa de campo, juntamente com os instrumentos de coleta de dados que utilizamos.
A análise das atividades didáticas e do questionário de avaliação é feita no Capítulo 5, no qual elencamos algumas categorias de discussão a partir de um contraste com nosso referencial teórico-bibliográfico.
Capítulo 1
A CONSTRUÇÃO DO CONCEITO DE LIMITE:
UM PERCURSO DO CÁLCULO PARA A ANÁLISE
Ao avaliar o desenvolvimento da Matemática, devemos sempre ter em mente que as ideias atrás das notações são de longe a melhor metade...
Carl Boyer
Entendemos que o foco do nosso trabalho é o processo de ensino e aprendizagem do conceito de limite, em particular, aqui falamos de limites de funções reais de uma variável. Sendo assim, faremos um breve histórico sobre o desenvolvimento do conceito de limite e, em seguida, uma revisão da literatura relacionada ao ensino desse conceito.
Ressaltamos que não pretendemos esgotar o assunto, mas situar o ensino e aprendizagem de limite como objeto de estudo dentro da Educação Matemática e levantar elementos que contribuam para uma melhor compreensão do nosso estudo em questão.
1.1. Um breve histórico sobre o desenvolvimento do conceito de limite
Foram necessários quase 2.500 anos de história para que o conceito de limite fosse estabelecido da forma como é hoje, desde os paradoxos de Zenão (cerca de 450 a.C), passando pela Aritmetização da Análise com Weierstrass, no século XIX quando, segundo Geraldo Ávila (2006), a definição de limite de Cauchy – correta, porém, ainda eivada da noção espúria de movimento – é substituída pela definição puramente numérica: f(x)tem
limite L com x tendendo a
x
0 significa que dado qualquer ε >0, existeδ >0 tal que seε
δ
−
<
<
−
<
x
x
f
(
x
)
L
0
0 .Zenão de Eléia foi um filósofo grego que entrou para a história por causa dos seus famosos dons de dialética, segundo Antônio Brolezzi (1996, p. 22):
compor uma reta de comprimento infinito; e se não têm nenhum comprimento, então uma quantidade infinita deles tampouco terá comprimento algum. Além disso, dirá também: aquilo que acrescentado a outro não o faz maior, e subtraído de outro não o faz menor, é simplesmente nada.
Ainda segundo o pesquisador, mais famosos ainda que esses argumentos são seus quatro paradoxos sobre a impossibilidade do movimento. Na forma que chegaram a nós, por meio de Aristóteles (384 – 322 a.C.) e outros, os que causaram maior agitação foram: o da Dicotomia, o de Aquiles, o da Flecha e o do Estádio. Apenas para ilustrar suas ideias, embora o mais conhecido seja o de Aquiles, iremos apresentar o paradoxo da Dicotomia, assim descrito por Brolezzi (1996, p. 22):
Zeno nos coloca frente à aparente impossibilidade de percorrermos um número infinito de distâncias num tempo finito. Imaginemos uma pessoa que deve atravessar uma sala de um lado a outro. Antes de chegar à parede oposta, deve evidentemente chegar à metade da sala. Antes disso, porém, deve percorrer a metade da metade, ou um quarto da distância. E assim por diante, sempre dividindo a distância pela metade, indefinidamente. Desse modo, a pessoa nunca chegará ao outro lado, pois terá que percorrer um número infinito de espaços, ainda que pequenos, num tempo evidentemente finito.
De acordo com Carl Boyer (2002), os argumentos de Zeno parecem ter influenciado profundamente o desenvolvimento da Matemática grega, influência que se compara com a da descoberta dos incomensuráveis, com a qual talvez se relacione. As grandezas deixam de estar associadas a números e passam a estar associadas a segmentos de reta. É a passagem da ideia do discreto para o contínuo; ao menos em parte, o reino dos números continuava a ser discreto, mas o das grandezas passava a ser contínuo.
Essa separação do discreto e do contínuo é quase uma separação completa entre a Teoria dos Números e a Geometria, mas que teve uma contribuição interessante: a Álgebra Geométrica, que consistia, segundo Brolezzi (1996), em resolver problemas algébricos utilizando a ideia de grandezas contínuas.
Antônio Lira (2008) destaca que os gregos não desenvolveram o Cálculo por duas razões: o mal-estar diante do infinito – chamado horror infiniti – e o fato de que eles não possuíam a linguagem algébrica.
banidos da Matemática grega por esta razão, sendo o trabalho de Euclides (300 a.C.) um monumento a esta exclusão”.
A partir desse ponto, vamos dar ênfase ao trabalho de Eudoxo de Cnido (morreu por volta de 355 a.C.), aluno de Platão (427 – 347 a.C.) que propôs outra definição de proporção, de caráter mais geral, uma vez que o conceito de proporção dos pitagóricos, associando a razão entre dois segmentos de reta à razão entre números inteiros, não podia ser aplicada no caso das grandezas incomensuráveis. Conforme Brolezzi (1996), com a nova definição de Eudoxo, os quatro termos da proporção puderam ser todos grandezas geométricas, evitando por completo qualquer extensão à ideia pitagórica de número. Dessa forma, Eudoxo constrói um instrumento útil que podia ser manuseado sem haver misturas entre números e grandezas geométricas, isto é, sem ferir o modo de pensar grego. Podia-se já falar da "razão entre as áreas de dois círculos" como sendo equivalente à "razão entre os quadrados construídos sobre os diâmetros dos círculos".
Segundo Boyer (2002, p. 63), de posse dessa definição, Eudoxo forneceu o lema que hoje tem o nome de “Lema de Arquimedes” e serviu de base para o método da exaustão, que é o equivalente grego de cálculo integral:
Dadas duas grandezas diferentes (ambas não nulas), se da maior subtrairmos uma grandeza maior que a sua metade, e do que restou subtrairmos uma grandeza maior que a sua metade, repetindo esse processo continuamente, restará uma grandeza que será menor que a menor grandeza dada.
A partir do método da exaustão, Arquimedes de Alexandria (287 – 212 a.C.), ocupou-se intensamente com o cálculo de áreas e volume de diversas figuras geométricas, inclusive do círculo e da esfera. Segundo Ávila (2006), o método da exaustão consistia em exaurir a figura dada por meio de outras; dessa forma, Arquimedes provou que a área do círculo é exatamente 2
r
⋅
π e provou que a razão da circunferência para o diâmetro está
compreendida entre
71 10 3+ e
70 10
3+ . Além disso, outro feito importante creditado a
Arquimedes foi a quadratura da parábola, ou seja, o cálculo da área do segmento de parábola, chegando à conclusão de que esta é
3
4 da área do triângulo nele inscrito,
A diferença entre o método de exaustão e o limite do Cálculo Diferencial e Integral reside apenas no fato de os gregos não realizarem essa passagem ao infinito, pois não tinham noção de um continuum aritmético. Mas o tipo de argumentação é o mesmo, tanto no caso do atual limite quanto no método de exaustão geométrico. Pode-se talvez dizer que a noção de limite tivesse sido vislumbrada pelos gregos.
Merece destaque também a obra de Fermat (1601 – 1665). Segundo Boyer (2002), é possível que desde 1629, Fermat já estivesse de posse da sua Geometria Analítica, pois nesse período, ele fez duas descobertas importantes que se relacionam com o seu trabalho sobre lugares geométricos. A mais importante foi o chamado “Método para achar máximos e mínimos” que lhe rendeu, nas palavras de Laplace (1749 – 1827), o título de descobridor do Cálculo Diferencial, bem como co-descobridor da Geometria Analítica. Boyer (2002, p. 240) descreve assim o método:
Fermat estivera considerando lugares dados (em notação moderna) por equações da forma
y
=
x
n; por isso elas são hoje frequentemente chamadas “parábolas de Fermat” se n é positivo ou “hipérboles de Fermat” se n é negativo. Aqui temos uma geometria analítica de curvas planas de grau superior; mas Fermat foi além. Para curvas polinomiais da forma y = f(x)ele notou um modo muito engenhoso para achar pontos em que a função assume um máximo ou mínimo. Ele comparou o valor de f(x) num ponto com o valor de f(x+E) num ponto vizinho. Em geral esses valores serão bem diferentes, mas num alto ou num baixo de uma curva lisa a variação será quase imperceptível. Portanto para achar os pontos de máximo e de mínimo Fermat igualava f(x) e f(x+E), percebendo que os valores, embora não exatamente iguais, são quase iguais. Quanto menor o intervalo E entre os dois pontos, mais perto chega a pseudo-equação de ser uma verdadeira equação; por isso Fermat, depois de dividir tudo por E fazia E = 0. Os resultados lhe davam as abscissas dos pontos de máximo e mínimo do polinômio. Aqui tem-se o processo hoje chamado de diferenciação pois o método de Fermat equivale a achar( ) E x f E x f E ) ( lim 0 − + →
e igualar isso a zero. [...] O processo de Fermat de mudar ligeiramente a variável e considerar valores vizinhos é a essência da análise infinitesimal (grifo do autor).
Boyer (2002) afirma que, de forma evidente, Fermat ainda não possuía em mãos, a definição formal de limite, mas podemos perceber que o seu método para achar máximos e mínimos se assemelha muito ao que utilizamos hoje no Cálculo. É importante citar que durante os anos em que Fermat estava desenvolvendo sua Geometria Analítica, ele descobriu também como achar a tangente a uma curva algébrica da forma y= f(x)usando
Enfim, no século XVII surgem os trabalhos de Isaac Newton (1642 – 1727) e Gottfried Wilhelm Leibniz (1646 – 1716) que são considerados os inventores do Cálculo Diferencial e Integral. O percurso de “invenção” do Cálculo traçado por eles teve interessantes diferenças, assim descritas por Brolezzi (1996, p. 29):
Newton e Leibniz chegaram ao Cálculo através de caminhos diferentes. Não só é diferente a linguagem com que ambos expressaram as ideias fundamentais do Cálculo, mas também em termos de concepção pode-se verificar uma diferença grande entre os trabalhos destes homens. Tanto Newton quanto Leibniz podem ser considerados como os primeiros a expressar a ideia da reciprocidade entre a diferencial e a integral, que constitui o Teorema Fundamental do Cálculo. Mas a maneira de ver o Cálculo era distinta.
Newton se referia a seu Cálculo como o “Método das Fluxões”, sendo a fluxão uma velocidade finita, e não uma quantidade infinitamente pequena. As variáveis eram consideradas como quantidades fluentes. Os conceitos mecânicos e cinemáticos eram usados como variáveis, o que equivale a considerá-las funções do tempo. Para Newton, o conceito fundamental do Cálculo é eminentemente cinemático e a ideia central é a de fluxão x, vetor velocidade de x, ou taxa de mudança da variável. “Trata-se da decomposição no eixo x do vetor velocidade do ponto” (BROLEZZI, 1996, p. 30). De acordo com Boyer (2002), Newton tentou definir o limite de uma função.
Já para Leibniz, a visualização do Cálculo se dá de forma estática, de acordo com Margaret Baron e Henry Bos (1985, p. 70). Ele considerava as variáveis como percorrendo sequências de valores infinitamente próximos. No seu Cálculo, há pouco uso de conceitos de movimento.
De acordo com Ávila (2006), o cálculo de Leibniz, na sua origem, é mais complicado que o de Newton. No entanto, a sua grande vantagem é a notação, os símbolos “d” para derivada e “ ” para a integral, utilizados até hoje, foram introduzidos por Leibniz em 1675, e ainda as notações dx, dy, ds para elementos infinitesimais tem a grande conveniência de “sugerir” os próprios resultados.
Brolezzi (1996, p. 30) também compara os estilos de cada um, da seguinte forma:
Podemos dizer assim que, em termos de tendência, ou estilo, Newton teria chegado ao Cálculo pela via do contínuo, e Leibniz, pela via do discreto. Ambas as maneiras de abordar o problema mostraram-se igualmente úteis, pois, enquanto não estava estabelecida a noção de limites, as ideias de movimento contínuo e de infinitésimos discretos surgiram como tentativas de esquematizar as impressões sensíveis a respeito da variação (grifo nosso).
Entretanto, em ambos os Cálculos faltavam os fundamentos; tanto Newton como Leibniz tinham problemas com os infinitesimais, visto por ambos de maneiras diferentes, mas que operavam de maneiras parecidas, pois esses infinitesimais às vezes eram cancelados como fatores diferentes de zero, outras eram desprezados como se realmente fossem zero. “Essas operações contraditórias dominaram o Cálculo por muito tempo, até que surgissem trabalhos decisivos para a fundamentação lógica da disciplina no começo do século XIX” (ÁVILA, 2006, p. 191).
Destacaremos agora, os trabalhos de dois matemáticos que foram fundamentais na busca de uma construção rigorosa dos fundamentos do Cálculo e, portanto, para o
movimento que ficou conhecido como Aritmetização da Análise: Cauchy (1789 – 1875) e Weierstrass (1815 – 1897).
O processo de Aritmetização da Análise foi uma busca pela fundamentação do Cálculo não mais de maneira geométrica, mas sim por meio dos números. Segundo Ávila (2006), esse processo era, de certo modo, uma volta a Pitágoras.
Uma das principais contribuições de Cauchy para a Análise foi a definição quase tão precisa de limite como a que utilizamos hoje: “Quando valores sucessivos atribuídos a uma variável se aproximam indefinidamente de um valor fixo de modo a acabar diferindo dele tão pouco quanto se queira, este último chama-se o limite dos outros dados” (CAUCHY, 1829 apud BOYER, 2002, p. 355).
No entanto, segundo Reis (2001), talvez a maior contribuição de Cauchy não esteja no rigor da definição de limite, mas sim na concepção de infinitésimo como uma variável dependente: “Diz-se que uma quantidade variável se torna infinitamente pequena quando seu valor numérico decresce indefinidamente de modo a convergir para o limite zero” (CAUCHY, 1829 apud BOYER, 2002, p. 355).
A partir desse conceito de limite, Cauchy desenvolveu os conceitos de continuidade, diferenciabilidade e integral, cujas definições são, em sua essência, as utilizadas até hoje.
Porém, a busca pelo rigor levava a uma questão: a fundamentação do sistema de números reais, uma vez que a teoria de limites de Cauchy estava baseada apenas em uma noção intuitiva desses números.
A partir de então, segundo Reis (2001), Weierstrass defendeu a necessidade de que o sistema de números reais fosse tornado rigoroso, o que se concretizou no final do século XIX, com os trabalhos de Dedekind (1831 – 1916) e Peano (1851 – 1932) que mostraram como o sistema dos números reais pode ser deduzido de um conjunto de postulados para o sistema dos números naturais, conhecidos como “Axiomas de Peano” e “Cortes de Dedekind”, os quais permitiram a demonstração rigorosa dos teoremas fundamentais sobre limites sem utilizar recursos geométricos, criando dessa forma, uma nova forma de lógica matemática.
1.2. Um pouco sobre o ensino de limites
Iniciaremos com um pequeno cenário de algumas pesquisas relacionadas ao ensino de limites.
Diante do que foi exposto até aqui, percebemos que houve um empenho de grandes matemáticos para que o conceito de limite fosse definido como hoje o é. Então, parece-nos natural pensar que, para nossos estudantes de Cálculo, não é fácil a compreensão / aprendizagem desse conceito.
De uma maneira geral, o estudo de limites de funções integra a ementa da disciplina de Cálculo I, a qual normalmente aparece nas estruturas curriculares de cursos como Matemática (Licenciatura e Bacharelado), Engenharias, Economia, dentre outros, nos primeiros períodos.
Uma das discussões presentes na literatura é a dificuldade de ensinar e aprender o conceito de limite, como mostra uma pesquisa de Bernard Cornu (1991), realizada em 1983, ao destacar a importância do conceito para o desenvolvimento de outros conceitos do Cálculo Diferencial e Integral sendo um tipo de “pensamento necessário” para a construção de uma Matemática avançada.
Aqui, cabe destacar que acreditamos que o conceito de limite realmente é necessário para a construção de conceitos como derivada e integral, principalmente na forma como o Cálculo está hoje estruturado nos currículos públicos dos cursos de Ciências Exatas. Entretanto, há de se considerar que a própria História do Cálculo nos mostra que o surgimento desses conceitos se deu na ordem inversa: integral, derivada e limite. Talvez a formalização da estrutura matemática tenha contribuído para a ordem atual do ensino de Cálculo.
Para o pesquisador, o conceito de limite é de difícil apreensão e, consequentemente, traz dificuldades também para quem o ensina. É possível perceber que os alunos, de uma maneira geral, são capazes de realizar longas listas de atividades envolvendo tal assunto, sem que realmente tenham compreendido o conceito.
Cornu (1991) acredita que a dificuldade no ensino e na aprendizagem do conceito de limite não se restringe à riqueza e complexidade do assunto, mas também reside no fato de que os aspectos cognitivos envolvidos nesse processo não podem ser gerados apenas a partir da definição matemática. Há alguns aspectos do conceito de limite que apenas são compreendidos pela intuição, que é o caso do caráter dinâmico deste conceito. O fato é que, de uma maneira geral, os estudantes acabam não se apropriando do conceito formal de limite: “Lembrar a definição de limite é uma coisa, adquirir a concepção fundamental é outra” (CORNU, 1991, p. 153).
Outra questão que Cornu (1991) discutiu foi o que chamou de concepções espontâneas, descritas como concepções relacionadas a uma noção, que ocorrem antes de seu ensino formal. Os estudantes trazem as suas próprias ideias, intuições e imagens que vêm da própria experiência, anterior ao ensino formal de um tema ou conceito. Segundo Cornu (1991), para a maioria dos conceitos matemáticos, o ensino não começa em um território virgem. No caso dos limites, um agravante é a linguagem coloquial, na qual expressões como “tender a” e “limite” tem significados diferentes para os estudantes (TALL e SCHWARZENBERGER, 1978) e para os professores que a utilizam no contexto técnico da aula de Matemática.
Ainda segundo Cornu (1991), é ilusão acreditar que, diante de uma teoria formal, tais concepções espontâneas desaparecem; ao contrário, misturam-se à linguagem técnica dando origem a uma concepção pessoal acerca da ideia apresentada, que nem sempre corresponde à concepção como entendida pela comunidade dos matemáticos.
Este último tipo, obstáculos epistemológicos, foi introduzido por Gaston Bachelard (1983). Para o pesquisador, os obstáculos epistemológicos têm duas características principais:
1) Eles são inevitáveis e essenciais na constituição do conhecimento a ser adquirido;
2) Eles são encontrados, ao menos em parte, no desenvolvimento histórico do conceito.
Para Cornu (1991), em relação ao conceito de limite, existem quatro obstáculos epistemológicos na sua construção histórica:
1) A ausência de relações entre a geometria e os números;
2) A noção do infinitamente grande e do infinitamente pequeno;
3) O aspecto metafísico da noção de limite;
4) A dúvida se o limite pode ser atingido ou não.
Os dois primeiros obstáculos levaram muito tempo para serem superados e possibilitar a construção formal do conceito. Cornu (1991) avalia que tal questão, da falta de ligação da geometria com os números, impediu que o conceito de limite fosse formulado ainda pelos gregos, pelo método da exaustão. A ideia do infinitamente grande e infinitamente pequeno gerou conflitos entre grandes nomes da matemática, tais como Newton, conforme visto no capítulo anterior, ou D’Alembert, que se opôs ao uso dos infinitesimais e tentou removê-los do Cálculo Diferencial.
Quanto aos dois últimos obstáculos mencionados, estes geram conflitos entre os estudantes até hoje. De fato, a questão do aspecto metafísico do conceito de limite gera perguntas tais como: “isto realmente é Matemática?” E dúvidas quanto ao limite ser atingido ou não são objetos de pesquisa em nossas salas de aula, refletindo a dificuldade na construção e apropriação do conceito formal expresso na definição de limite.
cometidos pelos alunos, os quais, quando analisados, permitem encontrar melhores estratégias de ensino.
Cornu (1991) finaliza seu trabalho ressaltando a importância dos professores reconhecerem as dificuldades relacionadas ao conceito de limite e que apenas uma exposição clara das ideias não é suficiente para que os estudantes compreendam tal conceito.
Uma sugestão de Cornu (1991) para os professores é que, antes de começar a trabalhar com a noção de limite, os estudantes tenham a possibilidade de trabalhar com atividades adequadas para ajudá-los a tomar consciência das próprias concepções espontâneas, imagens, intuições e experiências que virão à tona quando se iniciar o processo de aprendizagem de limites; em particular, deve-se discutir os diferentes significados das palavras utilizadas dentro desse contexto.
Enfim, de uma maneira geral, é possível perceber, pelos argumentos do autor e de nossa própria experiência, que o ensino e a aprendizagem do conceito de limite é uma tarefa difícil, mas que não pode passar despercebida nos cursos de Cálculo, uma vez que a compreensão desse conceito pode contribuir para uma real compreensão de outros conceitos, como continuidade, derivada e integral, especialmente na perspectiva como o Cálculo está hoje estruturado nos currículos públicos.
Outra pesquisa que também busca reconhecer os obstáculos epistemológicos em relação ao conceito de limite foi realizada por Anna Sierpinska (1985). A pesquisadora constatou, numa investigação junto a quatro estudantes de Cálculo, divididos em grupos de dois, a existência de diversos tipos de obstáculos ligados à aprendizagem da noção de limites, assim classificados por ela:
1) Obstáculos relacionados a um certo horror ao infinito;
2) Obstáculos relacionados à noção de função;
3) Obstáculos relacionados a fundamentos geométricos;
4) Obstáculos relacionados a fundamentos de lógica;