A técnica do super-passo na resolução numérica de equações diferenciais parciais...

(1)

.

A t´

ecnica do super-passo na

resolu¸

c˜

ao num´

erica de equa¸

c˜

oes

diferenciais parciais parab´

olicas

Aimberˆe Galdino

DISSERTAC¸ ˜AO APRESENTADA AO

INSTITUTO DE MATEM ´ATICA E ESTAT´ISTICA DA

UNIVERSIDADE DE S ˜AO PAULO PARA

OBTENÇ ÃO DO TÍTULO DE MESTRE EM

CIˆENCIAS

´

Area de Concentra¸c˜ao: Matem´atica Aplicada Orientador: Prof. Dr. Alexandre Megiorin Roma

Durante a elabora¸c˜ao deste trabalho o autor recebeu aux´ılio ﬁnanceiro do CNPq

(2)

A T´

ecnica do Super-Passo na Resolu¸

c˜

ao

Num´

erica de Equa¸

c˜

oes Diferenciais Parciais

Parab´

olicas

Este exemplar corresponde à reda¸cão final da disserta¸cão devidamente cor-rigida e defendida por Aimberê Galdino e aprovada pela Comissão Julgadora.

S˜ao Paulo, 2 junho de 2006.

Banca examinadora:

• Prof. Dr. Alexandre Megiorin Roma (Orientador) - IME-USP

• Prof. Dr. Clodoaldo Grotta Ragazzo - IME-USP

(3)

(4)

AGRADECIMENTOS

`

A meu orientador Prof. Dr. Alexandre Roma, pela paciência e dedica¸cão em me orientar durantes esses anos de pesquisa. Ao Prof. Dr. Vasilios Alexiades por estar, mesmo a distância, ajudando no desenvolvimento deste trabalho.

Aos meus pais, tio Alexandre, aos meus amigos de Santana de Parna´ıba e a Lilian que sempre me apoiaram, incentivaram e ajudaram na conclus˜ao deste trabalho.

Agrade¸co a todos os colegas de pós-gradua¸cão que me ajudaram na con-clusão do mestrado.

Aos professores que compuseram a banca examinadora, pela leitura cuida-dosa deste trabalho e sugest˜oes ou cr´ıticas decorrentes da mesma.

Agrade¸co ao IME-USP, em especial a Comissão de Pós-Gradua¸cão pela oportunidade de realizar meus estudos nesta institui¸cão.

(5)

Resumo

(6)

Abstract

(7)

Sum´

ario

Lista de Figuras iii

Lista de Tabelas v

Introdu¸c˜ao 1

1 Modelagem Matem´atica da Condu¸c˜ao do Calor 4

1.1 Equa¸c˜oes Diferenciais Parciais . . . 4

1.2 Classiﬁca¸c˜ao . . . 5

1.3 Modelagem Matem´atica da Propaga¸c˜ao de Calor . . . 6

2 Métodos Numéricos Clássicos 11 2.1 Discretiza¸cão: Diferen¸cas Finitas . . . 11

2.2 M´etodo de Euler Expl´ıcito . . . 18

2.3 M´etodo de Euler Impl´ıcito . . . 23

2.4 M´etodo de Crank-Nicolson . . . 27

3 A T´ecnica do Super-Passo 32 3.1 Condi¸c˜ao de Estabilidade . . . 35

(8)

4 Resultados Num´ericos 44

4.1 Análise Numérica de Convergência . . . 44

4.1.1 M´etodo de Euler Expl´ıcito . . . 47

4.1.2 M´etodo de Euler Impl´ıcito . . . 47

4.1.3 M´etodo de Crank-Nicolson . . . 48

4.1.4 T´ecnica do Super-Passo . . . 49

4.2 Compara¸c˜ao de Performance . . . 51

5 Conclus˜ao 55

Apˆendice: Polinˆomios de Chebyshev 57

(9)

Lista de Figuras

1.1 Propaga¸c˜ao do calor em uma barra. . . 7

2.1 Discretiza¸c˜ao do dom´ınio Ω. . . 12

2.2 Mol´ecula computacional do M´etodo de Euler Expl´ıcito. . . 19

2.3 Mol´ecula computacional do M´etodo de Euler Impl´ıcito. . . 24

2.4 Mol´ecula computacional do M´etodo de Crank-Nicolson. . . 29

(10)

Lista de Tabelas

3.1 Aproxima¸cão numérica para o limite (3.15). . . 39 4.1 Resultados numéricos obtidos pelo Método de Euler Expl´ıcito

na aproxima¸cão da solu¸cão do problema (4.6). . . 47 4.2 Resultados numéricos obtidos pelo Método de Euler Impl´ıcito

na aproxima¸cão da solu¸cão do problema (4.6) . . . 48 4.3 Resultados numéricos obtidos pelo Método de Crank-Nicolson

na aproxima¸cão da solu¸cão do problema (4.6). . . 49 4.4 Resultados numéricos obtidos pela Técnica do Super-Passo na

aproxima¸cão da solu¸cão do problema (4.6). . . 50 4.5 Erros cometidos nas aproxima¸cões da solu¸cão da equa¸cão (4.7). 52 4.6 Compara¸cão entre os pseudo-códigos da Técnica do

(11)

Introdu¸

c˜

ao

A modelagem matemática de problemas f´ısicos freqüentemente envolve a resolu¸cão de equa¸cões diferenciais parciais. Em particular, a condu¸cão de calor num meio f´ısico pode ser modelada por uma equa¸cão diferencial parcial do tipo parabólico.

Quando não é poss´ıvel explicitar a solu¸cão da equa¸cão diferencial parcial utilizam-se métodos numéricos para aproximar a solu¸cão do modelo. Neste trabalho utilizaram-se métodos impl´ıcitos e expl´ıcitos baseados em diferen¸cas finitas. Os métodos expl´ıcitos restringem a escolha do passo de integra¸cão no tempo ∆t em fun¸cão do passo de integra¸cão espacial ∆x. Essa restri¸cão é conhecida como condi¸cão de estabilidade e, em geral, os métodos impl´ıcitos ou não a possuem ou a apresentam de forma muito mais branda. Maiores detalhes podem ser encontrados em [3], [5], [4], [8], [14], [19], [22] e [25]. A condi¸cão de estabilidade impõe aos métodos expl´ıcitos uma maior quantidade de passos no tempo do que os métodos impl´ıcitos, tornando-os menos efi-cientes computacionalmente, entretanto como o tamanho do passo no tempo dos métodos impl´ıcitos é maior do que os permitidos pela condi¸cão de estabil-idade dos métodos expl´ıcitos, os erros cometidos na aproxima¸cão da solu¸cão do problema proposto também são maiores. É uma situa¸cão onde a rela¸cão custo benef´ıcio deve ser analisada.

(12)

esta-Introdu¸c˜ao

bilidade. O algoritmo do Super-Passo é baseado no relaxamento da condi¸cão de estabilidade em cada passo no tempo, para impô-la apenas ao final de um ciclo de N passos intermediários auxiliares. O esquema aqui apresentado é uma varia¸cão do Método de Gretzsch [13]. A implementa¸cão da Técnica do Super-Passo é simples; basta uma pequena modifica¸cão no código que emprega o método expl´ıcito para que o tempo de processamento seja até da ordem de 10 vezes menor, como pode ser visto em [2], [1], [10], [18], [20], [21] e [29].

O presente trabalho mostra que a Técnica do Super-Passo aplicada ao Método de Euler Expl´ıcito tem o tempo de processamento e erro cometido na aproxima¸cão similares aos obtidos pelo Método de Euler Impl´ıcito. Foram realizadas compara¸cões entre os erros cometidos na aproxima¸cão da solu¸cão e tempo de processamento para os Métodos de Euler Expl´ıcito, Impl´ıcito, Crank-Nicolson e Super-Passo aplicado ao Método de Euler Expl´ıcito.

No primeiro cap´ıtulo é realizada uma introdu¸cão às equa¸cões diferenciais parciais, as equa¸cões são classificadas em parabólicas, hiperbólicas e el´ıpticas e na última se¸cão do cap´ıtulo é deduzida, a partir fenômenos f´ısicos, a equa¸cão do calor com condutibilidade variável. Maiores detalhes sobre as equa¸cões diferenciais parciais podem ser encontrados em [9], [15], [16] e [17].

O Cap´ıtulo 2 apresenta a discretiza¸cão da equa¸cão do calor com con-dutibilidade variável utilizando diferen¸cas finitas e, para esta equa¸cão são, empregados os Métodos de Euler Expl´ıcito, Impl´ıcito e Crank-Nicolson e, para cada método numérico, são realizados os cálculos necessários para se obter as condi¸cões de estabilidade e consistência. Os métodos numéricos ap-resentados neste cap´ıtulo podem ser encontrados com uma abordagem mais ampla em [3], [5], [4], [8], [14], [19], [22] e [25].

(13)

Introdu¸c˜ao

do calor por esta técnica. A constru¸cão e aplica¸cões do Super-Passo podem ser encontrados em [2], [1], [10], [18], [20], [21] e [29].

No Cap´ıtulo 4 é feita a valida¸cão dos Métodos de Euler Expl´ıcito, Impl´ıcito, Crank-Nicolson e da Técnica Super-Passo por refinamento de malha e apre-senta os resultados obtidos pelos métodos ao aproximar a solu¸cão da equa¸cão do calor com condutibilidade variável.

O quinto cap´ıtulo apresenta a conclus˜ao do trabalho e sugest˜oes para a continuidade do mesmo.

(14)

Cap´ıtulo 1

Modelagem Matem´

atica da

Condu¸

c˜

ao do Calor

1.1 Equa¸

c˜

oes Diferenciais Parciais

A modelagem matemática de problemas f´ısicos freqüentemente resulta na formula¸cão de uma Equa¸cão Diferencial Parcial (ou de um sistema de equa¸cões diferenciais parciais) que é uma equa¸cão envolvendo duas ou mais variáveis independentes x1, x2, . . . , xn e derivadas parciais da fun¸cão u =

u(x1, x2, . . . , xn). A forma geral de uma equa¸c˜ao diferencial parcial de ordem

k ´e dada por

Ψ

µ

x1, x2, . . . , xn, u, , . . . ,

∂u ∂x₁, . . . ,

∂u ∂x_n,

∂2_u

∂x2 1

, ∂

2_u

∂x1∂x2

, . . . ,∂

k_u

∂xk n

¶

= 0.

(15)

§ 1.2 Equa¸cões Diferenciais Parciais-Classifica¸cão

ordem com duas vari´aveis x et, tem-se

a∂

2_u

∂x2 + 2b

∂2_u

∂x∂t +c ∂2_u

∂t2 =ϕ

µ

x, t, u,∂u ∂x,

∂u ∂t

¶

, (1.1)

onde a, be c s˜ao fun¸c˜oes de x, t, u, ux, ut, com ux =

∂u ∂x, ut=

∂u

∂t e u(x, t) a solu¸c˜ao de (1.1). Em outra nota¸c˜ao,

auxx+ 2buxt+cutt =ϕ(x, t, u, ux, ut),

onde a, be c s˜ao fun¸c˜oes de x, t, u, ux, ut, com ux =

∂u ∂x, ut=

∂u

∂t e u(x, t) a solu¸c˜ao de (1.1).

Se a _≡ b _≡ c _≡ 0 então a equa¸cão é de primeira ordem. Quando em (1.1) a, b e c são fun¸cões de x, t e u apenas ela é dita quase-linear; se, adi-cionalmente, ϕ não depender de ux e ut então é dita semi-linear; a equa¸cão

será linear se a, b, c eϕ forem fun¸cões apenas dex e t. Em quaisquer outras situa¸cões, a equa¸cão será não-linear.

Uma equa¸cão diferencial parcial como em (1.1) pode possuir uma fam´ılia de solu¸cões, uma solu¸cão única ou ainda não possuir nenhuma solu¸cão.

1.2 Classiﬁca¸

c˜

ao

Nesta Se¸cão são classificadas as equa¸cões diferenciais parciais quase-lineares de segunda ordem com duas variáveis independentes e coeficientes reais.

Considere apenas os termos com derivadas de segunda ordem de uma equa¸c˜ao diferencial parcial quase-linear, ou seja,

L(u) = a∂

2_u 2 + 2b

∂2_u

+c∂

2_u

(16)

§ 1.3 Equa¸c˜oes Diferenciais Parciais-Modelagem

onde a, b e c são fun¸cões de x, t, u, ux e ut, não simultaneamente nulos, e

u(x, t) a solu¸cão de (1.1). A classifica¸cão das equa¸cões diferenciais parciaisé feita por analogia com a teoria das cônicas no plano. O estudo das curvas planas de 2o _{grau é simplificado pela redu¸cão da equa¸cão a sua forma normal}

atrav´es de uma mudan¸ca linear de coordenadas.

Como no estudo das cônicas, pode-se fazer uma mudan¸ca de variáveis que reduz (1.2) à sua forma canônica; a classifica¸cão de (1.2) é feita analisando o sinal do discriminate b2 ₋_{ac. A mudan¸ca de variáveis que transforma}

a equa¸cão (1.2) em sua forma canônica é apresentada em [17], [16] e mais detalhadamente em [9]. Assim, o discriminante b2 ₋_4ac _{define o tipo da}

equa¸c˜ao diferencial parcial (1.2) em

• el´ıptica seb2₋_{4ac <} _0;

• parab´olica se b2₋_4ac_{= 0;}

• hiperb´olica se b2₋_{4ac >} _0.

A equa¸cão ut−µ∆u = 0 com (µ > 0) é do tipo parabólico e conhecida

como equa¸cão do calor e modela a condu¸cão de calor em meios cont´ınuos; ∆u = 0 é do tipo el´ıptico e denominada equa¸cão de Laplace e modela fenômenos estacionários; utt−c2uxx = 0 é do tipo hiperbólico e conhecida

como equa¸c˜ao da onda e pode modelar a propaga¸c˜ao de ondas num meio cont´ınuo.

1.3 Modelagem Matem´

atica da Propaga¸

c˜

ao

de Calor

(17)

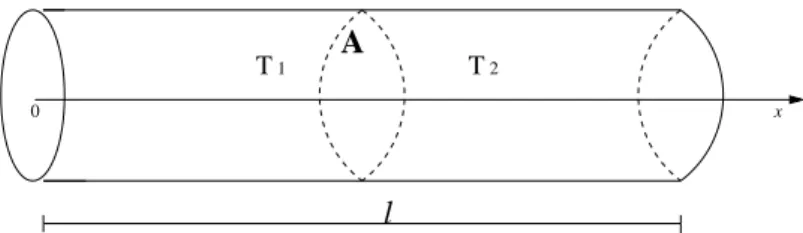
Considere uma barra de comprimento ℓ, com área de seçcão A, feita de um material condutor uniforme de calor. Suponha que a superf´ıcie lateral da barra esteja isolada termicamente de modo a não permitir, através dela, transferências de calor com o meio ambiente. Transferências podem, entre-tanto, ocorrer através das extremidades da barra.

A uniformidade do material e o isolamento térmico lateral implicam que o fluxo de calor se dê somente na dire¸cão longitudinal, e, portanto, tem-se um problema de condu¸cão de calor em uma dimensão apenas.

Considere que u(x, t) represente a temperatura em um ponto x desta barra no instante t, onde 0 _≤ x_≤ ℓ e 0 _≤ t _≤ T. Fixados dois pontos x0 e

x0+δcom 0< δ na barra, tˆem-se as respectivas temperaturasT1 =u(x0, t) e

T2 =u(x0+δ, t) para um dado instante de tempo t. Suponha que o ﬂuxo de

calor seja deT1 paraT2, ou seja,T1 > T2. A Figura (1.1) ilustra a propaga¸c˜ao

do calor para esta barra.

l

A

T2

T1

0 x

Figura 1.1: Propaga¸c˜ao do calor em uma barra. PelaLei de Condu¸c˜ao de Calor de Fourier, segue que

Q=µA|T2−T1| δ ,

(18)

Suponha que o limite lim

δ→0Q=µA|ux(x, t)| exista. Logo, o ﬂuxo de calor

entre as sec¸c˜oes x0 e x0 +δ pode ser expresso por

q(x, t) =₋µAux(x, t).

Se a condutibilidade térmica µfor dada em fun¸cão em x, ou seja, µ=µ(x), então o fluxo de calor entre as seçcões será dado por

q(x, t) = ₋Aµ(x)ux(x, t). (1.3)

Fixado um elemento da barra entre [x0 e x0 +δ] a quantidade de calor,

q, contida neste elemento da barra em um per´ıodo de tempo entret0 e t0+τ

´e expressa por

q=

Z t0+τ

t0

q(x0, t)dt−

Z t0+τ

t0

q(x0+δ, t)dt. (1.4)

Substituindo (1.3) na express˜ao (1.4) segue que

q =

Z t0+τ

t0

A[µ(x0+δ)ux(x0+δ, t)−µ(x0)ux(x0, t)]dt. (1.5)

Por outro lado, utilizando a densidade ρ(x), a quantidade de calor pode ser determinada da seguinte maneira:

Z t0+τ

t0

Z x0+τ

x0

cρ(x)Aut(x, t)dx dt, (1.6)

onde c é o calor espec´ıfico do material, dado em J/kgK, ou seja, Joules / kilograma Kelvin eρ(x) a densidade do material que a barra é feita e é dado em kilograma / metro cúbico, kg/m3_.

(19)

Z t0+τ

t0

Z x0+τ

x0

[µ(x)ux(x, t)]xdx dt=

Z t0+τ

t0

Z x0+τ

x0

ρ(x)Aut(x, t)dx dt.

Assim, segue que

cρ(x)ut(x, t) = [µ(x)ux(x, t)]x, (1.7)

onde ρ(x) e µ(x) são a densidade e a condutibilidade térmica da barra, re-spectivamente, e co calor espec´ıfico. Note que ρ(x), µ(x)>0,_∀x_{∈ ℜ}.

A equa¸cão (1.7) é a equa¸cão do calor com coeficientes variáveis para uma barra definida no dom´ınio Ω =_{(x, t)_{∈ ℜ}2_/0_≤_x_≤_ℓ _{e 0}_≤_t_≤_T_}_{, com}

ℓ,T positivos ﬁxos.

A equa¸cão (1.7), da forma que está definida, não garante a unicidade da solu¸cão u(x, t). Para que a equa¸cão possua solu¸cão são necessárias in-forma¸cões adicionais sobre a fun¸cãou(x, t) conhecidas como condi¸cão inicial e condi¸cões de contorno, maiores detalhes pode ser encontrados em [9], [11], [15], [16] e [17].

Considere a equa¸cão diferencial parcial do tipo parabólico dada em (1.7) em conjunto com as seguintes condi¸cões de contorno e condi¸cão inicial:

          

ρ(x)ut(x, t) = [µ(x)ux(x, t)]x,

u(x,0) = φ(x), x_∈[0, ℓ], u(0, t) =g(t), t_∈[0, T], u(ℓ, t) = h(t), t_∈[0, T],

(1.8)

(20)

teorema a seguir garante a existˆencia e unicidade da solu¸c˜ao do problema (1.8).

Teorema 1 Seja u cont´ınua em Ω¯, suas derivadas cont´ınuas em Ω. Ent˜ao

u ´e unicamente determinada em Ω¯ pelos valores de u em ∂Ω.

No Teorema 1 ¯Ω representa o interior do conjunto Ω, e∂Ω a sua fronteira, a demosntra¸c˜ao deste teorema encontra-se em [17] e [9].

(21)

Cap´ıtulo 2

M´

etodos Num´

ericos Cl´

assicos

Neste Cap´ıtulo são apresentados os métodos de Euler Expl´ıcito, Impl´ıcito e Crank-Nicolson. A condi¸cão de estabilidade para cada método também é determinada e mostra-se que os métodos numéricos obtidos são consistentes

com a equa¸cão diferencial parcial do tipo parabólico em (1.7) com densidade constante. Por simplicidade, tomar-se-á c= 1 eρ(x)_≡1, para todox, e um termo for¸cante f(x, t) de classe C∞_.

2.1 Discretiza¸

c˜

ao: Diferen¸

cas Finitas

Considere o seguinte problema de Dirichilet

          

ut(x, t)−[µ(x)ux(x, t)]x =f(x, t),

u(x,0) =φ(x) x_∈[0, L], u(0, t) =g(t) t_∈[0, T], u(L, t) =h(t) t_∈[0, T],

(2.1)

(22)

§ 2.1 Métodos Numéricos-Discretiza¸cão

O intervalo [0, L], da vari´avel espacial x, ´e dividido em N partes iguais de comprimento ∆x, obtendo-se N + 1 pontos xn = n∆x, n = 0,1, . . . , N,

onde ∆x = _NL. O instante de tempo final T do intervalo [0, T] da variável temporal t é dividido pelo passo de integra¸cão no tempo ∆t, determinado respeitando (quando existe) a condi¸cão de estabilidade do método numérico, obtendo-se a quantidade de passos no tempo M, ou seja, tem-se M + 1 pontos tm =m∆t, m = 0,1, . . . , M. Assim, procura-se aproximar a solu¸cão

da equa¸c˜ao diferencial nos pontos da malha (xn, tm), ilustrada na Figura

(2.1).

✁

✂✄

☎✆

✝✞

✟✠ ✡☛ ☞✌

0

T

L

t

x

n+1 n n−1

(x ,t )_{n m} m+1

m

m−1

Figura 2.1: Discretiza¸c˜ao do dom´ınio Ω.

O valor da solu¸c˜ao exata no ponto (xn, tm) ser´a representado por umn e a

aproxima¸cão obtida por um método numérico por Um n .

O problema (2.1) é discretizado utilizandodiferen¸cas finitas, ou seja, para aproximar a derivada de 1a _{ordem de} _{u(x, t) em rela¸cão a} _t _{utilizam-se as}

seguintes aproxima¸c˜oes:

ut(x, t)≈

u(x, t+ ∆t)₋u(x, t)

∆t (F´ormula Progressiva), (2.2) ut(x, t)≈

u(x, t)₋u(x, t₋∆t)

(23)

utiliza-se a seguinte aproxima¸c˜ao:

utt(x, t)≈

u(x, t₋∆t)₋2u(x, t) +u(x, t+ ∆t)

∆t2 . (2.4)

As aproxima¸cões acima são oriundas da manipula¸cão algébrica da ex-pansão em Série de Taylor da fun¸cão u em (x, t+ ∆t):

u(x, t_±∆t) =u_±∆t∂u ∂t +

∆x2 2!

∂2u ∂t2 ±

∆x3 6!

∂3u

∂t3 +O(∆t

4_). _(2.5)

Por intermédio da manipula¸cão algébrica das aproxima¸cões (2.2), (2.3) e (2.4) é poss´ıvel construir os Métodos de Euler Expl´ıcito, Euler Impl´ıcito e Crank-Nicolson, essas constru¸cões são detalhadas em [3], [4], [5] e [8].

Considere uma equa¸c˜ao diferencial parcial de segunda ordem deﬁnida no dom´ınio Ω.

P(u) = f(x, t, u, ut, ux) (2.6)

onde P(u) ´e dada por,

P(u) = a(x, t)uxx+b(x, t)uxt+c(x, t)utt+d(x, t)ut+e(x, t)ux,

com a, b, c, d, e, ue suas derivadas cont´ınuas em Ω. Um método de diferen¸cas finitas com passo de integra¸cão no tempo ∆te passo de integra¸cão no espa¸co ∆xpara (2.6) é denotado por P∆(U), as defini¸cões a seguir são discutidadas

em [25].

Defini¸cão 1 Um método de diferen¸cas finitas P∆Unm = 0 para uma equa¸cão

(24)

∆x

∞

X

j=−∞

|Unm|

2

≤CT∆x J

X

j=0

∞

X

i=−∞

¯ ¯U_ij

¯ ¯

2

, (2.7)

para 0_≤m∆t_≤T, com (∆x,∆t)_∈Λ.

A estabilidade é uma condi¸cão necessária para a convergência do método numérico, uma das formas funcionais de se determinar a condi¸cão de estabil-idade de um método numérico de passo único no tempo é a Análise de Von Neumann, que é ilustrada a seguir e, detalhada em [25].

An´alise de Von Neumann

Uma importante aplica¸cão dasTransformadas de Fourier é aAnálise de Von Neumann para a determina¸cão da condi¸cão de estabilidade de métodos numéricos baseados em diferen¸cas finitas. As Transformadas de Fourier fornecem condi¸cões suficientes e necessárias para a estabilidade dos métodos de diferen¸cas finitas.

POr intermédio daTransformada de Fourier a determina¸cão da condi¸cão de estabilidade de um método de diferen¸cas é reduzido a manipula¸cões algébricas. Considere a equa¸cãou(x, t)t=−µu(x, t)x, com 0< aeu(x, t)∈C2(Ω), onde

Ω é o dom´ınio da fun¸cão u(x, t), e o método de diferen¸cas dado a seguir: Um+1

n −Unm

∆t =−µ

Um

n −Unm−1

∆x , (2.8)

que pode ser reescrito como

U_nm+1 =

µ

1₋µ∆t ∆x

¶

U_nm+µ∆t ∆xU

m

n−1. (2.9)

Aplicando a Transformada Inversa de Fourier para Um

n, tem-se

U_nm = _√1 2π

Z π/∆x

−π/∆x

(25)

substituindo em (2.9) para Um

n eUnm−1, obt´em-se

U_nm+1 = √1

2π

Z π/∆x

−π/∆x

ein∆xξ

·µ

1₋µ∆t ∆x

¶

+µ∆t ∆xe

−i∆xξ

¸

ˆ

Um(ξ)dξ. (2.10)

Comparando a express˜ao (2.10) com a transformada Inversa de Fourier

U_nm+1 = _√1 2π

Z π/∆x

−π/∆x

ein∆xξUˆm+1(ξ)dξ,

e usando o fato que a Transformada de Fourier é única, segue que o integrando de (2.10) é igual ao da Transforma Inversa de Fourier, assim tem-se que

ˆ

Um+1(ξ) =

·µ

1₋µ∆t ∆x

¶

+µ∆t ∆xe

i∆xξ

¸

ˆ

Um(ξ) =g(∆xξ) ˆUm(ξ), (2.11)

onde

g(∆xξ) =

µ

1₋µ∆t ∆x

¶

+µ∆t ∆xe

i∆xξ_.

A expressão2.11 mostra que realizar um passo de integra¸cão no tempo do método numérico é equivalente a multiplicar a Transformada de Fourier da solu¸cão pelo fator de amplifica¸cão g(∆xξ). Assim, obtém-se a rela¸cão

ˆ

Um(ξ) = gm(∆xξ) ˆU0(ξ). (2.12)

(26)

∆x

∞

X

j=−∞

¯ ¯U_jm

¯ ¯

2

=

Z π/∆x

−π/∆x

¯ ¯ ¯Uˆ

m_(ξ)¯¯ ¯

2

dξ

=

Z π/∆x

−π/∆x|

g(∆xξ)_|2m¯¯ ¯Uˆ

0_(ξ)¯¯ ¯

2

dξ.

A desigualdade em (2.7) será satisfeita, com J = 0, se _|g(∆xξ)_|2m for apropriadamente limitada. Considereθ = ∆xξ, então o fator de amplifica¸cão para o método (2.8) é dado por

|g(θ)_|2 =

¯ ¯ ¯ ¯

µ

1₋µ∆t ∆x

¶

+µ∆t ∆xe −iθ ¯ ¯ ¯ ¯ = µ

1₋µ∆t ∆x +µ

∆t

∆xcos (θ)

¶2

+µ2

µ

∆t ∆x

¶2

sin2(θ)

=

µ

1₋2µ∆t ∆xsin 2 µ θ 2 ¶¶2

+ 4µ2

µ ∆t ∆x ¶2 sin2 µ θ 2 ¶ cos2 µ θ 2 ¶

=1₋4µ∆t ∆xsin 2 µ θ 2 ¶

+ 4µ2

µ ∆t ∆x ¶2 sin4 µ θ 2 ¶

+ 4µ2

µ ∆t ∆x ¶2 sin2 µ θ 2 ¶ cos2 µ θ 2 ¶

=1₋4µ∆t ∆x

µ

1₋µ∆t ∆x ¶ sin2 µ θ 2 ¶ .

Note que_|g(θ)_|´e limitado por 1 se 0_≤µ∆t

∆x ≤1. Assim, por (2.12), segue

que

∆x

∞

X

j=−∞

¯ ¯U_jm

¯ ¯

2

≤

Z π/∆x

−π/∆x

¯ ¯ ¯Uˆ

0_(ξ)¯¯ ¯

2

dξ= ∆x

∞

X

j=−∞

¯ ¯U_j0

¯ ¯

2

.

Pela defini¸cão (2.7) o método é estável. Entretanto, se o númeroµ_∆∆_xt não estiver fixado entre 0 e 1, quando ∆xe ∆ttenderem a zero, então_|g(θ)_|será maior do que 1 para alguns valores de θ, e o método será instável.

(27)

Teorema 2 Um método de diferen¸cas finitas de passo único (com coefi-cientes constantes) é estável, se e somente se, existir uma constante K (independente de θ, ∆x e ∆t) e alguns passos de integra¸cão ∆t0 e ∆x0 tais

que

|g(θ,∆x,∆t)_{| ≤}1 +K∆t, (2.13)

para todo θ, 0<∆t_≤∆t0, e 0<∆x≤∆x0.

Se g(θ,∆x,∆t) for independente de ∆x e ∆t, a condi¸c˜ao de estabilidade (2.13) pode ser substitu´ıda por

|g(θ)_{| ≤}1.

Este teorema mostra que para se determinar a condi¸cão de estabilidade de um método de diferen¸cas finitas considera-se apenas o fator de amplifica¸cão g(∆xξ) oriundo da análise de Von Neumann, este teorema, e as defini¸cões 2 e 3 são discutidas em [25].

Defini¸cão 2 Dada uma equa¸cão diferencial parcialP(u)definida num dom´ınio

Ω e um método de diferen¸cas finitas, P∆(U), com passos de integra¸cão no

tempo e espa¸co dados por ∆t e ∆x. O método de diferen¸cas finitas é dito consistente com a equa¸cão diferencial parcial se para qualquer fun¸cão suave

φ(x, t)

|P φ(x, t)₋P∆φ(x, t)| →0 quando ∆x,∆t →0, ∀(x, t)∈Ω

A consistência é uma condi¸cão necessária para a convergência do método numérico, pois, garante que o método de diferen¸cas finitas aproxima a equa¸cão diferencial quando os passos de integra¸cão no tempo tendem a zero.

(28)

§ 2.2 M´etodos Num´ericos-Euler Expl´ıcito

u(x, t), da equa¸c˜ao diferencial eUm

n a aproxima¸cão gerada pelo método numérico,

tais que,

U_n0 _−→u(x,0), quando n∆x_−→x,

ent˜ao

U_nm _−→u(x, t), quando (n∆x, m∆t)_−→(x, t),

com

∆x,∆t_−→0.

O Teorema de Lax-Richtmyer enuncia um resultado necessário e suficiente para a convergência de métodos de diferen¸cas finitas.

Teorema 3 Teorema de equivalência de Lax-RichtmyerUm método consistente de diferen¸cas finitas para uma equa¸cão diferencial parcial é con-vergente se e somente se o método for estável.

O Teorema de equivalência de Lax é demostrado em [25], as defini¸cões acima são encontradas em [8], [25].

2.2 M´

etodo de Euler Expl´ıcito

Na discretiza¸cão da equa¸cão (2.1) utilizou-se a seguinte aproxima¸cão para a derivada de primeira ordem no espa¸co:

ux(xn, tm)≃

um n+1

2 −

um n−12

∆x ,

onde um n+1

2

=u(x_n₊1 2, tm).

(29)

no tempo (2.2) obt´em-se: Um+1

n −Unm

∆t −

µ_n₊1 2(U

m

n+1−Unm)−µn−1 2(U

m

n −Unm−1)

∆x2 =f

m

n , (2.14)

ou seja,

Unm+1 =Unm+

∆t ∆x2

h

µ_n₊1 2(U

m

n+1−Unm)−µn−12(U

m

n −Unm−1)

i

+∆tfnm, (2.15)

onde µ_n₊1

2 =µ(xn+

∆x

2 ), e n= 1,2. . . , N −1 e m= 0,1. . . , M −1.

Lembrando que o intervalo espacial [0, L] possuiN+1 pontos e o intervalo temporal [0, T] cont´em M + 1 pontos.

No caso especial em que a condutibilidade térmica µ é constante, a ex-pressão (2.15) pode ser escrita como

U_nm+1 =U_nm+µ ∆t ∆x2

¡

U_nm₊₁₋2U_nm+U_nm₋₁¢

+ ∆tf_nm, (2.16) com n = 1,2. . . , N₋1 e m = 0,1. . . , M ₋1.

A Figura (2.2) ilustra a molécula computacional da fórmula (2.16) que é conhecida como Método de Euler Expl´ıcito.

∆

x

∆

t

n−1,m n,m n+1,m

n,m+1

(30)

´e necess´ario conhecer os valores Um

n−1, Unm e Unm+1 para que a aproxima¸c˜ao

Um+1

n possa ser calculada, a constru¸cão deste método numérico pode ser

encontrada em [3], [4], [5] e [8].

Condi¸c˜ao de Estabilidade do M´etodo de Euler Expl´ıcito

Considere o problema proposto em (2.1), com o dom´ınio discretizado e o M´etodo de Euler Expl´ıcito descrito em (2.16) e suponha que f(x, t)_≡0.

No Critério de Von Neumann, para determinar estabilidade do esquema, examina-se a propaga¸cão do erro global, tendo em vista que ele é a soma de erros mais simples chamados de harmônicos. O processo é inspirado na expansão de uma fun¸cão em série de Fourier. Substitui-se um

n por gmeinθ em

(2.16), e adotando µM = max

0≤x≤L{µ(x)}, tem-se:

gm+1einθ =gmeinθ+ ∆t ∆x2µM

¡

gmei(n+1)θ₋2gm+1einθ+gmei(n−1)θ¢

⇒

ggmeinθ =gmeinθ+ ∆t ∆x2µM

¡

gmeinθeiθ₋2gmeinθ+gmeinθe−iθ¢

,

logo,

g = 1 + ∆t ∆x2µM

¡

eiθ ₋2 +e−iθ¢

,

utilizando a identidadeea+bi₌_ea_{(cos (b)+}_i_{sin (b)) na express˜ao acima segue}

que:

g = 1 + ∆t

∆x2µM(2 cos (θ)−2) = 1 + 2

∆t

∆x2µM (cos (θ)−1),

pela seguinte rela¸c˜ao trigonom´etrica cos (x) = 1₋2 sin2¡_x

2

¢

tem-se

g = 1₋4 ∆t

∆x2µM sin 2

µ

θ 2

¶

(31)

Para que o método seja estável é necessário que haja amortecimento do erro, ou seja _|g_{| ≤}1.

Assim,

−1_≤1₋4 ∆t

∆x2µMsin 2 µ θ 2 ¶ ≤1, donde, ´e necess´ario que

−1_≤1₋4 ∆t

∆x2µMsin 2 µ θ 2 ¶ ⇒

2_≥4 ∆t

∆x2µMsin 2 µ θ 2 ¶ ⇒ 1 2 ≥ ∆t

∆x2µM sin 2

µ

θ 2

¶

Portanto, para que o Método de Euler Expl´ıcito seja estável é necessário que os parâmetros ∆x e ∆t atendam a seguinte condi¸cão de estabilidade:

∆t ∆x2 ≤

1 2µM

,

onde µM = max

0≤x≤L{µ(x)}.

Note que esta restri¸c˜ao para o tamanho do passo na dire¸c˜ao t pode ser interpretada como ∆t < ∆x2

2µM, assim, se a aproxima¸c˜ao for feita para um valor

de T grande, o esfor¸co computacional tamb´em ser´a alto.

Consistˆencia do M´etodo de Euler Expl´ıcito

Suponha que u(x, t) seja uma fun¸cão suficientemente suave, P u(x, t) a equa¸cão diferencial em (2.1) eP∆ua equa¸cão diferencial em (2.1) discretizada

com o M´etodo Euler Expl´ıcito, com um

n = u(xn, tm) e µM = max

0≤x≤L{µ(x)},

ent˜ao:

P∆u=

um+1

n −umn

∆t −µM um

n−1−2umn +umn+1

(32)

Aplicando as expansões em série de Taylor (2.5) acima obtém-se:

Pδu =

um

n + ∆tut+ 1₂∆t2utt+O(∆t3)−umn

∆t −µM

um

n−1−2umn +umn+1

∆x2 ,

= ∆tut+O(∆t

2₎

∆t −µM

∆x2_u

xx+O(∆x3)

∆x2 ,

= ut+O(∆t)−µM (uxx+O(∆x)),

logo

P∆u=ut+O(∆t)−µM(uxx+O(∆x)),

onde as derivadas s˜ao calculadas no ponto (xn, tm), ou seja, ut=ut(xn, tm).

Considerando a diferen¸ca entre P u e P∆u tem-se,

P u₋P∆u=ut−µMuxx−ut+O(∆t) +µM(uxx+O(∆x)),

P u₋P∆u=O(∆t) +µMO(∆x).

Assim

lim

∆t→0 ∆x→0

P u₋P∆u= lim ∆t→0 ∆x→0

O(∆t) +µMO(∆x) = 0.

Portanto, o Método de Euler Expl´ıcito é consistente com a equa¸cão diferen-cial.

(33)

§ 2.3 M´etodos Num´ericos-Euler Impl´ıcito

2.3 M´

etodo de Euler Impl´ıcito

A discretiza¸c˜ao de (2.1) foi realizada utilizando-se a seguinte aproxima¸c˜ao para aderivada de primeira ordem,

ux(xn, tm)≃

um n+1

2 −

um n−12

∆x ,

onde um n+1

2

=u(x_n₊1 2, tm).

Aplicando na parte espacial da equa¸c˜ao (2.1) e aproximando a derivada de primeira ordem no tempo por diferen¸cas regressivas no tempo obt´em-se,

Um+1

n −Unm

∆t −

µ_n₊1 2(U

m+1

n+1 −Unm+1)−µn−12(U

m+1

n −Unm−+11 )

∆x2 =f

m+1

n , (2.17)

agrupando as parcelas calculadas no mesmo instante de tempo tem-se

−_∆x∆t₂µ_n₊1 2U

m+1

n+1 +

µ

1 + ∆t ∆x2

³

µ_n₊1

2 +µn− 1 2

´¶

U_nm+1₋ ∆t

∆x2µn−12U

m+1

n−1 =Unm+∆tfnm+1,

(2.18) onde µ_n₊1

2 =µ(xn+

∆x

2 ), comn = 1,2, . . . , N −1 e m = 0,1, . . . , M −1.

O método descrito em (2.18) é chamado Método de Euler Impl´ıcito.

No caso em queµ(x) for uma fun¸c˜ao constante, a express˜ao (2.18) resume-se a

−ωUnm+1+1+ (1 + 2ω)Unm+1−ωUnm−+11 =Unm+ ∆tfnm+1, (2.19)

onde ω =µ_∆∆_xt2.

(34)

a resolu¸c˜ao do seguinte sistema linear:

AUm+1 =Um+Cm+1+Fm+1, m= 0,1, . . . , M −1,

onde: A=       

1 + 2ω ₋ω 0 . . . 0 0 ₋ω 1 + 2ω ₋ω . . . 0

... ...

0 . . . 0 ₋ω 1 + 2ω

      

, Um =

         Um 1 Um 2 ... Um

N−2

Um N−1

         ,

Cm+1 =ω

        

U₀m+1 0 ... 0 U_Nm+1

        

, Fm+1 = ∆t

        

f₁m+1 fm+1

2

... f_Nm₋+1₂ f_Nm₋+1₁

         ,

A molécula computacional do Método de Euler Impl´ıcito é ilustrada na Figura (2.3).

∆

x

∆

t n,m+1 n−1,m+1 n+1,m+1 n,m

(35)

seja, ´e necess´ario conhecer os valores U_nm₋+1₁ , Um

n e Unm+1+1 para que a

aprox-ima¸c˜aoUm+1

n possa ser calculada, a constru¸c˜ao do M´etodo de Euler Impl´ıcito

pode ser encontrada em [3], [4], [5] e [8].

Condi¸c˜ao de Estabilidade do M´etodo de Euler Impl´ıcito

Considere o problema proposto em (2.1), com dom´ınio discretizado e o M´etodo de Euler Impl´ıcito descrito em (2.18). Considerando f(x, t) _≡ 0 e µM = max

0≤x≤L{µ(x)}, substitui-seu m

n por gmeinθ em (2.19), obtendo-se:

− ∆t

∆x2µMg

m+1_ei(n+1)θ₊

µ

1 + 2 ∆t ∆x2µM

¶

gm+1einθ₋ ∆t ∆x2µMg

m+1_ei(n−1)θ _=gm_einθ

⇒

− ∆t

∆x2µMgg

m_einθ_eiθ₊

µ

1 + 2 ∆t ∆x2µM

¶

ggmeinθ ₋ ∆t ∆x2µMgg

m_einθ_e−iθ _=gm_einθ_,

e, portanto,

−_∆x∆t2µMge

iθ₊

µ

1 + 2 ∆t ∆x2µM

¶

g₋ ∆t

∆x2µMge−

iθ _{= 1}

Utilizando novamente a identidadeea+bi₌_ea_{(cos (b)+i}_{sin (b)), segue que}

−2 ∆t

∆x2µMgcos (θ) +

µ

1 + 2 ∆t ∆x2µM

¶

g =1_⇒ g

µ

2 ∆t

∆x2µM(1−cos (θ)) + 1

¶

=1.

Aplicando a rela¸c˜ao trigonom´etrica cos(x) = 1 ₋ 2 sin2¡_x

2 ¢ na express˜ao acima, tem-se g µ 4 ∆t

∆x2µMsin 2 µ θ 2 ¶¶ = 1. Logo,

g = 1

(36)

e segue que

|g_|<1 _∀θ.

Portanto, o Método de Euler Impl´ıcito é incondicionalmente estável, ou seja, independentemente do tamanho do passo de integra¸cão no tempo o Método de Euler Impl´ıcito não amplifica os erros cometidos na aproxima¸cão numérica da solu¸cão do equa¸cão diferencial.

Consistˆencia do M´etodo de Euler Impl´ıcito

Suponha que u(x, t) seja uma fun¸cão suficientemente suave, P u(x, t) a equa¸cão diferencial e P∆u o Método Euler impl´ıcito, com umn = u(xn, tm) e

µM = max

0≤x≤L{µ(x)}, ent˜ao

P∆u=

um

n −umn−1

∆t −µM um

n−1−2umn +umn+1

∆x2 . (2.20)

Substituindo um+1

n , umn−1 e umn+1 pelas suas expans˜oes em s´erie de Taylor na

equa¸c˜ao (2.20) tem-se

P∆u =

um

n −umn + ∆tut+O(∆t2)

∆t −µM

−∆xux+∆x

2

2 uxx+ ∆xux+ ∆x2

2 uxx+O(∆x 3₎

∆x2

= ut+O(∆t)−µM(uxx +O(∆x)),

logo,

P∆u=ut−µMuxx+O(∆t) +O(∆x),

onde as derivadas s˜ao calculadas no ponto (xn, tm), ou seja, ut=ut(xn, tm).

Considerando a diferen¸ca entre P ue P∆u tem-se

(37)

§ 2.4 M´etodos Num´ericos - Crank-Nicolson

assim,

P u₋P∆u=O(∆t) +O(∆x),

segue que,

lim

∆t→0 ∆x→0

P u₋P∆u= lim ∆t→0 ∆x→0

O(∆t) +O(∆x) = 0.

Portanto, o Método de Euler Impl´ıcito é consistente com a equa¸cão diferencial parcial. Pelos resultados obtidos em (2.3) o Método de Euler Impl´ıcito é convergente.

2.4 M´

etodo de Crank-Nicolson

O Método de Crank-Nicolson pode ser obtido tomando-se a média entre os métodos de Euler Expl´ıcito e Impl´ıcito. Assim, pelas expressões em (2.14) e (2.17), o Método de Crank-Nicolson é dado por:

Um+1

n −Unm

∆t =

µ_n₊1 2

¡

U_nm₊₁+1+Um

n+1−Unm+1−Unm

¢

2∆x2 +

fm+1

n

2

−µi− 1 2

¡

Um+1

n +Unm−Unm−1−Unm−+11

¢

2∆x2 +

fm n

2 ,

(2.21)

com µ_n₊1

2 =µ(xn+

∆x

2 ), comn = 1,2, . . . , N −1 e m = 0,1, . . . , M −1,

ou ainda,

−_2∆x∆t₂µ_n₋1 2U

m+1

n−1 +

µ

1 + ∆t 2∆x2

³

µ_n₊1

2 +µn− 1 2

´¶

U_nm+1₋ ∆t

2∆x2µn+12U

m+1

n+1 =

∆t

2∆x2µn−12U

m n−1+

µ

1₋ ∆t 2∆x2

³

µ_n₊1

2 −µn− 1 2

´¶

U_nm+ ∆t

2∆x2µn+12U

m

n+1+ ∆tf ,¯

(2.22)

onde ¯f = f

m+1

n +fnm

(38)

Se µ(x) for um fun¸cão constante constante então a expressão (2.22) pode ser escrita como:

−ωU_nm₋+1₁ + 2(1 +ω)U_nm+1₋ωU_nm₊₁+1 =ωU_nm₋₁+ 2(1₋ω)U_nm+ωU_nm₊₁+ ∆tf ,¯ (2.23) com ω =µ ∆t

∆x2, n = 1,2, . . . , N −1 e m= 0,1, . . . , M −1.

Note que, para obter a aproxima¸cão da solu¸cão no instantetm+1, é necessária

a resolu¸c˜ao do seguinte sistema linear:

AUm+1 =BUm+Cm+1+Fm, com m= 0,1, . . . , M −1.

onde, A=       

1 +ω ₋ω

2 0 . . . 0

0 ₋ω₂ 1 +ω ₋ω₂ . . . 0

... ...

0 . . . 0 ₋ω₂ 1 +ω

      

, Um+1 =

        

U₁m+1 U2m+1

... U_Nm₋+1₂ U_Nm₋+1₁

         , B =       

1₋ω ω₂ 0 . . . 0 0 ω₂ 1₋ω ω₂ . . . 0

... ...

0 . . . 0 ω

2 1−ω

      

, Cm+1 =

ω 2          Um

0 +U0m+1

0 ... 0 Um

N +UNm+1

(39)

e Fm =

∆t 2

        

fm

1 +f1m+1

fm

1 +f1m+1

... fm

N−2+fNm−+12

fm

N−1+fNm−+11

        

O método descrito em (2.22) é chamadoMétodo de Crank-Nicolson, e sua mólecula computacional é ilustrada na Figura (2.4).

∆

x

∆

t n,m+1

n−1,m+1 n+1,m+1

n+1,m n,m

n−1,m

Figura 2.4: Molécula computacional do Método de Crank-Nicolson. A Figura (2.4) ilustra a dependência que a aproxima¸cão obtida no ponto (xn, tm+1) em rela¸cão aos pontos (xn−1, tm+1), (xn+1, tm+1), (xn−1, tm), (xn, tm)

e (xn+1, tm), ou seja, ´e necess´ario conhecer-se os valores U₋m1+1, Unm+1+1, Unm−1,

Um

n e Unm+1 para que a aproxima¸c˜ao Unm+1 possa ser calculada, a constru¸c˜ao

deste método numérico é discutida em [3], [4], [5] e [8].

Condi¸c˜ao de Estabilidade do M´etodo de Crank-Nicolson

De maneira análoga a feita aos outros métodos faz-se a substitui¸cãoum n =

gm_einθ _{na express˜ao (2.23), adotando}_ω ₌ ∆t

∆x2µM, onde µM = max

0≤x≤L{µ(x)},

(40)

−_∆x∆t2µMg

m+1_ei(n−1)θ_{+ 2}

µ

1 + ∆t ∆x2µM

¶

gm+1einθ₋ ∆t ∆x2µMg

m+1_ei(n+1)θ ₌

= ∆t ∆x2µMg

m_ei(n−1)θ_{+ 2}

µ

1₋ ∆t ∆x2µM

¶

gmeinθ+ ∆t ∆x2µMg

m_ei(n+1)θ_.

Agrupando os termos semelhantes,

−_∆x∆t₂µMggmeinθe−θ+ 2

µ

1 + ∆t ∆x2µM

¶

ggmeinθ₋ ∆t ∆x2µMgg

m_einθ_eiθ ₌

= ∆t ∆x2µMg

m_einθ_e−iθ_{+ 2}

µ

1₋ ∆t ∆x2µM

¶

gmeinθ+ ∆t ∆x2µMg

m_einθ_eiθ_.

Logo,

−_∆x∆t₂µMg

¡

e−iθ₊_geiθ¢

+ 2

µ

1 + ∆t ∆x2µM

¶

g = ∆t ∆x2µM

¡

e−iθ₊_eiθ¢

+ 2

µ

1₋ ∆t ∆x2µM

¶

Lembrando que ea+bi ₌_ea_{(cos (b) +}_i_{sin (b)), tem-se}

−2 ∆t

∆x2µMgcos (θ) + 2

µ

1 + ∆t ∆x2µM

¶

g =2 ∆t

∆x2µMcos (θ) + 2

µ

1₋ ∆t ∆x2µM

¶

⇒

g

µ

1 + ∆t

∆x2µM(1−cos (θ))

¶

= ∆t

∆x2µM(cos (θ)−1) + 1

e utilizando a rela¸c˜ao trigonom´etrica cos (x)₋1 = ₋2 sin2¡_x

2

¢

, tem-se

g

µ

1 + 2 ∆t

∆x2µMsin 2

µ

θ 2

¶¶

= 1₋2 ∆t

∆x2µM sin 2 µ θ 2 ¶ , logo

g = 1−2

∆t

∆x2µMsin

2¡_θ

2

¢

1 + 2 ∆t

∆x2µMsin

2¡_θ

2

¢ <1, ∀ θ.

(41)

Consistˆencia do M´etodo de Crank-Nicolson

Suponha que u(x, t) seja uma fun¸cão suficientemente suave, P u(x, t) a equa¸cão diferencial e P∆u o método de Crank-Nicolson, comumn =u(xn, tm)

e µM = max

0≤x≤L{µ(x)}, ent˜ao

P∆u=

um+1

n −umn

∆t −

µM

2∆x2

¡

um

n−1+umn+1−2(umn +unm+1) +umn−+11 +umn+1+1

¢

, (2.24) Note que, aplicando as expans˜oes de (2.5), obt´em-se

• u

m+1

n −umn

∆t =ut+O(∆t),

• u

m

n−1−2umn +umn+1

∆x2 =uxx+O(∆x 2_),

• u

m

n−1−2umn +umn+1

∆x2 =u

+

xx+O(∆x2),

onde todas as derivadas são calculadas no ponto (xn, tm), única exce¸cão

feita a u+

xx que ´e calculada no ponto (xn, tm+ ∆t).

Substituindo as aproxima¸c˜oes na equa¸c˜ao (2.24) segue que

P∆u=ux+O(∆t)−µM

uxx+u+xx+O(∆x2)

2 .

Logo,

lim

∆t→0 ∆x→0

P u₋P∆u = lim ∆t→0 ∆x→0

µ

ut−µMuxx−ut+O(∆t) +µM

uxx+u+xx+O(∆x2)

2

¶

=_⇒

lim

∆t→0 ∆x→0

P u₋P∆u = ut−µMuxx−ut+µM

uxx+uxx

2 = 0.

(42)

Cap´ıtulo 3

A T´

ecnica do Super-Passo

A Técnica do Super-Passo é uma forma simples e eficiente de se reciclar códigos expl´ıcitos, melhorando a sua performace computacional. A Técnica do Super-Passo é baseada nos Métodos Runge-Kutta-Chebyshev, como pode ser visto em [28]. Assim como os Métodos Runge-Kutta, a Técnica do Super-Passo é composta por N sub-passos (estágios) e relaxa a restri¸cão temporal imposta pela condi¸cão de estabilidade do método numérico expl´ıcito.

Neste Cap´ıtulo, a fim de tornar a compreensão da técnica a mais simples poss´ıvel, é apresentada a formula¸cão da Técnica do Super-Passo aplicada ao Método de Euler Expl´ıcito para um sistema de equa¸cões diferenciais or-dinárias. O método aqui descrito poder ser aplicado em malhas estruturadas e não estruturadas na resolu¸cão numérica de equa¸cões diferenciais parciais do tipo parabólico lineares e não lineares para uma, duas ou três dimensões.

´

(43)

§ 3 Super-passo

Considere o sistema de equa¸c˜oes diferenciais ordin´arias

  

dU

dt +AU(t) = 0, t >0 U(0) =U0,

(3.1)

onde A é uma matriz n_×n simétrica definida positiva e U0 é um vetor em

ℜn _dado.

O M´etodo de Euler Expl´ıcito para o sistema (3.1) pode ser escrito como

(

Um+1 _{= (I}₋_∆tA)_Um_, _m_{= 0,}_{1, . . .}

U0 ₌_U 0,

(3.2)

sendo ∆t > 0 o passo de integra¸c˜ao no tempo, I a matriz identidade de ordem n e Um _{∈ ℜ}n _{um vetor que representa a aproxima¸c˜ao obtida pelo}

método numérico (3.2) para a solu¸cão do sistema (3.1) no instante de tempo tm =m∆t.

O esquema numérico em (3.2) é estável se

ρ(I₋∆tA)<1, (3.3)

sendo queρ(_·) denota oraio espectral da matriz (I₋∆tA),λmax o seu maior

autovalor e λmin o menor. A condi¸c˜ao em (3.3) ´e satisfeita com a escolha

∆t <∆texpl =

2 λmax

. (3.4)

(44)

§ 3.1 M´etodos Num´ericos-Super-Passo

Um passo de integra¸cão no tempo da Técnica do Super-Passo ∆T, con-siste de N sub-passos (estágios) τi, com i = 1, . . . , N, ou seja, para cada

super-passo de integra¸c˜ao no tempo ∆T s˜ao calculados os N sub-passos.

Um+1,1 = (I₋Aτ1)Um,

Um+1,2 = (I₋Aτ2)Um+1,1,

...

Um+1 =Um+1,N = (I₋AτN)Um+1,N−1.

Substituindo recursivamente até um cicloj obtém-se uma expressão para os primeiros j sub-passos,

Um+1,j =

j

Y

i=1

(I ₋Aτi)Um, j = 1,2, . . . , N m= 0,1. . .

A demonstra¸c˜ao desta igualdade segue por indu¸c˜ao sobrej.

A Técnica do Super-Passo aplicada ao Método de Euler Expl´ıcito comN sub-passos é dada por

Um+1 =

N

Y

i=1

(I₋Aτi)Um, m = 0,1, . . . , (3.5)

ondeAé uma matrizn_×nsimétrica definida positiva,Ié a matriz identidade de ordem n, N a quantidade de sub-passos, τi o i-ésimo sub-passo, que será

explicitado na próxima Se¸cão, e Um _{representa aproxima¸cão numérica para}

(45)

3.1 Condi¸

c˜

ao de Estabilidade

A Técnica do Super-Passo procura relaxar a restri¸cão ao passo de inte-gra¸cão no tempo imposta por (3.4), assim a condi¸cão de estabilidade não é atendida ao final de todo o passo de integra¸cão ∆t, mas apenas ao final de um ciclo de N passos no tempo. A condi¸cão de estabilidade é imposta sobre o super-passo ∆T, enquanto tenta-se maximizar a soma ∆T =PN

i=1

τi.

Uma condi¸cão suficiente para que a condi¸cão de estabilidade do algoritmo (3.5) dada em (3.3) seja atendida é,

N

Y

i=1

|1₋λτi|<1, ∀λ∈[λmin, λmax], (3.6)

onde QN

i=1|

1₋λτi| é o fator de amplifica¸cão do método e λmin e λmax são o

menor e maior autovalor da matriz A.

Existem v´arios valores de τi que satisfazem a condi¸c˜ao acima, mas o

objetivo ´e determinar τ′_s _{tais que:}

∆T =

N

X

i=1

τi seja o maior poss´ıvel.

Entretanto, o problema em (3.6) não é conveniente, pois a condi¸cão de es-tabilidade possui uma desigualdade estrita. A condi¸cão (3.6) será substitu´ıda por

N

Y

i=1

|1₋λτi| ≤k, ∀λ∈[ǫ, λmax], (3.7)

onde ǫ_∈(0, λmin] ek ∈(0,1), ambos ﬁxos.

(46)

O problema de encontrar os valores “´otimos”para osτ′_s_{pode ser reescrito}

como encontrar τ1, τ2, . . . , τN tais que

PN(λ) = N

Y

i=1

(1₋λτi) (3.8)

satisfa¸ca

|PN(λ)| ≤k, k <1 ∀λ∈[ǫ, λmax] (estabilidade),

¯ ¯ ¯ ¯

dPN

dλ (0)

¯ ¯ ¯ ¯=

N

X

i=1

τi, (valores ´otimos).

Considere o seguinte polinˆomio de grauN em λ,

QN(λ) =

TN

µ

λmax+ǫ−2λ

λmax−ǫ

¶

TN

µ

λmax+ǫ

λmax−ǫ

¶ , (3.9)

onde ǫ_∈(0, λmin] eλ ∈[ǫ, λmax].

O numerador é um Polinômio de Chebyshev de grauN definido no inter-valo [ǫ, λmax], e o denominador é uma constante.

Pelas propriedades dos Polinˆomios de Chebyshev, tem-se que,

¯ ¯ ¯ ¯

TN

µ

λmax+ǫ−2λ

λmax−ǫ

¶¯ ¯ ¯ ¯≤

1.

Assim, o polinˆomio em (3.9) ´e limitado por

k′ ₌ 1

TN

µ

λmax+ǫ

λmax−ǫ

(47)

note que

λmax+ǫ

λmax−ǫ

>1,

e, pelas propriedades dos polinˆomios de Chebyshev, tem-se que

¯ ¯ ¯ ¯ TN µ

λmax+ǫ

λmax−ǫ

¶¯ ¯ ¯ ¯

>1,

onde ǫ_∈(0, λmin] e 0< λmax.

Ent˜ao

|k′_|_<_1.

As ra´ızes do polinômio QN(λ) são as mesmas do Polinômio de Chebyshev

TN

³

λmax+ǫ−2λ

λmax−ǫ

´

e s˜ao dadas por:

λi =

1 2

µ

(₋λmax+ǫ) cos

µ

2i₋1 N

π 2

¶

+λmax+ǫ

¶

, i= 1, . . . , N.

onde ǫ_∈(0, λmin).

Voltando ao fator de amplifica¸cão da Técnica do Super-Passo, que é dado pela fun¸cão,

PN(λ) = N

Y

i=1

(1₋λτi). (3.10)

Procura-se determinar quais valores deτ′_s _satisfazem:

|PN(λ)| ≤k, ∀λ∈[ǫ, λmax], k <1, (3.11)

¯ ¯ ¯P ′ N(0) ¯ ¯ ¯= N X i=1

τi. (3.12)

Escolhe-se

τi =

1 λi

(48)

Ent˜ao, (3.10) pode ser escrito como,

PN(λ) = N

Y

i=1

µ

1₋λ 1 λi

¶

, com i= 1, . . . N.

Assim, asN ra´ızes de (3.10) s˜ao dadas por λi, i= 1, . . . , N.

Logo, tˆem-se dois polinˆomios, PN e QN de grau N com as mesmas N

ra´ızes λi, e PN(0) =QN(0) = 1.

Portanto,

PN(λ)≡QN(λ), ∀λ∈(ǫ, λmax].

A condi¸c˜ao em (3.11) ´e garantida escolhendok =k′_{, ou seja,}

|PN(λ)| ≡ |QN(λ)| ≤ |k′|<1, ∀λ∈(ǫ, λmax].

Pelos artigos [2], [1] e [18], sabe-se que o maior valor para a soma em (3.12) ´e obtido escolhendo,

τi =

1 λi

, com i= 1, . . . , N.

Os sub-passos de integra¸c˜ao no tempo τ′_s _{s˜ao dados explicitamente por,}

τi = 2

µ

(₋λmax+ǫ) cos

µ

2i₋1 N

π 2

¶

+λmax+ǫ

¶−1

, i= 1, . . . , N,

que podem ser reescritos mais convenientemente como,

τi = ∆texpl

µ

(₋1 +ν) cos

µ

2i₋1 N

π 2

¶

+ 1 +ν

¶−1

, i= 1, . . . , N, (3.13)

ondeν = _λ ǫ

max, 0< ν <1, ∆texpl =

2

(49)

Note que seN = 1 e ν = 0 segue que τ1 = ∆texpl, ou seja, a T´ecnica do

Super-Passo realiza as mesmas aproxima¸cões do Método de Euler Expl´ıcito. Utilizando a condi¸cão (3.12) e uma das formula¸cões dos Polinômios de Chebyshev o tamanho do super-passo, ∆T, pode ser expresso explicitamente como,

∆T =

N

X

i=1

τi = ∆texpl

N 2√ν

µ

(1 +√ν)2N ₋₍₁₋√_ν)2N

(1 +√ν)2N _{+ (1}₋√_ν)2N

¶

, (3.14)

Assim,

∆T _−−→

ν→0 N 2_∆t

expl,

isso ´e,

∆T

∆texpl −−→ν→0

N2. (3.15)

A Tabela (3.1) apresenta os diferentes valores do super-passo de inte-gra¸cão no tempo quando ν _→ 0, e a aproxima¸cão numérica para N2 _no

limite (3.15). Para se obter os resultados tabelados aplicou-se a (3.14) com 9 sub-passos, e o passo de integra¸cão no tempo, determinado pela condi¸cão de estabilidade do Método de Euler Expl´ıcito é ∆texpl = 1.851852×10−6.

ν ∆T N2

10−1 _2.635191_×₁₀−5 _14.23

10−2 _7.895230_×₁₀−5 _42.63

10−3 _1.356929_×₁₀−4 _73.27

10−4 _1.484056_×₁₀−4 _80.13

10−5 _1.498387_×₁₀−4 _80.91

10−6 _1.499839_×₁₀−4 _80.99

Tabela 3.1: Aproxima¸c˜ao num´erica para o limite (3.15).

(50)

§ 3.3 Ordem

Note queN passos de um m´etodo expl´ıcito de comprimento ∆texplcalcula

aproxima¸cões em um instante final N∆texpl, mas a Técnica do Super-Passo

com N sub-passos realiza aproxima¸c˜oes para um instante de tempo t = N2_∆t

expl quando ν →0.

Assim a T´ecnica do Super-Passo cobre um intervaloN vezes maior com custo computacional adicional de calcular (3.13) no primeiro ciclo dos N sub-passos no tempo.

3.2 Consistˆ

encia

A Técnica do Super-Passo será consistente se o método expl´ıcito a que ela for aplicada o for, pois a técnica altera apenas o tamanho do passo no tempo.

3.3 Erro Cometido na Aproxima¸

c˜

ao pela T´

ecnica

do Super-Passo

Para analisar o erro cometido entre a aproxima¸cão gerada pela Técnica do Super-Passo e a solu¸cão anal´ıtica de um problema, para manter a sim-plicidade e clareza dos resultados obtidos considerou-se o problema modelo proposto em (3.1) comn= 1, ou seja, considerou-se o caso em que o sistema de equa¸cões diferenciais é unidimensional. Assim o problema (3.1) possui como solu¸cão u(t) = u0e−λt, o erro cometido na aproxima¸cão pela Técnica

(51)

§ 3.3 Ordem

tempo ´e dado por:

¯ ¯e(k)

¯ ¯ ≡

¯

¯u(k∆T)−U(k) ¯ ¯= ¯ ¯ ¯ ¯ ¯

e−λk∆T

−

N

Y

i=1

(1₋λτi)U(k−1)

¯ ¯ ¯ ¯ ¯ = = ¯ ¯ ¯ ¯ ¯

e−λ∆T_e−λ(k−1)∆T

−

N

Y

i=1

(1₋λτi)U(k−1)

¯ ¯ ¯ ¯ ¯ = = ¯ ¯ ¯ ¯ ¯

e−λ∆T_u((k

−1)∆T)₋

N

Y

i=1

(1₋λτi)U(k−1)

¯ ¯ ¯ ¯ ¯ .

Somando e subtraindo

N

Q

i=1

(1₋λτi)u((k−1)∆T) segue

¯ ¯ek

¯ ¯ ≡ ¯ ¯ ¯ ¯ ¯

e−λ∆T_u((k

−1)∆T)₋

N

Y

i=1

(1₋λτi)u((k−1)∆T)+

+

N

Y

i=1

(1₋λτi)u((k−1)∆T)− N

Y

i=1

(1₋λτi)U(k−1)

¯ ¯ ¯ ¯ ¯ = = ¯ ¯ ¯ ¯ ¯ "

e−λ∆T

−

N

Y

i=1

(1₋λτi)

#

u((k₋1)∆T)+

+ £

u((k₋1)∆T)₋U(k−1)¤

N

Y

i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯ ≤ ≤ ¯ ¯ ¯ ¯ ¯

e−λ∆T ₋ N

Y

i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯

|u((k₋1)∆T)_|+

+ ¯

¯u((k−1)∆T)−U(k−1) ¯ ¯ ¯ ¯ ¯ ¯ ¯ N Y i=1

(1₋λτi)

(52)

§ 3.3 Ordem

Portanto,

¯ ¯e(k)

¯ ¯≤ ¯ ¯ ¯ ¯ ¯

e−λ∆T

−

N

Y

i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯

|u((k₋1)∆T)_|+¯

¯u((k−1)∆T)−U(k−1) ¯ ¯ ¯ ¯ ¯ ¯ ¯ N Y i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯ (3.16) Observe que,

• |u((k₋1)∆T)_|=¯

¯u₀e−λ(k−1)∆T ¯

¯≤ |u₀|,

• ¯ ¯ ¯ ¯ N Q i=1

(1₋λτi)

¯ ¯ ¯

¯<1, condi¸c˜ao de estabilidade.

Substituindo em (3.16), tem-se

¯ ¯ek

¯ ¯≤ ¯ ¯ ¯ ¯ ¯

e−λ∆T

−

N

Y

i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯

|u0|+

¯ ¯ek−1

¯ ¯.

Note que o erro cometido no instante de tempotk pela T´ecnica do

Super-Passo ´e dado em fun¸c˜ao do erro cometido no instante de tempo anterior. Logo,

¯ ¯ek−1

¯ ¯≤ ¯ ¯ ¯ ¯ ¯

e−λ∆T

−

N

Y

i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯

|u0|+

¯ ¯ek−2

¯ ¯.

Aplicando recursivamente at´e o termo _|e0_|_{= 0 obt´em-se}

¯ ¯ek

¯ ¯≤k

¯ ¯ ¯ ¯ ¯

e−λ∆T

−

N

Y

i=1

(1₋λτi)

¯ ¯ ¯ ¯ ¯

|u0|. (3.17)

A expansão em série de Taylore−λ∆T _{é dada por:}

e−λ∆T _{= 1}

−λ∆T +(λ∆T)

2

2 −

(λ∆T)3

6 +

(λ∆T)4

24 +O(∆T

5_).

(53)

§ 3.3 Ordem

¯ ¯ek

¯ ¯≤k

λmax

2

Ã _N X

i=1

τi2=1

!

|u0|. (3.18)

onde λmax = _∆_t2

expl.

A expressão (3.18) depende apenas de ∆texpl, assim o método é de ordem

(54)

Cap´ıtulo 4

Resultados Num´

ericos

O presente Cap´ıtulo apresenta as valida¸cões por refinamento de malha e a compara¸cão de performance dos métodos deEuler Expl´ıcito,Euler Impl´ıcitoe

Crank-Nicolson com o método resultante da conjun¸cão daTécnica do Super-Passo ao Método de Euler Expl´ıcito para a aproxima¸cão numérica da solu¸cão da equa¸cão do calor.

Os métodos foram implementados em linguagem de programa¸cão FOR-TRAN 90 utilizando precisão dupla. Para medir o tempo de processamento dos métodos numéricos utilizados foi utilizada a subrotina impl´ıcita da lin-guagem FORTRAN 90 timef. (maiores detalhes sobre a linguagem FOR-TRAN podem ser encontradas em [6]).

4.1 An´

alise Num´

erica de Convergˆ

encia

Antes de analisar a convergência dos métodos numéricos é necessário de-screver qual será a norma adotada e como a análise de convergência numérica será realizada.

(55)

§ 4.1 An´alise de Convergˆencia

deste vetor ser´a dada por

ke_k_∞ = max

0≤i≤n{|ei|}. (4.1)

Considere a seguinte equa¸cão diferencial parcial do tipo parabólico junta-mente com as suas condi¸cões de contorno e inicial

          

ut(x, t)−[µ(x)ux(x, t)]x =f(x, t),

u(x,0) =φ(x) x_∈[0, L], u(0, t) =g(t) t_∈[0, T], u(L, t) =h(t) t_∈[0, T],

(4.2)

deﬁnida no dom´ınio Ω = [0, L]_×[0, T], com µ(x)>0,_∀x_∈[0, L].

Dividiu-se o intervalo [0, L], da vari´avel espacial x, em N partes iguais de comprimento ∆x, obtendo os N + 1 pontos xi = i∆x, i = 0,1, . . . , N,

onde ∆x = L

N, particionando o intervalo [0, T] da vari´avel temporal t pelo

passo de integra¸cão no tempo ∆t, que é determinado respeitando a condi¸cão de estabilidade do método numérico, obtém-se a quantidade de passos no tempo M, ou seja, tem-se M + 1 pontos ti =i∆t,i= 0,1, . . . , M.

A solu¸c˜ao u(x, t) do problema (4.2) nos pontos do dom´ınio discretizado Ω∆t

∆x = {(xi, tj)∈Ω/xi =i∆x e tj =j∆t} ´e representada por u(xi, tj) =

ui,j e a aproxima¸cão numérica obtida por algum método numérico será

de-notada por Ui,j.

A aproxima¸cão obtida por um método numérico para aproximar a solu¸cão do problema proposto em (4.2), possui um erro que é dado por ei,j =|ui,j−

Ui,j|, comi= 0,1, . . . , N ej = 0,1, . . . , M.

(56)

§ 4.1 An´alise de Convergˆencia

pode se escrever a expans˜ao assint´otica.

U(x, t,∆x) = u(x, t) +Eq(x, t)∆xq+Eq+1(x, t)∆xq+1+. . . , (4.3)

onde u(x, t) é a solu¸cão exata, e com coeficientes funcionais Ei(x, t), i =

q, q+ 1, . . . independem de ∆x.

No problema apresentado na valida¸cão e na compara¸cão de performance dos métodos numéricos, a solu¸cão anal´ıtica u(x, t) é conhecida a priori. Para este problema, as expansões deU(x, t,∆x) eU(x, t,∆x

2 ), para o mesmo ponto

(x, t), podem ser expressas como

U(x, t,∆t)_≈u(x, t) +Eq(x, t)∆tq,

U(x, t,∆₂t)_≈u(x, t) +Eq(x, t)∆t

q

2q .

(4.4) Tais aproxima¸cões permitem estimar a razão de convergência do método numérico

|U(x, t,∆t)₋u(x, t)_|_∞

¯

¯U(x, t,∆t

2 )−u(x, t)

¯ ¯

∞

≈2q. (4.5)

A convergência da razão em (4.5) para 2, 4, 8,. . . , significa que o método numérico tem ordem q= 1,2,3, . . ., respectivamente.

A estimativa da razão de convergência em (4.5) será utilizada na valida¸cão dos métodos numéricos implementados.

A implementa¸cão dos métodos numéricos foi validada empregando a análise de convergência explicada anteriormente, utilizando o seguinte problema modelo:

            

ut−[µ(x)ux]_x =f(x, t),

u(x,0) = cos (πx), 0_≤x_≤ 1₄; 0_≤t_≤ 1₄, u(0, t) = cos (πt), u¡₁

4, t

¢

= √2

2 cos (πt),

µx(x) =

1

2, µ(x) = x 2 + 1,

(57)

§ 4.1.2 An´alise de Convergˆencia

onde f(x, t) =ut−[µ(x)ux]x e u(x, t) = cos (πx) cos (πt).

4.1.1 M´

etodo de Euler Expl´ıcito

O passo no tempo para o método de Euler Expl´ıcito foi ∆t = ∆₃x2, note que esta escolha respeita a condi¸cão de estabilidade do método, como visto em (2.2.1). Definiu-se ∆texpl = ∆x

2

3 como sendo delta t expl´ıcito.

As tabelas a seguir apresentam, Nx, NT as respectivas divis˜oes do

in-tervalo de defini¸cão nas dire¸cões x e t, o s´ımbolo ∆x representa o passo de integra¸cão no espa¸co, _||e_||_∞o erro máximo cometido na aproxima¸cão e razão a ordem do método numérico ao quadrado.

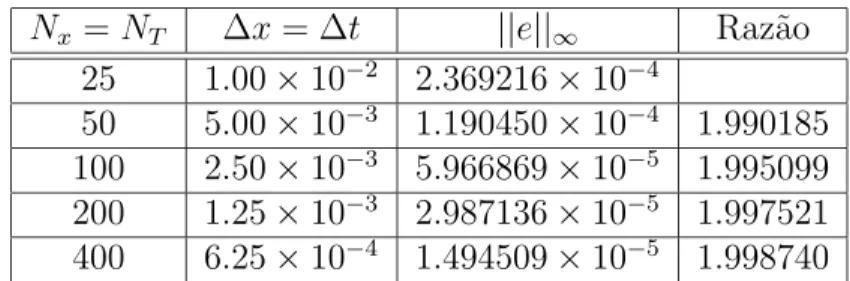
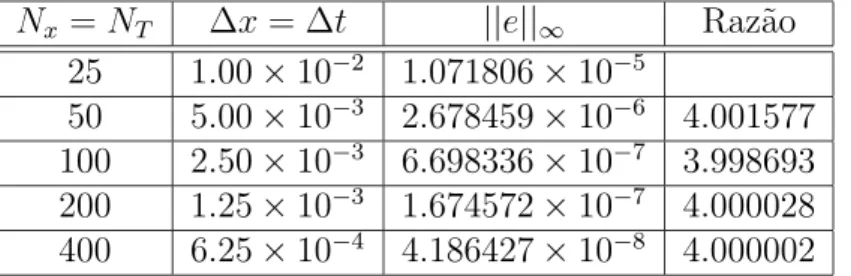
Nx ∆x NT ||e||∞ Raz˜ao

25 1.00_×10−2 ₈₄₃₈ _5.387633_×₁₀−6

50 5.00_×10−3 ₃₃₇₅₁ _1.347009_×₁₀−6 _3.999700

100 2.50_×10−3 ₁₃₅₀₀₀ _3.368690_×₁₀−7 _3.998613

200 1.25_×10−3 ₅₄₀₀₀₀ _8.421701_×₁₀−8 _4.000011

400 6.25_×10−4 _{2160000 2.105431}_×₁₀−8 _3.999989

Tabela 4.1: Resultados numéricos obtidos pelo Método de Euler Expl´ıcito na aproxima¸cão da solu¸cão do problema (4.6).

A tabela acima mostra que quando o passo de integra¸cão no espa¸co, ∆x, é dividido por dois o erro cometido na aproxima¸cão diminui e a razão entre os erros tende a 4.

Assim, como foi utilizado ∆texpl = ∆x

2

3µmax, onde µmax = µ(1) = 1.5,

conclui-se que o M´etodo de Euler Expl´ıcito tem ordem 1.