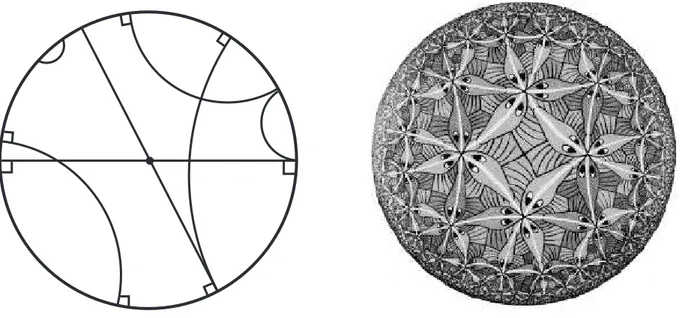
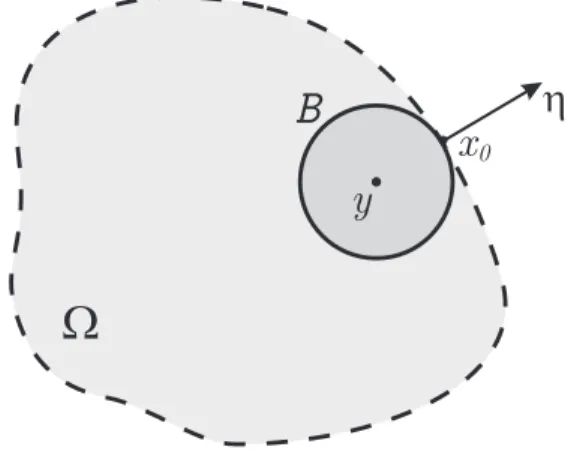
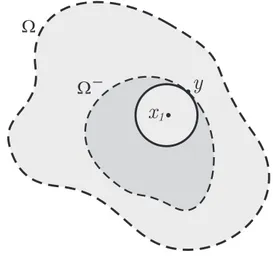
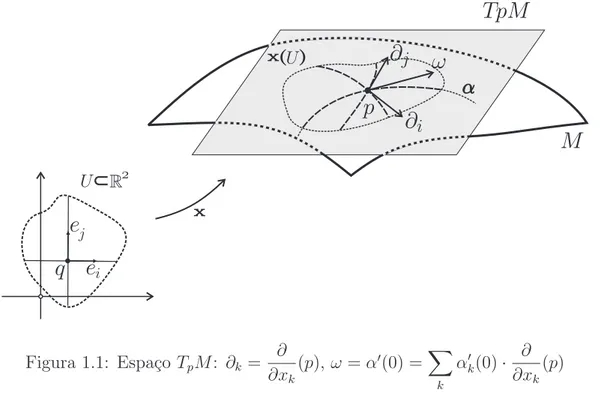
Gráficos Radiais com Curvatura Média Constante no Espaço Hiperbólico
Texto
Imagem
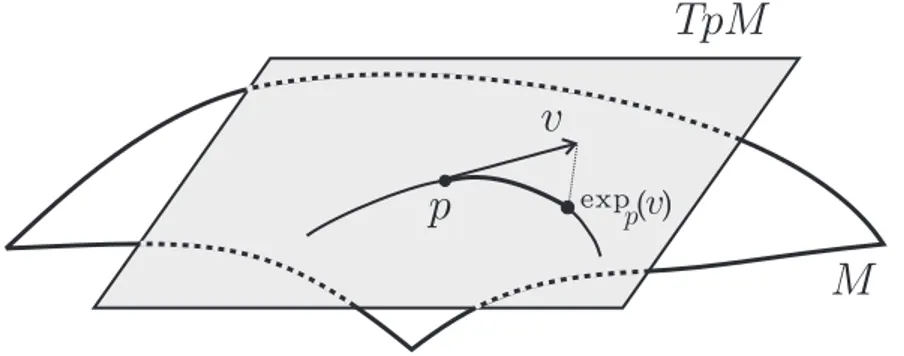

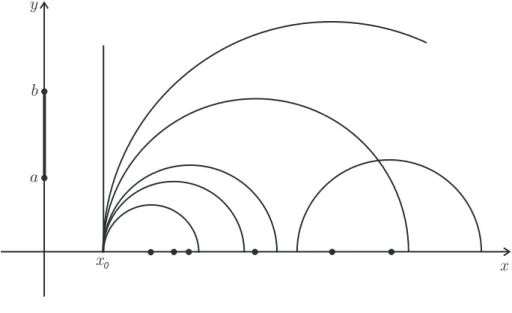
Documentos relacionados
ü A bibliografia sugerida tem apenas o propósito de orientar o estudo dos candidatos, não excluindo, em hipótese alguma, outros livros que abranjam a matéria indicada para
Tese (Doutorado em Zootecnia) - Universidade Estadual do Sudoeste da Bahia, Itapetinga. Segurança alimentar na cadeia do leite. Juiz de Fora: EPAMIG; Instituto
©2011 Enterasys Networks, Inc., A Siemens Enterprise Communications Company – All rights reserved. Entendendo
Chang’s Cecconi’s BLT Time Cheesecake Factory MIAMI BEACH BRICKELL DOWNTOWN REGIÃO DO AEROPORTO REGIÃO DE AVENTURA REGIÃO DE HALLANDALE BEACH NORTH MIAMI BEACH NORTH MIAMI BEACH
Quais fontes de informações você usou (se usou alguma) para ajudá-lo com a decisão em sua última compra de [MARCA & CATEGORIA].. Base: compradores de artigos de
لود عيمج يف يرست دعاوقل ماعلا راطلإا ددحت ةفصاوملا هذهو ةداعإو ةميدقلا ةزهجلأا ةداعتسا صوصخب يبرولأا داحتلاا ةمظنلاا ثدحا ةفرعمل
Por fim, irei examinar as ligações da elegia 2.12 com outros poemas eróticos dos Livros 1 e 2 de Propércio, com enfoque na relação de interdependência entre as figurações do
O Museu Virtual da Lusofonia é uma plataforma de cooperação académica em Ciências Sociais e Humanas, vinculada, sobretudo, aos estudos culturais, à comunicação da ciência,