Operações Unitárias na Engenharia Química - ( Marco Antonio Farah)

(1)

Operações Unitárias na Engenharia Química - ( 3-39

Entre eles listam-se o de McCabe-Thiele (1925) e o de Ponchon-Sacarit (1921-1922), que se baseiam em diagramas de equilíbrio (x-y) e (H-x-y, x-y) para sua resolução levando em conta também algumas hipóteses.

Ao contrário do método prato-a-prato rigoroso analítico, de tentativa e erros, desenvolvido por Sorel em 1891 e descrito anteriormente, estes métodos são de aplicação mais rápida.

O mais simples destes métodos é o método de McCabe-Thiele, sendo também o de mais fácil entendimento e excelente para compreensão dos conceitos envolvidos em uma destilação fracionada.

Pelo que já foi considerado, a equação 3.136 é uma reta e sua localização será:

se x = y ⇒ y = L V

Dx Sx_s _D

−

+ ₌

D

S

Dx

Sx

s D

+

Como a corrente lateral é normalmente líquida:

V = V e L - L = S (3.138)

∴ is =

S L

L− _{= 1} (3.139)

Pode-se definir uma linha is, tal como mostrado pelas equações 3.138 e 3.139, que

represente a interseção da reta da seção de enriquecimento com a intermediária. Esta linha tem como coeficiente angular o valor is , pois:

Seção Intermediária: Vy = xL + Sxs + DxD (3.140)

Seção de Enriquecimento: Vy = Lx + DxD (3.141)

Subtraindo 3.140 de 3.141, levando em conta 3.138 e 3.139; vem:

(L - L )x = Sxs

Como is = 1 x = xs (3.142)

Então, a interseção destas retas é uma vertical passando por x = xs, quando a

retirada lateral é líquido saturado.

A localização sobre o diagrama (x-y) desta reta é mostrado na Figura 3.39

••••

++++ ++++

(2)

3.14.10.2 Duas Cargas

Ocasionalmente, pode-se ter mais de uma mistura de mesmos componentes de diferentes composições, a qual se deseja separar. Poderíamos misturar as soluções e introduzi-las como uma única carga. Isto reduziria o custo do investimento na fracionadora, mas aumentaria o custo operacional pois se consumiria mais energia.

Separar uma mistura consome energia e se misturarmos soluções de composições diferentes, nós desperdiçamos uma separação parcial que já aconteceu. Por isto, é melhor introduzir as duas cargas em diferentes estágios na fracionadora, no estágio ótimo em cada caso.

Consideremos dois estágios de carga A e B, para as cargas G e F.

L = L + LG = L + i1 . G (3.143)

V = V - VG = VG = V - (1 - i1)G (3.144)

L'= L + LF = L + i2 . F (3.145)

V'= V - VF = V - (1 - i2) F (3.146)

Figura 3.40 - Duas cargas

Envoltória II:

    

+ + =

G D L V

Gz Dx x L y

V _s _G (3.147)

(3.148)

Envoltória I:

(3)

A interseção das equações acima dá:

( V - V)y = ( L - L)x - GzG

Se i1 = LG/G ∴ (1 - i1) G/y = i1 G/x - GzG

∴

1 i

z x 1 i

i y

1 G

1 1

− − −

= (3.150)

A equação 3.150 representa o lugar geométrico das interseções das seções de enriquecimento e intermediária.

Envoltória III:

V'y = L'x - B xB (3.151)

Fazendo a interseção entre 3.147 e 3.151:

(V' - V )y = (L' - L )x - BxB - DxD + GzG

Se i2 = LF/F

- (1 - i2)F/y = i2 F/x - F/Zy

∴

1 i

z x 1 i

i y

2 F

2 2

− − −

= (3.152)

Esta equação representa o lugar geométrico das interseções das retas de operação das seções de esgotamento e intermediária.

Definindo z combinado como

G F

Gz

Fz_F _G

+

+ _{, podemos traçar as retas sobre o gráfico (x, y),}

tal como mostrado na Figura 3.41:

••••

∆∆∆∆

••••

++++!

(4)

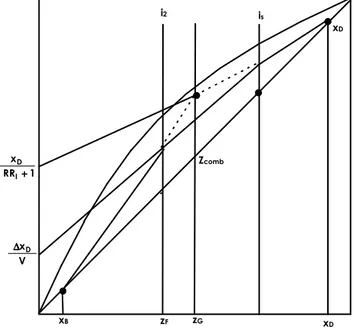
Resumindo as equações das retas de operação:

• Região de topo: y =

1 RR

x x V

L _D

+ +

• Região intermediária:

y =

V GZ Dx x V

L ₊ _D − _G ₌ ₊ ∆ _x_∆

V x V L

(3.153)

• Para x = 0 ⇒ y = ∆ x∆

V onde ∆ = D - G

x_∆ = V

Gz Dx_D− _G

(3.154)

3.15 Eficiência dos Estágios Reais

Nos estágios reais, as correntes que os deixam não estão realmente em equilíbrio, como aconteceria idealmente, em virtude de o tempo de contato ser insuficiente para a mistura ideal das fases nos estágios. Isto implica em menores variações nas composições efluentes dos estágios, tornando necessário um aumento do número de estágios para compensar esta perda. A eficiência deve ser calculada para definir o número de estágios reais para efetuar a separação desejada.

O desempenho de um estágio depende de muitas variáveis físicas. Contatos mais íntimos em maior tempo levam a uma proximidade do equilíbrio ideal, entre as correntes efluentes.

As variáveis que influem na eficiência são a área interfacial das fases, a taxa de transferência dos componentes de uma fase para outra e o tempo de contato. Estas variáveis são por sua vez funções das características de construção dos estágios, das propriedades físicas das fases e de suas vazões.

3.15.1 Eficiência Global

A eficiência mais comumente usada é a eficiência global da torre, definida como:

Eg =

s necessário reais

estágios de

número

equilíbrio de

estágios de

número

(3.155)

É largamente usada e de fácil aplicação, mas tem limitações práticas e teóricas. Do lado prático, a eficiência global somente pode ser determinada com base em resultados de colunas em operação. Do lado teórico, carece de base fundamental, pois combina os efeitos de muitas e complexas variáveis em apenas um único valor para a coluna inteira.

3.15.2 Eficiência de Murphree

(5)

Operações Unitárias na Engenharia Química - ( 3-43 " #$%&'( %'(!)

* '

%&'

%'

%&'( %'(!

%'( %'(!

%'(!

Figura 3.42 - Eficiência de Murphree

Neste caso, admite-se que o vapor no estágio esteja completamente misturado e tenha composição uniforme yn+1. O vapor que sai do estágio tem composição média yn. É possível que o

vapor esteja uniformemente misturado ao atingir o estágio, mas nas vizinhanças da superfície do líquido no estágio n, a sua composição pode variar, pois está em contato com um líquido, cuja composição é variável. A Eficiência Murphree do Vapor é definida por:

Ev =

1 n * n

1 n n

y y

+ + −

− _{x 100}

(3.156)

em que:

* n

y − a composição hipotética do vapor que estaria em equilíbrio com o líquido efluente do estágio real n (xn);

yn e yn+1 − composição vapor que deixa e que chega ao estágio n, respectivamente.

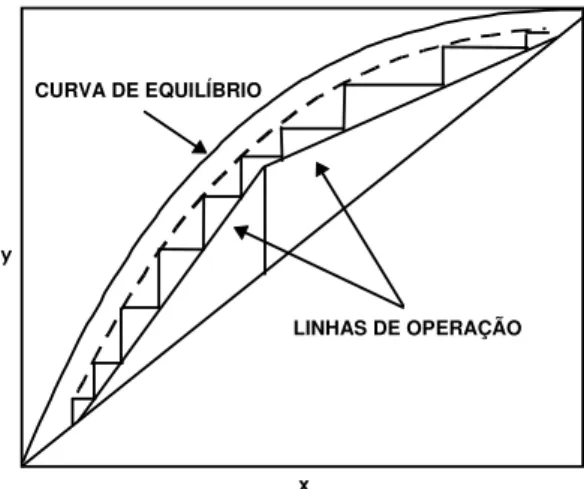
CURVA DE EQUILÍBRIO

LINHAS DE OPERAÇÃO

x %

Figura 3.43 - Incorporação da eficiência ao cálculo do número de estágios

EMV =

1 n * n

1 n n

y y

+ + −

− _(3.157)

EMV − é a razão entre a variação da composição média real que ocorre na composição do vapor e a

(6)

A Eficiência Murphree de Líquido é definida por:

EML = _*

n 1 n

x x

− − −

− _{x 100} _(3.158)

em que:

* n

x − composição do líquido hipotético, que deixaria o estágio em equilíbrio com o vapor, cuja composição fosse a do vapor que eflui realmente do estágio yn;

xn e xn+1 − composição do líquido que deixa e que chega ao estágio n, respectivamente.

Desde que a composição do líquido pode variar consideravelmente em diferentes pontos no estágio de equilíbrio, é necessário definir uma eficiência de Murphree local restrita às condições de um ponto do estágio. Isto pode acontecer em colunas de grande diâmetro, se ocorrer um gradiente de concentração do vapor ou do líquidoemummesmoestágio.EficiênciadeMurphreeLocalparao Vapor:

1 n ’* n

’ 1 n ’ n

v _y _y

y y E

+ + − −

= (3.159)

’* n

y − concentração do vapor em equilíbrio com um líquido situado em um dado ponto do estágio;

’ n

y e ’ 1 n

y ₊ − composição do vapor que deixa e que chega a dado ponto do prato.

A eficiência local nunca pode ser maior que 1, pois y* é o valor máximo que pode ser atingido por y, no ponto em consideração, enquanto que a eficiência de Murphree do estágio, por se tratar de valores médios, pode ser maior do que 1.

3.15.3 Relação entre Eficiência de Murphree e a Eficiência e Global

Para sistemas cujo equilíbrio possa ser representado por uma reta (y = mx), a seguinte relação é valida:

(

)

(

mVL

)

log

] 1 L V m E 1 [ log

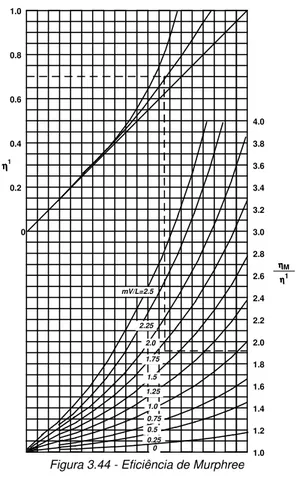
Eg= + v − (3.160)

a qual pode ser resolvida graficamente (Figura 3.44).

1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8

0 0.2 0.4

4.0 0.6

0.8 1.0

ηηηη1

1 M

ηηηη ηηηη

0 0.25 1.25

1.0 0.75 0.5 1.5 1.75 2.0 2.25 mV/L=2.5

(7)

3.15.4 Utilização da Eficiência de Murphree

Quando se conhece a Eficiência de Murphree, pode-se substituir os valores da composição do vapor em equilíbrio, por aqueles que efetivamente deixam o estágio, construindo uma outra curva que substitui a do equilíbrio ideal (Figura 3.42).

A curva de equilíbrio efetiva seria usada no método de McCabe-Thiele, para calcular o número de estágios.

Nos casos em que a curva de equilíbrio for uma reta, pode-se calcular o número de estágios pela equação seguinte:

N =

[

(

) (

)

]

(

)

(

)

[

*

]

B * D B D

* B B * D D

y y / y y log

− −

(3.161)

yD , yB − concentração do mais volátil no vapor que deixa o primeiro e o último estágio da torre;

* D

y , x *_B − concentrações do mais volátil no vapor, que estaria em equilíbrio com o líquido, que deixa o primeiro e o último estágio.

A eficiência global seria calculada pela equação (3.161) e aplicada a toda a torre. Assim, o número real de estágios seria o número de estágios ideais dividido pela eficiência global.

MÉTODO DE PONCHON-SAVARIT

A solução gráfica dos problemas de destilação "flash" ou fracionada pode ser obtida também, pelo método de Ponchon-Savarit. A diferença deste método para o de McCabe-Thiele, se encontra no fato de que o primeiro não necessita efetuar simplificação a respeito da quantidade de calor latente das fases. O método utiliza diagramas de entalpia versus composição e de equilíbrio líquido-vapor, podendo ser empregado para outras operações unitárias como a extração, absorção e cristalização. O método de Ponchon-Savarit também é aplicável a outras operações unitárias como a extração e a absorção.

3.16 Diagrama Entalpia versus Concentração

Antes de apresentarmos o método, serão descritos os princípios da construção do diagrama entalpia versus composição e as informações que este diagrama contem. O diagrama é construído a partir da:

− determinação da composição e do estado térmico do produto para o qual se deseja determinar a entalpia;

− definição de uma seqüência de processos físicos de troca de calor, que levarão o produto de um estado inicial a um desejado estado final;

− avaliação das variações de entalpia em cada etapa. A soma destas variações é a variação total de entalpia.

Para estes cálculos poderão ser necessárias as seguintes informações: a) capacidade calorífica de líquidos e de gases puros;

b) capacidade calorífica de misturas líquidas e gasosas em várias proporções; c) calor de vaporização e/ou de condensação;

d) calor de solução;

(8)

O diagrama da Figura 3.45 mostra as curvas de ponto de bolha e de orvalho, enquanto que na Figura 3.46, observa-se as linhas de amarração ("tie-line') que definem o equilíbrio entre um líquido e um vapor a uma dada temperatura. As concentrações x_B e y_D são as das fases B e D em equilíbrio a uma dada pressão e temperatura.

+ ,

-., ,

/ %

0

/ % 0

0 ••••

••••

%

Figura 3.45 - Diagrama Entalpia Composição Figura 3.46 - Diagrama Entalpia-Composição ("Tie-Lines")

3.17 Destilação "Flash" por Ponchon-Savarit

Como já foi visto, as equações de balanço material, energético, de equilíbrio e relações estequiométricas de um "flash" são as seguintes:

F = B + D (3.162)

Fz_F= Bx_B + Dy_D (3.163)

F

h

F = Bh_B + DH_D (3.164)

Onde h , _F h e _B H , representam a entalpia em base _D molar das correntes F, L e V conforme Figura 3.47.

Para uma dada carga de composição, pressão e temperatura definidas, podemos calcular o valor de h e localizar o ponto (z_F F, h ) no diagrama F

da Figura 3.46.

Analisando-se este sistema, verificamos que existem seis incógnitas (h ,_F H , x_v L, yv, L e V) e

dispomos das seguintes informações:

− três equações (3.162 a 3.164);

− relação de equilíbrio líquido-vapor, sob a forma gráfica;

− entalpia do líquido e do vapor em função da composição, sob a forma gráfica.

Uma vez que três das informações são gráficas, a solução do problema não é direta, a não ser que tenhamos as equações correspondentes aos gráficos. Ainda que isto ocorra, dependendo do tipo destas equações, as soluções algébricas poderão ser complicadas.

20.000

15.000

10.000

5.000

h

0

5.000

1,0

0,8

0,6

0,4

0,2

0 RELAÇÕES ENTRE FASES

h

______________________

H H

(9)

O modo mais fácil de resolver o problema é o de fazer uso conjugado dos gráficos y - x e h-x-y, os quais devem estar dispostas um sobre outro, tal como na Figura 3.47.

Considerando-se que as correntes B e D estejam em equilíbrio, elas estão a mesma temperatura e sobre uma mesma "tie-line". Podemos mostrar que a "tie-line" que liga F e B tem a mesma inclinação que aquela que passa por F e D.

F = B + D

(L + V) zF = B_XB + y_B

F D

B F

z y

x z B D

− −

= (3.165)

(B + D) hF = B hL + HD V

F V

L F

h H

h h B D

− −

= (3.166)

Combinando 3.165 e 3.166

F D

B F

z y

x z

−

− ₌

F D

L F

h H

h h

− −

(3.167)

ou ainda

L f

B F

h h

x z

−

− ₌

F D

h H

z y

− −

tg α_FB = tg α_FD (3.168)

Logo, a reta que passa por F e B é a mesma que passa por F e D.

A solução gráfica do problema consiste em achar, por um processo de tentativas que utiliza os dois diagramas de forma conjugada, a "tie-line" que passa por F.

Nos casos em que se fixa a porcentagem vaporizada e se deseja determinar a tempera-tura, a solução é mais simples, pois pode-se, tal como já foi visto, determinar as concentrações x_B e y_D, sobre o diagrma y-x, e daí determina-se a "tie-line", a qual corresponde a uma temperatura constante.

3.18 Destilação Fracionada por Ponchon-Savarit

3.18.1 Condensador Total

A resolução de uma destilação fracionada pelo método de Ponchon-Savarit é uma exten-são da aplicação a destilação integral, acrescida de que, neste caso, a transferência de matéria e ener-gia se faz em N estágios, havendo fornecimento de enerener-gia no fundo da torre e retirada em seu topo.

Vamos admitir conhecidas as condições da carga (F, zF e h ), as composições dos F

produtos de fundo e de topo e a razão de refluxo. Deseja-se determinar o número de estágios para se obter a separação desejada.

O método de Ponchon-Savarit não necessita da premissa de que os fluxos molares de líquido e vapor em cada seção sejam constantes, pois pode usar combinadamente os diagramas de equilíbrio (y, x) e de entalpia versus composição (h, x, y).

(10)

Fh + q_F R = DhD + BhB + qC (3.169)

qC = VHv - (Lo + D) h D

V = Lo + D

qC = (Lo + D) (H - v h ) D

qC = D(1 + RR) (H - v h ) D (3.170)

onde H - h_v D = calor latente de condensação do produto de topo, no caso de condensação total, sem

sub-resfriamento.

L

Lo

y1

B F

D qc

qR

Figura 3.48 - Destilação fracionada por Ponchon-Savarit

Combinando a equação F = D + B com a equação 3.169, tem-se:

(D + B) h = (_F h - _B B q_R

) B + (h + _D D q_C

) D (3.171)

D 

  

 

   

 

− − =

   

 

−

   

 

+

B q h h B h D q

h R

B F F C

D (3.172)

Levando em conta que:

D (xD - zF) = B (zF - xB) (3.173)

Dividindo a equação 3.173 pela 3.172.

   

 

− −

− =

−

   

 

+ −

B q h h

x z

h D q h

z x

R B F

B F

F C D

F D

(3.174)

No diagrama entalpia versus composição, a equação (3.174) indica que os pontos:

(11)

A : coordenadas (zF, hF) e

C : coordenadas (xD, hD+ q_DC ).

estão alinhados sobre a mesma reta. Então, se conhecemos qC (por balanços material e energético,

equação 3.170), podemos localizar o ponto    

 

D q + h ,

x C

D

D .

Como conhecemos as condições da carga podemos traçar a reta que passa por F e C (Figura 3.49). Como é conhecida a composição xB, a interseção da reta vertical que

passa por xB com a extensão da reta FC dá o

ponto R e, como consequência, o valor de (H - _B

B qR _).

Para se calcular número de estágios na seção de retificação, localiza-se os pontos C, A, R, D e V1 sobre a curva H versus

x-y o vapor (V1) que deixa o primeiro estágio e que

está em equilíbrio com L1, líquido que deixa este

prato. Assim usando o diagrama y versus x, determina-se o ponto x1. A vertical que passa

por ele intercepta a curva h versus x em L1.

Repetimos o procedimento anterior, unindo L1 a

C, levando em conta que L1, C e V2 estejam

em linha reta, o que pode ser deduzido efetuando-se balanço material e energético em torno deste ponto.

Assim marca-se o ponto V2 sobre a

curva h versus y. Repetindo-se os mesmos pro-

' 1

V

D Q' c

' c

Q

' m

V

' o

V

zo

a A

1

W m

xa

J n

2

1

' 1

L '

m

L

B _L

n

Lo

' 1 m

L

' 1 n

V

Va

F

L2 _L

1

yo

V2

D

xd

D V1

C

H1

hd

0

R

xB

hR

B 0

' R

Q R Q' r

CONCENTRAÇÃO MOLAR

Figura 3.49 - Número de estágio de destilação

cedimentos (V2 e L2 em equilíbrio), define-se L2, o que pode ser aplicado sucessivamente até o prato de

carga, por raciocínios análogos.

Quando alguma linha de amarração cruzar a reta RAC, indica que completou-se a seção de retificação, implicando em procedimento diferente. A partir deste ponto, alcançou-se a

seção de esgotamento e deve-se trabalhar com os dados de balanço material e energético desta seção.

Pode-se mostrar que similarmente à seção de retificação, os pontos R, Lm e Vm+1 estão

alinhados. Assim o líquido que deixa o prato de carga está alinhado com o vapor que a ele chega. Este procedimento é repetido até que se alcance a concentração xB, indicando que o número de estágios na

torre foram suficientes para se efetuar a separação desejada.

(12)

Pelo método de Ponchon-Savarit é possível calcular as vazões molares de líquido e vapor em qualquer ponto da coluna, obtidas por balanço nos pratos:

1 n n

V L

C V D

L

+ +

= (3.175)

n 1 n

1 n n

V L

C L D V

+ +

= (3.176)

A razão de refluxo RR seria igual a D L_o

ou

RR' =

C L

C V D L

o 1

o ₌

(3.177)

Como conseqüência, se conhecemos RR podemos localizar o ponto C, sem que seja necessário calcular qc.

3.18.2 Razão de Refluxo Total e Mínima

A razão de refluxo total corresponde a D = 0, o que corresponde a localização dos pontos R e C no infinito como mostra a Figura 3.50, pois DV1, LV1 etc. são verticais.

A condição de refluxo mínimo corresponde a uma zona de acumulação ("pinch"), o que se traduz em linhas de amarração paralelas a reta CAR, (Figura 3.51).

W 3

2

1

V3

V2

D

V1

0

L1

L2

L3

W

xB

R

xd

CONCENTAÇÃO MOLAR

Figura 3.50 - Refluxo total - número de estágios

W

3 2

1

Va

Cm

D

V 0

D La

Rm

W

xr

R

xd

A

1 2

ya

xa

ha

Ha

' çm

Q

CONCENTRAÇÃO MOLAR m=∞∞∞∞

n=∞∞∞∞

Figura 3.51 - Refluxo mínimo - número infinito de estágios

Como jáfoiditoométododePonchon-Savaritémaisrigorosodoqueométodode McCabe- Thiele, apresentando melhores resultados, sendo que este último é de aplicação bem mais simples.

(13)

paralelas no intervalo de concentrações considerado, pode-se tomar como verdadeira a premissa de vazões molares constantes de líquido e vapor em cada seção.

Isto é mostrado a partir das equações 3.175 e 3.176:

C V

C L L

V

1 n

n 1 n

+ −

+ ₌ _(3.178)

Quando as linhas de entalpia de líquido e vapor são paralelas, a relação

D V

D L

1 n

′′′′ ′′′′

++++ −−−− _é

constante em toda a seção, indicando que

n 1 n L

V₊₊₊₊ _{é constante nesta seção. Em geral, a aplicação}

de um ou outro método, depende da disponibili-dade de dados e da precisão desejada em cada caso.

3.18.3 Condensador Parcial

Quando a condensação for parcial, a resolução pelo método de Ponchon-Savarit muda ligeiramente, pois tem-se agora que considerar um produto vapor ou um produto vapor e um líquido, obtidos pela condensação.

Similarmente ao método de McCabe-Thiele a alteração se deve a que no caso de:

a) um produto vapor, o ponto C estará sobre a vertical que passa pela concentração y do produto gasoso (Figura 3.52c), ao contrário da condensação total (Figura 3.52a); b) dois produtos (um vapor e um líquido), o ponto C estará sobre a linha vertical que

passa por xn (Figura 3.52b).

xT =

G D

Gy Dx_D _G

+

+ _(3.179)

T

h =

G D

G H D hD G

+ +

(3.180)

Y1

Yd

Y2

C

V2 V1

G

L2 L1

D hd

Yd Xd = Zd

D

Y1

Yd

Y2

T

C

V2 V1

G

L2

L1 D hd

Yd Xd D

' c Q

T Hd

xd

Zd

Y1

Yd

Y2

G

C

V2 V1

G

L2

L0

X0 = Xd

Hd

L1 Yd

L0

Zd = Yd

Figura 3.52a Condensador total

Figura 3.52b

Condensador parcial - destilado misto

Figura 3.52c