Análise estrutural de um compledo de níquel e de vários triterpenos por difração...

(1)

Universidade

de São Paulo

Instituto

de Física

e Química de São Carlos

Análise Estrutural

de um

Complexo de Níquel e de

Vários Triterpenos por

Oifraçãodf! Raios

%

Dissertação apresentada

ao Instituto

de Física e Química de São Carlos

-uSP, para

obtenção

do título

de

Mestre em Física Aplicada.

_~~~~ __ ~._,.~. ~.+_i~---._,

SEkYIÇO DE BI8L:OTEC:" F !f";~;". ' ", \. li,,)SC FISICA

Departamento de Física de Ciência dos Materiais

(2)

Dr.

_{Yvonne P.Mascarenhas}

_Orientador

,,--.

. .

/ ' " , . ',

~ . .-.. . /< .., ""'...

-'<i-s>,:,-',·, ..:~,.

".-Dr. Glaucius

Oliva

r

(-/;"2; ,

1",/ '/ ~

L'- "0.01.,- .••••• ' ~ f / '

r/d.

_José

I

i

I .

(3)

A realização deste trabalho foi possível graças ao suporte financeiro

dado pelos Instituições de apoio

à

pesquisa: FAPESP, FINEP, CAPES e CNPq e

aos Departamento

de Física da Universidade

Federal de Ouro Preto e do

(4)

Para minha esposa Renata e minha

filha Maristella. ternas

companheiras

e

(5)

A g r a d e c

i m e n t o s

Profª. Drª. Yvonne P. Mascarenhas.

meu agradecimento

especial pela

orientação, apoio e pelos ensinamentos.

ProL Dr. Eduardo E. Castellano. pelo apoio e pela constante

disposição

em colaborar.

ProL Dr. José Rego de Souza e a Sra. Grácia Silva. pelo fornecimento

das

amostras cristalinas dos tríterpenos.

ProL Dr. César V. Franco e ao Sr. Noel M. Levy. pelo fornecimento

da

amostra cristalína do complexo de níquel.

Aos colegas: Carlos Alberto Simone, Carlos Paiva Santos e Stellu Muris

Fabiane. pelo apoio. estímulo e amizade.

(6)

L i s t a

d e s í m b o l o s

u s a d o s

Mr

peso molecular

a, b, c

parâmetros que definem a cela unitária

_..•

a

àngulo entre os vetores b e

ê

R ~

1 ....• ...•

p

angu o entre os vetores a e c

...•

y

ângulo entre os vetores

ã

e b

V

volu me da cela unitária

de

densidade do cristal calculada

ll

fator de absorção linear

À

com primento de onda

R. índice de discordâncía entre o fator de estrutura observado e

o calculado

FlV)

fator de estrutura

Hv.J

intensidade

Z

número de moléculas por cela

rj

vetor de posição do

j

-ésimo átomo em relação à orige m

S. vetor de espalhamento

p(r

L

densidade eletrônica

HIb-IL

fator de espalhamento atômico

$0.1)

fase

L. fator de Lorentz

p

fator de polarização

a(x)

desvio padrão estimado

(7)

Tabela de

Conteúdo

Agradeci men tos

Ü

Tabela de Conte

ú

do

:

ív

Lista de Tab eIas

víi

Lista de Figur as

~

ix

Resu mo

"

xi

~t»stl"aLc:t

][i17

I

ntl"od ução

_

1 CaLpítulo

I

~lguns

Fundamentos

daLTeol"ÍaLde Difl"aLçãode RaLios

X

pOI"

Cl"istai s

:

4

1.1 Geometria dos Cristais

5 1.1.1'

Introduç·ão

5

1.1.2 Sistemas Cristalinos-Simetrias

7

1.1.3 Retículos de Bravais

8

1.1.4 Grupos Puntuais

9

1.1.5 Grupos Espaciais

10

1.2 Espalhamento de Raios X por um Elétron

11

1.3 Espalhamento de Raios X por um Atomo

14 IA

Espalhamento de Raios X por um Grupo de Atomos

16

1.5 Difração de Raios X por um Cristal

17

1.5.1 Fator de Estrutura

17

1.5.2 Lei de Bragg

19

1.5.3 Retículo Recíproco

:

21

1.5.4 Construção de Ewald

22

1.5.5 Síntese de Fourier

23

1.5.6 Lei de Fríedel

24 Capítulo

1 1

Coleta e Análise

dos DaLdos

2 6

. I 1.1

Coleta de Dados

27

11.1.1 Descrição do Arranjo ExperimentaL

27

11.1.2 Obtenção dos Paràmetros da Cela ~

28

11.1.3 Medida das Intensidades

30 I 1.2

Red ução dos Dados

32 I I.2.1

Fator de Polarização

33

11.2.2 Fator de Lorentz

34

11.2.3 Fator de Trans missão

34

11.3 O Fator de Temperatura

3 S

(8)

I I

.5

Método de Wilson

37 Capítulo

I I I

Introdução aos Métodos de Determinação de Estruturas

39. 111.1 O'Problema da Fase

40 I I 1.1.1

Método de Patterson

40 a) Síntese de Fourier

42 b) Síntese de Fourier Diferença

44 I I 1.1.2

Métodos Diretos

44 a) Fatores de Estrutura Unitário e Normalizado

45 b) Estatística das Intensidades

47 c)

Teoria das Desigualdades

:

48 c.l)

Desigualdade de Harker-Kasper

48 c.2)

Determinante de Karle-Hauptman

49 c.3)

Equação de Sayre

52 d) Invariante e Semi-invariante

de Estrutura

53 e)

Definição da Orige m

55 e.l)

No Grupo Espacial P 1

55 e.2)

No Grupo Espacial P 1

56 e.3)

Origens Equivalentes

57 eA)

Regra Geral para Específicação da

Origem

) 8

f)

RelaÇÔesde Probabilidades

60 f.I)

Caso Centrossimétrico

61 f.2)

Caso não Centrossimétrico

63 g) O Método de Multi-solução

66 g.l )

Cálculo de lEI

67 g.2)

Determinação das Fases

:

68 g.2.1) Relações de fases

68 g.2.2) Escolha do Conjunto Inicial de

Fases

68 &.2.3) Deter minacão das Fases

69 g.2A) Fórmula da Tangente

:70

g.2.)

Figuras de Mérito

:

71 g.3)

Mapas de E(b)

72 I I 1.2 Refinamento por Mínimos Quadrados

72 I 11.2.1 Álgebra do Método

72 I I 1.2.2

Estimativa do Desvio Padrão

75 I I 1.2.3

IÍldices de Discordância

77 Capítulo IV

A Estrutura Cristalina e Molecular de um CompleIo de

Níquel: (Nill(DPEHhJ(NOd2' 2H20

~

78

(9)

I

V.1 Introd ução

~

79 IV.2

Obtenção da Cela Unitária e a Coleta de Dados

80 IV,3

Análise dos Dados e Determinação do Grupo EspaciaL

81 IV.4 Solução e Refina mento da Estrutura

83 I

V .s

Descrição da Estrutura

87 Capítulo

V

As Estruturas

Cristalinas

e Moleculares

de .Alguns

T

r íter penos

9 2

V.1 Introd ução

93

V.2 Obtenção das Celas Unitárias e as Coletas de Dados

95

V.3 Análise dos Dados e Determinação dos ,Grupos Espaciais

96

V.4 Solução e Refinamento das Estruturas

99 a)

Triterpeno T 1

102 b)

Triterpeno T2

104 c)

Triterpeno T3

105 d)

Triterpeno T4

107 e)

Triterpeno T5

109

V.5 Descrição das Estruturas

111 a)

Triterpeno T 1

111 b)

Triterpeno T2

113 c)

Triterpeno T3

116 d)

Triterpeno T4

118 e)

Triterpeno T5

120 Capítulo

VI

Consi der ações Finais

13 3

Apêndice

A

135 A pên dice B

144 A pên dice C

152 A pên dice D

166 A pêndice

E

172 A pên dice F

18 I

Bib liograf ia

188

(10)

Tabela 1.1

-Tabela

II!.l

-Tabela

II

1.2 Tabela III.3

Tabela IV.I

Tabela IV.2

-Tabela

I V A

-Tabela

IV.s

Tabela IV.6

Tabela V.1

Tabela V.2

-Tabela

V.7Tabela V.8

Tabela V.l O

Tabela V.II

-L i s t a

d e T a b e l a s

Os sete siste mas cristalinos

8 Alguns planos e linhas de Harker

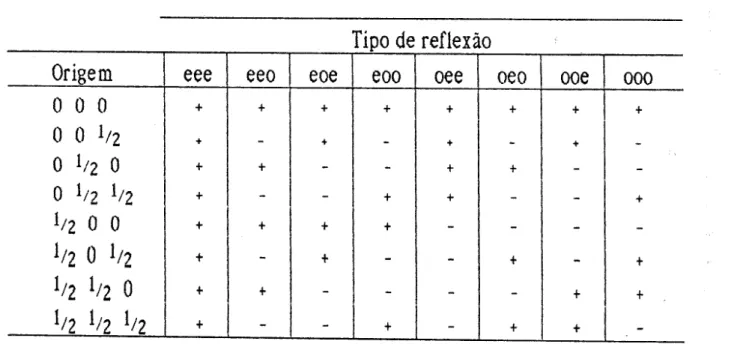
42 Valores e distrib uições teóricas dos IErs

47 Mudança do sinal das reflexões com a mudança de

or ige m no gr u po es pacial P 1

56 Resumo dos dados cristalogrâficos

- complexo de NL

82 Picos e vetares interatômicos

do mapa de Patterson

-co

fil

p

lex o de Ní.

:

83 Coordenadas fracionárias

e os fatores de temperatura

isotrópicos equivalentes

- complexo de Ní..

85 Parâmetros

térmicos anisotrópicos - complexo de Ni.

86 Distâncias e ângulos das ligações - complexo de Ní.

88 Coordenadas ortogonalizadas

dos átomos dos dois

anéis piridil - com plexo de NL

89 Distâncías e ângulos das pontes de hidrogênio

-complexo de Ni

9O

Parâmetros das celas unitárias dos

5 triter penos

95 Parâmetros usados nas coletas de dados e o número

de refle xõe s coletad as

96 Grupos espaciais, número de moléculas e condições de

possíveis reflexões para os

5 triterpenos

97 Fatores de escala e de temperatura isotrópico médio

dados pelo método de Wilson para os cinco

tr iter penoso

99 Parâmetros relacionados com o refinamento das

es tr u

t

uras

1OO

Coordenadas fracíonárías e os fatores de temperatura

isotrópicos equivalentes - triterpeno T 1

102 Parâmetros térmicos anisotrópicos - triterpeno Tl.

I03

Coordenadas fracíonárias e os fatores de temperatura

isotrópicos equivalentes - tríterpeno T2

104 Coordenadas fracionárias e os fatores de temperatura

isotrópicos equivalentes - triterpeno

T 3

105 Parâmetros térmicos anisotrópicos - triterpeno T3

l06

Coordenadas fracionárias e os fatores de temperatura

(11)

Tabela

V.13 -

Coordenadas fracionárias e os fatores de temperatura

isotrópicos equivalentes - triterpeno TS

109 Tabela V.14 -

Parâmetros térmicos anisotrópicos - triterpeno T5

110 Tabela V.15 -

Angulos médios das Egações sp2 e sp3 para os 5

tr iter penos

122 Tabela

V.16 -

Conformação dos anéis de cada tríterpeno

122 Tabela V.17 -

Distâncias relevantes das pontes de hidrogênio no

tr

í

ter peno T

2

123 Tabela V.18 -

Angulos de torção (') do triterpeno T 1..

124 Tabela V.19.a - Ângulos de torção (") da 1

ª

molécula do triterpeno

T 2

125 ~

Tabela V.19.b - Angulos de torção (') da

2ª

molécula do tríterpeno

T 2

126 Ângulos de torção (') do triterpeno T

3.

127 Ângulos de torção

(0)

do triterpeno T4

128 Ângulos de torção (') do triterpeno T5

129

(12)

-Figura I.1.a:

Figura 1.I.b:

Figura 1.2:

Figura 1.3:

Figura 1.4:

Figura 1.5

Figura 1.6

Figura 1.7

Figura 1.8

Figura 1.9

Figura 1.10

Figura 1.11

Figura 1.12

Figura I LI

Figura 11.2

Figura 11.3

Figura II 1.1

Figura II 1.2

Figura III.3

Figura 1IIA

Figura lII.5

Figura II I.6

Figura II I.7

Figura lV.1

Figura lV.2

Figura lV.3

Figura IV.4

Figura IV.5

Fig. lV.6

Figura V.1

Figura V.2

Figura V.3

-Figura

V.4-Figura

V.5-Lista de

_Figuras

o

retícul0 tridimensional, mostrando a cela unitária

6 Parâ

fi

etros da cela unitária

6 Plano do retículo cujos índices de Míller são hkl..

7 Os 14 retículos de Bravais

9 Projeção do grupo P2j / c

11 Espalhamento por um elétron

13 Espalhamento por um átomo

15 Curvas de

f

x

sen

a

16 ~

Grupo de átomos em uma ceia unitária

17 Reflexão nos planos (hkl)

19 Representação do vetor ~ perpendicular

ao plano

(hk1)

,

2 O

O

vetor de esp alha men to

2 O

Construção de Ewald

23 Dífratômetro automático CAD-4

28 Perfil da intensidade do feixe dífratado

31 Caminho do feixe dífratado em um cristaL

35 Diagrama representando

FU.Ü.• FcOJ.)+

FdtJJ

43 Varíação do valor do deter minante D3 com

$(

tJJ

+

$U;.)

+

$(

h - k )

5 O

Interpretação

da desigualdade

ID(b.) -

.sI ::;

r..

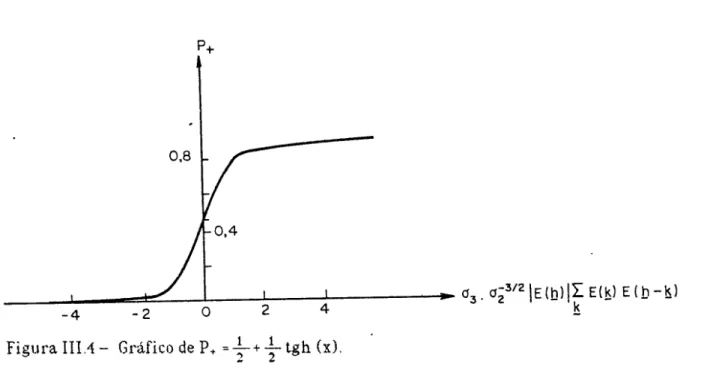
52 Gráfico de P+ .•

+

+ ~

tgh x, onde x .• E(I}). E(!5)E(l}-!5L

62 Gráfico de P(~) versus ~

65 Gráfico de V

(h' ~)

vers us K

(h' ~)

66 Etapas do método de mu1ti-solução

67 Estrutura do ligante DPEH

79 Estrutura do complexo {Ni

ll

_(DPEH)z]2+

₈₀

O

gr u po es pacial Cc

82 Vista em perspectiva da molécula do complexo de Ni

87 Perspectiva do poliedro de coordenação do complexo

de N i

9 O

Projeção estereoscópica do complexo de Ni...

91 Fór mula estrutural dos tr iterpenos

93 O

gru po espacial P21

97 O

gr u po es paGial C2

98 O

gru po espacial P2 ,2,21

98

(13)

Figura V.6

Figura

V.7-Figura V.8

Figura V.9

Figura V.1 O

Figura V.11

Figura V.12

-Figura

V.13Figura V.14

Figura V.15

Figura V.16

Figura V.17

-Figura

V.l8Figura V.19

Figura V.20

-a e b - Distânci-as e ângulos d-as lig-ações - triterpeno

T

1...

1 12

Vista em perspectiva da molécula do triterpeno

T2

113 a e b - Distâncias e ângulos das ligações da 1

ª

molécula do triterpeno

T2

114 a e b - Distâncias e ângulos das ligações da 2ª

molécula do triter peno T2

115 Vista em perspectiva da molécula do triterpeno

T3

116 a e b - Distâncias e ângulos das ligações - triterpeno

T

3...

11 7

Vista e m perspectiva da molécula do triterpeno T4

118 a e b - Distâncias e ângulos das ligações - triterpeno

T 4

1 19

Vista em perspectiva da molécula do triterpeno T5

120 a e b - Distâncias e ângulos das ligações - triterpeno

T 5

12 1

(14)

(15)

Este trabalho consiste em uma introdução teórica dos fundamentos

básicos da difração de raios X por cristais, de uma descrição sucinta do

difra-tõmetro automático CAD-4 da Enraf -Nonius, e do método de Patterson e dos

metodos diretos usados na determinação de estruturas.

Foram resolvidas as estruturas cristalinas e moleculares de um

com-plexo de níquel(II) e de cinco triterpenos.

Os cinco triterpenos são produtos naturais extraídosl

77 _{1 da casca de}

madeira

A

lI s t r o p le n c k ia

p o p llln e a

( C e la s t r a c e a e

) .

Monocristais desses

produtos foram analisados por difração de raios X usando um difratômetro

automático

CAD-4

e com radiação de MoKa

(1..

=

0,71 073Á) monocro~

matizada por cristal de grafita. Os principais dados cristalográficos estão

resumidos na tabela abaixo:

TI

T2

T3

T4

T5

Fórmula Química

I

_C31H

48

0

4 C30H

4S

03 C31H.~803 C31H5003 C30H

48

0

4 M

r

I

484,73

456,71

468,73

470,74

I

472,71

Grupo Espacial

P2t

Pl

C2

P2t2t2t

P2t

a(A)

6,697(2)

7,271(2)

12,109(2)

6,815(2)

14,695(2)

b(A)

14,714(7)

12,389(8)

7,346(2)

16,127(2) 13,699(2)

dA)

13,866(3)

15,632(2)

30,570(6)

24,695(4)

6,622(3)

atO)

₉₀

_74,95(2)

₉₀

P'

_{t .}

0)

_103.53(2)

_87.55(2)

_99,83(2)

₉₀

_104,45(2)

y(O)

₉₀

_86,76(4)

₉₀

I

₉₀

Z

2

4 I

2 V(A3)

1328( 1)

1357(1)

2679(2)

2714(2)

1288(1)

d

ç

(g. cm-3)

1,211

1,118

1,162

1,152

1,219

Jl(cm-t)

0,726

0,651

0,675

0,668

I

0,733

F(QOO)

_I

₅₃₂

I

₅₀₄

₁₀₃₂

₁₀₄₀

I

₅₂₀

R

I

0,0485

0,0996

0,0574

0,0545

0,0420

NQ refI.: 1 ) 30(1)

I

₁₃₉₅

1972

751 1438

838 o

complexo de níquel, [NiII(DPEHh](N03h· 2H20, foi sintetizadol70\ a

partir de uma solução alcoólica de 2 moles do ligante

DPEH(Diacetilmonooxi-ma-p-Piridil-(2)-Etilimina)

para cada moI de [Ni(OH2)6](N03h. Um

mono-cristal desse composto foi analisado por difração de raios X, usando um

difra-tômetro automático CAD-4 e radiacão de MoKa

(À

=

0,71 073A)

(16)

~ =

103,22(2)", V

=

2887(Z)À3, 2

=

4, de

=

1,448g· cm-

3, ~ =

7,36cm-

Jf

EOOO)

=

1312, R '"

0,0594 e 1656 refleções com I

> 20(1).

O

átomo de Ni está

t:oordenado por seis átomos de N com uma configuração octaédríca dístorcída.

(17)

(18)

(19)

(20)

(21)

o

objetivo deste trabalho foi o domínio das técnicas de resolução de

estruturas

cristalinas de pequenas moléculas por difração de raios X e a

fa-mi1iarização com o uso do difratômetro automático CAD-4 da Enraf -Nonius e

com os programas correlatos.

A determinação da estrutura cristalina e molecular de compostos por

difração de raios

X

se faz necessário porque as informaçôes que são obtidas

da análise estrutural. tais como: existência de ligações de hidrogênio

inter-molecular e intrainter-molecular. o estudo das conformações de anéis, a

deter-minação de poliedros de coordenação e do empacotamento cristalino e o

cálculo das distâncias e ângulos interatômicos, são essenciais

à

Física do

Estado Sólido, Mineralogia, Metalurgia, Química, Biologia e outros ramos do

conhecimento.

Em função deste objetivo foram resolvidas as estruturas

cristalinas e

moleculares de alguns compostos. os quais representam

um trabalho de

pesquisa em colaboração com vários pesquisadores de outras instituições que

os obtiveram por síntese ou extração. São seis compostos, a saber:

- um

c o m p l e x o d e

Ni: [Nill(DPEHh](N03h· 2H20 ~ Dinitrato· de bis

(Díacetilmonooxima-p-Piridil-(2)-Etilimina)

níqueHIl)

dihidratado.

°

inte-resse no estudo cristaloquímico desse complexo de niquelO I) está

relacio-nado com o fato de que muitos complexos de metais de transição são

essenci-ais para regular o metabolismo de organismos vivos.

- cinco triterpenos extraídos da casca da madeira do

A u stro p /e n c.kia

p o p u /n e a (

C e /a stra ce a e );

T r i t e r p e n o T 1 :

C31H4804~ 3-hidroxl-2-oxo-friedelan-

3-en-20a-carbometoxila.

T r i t e r p e n o

T2: C3oH4803"'" ácido- 3P-hidroxiolean-12-en-20a-óico.

T3: C31H4803~ 3-oxo-olean-12-en-20a-carbometoxíla.

T4:

C31H5003~ 3-oxo-friedelan-20a-carbometoxíla.

T5:

C3ÜH4804"'"ácido-3P-hidroxi-2-oxo-.

20a-óico.

°

estudo desses triterpenos deve-se ao fato de que vários triterpenos

pentacic1icos apresentam

atividades farmacológicas (antíleucêmícos.

(22)

Este trabalho segue o padrão de desenvolvimento

usual de

determina-ção de estruturas e foi subdividido em seis capítulos, a saber:

C a p í t u l o

I :

são dados alguns fundamentos da teoria de difração de

raios X. De uma forma sucinta

é

feito o estudo da

geo-metria interna dos cristais e da interação dos raios X

com a matéria.

C a p í t u l o

lI:

é feita u ma descrição do difratõmetro automático

CAD-4 usado na coleta de dados e dos fatores que afetam a

intensidade.

C a p í t u l o 1 1 1 :

são descritos os métodos de Patterson e os metodos

diretos, os quais foram usados para resolver o

pro-blema da fase neste trabalho. Resolvido o propro-blema da

fase são descritos os processos para se completar a

estrutura

e o processo de refinamento

por mmimos

quadrados.

IV: se refere à determinação da estrutura cristalina e

mo-lecular do complexo de níquel(I I).

V:

se refere à determinação

das estruturas

cristalinas e

(23)

Capítulo

I

Alguns

Fundamentos

da Teoria

de Difração

de

(24)

II

Geometriados Cristais

_It

_I

A

forma externa regular dos cristais induziu os primeiros

observado-res a acreditar que eles eram formados pela repetição uniforme de blocos

constituintes

elementares.

Quando um cristal cresce, num ambiente mantido

em condições físicas constantes, sua forma permanece

imutável

durante

o

crescimento como se os blocos constituintes

elementares

estivessem

sendo

empílhados continuamente. Os blocos elementares

são contituídos por átomos

ou por grupos de átomos. Assim, um cristal é um arranjo tridimensional

peri-ódico de átomos.

As

primeiras observações experimentais

sobre a difração de raios

X

produzida por cristais foram relatadas

por Fríedríck e Kinipping. Em

1912.

Lauel21 apresentou

uma teoria elementar

para a difração de raios X

produ-zida por uma estrutura

periódica de átomos. Ficou decisivamente

mostrado

que os cristais são constituídos por uma estrutura

periódica de átomos.

O arranjo ordenado de átomos que constitui um cristal é conhecido

co-mo

e s tr u tu r a c r is tfJ 1 in a

Um cristal ideal

é

construido pela repetição infinita de uma mesma

unidade estrutural.

A unidade estrutural

pode ser um único átomo, um

con-junto de átomos ou um grupo de moléculas. Logo, a estrutura

de todos os

cristais pode ser descrita em termos de um retículo com um grupo de átomos

ligados a cada ponto do reticulo. Este grupo

é

denominado de

b a s e

e se

repe-te no espaço para formar a estrutura cristalína.

Um cristal ideal

é

composto por um arranjo de átomos num retículo

definido por três vetores fundamentais

ª'

º

e

ç,

de modo que as

configura-ções atômicas sejam exatamente iguais tanto para um observador

situado em

r

quanto para um observador situado em

r',

dado por:

o

conjunto de pontos

r'

especificados para todos os valores dos inteiros

fit,

n2 e n3 define um reticulo. que

é

um agrupamento

periódico regular de

pontos no espaco. O retículo assim definido

é

uma abstracão matemática.

Pa-ra se formar a estrutuPa-ra

cristalina

é

necessário que exista uma base de

(25)

Os

vetores

ª,

º

e ç

de translação são usualmente utilizados para definir

os eixos cristalográfícos.

O

paralelepípedo formado por estes vetares

é

deno-minado de

c e la u n itá r ia

e corresponde

à

cela de menor volume, dado por:

A cela unitária preencherá todo o espaço pela ação de operações de

translação conveníentes. A figura I.1.a mostra um retículo tridimensional,

mostrando também a cela. A figura I.l.b mostra os parâmetros

a, b, c e os

ângulos

a, ~,

y

entre os vetores

ª'

º

e

ç,

que definem a cela unitária.

Figura I.1.a: O retlculo

tridimensiona1.

Figura I.1.b: Parâmetros da cela unitária.

mostrando a cela unitária.

r·

_-1

=

x .. a

_{1 -}

+

Y"b

_{I -}

+

z.. c

1-em que as componentes

Xj, Yj

e

Zj

são as coordenadas atômicas do l-eSlmo

átomo, cujos valores são frações dos comprimentos axíais a, b, c na direção da

respectiva coordenada, sendo a origem um vértice da cela.

E de interesse especificar índices que definam os planos do retículo.

Esses indices são denominados de

in d ic e s

d e

A 1 .J 1 J e r

e são relacionados a uma

(26)

dos índices de Miller

é

feita da seguinte maneira: toma-se os inversos dos

números que caracterizam a interseção, reduzindo-os a três inteiros de

mes-ma razão e tem -se os índices de Miller (hkl).

o

-º-h

Como exemplo, se considerarmos um plano interceptando os eixos em:

-

-OA

=

6a, OB

=

2b e OC

=

3c, os índices de Miller do primeiro plano a partir da

origem são (132).

Existem 7 sistemas de coordenadas tridimensionais

que são úteis para

descrever os cristais e que são a base de sua classificação. Em geral, a cela

unitária é caracterizada por seis parâmetros:

a,

p,

y,

a, b, c, já definidos.

A tabela 1.1 fornece a lista dos sistemas cristalinos com os parâmetros

da cela unit.ária que caracterizam cada uma.

No sistema monoclínico um dos eixos é único, no sentido de que ele é

perpendicular

aos outros dois. Por convenção esse eixo único é escolhido

como sendo o eixo b, de modo que

p )

90°.

As operações de simetria de um retícul0 são as operações que

trans-formam o retículo nele próprio. Estas operações são de dois tipos: rotação e

reflexão.

A

r o t a ç ã o

é

necessariamente em torno de um eixo e

é

designada como

sendo de ordem n se

é

uma rotação de 360

0

(27)

de-signados por um inteiro e são possíveís somente rotações de ordem 1. 2,

3,

4,

e

6. Sistema cristalino

Triclínico

Monoc1ínico

Ortorrômbico

Tetragonal

Romboédrico

Hexagonal

Cúbico

Parâmetros

a ;: b ;: c,

a ;:

p

;=

y

a;:

b ;:

c,

a

= y=

90°,

P

;=

90°

a

;=

b ;:

c,

a

= ~ = y =

9 0°

a

=

b

;=

c,

a

=

P

= y =

9 O

o

a

=

b

=

c,

a

=

P

=

y;=

9 O

o

a

=

b

=

c,

a

=

P

=

9 O

o,

y =

12 O

o

a

=

b

=

c, a

= ~ = y =

9 O

°

-1

2 1 m

mmm

4 / m m m

-3m

6 / m m m

m3m

Se existe um plano no retículo tal que a parte de um lado do plano está

relacionada especular mente com a parte do outro lado, o retículo possui um

p / m o

d e s i m e t r i a

ou um

p / a n o d e r e l l e x ã o

designado pela letra m.

Estes elementos podem ser combinados, tal como a operação

2 1 m ,

que

combina um eixo de ordem 2 com um plano especular perpendicular a ele.

A operação 1, denominada de

i n v e r s ã o ,

é caracterizada por uma

refle-xão através de um ponto denominado

c e n t r o d e i n v e r s i a

Pode ocorrer também um outro conjunto de elementos de simetria que

combina um eixo de rotação com um centro de inversão (são os chamados

eixos impróprios).

C o m o e . 1 'e m p k ~

a operação 4 combina uma rotação de 90°

com uma inversão através do centro de simetria. Nesta operação, se um

ob-jeto tem coordenadas xyz, os demais obob-jetos a ele ralacionados por esta

ope-ração de simetria terão coordenadas:

y,

x,

z;

y,

x, z;

X,

y,

z, sendo o eixo de

rotação coincidente com o eixo z.

Existem sete retículos relacionados aos sete sistemas cristalinos (tabela

1.1), os quais têm o equivalente a um ponto por cela unitária. Tais retículos

são denominados de

p r i m i t i v o s

e são designados pela letra P precedendo o

símbolo de simetria (exceto para o romboédríco, para o qual se usa a letra R).

No seu estudo dos retículos, Bravais descobriu os retículos

n ã o p r i m i t i v o s

(28)

(faces ab). Se o retículo tem um ponto no centro da cela,

é

designado por L Se

todas as faces têm pontos em seus centros, o retículo

é

designado de

F.

~\ \0

\~---~

"'~ ~ ••••• --

0""""----.Jct-c

pj P2Im

b Q

lí-l

I

7i

0~11

1 ,1

l~

N

;-- -o

f

:L-

~o

,h

0/ 0

V

h'

1/

PrIlmm Cmmm

b c b c

/~\

\) .X \

, ~ , W

Q R3m

/~--o

:...+-I

I I I

)_ -o

c /'

V

,g-

_P4/mmm

o a

(29)

Considerando todos os grupos de elementos de simetria tem-se

.12

g r u p o s p l J n t l J i 1 1 : ~

Esses são divididos entre as 7 classes cristalinas. O retículo

que é caracteristico de cada classe sempre tem a simetria mais alta possível

dentro da classe e define o grupo puntual

holoédrico

que pode ser

acomodado dentro da classe. Veja tabela 1.1.

Quando se combina os 32 grupos puntuais com os 14 retículos de

Bravais resultam 230 grupos espaciais, os quais descrevem os únicos meios

em que objetos idênticos podem ser arranjados em um reticulo infinito. A

operação de translação no retículo introduz duas novas espécies de operações

de simetria:

e i x o s l J e J i c o i d a i s

e os planos de

r e l J e x ã o - t r i 1 1 l s / a ç a a

("gUde"),

Quando essas operações são combinadas com os elementos de simetria

já

descritos resultam nos mesmos 230 grupos espaciais.

E i r a 1 l e J i c o i d a J :

é

a combinação de uma rotação e uma translação

correspondente a uma fração do parâmetro reticular paralela ao eixo de

rota-ção.

E

designado pelo inteiro n e um sub-índice m. Assim, 31 designa um eixo

helicoidal de ordem 3 (rotação de 120°) com uma translação entre os

suces-sivos pontos de 1/3 (m/n). Os eixos helicoidais possíveis são: 21; 31. 32; 41,

42;

61,62,63,64.6

5,

P / a n o d e r e l J e x a o - t r i 1 1 l s l a ç a o :

é

a combinação de um plano de reflexão

e uma translação paralela no plano. A translação em tal plano é ao longo de

um eixo ou ao longo da diagonal da face da cela unitária, de magnitude igual

à

metade do comprimento do eixo ou da diagona1.

E

designado por a, b ou c

se a translação

é

a/2, b/2 ou c/2, respectivamente,

por n se for (a+b)/2,

(a+c)/2 ou (b+c)/2 e d se for a/2 + b/2 + c/2.

Um grupo espacial

é

designado pela letra maiúscula identificando o

tipo do retículo (P, C etc.) seguido pelo símbolo do grupo puntual modificado

pela introdução dos elementos de simetria translacional se necessário.

O volume I da Internatíonal Tables for X-ray Crystallography!41

des-creve os 32 grupos puntuais e os 230 grupos espaciais.

C o m o

e x e m p l o .

seja o grupo espacial P21/C, o qual

é

relacionado ao

(30)

I

_o-+-l ~~o_

1 / 4

I

1 / 4

I

plano de reflexão-translação

c, perpendicular

ao plano de

prol' eção

(y

=

1 e

y

= ~.).

4

4 I

I

I~ol~o

I

~

eixo

21 paralelo ao plano de

projeção (z

~; x = 0, x = ~

e x

=

1).

r~

objeto.

(1) --"

x.

y,

z. Operando

primeiro

21 tem-se:

(2)

-+

X, Y

+

1. Z

+

1,

lem-brando que

1 -

x

==

-x. De

(1).

operando

o plano de reflexão-translação

c,

tem-se

t3)

-+

x.

i-

y. z

+

i.

De (2), operando

o plano de reflexão-translação

c.

tem-se

(4)

-+

X. V .

z.

O eixo

21 e o plano de reflexão-translação

produz um

centro de inversão. Logo (I) e (4), (2) e (3) estão relacionados

por este centro

de inversão.

L2

Espal.bameotode Haios

.r

P o r

um

fflétroo

15)

o

r 'a io

X é uma radiação eletromagnética

que se encontra

na região do

espectro eletromagnético

entre a radiação

ultra-violeta

e a radiação

gama. O

comprimento

de onda dos raios X tem um alcance aproximado

de

0.1 a

IOoA.

Estaremos

interessados

em raios X monocromáticos,

tendo um comprimento

de onda da ordem de lÁ.

A interação

do feixe de raios X com um centro

espalhador

é

usual-mente considerada

em termos do espalhamento

por um único elétron e isso

ocorre em dois processos: o espalhamento

Thomson ou coerente

e o espalha,:"

mento Compton ou incoerente.

Além das duas radiaçõés

oriundas

desses dois

processos

de espalhamento.

uma terceira

radiação

denominada

de radiação

fluorescente

deve ser considerada.

Essa radiação surge do processo de

(31)

Quando um fóton de raio X incide em um átomo ocorrem transições

eletrôni-cas dentro do átomo, havendo emissão da radiação fluorescente.

No espalhamento Compton

l61

o comprimento de onda da radiação

es-palhada é maior que o comprimento de onda da radiação incidente, devido a

uma perda de energia no proce~sso de colisão dos f~tons de raios X com o

elétron. A diferença

de comprimento

de onda depende

do ângulo de

espalhamento, sendo maior quanto maior for o ângulo de espalhamento.

Na difração de raios X por um cristal o espalhamento coerente e

coope-rativo de muitos átomos é significativamente

maior que a soma das

contri-buições incoerentes, o que faz com que, normalmente,

se ignore o

espalha-mento incoerente na cristalografia de raios X e a fluorescência pela escolha

adequada do comprímento de onda da radiação utilizada.

Assím, será descrito apenas o espalhamento

Thomson ou coerente,

quando um feixe de raios X incide sobre um elétron.

E s p a l h a m e n t o

T h o m s o n

I7.

8 )

Quando uma onda eletromagnética choca-se com um elétron, o campo

eletromagnético oscilante incidente força o elétron a oscilar com a mesma

freqüência da onda incidente. A carga oscilante (acelerada) age como uma

fonte secundária de emissão de ondas eletromagnéticas, as quais têm a

mes-ma freqüência da radiação incidente.

o

feixe de raios X é espalhado em todas as direções por um elétron,

mas a intensidade do feixe espalhado depende do ângulo de espalhamento.

j.

Thomson encontrou que a intensidade I

_e

do feixe espalhado por um único

elétron de carga e, massa m e a uma distância r do elétron, válida para uma

onda plana e polarizada é dada por:

10 ~

intensidade do feixe incidente,

e ~

carga do elétron,

m ~

massa do elétron,

c

=

3 x

1 08

m/s, velocidade da luz,

(32)

Seja um feixe incidente

na direção

01 (fígura

1.5),

o qual encontra

o

-+

e l é t r o n

em O. Esse feixe não polarizado tem o vetor campo elétrico

E situado

no plano yz. Esse feixe pode ser resolvido

em duas componentes

plano

pola-2

2

2 fizadas, tendo os vetores campo elétrico E

y

e

E

z,

onde E

=

Ez

+

E

y.

Na média

-+

E

y =

Ez, desde que a direção do vetor E é aleatória. Como I

o:

E2, vem:

1 :r

10 =

Ioy

=

Io

z

Supondo um feixe espalhado

na direção OD, a qual faz um ângulo 28

com a direção do feixe incidente,

a intensidade

do feixe espalhado

nessa

di-reção e a uma distância r do elétron será a soma das duas componentes

es-palhadas

I

ey

e I

ez.

A componente

E

y

do feixe incidente

acelera

o elétron

na direção y

( a

90'). Logo, a intensidade

espalhada

I

ey

é dada por:

A componente

_{Ez do feixe incidente}

acelera

o elétron

na direção

z

(a

90' -

28),

resultando

para a intensidade

espalhada

Iez:

~,,,~-~~-,.~ ...~.-.",'.. ,•....•..."..•.•. _~....,:"."~-'--"'-.•...•.•..•.

~

'SERViÇO DE BIBLIOTECA ;: '~H 21.\ "".' .. (~

(33)

A intensidade da radiação espalhada na direção ODe a u ma distância r

do elétron vale:

A quantidade

1 +

~s2

28 =

P é denominada de

f a t o r d e p o J a r i z a ç ã a

Como I

e

O<:

_1_, implíca que os elétrons são os únicos espalhadores

efe-m

2 tivos, poís a massa do próton é

1837

vezes a massa do elétron, tornando o

próton um espalhador secundário.

1 . 3

E s p a l ó a m e n / o d e B a i o s X p o r u m A / a m o

191 Em um átomo, os elétrons ocupam um volume finito. sendo necessário

encontrar uma distribuição espacial para os mesmos. Essa distribuição pode

ser caracterizada pela função densidade eletrônica p(r), isto

é,

em cada

ele-mento de volume dV do átomo o número de elétrons é p(r)dV. Se o átomo

é

atingido por uma onda eletromagnética plana (caracterizada pelo versor §o),a

amplitude da onda esférica espalhada (caracterizada pelo versor

§)

pelo

ele-mento de volume dV

é

proporcional ao número de elétrons nesse elemento

de volume. A amplitude total da onda espalhada pode ser obtida por

super-posição das ondas parciais emitidas por cada elemento de volume. Para se

realizar essa soma, deve-se levar em conta que as fases dessas ondas parciais

são diferentes para cada elemento de volume dV. Como referência para os

cálculos das fases será usada a figura 1.6.

Para simplificar as fórmulas finais, é conveniente que os versores ~ e

§o tenham módul0 ~.

A diferença de percurso entre a onda espalhada pelo elemento de

vo-lume na orígem e o elemento vovo-lume em r é dada por:

oc -

OP

=

I{

r .~-r .~)

=

Àr' (~- ~)

=

Àr' ~

onde ~

é

o

v e t o r d e e s p a J ! J a m e n t o .

õ.+.

=

2n . Àr' S

=

2n r· S

(34)

-Figura 1.6 - Espalhamentl) plH' um át·omo.

A onda espalhada

na direção ~ pelo elemento

de volume

em [, será:

plr)d V exp( 2ni r· ~).

f(~)

=

J

P(t)exp(2Jlit~) dV

Vohme d>atomo

A expressão

(1.2)

representa

o

f a t o r d e e s p a J . b a m e n t o a t ô m i c a

Os

fato-res de espalhamento

atômico dependem

do comprimento

de onda e do

mó-dul0 de ~, supondo que o átomo tenha simetria

esférica. Com isso, f depende

de

Â

e do ângulo de espalhamento

2B.

Se o átomo tem simetria

esférica, f é

real, pois plr)

=

p(-r). Os valores de f foram calculados e são tabelados

na

In-ternational

Tables for X-ray Crystallography14l,

voI. II L A figura

1.7 abaixo

mostra algu mas curvas de

f

x

sen

B .

Â

Se ~

=

O, f(0)

=

f

p(r) dV

=

Z, onde Z é o número

total de elétrons

no

atamo.

Efeitos secundários

surgem

quando o comprimento

de onda do feixe

incidente

está perto da borda de absorção do elemento

espalhado!'.

A

corre-ção desse efeito faz-se necessária.

Esse efeito é denominado

de

e s p f J 1 . b a O l e n t o

': l t l O m f J 1 o[101

e ao considerá-io

duas correções no fator de espalhamento

atô-mico são introduzidas:

M'

e

M " ,

para cada espécie de átomo.

M'

é um termo

de correção real (usualmente

negativo)

e M" é o termo de correção da

(35)

f

= f + M '+ í M "

anômalo

. Figura. 1.7 - Curvas de

f

x

sen

9 .

1

f .

4'

Espal1Jamcoto dc Haios X por um Grupo dc Atamos

19J

Seja um grupo de N átomos, em que

rj

é o vetar de posíção do j-esímo

átomo em relação à origem da cela unitária. Na equação (1.2), o vetar

r

no

es-palhamento pelo j-ésímo átomo torna-se: (

+

fi.

Assím, o espalhamento

do

átomo

j

em relação

à

origem da cela vale:

GCat)j

=

f

p(r)ex~ 2Jti(r

+

ri}~JdV

Volane do ó.tomo

ou

G(at)i

=

fiel ~

l)ex~2Jti{j"~)

(36)

G(§)

=

.!

fíex~21tití'§)

1=1

onde G(S) é uma função complexa.

I.5 Oifraçao

de

.Haios

r

por

um

Crista/I

,l

Para se analisar em detalhe a influência de um arranjo atômico

perió-dico na duração de raios X por um cristal, primeiro analisa-se a difração de

um arranjo unidimensional, composto de n átomos, sendo cada átomo

separa-do separa-do seu vizinho por um vetar distância

ª'

Na direção correspondente

ao vetar de espalhamento

~, a onda total

espalhada é dada por:

A(

§)

=

f

a .

f

ex

J

21t

i

(j -

1) ~.

§J

(

1.5 )

1=1

tt

onde f

a

é o fator de espalhamento. atômico. Esta expressão pode ser

simplifi-cada, de modo que a intensidade de espalhamento esteja relacionada com

Pela expressão vê-se que a intensidade será máxíma, ísto

é,

a difração

somente será observada se a diferença de fase

2n

ª'

§

entre as sucessivas

on-das espalhaon-das for igual a um múltiplo de

21t.

Logo,

SERViÇO DE BI8L.,ºH~,A E INFORMAÇÃO _ IFQSC

(37)

2n a· S

=

2nh ou a·

S

=

h, onde h é inteiro.

-

-Em três dimensões, onde a cela unitária

é

definida pelos vetores

ª,

º

e

ç.

as condiÇÕes de difração tornam -se:

onde h. k. 1 são inteiros. Essas equações são conhecidas como as

e q u a ç õ e s d e

L a u e .

Pelo teorema da convolução (símbolo

* ) 1111 ,

a densidade eletrônica do

cristal

é

dada pela convolução de densidade eletrônica da cela com um

con-junto de funções

t >

de Dirac, caracterizando o retículo direto

Periltal(r)

=

Pcela(r)

-1

r-

(n

i ~ +

n2

º

+

n3

ç)J

onde nla n2 e n3 são inteiros.

A onda total dífratada

pelo cristal tem amplitude Gcristal(§)

determi-nada pela transformada

de Fourier (TF) de Pcristal(r),

A transformada

de Fourier de

~r-nlª-n2º-n3çJ

é uma nova função

t >

de Dirac, caracterizando o reticulo recíproco.

Assim, G

c

ristal(§) ... F(b)

ao

F(hkl), é dado por: F(b) ... TF[Pcela(r))

. t > ( § - h ª * - k Q * - I F )

que fornece uma amostragem da transformada

de Fourier

da densidade

eletrônica da cela unitária em pontos discretos do retículo

recíproco, em que

b-

= =

(h ..k,

O. Logo,

F(hkl)

=

F(~)

=

. !

fi

( I ~ I)

ex~2n

itj'~)

( 1 .1 O )

. 1 = 1

onde F(b)

é

o fator de estrutura, que

é

uma quantidade complexa, para o caso

de grupos espaciais não centrossimétrícos.

r " h

=

x · a · h + Y . b · h + z · C · h

=

x ·h+ v . k + z ·1

(38)

N

Se

h

""

º,

F(OOO)

==

!

fi ""

n

Q

de elétrons na cela unitária.

i

=

1 A intensidade do feixe dífratado é relacionada com o fator de

estrutu-ra, através da equação

1 . 5 . 2

L e i d e B r a g g l t 2 1

Bragg(l913)113J deduziu uma equação muito simples tratando a

dura-ção de raios X como "reflexão" nos planos do retículo. Considere um feixe de

raios X incidindo em alguns planos paralelos, cuja distância interplanar

é

dhkl.

o

feixe difratado terá intensidade máxima se as ondas estão em fase. A

diferença de percurso vale:

BD

+

CD

=

2d

sen

e

(39)

2 sen

e

=

_1_

(I .13 )

Á

dhkl

pois a reflexão de planos com índices (nh nk nO é a reflexão de n-ésíma

or-dem dos planos com índices (hkl).

Essencialmente a lei de Bragg contribui para identificar os inteiros h, k,

1 das equações de Laue, com os índices de Miller dos planos do retículo. As

equações

0.7)

podem ser reescritas na seguinte forma:

a

b

c

h . ~

=

1,

k . ~

=

1 e

T' ~

=

1 A subtração das duas primeiras equações dá:

(~-~).s=o

h k

~

a qual significa l'ue o vetar S

_~

_-

é

perpendicular

ao vetar

ª _

_h

º .

_k

De modo

sími-a

c

lar pode ser mostrado

que o vetar ~ é perpendicular

ao vetar

~

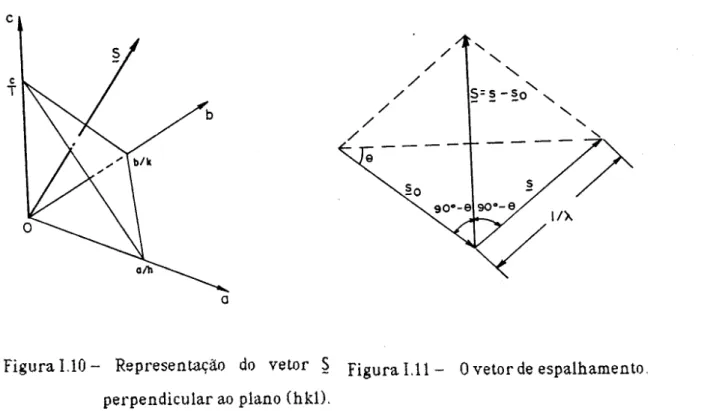
_ ~. Esses

dois vetares definem um plano cujos índices de Miller são hkl. Então o vetar

~ é perpendicular

ao plano (hkl). Figura 1.10.

Mas ~ é um vetar na direção do bissetor do feixe incidente e difratado.

desde que Isol

=

Is\

=

_1 ,

Figura 1.11.

- - j..

/

Figura 1.10 -

Representação

do vetor

S Figura 1.11 -

Ovetor de espalhamento,

perpendicular

ao plano (hkD.

A distãncia

dhkl dos planos

(hkl) é a distância

perpendicular

do

(40)

a

P

c

d'

- d S .

vé-se que dhkl é a projeção

de ~, ~

ou

T

sobre o versor

da

Ireçao e~, Isto

a

S

1 dhkl

=

11'

N

=

I

SI

A expressão mostra que a distância interplanar

é

o inverso do módulo do

ve-tor de espalhamento.

(L14)

Da figura 1.11, tem-se:

logo,

'1

2 sen

e

=

---dbkl

À

a qual

é

idêntica

à

equação

0.13),

que foi obtida por Bragg.

As direções dos feixes de raios X difratados são determinadas a partir

do conhecimento

dos valores de ~ que são soluções das equações de

Laue (1.7).

A primeira equação, ~.

ª

=

h,

é

equivalente a estabelecer que a

proje-ção de ~ em

ª

é

constante para um valor fixo de h, isto

é,

as extremidades do

vetar ~ se encontram sobre um plano perpendicular a

ª'

Se h

é

zero. o plano

passa pela origem; se h

=

1. o plano faz um certo intercepto em

ª;

se h

=

2, ele

faz o dobro do intercepto; e assim por diante. Em. outras palavras, um

con-junto de planos de espaçamento

constante

é

estabelecido, cada plano do

conjunto correspondendo

a um particular valor de h. De modo similar, um

conjunto de planos equidístantes

perpendiculares

a

º

serão estabelecidos,

cada plano correspondendo a um valor particular de k; um último conjunto

de planos perpendiculares

a ç corresponderão

a diferentes valores de 1. A

interseção desses planos representa os pontos que são as extremidades

dos

vetares ~ que satisfazem simultaneamente

as três equações de Laue. Estes

conjuntos de planos definem um retícul0 de pontos -

o

r e i / c u J o r e c i p r o c a

A cela unitária do retículo recíproco

é

definida por três vetores

ª.~,

!?>: e

(41)

~. ~* = 1,

~* .

º

= ª*.

ç

=

o

b'b*=l,

b·a=b·c=O

_-

-bXc

cXa

aXb

a*

=

-=---=--

b*

= --

e c*

=

-=--=--

V'

-

V

-

V

em que

V

=

I

~(Q

x~)

I

é

o volume da cela unitária no espaço direto.

(1.16)

o

vetar de espalhamento tem como componentes, no espaço reciproco,

os vaiores h, k, 1,isto

é

S ;;: h

=

ha'«

_-

+

kb

_-

* +

1c*

_-

(1.17)

A condição de difração de raios X por cristais pode ser expressada em

termos da lei de Bragg ou em termos das equações de Laue. Ewald propõs

uma construção geométrica simples que encerra as duas leis acima, a qual

é

muito útil na descrição da difração.

Uma esfera é desenhada com centro no cristal (C) e raio

1. A origem do

À

retículo

é

colocada em O, onde o feixe direto intercepta a esfera. A condição

de que um raio CB seja um raio difratado

é

que B seja um ponto do retículo

-recíproco (hkl), isto

é ,

o vetar OB

é

o vetor do retículo recíproco,

Q.

=

hª*

+

kQ*

+

lç*.

Para que a reflexão hkl se encontre na posição de difração o cristal

deve girar, para que este ponto particular do retículo recíproco corte a esfera

de reflexão.

E

conveniente. em termos práticos, trabalhar com uma esfera de

refle-xão de raio unitário, de modo que os vetares do espaço recíproco tornam-se

quantidades adimensionais. Assim, o módulo de

S

ou

D

é

dado por

1 I

À

S

=-- dhltl

para que seja mantida a relação com a lei de Bragg. Nestas condições a esfera

de reflexão terá sempre o mesmo diâmetro. independente

do comprimento

de onda. Mas, uma variação em

À

tem o efeito de encolher (pequenos ;() ou

(42)

Considerando

p(r)

como sendo a densidade eletrônica no ponto

[(x, y.

z), o qual encerra um elemento de volume dV da cela unitária, o fator de

es-trutura pode ser determinado da equação:

F(b) =

f

PCr.)exr{2n

i

f.'

b) dV

v

onde a integral

é

sobre todo o volume da cela unitária.

A densidade eletrônica é calculada pela transformada

de Fourier de

F(g), isto

é,

pCr.) =

f

F(b)ex~-2nir.'

b)dV*

(1.19)

V*

onde a integral

é

feita sobre todo o volume do espaço recíproco em que

9 é

definido.

(43)

eletrônica seja

periódica em três dimensões, o que implica que a mesma pode

ser representada por uma série de Fourier tridimensional. Esta suposição é

justifícada pela própria definição de um cristal. Então,

(6

pCr)

=

l, l, l,

C(h'.k',1')exp2ni(h'x+k'y+l'z)

(1.20)

h'k'l'=-'h

onde h', k' e

r

são inteiros.

Inserindo este valor de

p(r)

na equação

(1.18),

vem:

F(

h)

=

F(hId)

=

J

h',k~

= _

C(h'.k:,l')

exp 2n

{(h

+

h')x

+

(k

+

k')y

+

(I

+

l'

lzJdV

v

A exponencial

é

periódica e a integral num período

é

zero em geral, exceto se

h

=

_h', k

=

-k' e I

=

-1'. Nestas condições.

F(W)

=

_J

(C(h' ,k',1')- dV

=

V· C{-h,-k.-1)

v

C(-h.-k.-l)

= ~

F(hId)

Inserindo o valor de C(-h. -k. -1) na equação

0.20),

vem:

Esta expressão fornece a densidade eletrônica no espaço direto em termos

dos fatores de estrutura no espaço recíproco.

o

fator de estrutura sendo uma quantidade complexa pode ser

deter-minado conhecendo-se o módul0 do fator de estrutura e a fase

$(.b),

isto

é.

(44)

A

=

\F(h)\' cos[4J{h)l

B

=

IF(~)\·

senl$(h)]

Se

a estrutura é centros simétrica (para um átomo na posição

x,

y,

z

existe um outro átomo em -x,

-y,

-z), B

=

O.A fase

é $

=

Oou

Ir

e

Fel})

é

real.

A lei de Friedel se refere

-

--

à

relação entre a reflexão hkl e seu par

cen-trossimétríco h, k, 1 (índíces negativos). Esta relação pode ser deduzída como

se segue:

Logo

ou, como

I(!!) ~ IF(!!l!2,

vl:(~)1

=

IF(~)I

e ~~)

= -~~)

0.24)

0.25 )

A relação

(1.25),

lei de Friedel, sofre desvios no caso de ocorrer

espa-lhamento anômalo, sempre que o grupo espacial for não centros simétrico.

(45)

25-Capítulo

II

(46)

/ll

Coleta de Dadosl

2 _tl

As intensidades dos feixes de raios X difratados por cristais foram

co-letadas utilizando um difratômetro automático CAD-4 da Enraf Nonius, no

la-boratório de Cristalografia do Departamento

de Física e Ciência dos Materiais

da USP de São Carlos.

Os cristais a serem utilizados devem possuir uma estrutura

interna

uniforme (não devem ser geminados ou compostos de sub-cristais

micros-cópicos), isto

é,

devem ser monocristais e serem de tamanho e forma

ade-quados para minimizar e eventualmente

possibilitar a correção dos efeitos de

absorção (dimensões não superiores a O,5mm).

Descrição do Arranjo Experimental

O difratômetro

consta de um goniômetro de três graus de liberdade

(goniômetro Kappa), mais um quarto grau de liberdade

para a posição do

detetor. O goniômetro Kappa suporta a cabeça goniométrica que mantém o

cristal no centro do difratômetro

e consta de três partes associadas a três

eixos de rotação independentes,

como mostra a figura 11.1.Estes três eixos se

interceptam

no centro do difratômetro.

A cabeça goniometrica está montada no eixo

$.

o qual

é

suportado pelo

bloco kappa. O bloco kappa pode girar em torno do eixo k e é suportado pelo

bloco ômega. Por sua vez, o bloco ômega pode girar em torno do eixo

ül,

su-portado pela base do difratômetro. O ângulo

a

entre os eixos k e

ül

é

nomi-nalmente de 50°, que

é

o mesmo ângulo entre os eixos k e

$.

o

plano horizontal que passa pelo centro do difratômetro

é

perpendi-cular ao eixo

ül.

Os feixes incidente e difratado se encontram sobre esse plano,

sendo as intensidades e posições do feixe difratado medidas sobre o mesmo.

Um sistema de coordenadas

m

é

definido. O eixo X está dirigido do

centro do difratômetro

à

fonte de raios X.O eixo Z está dirigido para cima, na

direção de

ül

e o eixo Y completa o sistema tríortogonal direto.

O difratômetro contém um eixo 28 independente,

o qual está associado

ao detetor, coincidente com o eixo

ül.

As posições zero dos ângulos k,

ül

e 28 são definidos em termos da

geometria do aparelho. O ângulo k, para os quais os eixos

ül

e

$

coincidem, é

definido como k

=

O.

ül =

O é definido como a posição na rotação do eixo

ül

para o qual o eixo k fica no plano

Xl.

e o bloco kappa

é

oposto

à

direção +X. A