Pró-Reitoria de Pós-Graduação e Pesquisa
Programa de Pós-Graduação Stricto Sensu
Doutorado em Economia
CONHECIMENTO COMUM IMPERFEITO NO TEOREMA DE
CONCORDÂNCIA DE AUMANN
–
DIFERENCIAÇÃO DE
PREÇOS E CUSTOS DE MENU NOS PAGAMENTOS COM
CARTÃO DE CRÉDITO
Brasília - DF
2013
MARCOS VALLI JORGE
CONHECIMENTO COMUM IMPERFEITO NO TEOREMA DE CONCORDÂNCIA DE AUMANN – DIFERENCIAÇÃO DE PREÇOS E CUSTOS DE MENU NOS
PAGAMENTOS COM CARTÃO DE CRÉDITO
Tese apresentada ao Programa de Pós-Graduação Stricto Sensu em Economia da Universidade Católica de Brasília, como requisito parcial para obtenção do Título de Doutor em Economia.
Orientador: Prof. Dr. Wilfredo L. Maldonado
Ficha elaborada pela Biblioteca Pós-Graduação da UCB
27/08/2013 G82c Jorge, Marcos Valli.
Conhecimento comum imperfeito no Teorema de Concordância de Aumann: diferenciação de preços e custos de menu nos pagamentos com cartão de crédito. / Marcos Valli Jorge – 2013.
98f.; il : 30 cm
Tese (doutorado) – Universidade Católica de Brasília, 2013. Orientação: Prof. Dr. Wilfredo L. Maldonado
1. Economia. 2. Teoria dos jogos. 3. Pagamento. 4. Preços. 5. Cartões de crédito. I. Maldonado, Wilfredo L. orient. II. Título.
Tese de autoria de Marcos Valli Jorge, intitulada “Conhecimento Comum Imperfeito no Teorema de Concordância de Aumann – Diferenciação de Preços e Custos de Menu nos Pagamentos com Cartão de Crédito”, requisito parcial para obtenção do grau de Doutor em Economia, defendida e aprovada, em 23 de agosto de 2013, pela banca examinadora constituída por:
__________________________________________________________ Prof. Dr. Wilfredo L. Madonado
Orientador
Universidade Católica de Brasília – UCB
__________________________________________________________ Prof. Dr. José Ângelo Costa do Amor Divino
Examinador Interno
Universidade Católica de Brasília - UCB
__________________________________________________________ Prof. Dr. Rogério Mazali
Examinador Interno
Universidade Católica de Brasília - UCB
__________________________________________________________ Prof. Dr. Gil Riella
Examinador Externo Universidade de Brasília - UnB
__________________________________________________________ Dr. Mardilson Fernandes Queiroz
Examinador Externo Banco Central do Brasil - BCB
AGRADECIMENTOS
Meu sincero agradecimento ao amigo Wilfredo Maldonado pelo incentivo para que eu retomasse o doutorado após um par de décadas, assim como pela orientação, atenção e apoio durante a elaboração desta tese.
Aos professores Benjamin Tabak, Jaime Orillo, José Ângelo Divino, Rogério Mazali, Tito Belchior e Wilfredo Sosa pela contribuição para o meu aprimoramento acadêmico, assim como, pelas críticas e sugestões que em muito colaboraram para elevar a qualidade deste trabalho. Obviamente, os eventuais erros que, por ventura, remanesçam são de minha inteira responsabilidade.
Agradeço aos colegas Alexandre Moody, Fábio Trajano, Mardilson Queiroz e Ricardo Mourão pelos debates instigantes sobre o mercado de cartões de crédito, responsáveis por despertar meu interesse em aprofundar o estudo do tema e produzir a segunda parte deste trabalho.
“The whole problem with the world is that fools and fanatics are always so certain of themselves, but wiser people so full of doubts.”
RESUMO
Referência: VALLI JORGE, Marcos. Título: Conhecimento Comum Imperfeito no
Teorema de Concordância de Aumann – Diferenciação de Preços e Custos de Menu nos
Pagamentos com Cartão de Crédito. Ano da defesa: 2013. Quantidade de folhas: 98. Tese
de Doutorado (Economia) – Universidade Católica de Brasília, Brasília, 2013.
Na primeira parte deste trabalho estendemos o conceito de conhecimento comum (common knowledge), introduzido por Aumann (1976), para um contexto em que os indivíduos não conheçam perfeitamente as partições de informação privada de outros indivíduos, situação que denominamos de conhecimento comum imperfeito. Fazemos extensões de duas versões do Teorema de Concordância (Agreement Theorem) apresentado originalmente em Aumann (1976). A primeira versão, apresentada em Geanakoplos (1992), na qual a informação é do tipo particional, os estados não trazem nenhuma informação sobre o conhecimento de cada indivíduo a respeito da partição dos outros, e as regras de decisão individuais são distintas, é estendida aqui para um contexto com conhecimento comum imperfeito. A segunda versão, apresentada em Samet (1990), em que os estados incorporam a informação sobre o conhecimento de cada indivíduo sobre o que outros possam saber e a informação não é particional, é estendida aqui para o caso em que as regras de decisão individuais são distintas, como na versão de Geanakoplos. De fato, apresentamos uma demonstração alternativa que, além de mais geral, é muito mais curta e direta do que aquela adotada em Samet, e na qual fazemos uso de uma definição distinta de evento comumente conhecido que entendemos mais adequada. Finalmente, apresentamos um exemplo para ilustrar como o conhecimento comum imperfeito surge no contexto de um jogo simples. Na segunda parte, construímos um modelo para os pagamentos com cartão de crédito no qual os lojistas podem cobrar preços diferenciados dependendo dos instrumentos de pagamento escolhidos pelos consumidores. Segue-se uma abordagem similar à adotada em Rochet e Wright (2010), exceto por assumirmos um sistema de cartões livre de regras de não-sobrepreço ou de qualquer desincentivo à diferenciação. Calculam-se os preços de equilíbrio competitivo, num arcabouço de competição do tipo Hotelling entre os lojistas, supondo que o crédito fornecido diretamente pelos próprios lojistas é menos eficiente em custos do que o crédito proporcionado pelo cartão de crédito. De acordo com a literatura, obtém-se que a tarifa de intercâmbio se torna neutra ao se eliminar a regra de não-sobrepreço, quando esta tarifa perde sua capacidade de afetar as decisões individuais no sentido de deslocar o bem-estar agregado dos consumidores do seu nível máximo. Prova-se que o preço médio praticado no equilíbrio com diferenciação de preços é menor que o preço único praticado sob a regra de não-sobrepreço, a despeito da margem dos lojistas serem as mesmas em ambos cenários. Em seguida, mostramos como alguns subsídios são eliminados quando a diferenciação de preços é permitida. Adicionalmente, introduz-se um custo de menu de preços por instrumento de pagamento para provar que existe um valor limite para a tarifa de intercâmbio tal que, acima deste valor, o preço único não é mais equilíbrio e passa a existir um equilíbrio de preços diferenciados. Este valor limite pode ser interpretado como com um teto endógeno para a tarifa de intercâmbio fixada pela indústria de cartões. Finalmente, demonstra-se que, mesmo existindo custos de menu, o bem-estar dos consumidores pode ser maior no equilíbrio com preços diferenciados do que no equilíbrio com preço único sob uma regra de não-sobrepreço.
Palavras-chave: Conhecimento comum. Teorema de concordância. Partição de informação.
ABSTRACT
In the first part of this work, we extend the concept of common knowledge, introduced by Aumann (1976), for a context where the individuals do not know the private information partitions of other individuals, situation that we denominate “imperfect common knowledge”. We provide extensions of two versions of the Agreement Theorem originally presented in Aumann (1976). The first version, given in Geanakoplos (1992), where the information is partitional, the states do not bring any information about the knowledge of each individual with respect of the others partitions, and the decision rules may be different, is extended here to the context of imperfect common knowledge. The second version, approached by Samet (1990), where information is not partitional, and the states incorporate the information about the knowledge of each individual with respect to what the other individuals could know, is extended here for the case of different decision rules, as in the Geanakoplos version. In fact, we provide and alternative proof which, besides being more general, is shorter and straightforward than that used by Samet, includes a different and more suitable definition of common knowledge event. Finally, we present an example to illustrate how the imperfect common knowledge emerges in the context of a simple game. In the second part, we build a model of credit card payments where the retailers are allowed to charge differential prices depending on the instrument of payment chosen by the consumer. We follow the Rochet and Wright (2010) approach, but assuming a credit card system without a no-surcharge rule or any type of price differentiation disincentive. In a Hotelling competition framework at the retailers level, the competitive equilibrium prices are computed assuming that the store credit provided by the retailer is less cost efficient than the one provided by the credit card. In accordance with the literature, we obtain that the interchange fee becomes neutral if we eliminate the no-surcharge rule, when the interchange fee loses its ability to distort the individual consumer’s decisions displacing the aggregated consumers’ welfare from its maximum. We prove that the average price obtained under price differentiation is smaller than the single retail price under the no-surcharge rule, despite the retailer’s margins being the same in both scenarios. Furthermore, we show how some cross subsidies are eliminated when price differentiation is allowed. In addition, we introduce menu costs to prove that there is a threshold value for the interchange fee such that price differentiation is equilibrium if that fee is above this value. The threshold may be interpreted as an endogenous cap for the interchange fee fixed by the credit card industry. Finally, even with menu costs associated to price differentiation, we
conclude that the consumers’ welfare is greater in the price differentiated equilibrium than in
the single price equilibrium under the non-surcharge rule.
Keywords: Common knowledge. Agreement theorem. Information partition. Common prior.
LISTA DE ILUSTRAÇÕES
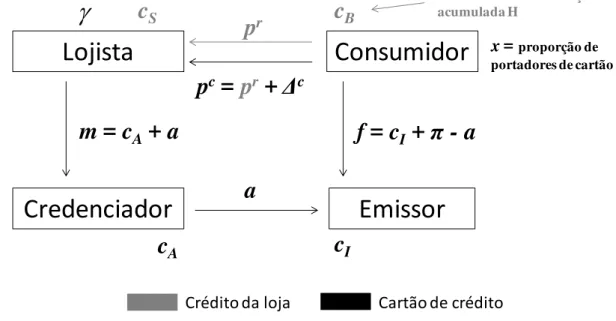
Figura 1: Preços, custos e tarifas dos instrumentos de pagamento...57
Figura 2: Consumidor indiferente no modelo Hotelling...60
Figura 3: Decomposições do preço único de equilíbrio...67
Figura 4: Movimento unilateral para a estratégia de preço único...68
Figura 5: Lucros com a possibilidade de diferenciação de preços...69
LISTA DE TABELAS
Tabela 1: Estados do jogo...39
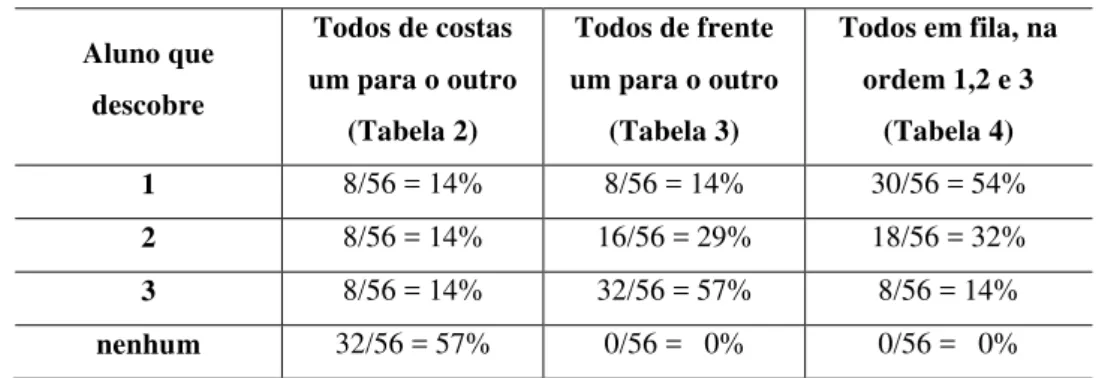
Tabela 2: Alunos dispostos um de costas para o outro...42
Tabela 3: Alunos dispostos um de frente para o outro...43
Tabela 4: Alunos dispostos em fila, na ordem 1, 2 e 3...45
SUMÁRIO
1 INTRODUÇÃO ... 13
2 CONHECIMENTO COMUM IMPERFEITO NO TEOREMA DE CONCORDÂNCIA DE AUMANN ... 19
2.1. PRELIMINARES À ANÁLISE DO CONHECIMENTO COMUM IMPERFEITO ... 19
2.2. O TEOREMA DE CONCORÂNCIA DE AUMANN ... 20
2.2.1.Espaço de estados restrito e conhecimento particional ... 21
2.2.2.Espaço de estados abrangente e conhecimento não particional ... 24
2.3. EXTENSÕES DAS VERSÕES DO TEOREMA DE CONCORÂNCIA DE AUMANN ... 28
2.3.1.Espaço de estados restrito e conhecimento particional ... 29
2.3.2.Espaço de estados abrangente e conhecimento não particional ... 31
2.4. EXEMPLO DE CONHECIMENTO COMUM IMPERFEITO DAS PARTIÇÕES ... 38
2.4.1.Conhecimento comum perfeito ... 40
2.4.2.Conhecimento comum imperfeito ... 43
2.4.3.Probabilidades posteriores ... 47
2.5. CONSIDERAÇÕES FINAIS SOBRE A SEÇÃO 2 ... 50
3 DIFERENCIAÇÃO DE PREÇOS E CUSTOS DE MENU NOS PAGAMENTOS COM CARTÕES DE CRÉDITO ... 52
3.1. PRELIMINARES À ANÁLISE DO MERCADO DE CARTÕES DE CRÉDITO ... 52
3.2. O MODELO COM DIFERENCIAÇÃO DE PREÇOS ... 52
3.3. ANÁLISES E RESULTADOS ... 58
3.3.1.Preços de equilíbrio com diferenciação ... 63
3.3.2.Custo de menu ... 70
3.4. CONSIDERAÇÕES FINAIS SOBRE A SEÇÃO 3 ... 74
4 CONCLUSÕES ... 76
REFERÊNCIAS ... 80
1 INTRODUÇÃO
A Seção 2 deste trabalho trata do Teorema de Concordância (Agreement Theorem),
originalmente apresentado por Aumann (1976), que estabelece que dois indivíduos Bayesianos, que tenham as mesmas crenças iniciais (common prior belief), mesmo que
tenham acumulado informações privadas assimétricas, possuem crenças posteriores idênticas sobre algum evento, sempre que estas crenças forem de conhecimento comum (common knowledge). Em outras palavras, o teorema estabelece a impossibilidade de dois indivíduos
concordarem a respeito de qualquer eventual discordância sobre o valor de suas probabilidades revisadas calculadas com base nas suas informações privadas, ou seja, a impossibilidade de concordarem que discordam sobre algo (agree to disagree).
Os indivíduos, cotidianamente, costumam discordar publicamente sobre diversos assuntos. Em particular, a discordância entre as expectativas dos indivíduos é o que os leva a apostarem uns contra os outros, motivando, portanto, as transações nos mercados financeiros. De fato, tais discordâncias são encaradas naturalmente, em geral, tende-se a acreditar que elas decorreriam, fundamentalmente, das informações privadas distintas que cada um teria acumulado ao longo do tempo. Ou seja, decorreria da informação assimétrica. No entanto, se supusermos que as crenças iniciais dos agentes são iguais, o teorema de concordância implica em que as informações assimétricas dos agentes não justificariam suas diferentes expectativas, quando estas últimas são de conhecimento comum. Portanto, não se explicariam as transações financeiras entre agentes racionais, veja Milgrom e Stokey (1982).
pequenas perturbações. Existe uma parte da literatura focada em estabelecer as condições para existência de crenças iniciais comuns, onde se destacam os trabalhos de Samet (1998a), que utiliza a técnica de separação de convexos, Samet (1998b), que faz uso de expectativas iteradas, Feinberg (2000) que adota uma abordagem sintática que não utiliza espaços de estados e Rodrigues-Neto (2009) que usa as equações de ciclos baseadas na teoria dos grafos.
Entre as principais extensões do Teorema de Concordância de Aumann, Cave (1983) mostrou que a lógica da demonstração de Aumann também vale quando as regras decisão que são consistentes com a operação de união entre eventos. Por sua vez, Bacharach (1985) identificou a propriedade de consistência com a união com o chamado “princípio da coisa
certa” (sure-thing principle), segundo o qual: se os valores esperados de uma mesma variável
aleatória condicionados a dois eventos disjuntos são iguais, então o valor esperado desta variável aleatória condicionado a união dos dois eventos será o mesmo. Por sua vez, Geanakoplos (1987 e 1992) estendeu um pouco mais a abordagem de Bacharach, quando tratou do caso em que a concordância possa ocorrer com base em regras de decisão distintas entre os indivíduos. Ou seja, sob a hipótese de crenças iniciais comuns, a existência de conhecimento comum sobre decisões individuais distintas é justificada exclusivamente pelo fato das regras de decisões serem distintas, e não pelo fato das informações privadas acumuladas serem distintas.
No sentido de estender o resultado para racionalidade limitada, Samet (1990) provou que o Teorema de Concordância de Aumann permanece válido num contexto em que os indivíduos desconsideram aquilo que eles não conhecem. A abordagem adotada por Samet faz uso de um espaço de estado mais abrangente, que incorpora no espaço de estado o conhecimento que cada indivíduo tem sobre o que os outros indivíduos possam saber. Esta abordagem se distingue da abordagem adotada tanto na versão original de Aumann, quanto nas extensões de Bacharach e Geanakoplos.
bem-estar deveria ser objetivo principal de qualquer regulador. No entanto, atingir tal objetivo se constituir num desafio complexo, que envolve a avaliação de aspectos distributivos, como a atribuição da importância relativa do bem-estar de cada segmento da sociedade.
Entre os assuntos mais instigantes do debate sobre a regulação do mercado de cartões de crédito é aquele sobre os efeitos da regra de não-sobrepreço, ou de qualquer outro desincentivo à diferenciação, sobre o bem-estar dos consumidores. Existe na literatura estudos enfatizando que o sobrepreço pode ter efeitos positivos sobre comerciantes e consumidores, como nos trabalhos de Chakravorti e Emmons (2003) e Bolt e Chakravorti (2008). Assim como existem estudos mostrando efeitos ambíguos sobre o sistema, como nos trabalhos de Rochet (2003) e Rochet e Tirole (2011). Um aspecto peculiar do sistema de cartões de crédito é que, a despeito do fato dos usuários de cartões poderem escolher seus instrumentos de pagamento, os custos da transação são percebidos apenas pelo comerciante, que, em geral, recupera tais custos por meio da estratégia de preço único. Na prática, a estrutura de tarifas tende a induzir o repasse das taxa de desconto cobrada do comerciante para premiar a emissão (tarifa de intercâmbio) e a utilização dos cartões (recompensas), comportamento característico de uma estrutura de mercado de dois lados. A questão central é se a indústria de cartões de crédito poderia exercer poder de mercado impondo regras aos comerciantes credenciados que proíbam a prática de sobrepreço nas aquisições com cartão de crédito. Em outras palavras, as regras de não-sobrepreço poderiam impedir a sinalização aos usuários dos cartões sobre os custos relativos dos diferentes instrumentos de pagamento, reforçando um padrão em que quanto maior a taxa de desconto cobrada do comerciante, maior a capacidade de recompensar os usuários de cartão, levando a uma alocação menos eficientes dos recursos no sistema de pagamentos (“excesso” de utilização dos cartões de crédito).
Chakravorti e To (2007). Existem estudos empíricos que medem estes subsídios cruzados em algumas jurisdições, em geral, indicando que estes subsídios não são negligíveis1.
A regra de não-sobrepreço, por causa da sua natureza anticompetitiva, tem sido proibida em algumas jurisdições. Por exemplo, no Reino Unido desde 1991, na Holanda desde 1994, na Suécia desde 1995 e na Austrália desde 20032. As autoridades entenderam que a liberdade de preços é essencial para uma efetiva competição de preços, em particular, para a competição entre arranjos de pagamentos.
Na Austrália, a proibição das regras de não-sobrepreço é determinada pela regulação nos seguintes termos: “Nem as regras dos arranjos de pagamento, nem qualquer um dos seus participantes, podem proibir o comerciante de cobrar do usuário de cartão uma tarifa ou sobrepreço pela transação com o cartão de crédito” (tradução do autor). Ademais, numa avaliação dos efeitos da limitação na tarifa de intercâmbio imposta naquele país mostrou que os emissores recuperaram parte de suas perdas no curto prazo com a diminuição de suas receitas com as tarifas de intercâmbio, veja Chang, Evans e Garcia-Swartz (2005). Os autores também mostraram que os comerciantes obtiveram benefícios que não foram substancialmente repassados aos consumidores. A despeito disso, os reguladores ainda reconhecem que as reformas regulatórias sobre a prática do sobrepreço na Austrália foram bem sucedidas, no sentido de terem proporcionado significativos benefícios à sociedade. No entanto, nos últimos anos surgiu a preocupação com ocorrência frequente de situações em que o sobrepreço praticado acima do custo de aceitação da transação com cartão de crédito pelo comerciante. Como as evidências obtidas mostram que em algumas instâncias a prática do sobrepreço se desenvolveu de uma maneira que poderia potencialmente comprometer a sinalização de preços e reduzir a efetividade das reformas, os reguladores estão revisando os padrões regulatórios no sentido de permitir que os arranjos de pagamentos possam impor um limite ao sobrepreço que seja próximo do custo de aceitação dos pagamentos com cartão de crédito, cujo principal componente é a taxa de desconto do comerciante3.
Quando se analisa a conveniência de se eliminar a regra de não-sobrepreço para os pagamentos com cartão de crédito, seria correto afirmar (o que provaremos mais adiante neste
1 Schuh, S.; Stavins, J. (2010), assim como, Banco Central do Brasil (2011a) e (2011b), trazem exemplos de estudos que estimaram os subsídios cruzados nos Estados Unidos e no Brasil, respectivamente.
2 Veja, respectivamente, United Kingdom Parliament (1990), Vis, E.; Toth, J. (2000), MA Market Development AB (2000) e Reserve Bank of Australia (2012).
trabalho) que alguns comerciantes teriam incentivos para praticar um sobrepreço em relação ao preço único para os cartões de crédito, sem promover nenhuma redução nos preços para as outras transações. No entanto, este fato está longe de representar um argumento válido contra a diferenciação de preços, pois pressupõe que o comerciante varejista teria poder de mercado para manter esta prática sem ser contestado. Uma análise correta deveria levar em consideração a existência de um novo equilíbrio de dois preços que surgiria quando se passa a permitir a diferenciação, assim como, comparar bem-estar do consumidor nos dois equilíbrios. Este é, exatamente, um dos principais objetivos deste trabalho.
Como ilustraremos na Seção 3, por meio de nossa análise teórica de um modelo simples, o fato do comerciante ter a possibilidade de obter um lucro extra quando ele decide se desviar do preço único não garante que tal estratégia seja sustentável. De fato, uma análise coerente e completa precisaria, antes de qualquer coisa, identificar os novos preços de equilíbrio, os quais dependerão do ambiente competitivo em questão e dos seus efeitos sobre as possibilidades de lucro. De posse dos dois equilíbrios, podemos compará-los, medindo os ganhos, ou perdas, de bem-estar para o consumidor.
externalidades inerentes ao sistema de cartões de pagamento e discute em que situação o bem-estar do consumidor, ou o bem-bem-estar social, seria o referencial adequado para o estudo sobre a regulação da indústria de cartões de crédito. Eles apresentam uma análise teórica que fundamenta as recentes ações antitrust promovidas pelos reguladores e comerciantes contra as
associações de cartões de crédito na Austrália, no Reino Unido e nos Estados Unidos. Wrang (2010) afirma que as redes de cartões demandam tarifas de intercâmbio altas para maximizar o lucro dos emissores, à medida que os cartões se tornam mais eficientes e convenientes. Ele discute, também, os aspectos positivos e negativos das políticas de intervenção.
2 CONHECIMENTO COMUM IMPERFEITO NO TEOREMA DE CONCORDÂNCIA DE AUMANN
2.1. PRELIMINARES À ANÁLISE DO CONHECIMENTO COMUM IMPERFEITO
Nesta seção estendemos o Teorema de Concordância de Aumann para uma situação em que o conhecimento comum das decisões surge num contexto em que os indivíduos não conhecem perfeitamente as partições dos outros, situação que denominamos de “conhecimento comum imperfeito”. Ou seja, provamos que não é necessária a hipótese, assumida por Aumann, de que os indivíduos conheçam perfeitamente a partição de informação dos outros indivíduos para a validade do Teorema de Concordância. Na segunda parte deste capítulo, mostramos que a versão de Samet para o Teorema de Concordância, em que a informação não é particional, pode ser estendida para o caso de regras de decisões distintas. Na última parte deste capítulo, apresentamos um exemplo que ilustra o surgimento do conhecimento comum imperfeito.
Na Seção 2.2, a seguir, além de fixarmos a notação que será utilizada nas seções seguintes, fazemos uma revisão dos conceitos de conhecimento comum, do Teorema de Concordância de Aumann, além de apresentar duas versões deste teorema, para as quais apresentamos suas extensões na seção seguinte.
Na Seção 2.3 deste trabalho propomos uma estrutura para modelar o conceito de conhecimento comum num contexto em que cada indivíduo possui uma estrutura de informação, ou partição, que não é perfeitamente conhecida pelos outros indivíduos. Na Seção 2.3.1, num contexto em que o conhecimento comum é do tipo imperfeito, demonstramos que o Teorema de Concordância de Aumann (1976), na sua versão para regras de decisão distintas dada por Geanakoplos (1992), continua válido.
versão de Geanakoplos (1992) do Teorema de Concordância de Aumann, para regras de decisão distintas permanece válida no contexto de Samet (1990). Ademais, propomos uma demonstração muito mais curta e direta do que aquela adotada por Samet.
Na Seção 2.4, apresentamos um exemplo para ilustrar como o conhecimento comum imperfeito surge no contexto de um jogo simples. O exemplo é uma variação da versão tradicional do exemplo formalmente tratada em Geanaloplos (1992). Explicitamos os conjuntos de conhecimento comum imperfeito e calculamos as probabilidades posteriores, mostrando como o arcabouço que propomos pode ser utilizado para modelar um caso em que os indivíduos podem não conhecer perfeitamente a partição do outro. Finalmente, na Seção 2.5, apresentamos um resumo das conclusões de todo este trabalho.
2.2. O TEOREMA DE CONCORÂNCIA DE AUMANN
Esta seção trata do teorema originalmente apresentado em Aumann (1976), e de duas outras versões dele apresentadas em Geanakoplos (1992) e Samet (1990). Primeiramente, na Seção 2.2.1, tratamos especificamente de um contexto de espaço de estados restrito, ou seja, modelos em que os estados não trazem informação sobre os variados níveis de conhecimento que cada um dos indivíduos poderia ter sobre a estrutura de informação particular (partição) de outros indivíduos. Neste contexto, apresentamos o teorema original e a versão de Geanakoplos, com o objetivo de fixar a notação para a extensão que introduziremos na Seção 2.3.1.
2.2.1. Espaço de estados restrito e conhecimento particional
Seja um espaço de probabilidade, onde representa o espaço de estados, a sigma-álgebra de subconjuntos em e a medida probabilidade definida para os eventos de . Suponha que seja a probabilidade a priori comum (common prior) de um conjunto finito
indivíduos.
Assuma que o conhecimento de um indivíduo a respeito da ocorrência de um estado seja representado por uma partição de , que denotaremos por . Isto é, para cada estado , existe um único elemento da partição que contém , o qual denotaremos por . Na ocorrência do estado , o indivíduo apenas tem conhecimento da ocorrência do evento da partição, que pode ser interpretado como “sinal” indicando onde estaria localizado o estado ocorrido. No entanto, o indivíduo não teria conhecimento específico a respeito de qual estado pertencente a teria ocorrido, ou seja, não consegue distinguir entre e qualquer outro estado em .
Desta forma, na ocorrência de um evento , o indivíduo Bayesiano revisa suas probabilidades. Isto é, calcula a probabilidade posterior de um evento ocorrer, usando a probabilidade a priori (a mesma para todo indivíduo) e aplicando a definição de probabilidades condicionais. Portanto, a probabilidade a posteriori é dada por
Fixado um evento e um número , considere o evento
. Este evento representa o conjunto dos estados para os quais o indivíduo atribui probabilidade posterior igual a , ao evento .
Denotemos por , ou simplesmente , a partição mais refinada que tenha todas as partições individuais como seu refinamento. Diremos que é uma partição de conhecimento comum perfeito (perfect common knowledge). Fixado ,
diremos que um evento é de conhecimento comum perfeito em se o conjunto contém algum evento da partição que contém .
Note que está implícito na definição de conhecimento comum perfeito o fato de que não existe nenhum estado no que algum indivíduo não consiga identificar os estados que formam o evento para todo indivíduo . Na Seção 2.3, a seguir, são abordadas situações em que esta hipótese não é válida. Ou seja, situações em que possa haver conhecimento comum sem que os indivíduos conheçam perfeitamente a partição dos outros, que chamamos de conhecimento comum imperfeito.
Teorema (Aumann, 1976): Dado e , se os eventos e são de
conhecimento comum perfeito em (perfect common knowledge), então .
Vale enfatizar que a implicação inversa do teorema acima não é valida. Isto é, pode ocorrer que , sem que os eventos e correspondentes sejam de conhecimento comum perfeito para algum . Este fato pode ser ilustrado por meio do exemplo abaixo.
Exemplo: Seja o espaço de estados, e denote por a medida de probabilidade
uniforme em . Se e representarem as respectivas partições individuais, a partição representa a partição de conhecimento comum perfeito. Fixando e , teremos ,
e . Podemos concluir que não contém nenhum conjunto da partição de conhecimento comum perfeito . Portanto, os eventos e não são de conhecimento comum perfeito para nenhum .
observado no espaço de estados , a regra atribui uma única decisão no espaço de decisões . Diz-se que uma regra de decisão satisfaz o “princípio da coisa certa” ( Sure-Thing-Principle ou STP) se sempre que e então .
O principal exemplo de regra de decisão que satisfaz o STP é o obtido num contexto onde um indivíduo tem uma probabilidade a priori, e sua regra de decisão corresponde à probabilidade posterior de um determinado evento fixo em função dos eventos condicionados. De fato, dada uma probabilidade a priori e fixado um evento , pode-se definir a regra de decisão
. Note que se e , então
Uma extensão do Teorema de Concordância de Aumann (Aumann’s Agreement
Theorem), enunciado acima, para indivíduos que seguem regras de decisão que satisfaçam o
STP foi obtida por Geanakoplos (1992). Considere a regra de decisão do indivíduo . Dada uma decisão , considere o evento
composto pelos estados nos quais a decisão do indivíduo é igual a d.
Teorema (Geanakoplos, 1992): Suponha que, para cada indivíduo , a regra de
decisão satisfaça o STP. Dado um estado e uma sequência de decisões , se evento for de conhecimento comum perfeito em (perfect common knowledge)
para todo , então existe um evento de conhecimento comum (symmetric information) tal que , para todo . Se as regras de decisão são todas iguais a
Note que, sob a hipótese da partição ser perfeitamente conhecida pelos outros indivíduos, dois indivíduos conseguem identificar os elementos pertencentes ao conjunto
. No caso geral, se tivermos ainda que a regra de decisão do indivíduo é conhecida pelo outro indivíduo,dois indivíduos conseguem identificar os elementos do conjunto . No entanto, esta hipótese pode ser muito restritiva se pretendemos abordar diversas situações reais, quando seria mais factível que cada um dos indivíduos tenha um conhecimento imperfeito sobre a partição do outro, e conheçam pouco sobre a regra de decisão do outro.
Por exemplo, imagine que dois indivíduos participem de um jogo, e que o jogador saiba da ocorrência de um evento . Se o jogador conhecer perfeitamente a partição
do jogador , aquele poderia, eventualmente, usar esta informação para deduzir sobre se alguns eventos da partição poderiam ter ocorrido, ou não, do ponto de vista do jogador . Este tipo de informação permitiria ao jogador tomar decisões estratégicas levando em consideração o comportamento do jogador , que não seriam possíveis se o jogador não soubesse nada sobre a partição .
2.2.2. Espaço de estados abrangente e conhecimento não particional
Outra extensão do Teorema de Concordância de Aumann foi apresentada em Samet (1990), que incorporou nos estados a informação sobre o conhecimento de cada indivíduo sobre o que os outros indivíduos possam saber, e tratou de casos em que as informações dos indivíduos não podem ser representadas por uma partição, ou seja, não é particional. No caso em que a informação do indivíduo não é particional, a classe dos conjuntos , composta pelos conjuntos de estados que o indivíduo não é capaz de distinguir do estado , não formam uma partição de .
Para cada indivíduo considere a função , onde, para todo , corresponde à proposição que afirma que “o indivíduo sabe a proposição ”. Considere, também, a função , onde representa a proposição “não ”, donde, portanto, e .
Considere o conjunto de estados , tal que para todo estado e toda proposição , temos que:
significa que a proposição é verdadeira no estado ; significa que a proposição é falsa no estado ; ;
Se então ;
O conteúdo informacional do indivíduo , quando ocorrer o estado , pode ser representado pelo conjunto de afirmações que são conhecidas como verdadeiras por ele, isto é:
Ou ainda, pelo conjunto
dos estados que são indistinguíveis para ele.
Neste contexto, Samet (1990) demonstra que e que, se , então
. A igualdade somente poderia ser garantida num subespaço
, em que para todo , e , sempre tivermos
. Ou seja, a informação seria particional apenas se os indivíduos tiverem
conhecimento das proposições que eles não sabem ou, em outras palavras, se os indivíduos não “ignoram a sua própria ignorância”.
onde a união percorre todas as sequências de indivíduos, de qualquer tamanho finito e permitindo repetição; e onde .
Uma proposição é dita de conhecimento comum em um estado (common knowledge proposition) se para qualquer inteiro e qualquer sequência de indivíduos
tivermos que . O Teorema 3 de Samet (1990) demonstra que, se e é de conhecimento comum no estado , então é de conhecimento comum em e, em particular,
No entanto, não se demonstra naquele trabalho se os estados que não estão em de fato poderiam ser comumente distinguíveis do estado . Ou seja, não se demonstra se
implica em que existiria uma proposição de conhecimento comum em que não seria verdadeira em Na Subseção 2.3.1 voltamos a tratar desta questão, quando definimos o conjunto dos estados indistinguíveis de um determinado estado , o qual propomos como uma alternativa ao conjunto definido acima, por entendermos como sendo um conjunto mais adequado para representar o evento de conhecimento comum, ou informação simétrica, necessário para um Teorema de Concordância.
Definindo os conjuntos de estados e
, pode-se usar a família de conjuntos como base para a topologia produto em . Esta topologia induz uma topologia no espaço de estados . Samet (1990) demonstra que, nesta topologia, o conjunto é fechado e, portanto, compacto. Samet mostra, também, que os conjuntos são fechados, que é fechado sempre que for fechado. Seguindo daí, portanto, que é uma união enumerável de conjuntos fechados.
como a probabilidade a priori da proposição ser verdadeira. Note que, como é fechado e é uma união enumerável de fechados, ambos são mensuráveis.
Fixada uma proposição , para cada e tal que denote por
a probabilidade posterior da proposição ser verdadeira, dado o conhecimento do indivíduo decorrente da ocorrência do estado .
Seja o conjunto das probabilidades posteriores factíveis. Como conjunto é enumerável, segue do Teorema 4 em Samet (1990) que o conjunto também é enumerável. Fixado um , seja a proposição que
afirma que “a probabilidade posterior da proposição ser verdadeira, calculada pelo
indivíduo , é igual a ”.
A condição de regularidade da probabilidade a posteriori é satisfeita em
quando, para cada estado e cada indivíduo , se então
para todo , e se então se, e somente se, .
Diz-se que o conhecimento privado é finitamente gerado em quando, para
cada estado e cada indivíduo , existir um conjunto finito de proposições
tal que, para qualquer , tivermos sempre que
para todo . Diz-se que é o conjunto gerador finito da informação em . Em
outras palavras, o conhecimento privado é finitamente gerado se, para cada estado e indivíduo, existir um conjunto finito (gerador) de proposições conhecidas por ele neste estado, tal que, dada qualquer proposição conhecida por ele neste mesmo estado, esta mesma proposição também será conhecida por este indivíduo em qualquer outro em que ele conheça todas as proposições do conjunto finito (gerador).
Teorema (Samet, 1990): Suponha o conhecimento privado seja finitamente gerado e a que condição de regularidade da probabilidade a posteriori seja satisfeita em um determinado subconjunto de estados . Se, para todo indivíduo , a proposição for de conhecimento comum em , então para quaisquer indivíduos .
Na Seção 2.3, a seguir, introduziremos extensões para as versões dos teoremas apresentados acima.
2.3. EXTENSÕES DAS VERSÕES DO TEOREMA DE CONCORÂNCIA DE AUMANN
Na Seção 2.2, acima, foram apresentadas as versões de Geanakoplos (1992) e Samet (1990) para o teorema originalmente apresentado em Aumann (1976). Nesta seção introduzimos extensões para cada uma destas versões.
Primeiramente, na Subseção 2.3.1, tratamos de um contexto com espaço de estados
restrito, no qual apresentamos uma abordagem para modelar situações onde o conhecimento
sobre a partição alheia é imperfeito, ou seja, a partição de conhecimento privado não é perfeitamente conhecida pelos outros indivíduos. O conhecimento comum que possa surgir neste contexto é chamado aqui de conhecimento comum imperfeito. Demonstramos que o Teorema de Concordância de Aumann, na versão de Geanakoplos (1992), pode ser estendido para o caso em que as decisões dos indivíduos são de conhecimento comum imperfeito.
Teorema de Concordância de Aumann, por meio de uma estratégia de demonstração mais curta e direta, e utilizando um conjunto de conhecimento que entendemos mais adequado.
2.3.1. Espaço de estados restrito e conhecimento particional
Considere uma partição que tenha como seu refinamento. Suponhamos que a partição represente o conhecimento imperfeito (ou incompleto) que o outro indivíduo tem a respeito da partição do indivíduo .
No caso com apenas dois indivíduos, imagine que o próprio indivíduo tenha revelado a partição ao outro indivíduo, e que, portanto, o indivíduo sabe que esta partição representa a percepção limitada sobre seu conhecimento que o outro indivíduo possui. Denotemos por a partição mais refinada que tenha as partições e como seus
refinamentos. Neste caso, a partição representa o conhecimento comum imperfeito dos dois indivíduos, diferentemente do conhecimento perfeito representado pela partição mais refinada .
Em geral, para um conjunto enumerável de indivíduos, denotemos por a partição mais refinada que tenha todas as partições individuais como seu refinamento. Diremos que é uma partição de conhecimento comum perfeito (perfect common knowledge). Fixado , diremos que um evento é de conhecimento comum perfeito em
(perfect common knowledge) se o conjunto contém algum evento da partição que
contém .
Uma partição de é uma partição de conhecimento comum imperfeito, se, para
cada indivíduo , existir uma partição que tenha a partição privada como seu refinamento, tal que . Consequentemente, como é um refinamento de , que por sua vez é refinamento de , então segue que é um refinamento de , para todo
.
se para algum , então , caso em que não existiria conhecimento comum imperfeito.
Fixado um , diremos que é um evento de conhecimento comum imperfeito em segundo a partição (imperfect common knowledge) se for uma
partição de conhecimento comum imperfeito e se o evento contém o elemento da partição
que contém .
O Teorema 2.1 a seguir estende o Teorema de Concordância de Aumann para o caso em que os indivíduos não conhecem perfeitamente as partições uns dos outros, mas ainda assim existir conhecimento comum. Nestes casos, o conhecimento comum é representado pelos elementos de uma partição de conhecimento comum imperfeito . O Teorema 2.1 a seguir também estende para os casos de conhecimento comum imperfeito a versão do Teorema de Concordância de Aumann para regras de decisão que satisfazem o STP, apresentada em Geanakoplos (1992).
Teorema 2.1: Seja um conjunto enumerável de indivíduos e uma partição de
conhecimento comum imperfeito em (imperfect common knowledge). Suponha que todos
os indivíduos saibam que cada uma das regras de decisão satisfaz o STP e que cada uma das partições privadas é enumerável. Dado um estado e uma sequência de decisões , se cada um dos eventos (definido na Seção 2.2.1) é de conhecimento comum imperfeito em segundo a partição (imperfect common knowlegde), então todos os indivíduos são capazes de concluir que , para
todo , onde é um evento de conhecimento comum (informação simétrica) que contém .
Demonstração: Seja o elemento da partição de conhecimento comum que
para todo . Segue daí que todos os indivíduos, mesmo sem conhecerem as regras de decisão do outros, sabem que , para todo e . Como todos sabem que as regras de decisão satisfazem o STP, podem concluir que , para todo . Isto é,
, para todo .
Dado que as decisões comumente conhecidas dos indivíduos seriam as mesmas na ocorrência de um mesmo evento de conhecimento comum (simétrico) , conclui-se que estas mesmas decisões só poderiam ser diferentes umas das outras no caso em que as regras de decisão forem distintas. O Corolário 2.1 abaixo formaliza este resultado particular.
Corolário 2.1: Se, adicionalmente às hipóteses do Teorema 2.1 acima, todos os indivíduos
em souberem que as regras de decisão são todas iguais, então todos concluem que , para quaisquer indivíduos .
Demonstração: Se todos sabem que as regras de decisão são iguais, onde para todo ,
segue do Teorema 2.1 que para todo . Portanto, todos os indivíduos em concluem que , para todo e .
2.3.2. Espaço de estados abrangente e conhecimento não particional
Vimos que, de acordo com a definição estabelecida em Samet (1990), uma proposição é de conhecimento comum (common knowledge) em um estado se, para todo
inteiro e toda sequencia de indivíduos , tivermos que .
Para cada e , defina o conjunto
. Note que as proposições que são conhecidas exclusivamente pelo indivíduo , isto é, aquelas proposições que nenhum outro indivíduo sabe que sabe, não pertencem a .
Note que, no que diz respeito exclusivamente às informações privadas de um indivíduo , este indivíduo seria capaz de distinguir outro estado do estado se existisse uma proposição conhecida por em que não fosse verdadeira em .
Por outro lado, no que diz respeito ao que outros indivíduos sabem sobre o que um indivíduo possa saber, um indivíduo saberá se o indivíduo distingue o estado do estado se existir uma proposição que saiba que sabe em , mas que não seja verdadeira em . Em outras palavras, mesmo existindo uma proposição tal que e
, quando é capaz de distinguir de , pode ser que para algum indivíduo . Neste caso, não saberia que , ou seja, não distingue do estado que difere de apenas pelo fato de . Portanto, não saberia se seria capaz de distinguir de .
Considere o conjunto
composto pelos estados nos quais as proposições em são verdadeiras. Os estados pertencentes a são todos aqueles nos quais seria de conhecimento comum que o indivíduo não consegue distingui-los do estado . De fato, como , conclui-se diretamente das definições que .
Note que, para todo , temos para toda sequência de indivíduos e todo . Segue daí que . Portanto, temos que
.
Lema 2.1: se, e somente se, .
Demonstração: Seja e é uma sequência qualquer de indivíduos. Como
temos , de onde se segue que é de conhecimento comum em , isto é, . Supondo que , segue que para todo . Como o resultado anterior vale para toda sequência de indivíduos , conclui-se que é de conhecimento comum em para todo . Segue que . Portanto, .
Suponha agora que . Se , segue da hipótese que
, ou seja, é de conhecimento comum em para todo . Isto é,
para toda sequência de indivíduos e . Segue daí que
. Provamos que, para qualquer então , ou seja, que
.
Lema 2.2: se, e somente se, .
Demonstração: Seja . Daí segue que para todo . Como
, tem-se, em particular que para todo . Portanto,
.
Seja , então é de conhecimento comum em para todo . Donde segue que, para toda sequência de indivíduos e todo , é de conhecimento comum em . Em particular, . Assumindo
, como , temos . Portanto,
, para toda sequência de indivíduos e todo . Isto é, .
De forma análoga à definição , definimos um conjunto composto de estados que são comumente possíveis para todos os indivíduos na ocorrência do estado por
Lema 2.3: Se for de conhecimento comum em e , então é de conhecimento comum em e, consequentemente, .
Demonstração: Como , existe uma sequência de estados e um
conjunto de indivíduos , onde , , . Por outro lado, como a proposição é de conhecimento comum em , então, para toda sequência de indivíduos , onde , toda sequência de inteiros positivo , e todas as sequências de indivíduos , temos que
Daí segue que
e como segue que
Portanto, por indução, teremos que
para e que
. Como , da última igualdade conclui-se que a proposição é de conhecimento comum em . Como consequência imediata, temos que .
Lema 2.4: Para todo temos que para qualquer .
Demonstração: Seja . Dado um indivíduo qualquer, se então
Em particular, segue daí que , ou seja, . Por outro lado, da definição de , sabemos que para todo indivíduo . Provamos, portanto, que
Dizemos que o estado é comumente distinguível do estado se existe uma proposição de conhecimento comum em que é não verdadeira em . Por outro lado, diremos que o estado é comumente indistinguível do estado se toda proposição de conhecimento comum em for verdadeira em . Neste sentido, o conjunto
dos estados comumente indistinguíveis de será denominado de evento de conhecimento
comum que contém o estado , ou evento de informação simétrica. Note que, como
consequência do Teorema 3 em Samet (1990), temos que . No entanto, sem demonstrar a igualdade não poderíamos afirmar que o evento seja um evento de conhecimento comum, no sentido de conter todos os estados que são, de fato, comumente indistinguíveis. Por se tratar de um Teorema de Concordância, se deveria mostrar que as decisões são as mesmas num evento de conhecimento comum. No Teorema 2.3 abaixo usaremos o conjunto no lugar do utilizado em Samet (1990).
O Teorema 2.2 abaixo demonstra que os estados comumente indistinguíveis de , definido acima, coincide exatamente com os estados que todos os outros indivíduos comumente supõem serem indistinguíveis de para um indivíduo em particular, qualquer que seja este indivíduo.
Teorema 2.2: Para todo que para qualquer .
Demonstração: Suponha que . Se uma proposição for de conhecimento comum
em , teremos, pelo Lema 2.3 acima, que . Segue daí que . Portanto, temos que .
, temos que é de conhecimento comum em para todo , e segue da hipótese inicial que . Consequentemente, . Provamos que
para todo , ou seja, . Segue do Lema 2.4 acima que e, consequentemente, que .
Provamos, portanto, que . Do Lema 2.4, segue que
para todo indivíduo .
Note que, no contexto da subseção 2.3.1 anterior, o espaço de estados não incluía a informação dos indivíduos a respeito do que os outros poderiam saber (partição). Consequentemente, poderia haver diferenças entre as partições , que naquele contexto representa que todos os outros indivíduos comumente sabem sobre a partição do indivíduo , e a partição de conhecimento comum . Do Teorema 2.2 acima, temos que, se o espaço de estados é abrangente, isto é, se ele incorpora o conhecimento sobre o que os outros possam saber, não há distinção entre o que todos os outros indivíduos comumente sabem sobre o conhecimento privado de um indivíduo em particular e o conhecimento comum de todos os indivíduos.
Considere um conjunto enumerável contento todas as decisões factíveis e a regra de decisão do indivíduo , definida em uma classe nos subconjuntos de
. Em particular, representa a decisão do indivíduo quando ocorre o estado , e a ocorrência do evento é informada a ele. Para cada , denota-se por a proposição pertencente a que afirma que “a decisão do indivíduo é igual a ”.
As regras de decisão dos indivíduos são regulares em quando: para cada
estado e cada indivíduo , se então para todo ; e se então se, e somente se, .
Note que essa definição de regularidade para uma regra de decisão estende a noção de regularidade presente na regra Bayesiana de revisão de probabilidades. No caso em que a probabilidade a priori é a mesma, teremos , e
O Teorema 2.3 a seguir estende o Teorema 7 de Samet (1990) para regras de decisões regulares que satisfazem o STP, princípio definido em Geanakoplos (1992). Neste contexto estendido, o Teorema 2.3 mostra que, se as decisões individuais são de conhecimento comum, então existe um evento de conhecimento comum, representado por , onde as decisões individuais são as mesmas. Mesmo sendo uma extensão do resultado em Samet (1990), note que a estratégia de demonstração desenvolvida aqui é muito mais curta e direta que a aquela utilizada por Samet (1990).
Teorema 2.3: Seja o conjunto enumerável de indivíduos cujas regras de decisão
satisfazem o STP. Seja um subconjunto de estados onde os conhecimentos privado e comum sejam finitamente gerados, e onde as regras de decisão são regulares. Se, para todo indivíduo , a proposição for de conhecimento comum em , teremos
para todo , onde é o evento de conhecimento comum em (informação simétrica).
Demonstração: Como temos que . Por outro lado,
pelo Lema 4 e Teorema 2, temos que . Consequentemente, pelo Lema 3 sabemos que se uma proposição for conhecimento comum em e então também é de conhecimento comum em . Em particular, , ou seja, . Daí, se então , donde segue que . Portanto, conclui-se que .
Do Teorema 4 em Samet (1990), sabe-se que a partição é enumerável. Segue daí que, para todo , existe uma sequência tal que o conjunto
. Como, para todo , temos que do Lema 2.3 acima, temos que , para todo indivíduo . Portanto, segue da condição de regularidade da regra de decisão que . Como a regras satisfazem o STP, concluímos que
.
Corolário 2.2: Se, adicionalmente às hipóteses do Teorema 2.3 acima, as os indivíduos
Demonstração: Se as regras de decisão são iguais, onde para todo indivíduo , segue do Teorema 2.3 que . Daí, como o lado esquerdo da última igualdade não depende do indivíduo, todos concluem que as decisões de todos os indivíduos são iguais.
O Corolário 2.2 acima se aplica ao caso particular em que as regras de decisão são todas iguais à regra de revisão Bayesiana de revisão de probabilidades, como em Aumann (1976). No entanto, note que o espaço de estados aqui incorpora o conhecimento sobre o que o outro possa saber (abrangente) e a estrutura de informação não é do tipo particional, sendo ainda uma extensão do caso tratado em Aumann (1976).
Vale enfatizar que a estratégia de demonstração do Teorema 2.3 acima se diferencia daquela utilizada em Samet (1990) nos seguintes aspectos:
Utilizar o evento de conhecimento comum , ou seja, o conjunto dos estados comumente indistinguíveis, e não o evento ;
Selecionar uma sequência de estados formada por representantes das classes de equivalência da partição enumerável , onde todos pertencem ao evento de conhecimento comum
Utilizar o fato da proposição ser de conhecimento comum em e de
, para concluir, pelo Lema 2.3, que a proposição é verdadeira em ;
Utilizar a hipótese de regularidade das regras de decisão para concluir que, se a proposição é verdadeira num representante de classe , então que .
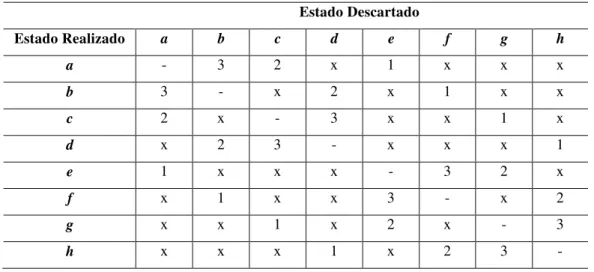
2.4. EXEMPLO DE CONHECIMENTO COMUM IMPERFEITO DAS PARTIÇÕES
parcial ou imperfeito sobre as partições dos outros. A segunda e a terceira situações representam variações de um exemplo clássico da literatura de “common knowledge”, no qual existe conhecimento perfeito das partições dos indivíduos envolvidos, e cuja apresentação rigorosa pode ser encontrada em Geanakoplos (1992).
Como na sua versão clássica do jogo, suponha que um professor coloque um chapéu em cada um dos seus três alunos, quando estes estão posicionados um de costas para o outro. Isto é, sem que eles possam ver a cor de nenhum chapéu, nem de seus próprios. O professor anuncia publicamente a todos eles que os chapéus colocados podem ser de cor branca (W) ou
vermelha (R) e que nenhum deles consegue ver a cor do próprio chapéu.
Diferentemente da versão clássica, suponha que o professor tenha se reunido, anteriormente, com cada um dos seus três alunos, para revelar a cor dos chapéus que colocará nos outros dois colegas, no entanto, cada aluno desconhece a possibilidade desta reunião como os outros colegas.
Note que, nestas condições, cada um dos três alunos tem informação privada sobre os chapéus de seus colegas, no entanto, nenhum deles sabe sobre o que seus colegas teriam a capacidade de conhecer sobre as cores dos chapéus alheios. Portanto, temos uma situação onde cada um dos indivíduos é capaz de conhecer mais do que seus colegas poderiam imaginar, em outras palavras, não existe conhecimento perfeito das partições que representam as informações privadas.
Na Tabela 1 abaixo, define-se cada um dos oito estados possíveis, os quais correspondem às combinações de cores possíveis para os três chapéus.
Tabela 1 – Estados do jogo:
Configurações dos chapéus
Alunos a b c d e f g h
1 R R R R W W W W
2 R R W W R R W W
Desta forma, temos que e, como cada um dos alunos apenas não sabe a cor do seu próprio chapéu, as informações privadas são representadas pelas partições:
Visto que nenhum dos alunos conhece nada sobre o que outro aluno poderia saber, tem-se uma situação onde ninguém conhece a partição de seus colegas. Como consequência, não existe nenhum conhecimento comum entre quaisquer dois alunos e, portanto, não existe conhecimento nenhum comum entre todos os três alunos.
2.4.1. Conhecimento comum perfeito
Como no caso clássico, suponha agora que os alunos sejam reposicionados um de frente para o outro. Neste momento, cada um dos alunos passa a perceber que cada um de seus colegas agora consegue ver a cor dos chapéus dos outros, mesmo que ainda não sejam capazes de ver a cor do seu o próprio chapéu. Portanto, nesta situação, tudo o que cada aluno é capaz de saber é de conhecimento dos outros, isto é, cada um dos alunos conhece perfeitamente a partição dos outros alunos. Desta forma, o conhecimento comum perfeito entre os pares de alunos pode ser representado, respectivamente, pelas partições de conhecimento comum perfeito:
Note, no entanto, que . Isto é, não existe conhecimento comum aos três alunos.
O professor informe que existe pelo menos um chapéu vermelho;
O Aluno 1 informe que ainda não é capaz de deduzir qual é a cor do seu chapéu; O Aluno 2 informe que ainda não é capaz de deduzir qual é a cor de seu chapéu.
De posse destas informações é possível mostrar que o Aluno 3, diferentemente dos outros dois, consegue agora deduzir a cor de seu chapéu. De fato, como todos conhecem a partição , todos foram informados pelo professor que não ocorreu o estado da natureza (=WWW) e o Aluno 1 não descobriu a cor de seu chapéu, todos podem deduz daí que não
ocorreu o estado (=RWW). Isto é, o Aluno 1 não está vendo dois chapéus brancos em seus
colegas, caso contrário teria deduzido, com base na informação passada pelo professor, que o seu chapéu seria vermelho.
Analogamente, como todos conhecem a partição , todos foram capazes de concluir que não ocorreu e o Aluno 2 não descobriu a cor do seu chapéu, conseguem deduzir que não ocorreu (=RRW) e nem (=WRW). Isto é, se o chapéu do Aluno 3 fosse branco, o
Aluno 2 deduziria que o seu chapéu é vermelho, pois já sabemos que os dois chapéus, do Aluno 1 e do Aluno 3, não podem ser os dois brancos. Finalmente, como o Aluno 2 não descobriu a cor de seu chapéu, conclui-se que o chapéu do Aluno 3 é vermelho. Dito de outra forma, após estes três pronunciamentos públicos, todos são capazes de concluir que não ocorreu . Portanto, ocorreu o evento complementar , composto de todos os estados em que o chapéu do Aluno 3 é vermelho.
Em particular, suponha que os chapéus fossem todos vermelhos, isto é, o estado da natureza fosse, de fato, . Note que, nesta situação específica, a nova informação do professor pareceria irrelevante, visto que já seria de conhecimento de cada um dos três alunos que existiam pelo menos dois chapéus vermelhos. Ademais, cada um sabe ainda que os outros estão vendo pelo menos um chapéu vermelho. No entanto, sem a informação adicional do professor, o Aluno 3, por exemplo, não pode deixar de considerar a possibilidade do Aluno 2 achar possível que o Aluno 1 possa estar vendo dois chapéus brancos.