André Gustavo Campos Pereira
Joaquim Elias de Freitas
Roosewelt Fonseca Soares
Cálculo I
D I S C I P L I N A
Derivadas de
funções compostas
Autores
aula
Divisão de Serviços Técnicos
Catalogação da publicação na Fonte. UFRN/Biblioteca Central “Zila Mamede” Governo Federal
Presidente da República Luiz Inácio Lula da Silva Ministro da Educação Fernando Haddad
Secretário de Educação a Distância – SEED Carlos Eduardo Bielschowsky
Universidade Federal do Rio Grande do Norte
Reitor
José Ivonildo do Rêgo
Vice-Reitora
Ângela Maria Paiva Cruz
Secretária de Educação a Distância Vera Lúcia do Amaral
Secretaria de Educação a Distância- SEDIS
Coordenadora da Produção dos Materiais Marta Maria Castanho Almeida Pernambuco
Coordenador de Edição Ary Sergio Braga Olinisky
Projeto Gráfico Ivana Lima
Revisores de Estrutura e Linguagem Eugenio Tavares Borges
Jânio Gustavo Barbosa Thalyta Mabel Nobre Barbosa
Revisora das Normas da ABNT Verônica Pinheiro da Silva
Revisoras de Língua Portuguesa Janaina Tomaz Capistrano Sandra Cristinne Xavier da Câmara
Revisores Técnicos Leonardo Chagas da Silva Thaísa Maria Simplício Lemos
Revisora Tipográfica Nouraide Queiroz
Ilustradora Carolina Costa
Editoração de Imagens Adauto Harley Carolina Costa
Diagramadores Bruno de Souza Melo Dimetrius de Carvalho Ferreira Ivana Lima Johann Jean Evangelista de Melo
Adaptação para Módulo Matemático André Quintiliano Bezerra da Silva Kalinne Rayana Cavalcanti Pereira Thaísa Maria Simplício Lemos
Colaboradora Viviane Simioli Medeiros Campos
Apresentação
N
a aula 4 (A derivada), vimos como utilizar as propriedades para calcular as derivadas de somas, produtos e quocientes de funções deriváveis. Entretanto, existem funções que não são expressas como somas, produtos ou quocientes de funções deriváveis. Se voltarmos às aulas 8 (Funções (I)) e 9 (Funções (II)) de Pré-Cálculo, nos depararemos com funções obtidas pela composição de funções e funções que são inversas de uma outra função. Nesta aula, estudaremos a regra da cadeia, que é utilizada para calcular a derivada de composta de funções, e aprenderemos como calcular a derivada da inversa de uma função.Objetivos
Regra da cadeia
Se você não está lembrando o que significa composta de funções retome seu material de Pré-Cálculo, mais precisamente a página 15 da aula 8 e faça uma leitura rápida para relembrar. Lembre-se de que relembrar é viver.
Vamos começar a regra da cadeia considerando um exemplo em que desejamos calcular a derivada da função hx) =snx+ 1). Observe que a função h pode ser vista como a composta das funções fx) =sn x e x) =x+ 1.
Usando a definição de função composta, temos
f g)x) =fgx)) =sngx)) =snx+ 1). Ou seja, a função h realmente pode ser vista como:
hx) = g)x)
ou
hx) =gx)).
Nosso objetivo agora é obter a derivada hx) = 2x em termos das derivadas fx) = 2xe
g
x) = 2x. Sabemos que a função fx) =sn x é derivável e que sua derivada é fx) =os x. Com relação àfunção polinomial x) =x+ 1, sabemos que sua derivada é x) = 2x.
Para determinarmos a derivada da função hx) =snx+ 1), devemos aplicar a regra da cadeia. Essa regra aplica-se à derivada de funções compostas do tipo g)x) =gx)).
Teorema 1 (regra da cadeia)
Sejam f e
g duas funções deriváveis, e suponhamos que seja possível obter a função
composta g)x) =gx)). Em outras palavras, estamos supondo que x pertence aodomínio de
g, que
x) pertence ao domínio def, e que existem as derivadas
gx)egx)).Então, a função composta, g, é derivável em x e sua derivada é dada por
◦g)x) =gx))gx).
A seguir, apresentamos outras notações que você pode encontrar em alguns livros de cálculo.
Fazendo u=x), podemos escrever a regra da cadeia da seguinte forma, usando a notação de Leibniz, vista na aula 4 (A derivada):
xfux)) = f u
Na notação que omite a variável independente, temos
xfux)) =f
u)u,
ou ainda
[ux))] =u)u.
Observação – Embora a regra da cadeia seja de fundamental importância para o estudo do cálculo, sua demonstração não faz parte dos objetivos desta disciplina.
Exemplo 1
Vamos voltar a considerar as funções hx) =senx+ 1) fx) =sen x e x) =x+ 1. Desejamos encontrar a derivada x) em termos das derivadas x)egx). Como vimos anteriormente, fx) =ox xegx) = 2x. Então, pela regra da cadeia, a derivada x) será obtida do seguinte modo
hx) = [fgx))] =fgx))gx) =osgx))gx) =osx+ 1)2x,
hx) =osx+ 1)2x.
A função exponencial
e
x
e sua derivada
Uma pergunta interessante que se pode fazer é “existe uma função cuja derivada seja ela própria?”. Surpreendentemente, a resposta é sim. Para isso, vamos tentar uma função exponencial aa >0ea= 1). Nesse caso,
() = lim
0
(+)
x = lim0
(1)
x =
lim
0
· lim
0
1
x =·lim0
1
Atividade 1
1
2
Para concluir que existe uma função cuja derivada é a própria função, basta mostrar que existe um número a tal que
lim
0
1 x = 1.
Esse número especial a existe e o chamaremos de e, o qual é definido pelo limite
= lim
0(1 + x) 1 x.
Em cursos mais avançados de cálculo, prova-se que esse limite existe e que é um número irracional com valor e= 27828 . Agora com e, procedamos ao cálculo do limite
() = lim 0
· lim 0
1
x =
·1 =.
Resumindo, ) =.
Observação – Devido à propriedade vista anteriormente a respeito do número e, diz-se que ele é a base natural das funções exponenciais. Note que se c é uma constante também temos e) =e.
Considere fx) =egx) =u= 3x Então, a função composta de f com g é dada por
fg)x) =fgx)) =fu) ==x.
Determine a derivada da função f g)x) =.
Determine a derivada da função composta de g com f que é dada por
Derivada da função inversa
Agora é um bom momento para você reler a aula 9 de Pré-Cálculo, a partir da página 14, quando tratamos de funções invertíveis. Seria bom termos em mente que x)= 1
x).
Teorema 2
Se f tem derivadas em todos os pontos de um intervalo I, no qual fx)0 ou no qual
fx)0, é possível mostrar que:
a) se
y=x), então, a imagem de f é um intervalo J e existe uma função x=y) que satisfaz às relações x)) =xey)) =y, dita a inversa de f, e possui derivadas em todo intervalo J;b) a derivada da função inversa é
yf
y) = 1
ffy))
yfy) = 1 fx).
Note que yf
y) = x
y efx) =
xfx) = y
x, o que nos permite escrever
dx dy =
y x
.
Isto é, a derivada da função inversa é o inverso da derivada da função dada.
Demonstração
Não faremos a demonstração do item (a). Uma demonstração rigorosa desse item é feita em cursos mais avançados de cálculo.
Para uma demonstração do item (b), derivamos ambos os membros da igualdade
y) =x
xfy) = x),
e usando a regra da cadeia pelo fato de y=x) temos:
yf
y)y = 1,
xf
y) = 1 y =
1 fx)
Logo,
yfy) = 1 fx)
Como na função inversa a variável independente é y, devemos expressar x)
em termos de y,
portanto, yf
y) = 1
fx) = 1 ffy))
Resumindo, yf
y) = 1
ffy))
Observação - Note que foi extremamente importante o fato de termos fx)0 ou fx)0 (na verdade, x)= 0) para que o quociente anterior fizesse sentido.
Exemplo 2 (Derivada do logaritmo natural)
Como visto na aula 13 de Pré-Cálculo (Funções exponenciais e logarítmicas), a função inversa da exponencial y é a função logaritmo natural lny. Aplicando a fórmula da derivada da função inversa a lny, e sabendo que fx) =e fx) =eefy) =lny,
temos:
y lny= 1
ffy)) = 1 flny) =
1 eln =
1 y.
Resumindo,
y lny=
y. Finalmente, podemos reescrever essa fórmula usando
x
como variável independente, conforme é mais usual, obtendo:
Exemplo 3 (Derivada da função exponencial
a
x
,
a
>
0
)
Ainda remetendo à aula 13 de Pré-Cálculo, vimos que eln e a regra de potências
)d=d, portanto, elevando ambos os membros a x, obtemos
x= eln)x=exln,
ou seja,
xexln.
Derivando a igualdade anterior, obtemos
d dx
x) = d dxe
xln),
e utilizando a regra da cadeia, fazendo uxln, temos
d dx
x) = d
due
u) d
dxu) =e
uln=exlnln=xln.
Resumindo, d dx
) =ln.
O logaritmo natural também é chamado de logaritmo neperiano.
Exemplo 4 (Derivada da função
x
r
,
x
>
0
,
r
∈
R
,
r
fixo)
Como xn elevando ambos os membros a r, obtemos:
xnxnx
xx
) = x
enx
Utilizando a regra da cadeia, fazendo u
=
r
Inx temos xx
) = ue
u)u x =e
ur 1 x =e
lnx r x =x
r
x =rx
Resumindo,
xx
Atividade 2
1
2
3
Polinômios centrados em
a
Denominamos de polinômio centrado em
a de grau
n o polinômio
apresentado na forma:Pnx) = n
=
axa)=axa)+a1xa)1+ +axa)+ +anxa)n ,
Pnx) =a+a1xa) + +axa)+ +anxa)n,
onde a, a, a1, , a são números reais com = .
Exemplo 5
Consideremos o polinômio x) = 1 + 2x1) + 3x1). Então,
= , = , 1= 2 e = .
Exemplo 6
No polinômio x) = 1 + 3x1), temos
= 1 , = 1 , 1= e 2 = 3
Considerando a função x) =x+ 13, encontre sua derivada x).
Dada a função x) =x3x+ 134, encontre sua derivada x).
Encontre a derivada de xa) , x > a , a r ∈. com
a
er
fixos.Exemplo 7
No polinômio x) =x+ 5x, temos = , = , 1 = 1 , 2 = e 3= 5,
o que dá um polinômio centrado em 0, a saber
3x) =x+ 5x3= 0 + 1x0)+ 0x0)2+ 5x0)3
Derivada do polinômio centrado em a, nx) = n
=
axa). Neste caso, usamos a notação de Newton para derivadas.
Pnx) = n
=
axa)
=
a+a1xa)1+ +axa)+ +anxa)n.
Como a derivada de uma soma é a soma das derivadas, temos
Pnx) = n
=
axa)
= a)+ [a1xa)]+ + [anxa)n]
Pnx) = n
= a
xa) = 0 +axa)+a2xa)2+ +anxa)n)
Pnx) =
n
=
akxa) =
0 +a·1·xa)+a2·2·xa)2+ +an·n·xa)n
Pnx) =
n
=
kaxa) =a+ 2a2xa) + +nanxa)n
Observe que nos últimos somatórios o k varia de 1 a
n, pois a primeira parcela para
k = 0 a derivada é nula, uma vez que
= , sendo totalmente desnecessário explicitá-la.Resumindo,
nx) = n
=
kaxa) ou n
=
x)
=
n
=1
Calcule a derivada das funções dos exemplo 5, 6 e 7.
Atividade 3
Funções
trigonométricas inversas
Vimos na aula 15 de Pré-Cálculo (Funções trigonométricas inversas) que as funções trigonométricas seno, co-seno, tangente, quando restritas a domínios adequados, admitem função inversa. Vejamos mais alguns exemplos.
Exemplo 8 (Função
arcsec(x)
)
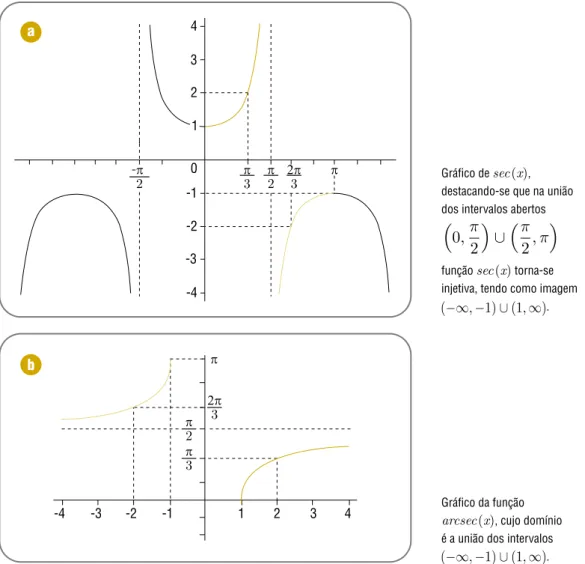
Na Figura 1a, vemos que a função secante não possui inversa em todo seu domínio, mas se considerarmos essa função restrita à união dos intervalos abertos ,
2
2, , como vemos nessa figura, a função secante torna-se injetiva. Desse modo, admite uma função inversa, a qual denominamos de arco secante e representamos por rcsecx), definida no domínio ∞1)∪1∞) com imagem ,
2
2, , como mostrado na Figura 1b.
Cabe observar que na função rcsecx), usualmente, quando tentamos encontrar seus valores, lê-se o arco cuja secante é x.
Se y=rcsecx), então, x=sey)
Exemplo 9
Na Figura 1a, sec3
= e na Figura 1b, arcsec2) =
3, as quais estão de acordo
com a leitura: o arco cuja secante é 2 é
As funções arccos), rccotgx) e rccosecx) podem ser determinadas da mesma forma que as outras vistas anteriormente, no entanto, é mais simples usar as identidades seguintes:
arc cosx)≡
2 arc senx),
arc cotgx)≡ 2 arc tgx),
arc cosecx)≡
2 arc secx).
Figura 1 - Gráficos da sec(x) e de sua função inversa arcsec(x)
Gráfico de sec(x),
destacando-se que na união dos intervalos abertos
, 2
2,
função sec(x) torna-se
injetiva, tendo como imagem ∞1)∪1∞).
Gráfico da função
arcsec(x), cujo domínio
é a união dos intervalos ∞1)∪1∞). a
Cálculo das
derivadas das funções
trigonométricas inversas
Exemplo 10 (Derivada da função
arcsen(x)
)
Observação - Para facilitar a aplicação das fórmulas da derivada da função inversa, optamos considerar x=rcseny), sendo
y tratada como a
variável independente.
Como visto anteriormente, arco seno é a função inversa da função seno. Quando
ysn x, tem-se x=rcseny). Aplicando a fórmula da derivada da função inversa,
yf
y) = 1
ffy)),
a x=rcseny), com y=fx) =sen x,fx) =cos xex=fy) =rcseny), temos:
d
dyrcseny) = 1
ffy)) =
1
cosrcseny)),
pois fx) =cos x,x=rcseny), e mais
cosrcseny)) =cosx) =1sen x) =1y,
a raiz quadrada é positiva, porque cos
(
x
)
é sempre maior ou igual a zero, quando x está no intervalo ,
..
Concluímos que
d
dyrcseny) =
1
Finalmente, podemos reescrever essa fórmula usando x como sendo a variável independente,
de acordo com o que é mais usual, obtendo:
d
dxrcsenx) =
1
√
1x.
Exemplo 11 (Derivada do
arctg
(x)
)
Observação - Para facilitar a aplicação das fórmulas da derivada da função inversa, optamos por considerar x=rc tgy), sendo
y tratada como a
variável independente.Conforme vimos anteriormente, arco tangente é a função inversa da função tangente. Quando yt x, tem-se x=rctgy).
Aplicando a fórmula da derivada da função inversa a x=rctgy), com y=fx) =tg x,fx) = 1 +tg2 xex=fy) =rctgy), temos:
d
dyrctgy) =
1
ffy)) =
1
1 +tg2rctgy)) =
1
1 + [tgrctgy))]2 =
1 1 +y2.
Resumindo,
d
dyrctgy) = 1 1 +y.
Finalmente, podemos reescrever essa fórmula usando x como variável independente, conforme o que é mais usual, obtendo:
d
dxrctgx) =
1 1 +x.
Exemplo 12 (Derivada da função
arcsec
(x)
)
Observação - Para facilitar a aplicação das fórmulas da derivada da função inversa, optamos por considerar x=rcsecy), sendo
y tratada como a
variável independente.Aplicando a fórmula da derivada da função inversa a x=rc secy), com
y=fx) =sec x,fx) =sec x tg xex=fy) =rc secy), temos:
d
dyrcsecy) =
1
ffy)) =
1
secrc secy))tgrc secy)),
pois fx) =sec x tg x,x=rcsecy),tg x) = sec x)1,|tg x|=
sec x) 1
e mais
tgrcsecy)) =tgx) =±
sec x)
1 =±y1 d
dyrcsecy) =
1 ±yy1,
a indefinição do sinal (+) ou (-) é decorrência da descontinuidade da função arco secante, mas, como vemos no gráfico dessa função, para pequenos valores positivos do acréscimo
, temos valores positivos de , portanto, essa derivada sempre será maior ou igual a zero. Podemos então eliminar o sinal (-) utilizando a função valor absoluto:
d
dyrcsecy) = 1
|y|y1.
Finalmente, reescrevemos essa fórmula usando
x como variável independente,
conforme é mais usual, obtendo:d
dxrcsecx) =
1
|x|√x1.
Derivadas laterais
Poderíamos ter procedido ao estudo da derivada de uma função de modo análogo ao que fizemos em limites. Assim, definimos, primeiramente:
a)
derivada à direita: chamamos de derivada à direita da função f no ponto o limite da taxa de variação média quando tende a 0 por valores sempre positivos, desde que esse limite exista. Deste modo, a derivada à direita da funçãof no ponto
, denotada por x), é
(x0) = lim 0
y
x = lim0
(x0 + x)(x0)
x ;
b)
derivada à esquerda: chamamos de derivada à esquerda da função f no ponto limite da taxa de variação média quando tende a 0 por valores sempre negativos, desde que esse limite exista. Desse modo, a derivada à esquerda da função f no ponto , denotada por x), é
(x) = lim 0
y
x = lim0
(x + x)(x)
Em seguida, com a ajuda do Teorema 3, diríamos que uma função é derivável num ponto se, e somente se, as derivadas laterais em x,x)e x), existem e são iguais; a esse valor comum daríamos o nome de derivada da função f no ponto .
Definição
Uma função f é derivável no intervalo fechado [a
,
b] se for derivável em todos
os pontos do intervalo aberto(a
,
b), possuir derivada à esquerda em
a e
derivada à direita em b.Exemplo 13
Calcular as derivadas laterais da função valor absoluto de
x, ou módulo de
x,
x) =x, emx.Derivada à direita em = :
(0) = lim 0
y
x = lim0
(0 + x)(0)
x =
lim
0
|0 + x| |0|
x = lim0
|x|
x .
Como tende a 0, por valores sempre positivos, temos que = , portanto,
(x0) = lim 0
x
x = lim0
x
x = 1. Derivada à esquerda em = :
(0) = lim →0
y
x = lim→0
(0 + x)(0)
x
= lim
→0
|0 + x| |0|
x = lim→0
|x|
x
Como tende a
0 por valores sempre negativos, temos que
||=,portanto,
(0) = lim 0
|x|
x = lim0
x
x =1.
Como as derivadas laterais em = são diferentes, temos que a x) =x não é
Teorema 3
Atividade 4
Resumo
1) Monte uma tabela com as funções vistas até o momento, de modo
que na primeira coluna tenhamos a função e na segunda sua derivada. Por exemplo:Função Derivada
x) =x x) =nx
2)
Considere a função x) = x3+ 3x4x+ 1)5 e encontre a derivada x).3) Considere o polinômio
x) = 1 + 2x1) + 3x1) e obtenha a derivada
x) do polinômio x).
4) Considere o polinômio
2x) = 1 + 2x1) + x1)2 e obtenha a derivada 2x) do polinômio 2x).
5) Considere a função x) = x
2)5 e obtenha a derivada x).6)
Considere a função fx) = e obtenha a derivada x).7) Considere a função
fx) =e obtenha a derivada x).
8) Considere a função x) = 2
e obtenha a derivada x).
9) Considere a função
fx) =rcsen2x) e obtenha, aplicando a regra dacadeia, a derivada x).
Auto-avaliação
Imagine um processo qualquer composto de duas fases em que a última só se realiza depois da primeira ter sido encerrada. Ou seja, o processo total pode ser visto como uma composição dos dois estágios. Seja hx) =gx)) a função que representa tal processo, no qual a função x) representa a primeira etapa e a função x) representa a segunda.
a) Qual o sinal da derivada de x) se as derivadas de
gx)ex) têm sinaisiguais?
b) Qual o sinal da derivada de x) se as derivadas de
gx)ex) têm sinaisdiferentes?
Referências
ANTON, Howard. Cálculo: um novo horizonte. 6. ed. Porto Alegre: Bookman, 2000. v 1.