Modelos de Randall Sundrum e estabilização do raio da dimensão extra

(1)

CENTRO DE CIˆENCIAS DEPARTAMENTO DE F´ISICA

PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

RAIMUNDO IVAN DE OLIVEIRA JUNIOR

Modelos de Randall Sundrum e Estabilizac

¸˜

ao do

Raio da Dimens˜

ao Extra

(2)

Modelos de Randall Sundrum e Estabilizac

¸˜

ao do

Raio da Dimens˜

ao Extra

Disserta¸cão de Mestrado apresentada ao Programa de Pós-Gradua¸cão em F´ısica da Universidade Federal do Ceará como requisito parcial para a obten¸cão do t´ıtulo de Mestre em F´ısica. Área de concentra¸cão: F´ısica da matéria condensada.

Orientador: Prof. Dr. Geov´a Maciel de Alencar Filho

Co-orientador: Prof. Dr. Ricardo Renan Landim de Carvalho

(3)

Biblioteca Universitária

Gerada automaticamente pelo módulo Catalog, mediante os dados fornecidos pelo(a) autor(a)

O51m Oliveira Júnior, Raimundo Ivan de.

Modelos de Randall Sundrum e estabilização do raio da dimensão extra / Raimundo Ivan de Oliveira Júnior. – 2017.

54 f. : il. color.

Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Ciências, Programa de Pós-Graduação em Bioquímica, Fortaleza, 2017.

Orientação: Prof. Dr. Geová Maciel de Alencar Filho. Coorientação: Prof. Dr. Ricardo Renan Landim de Carvalho.

(4)

Modelos de Randall Sundrum e Estabilizac

¸˜

ao do

Raio da Dimens˜

ao Extra

Disserta¸cão de Mestrado apresentada ao Programa de Pós-Gradua¸cão em F´ısica da Universidade Federal do Ceará como requisito parcial para a obten¸cão do t´ıtulo de Mestre em F´ısica. Área de concentra¸cão: F´ısica da matéria condensada.

Aprovada em 15/09/2017

BANCA EXAMINADORA

Prof. Dr. Geov´a Maciel de Alencar Filho (Orientador) Universidade Federal do Cear´a (UFC)

Prof. Dr. Roberto Vinhaes Maluf Cavalcante Universidade Federal do Cear´a (UFC)

(5)

(6)

A Deus por me dar for¸cas para seguir enfrentando os obst´aculos.

A minha querida m˜ae, Luzia Oliveira Lima, pelo apoio incondicional.

A minha namorada, Claudiane Chagas da Silva, pela paciˆencia e dedica¸c˜ao.

Ao professor Dr. Makarius Oliveira Tahim, por me fazer acreditar que eu era capaz.

Ao professor Dr. Geov´a Maciel de Alencar Filho, pela paciˆencia e disponibilidade em

me ajudar.

Ao professor Dr. Carlos William de Ara´ujo Paschoal, por me ajudar em um dos

momentos mais dif´ıceis durante essa jornada.

A todos os integrantes do CREU: Raul Crowley, Rodrigo Almeida, Francisco

Eman-nuel, Wendel Macedo, Emanuel Wendel, Luis Felipe, Jason, Stanley Frota, Ancelmo

Pi-nheiro e Márcio, pela ajuda nos momentos de dúvidas (não foram poucos).

(7)

Nessa disserta¸cão estudamos os modelos Randall Sundrum Tipos I e II e a estabiliza¸cão do raio da dimensão extra. Tanto o tipo I quanto o II foram elaborados por Lisa Randall e Ramman Sundrum. O tipo I foi desenvolvido para resolver o problema da hierarquia de gauge ( grande discrepância entre a escala de energia do modelo padrão (103 _GeV₎ e a escala de energia da gravidade (1019 _GeV _{) . O tipo II trata, detalhadamente, o} comportamento da gravidade. Iniciamos falando dos modelos de dimensões extra que antecederam os modelos de Randall Sundrum: Kaluza-Klein, Arkani-Hamed-Dimopoulos-Dvali (ADD) e o modelo de Rubakov (O Universo como uma parede de dom´ınio). Em seguida, fazemos uma revisão dos trabalhos de Lisa Randall e Ramman Sundrum. Após isso, focamos no problema da estabiliza¸cão do raio. Esse problema surge no modelo tipo I. Por fim, explicamos a solu¸cão dada para ele: O mecanismo de Goldberger Wise.

(8)

In this dissertation we study The Randall Sundrum models type I and II and the sta-bilization of the radius of the extra dimension. Both the types were elaborated by Lisa Randall and Ramman Sundrum. The type I was developed to solve the gauge hierarchy problem (big discrepancy between the energy scale of the standard model(103_GeV_{) and} the energy scale of the gravity (1019_GeV_{) . The type II explain, in details, the} beha-vior of the gravity. We begin speaking of the extra dimensions models that preceded the Randall Sundrum model: Kaluza Klein, Arkani-Hammed- Dimopoulus-Dvali (ADD) and the Rubakov’s model ( The universe as a domain wall). Then, we make a review of the Lisa Randall and Ramman Sundrum papers. After that,we focus on the problem of the stabilization of the radius. This problem arises in the type I model. Lastly, we explain the solution that was created to it: The Goldberger Wise mechanism.

(9)

3.1 Potencial escalar em fun¸c˜ao do campo . . . 16

3.2 Solu¸c˜ao do tipo parede de dom´ınio . . . 17

3.3 Densidade de energia da parede de dom´ınio localizada em z=0 . . . 18

4.1 Simetria Orbifold . . . 21

4.2 Setup do modelo Randall Sundrum . . . 21

4.3 A gera¸c˜ao de uma hierarquia exponencial . . . 28

5.1 Potencial Gravitacional V(z) . . . 36

(10)

1. Introdu¸c˜ao . . . 1

2. Modelo de Kaluza-Klein . . . 4

2.1 Introdu¸c˜ao . . . 4

2.2 Condi¸c˜ao Cil´ındrica . . . 6

2.3 Decomposi¸c˜ao de KK . . . 8

2.3.1 Decomposi¸c˜ao do campo escalar . . . 9

2.3.2 Escala Pequena . . . 10

3. Modelo ADD e o Universo Como uma Parede de Dom´ınio . . . 11

3.1 Escala Natural de Energia . . . 11

3.2 O Modelo ADD . . . 14

3.3 O Universo Como Uma Parede de Dom´ınio . . . 15

3.4 Densidade de Energia da Brana . . . 17

4. Modelo Randall-Sundrum Tipo I . . . 20

4.1 A configura¸c˜ao do Modelo . . . 20

4.1.1 A m´etrica . . . 21

4.2 A¸c˜ao e Equa¸c˜oes de Movimento . . . 23

4.3 Implica¸c˜oes F´ısicas . . . 25

5. Modelo Randall Sundrum Tipo II . . . 30

5.1 Modos Gravitacionais . . . 30

5.2 Equa¸c˜oes de Einstein Linearizadas . . . 31

5.3 Equa¸c˜ao Tipo Schrodinger . . . 34

5.3.1 Modo-zero . . . 37

5.3.2 Modos Massivos . . . 39

5.4 Espectro Gravitacional . . . 41

5.5 Limite Newtoniano . . . 43

6. Estabiliza¸c˜ao do Raio da Dimens˜ao Extra . . . 46

6.1 Mecanismo de Goldberger Wise . . . 46

6.2 A¸c˜ao Proposta e equa¸c˜oes de movimento . . . 47

6.3 O sistema gravidade-escalar . . . 49

7. CONCLUS ˜OES E PERSPECTIVAS . . . 51

(11)

1. Introdu¸

c˜

ao

A F´ısica sempre tenta dar explica¸cões para os fenômenos naturais através da

cons-tru¸cão de modelos. Esses modelos são versões simplificadas da natureza, no intuito de

descrevˆe-la da melhor maneira poss´ıvel. Um dos mais bem sucedidos modelos j´a

cria-dos na F´ısica ´e o modelo padr˜ao das part´ıculas elementares. Ele descreve as part´ıculas

elementares do nosso universo, bem como as intera¸c˜oes entre elas [1].

De acordo com esse modelo existem quatro intera¸c˜oes fundamentais na natureza, a

saber: Forte, fraca, eletromagn´etica e gravitacional. Nele existem basicamente dois tipos

de part´ıculas: Os férmions e os bósons. Os primeiros são part´ıculas com spin semi-inteiro

enquanto que os bósons tem spin inteiro. De maneira simples, os férmions são as part´ıculas

que constituem a matéria e os bósons são as part´ıculas que transmitem as for¸cas.

Este modelo é uma teoria de campos consistente com a mecânica quântica e a

re-latividade especial [2]. Ele consegue descrever muito bem as intera¸c˜oes forte, fraca e

eletromagn´etica, mas falha ao tentar descrever a gravidade. Esse ´e apenas um de seus

problemas, ele possui muitos outros, de car´ater experimental e te´orico. Os problemas

de caráter experimental são: Oscila¸cões de neutrinos, assimetria matéria-antimatéria,

matéria escura e infla¸cão cósmica. Os problemas de caráter teórico são: Origem da massa

das part´ıculas, excesso de parˆametros livres, problema de hierarquia da fam´ılia de l´eptons

e problema da hierarquia de gauge.[1]

Neste texto trataremos basicamente do problema da hierarquia de gauge. Esse

pro-blema trata da grande discrepˆancia entre a escala de energia da intera¸c˜ao gravitacional

( 1019_GeV _{) e a escala de energia do modelo padrão(escala eletrofraca) (10}3_GeV _{). A} primeira é conhecida como escala de Planck. Nessa escala a intera¸cão gravitacional seria

(12)

todas as outras [2], o bóson de Higgs. No entanto, o próprio bóson de Higgs tem massa.

Surge então a pergunta: Quem dá massa para o bóson de Higgs? (isso é um parâmetro

livre na teoria). Nos modelos de grande unifica¸cão é necessário duas quebras espontâneas

de simetria, uma na escalaT eV e outra na escala GeV. Dessa forma são necessários dois bósons de Higgs; um com energia da ordem de (103_GeV_{) e outro com massa da ordem} de (1019_GeV_{). As razões para essa disparidade de massa são imposi¸cões experimentais,} isto é, a hierarquia MPl

Mw ∼10

16 _{deve existir para reproduzir efeitos f´ısicos observ´aveis em}

baixas energias.[2]

O grande Gap de energia entre a escala eletrofraca e a escala de Planck, necessita um

”fine tunning”da ordem de 16 d´ıgitos [3]. Mas o que significa o fine tunning? Basicamente

isso significa que temos que colocar os parˆametros a m˜ao em ordem de conciliarmos a

teoria com a experiˆencia. Isso pode ser entendido melhor atrav´es de um ”toy model”.

Suponha que observamos uma part´ıcula atrav´es de um experimento e encontramos para

sua massa um valor deMexp ≈1.100GeV_c2 (massa experimenttal). No entanto, essa mesma medida, de acordo com a teoria quˆantica de campos, tem que sofrer uma corre¸c˜ao da

ordem de 1019_GeV_{. Isso independentemente da massa teórica (prevista na lagrangeana} clássica). Naturalmente esperamos que a massa teórica da part´ıcula deveria coincidir,

aproximadamente, com o experimentoMexp ≈Mteo. Mas um simples c´alculo nos mostra

que não é isso o que acontece. A massa experimental é dada porMexp =Mteo+δmquantum,

ondeδmquantum corresponde a corre¸c˜ao quˆanica. Dessa forma,Mteo≈Mexp−δmquantum ≈

1.100GeV ₋1019_GeV_{. Isso mostra que um ajuste de 16 d´ıgitos se faz necess´ario. Isso nos} mostra que precisamos de teorias alternativas para explicar o problema da hierarquia de

gauge.[3]

Temos ent˜ao a pergunta: como gerar essa hierarquia de energias? Existem trˆes modelos

que propõe uma solu¸cão para esse problema. O primeiro é o modelo Technicolor. este

modelo prop˜oe uma F´ısica de part´ıculas em que n˜ao existem campos escalares como

part´ıculas fundamentais. Dessa forma o higgs n˜ao existe e consequentemente a hierarquia

também não. O segundo modelo é a supersimetria. Neste se propõe o acréscimo de

(13)

em dimens˜oes extras.

O primeiro modelo de dimens˜ao extra criado para tentar resolver o problema da

hi-erarquia ´e o modelo de Arkani-Hamed Dimopoulos e Dvali (ADD) [4]. Em 1998 ADD

propuseram um modelo com duas dimens˜oes extras grandes, da ordem de 1mm, e uma

hipersuperf´ıcie onde n´os vivemos. Eles consideravam que a gravidade se diluia no grande

volume da dimens˜ao extra. Dessa forma a hierarquia, em 4D, entre a escala de Planck e a

escala elerofraca seria apenas aparente. No entanto, isso apenas transferiu a hierarquia de

um lugar para outro. Pois ao considerar uma dimens˜ao extra grande resolvia a hierarquia

entre as escalas de energia, mas criava a hierarquia entre os tamanhos das dimens˜oes

ex-tras. Naturalmente esperava-se uma dimens˜ao extra da ordem do comprimento de Planck

LP l≈10−33cm . [5]

O outro modelo de dimens˜ao extra foi criado por Lisa Randall e Raman Sundrum,

em 1999. Eles propuseram uma dimens˜ao extra que, diferente da proposta de ADD, era

compacta. Nesse modelo existem duas branas, uma em que ”vive”a gravidade e outra

onde os campos do modelo padr˜ao ficam confinados, nosso universo. A hierarquia entre as

escalas ´e gerada apenas com argumentos de geometria, atrav´es de um fator exponencial

que ´e colocado na m´etrica que descreve o modelo. Antes de estudarmos com detalhes o

modelo Randal Sundrum, veremos outros modelos de dimens˜oes extras que surgiram antes

do RS: O modelo de kaluza-Klein, Rubakov Shaposhnikov (Universo como uma parede

(14)

2. Modelo de Kaluza-Klein

Um dos primeiros modelos de dimens˜ao extra foi criado por Theodor Kaluza e Oscar

Klein. A inten¸cão desse modelo é unificar a gravidade com o eletromagnetismo. Isso é feito

supondo uma dimens˜ao extra do tipo espa¸co. Nesse modelo o tensor m´etrico de um espa¸co

tempo curvo 5-dimensional ´e decomposto em um tensor m´etrico de um espa¸co curvo

4-dimensional, o potencial vetor do eletromagnetismo e um campo escalar. A proposta do

modelo é muito boa, mas aparece inconsistências muito fortes na teoria. A equa¸cão de

movimento para o campo escalar φ s´o ´e consistente no caso em que FµνFµν = 0. O raio

de compactifica¸c˜ao dessa teoria ´e muito pequeno, o que faz com que a escala de energia

da teoria seja muito grande, impossibilitando a deteçcão da dimensão extra. Isso motiva

o surgimento de outras teorias de dimens˜oes extras. Faremos nesse cap´ıtulo uma breve

revis˜ao da teoria de KK.

2.1 Introdu¸c˜ao

Em 1914 Gunnar Nordstrom unificou o eletromagnetismo e a gravidade

Newtoni-ana [6]. Ele fez isso utilizando um tensor de energia momento totalmente sim´etrico em

um espa¸co de Minkowski de 5 dimensões. Para nós, isso pode não ser muito relevante,

uma vez que ele usou a relatividade Newtoniana, a qual sabemos que n˜ao ´e correta. No

entanto, vale lembrar que ele fez isso antes do descobrimento da teoria da relatividade

geral.

Sete anos depois em 1921 o matem´atico Theodor Kaluza descobriu que o tensor m´etrico

de um espa¸co curvo 5-dimensional pode ser decomposto em um tensor m´etrico de um

espa¸co curvo 4-dimensional, o potencial vetor do eletromagnetismo e um campo escalar.

Kaluza enviou seu trabalho para Einstein que encorajou o mesmo a public´a-lo.

(15)

da quinta dimensão), que não era bem explicada pelo mesmo. É ai que entra o F´ısico

Oscar Klein. Ele dá uma explica¸cão sobre a condi¸cão cil´ındrica propondo que a quinta

dimensão é pequena e periódica e compactada em forma de um c´ırculo. Se a quinta

dimensão é um c´ırculo, ela pode ser feita tão pequena que a métrica não depende mais

dela.

A teoria de Kaluka-Klein (KK) buscava unificar a gravidade de Einstein com o

ele-tromagnetismo de Maxwell por meio da inclus˜ao de uma dimens˜ao extra do tipo espa¸co.

Dessa forma o conjunto completo das coordenadas em um espa¸co-tempo (4 + 1)₋

dimen-sional seria (xµ_{, y) com}_µ_{= 0,}_1,_2,_{3 .}

Nessa teoria o espa¸co 5-dimensional seria composto apenas pela gravidade [7]. Dessa

forma não teriamos matéria e as equa¸cões de Einstein em 5-D seriam:

GAB = 0. (2.1)

Aqui (A, B = 0,1,2,3,5) representam os ´ındices da m´etricagAB em 5-D.

Ao considerarmos quatro coordenadas espaciais e uma do tipo tempo, pode-se dividir

a m´etrica da seguinte forma:

gµν(µ, ν = 0, ...,3) a m´etrica do espa¸co tempo ordin´ario 4-dimensional;

gµ5 =g5ν um 4-campo vetorial;

g55 = φ um campo escalar. Dessa forma podemos parametrizar gAB, considerando

φ= 1, da seguinte forma:

˜ gAB =



 

gµν +AµAν Aµ

Aν 1





 (2.2)

e a m´etrica inversa:

˜ gAB =



 

gµν ₋_Aµ

−Aν _{1 +}_A µAµ





. (2.3)

(16)

2.2 Condi¸c˜ao Cil´ındrica

Em sua teoria Kaluza considerou uma condi¸c˜ao cil´ındrica [7]: a derivada da m´etrica

gAB com rela¸cão a dimensão extra é nula

∂gAB

∂x5 = 0. (2.4)

Segundo ele isso era devido ao fato de não vermos a dimensão extra, todos os fenômenos

f´ısicos observ´aveis ocorrem em 4-D. Posteriomente Klein deu uma melhor explica¸c˜ao para

essa condi¸cão. Ele supôs que a dimensão extra fosse compactada em um c´ırculo de raio

muito pequeno que n˜ao poderia ser observado para energias menores que 1019_GeV_. Podemos calcular o escalar de Ricci em 5-D da mesma forma que fazemos em 4-D.

Primeiro calculamos os simbolos de Christoffel, onde os termos n˜ao nulos s˜ao:

˜ Γ5 µν = 1 2

∇µAν+∇νAµ−AσFµσAν −AσFνσAµ

; (2.5)

˜ Γσ

µ5 = 1 2F

σ µ;

˜

Γ5_µ₅ = ₋1 2AσF

σ µ;

˜ Γσ

µν = Γ

σ µν +

1 2(AµF

σ

ν +AνFµσ);

˜ Γσ

µσ = Γ

σ µσ+

1 2AσF

σ µ.

Onde Fµν = ∂µAν −∂νAµ e ∇ denota a derivada covariante. Com as conex˜oes em

mãos os tensores de Ricci não nulos são:

˜

R55 = ₋1 4FγηF

γη_; _(2.6)

˜

Rµ5 = − 1 2∇σF

σ µ −

1

4AµFγηF

γη_;

˜

Rµν = Rµν −

1 4

2 Aµ∇σFνσ +Aν∇σFµσ

−Fσ

µFνσ−FνσFµσ+AµAνFγηFγη

(17)

De forma que o escalar de Ricci ´e dado por:

˜

R = ˜gABR˜AB =R+

1 4FγηF

γη

. (2.7)

Utilizando uma a¸c˜ao de Einstein Hilbert em 5-D,

S5D =

Z

d5xp₋˜gR.˜ (2.8)

De 2.2 temos que det˜gAB = detgµν, logo √−g˜ = √−g, substituindo essa condi¸c˜ao e 2.7

em 2.8, obtemos:

S5D =

Z

d5x√₋g

R+ 1 4FγηF

γη

. (2.9)

Podemos integrar a dimens˜ao extra, obtendo uma a¸c˜ao puramente 4-dimensional

S4D =V

Z

d4x√₋g

R+1 4FγηF

γη

. (2.10)

OndeV ´e o volume de S1_{. Ao variarmos a a¸c˜ao 2.10 encontramos}

Gµν = 8πGTµνEM. (2.11)

Onde TEM

µν = gµν FαβFαβ

4 − F

α

µFνα ´e o tensor energia-momento do eletromagnetismo e

Fαβ =∂αAβ−∂βAα, corresponde ao tensor eletromagn´etico de Maxwell.

Reduzimos assim a a¸c˜ao de Einstein-Hilbert 5-dimensional a soma de uma a¸c˜ao

gra-vitacional 4-dimensional e a a¸c˜ao de Maxwell [8]. Dessa forma o eletromagnetismo e a

gravidade em quatro dimens˜oes s˜ao unificados, sendo diferentes aspectos da gravidade em

um espa¸co-tempo com uma dimens˜ao extra compacta.

A teoria de KK parece totalmente consistente, mas ela não é. Se para nossa métrica

inicial tivesemos considerado uma m´etrica em que n˜ao fizessemosφ= 1 inicialmente, por exemplo:

gAB =



 

gµν −k2φ2AµAν −kφ2Aµ

−kφ2_A

ν φ2





(18)

Ter´ıamos as seguintes equa¸c˜oes de movimento:

Gµν =

k2_φ2 2 T

EM µν −

1

φ[∇µ(∂νφ)−gµνφ] ; (2.13) ∇µFµν = −

3∂µ_φ

φ ;

φ = k

2_φ3 4 FµνF

µν_.

Agora se escolhermos φ = cte , as duas primeiras equa¸cões acima são exatamente a equa¸cão de Einstein e a equa¸cão de Maxwell:

Gµν = 8πGTµνEM (2.14)

∇µFµν = 0.

No entanto, a terceira equa¸cão só é consistente quandoFµνFµν = 0.

N˜ao nos preocuparemos muito com as inconsistˆencias da teoria de KK. Vamos

apre-sentar a decomposi¸c˜ao de KK e encontrar a escala de energia natural dessa teoria. ´E essa

escala que motiva o surgimento dos cen´arios de branas.

2.3 Decomposi¸c˜ao de KK

Em 1926 o F´ısico Oscar Klein fez algums aperfei¸coamentos na teoria de Kaluza. Ele

supˆos que a quinta dimens˜ao deveria ter a topologia de um c´ırculo e a escala de

compri-mento muito pequena. Discutiremos agora os efeitos dessa hip´otese.

Se a quinta dimens˜ao tem a topologia de c´ırculo, um campo escalar φ(xµ_{, y}_{) tem a}

propriedadeφ(xµ_{, y) =} _φ(xµ_{, y}_{+ 2πR), onde} _R_{´e o raio da dimens˜ao extra. Na realidade,}

qualquer campo será periódico na dimensão extra. Assim podemos expand´ı-los em série

(19)

gµν(xµ, y) =

X

n

g(µνn)(x µ

)einyR ; (2.15)

φ(xµ, y) = X

n

φ(n)(xµ)einyR ;

Aµ(xµ, y) =

X

n

A(n)

µ (xµ)e

iny R .

Ondenrefere-se ao n-ésimo modo de Fourier. Os campos são independentes da dimensão extra apenas paran = 0. Que é conhecido como modo zero.

2.3.1 Decomposi¸c˜ao do campo escalar

Por quest˜ao de simplicidade mostraremos a decomposi¸c˜ao do campo escalar sem massa

em modos de KK na quinta dimens˜ao. A decomposi¸c˜ao para outros campos(vetorial,

tensorial e spinorial) ´e semelhante.

A a¸c˜ao para um campo escalar sem massa em 5-D ´e dada por:

S =

Z

d5x1 2

gM N∂Mϕ(xM)∂Nϕ(xN)

, (2.16)

onde gM N = ηµνdxµdxν +dy2 ´e a m´etrica 5-dimensional, com xM ∼ (xµ, y) e y ∈ S1.

Devido a periodicidade da dimens˜ao extra, podemos expandir o campo em uma s´erie de

Fourier:

ϕ(xµ, y) = √1 2πR

∞

X

−∞

φ(n)(xµ)einyR . (2.17)

Substituindo 2.17 em 2.16 obtemos

S=

Z

d4x1 2

X

n

∂µφ(−n)∂µφ(n)+

n2 R2φ

(−n)_φ(n)

. (2.18)

Como ϕ(xµ_{y) ´e real, temos} _φ(−n)₌_φ(n)†

, de modo que a a¸c˜ao efetiva em 4-D ´e:

S =

Z

d4x 1 2∂µφ

(0)_∂µ

φ(0)+ ∞ X n=1 1 2

∂µφ(n)∂µφ(n)

†

+ n 2

R2φ

(n)_φ(n)† !

(20)

Vemos que obtemos a a¸c˜ao efetiva para um campo escalar n˜ao massivo em 4-D, o modo

zero da expansão, e uma série infinita de campos cuja a massa é dada porm(n) = _Rn. Os modos dessa expansão são ditos modos de KK e a série infinita de campos massivos é

chamada de torre de KK.

Se considerarmos um campo escalar massivo com massa m0 na quinta dimens˜ao, a massa dos modos de KK ser´am2

(n) =m2(0)+

n R

2

. Quando o n´umero de dimens˜oes extras

´e arbitr´ario, temosm2

(n) =m2(0)+

n1

R

2

+ n2

R

2

+.... Cada modo carrega uma energia da ordem de n

R (massa de repouso), e assim, n˜ao podem ser excitados para energias abaixo

desse patamar. Do ponto de vista quadrimensional cada modo de KK mn = _Rn pode ser

interpretado como um tipo diferente de part´ıcula.

2.3.2 Escala Pequena

Se R for muito pequeno, a energia necess´aria para estimular modos com n ₆= 0 seria muito grande, fora do alcance experimental atual. Dessa forma, apenas o modo zero pode

ser detectado.

Poderemos observar a dimens˜ao extra quando os aceleradores chegarem a energias

da ordem E _∼ 1

R. Dessa forma para tentar explicar o fato de que at´e agora nenhuma

dimens˜ao extra foi observada, adota-se como escala de compactifica¸c˜ao a escala de Planck

LP l =

_~

G c3

1₂

≈1,6x10−35m. (2.20)

Dessa forma a massa dos estados excitados seria da ordem da escala de Planck,

MP ≈1019GeV. Tal escala de compactifica¸c˜ao impede que os experimentos atuais nos

ace-leradores de part´ıculas, que tˆem energias da ordem de 1T eV, detectem sinais da existˆencia

(21)

3. Modelo ADD e o Universo Como uma Parede de Dom´ınio

No cap´ıtulo anterior vimos que a escala de energia gerada no modelo de KK ´e muito

grande, impossibilitando a deteçcão da dimensão extra. Dessa forma surgem outros

mo-delos de dimes˜oes extras propondo um tamanho maior para as mesmas. Um modelo

bastante conhecido ´e o modelo de Arkani-Hamed Dimopoulos e Dvali (ADD). Nele se

propõe a existência de dimensões extras grandes (_≈1mm) dessa forma a escala de

ener-gia é menor e as dimensões extras poderiam ser detectadas. Esse modelo não obteve

sucesso pois as dimensões extras não foram detectadas e ele não resolveu por completo o

problema que se propˆos, que era o problema da hierarquia. Ele resolveu o problema da

hierarqua entre as escalas de energia, mas criou outra hierarquia, agora entre os

tama-nhos das dimens˜oes extras. Neste cap´ıtulo tamb´em falaremos de como gerar uma brana

(hipersuperf´ıcie 4-dimensional que ´e considerada como sendo o nosso universo). A brana

é gerada através da solu¸cão tipo kink para a equa¸cão de movimento de um campo escalar.

3.1 Escala Natural de Energia

Vimos que na teoria de KK não é poss´ıvel fazer a deteçcão da dimensão extra. No

entanto, se compararmos a a¸c˜ao de Einstein-Hilbert em teorias n-dimensional com a

a¸c˜ao de Einstein-Hilbert usual em 4-D, podemos encontrar o tamanho para dimens˜ao

extra. Consequentemente, encontramos a escala de energia em que os efeitos podem ser

detectados em quatro dimensões. A a¸cão de Eintein-Hilbert n-dimensional é [9]

S4+n ∼

Z

d4+n_xp

−g(4+n)_R(4+n)_. _(3.1)

A dimensão de massa deS4+né−n−2. Mas como sabemos, a a¸cão necessita ser

(22)

Planck fundamental M∗. Dessa forma a a¸c˜ao de Einstein-Hilbert n-dimensional fica:

S4+n =−M_∗n+2

Z

d4+nxp₋g(4+n)_R(4+n)_. _(3.2)

Precisamos saber como a a¸c˜ao usual de Einstein-Hilbert

S4 =₋MP L2

Z

d4xp₋g(4)_R4 _(3.3)

esta contida na express˜ao n-dimensional. Assumindo que o espa¸co-tempo 4-dimensional

é plano e que a dimensão extra é compacta. Temos as seguintes rela¸cões:

p

−g(4+n) ₌_rnp

−g4 _e _R(4+n) ₌_R4_. _(3.4)

Substituindo 3.4 em 3.2, temos

S4+n=−M_∗n+2

Z

dV rn

Z

d4xp₋g4_R4_. _(3.5)

O fator R

dV rn _{é o volume da dimensão extra que é denotado por} _V

n. Assumindo a

compactifica¸cão da dimensão extra como um toroVn= (2πr)n . Temos então,

S4+n =−M_∗n+2Vn

Z

d4xp₋g4_R4_. _(3.6)

Comparando 3.6 com 3.3, obtemos:

MP l2 =M n+2

∗ Vn=M_∗n+2(2πr)n. (3.7)

Assumindo que os campos de gauge vivem na dimens˜ao extra, podemos fazer um

procedimento parecido com o anterior para obtermos os acoplamentos de gauge. A a¸c˜ao

para campos de gauge em altas dimens˜oes pode ser escrita como

S(4+n) =₋

Z

d4+nx 1 4g2

∗

FM NFM N

p

(23)

Onde g∗ é a constante de acoplamento dos campos de gauge em altas dimensões. É razoável se pensar que a parte quadridimensional do Field-Strength esta inclusa no tensor

de altas dimens˜oesFM N. Fazendo novamente a integral na dimesns˜ao extra obtemos:

S4 =₋

Z

d4xVn 4g2

∗

FµνFµν

p

−g4_. _(3.9)

Assim a rela¸c˜ao entre os acoplamentos dos gauges efetivos com os gauges em altas

di-mens˜oes ´e:

1 g2

ef f

= Vn g2 ∗

. (3.10)

Vamos agora ver as consequˆencias de 3.7 e 3.10. Assumindo-se que a mesma F´ısica

que dá a intensidade do acoplamento gravitacional, também dá o acoplamento de gauge,

g _∼ 1

M∗n/2

. Dessa forma, temos

1 g2 4

= VnM_∗n ∼rnM_∗n (3.11)

MP l2 = VnM∗n+2 ∼rnM∗n+2,

isso nos leva ar _∼ _M1

P l. Dessa forma em uma teoria natural de altas dimens˜oes r∼

1

MP l.

Assim não se tinha muita esperan¸ca de encontrar evidências de uma dimensão extra. Esse

era o pensamento que se tinha at´e os anos 90. No entanto, esse resultado foi alcan¸cado

considerando-se que todos os campos se propagam na dimens˜ao extra. Se considerarmos

que os campos de gauge ficam localizados em uma hipersuperf´ıcie denominada brana,

podemos encontrar um tamanho maior para a dimens˜ao extra.[9]

Se considerarmos que apenas a gravidade se propaga na dimens˜ao extra, teremos um

valor maior para essa dimens˜ao. Mas qu˜ao grande ela tem que ser? Considerando apenas

a gravidade se propagando na dimens˜ao extra, teriamos uma nova F´ısica apenas na escala

gravitacional. Assim as restri¸c˜oes no tamanho da dimens˜ao extra estariam ligadas as

medidas da gravidade.

A gravidade ´e muito dif´ıcil de ser testada para distˆancias pequenas. Para grandes

(24)

for¸ca. Até o presente momento ela so foi testada até 0.1mm. Dessa forma a dimensão

extra tem que ser menor que isso uma vez que se ela fosse dessa ordem de grandeza ja

teriam encontrado evidˆencias dela.

Desde que temos a rela¸c˜ao M2

P l ∼ M∗n+2rn, se r > M1P l , a escala fundamental de

Planck M∗ seria reduzida para MP l. Quão baixo poderia M∗ ir? Se M∗ < 1T eV, isso implicaria que a gravidade quântica devia ja ter detectado algum aspecto de dimensão

extra. Como nenhuma evidência foi encontrada, tem-se que impor queM∗ _≥1T eV. Dessa forma o valor mais baixo (maior valor poss´ıvel para a dimensão extra) seriaM∗ _∼1T eV. Esse modelo é chamado de ”Modelo de Grandes Dimensões Extras”e foi proposto por

Arkani-Hamed, Dimopoulus e Dvali (ADD).

3.2 O Modelo ADD

Quão grande seria o raio da dimensão extra se M∗ fosse da ordem de 1T eV ? Rever-tendo a expressão M2

P l∼M∗n+2rn. temos

1 r =M∗

M∗ MP l

_n2

= (1T eV)10−n32, (3.12)

onde usamosM∗ _∼103_GeV _e_M

P l ∼1019GeV. Considerando que 1GeV−1 = 2x10−14cm,

obtemosr_∼2x10−17_x1032

ncm.

Para n = 1 temos o absurdo resultado r = 2x1015_{cm, que claramente não pode} ser poss´ıvel. Para n = 2, obtém-se r = 2mm. Isso também não seria poss´ıvel pois o experimento mais preciso realizado para a gravidade tem-se r_∼0,2mm = 1012 1

T eV.

Para n > 2 o tamanho da dimensão extra é menor que 10−6_{cm, e isso pode ser um} tamanho poss´ıvel para a dimensão extra. Assim para n _≥ 2 M∗ _∼ 1T eV é de fato uma possibilidade que pode ser testada. SeM∗ fosse realmente da ordem de 1T eV não existiria Problema da Hierarquia. A intera¸cão gravitacional seria mais fraca em 4-D porque ela se

dilui no grande volume da dimens˜ao extra.

No modelo ADD s˜ao consideradas 2 dimens˜oes extras compactadas em um 2-toro ou

(25)

na brana at´e a ordem de energia da teoria (1T eV). Acima dessa energia eles se propagam

para o Bulk (uma esp´ecie de volume 5-dimensional).

A largura da brana ´e dada por δ _∼ _{T eV}1 , de acordo com 3.12 r _∼ 1016_{T eV}−1_{, uma} nova hierarquia surge. Agora n˜ao mais uma hierarquia entre escalas de energia, mas sim

entre o tamanho da brana e o tamanho da dimens˜ao extra.

3.3 O Universo Como Uma Parede de Dom´ınio

Anteriormente falamos da mat´eria ficar confinada em uma hipersuperf´ıcie denominada

de brana. Mas como ´e gerada essa brana? No cap´ıtulo seguinte, onde falaremos do modelo

Randall- Sundrum, as branas são colocadas a mão. Não existe um processo que gere as

mesmas. No entanto, ´e poss´ıvel gerar uma brana atrav´es de um campo escalar [10].

Consideremos um campo escalarφ=φ(xµ_{, z) cuja a¸c˜ao ´e dada por:}

S =

Z

d4xdz

1

2 ∂Aφ∂

A

φ₋V(φ)

. (3.13)

No intuito de obtermos uma solu¸c˜ao tipo kink, consideramos o seguinte potencial:

V(φ) = λ 2

8(φ 2

(26)

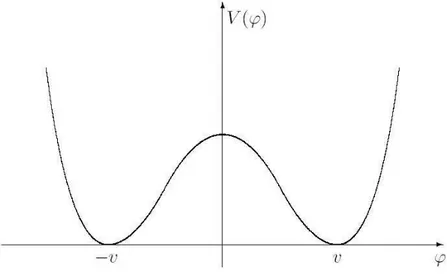
Figura 3.1: Potencial escalar em fun¸c˜ao do campo

Fonte: Adaptado Rubakov et al. [10].

Podemos observar que existem dois valores de menor energia φ =v e φ =₋v. Para φ= 0 temos um máximo instável. Ao variarmos a a¸cão 3.13, obtemos:

5φ+dV(φ)

dφ = 0. (3.15)

Onde 5 =− ∂ 2

∂z2 ,assim temos

φ₋ ∂

2_φ ∂z2 +

λ2 2 φ(φ

2

−v2) = 0. (3.16)

Buscando obter uma solu¸c˜ao conhecida na literatura como parede de dom´ınio,

con-sideramos uma solu¸cão estacionária e que dependa apenas da dimensão extra. Assim a

equa¸c˜ao de movimento reduz-se a:

−d 2_φ dz2 +

λ2 2 φ(φ

2

−v2) = 0. (3.17)

A solu¸c˜ao para essa equa¸c˜ao tem a forma [7] :

φ(z) = tanh

λvz 2

(27)

Graficamente temos:

Figura 3.2: Solu¸c˜ao do tipo parede de dom´ınio

Fonte: Adaptado de Rubakov et al. [11].

Atente para o fato de que φ(z _{−→ −∞}) = ₋v e φ(z _{−→ ∞}) = v. É por isso que essa solu¸cão é conhecida como parede de dom´ınio, porque ela separa os dois estados de

menor energia do campo. Ou seja, ela liga os dois estados fundamentaisφ=v emz =_∞ eφ =₋v em z =_−∞. É comum também atribuir-se o nome de kink para essa solu¸cão. ( um kink é um defeito topológico que separa dois espa¸cos, cada um com um vácuo

diferente).

3.4 Densidade de Energia da Brana

Vamos agora ver qual ´e a densidade de energia desse kink. SejaH0 a Hamiltoniana ou densidade de energia no 4-volume, podemos definir a densidade de energia no 3-volume

como:

σ =

Z ∞

−∞

(28)

Uma vez que H0 ´e a energia dividida por 4-volume.

Como ´e do nosso conhecimento, a hamiltoniana pode ser escrita da seguinte forma

H0 = πφ˙ _{− L}, onde π = ∂L

∂φ˙ ´e o momento canonicamente conjugado a φ. Dessa forma,

temos para o campo escalar:

H0 = 1 2(∂Aφ)

2₊ λ2 8 (φ

2

−v2)2 (3.20)

observe que φ =v eφ =₋v são solu¸cões da equa¸cão de movimento 3.17 com energia zero, pois para essa solu¸cão H0 = 0 . Considerando a solu¸cão tipo kink para φ , 3.18 encontramos

H0 = 1 4

λ2_v4 cosh(λvz

2 )

, (3.21)

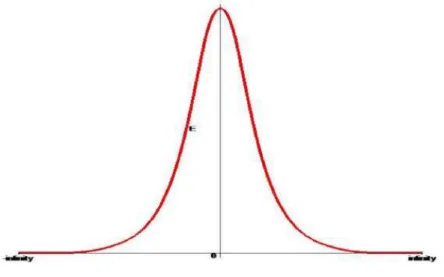
onde a representa¸cão gráfica é dada por:

Figura 3.3: Densidade de energia da parede de dom´ınio localizada em z=0

Fonte: Adaptado de Alex et al. [7].

(29)

Agora que conhecemos H0 , podemos calcular a densidade de energia da parede de dom´ınio. De acordo com 3.19, temos:

σ =

Z ∞

−∞ 1 4

λ2_v4 cosh(λvz

2 )

dz = 2λv 3

3 . (3.22)

No limite λ _{−→ ∞} a expessura da parede de dom´ınio vai a zero, isso se σ for mantido constante. Nesse caso a parede de dom´ınio da origem a uma estrutura denominada

(30)

4. Modelo Randall-Sundrum Tipo I

Neste cap´ıtulo estudamos o modelo Randall-Sundrum tipo I. Esse modelo foi criado

para resolver o problema da hierarquia, uma vez que o modelo ADD n˜ao obteve sucesso.

Nesse modelo considera-se a existˆencia de uma dimens˜ao extra, mas diferentemente do

modelo ADD, essa dimens˜ao ´e compactada em um c´ırculo. Lisa Randall e Ramman

Sundrum propõem um fator de deforma¸cão na métrica de Minkowski, e é justamente esse

fator que faz aparecer a hierarquia entre as escalas de energia.

4.1 A configura¸c˜ao do Modelo

O modelo Randall Sundrum considera o espa¸co tempo com 5 dimens˜oes. Sendo quatro

do tipo espa¸co e uma do tipo tempo. Nesse modelo considera-se a existˆencia de duas

p-branas , onde p é o número de coordenadas espaciais da brana, no nosso caso p = 3, e uma dimensão temporal. Uma dessas branas é o nosso universo, enquanto que a outra é

um universo paralelo ao nosso. Esses dois universos possuem escalas de energia diferentes.

O primeiro estando na escalaT eV e o segundo na escala GeV.

A dimens˜ao extra ´e compactada em um c´ırculo [5] ver figura 4.1, parametrizada por

um ângulo φ e com simetria (x, φ) _→ (x,₋φ). Formalmente o modelo é construido no S1_/Z2 _{orbifold [12]. Onde}_S1 _{é a esfera unidimensional e} _Z2 _{é o grupo multiplicativo}_{_1,– 1_}[5]. Tomamos o dom´ınio deφcomo sendo de₋πaπ, mas a métrica fica completamente definida se pegarmos apenas valores no intervalo 0_≤φ _≥π. Os pontos fixos do orbifold φ = 0 e φ = π são os pontos onde estão localizadas as duas branas. De forma simples podemos pensar essas branas como sendo as fronteiras do espa¸co tempo 5-dimensional

chamado de Bulk ver figura 4.2, com o nosso universo situado em φ=π e a outra brana em φ= 0. Essas branas, caracterizadas por coordenadasxµ_{, suportam teorias de campos}

(31)

presos na brana localizada em φ = π e o único campo que consegue se propagar na dimensão extra é o campo gravitacional.

Figura 4.1: Simetria Orbifold

Fonte: Adaptado de Gabella et al. [5].

Figura 4.2: Setup do modelo Randall Sundrum

4.1.1 A m´etrica

O modelo ´e baseado na relatividade geral de Einstein, logo teremos que fazer uso das

ferramentas básicas dessa teoria. A primeira coisa que devemos ter em mente é: Qual é a

(32)

a p-branaxi _{e a dimens˜ao extra} _{φ. A geometria do espa¸co-tempo curvado ´e descrito pela}

m´etrica:

ds2 = gM NdxMdxN (4.1)

= gµνdxµdxν + 2gµφdxµdφ+gφφdφ2

= g00dt2+ 2g0idtdxi+gijdxidxj+ 2gµφdxµdφ+gφφdφ2

Onde os ´ındices Romanos ma´ısculos (M, N, ..., p, p+ 1) s˜ao os ´ındices do Bulk (D =

p+ 2), os ´ındices gregos (µ, ν, ... = 0,1, ..., p) s˜ao os ´ındices do espa¸co tempo da brana e os ´ındices relacionados somente as coordenadas da membrana s˜ao os ´ındices Romanos

minúsculos (a, b, ...i, j, k, ..., p). A dimensão extra é transversa a brana.

Considera-se a m´etrtica como sendo diagonal. Ou seja, elementos da forma dxµ_dφ _e

dtdxi _{s˜ao eliminados. Isso se deve as simetrias que o modelo leva em considera¸c˜ao. Termos}

da forma dxµ_dφ _{s˜ao eliminados devido a simetria orbifold, e termos da forma} _dtdxi _s˜ao

nulos devido as simetrias de revers˜ao temporal (t _{→ −}t) e espacial (xi

→ −xi_).

Basicamente, vamos procurar solu¸c˜oes para as equa¸c˜oes de Einstein em 5Dque estejam

de acordo com o mundo real. Ou seja, impomos que a m´etrica deve preservar a invariˆancia

de Poncar´e: O universo em 4D derivado dessa teoria deve ser plano e est´atico. Isso nos

leva a propor um Ansatz para a m´etrica da forma:

ds2 =e−2σ(φ)ηµνdxµdxν +r2cdφ2 (4.2)

Onde ηµν = dia(−1,1,1,1) é a métrica de Minkowski. O fator exponencial é colocado

nessa m´etrica propositalmente. Veremos que ele ´e quem vai fazer com que surga a

hie-rarquia entre as escala T eV e GeV. Devido o fator exponencial depender da dimensão extra, essa métrica é não fatorável. Ou seja, não podemos escrevê-la como um produto

(33)

As condi¸cões de contorno impostas sobre a métrica de fundo são:

gµνvis ≡gµν(xµ, φ=π) , gocuµν ≡gµν(xµ, φ= 0) (4.3)

Levando em considera¸cão à constante cosmológica em 5D Λ que, diferentemente da

constante cosmol´ogica em 4D, n˜ao precisa ser nula ou mesmo pequena. Vamos agora

mostrar qual a a¸c˜ao fundamental para esse modelo.

4.2 A¸c˜ao e Equa¸c˜oes de Movimento

A a¸cão que descreve esse modelo satisfatoriamente é composta por três partes: Uma

relativa a gravidade e outras duas referente as duas branas. Usamos os termosSvis eSocu

para representar as a¸c˜oes nas branas vis´ıvel e oculta, respectivamente.

S = Sgravidade+Svis+Socu (4.4)

Sgravidade =

Z

d4x

Z π

−π

dφ√₋g_{−Λ + 2M3R_}

Svis =

Z

d4x√₋gvis{Lvis−Vvis}

Socu =

Z

d4x√₋gocu{Locu−Vocu}

Para cada Lagrangeana na 3-brana temos um potencial de v´acuo que funciona como

uma fonte de gravidade. O modelo foi inicialmente construido para a gravidade pura,

dessa forma n˜ao vamos considerar que as branas possuam mat´eria, logo_Lvis=Locu = 0.

Usando o princ´ıpio de Hamilton variamos a a¸cão acima com rela¸cão a métrica do Bulk.

Variando a a¸c˜ao gravitacional, obtemos:

δSgravidade=

Z

d4x

Z π

−π

dφδgM N

Λ 2

√

−ggM N + 2M3√−g

RM N−

R 2gM N

(34)

A varia¸c˜ao das a¸c˜oes nas branas vis´ıvel e oculta tem como resultado:

δSvis=−

Z

d4x

Z π

−π

dφδgM N

−1 2

√

−gvisgvisµνδ µ Mδ

ν NVvis

δ(φ₋π) (4.6)

δSocu=−

Z

d4x

Z π

−π

dφδgM N

−1 2

√

−gocugµνocuδ µ Mδ

ν NVocu

δ(φ)

Ao juntarmos as duas equa¸c˜oes anteriores, obtemos a seguinte equa¸c˜ao de movimento:

√ −g

RM N−

1 2gM NR

=₋ 1 4M3[Λ

√

−ggM N +Vvis√−gvisgvisµνδ µ Mδ

ν

Nδ(φ−π) + (4.7)

Vvis√−gvisgµνvisδ µ Mδ

ν Nδ(φ)]

Essa é a equa¸cão de Einstein 5-dimensional. O nosso objetivo agora é resolver essa

equa¸cão usando o Ansatz para a métrica. A resolu¸cão dessa equa¸cão vai nos fornecer

a fun¸cão σ(φ) que foi proposta na métrica. Esse fator de deforma¸cão é o que vai ser responsável por gerar a hierarquia entre as duas escalas. O coeficiente rc presente na

mérica é independente de φ , ele é o raio de compactifica¸cão da dimensão extra. Usando o nosso Ansatz para a métrica 4.2. Obtemos duas equa¸cões de movimento, uma referente

a dimens˜ao extra e outra relacionada ao espa¸co 4-dimensional.

6σ′2 r2

c

= −Λ

4M3, (4.8)

3σ′′ r2

c

= Vocu 4M3_r

c

δ(φ) + Vvis 4M3_r

c

δ(φ₋π). (4.9)

A solu¸cão para a equa¸cão 4.8 consistente com a simetria orbifold φ_{→ −}φ é:

σ=rc|φ|

r

−Λ

24M3 (4.10)

,

Omitimos a constante aditiva que aparece por que ela pode ser englobada em um

rescalonamento de xµ_{. Claramente vemos que a solu¸c˜ao s´o faz sentido se Λ<0, o modelo}

(35)

da geometria AdS5. Basicamente esse é um espa¸co com constante cosmológica negativa. Calculando a primeira e a segunda derivada dessa fun¸cão obtemos:

σ′ ₌_r

csng(φ)

r

−Λ

24M3 (4.11)

σ′′ = 2rc

r

−Λ

24M3[δ(φ)−δ(φ−π)], (4.12)

substituindo 4.12 na 4.9 obtemos a seguinte rela¸c˜ao entre os pontenciais:

Vocu =−Vvis = 24M3k,Λ =−24M3k2, (4.13)

Onde M é um parâmetro de massa natural da quinta dimensão, Λ é a constante cosmológica em 5-D e k é uma escala de energia da ordem da escala de Planck. Essas rela¸cões entre os potenciais nas branas e o termo cosmológico do Bulk são necessários

para obter-se uma solu¸cão que respeite a invariância de Poincaré em 4-D. Isso é tido na

teoria como um ”fine-Tunning”. Ou seja, s˜ao termos colocados a m˜ao no intuito de obter

um universo em 4-d est´atico. Poder´ıamos escolher outros valores paraVvis e Vocu, sendo

perfeitamente poss´ıvel obtermos um universo em 4-D n˜ao plano. Ap´os substituirmos 4.10

em 4.2, obtemos nossa solu¸c˜ao final para a m´etrica do Bulk:

ds2 =e−2krc|φ|_η

µνdxµdxν +rc2dφ2. (4.14)

O raio de compactifica¸cãorc é efetivamente uma constante de integra¸cão nessa métrica.

4.3 Implica¸c˜oes F´ısicas

Embora estejamos considerando uma dimens˜ao extra em nosso modelo, evidˆencias

de dimensões, além das quatro que estamos adaptados, ainda não foram encontradas

[12]. Portanto, precisamos ver quais as implica¸c˜oes F´ısicas desse modelo. Em outras

palavras, quais os resultados que obtemos na teoria efetiva ao fazer a redu¸c˜ao dimensional?

(36)

(T eV), com os parˆametros associados com a quinta dimens˜ao; M, k e rc.

O primeiro passo é encontrar flutua¸cões sem massa em torno da nossa solu¸cão 4.14.

Isso vai nos dar o campo gravitacional da nossa teoria efetiva[12]. Eles s˜ao os modos-zero

dessa solu¸c˜ao e tˆem a forma:

ds2 =e−2kT(x)|φ|_[η

µν+hµν(x)]dxµdxν+T2(x)dφ2. (4.15)

Aqui,hµν representa flutua¸c˜oes tensoriais em torno do espa¸co de Minkowski e ´e chamado

de gráviton na teoria efetiva em 4-D. Percceba que a métrica 4.15 é localmente igual a

m´etrica 4.14 , desde que qualquer m´etrica suave em 4-D,

˜

gµν(x)≡ηµν +hµν(x), (4.16)

é localmente Minkokwskiana, enquanto que qualquer fun¸cão real suaveT(x) é localmente constante.

O raio de compactifica¸cão rc, é o valor esperado de vácuo do campo modular T(x).

Como em muitas teorias de dimensões extras, é importante que o campo modular T(x) seja estabilizado para um valor esperado de vácuo rc , com uma massa de pelo menos

10−4_eV_{. Isso é um problema essencial da teoria; estabiliza¸cão das distâncias entre as duas} branas [13] [14]. Isso será tratado com mais detalhes em um cap´ıtulo seguinte.

Para entendermos se a supressão exponencial realmente é útil para resolver o

Pro-blema da Hierarquia, precisamos saber como a escala efetiva da gravidade se comporta

com rela¸cão a dimensão extra. Obtemos essa informa¸cão ao analisarmos como a a¸cão

gra-vitacional em 5-D contˆem a a¸c˜ao gragra-vitacional em 4-D. Focamos no termo de curvatura,

pois com ele podemos obter a escala da intera¸c˜ao gravitacional. Substituindo 4.15 na

a¸cão da gravidade e fazendo as mudan¸cas necessárias na métrica, no seu determinante e

no tensor de Ricci: (˜gµν =ηµν+hµν ,g = detgM N ,√−g =rce−4krcφ√−g˜eR⊃e2krcφR)˜

obtemos:

Sef e ⊃

Z

d4x

Z π

−π

dφ2M3rce−2krc|φ|

p

(37)

onde ˜R´e o tensor de Ricci 4-dimensional obtido apartir de ˜gµν(x) , em contraste com

o tensor de Ricci R 5-dimensional, obtido de gM N(x, φ). Devido as flutua¸c˜oes em 4-D

não dependerem de φ (os campos na teoria efetiva dependem apenas de x) , podemos fazer a integra¸cão explicita em φ e obtemos uma a¸cão puramente 4-dimensional. Após a integra¸cão emφ obtemos:

M_pl2 = M 3

k [1−e

−2krcπ_], _(4.18)

este ´e um resultado importante.

Ele nos revela que a massa de Planck efetivaM2

pl , depende fracamente de rc no limite

de grandekrc. Embora a exponencial tenha um papel pouco importante na determina¸c˜ao

da escala de Planck 4-dimensional, ela tem um papel muito importante na determina¸c˜ao

do setor vis´ıvel da massa.

Para determinar a lagrangeana dos campos de mat´eria, precisamos saber o

acopla-mento dos campos nas 3-branas com os campos gravitacionais de baixa energia [12],

particularmente precisamos saber quem ´e ˜gµν. Fazendo uma transforma¸c˜ao conforme na

m´etrica , temos:

gµν =e−2krcφ˜gµν. (4.19)

E usando 4.3, obtemos:

gvis

µν = e−2krcπ˜gµν (4.20)

gvis _{= detg}vis µν =e−8

krcπ_g_˜

p

−gvis ₌ p₋_e−8krcπg˜=p−ge˜ −4krcπ_.

Vamos considerar um campo de Higgs fundamental, posssuindo a seguinte a¸c˜ao:

Svis⊃

Z

d4x√₋gvis{g µν

(38)

onde o parâmetro v0 é um parâmetro de massa. Fazendo uma renormaliza¸cão na fun¸cão de onda H _→ ekrcπ_H _e _H† _→ _ekrcπ_H† _{e utilizando as rela¸cões entre as métricas acima ,}

obtemos:

Sef e ⊃

Z

d4_xp

−g˜_{g˜µν_D

µH†DνH−λ(|H| −e−2krcπv02)2}. (4.22)

Essa é a a¸cão de um Higgs escalar normal , exceto pelo valor esperado de vácuo

(VeV) v2 ₌_v2

0e−2krcπ que é exponencialmente suprimido. Como o (VeV) nos da todos os parâmetros de massa no modelo padrão, isto significa que todos os parâmetros de massa

s˜ao submetidos a uma supress˜ao exponencial na segunda brana. Se o valor da massa do

Bóson de Higgs é da ordem da escala de Planck, o bóson de Higgs f´ısico pode ser suprimido

na escala TeV. Obtendo a seguinte massa F´ısica:

m=m0e−krcπ (4.23)

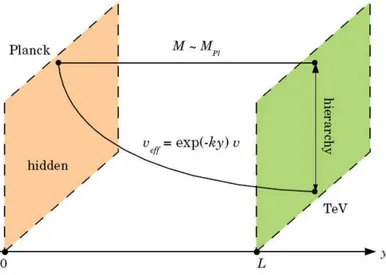
A supressão exponencial pode ser melhor entendida fazendo-se à análise da figura:

Figura 4.3: A gera¸c˜ao de uma hierarquia exponencial

(39)

Em conclusão, podemos ver que em uma teoria onde todos os parâmetros da dimensão

extra (M,Λ,Vocu,v ) s˜ao determinados pela escala de planck, uma hierarquia exponencial

´e gerada naturalmente entre a escala fraca e da gravidade. Dessa forma o modelo Randall

Sundrum fornece uma solu¸c˜ao original para o Problema da Hierarquia.

´

E importante notarmos que se tomarmos a segunda brana infinitamente distante da

segunda, a massa de Planck efetiva continua finita, veja 4.18. Isso nos revela que podemos

ter uma dimens˜ao extra infinita e ainda continuamos a sentir `a gravidade da maneira

normal. Dessa forma podemos dizer que `a gravidade est´a localizada em torno da brana em

(40)

5. Modelo Randall Sundrum Tipo II

O modelo Randall Sundrum tipo II lida, basicamente, com a gravidade. Veremos que

a gravidade como sentimos no nosso mundo ´e dada, quase que totalmente, pelo modo zero

de Kaluza-Klein (gráviton). A contribui¸cão dos outros modos de K.K são insignificantes,

pelo menos, para os experimentos que conseguimos realizar at´e o momento. Veremos que

no limite Newtoniano, o modelo reproduz, em 4-D, o potencial Newtoniano. Mostrando

assim que o mesmo ´e consistente.

5.1 Modos Gravitacionais

Para entendermos como a gravidade funciona no modelo Randall Sundrum temos que

encontrar expressões para os grávitons, que são pequenas flutua¸cões em torno da métrica

de fundo dada por:

ds2 =e−2k|y|ηµνdxµdxν +dy2, (5.1)

observe que fizemos a seguinte mudan¸ca na m´etrica;dy=rcdφerc|φ|=|y|. As express˜oes

expl´ıcitas para o gráviton serão encontradas através da solu¸cão das equa¸cões de Einstein

linearizadas.

Por conveniˆencia, trabalharemos com uma m´etrica conformalmente plana (

proporci-onal ao espa¸co plano). Para fazermos isso definimos uma nova variável para à dimensão

extra, z, relacionada comy da seguinte forma:

(41)

integrando essa equa¸c˜ao, obtemos como resultado:

e−2k|y|= 1

(k_|z_|+ 1)2. (5.3)

Com essa nova coordenada a m´etrica ´e dada por

ds2 = 1

(k_|z_|+ 1)2(ηµνdx

µ

dxν+dz2).

Para enfatizarmos o fato de a m´etrica ser conformalmente plana reescrevemo-a como

ds2 =e−2A(z)ηM NdxMdxN.

Usamos x5 ₌_z _{e a fun¸c˜ao} _{A(z) dada por:}

e−2A(z) = 1

(k_|z_|+ 1)2, (5.4)

e dessa formaA(z) = ln(k_|z_|+ 1).Como vamos precisar mais adiante, daremos a primeira e a segunda derivada deA(z) :

A′(z) = sgn(z)k

k_|z_|+ 1 (5.5)

e

A′′(z) = 2k(δ(z)−δ(z−Lz)) k_|z_|+ 1 −

k2

(k_|z_|+ 1)2. (5.6)

5.2 Equa¸c˜oes de Einstein Linearizadas

Para continuar nossos c´alculos vamos trabalhar com as equa¸c˜oes de Einstein

lineari-zadas. Quando duas métricas estão relacionadas por uma transforma¸cão conforme,veja

(42)

Einsteins relacionados:

GM N(gM N) = ˜G(˜gM N) + (n−2)[ ˜∇MA∇˜NA+ ˜∇M∇˜NA− (5.7)

˜

gM N( ˜∇R∇˜RA−

n₋3

2 ∇˜RA∇˜

R

A)],

ondené o número de dimensões espaciais. Nesse caso a métrica perturbada tem a seguinte forma

gM N =e−2A(ηM N+hM N) (5.8)

en = 5, dessa forma o tensor de Einstein tem como resultado,

GM N = ˜GM N+ 3[∂MA∂NA+∂M∂NA−Γ˜RM N∂RA (5.9)

−g˜M N(∂R∂RA−Γ˜RRS∂ S

A₋∂RA∂RA)].

O simbolo de Christoffel de ordem linear ´e facilmente encontrado, basta aplicarmos

˜

gN M =ηM N+hM N na sua forma tradicional, e encontramos:

˜ ΓRM N =

1 2(∂Mh

R

N +∂NhRM −∂ R

hM N), (5.10)

aqui usamosηM N _{para levantar ´ındices. Para simplificar os c´alculos vamos trabalhar com}

alguns gauges importantes. São eles: as flutua¸cões não têm componentes na dimensão

extrahM5 = 0, as flutua¸cões que geram o gráviton são perpendiculares ao mesmo∂µhµν =

0 e o tra¸co dessas flutua¸c˜oes ´e nulo ηµν_h

µν =hµν = 0.

As flutua¸cões em torno da métrica de Minkowski representam um tensor simétrico

5x5 , hM N. O mesmo possui 15 graus de liberdade. No entanto, levando em considera¸c˜ao

os gauges acima ralatados, o n´umero de graus de liberdade das flutua¸c˜oes tensoriais se

reduz de 15 para 5. Ainda levando em considera¸c˜ao esses gauges, o segundo s´ımbolo de

Christoffel em (5.9) anula-se. Enquanto que o primeiro se reduz a 1 2∂

5_h

M N. Al´em do

(43)

por :

˜

GM N =−

1 2∂R∂

R

hM N. (5.11)

Nosso pr´oximo passo ´e calcular a componente µν do tensor de Einstein linearizado. SubstituindoM N por µν, os simbolos de Christoffel e calculando as derivadas em (5.9) :

Gµν =−

1 2∂R∂

R_h µν +

3 2h

′

µνA

′

−3(ηµν+hµν)(A′′−A′2). (5.12)

Agora temos que calcular o outro lado da equa¸c˜ao de Einstein GM N = k2TM N. Ou

seja, temos que calcular o tensor de energia momento para `a m´etrica pertubada. Tendo

aten¸c˜ao no fato de que o determinante da m´etrica induzida na brana esta relacionado com

o determinente da m´etrica completa por:

gM N = e−2Ag˜M N (5.13)

g = e−2Agi

√

−gi = eA√−g,

onde i = 1,2 são ´ındices referentes as duas branas. Os ´ındice 1 esta relacionado com a brana oculta e o ´ıdice 2 com a brana vis´ıvel. As a¸cões nas branas são agora dadas por:

Socu = −

Z

d4x√₋geA(z)Vocu =−

Z

d4x

Z

dz√₋geA(z)Vocuδ(z) (5.14)

Svis = −

Z

d4x√₋geA(z)Vvis=−

Z

d4x

Z

dz√₋geA(z)Vvisδ(z−Lz).

Usando a defini¸c˜ao do tensor energia momento :

TM N =−

2 √

−g δSM

(44)

podemos calcular os tensores de energia momento em cada brana. S˜ao eles:

Tµνocu = −e A(z)_V

visδ(z)gµν (5.16)

Tµνvis = −e A(z)_V

ocuδ(z−Lz)gµν.

Dessa forma, levando em considera¸c˜ao a constante cosmol´ogica Λ em 5-D, a segunda parte

da equa¸c˜ao de Eisntein ´e:

k2Tµν =

1

4M3[−Λ−Vocue

A(z)_δ(z)

−VviseA(z)δ(z−Lz)]gµν. (5.17)

Lembrando das rela¸c˜oes Vvis = −Vocu = 24M3k e Λ = −24M3k2 , bem como 5.5 , 5.6 e

5.8 temos:

k2Tµν = [6k2e−2A−

Vvis

4M3e −A

(δ(z)₋δ(z₋Lz))](ηµν +hµν) (5.18)

k2_T

µν = [6A′2−

Vvis

4M3e

−A_(δ(z)

−δ(z₋Lz))](ηµν+hµν)

k2Tµν = 3(A′2−A′′)(ηµν+hµν).

Juntando 5.12 com `a equa¸c˜ao anterior:

−1₂∂R∂Rhµν+

3 2h

′

µνA′(z) = 0. (5.19)

5.3 Equa¸c˜ao Tipo Schrodinger

Uma forma de resolver 5.19 ´e transformando-a numa equa¸c˜ao tipo Schrodinder. Para

fazermos isso temos que nos livrar das primeiras derivadas h′

µν, atrav´es do seguinte

rees-calonamento:

(45)

ondeαé uma constante. Resolvendo a primeira parte da equa¸cão 5.19 referente a ´ındices da dimensão extra:

−1 2∂5∂

5_h

µν =−

1 2e

αA_[αA′′_h

µν + 2αA′h′µν+α2A′2hµν+h′′µν]. (5.21)

A parte relativa ao espa¸co tempo, ainda relacionado a primeira parte da equa¸c˜ao 5.19 ´e

dada por:

−1₂∂λ∂λhµν =−

1 2e

αA

∂λ∂λhµν. (5.22)

O segundo termo de 5.19, fica

3 2h

′

µνA

′_{(z) =} 3 2e

αA_(αA′2_h

µν+h′µνA

′_(z)). _(5.23)

Juntando 5.21, 5.22 e 5.23 e ap´os algum algebrismo, chegamos em

−1 2∂R∂

R₊

3 2 −α

A′h′_µν +

3 2α−

1 2α2

A′2₋ 1 2αA

′′

hµν = 0 (5.24)

Escolhemos α= 3₂, de modo `a anular h′

µν, obtendo:

−1 2∂R∂

R_h µν+

9 8(A

′₎2 − 3

4A ′′

hµν = 0 (5.25)

Fazemos agora uma redu¸c˜ao de Kaluza-Klein para quatro dimens˜oes. Para fazer isso,

precisamos aplicar uma separa¸cão de variáveis. Escrevemos as flutua¸cões gerais como uma

superposi¸c˜ao de modos :

hµν(x, z) =

∞

X

n=0 hn

µνψn(z), (5.26)

e fazendo a redu¸c˜ao chegamos nas duas equa¸c˜oes:

hnµν =m2nh n

(46)

e

−ψ′′n(z) +

9 4A

′2_(z)

−3₂A′′(z)

ψn(z) = m2nψn(z) (5.28)

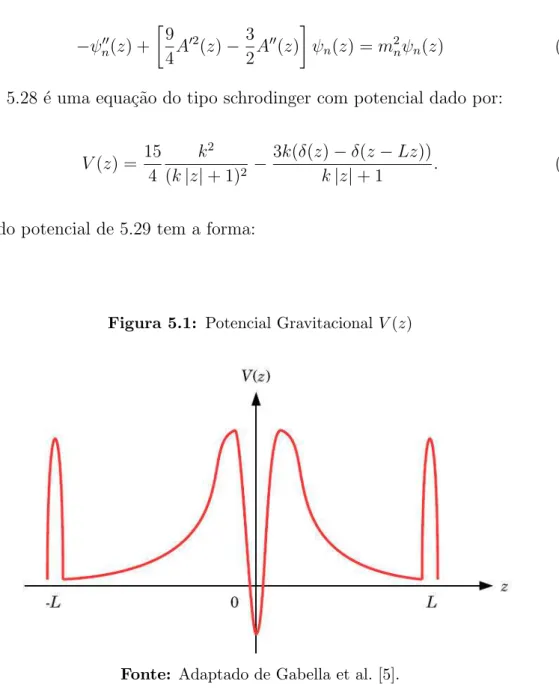
A equa¸cão 5.28 é uma equa¸cão do tipo schrodinger com potencial dado por:

V(z) = 15 4

k2

(k_|z_|+ 1)2 −

3k(δ(z)₋δ(z₋Lz))

k_|z_|+ 1 . (5.29)

O gr´afico do potencial de 5.29 tem a forma:

Figura 5.1: Potencial GravitacionalV₍z₎

As condi¸cões de contorno que as solu¸cões da equa¸cão 5.28 vão obedecer, são obtidas

integrando-se essa equa¸c˜ao para pequenos dom´ınios em torno das branas. Para a brana

em z = 0 temos:

Z 0+

0−

dz(₋ψ_n′′+V ψn) =

Z 0+

0−

dzm2ψn

(47)

A fun¸cão de onda tem que ser uma fun¸cão par sob a transforma¸cão z _{→ −}z, isso devido a simetria orbifold. Dessa forma, a derivada primeira da fun¸cão é ´ımpar: ψ′

n(0−) =

−ψ′

n(0+). A condi¸cão de contorno na brana em z = 0 é então:

ψ′

n(0) =−

3k

2 ψn(0). (5.30)

De forma similar, chegamos a condi¸c˜ao de contorno na branaT eV :

ψ′n(Lz) = −

3k

2(kLz+ 1)ψn(Lz). (5.31)

5.3.1 Modo-zero

O modo-zero é a solu¸cão de uma equa¸cão tipo Shcrodinger com mn= 0;

−ψ0+

9 4A

′2

− 3₂A′′

ψ0 = 0. (5.32)

Fazendoψ0 =eλA _{e substituindo em 5.32, obtemos :}

λ+ 3 2

A′′+A′2

λ2₋ 9 4

= 0.

Isso nos mostra queλ=₋3₂. Ou seja,ψ0(z) =e−3

2A(z), ou ainda:

ψ0(z) = (k|z|+ 1)− 3

2. (5.33)

Vemos que o modo zero tem uma fun¸cão de onda cujo pico ocorre emz = 0 [5]. Como iremos ver, as intera¸cões gravitacionais são mediadas predominatemente pelo modo-zero.

A gravidade ´e ent˜ao localizada na brana de Planck, enquanto que na brana TeV sentimos

apenas a ”cauda”dessa fun¸c˜ao de onda. Dessa forma, no modelo Randall-Sundrum, a

explica¸c˜ao para a fraqueza da gravidade est´a relacionada ao fato dela estar localizada

longe de onde vivemos. Isso contrasta com o modelo ADD, que explica a fraqueza da

gravidade devido ela se diluir no grande volume da dimens˜ao extra.

(48)

localizado, veja figura abaixo. Para fazermos isso vamos considerar a a¸c˜ao de

Einstein-Hilbert em 5-D

Z

d5x√₋gR, (5.34)

com o tensor de Ricci dado por sua forma linearizada R _∼ h _∼ ηµν

hµν , e com as

devidas modifica¸cões no determinante da métrica devido a transforma¸cão conforme.

O modo zero ´e normaliz´avel, isso significa que podemos fazer

Z ∞

−∞

dz_|ψ(z)_|2<_∞ (5.35)

Z

dze−3A

Z

d4xe−Ap₋˜gηµνhµν

Z

dze−4A

Z

d4_x√₋_gR.

Integrando na dimens˜ao extra, obtemos:

Z L

0

dze−4A =

Z L

0

dze−4ln(k|z|+1) (5.36)

Z L

0

dze−4A = ₋4

k{1 + (k|z|+ 1)[ln(k|z|+ 1)−1]}.

(49)

Figura 5.2: Localiza¸c˜ao do gr´aviton em torno da brana de Planck

5.3.2 Modos Massivos

A fun¸c˜ao de onda para os modos massivos de KK ´e:

−ψ”n(z) +

15 4

k2

(k_|z_|+ 1)2 −

3k(δ(z)₋δ(z₋Lz)) k_|z_|+ 1

ψn(z) =m2nψn(z). (5.37)

Com excessão do modo zero, que tem energia zero, os outros modos de KK não estão

ne-cessariamente localizados nas branas, dessa forma eles podem estar ao longo da dimens˜ao

extra. Resolveremos agora a equa¸c˜ao 5.37 na regi˜ao fora das branas.

Dessa forma `a equa¸c˜ao 5.37, fica:

ψn′′(z) +

m2n−

15k2 4(k_|z_|+ 1)2

ψn(z) = 0. (5.38)

Essa é uma equa¸cão de bessel de segunda ordem, cuja solu¸cão geral é dada por:

ψn(z) =

|z_|+1 k

1₂

ζ2

mn

|z_|+ 1 k

. (5.39)

(50)

solu¸c˜ao geral ´e dada por:

ψn(z) =

|z_|+ 1 k

12 anJ2

mn

|z_|+ 1 k

+bnY2

mn

|z_|+ 1 k

. (5.40)

Aquian e bn s˜ao coeficientes a serem determinados.

Para determinar esse coeficientes usamos os limites assintóticos deJ2 eY2 para peque-nos valores demn|z|, a condi¸cão de contorno 5.30 e uma mudan¸ca de variávelU =|z|+_k1.

No limite assint´otico para valores pequenos de mn|z| encontramos os valores de J2 e Y2

dados por:

J2

mn

|z_|+ 1 k ≈ m 2 n 8

|z_|+ 1 k 2 (5.41) Y2 mn

|z_|+ 1 k

≈ −1_π − _π1 4 m2

n |z|+1k

2.

Com esses resultados e a mudan¸ca de vari´avelU =_|z_|+ 1

k , o que leva a dU

dz = sng(z),

e fazendo sng(z) = 1 , pois estamos considerando a região à direita da brana em y = 0, encontramos os seguintes resultados para a fun¸cão de onda e a derivada primeira dos

modos de KK :

ψn(z) =

|z_|+ 1 k

1₂ (

an

m2

n

8

|z_|+ 1 k

2

−bn

1 π + 1 π 4 m2

n |z|+ 1k

2 !)

(5.42)

ψ_n′(z) = 1 2

|z_|+ 1 k

−12

( an m2 n 8

|z_|+1 k

2

−bn

1 π + 1 π 4 m2

n |z|+1k

2 !)

+ (5.43)

|z_|+ 1 k

1₂ (

an

m2

n

8

|z_|+ 1 k

+bn

8 πm2

n

1 |z_|+ 1_k3

)

E usando a condi¸c˜ao de contorno 5.30, encontramos o seguinte valor para an:

an =

4k2_b

n

m2

nπ

(51)

Dessa forma ficamos com a fun¸c˜ao de onda dada por:

ψn(z) =Nn

|z_|+ 1 k

12 Y2

mn|z|+

1 k + 4k 2 m2 nπ J2 mn

|z_|+ 1 k

. (5.45)

Onde Nn ´e uma constante de normaliza¸c˜ao. Como _mk_n>1 o termo com J2 domina a

express˜ao da fun¸c˜ao de onda.

Usando a condi¸c˜ao de normaliza¸c˜aoRL

−L|ψ|

2

dz = 1 , encontramos:

Nn =

r π 2 πm 5 2 n

4k2√_L. (5.46)

Dessa forma à aproxima¸cão para à fun¸cão de onda dos estados de KK no limite de grande

mn|z| ´e:

ψn(z) =

cos mn|z| − 5₄π

√

L . (5.47)

5.4 Espectro Gravitacional

Se considerarmos as duas branas, teremos duas condi¸c˜oes de contorno. Dessa forma,

podemos quantizar as massas dos modos de KK. A derivada da fun¸c˜ao de onda 5.40, sem

considerar as aproxima¸c˜oes feitas nos limites de grande e pequenomn|z|´e, de acordo com

[16], dada por:

ψ′

n(z) =mn

|z_|+ 1 k

12 anJ1

mn

|z_|+ 1 k

+bnY1

mn

|z_|+ 1 k + (5.48) −3 2

|z_|+ 1 k

−12 anJ2

mn

|z_|+ 1 k

+bnY2

mn

|z_|+ 1 k

.

Utilizando as condi¸c˜oes de contorno 5.30 e 5.31, juntamente com a equa¸c˜ao acima,

obtemos a seguinte equa¸c˜ao:

J1 m_n k Y1 mn

|z_|+ 1 k

−Y1

m_n k J1 mn

|z_|+ 1 k

= 0. (5.49)

(52)

di-mens˜ao extra, lembrando a equa¸c˜ao 5.4, temos:

z+ 1 k ≈

ekz

k . (5.50)

Podemos escrever ent˜ao:

J1

mn

|z_|+ 1 k ≈J1 mn ekz k (5.51) Y1 mn

|z_|+ 1 k ≈Y1 mn ekz k .

Na aproxima¸c˜ao para massas pequenas mn

k ≪ 1, as fun¸c˜oes de bessel do primeiro tipo

comportam-se, como:

J1mn k

≈ m_kn (5.52)

Y1mn k

≈lnmn 2k

m_n

k .

Numericamente ₋Y1(x) ≫ J1(x). Como m_kn ≪1 o primeiro termo em 5.49 ´e nulo, e no segundo, devido₋Y1(x)_≫J1(x) , temos que:

J1

mn

|z_|+ 1 k

= 0 (5.53)

J1 mn ekL k = 0

Jn=

mnekL

k mn=e−kLJnk

OndeJn s˜ao so zeros da fun¸c˜ao de bessel J1(Jn) = 0 .

Como k ´e um valor da ordem da escala de Plack, e o fator exp(₋kL) na brana TeV foi fixado para resolver o problema da hierarquia, as massas dos estados de KK s˜ao da

ordem de TeV. Isso implica na possibilidade da observa¸c˜ao de ressonˆancias individuias