Localização de campos em membranas deformadas

Loalização de ampos em membranas deformadas

WilamiTeixeira da Cruz

UNIVERSIDADE FEDERAL DO CEARÁ

DEPARTAMENTO DE FÍSICA

WilamiTeixeira da Cruz

Tese submetida ao Departamento de Físia

omo requisito para obtenção do grau

de Doutor em Físia.

Orientador

à minha família,a

fonte de toda minha

Gostaria de agradeer a todos que ontribuírampara aonlusão deste trabalho.

Ao professor Dr. Carlos Alberto Santos de Almeida pela orientação e pelos grandes

onselhos.

Todaminha famíliapeloapoiopermanentee inondiional.

Aos meus pais por mesmo depois de muito tempo terem aeitado minha esolha

prossional.

Agradeço àminha noiva Joelma pelapaiênia.

Ao professorDr. Riardo Renan Landimpelas disussões.

Ao professorDr. Adalto Gomes pelaajuda naparte omputaional.

AoprofessorDr. Makarius Oliveira Tahimpelas disussõese importanteolaboração

durante o urso.

AosolegasdoLASSCO,Ivan(brother),Vitor, Alex,Diego,Luis, Hudson, Wagner,

Luiana,Mário, Gonzaga eEulides.

Ao professorDr. Juselino Silvapelas onversas e exemplo de vida.

Aosprofessores do Departamento de Físia daUFC.

Aosfunionários dodepartamento de Físia daUniversidade Federal doCeará.

À oordenação do urso de pós-graduação emFísia daUFC.

À pró-reitoria de Pesquisa e Inovação do IFCE.

Analisamos o omportamento de ampos de vários ranks em modelos de dimensões

extras e enários de membranas om estrutura interna. Trabalhamos em um

espaço-tempo AdS (anti de Sitter) de ino dimensões onde o fator de warp é denido em

termos de uma função suave daquinta oordenada.

O fator de warp, assim omo o bakground, são obtidos a partir da deformação de

modelos de membrana grossa. Tal enário imitaos modelos de Randall-Sundrum (RS),

quepodemserobtidossobertolimite. Noentanto,avantagemdemodelosdemembrana

grossa é querepresentam versõesnão-singulares de enários RS(Randall-Sundrum).

Apartirdaaçãodeaoplamentodeumampoesalarrealomgravidadedesrevemos

ageometriadoenárioapartirdasequaçõesde Einstein. Enontramosentão,apartirde

um potenial

λφ

4

, soluçõesdo tipo kink para o ampo esalar que representa a própria

membrana. Nesse aso, a solução interpola assintotiamente dois espaços

AdS

, omo uma parede de domínio.

A partirde um proedimentodedeformação nopotenial,podemosobteruma lasse

de soluções de membrana. A vantagem desses novos modelos é que apresentam uma

estrutura interna. As soluções também interpolam dois espaços

AdS

om uma nova estrutura de transição entre osdomíniosonde o ampo esalarassume valornulo. Essas

estruturas têm inuênia na geometria do enário e onsequentemente nos métodos de

loalização.

Nesse enáriode membrana,obtivemosnovosresultadossobrealoalizaçãode modos

zero para o ampo esalare para ampos ferminios. Quando tomamosos modos

mas-sivos resultantes das omponentes dos ampos na quinta dimensão, enontramos novas

estruturas de ressonânia. Tais estruturas nos auxiliam aentender a relação dos modos

sorial de gauge. Nesses asos, para garantir aloalizaçãodos ampostivemos que

intro-duzir no enário um novo ampo esalar, o dílaton. Neste ponto proedemos om uma

nova análise sobre a interação do dílaton om a estrutura deformada. O meanismos

de loalização dos ampos de gauge e de Kalb-Ramond são diretamente afetados pela

estrutura interna damembrana. Novamente, analisando oespetro massivo,detetamos

signiativasalteraçõesnos poteniaisdaequação de Shroedingerresultante quandoos

omparamos om modelos de membrana grossa usuais. Detetamos estruturas de

resso-nânia no espetro massivo para o ampo de gauge. Estruturas semelhantes apareem

We analyze the behavior of elds of various ranks in models of extra dimensions and

senarios ontainingmembraneswith internalstrutures. Forthispurpose westartfrom

a ve dimensions AdS spae-time where the warp fator is dened interms of a smooth

funtion of the fth oordinate.

The warp fator, as well as the bakground, are obtained from the deformation of

thik brane models. This senario mimis the Randall-Sundrum senario (RS), whih

an be obtained under ertain limit. However, the advantage of thik brane models is

that they represent a non-singularversion of RS (Randall-sundrum)senarios.

Startingfromtheationwiththeouplingofarealsalareldandgravitywedesribe

the spae-timegeometryfromthe Einstein'sequation. Choosing a

λφ

4

potential,wend

kink-like solutions for the salar eld that represents the membrane itself. In this ase,

the solution interpolatestwo asymptotiallyAdS spaes,suh asa domain wall.

From adeformation proedure of the potential, we obtain alass of brane solutions.

The advantage of these new models is that they host internal strutures. The solutions

also interpolate two AdS spaes with a new transition struture where the salar eld

has zero value between the domains. These strutures have inuene on the senario's

geometry and thereforethe loalizationmethods.

In this brane senariowe obtained new results on the loation of zero modes for the

salar andfermioni elds. Takingthe massive modes resultingfromthe fthdimension

omponents of the elds, we nd new resonane strutures. These strutures help usto

understand the relationship of massivemodes with the membrane.

New results were also obtained when we take the vetor and tensor gauge elds.

In suh ases, to ensure the loation of these elds, we had to introdue a salar eld

on the senario, the Dilaton eld. At this point we proeed with a new analysis of

Again, analyzing the massive spetrum, we deteted signiant hanges inthe potential

of the resulting Shroedinger's equation when ompared with models of usual branes.

Resonane strutures are deteted in the spetrum for the massive gauge eld. Similar

strutures appear in the study of the Kalb-Ramond eld by the two detetion methods

Agradeimentos . . . i

Resumo . . . ii

Abstrat . . . iv

Conteúdo . . . 1

Introdução 4 1 Interação gravitaional 14 1.1 Campo esalar. . . 16

1.2 Espinorde Dira . . . 18

2 Membrana gerada por kink 21 2.1 Introdução . . . 21

2.2 A membrana omo kink . . . 22

3 A estrutura de membrana deformada 30 3.1 Motivação . . . 30

3.2 Oproedimentode deformação . . . 31

4 Loalização de ampo esalar 36 4.1 Modozero de ampoesalar . . . 36

5 Férmions 47

5.1 Motivação . . . 47

5.2 Modozero . . . 48

5.3 Modos massivos . . . 53

5.4 Ressonânias . . . 60

5.4.1 Quiralidade direita . . . 61

5.4.2 Quiralidade esquerda.. . . 67

5.5 Disussão de resultados . . . 69

6 Membrana deformada dilatnia 71 6.1 Motivação . . . 72

6.2 Adiionando o dílatonao enário . . . 73

6.3 Métodosuperpotenial . . . 75

7 Campo de gauge 78 7.1 Motivação . . . 78

7.2 Loalizaçãonamembrana deformada . . . 80

7.3 Modozero namembranadilatnia . . . 82

7.4 Modos massivos . . . 86

7.5 Ressonânias . . . 90

7.6 Disussão dos resultados . . . 93

8 Campo de Kalb-Ramond 96 8.1 Motivação . . . 97

8.2 Modozero namembranadeformada. . . 97

8.5 Modomassivo namembrana deformadadilatnia . . . 103

8.6 Disussão dos resultados . . . 106

Conlusões e Perspetivas 109

Apesar de não existir nenhuma evidênia experimental de que o nosso universo possui

mais do quequatro dimensões, teorias de dimensõesextras têm sido ada vez mais

usa-das para resolver problemas em físiade altas energias. Um universo quadridimensional

possui araterístias importantes omo a renormalizabilidadede teorias de gauge para

as interações fraa, forte eeletromagnétia. No entanto,é possívele bastante instrutivo

onstruir tais teorias em modelos de universo om mais ou menos doque o padrão

qua-dridimensional. Podemos itar por exemplo o estudo de vórties em sistemas planares

(2+1)D e suas apliações em físia da matéria ondensada, espeíamente em

super-ondutividade [1℄. Por outro lado, onsiderar aexistênia de dimensões extras tem sido

uma importanteferramentateória para a solução de problemas emteorias om quatro

dimensões. Namesmamedida,ointeressenarealizaçãodeexperimentosapazesde

reve-lara existêniadessas dimensões adiionaistem aumentado nos últimosanos. Emfísia

de altas energias, a prinipal motivaçãopara o estudodesses tópios resultada proura

por uma teoriaapaz de uniargravidade om as outrasforças fundamentais.

O primeiroesforço noontexto de uniação de gravidadeom eletromagnetismovia

dimensõesextras foiexeutado porKaluza[2℄eKlein [3℄. Aidéia adotadafoionsiderar

um espaço plano om ino dimensões, sendo quatro espaiaise uma temporal, om um

ampo gravitaional de 15 omponentes. No espaço-tempo quadridimensional (3+1),

esses 15 graus de liberdadeforam deompostos entre um tensor de rank 2 assoiado ao

mais dimensões, o modelo de Kaluza-Klein (KK) onsidera a idéia de dimensões extras

ompatas sendo representadas por uma esfera

S

1

de raio mirosópio. Esta esolha

promove a disretização dos auto-modos da teoria ujas massas são relaionadas om

o raio de ompatiação, os quais são os hamados modos KK. Neste modelo, estes

estadosexitadossãotão pesadosqueultrapassamoslimitesde energiaalançadospelos

aeleradores atuais.

Uma outra vertente de pesquisas onsiderando universos multidimensionais surgiu

nos anos 60 a partir do estudo de espalhamento de hádrons. Neste enário, um modelo

de ressonânia dupla foi desrito [4℄, sendo que o espetro dos estados no modelo foi

veriado ser reproduzido pelo espetro de uma orda vibrante. A motivação referente

a dimensões extras é devido ao fato de o modelo ser onsistente om 26 dimensões se

bosnio ou 10 se supersimétrio. Conheida atualmente omo teoria de ordas, foi

iniialmenteestabeleidaparadesreverinteraçõesfortestendouma esalahadrniada

ordem de Gev, esalaesta denida pelatensão da orda. Neste pontoa presença de um

modonão massivode spin2,sempartíulahadrniaequivalenteonheida,mostrava-se

inonsistente. Foientão quesepropsrelaionar talmodoomográviton, substituindo,

então, a esala hadrnia pela esala de Plank gravitaional

M

P L

= 10

19

_Gev

. A partir

desta substituição, a teoria de ordas foi então reformulada dando origem à primeira

fusão da teoria gravitaional om a meânia quântia. As dimensões adiionais são

regularmente mirosópias devido a esala natural de omprimento ser da ordem da

esala de Plank de

10

−33

_cm

. Outro ponto importante é que as massas dos estados

exitados são da ordem da esala de Plank

M

P L

, o que infelizmente impossibilita a teoria de ser testada experimentalmente. No entanto, om os desdobramentosda teoria

de Kaluza-Klein apliadas à inlusão de teorias de Yang-Mills em supergravidade, os

Em outra linha de idéias, modelos de dimensões extras surgiram num ontexto de

quebra espontânea de simetria por ampo de Higgs em teorias de gauge não abelianas.

Nesse aso, a dependênia espaial do valor esperado para o ampo de Higgs demanda

por defeitos topológios para modelar partíulas elementares [5, 6℄. Tal motivação foi

resultado dosurgimentode modelos emqueo universo quadridimensionalédesritopor

um defeito tipo parede de domínioo qual está ontido em um mundo multidimensional

[7℄. Nesse aso todaamatériadomodelopadrãoéonnada àparedede domínio,oque

oulta adimensão omplementar paraas forças forte,fraae eletromagnétia. Omesmo

não pde ser feito para gravidade, o que nesse aso, restringe qualquer dimensão extra

à uma esala mirosópia. Esta éa idéia primordialdo que onheemos sobre modelos

de mundos de membranas ou brane-worlds. Posteriormenteum tipo similar de parede

de domíniofoi onsiderado emteorias de superordas sendo adotada omo o loal onde

terminamas ordas [8℄. Osreferidos defeitos aram onheidos nessa onjetura omo

D-branes, onde o D diz respeito às ondições de ontorno de Dirihlet. Nesse aso o

tamanhoda dimensão extra também é onsiderado mirosópio.

Ooneitodedimensõesextrasmirosópiasfoiiniialmentevioladoomasidéiasde

Arkani-Hamed, Dimopoulos e Dvali(ADD) [9℄ sobre as vantagens de onsiderar

dimen-sõesomplementaresdetamanhoonsiderável. Omodeloespeulainlusivesobreo

tama-nhopermitidoparataisdimensões,tendoomoprinipalpropósitosoluionaroproblema

dehierarquia. Oreferidoproblemadizrespeitoàgrandedisrepâniaentreasesalas

gra-vitaionaisde massa eletrofraa

M

EF

= 10

3

_GeV

ede Plank

M

P L

= 10

19

_GeV

. A esala

dePlankédenidapelaequivalêniaentremassaeenergiaapartirdamassadePlank,

que por sua vez é representada pela unidade de massa no sistema natural de unidades.

Mais preisamente esse valor de massa é dado por

m

p

=

q

~

_c

de Plank reduzida. A esala eletrofraa por sua vez é determinada por

v

= (

G

F

√

2)

1

/

2

onde

G

F

é aonstante de Fermi.

Um aspeto interessantedo modelo ADD é que apesar de serem ompatiadas, as

n

dimensões espaiais extras possuem um raio omum não neessariamente mirosó-pio. Outro ponto importante é que neste enário de mundo om

(4 +

n

)

dimensões, a gravidade é ontrolada pela esala eletrofraa ao invés daesala de Plank, obviamente

om intenção de uniar as interações gravitaional e eletrofraa. As linhas de uxo

gravitaionalpodempotenialmentearonnadasaonossomundoquadridimensional,

sendoqueo potenialgravitaionalem

M

(3 +

n,

1)

entre dois orposestátiosde massas

m1

e

m2

,

V

(

r

) =

m1m2/M

n

+2

P L

(4+

n

)

r

n

+1

é onvertido em

V

(

r

) =

m1m2/M

n

+2

P L

(4+

n

)

rR

n

om

M

(3

,

1)

_×

S

n

. Isto resulta em um aoplamento gravitaional quadridimensional dado por

M

2

P L

=

M

P L

n

+2

(4+

n

)

R

n

, onde devemos ter

M

P L

(4+

n

)

∼

M

EF

. Como

M

P L

é da ordem de

10

19

_GeV

, o valor

n

= 1

, que resulta em

R

∼

10

13

_cm

, deve ser desartado para não

haver disordânia om o observado experimentalmente na gravidade de Newton nessa

esala de distânia. No entanto,

R

assume valores da ordem de milímetrospara

n

= 2

, o que é importante porque nesta esala de omprimento, a gravidade nuna tinha sido

testada. Aslinhas de uxogravitaionalpodemempriípiovazarpara dimensõesextras

manifestando-se omo modiações em esala milimétria para gravidade em 4

dimen-sões. Com os grávitons propagando-se nas dimensões adiionais, os ampos do modelo

padrão devem ser loalizadosemuma variedade quadridimensional. Estes fatoszeram

surgir a possibilidade de detetar em aeleradores de partíulas, no aso de duas

di-mensões extras, modiações na lei de gravidade Newtoniana em nível milimétrio. As

idéias aima foram posteriormente estendidas ao oneito de membranas originário de

teorias de ordas a partir do trabalho [10℄ de Antoniadis,Arkani - Hamed, Dimopoulos

e Dvali em (1998), e ganharam assim mais abrangênia. O setor gravitaional onsiste

sões podemteoriamente ser testadas pelaperda de energia levada pelos grávitons para

fora da membrana. Apesar de até 2003 [11℄ não terem sido detetadas disrepânias a

nível milimétrioou sub-milimétrio na teoria Newtoniada de gravidade, o trabalho de

Arkani-Hamed, Dimopoulos eDvali fez surgir,pelomenos teoriamente, a possibilidade

de experimentarevidêniasde dimensõesextrasemníveisde energiaedistânia

alançá-veis atualmente. Infelizmente, apesar do formalismoADD soluionar a hierarquiaentre

asesaladePlankeeletrofraa,introduzumanovahierarquiaentreasesalaseletrofraa

e de ompatiação.

Uma solução mais ompleta para oproblema de hierarquia foi apresentada por Lisa

Randall e Raman Sundrum em 1999 (RS-I) [12℄, e podemos itar omo aspetos mais

importantes domodelo:

1. existênia de apenas uma dimensão extra não mirosópia ompatiada, uma

variedade de simetria

Z2

, na qual pontos opostos da quinta dimensão são identi-ados;

2. duas membranasloalizadasempontos diametralmenteopostos dessa variedade;

3. a geometria do volume multidimensionalnão é mais onsiderada plana. Ao invés

disso adota-seuma geometria de ino dimensõesanti-de Sitter;

4. umahierarquiaexponenial,gerada pelamétria,determinaaesala fraaapartir

daesala de Plank.

A métriautilizadanão é fatorizávele aparte quadridimensionalémultipliadapor um

fator de warp, que é função da dimensão adiional,

ds

2

₌

_e

−2

kr

c

φ

_η

µν

dx

µ

dx

ν

+

r

2

c

dφ

2

, onde

x

µ

M

_{P L}

2

=

M

3

k

[1

−

e

−2

kr

c

π

_]

_,

(1)

onde

M

éaesala fundamentalem

5

D

. Ovalorde

M

P L

,nolimitequando

kr

c

égrande, depende muito pouo de

r

c

. Dessa forma, a exponenial tem muito pouo efeito na determinação da esala de Plank e teremos

M

P L

∼

M

∼

k

. Ao invés da supressão ser regulada pelo tamanho da dimensão extra omo no formalismo ADD, neste enário, a

supressão é dada pela urvatura do espaço fora da membrana que atua omo um meio

refrativo para o ampogravitaional. Outro ponto importanteé que a partir daanálise

dateoria efetiva para o ampo de Higgs om a métrianão fatorizávelhega-se a esala

T ev

om

kr

c

≈

10

e sem grandes hierarquias entre outros parâmetros fundamentais. A onguração de duas membranas do enário de Randall Sundrum (RS-II) foi

al-terada em [13℄ introduzindo-se a idéia de uma dimensão extra de tamanho innito. A

gravidade quadridimensional Newtoniana bem omo da relatividade geral puderam ser

reproduzidas nesse ontexto. Para entender melhor o enário RS-II (Randall Sundrum

II), podemos relembrar o enário ADD, onde a preaução para evitar onitos om a

observação emenáriodedimensão extrafoionnar todos osamposdomodelopadrão

auma membranasubespaçode um espaçoomino dimensões. Esta idéiaé

inompatí-velom agravidade, que sendoonstituinte daprópriaestrutura doespaço-tempo,deve

propagar-se emtodas as dimensões [13℄. De fato,se não queremos irde enontro a

vali-dadeexperimentaldaleideNewton edarelatividadegeral, devemos onsiderarsomente

dimensõesadiionaisompatas emilimétrias. Noentanto,nomodelo RS-II[13℄, o uso

de uma métria não fatorizável foi o ponto have para resolver essa inompatibilidade.

O oneito de duas membranas, uma oulta e outravisível, onde afunção de onda para

omodozerodográvitonémais fortenamembranaoulta [12℄,éinvertido quandosefaz

importanteé que mesmo no limite

r

c

→ ∞

o valor da esala de Plank é bem denido, o quemantém a utilidadedateoria nasolução doproblema de hierarquia.

A prinipal onstatação do modelo RS-II vem da forma do potenial gravitaional

não-relativístioentre duas partíulas de massas

m1

e

m2

na membrana

V

(

r

) =

G

m

1

m

2

r

1 +

1

kr

,

(2)

onde observamos laramente que om

k

da ordem da esala de Plank, a orreção

1

kr

é

extremamente suprimida, dando lugar ao potenial Newtoniano usual. Dessa forma é

possível onsiderar a dimensão extra de tamanho innito, sendo que a sua presença é

oultada pela supressão exponenial de toda troa de informação gravitaional entre a

membranae o espaçofora dela.

Como denido no modelo de Randall Sundrum todos os ampos do modelo padrão

devem aronnados à membrana. Então, é naturalsurgir oseguintequestionamento:

poderão os ampos dos mais variados ranks ser efetivamente loalizados na membrana

desrita nesse modelo? Tomando-se essa pergunta omo motivação, vários trabalhos,

prouraramtestar o omportamento dos mais variados ampos noenário RS.

Resumi-damente, podemositarotrabalho[14℄,mostrandoaloalizaçãode umampoesalarna

membranavisíveleosartigos[15℄,sobre loalizaçãode amposferminiosnãomassivos

om aajudade um aoplamentoYukawa. Apesar do modelode RandallSundrum

apre-sentar uma solução para problema de hierarquia, não suporta loalizaçãona membrana

de modos zeros para oampode gauge[16℄.

Diante dessas diuldades, outros modelos, omo aqueles que apresentam enários

de membranasmodeladaspor defeitostopológios,foramapresentados omo alternativa

para o problema da não loalizaçãodo ampo de gauge. Em taismodelos o número de

dimensões extras determina o tipo de defeito mais adequado para moldar a estrutura.

Por exemplo, se onsideramosapenas uma dimensão extra podemos modelar ouniverso

de dominio[17, 18, 19℄. Estasmembranasnão são innitamentenas sob pontode vista

de dimensão extra, o que resulta em um enário livre de singularidades. Neste aso, a

ondição de ajuste no é resultado daprópria teoria de membranainduzida. O fatorde

warp é uma função suave e determinado pela forma dopotenialesalar. Denominadas

espessas, estas membranas mimetizam um enário de Randall Sundrum e podem sob

erto limite voltar a ser innitamentenas.

Membrana geradasporkinksnão suportamnaturalmenteloalizaçãode modos zeros

para osamposvetoriaise tensoriaisde gauge. Oampotensorialao qualnos referimos

é o ampo de Kalb-Ramond (KR). Uma alternativa para ontornar esse problema é

introduzir um ampo do "bulk". Como mostrado em [19℄ num ontexto de membrana

modelada por kink, o aoplamento om o dílaton possibilita a loalização de modos

zeros para o ampo de gauge. Este tipo de aoplamentotambém foi usado emdiversos

modelosomomeanismode loalizaçãodoampodegauge[20,21℄, inlusiveemparedes

dedomínio. AloalizaçãodemodoszerosparaoampodeKR[22℄tambémfoialançada

pelo mesmomeanismo num enáriode membrana geradapor kink.

Como podemos notar, um importanteproblema no estudo de modelos de dimensões

extrasatualmenteonsisteemdeterminar,entreosdiversosenáriosdemembrana,

aque-lesapazes de loalizarosamposdomodelo padrão. Nonosso, aso dediamosatenção

aoestudode amposde vários ranks emum tipobastantepeuliarde membranagerada

por um ampo esalar real. Como veremos, a partir de um proedimento de

deforma-ção de um potenial

φ

4

, obteremos uma lasse de soluções lassiadas omo two-kink

[23℄. Como mostrado em[24℄, este tipo de modelo de membrana suporta loalizaçãode

modos zeros obtidos de utuações no setor transversal de traço nulo (TT) da métria.

Estes defeitos fazem surgir uma estrutura interna na membrana, tendo impliações na

in-matéria ondensada. Podemos itar omo exemplo um aso de aoplamento de ampo

esalaromplexoomgravidadeonde umatransição defasegera um"splitting"na

mem-brana espessa [25℄. Em matéria ondensada este fenmeno é onheido omo omplete

wetting.

Podemosdenir nossoobjetivoomosendo analisaroomportamentodos modos

ze-ros e massivos para ampos esalares, ferminios, de gauge, e de Kalb-Ramond nessas

estruturas de membranas deformadas. Como veremos, o parâmetro resultante do

pro-edimento de deformação terá impliações nos métodos de loalização, assim omo na

araterístia doaoplamento dos modos de Kaluza-Klein om a membrana. O método

utilizadopara armar que os modos zero (massa zero) dos ampos são loalizados,

on-siste emanalisar, na ação efetiva, o resultado das soluções das equações de movimento.

Para soluções normalizáveis (ação efetiva nita) dizemos que os modos são loalizados.

Transportandonossoproblemaparaum enáriodemeâniaquântia, obteremos

impor-tantes interpretações a respeito dos modos KK que nos auxiliaramna busa de estados

ressonantes. Como desrito em [17℄, no estudo de loalizaçãode gravidade em peredes

de domínio,a existênia dessas estruturas pode nos forneer um espetro de modos KK

om aoplamentonão suprimidoom a matériada membrana.

Ateseéapresentadanaseguintesequênia; noapítulo1,desrevemos oaoplamento

deférmionseoampoesalaromgravidade;noapítulo2,mostramososdetalhesdeum

enáriodemembranagrossa;nopasso seguinte, apresentadonoapítulo3,apresentamos

a estrutura de membrana deformada; nos dois apítulosseguintes mostramos os

resulta-dos de loalizaçãodos amposesalareferminios. Noapítulo6,analisamososefeitos

da introdução do ampo esalar dílaton ao enário. Nos dois apítulos seguintes,

anali-samos osdetalhes daloalizaçãodos ampos vetorial e tensorialde gauge na membrana

omestruturainternaénovanaliteratura. Umasopartiulardenossosresultadossobre

ressonânias no espetro massivo do ampo de gauge foi publiado no trabalho [22℄, de

nossa autoria. O método numério utilizadona análise dos modos massivos e deteção

Interação gravitaional

Neste apítulo,apresentamos tópiosbásiosaodesenvolvimentodos modelos de mundo

om ino dimensões. Mostraremos omo deve ser feito o aoplamento de um ampo

esalar om agravidade, oque será importantenadesrição dos modelosde membrana.

Também mostramos omo oorre o aoplamento de férmions om gravidade, o que será

útilno estudoda loalizaçãodestes ampos.

Apartirdooneitomatemátiodeação,podemosonstruirtodasaleisfundamentais

da Físia Clássia. Podemos, então, a partir da análise da invariânia das equações de

movimento, denir quantidades onservadas. O oneito de ação pode ser estendido ao

estudo de FísiaQuântia a partirda introduçãodas integraisde aminhode Feynman.

Essa ferramentamatemátia nos revelauma linguagem para desrevera transição entre

Meânia Clássiae Quântia [26℄.

Para obtermos as leis de onservação da Relatividade Espeial, preisamos ter

in-variânia sobre transformações de Lorentz globais e translações. Se queremos inluir

gravidade ao nosso enário, devemos realizar a transição da Relatividade Espeial para

a Geral, assim o prinípio daequivalênia deve então ser onsiderado. De uma maneira

geral, este prinípionos dizque um referenialem queuma partíulaé submetida a um

Iniialmente, onsideremos uma partíula em um ampo gravitaional onstante. A

partir das leisde Newton temos

m

I

−

→

a

=

m

G

−

→

g .

(1.1)

Qualquer força externa atuando na partíula é igual ao produto da sua aeleração pela

massa daprópriapartíula, denominadamassa inerial

m

I

. Uma forçagravitaional ex-ternaéproporionalaquantidade

m

G

,quehamamosdemassagravitaionaldepartíula. As duas massas denidas aima são, om uma grande preisão, numeriamente iguais,

embora pertençam à enários diferentes. Dessa forma, onsiderando

m

I

=

m

G

=

m

, podemosreesrever a equação (1.1) daseguinte forma

m

d

2

dt

2

[

−

→

r

(

t

)

−

−

→

_{g t}

2

2

] = 0

.

(1.2)

Podemosinterpretar queoampogravitaionalexternopodeser geradoa partirde uma

mudança de referenial

−

→

_r

_{→ −}

→

_r

′

₌

−

→

_r

−

−

→

g t

2

2

.

(1.3)

Assim,vistade umreferenialemquedalivre(

g

=

constante

),apartíulaestarialivrede gravidade. Chegamosa estaonlusão tomandoum ampo gravitaionalonstante, mas

geralmente o ampo gravitaional varia emtodos os pontos dos espaço. No entanto, de

aordoomEinstein,oampogravitaionalétalqueemtodosospontosdoespaço-tempo

existe umsistemade oordenadas

ξ

a

noqualagravidade pareenãoexistir. Élaroque, de pontoa ponto,esse sistemade oordenadas varia. Dessa forma,dado um sistemade

Iniialmente, na ausênia de gravidade tomemos a ação para um ampo esalar em 4D

sujeito a um potenial

V

(

φ

)

S

=

Z

d

4

x

1

2

∂

µ

φ∂

µ

_φ

₊

_V

₍

_φ

₎

.

(1.4)

Oelementode volume é dado por

d

4

x

=

dx

1

dx

2

dx

3

dx

4

.

(1.5)

Pelo prinípio da equivalênia, para inluir o ampo esalar num ampo gravitaional,

devemos reesrever asoordenadas

x

µ

, assim omo suas derivadas, omo um sistemade

oordenadas planas, omo se estivessem no referenial de queda livre que usamos para

exempliar noiníio. Devemos então tomar a seguintetransformação,

x

µ

_→

_ξ

a

_,

(1.6)

onde

ξ

a

será o sistema de oordenadas planas, om

a

= 1

,

2

,

3

,

4

. O elemento de linha nesse sistema será dado por

ds

2

=

η

ab

dξ

a

dξ

b

,

(1.7)

onde

η

ab

é a métriade Minkowski. A nova ação, inluindoagravidade, será

S

=

Z

d

4

ξ

1

2

η

ab

_∂

a

φ∂

b

φ

−

V

(

φ

)

,

(1.8)

om as derivadas em relaçãoàs oordenadas planas

∂

a

≡

∂

∂ξ

a

.

(1.9)

Oelementode volume tambémdeve ser esritoem termosdas oordenadas planas

pontoa ponto noespaço. As oordenadas

ξ

a

devem ser desritas omo funçõesloaisde

um sistema de oordenadas não-inerial

x

µ

daseguinteforma

dξ

a

(

x

) =

∂ξ

a

∂x

µ

dx

µ

_.

(1.11)

As matrizes de transformação do sistema de oordenadas planas para um sistema

arbi-trário são hamadas tetradas e dadaspor

e

a

_µ

=

∂ξ

a

∂x

µ

.

(1.12)

A tetradaarregaíndiesdosistemaplano

a

eurvo

µ

. Tambémtemosatransformação inversa

dx

µ

=

∂x

µ

∂ξ

a

dξ

a

≡

e

µ

_a

dξ

a

,

(1.13)

de onde podemos esrever a seguinterelação

dξ

a

=

e

a

_µ

dx

µ

=

e

a

_µ

e

µ

_b

dξ

b

.

(1.14)

Logo

e

a

_µ

e

µ

_b

=

δ

_b

a

, e

µ

_a

e

a

_ν

=

δ

µ

_ν

.

(1.15)

As derivadas devem ser esritasemtermos das tetradas omo

∂

∂ξ

a

=

∂x

µ

∂ξ

a

∂

∂x

µ

=

e

µ

a

∂

µ

.

(1.16)

A lagrangeana da ação (1.8) poderá ser reesrita em termos do sistema de oordenadas

x

µ

omo

L

=

1

2

η

ab

_e

µ

a

e

ν

b

∂

µ

φ∂

ν

φ

−

V

(

φ

)

,

(1.17) onde identiamosa métriainversa

de oordenadasarbitrárias

ds

2

=

η

ab

dξ

a

dξ

b

=

η

ab

e

a

µ

e

b

ν

dx

µ

dx

ν

=

g

µν

dx

µ

dx

ν

(1.19)

onde

g

µν

=

η

ab

e

a

µ

e

b

ν

Para esrever a ação (1.8) no sistema de oordenadas

x

µ

, devemos relaionar o

ele-mentode volume

d

4

_ξ

om

d

4

_x

. Usando (1.11),obtemosa seguinterelação

d

4

ξ

=

dξ

1

dξ

2

dξ

3

dξ

4

= (det

e

a

_µ

)

dx

1

dx

2

dx

3

dx

4

.

(1.20)

Otermo

det

e

a

µ

éonheidoomoojaobianodatrasformação. Apliandoodeterminante

à métria

g

µν

, denida em(1.19), obtemoso jaobiano

(det

e

a

_µ

)

2

=

₋

det

g

µν

.

(1.21)

Dessa forma,oselementos de volume relaionam-sedaseguintemaneira

d

4

ξ

=

p

₋

det

g

µν

d

4

x.

(1.22)

Finalmente, poderemos reesrever a ação para o ampo esalar (1.8) num enário om

gravidade omo,

S

=

Z

d

4

x

p

₋

det

g

µν

1

2

g

µν

_∂

µ

φ∂

ν

φ

−

V

(

φ

)

.

(1.23)

1.2 Espinor de Dira

Ogrupode Lorentzem representação espinorial

1

2

,

0

e

0

,

1

2

édesritopelos espinores

omplexos

ψ

L

e

ψ

R

respetivamente. Na ausênia de gravidade, oinvariantede Lorentz usado para termo inétioespinorialnaação é dado por,

L

Dirac

=

1

2

Ψ

γ

µ

←

_∂

→

onde

Ψ

é hamado espinorde Dira

Ψ

_≡







ψ

R

ψ

L







.

(1.25)

Oobjeto

Ψ

representa oadjunto de

Ψ

dadopelarelação

Ψ = Ψ

†

γ

0

,

(1.26)

onde

γ

0

=







0

1

1

0







γ

i

=







0

−

σ

i

σ

i

₀







.

(1.27)

Ostermos

σ

i

são as matrizesde Paulidadas por

σ

1

=







0

1

1

0







σ

2

=







0

−

i

i

0







σ

3

=







1

0

0

₋

1







.

(1.28)

Poderíamos montar uma ação invariante envolvendo ampos espinoriais da forma

∂

µ

Ψ

¯

∂

µ

Ψ

. No entanto,termos desse tiponão levama teoriasonsistentes tendo emvista queviolamarelaçãoentrespineestatístiaenãosãorenormalizáveisperturbativamente.

ParainluirainteraçãogravitaionalaoespinordeDiradevemos,omozemosom

o ampo esalar, apliar o prinípio da equivalênia. A diferença em relação ao ampo

esalar é que o ampo de Dira transforma-se omo um espinor sob a transformação de

Lorentz

Ψ

_→

e

(

2

i

ǫ

µν

_σ

µν

)Ψ

_,

(1.29)

onde

ǫ

µν

são os parâmetros da transformação e

σ

µν

representam os geradores da trans-formação de Lorentzno espinor. Emtermos das matrizes

γ

µ

, temos

σ

µν

=

i

2

[

γ

µ

_{, γ}

ν

_]

_.

(1.30)

De aordo om o prinípio da equivalênia, em ada ponto do espaço, o ampo

oordenadas favoreido deve mudar de ponto a ponto no espaço. De uma forma geral,

para generalizar a equação de Dira em um ampo gravitaional, devemos preservar a

invariânialoalsob as transformaçõesde Lorentz.

Denimosumanovaderivadademodoque,quandoatuandonoespinor,transforme-se

damesma formaque a derivada na ausênia de gravidade

D

a

≡

e

µ

a

(

∂

µ

+

iω

µ)

.

(1.31)

Esrevendo

ω

µ

em termosdaonexão de spin,teremosaderivada ovarianteatuandono espinorde Dira naforma

D

a

≡

e

µ

a

(

∂

µ

+

i

2

ω

cd

µ

σ

cd)

.

(1.32)

A nova lagrangeanade Dirano ampo gravitaionalserá

L

Dirac

=

1

2

Ψ

γ

a

_e

µ

a

(

∂

µ

+

i

2

ω

cd

Membrana gerada por kink

2.1 Introdução

A idéia de onsiderar uma estrutura adiional de ampo no bulk 5-dimensional foi

proposta por vários trabalhos [17, 18, 27℄ sendo que em todos os modelos o enário de

Randall-Sundrum pode ser reestabeleido em um limite apropriado. As estruturas de

membrana apresentadas nesses modelos não são innitamentenas em relaçãoà quinta

dimensão. Dessa forma, o que hamaremos estruturas de membranas grossas são

se-melhantes a paredes de domínio ferromagnétias, podendo se espalhar pela dimensão

extra.

Uma estrutura de parede de domínio é araterizadapelaexistênia de um

parâme-troque assumevalores diferentes emada domínioe quetransitagradualmenteentre os

domínios adjaentes. Dessa forma, o que podemos hamar de espessura da parede de

domínio é o tamanho da região onde esse parâmetro sofre a transição. Uma estrutura

análoga à parede de domínio pode ser onebida em teorias de ampos a partir de um

ampo esalar ujo potenial apresenta diferentes mínimos em diferentes domínios.

As-sim, o ampo esalar atravessa a parede de domínio, alternando-se entre os diferentes

Dessaforma,alémdaenergiapotenial,aenergiade gradientedoampoesalartambém

ontribui para o tensor momento-energia estabeleendo uma fonte de gravidade

depen-dentedoespaço-tempo,diferentedosasosdeparedededomínioemqueoampoesalar

é onstanteno espaço,permaneendo apenas emum dos mínimosdopotenial.

OespaçoantideSitter(AdS)podeseraraterizadoomoumavariedadeLorentziana

de simetria máxima om urvatura esalar negativa e onstante. Nos asos em que

o ampo esalar varia no espaço, a geometria gerada nas equações de Einstein pela

fonte não é exatamente de simetria

AdS

5

do espaço-tempo, omo aquela gerada por uma onguração de ampo esalar onstante. Como veremos, assim omo o ampo

esalar, a própria urvatura esalar varia espaialmente em regiões próximas à parede

de domínio, tendendo a valores onstantes e negativos longe dela. A solução pode ser

interpretada omouma paredede domíniogrossaque alternaentre doisespaços

AdS5

,o que arateriza umaversão sem singularidades doenário RS.

2.2 A membrana omo kink

Para desrever nosso enáriousaremos amétria

ds

2

=

e

2

A

(

y

)

η

µν

dx

µ

dx

ν

+

dy

2

,

(2.1)

onde o fator de warp é gerado pela função

A

(

y

)

da dimensão extra

y

. O tensor

η

µν

é a métria de Minkowski e os índies

µ

e

ν

variam de 0 a 3. Para gerar nossa estrutura de membrana, introduzimosuma ação om aoplamento entre gravidade 5-dimensional

e um ampo esalar daseguinte forma

S

=

Z

d

4

xdy

√

₋

G

(

₋

1

4

R

−

1

2

(

∂φ

)

2

naqual, o ampo

φ

onstituia própria membrana e

R

é a urvatura esalar. É possível obtermos, a partir do modelo desrito pela ação aima, soluções do tipo kink para o

ampo

φ

que dependemapenasda dimensão extra.

As equações de movimento resultantes da ação (2.2) serão extraídas da equação de

Einstein

R

M N

−

1

2

G

M N

R

+

G

M NΛ =

8

πg

c

4

T

M N

,

(2.3)

e daequação de Euler-Lagrange

∂

M

∂

_L

∂

(

∂

M

φ

)

−

∂

_∂φ

L

= 0

,

(2.4)

onde índiesom letras maiúsulas

M

= 1

,

2

,

3

,

4

,

5

,

e aonstante osmológia

Λ = 0

. O tensor energia-momentoédado por

T

M N

= 2

δ

_L

mat

δG

M N

+

G

M N

L

mat,

(2.5)

que omo havíamos dito terá ontribuições tantoda energiade gradienteomo da

ener-gia potenial do ampo esalar. Calulando o valor de

T

M N

a partir da ação (2.2) e substituindo naequação de Einstein, teremosas seguintes equações de movimento

R

M N

−

1

2

G

M N

R

= 2

∂

M

φ∂

N

φ

−

G

M N

1

2

∂

P

φ∂

P

_φ

₊

_V

₍

_φ

₎

,

(2.6)

∂

P

[

√

−

GG

P N

_∂

N

φ

] =

√

−

G

∂V

∂φ

.

(2.7)

Dessa forma, preisamos onheer o tensor de Rii

R

M N

e a urvatura esalar

R

. O tensor de Riié obtido pelaontração dotensor de urvatura daseguinte forma

R

M N

=

R

M P N

P

,

(2.8)

onde

R

P

M QN

=

∂

QΓ

P

M N

−

∂

N

Γ

P

M Q

+ Γ

R

M N

Γ

P

RQ

−

Γ

R

M Q

Γ

P

RN

.

(2.9)

A urvaturaesalar é obtidado tensor de Riipela ontração

Γ

P

_{M N}

=

1

2

G

P Q

₍

_∂

M

G

QN

+

∂

N

G

QM

−

∂

Q

G

M N)

.

(2.11)

A partir da métria

G

M N

=



























−

e

2

A

(

y

)

₀

₀

₀

₀

0

e

2

A

(

y

)

₀

₀

₀

0

0

e

2

A

(

y

)

₀

₀

0

0

0

e

2

A

(

y

)

₀

0

0

0

0

1



























(2.12) onde

√

−

G

=

q

−

(

₋

e

8

A

(

y

)

_{) =}

_e

4

A

(

y

)

(2.13)

hegamos aos seguintes resultados

Γ

1

₅₁

= Γ

2

₅₂

= Γ

3

₅₃

= Γ

4

₅₄

=

A

′

(

y

)

, A

′

(

y

) =

dA

(

y

)

dy

,

(2.14)

Γ

5

₂₂

= Γ

5

₃₃

= Γ

5

₄₄

=

₋

Γ

5

₁₁

=

₋

e

2

A

A

′

(

y

)

,

R

22

=

R

33

=

R

44

=

−

R

11

=

−

e

2

A

[4

A

′

(

y

)

2

+

A

′′

(

y

)]

(2.15)

R55

=

₋

4[

A

′

(

y

)

2

+

A

′′

(

y

)]

,

R

=

₋

4[5

A

′

(

y

)

2

+ 2

A

′′

(

y

)]

.

(2.16)

Com o ampo esalar dependendo apenas de

y

, substituimos as relações (2.15) e (2.16) naequação de movimento(2.6) eobtemos, para

M

=

N

= 5

6

A

′2

₌

_φ

′2

₋

₂

_V

₍

_φ

₎

_,

(2.17)

e para

M

=

N

= 1

,

2

,

3

,

4

-

3

-

2

-

1

1

2

3

Φ

0.5

1

1.5

2

V

HΦL

Figura2-1: Potenial

V

(

φ

) = (1

−

φ

2

₎

2

.

Finalmente, para ompletar as equações de movimento, obtemos da equação de

Euler-Lagrange(2.4) om a métria

G

M N

4

A

′

φ

′

+

φ

′′

=

∂V

∂φ

.

(2.19)

Neste ponto é importante notar que poderemos enontrar a forma do fator de warp

a partir da solução para o ampo esalar. Se queremos uma solução tipo parede de

domínio,afunção

φ

(

y

)

devetenderassintotiamenteparaosmínimosdopotenialquando

y

_{→ ±∞}

. Noasosemgravidadeopotenial

(1

−

φ

2

₎

2

,mostradonagura(2-1),suporta

solução tipokink

φ

(

y

) = tanh(

y

)

,

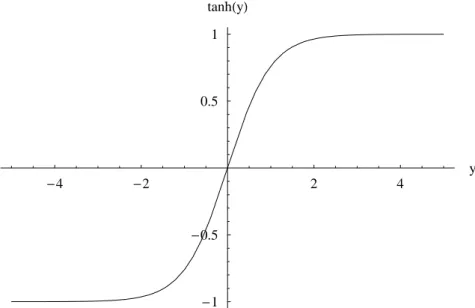
(2.20)

que traçamos nagura 2-2.

Somando as equações(2.17) e (2.18)teremos,

A

′′

=

₋

2

3

φ

′2

_,

-

4

-

2

2

4

y

-

1

-

0.5

0.5

1

tanh

H

y

L

Figura2-2: Função

φ

= tanh(

y

)

.

e integrando duas vezes

A

(

y

)

esubstituindo a solução

φ

(

y

) = tanh(

y

)

, teremos

A

′′

(

y

) =

₋

2

3

sech

2

(

y

)

2

(2.22)

A

′

₍

_y

_{) =}

₋

2

9

(2 +

sech

2

₍

_y

_{)) tanh(}

_y

₎

A

(

y

) =

₋

4

9

ln[cosh(

y

)]

−

1

9

tanh

2

₍

_y

₎

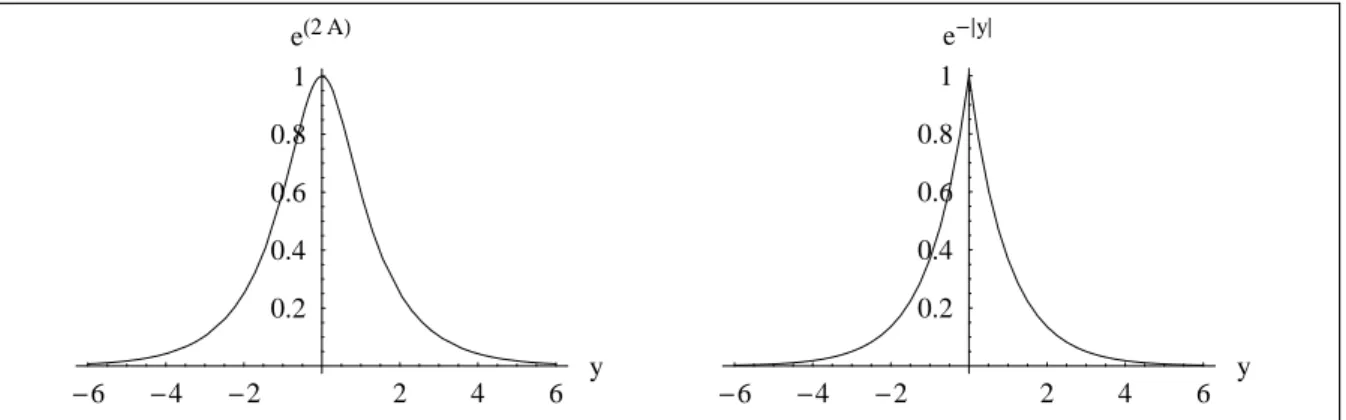
Podemos notar que a função

A

(

y

)

ésuave e representa um fatorde warp loalizado,ou seja

e

2

A

(

y

)

∝

e

−|

y

|

(

y

→ ∞

)

,

(2.23)

tendo a forma do fator de warp do modelo Randall-Sundrum para regiões distantes da

membrana. Nagura(2-3)plotamosofatordewarpgeradopelafunção

A

(

y

)

juntamente om aquele do modelo RS.

Éinteressantetambémompararoesalardeurvaturageradopelafunção

A

(

y

)

om odomodeloRS.Para istotraçamos

R

=

−

4[5

A

′

₍

_y

₎

2

_{+ 2}

_A

′′

₍

_y

_)]

nagura(2-4),onde

A

(

y

)

é dado pelaequação (2.22).

-

6

-

4

-

2

2

4

6

y

0.2

0.4

0.6

0.8

1

e

H2

AL

-

6

-

4

-

2

2

4

6

y

0.2

0.4

0.6

0.8

1

e

-

ÈyÈ

Figura2-3: Fator de warp para

A

(

y

)

(esquerda) e

−|

y

|

(direita).

próximas ao salto do ampo esalar tendendo assintotiamente quando

y

→ ±∞

a um valor onstante e negativo. Dessa formapodemos onluir que nas regiões distantes da

membrana

(

y

→ ∞

)

, a geometria doespaço-tempo adquire a mesma estrutura

AdS5

do modeloRandall-Sundrum. Aespessuradamembranaenurvaoespaço-tempofailitando

a loalizaçãode ampos. Comparando om o modelo RS om a função

A

(

y

) =

−

k

|

y

|

, a urvatura teriavaloronstanteem todobulk.

Uma forma alternativa de obter soluções para as equações de movimento onsiste

no método de superpotenial [18, 28℄. Com esse método derivamos o potenial para o

ampoesalar a partir de uma função denominada superpotenial

W

(

φ

)

,denida omo

∂W

∂φ

=

φ

′

. Para isso, esrevemos opotenial esalarem termosda função

W

omo

V

(

φ

) =

1

2

∂W

(

φ

)

∂φ

2

−

1

3

W

(

φ

)

2

_,

(2.24)

que omparandoom (2.17), obtemosas equações de primeira ordem

∂W

(

φ

)

∂φ

=

φ

′

_,

(2.25)

W

(

φ

) =

₋

3

A

′

.

(2.26)

No aso doespaço-tempoplano, ondeopotenialéesritoemfunção dosuperpotenial

omo

V

(

φ

) =

1

2

∂W

(

φ

)

∂φ

2

-

4

-

2

2

4

y

-

4

-

2

2

4

R

Figura2-4: Curvatura esalarpara

A

(

y

)

.

afunção

W

(

φ

) =

φ

−

φ

3

3

araterizao potenial

1

/

2(1

−

φ

2

₎

2

. Com estaesolhapara

W

, usando arelação (2.25)obtemos novamentea solução

φ

= tanh(

y

)

, ouseja

1

2

∂W

(

φ

)

∂φ

2

=

1

2

(1

−

φ

2

₎

2

_,

(2.28)

∂W

∂φ

= 1

−

φ

2

₌

_φ

′

_,

1

₋

tanh

2

(

y

) =

sech

2

(

y

)

.

Comeste métodopodemosalternativamenteobterafunção

A

(

y

)

,queompõeofatorde warp, a partir daesolha para

W

(

φ

) =

φ

−

φ

3

3

substituída narelação (2.26)

A

(

y

) =

₋

1

3

Z

W

(

φ

)

dy

=

₋

1

3

Z

(

φ

₋

φ

3

3

)

dy

=

−

4

9

ln[cosh(

y

)]

−

1

9

tanh

2

₍

_y

₎

_.

(2.29)

Voltandoaoaso om gravidade,onde o potenial édado por(2.24) obtemos

V

(

φ

) =

1

2

(1

−

φ

2

₎

2

−

1

₃

(

φ

₋

φ

3

3

)

2

_,

(2.30)

que é traçado na gura 2-5. Ao invés de um potenialquádruplo usado no modelo sem

-

4

-

2

2

4

Φ

5

10

15

20

25

V

HΦL

Figura2-5: Potenial

V

(

φ

) =

1

2

(1

−

φ

2

₎

2

₋

1

3

(

φ

−

φ

3

3

)

2

.

potenial resultantepossui dois mínimosdegenerados em

φ

=

±

1

ondeassume o valor

V

(

_±

1) =

₋

4

27

,

(2.31)

om asolução

φ

= tanh(

y

)

interpolandoentre osdois mínimosde aordo om

φ

(+

∞

) =

1

, φ

(

_−∞

) =

₋

1

. Devido aessa interpolação

φ

(

y

)

éuma função ímparde

y

,oque oma formadasequaçõesdemovimentolevamàfunçãopar

A

(

y

)

. Tambémédevidoàestrutura de kink que a função

A

(

y

)

determina um fator de warp de simetria

Z2

neessária para o enáriode membrana. Podemos dizer que essa simetriaé gerada dinamiamente, uma

vantagem em relação ao enário RS onde a simetria é imposta. Alémdisso, a formado

A estrutura de membrana deformada

3.1 Motivação

Atualmente existe grande interesse em estudar ampos esalares aoplados om

gravi-dade. Onúmerodedimensõesextrasqueseusa paradesreveromundoomomembrana

dene o tipode defeito quese deve abordar. Se onsideramos uma membrana

quadridi-mensional om apenas uma dimensão extra devemos montar nosso modelo baseado em

kinks. Normalmentedesrevemos esses defeitosapartirde amposesalaresemmodelos

do tipo

λφ

4

ou sine-Gordon. No nosso aso, obteremos uma lasse espeial de defeitos

a partir de uma deformação do potenial

λφ

4

[29℄. Mais espeiamente, introduzimos

um potenial para o ampo esalar dependente de números inteiros ímpares [23℄. Este

proedimentoé muitointeressantesendo quealém de fazersurgir uma estrutura interna

namembranatemimpliaçõesnadistribuiçãode densidadedeenergiaematériaaolongo

da dimensão extra [24℄. Algumas araterístiasdesses defeitos também foram

onside-radas noestudo de transiçõesde fasenageometria "warped"[25℄. Como mostraremos,o

bakground resultanteapresenta um "splitting"naurvatura doespaço.

Dessa formapoderemos analisara loalizaçãode amposde ranks variadosde forma

Como veremos mais adiante esta esolha também nos previne do apareimento de

singularidadesno espaço-tempo omoem enáriostipo Randall-Sundrum.

3.2 O proedimento de deformação

Iniialmente, tomamos novamente a ação de onde obtivemos a estrutura de membrana

grossaequeonsistedoaoplamentoentre umampoesalarrealeagravidadeemino

dimensões

S

=

Z

d

4

xdy

√

₋

G

(

₋

1

4

R

−

1

2

(

∂φ

)

2

−

V

(

φ

))

.

(3.1)

Com a métria

ds

2

=

e

2

A

(

y

)

η

µν

dx

µ

dx

ν

+

dy

2

,

(3.2)

enontramos asequações de movimento

6

A

′2

=

φ

′2

₋

2

V

(

φ

)

,

(3.3)

−

3

A

′′

₋

6

A

′2

= 2

V

(

φ

) +

φ

′2

.

(3.4)

Usaremos novamenteo métodosuperpotenial [18, 28℄onde o potenialé esrito omo,

V

(

φ

) =

1

2

∂W

(

φ

)

∂φ

2

−

1

₃

W

(

φ

)

2

,

(3.5)

de onde obtemos asequações de primeiraordem

∂W

(

φ

)

∂φ

=

φ

′

_,

(3.6)

W

(

φ

) =

₋

3

A

′

.

(3.7)

Emum enáriode espaço-tempoplano e om a esolhadafunção superpotenial

f

W

(

φ

) =

φ

₋

φ

3

-

4

-

2

2

4

Φ

0.5

1

1.5

2

V

P

HΦL

Figura 3-1:

V

p

(

φ

)

para

p

= 1

(linha sólida),

p

= 3

(linha pontilhada) e

p

= 5

(linha traejada).

obtemoso potenialo

1

/

2(1

−

φ

2

₎

2

que determina a solução

φ

= tanh(

y

)

.

Neste ponto usaremos o proedimento de deformação enontrado em [29, 23, 24℄

baseado nafunção

f

(

φ

) =

φ

1

p

,bemdenidapara qualquer

φ

,om

p

inteiroímpar. Dessa forma,enontraremos uma nova função

f

W

p

(

φ

)

a partir darelação

d

W

f

p

dφ

=

d

W

f

dφ

[

φ

→

f

(

φ

)]

df

dφ

,

(3.9)

de onde obtemos

d

f

W

p

dφ

=

p

φ

p

−

p

1

−

φ

p

+1

p

.

(3.10)

Integrando emrelação a

φ

hegamosà função

W

f

p(

φ

) =

pW

p

(

φ

)

onde

W

p(

φ

) =

p

2

p

₋

1

φ

2

p

−

1

p

−

p

2

p

+ 1

φ

2

p

+1

p

.

(3.11)

-

20

-

10

10

20

y

-

1

-

0.5

0.5

1

Φ

p

H

y

L

Figura 3-2:

φ

p(

y

) = tanh

p

₍

y

p

)

para

p

= 1

(linha pontilhada),

p

= 3

(linha traejada) e

p

= 5

(linha sólida).

potenial resultante

V

p

araterizam um novo enário de membrana mais rio do que aquele gerado por uma soluçãotipo kink padrão. Oapareimentoda transição entre os

mínimosdo potenialterá reexos na geometria daregião.

A solução para o ampo esalar é obtida da equação

∂W

p

(

φ

)

∂φ

=

φ

′

onde usaremos a

solução deformada

W

p

(

φ

)

,logo

∂W

p

(

φ

)

∂φ

=

φ

p

−

1

p

−

φ

p

+1

p

=

φ

′

(

y

)

,

(3.12)

eo resultado será

φ

p(

y

) = tanh

p

(

y

p

)

.

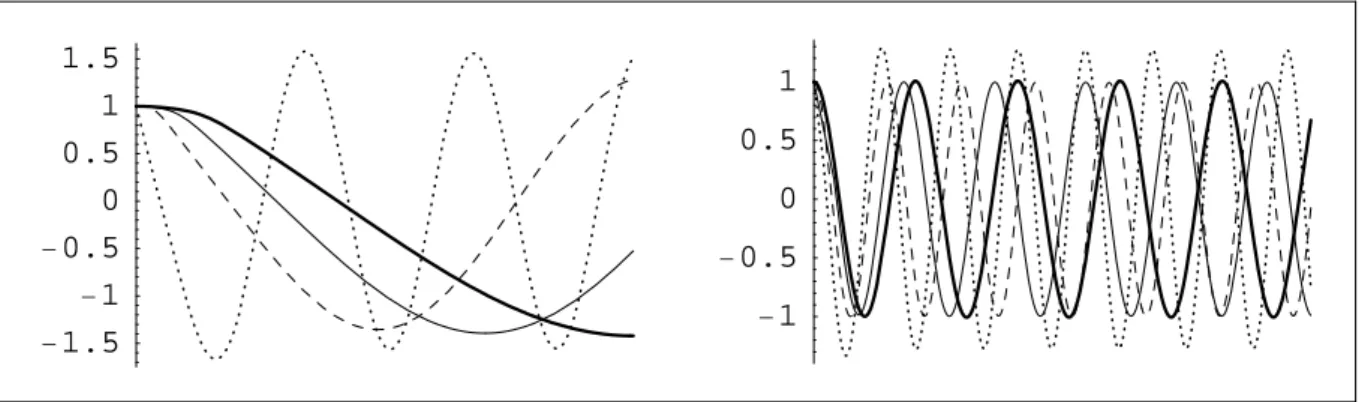
(3.13)

Como observamos na solução, que é traçada na gura (3-2) para

p

= 1

,

3

,

5

.

, a mesma tende para

φ

=

±

1

quando

y

→ ∞

, que orresponde aos dois mínimos do potenial. Veriamostambémuma regiãode derivada nulaem

φ

= 0

ujaespessura aumentaom

-30

-20

-10

10

20

30

y

0.2

0.4

0.6

0.8

1

e

2

A

P

Figura 3-3:

e

2

A

p

(

y

)

para

p

= 1

(linha pontilhada),

p

= 3

(linha traejada)e

p

= 5

(linha sólida).

A partir daequação de primeiraordem

W

p

=

−

3

A

′

p

(

y

)

, enontra-se analitiamentea solução para

A

p(

y

)

[24℄,

A

p

(

y

) =

−

1

3

p

2

p

+ 1

tanh

2

p

y

p

−

2

3

p

2

2

p

₋

1

−

p

2

2

p

+ 1

(3.14)

ln

cosh

y

p

−

p

−1

X

n

=1

1

2

n

tanh

2

n

y

p

.

Afunção

A

p

(

y

)

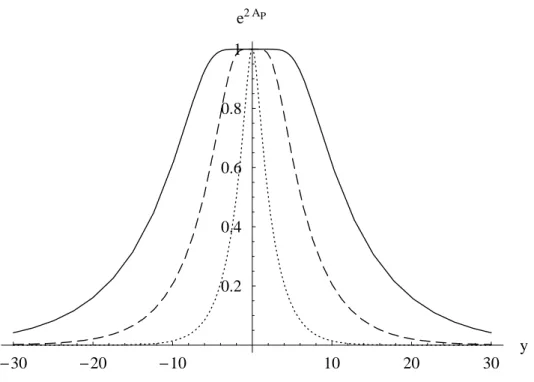
ompõeofatordewarpdamétria

e

2

A

p

(

y

)

,quemostramosnagura(3-3).

Dessaforma,afunção

A

p(

y

)

ontinua representando umageometria loalizadaemtorno de

y

= 0

. Apesar do apareimento de uma região onde permanee onstante, a função

e

2

A

p

(

y

)

ésuave,oquenos previnede singularidades,assumindoomesmoomportamento

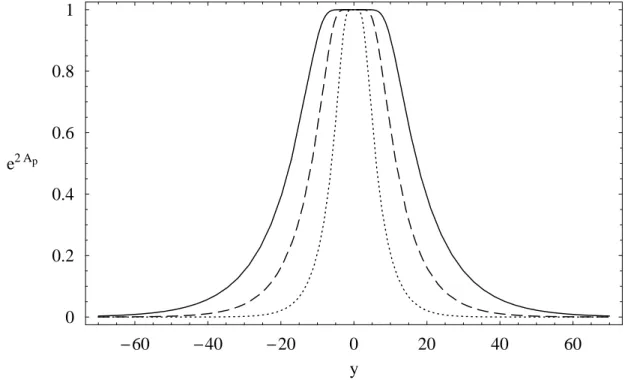
dofator de warp domodelo Randall-Sundrum pararegiões distantes damembrana.

A partir da solução para

A

p(

y

)

podemos determinar a urvatura esalar para bak-ground

-

4

-

2

2

4

y

-

4

-

2

2

4

RHyL

-

20

-

10

10

20

y

-

0.2

-

0.1

0.1

0.2

0.3

Rp

HyL

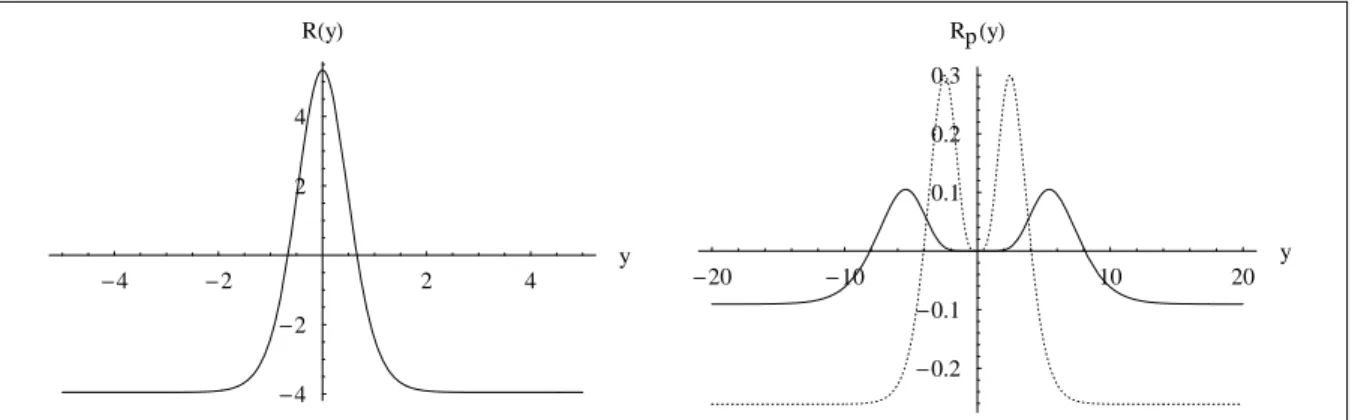
Figura 3-4: Curvatura esalar

R

p(

y

)

lado esquerdo para

p

= 1

e lado direito para

p

= 3

(linha pontilhada)e

p

= 5

(linha sólida).

Podemospereberumaaraterístiaimportantedaestruturadeformadaemomparação

aos modelos de membranas grossas geradas por kink. Observando a gura (3-4), para

p

= 1

, temos o esalar de urvatura para um modelo não-deformado. Neste aso a