TAMPEREEN YLIOPISTO Pro gradu -tutkielma
Jessica Glassar
Momentit generoiva funktio
Informaatiotieteiden yksikkö Matematiikka
Joulukuu 2012
Tampereen yliopisto
Informaatiotieteiden yksikkö
GLASSAR, JESSICA: Momentit generoiva funktio Pro gradu -tutkielma, 30 s.
Matematiikka Joulukuu 2012
Tiivistelmä
Tutkielman pääaihe on momentit generoiva funktio. Se on funktio, jonka avulla voidaan nimensä mukaisesti generoida jakauman momentteja. Lisäksi se on työväline, jonka avulla voidaan luonnehtia jakaumaa muodossa, jota on tietyissä tilanteissa helpompi käsitellä.
Tutkielman alussa pohjustetaan aihetta käyden läpi tarvittavia perus- määritelmiä satunnaismuuttujasta, odotusarvosta ja momenteista. Toinen esitietoja käsittelevä luku taas sisältää asiaa yleisesti generoivista funktioista sekä tarkemmin karakteristisesta funktiosta.
Itse momentit generoivaan funktioon päästään luvussa 4, jossa käsitel- lään määritelmän ja perusominaisuuksien lisäksi jakauman määrittämistä momenteista, momenttiepäyhtälöitä sekä riippumattomien muuttujien sum- maa.
Lukijan oletetaan tuntevan matemaattisen tilastotieteen perusteet sekä todennäköisyyslaskentaa. Tutkielman päälähteenä on käytetty Vijay K. Ro- hatgin ja A.K. Md. Ehsanes Salehin kirjan An Introduction to Probability and Statistics toista painosta.
Sisältö
1 Johdanto 4
2 Satunnaismuuttuja ja siihen liittyviä käsitteitä 4
2.1 Satunnaismuuttuja . . . 4
2.2 Riippumattomuus . . . 5
2.3 Odotusarvo . . . 6
2.4 Momentit . . . 8
3 Tarvittavia ennakkokäsitteitä 10 3.1 Generoivat funktiot . . . 10
3.2 Karakteristinen funktio . . . 12
4 Momentit generoiva funktio 13 4.1 Momentit generoivan funktion määritelmä ja perusominaisuuk- sia . . . 13
4.2 Jakauman määrittäminen momenteista . . . 19
4.3 Momenttiepäyhtälöitä . . . 22
4.4 Riippumattomien muuttujien summa . . . 26
Viitteet 29
1 Johdanto
Tämän tutkielman pääaiheena on momentit generoiva funktio. Aluksi on kui- tenkin hyvä pohjustaa aihetta hiukan, joten luvussa 2 kerrataan matemaatti- sessa tilastotieteessä käytettäviä käsitteitä siinä suhteessa, miten tarpeellisia ne ovat tutkielman aiheen kannalta. Ensin kerrotaan satunnaismuuttujasta (alaluvut 2.1 ja 2.2), joka on ehkä koko tutkielman eniten toistettu käsi- te. Sen jälkeen käydään läpi vielä odotusarvo (2.3) ja momentit (2.4), jotta lukijalla olisi tuoreessa muistissa nämä aiheen kannalta tärkeät asiat.
Luku 3 pitää sisällään kaksi osaa, joista ensimmäinen (3.1) kertoo generoi- vista funktioista yleensä. Se pyrkii hiukan valottamaan sitä, mitä generoivat funktiot oikein tekevät. Toinen osa (3.2) kertoo karakteristisesta funktiosta, joka on oikein hyödyllinen funktio, mutta joka käydään tässä tutkielmassa läpi oikeastaan vain siksi, että sitä tarvitaan erään lauseen todistuksessa.
Karakteristinen funktio on myös generoiva funktio.
Viimein luvussa 4 päästään itse asiaan. Ensin määritellään momentit ge- neroiva funktio ja käydään läpi sen perusominaisuuksia (alaluku 4.1). Sit- ten mietitään, voisiko tietyn jakauman määrittäminen momenteista onnis- tua (alaluku 4.2). Alaluku 4.3 käsittelee momenttiepäyhtälöitä ja viimeinen alaluku 4.4 tilanteita, joissa satunnaismuuttujia onkin enemmän kuin yksi.
Lukijalta odotetaan, että hän tuntee matemaattisen tilastotieteen pe- rusteet sekä hieman erilaisia jakaumia, kuten normaalijakauma ja Poisson- jakauma. Myös matemaattisen analyysin perusteet oletetaan tunnetuiksi.
Tutkielman päälähteenä on käytetty Vijay K. Rohatgin ja A.K. Md. Eh- sanes Salehin kirjaa An Introduction to Probability and Statistics, Second edition.
2 Satunnaismuuttuja ja siihen liittyviä käsit- teitä
Pohjustetaan aihetta hieman tarvittavilla ennakkotiedoilla. Tässä kappalees- sa käydään läpi pääpiirteittäin satunnaismuuttuja, sen ominaisuuksia sekä odotusarvo. Niiden jälkeen tarkastellaan vielä momentteja, jotka nimensäkin perusteella liittyvät kiinteästi momentit generoivaan funktioon.
2.1 Satunnaismuuttuja
Tutkimustuloksia on usein helpompi käsitellä jonkinlaisen tiivistetyn muut- tujan avulla. Esimerkiksi vaikka kyselytutkimus, jossa vastaukset on jaoteltu myönteisiin, ”1”, ja kielteisiin, ”0”, ja vastauksia on saatu 50 henkilöltä. Nyt otosavaruudessa on 250 elementtiä, joista jokainen on 1:n ja 0:n muodosta- ma 50 alkion merkkijono. Tällainen tietomäärä on saatava pakattua tiiviim- mäksi, jotta sitä voidaan käsitellä helpommin. Voidaan määrittää muuttuja
X = ”1”:n määrä 50 vastauksen joukossa. Tällöin otosavaruus on pienenty- nyt kokonaislukujen joukoksi{0,1,2, . . . ,50}, mitä on paljon helpompi käsi- tellä. [2, s. 27]
Kun määritetään X tällä tavoin, on luotu kuvaus alkuperäiseltä otosava- ruudelta uudelle sellaiselle, useimmiten joukolle reaalilukuja. Yleisesti käyte- tään seuraavanlaista määritelmää:
Määritelmä 2.1. Satunnaismuuttuja X on funktio otosavaruudestaS reaa- liluvuille, toisin sanoen X :S →R. [2, s. 27]
Esimerkki 2.1. Taulukossa 1 on muutamia esimerkkejä erilaisista satun- naiskokeista ja niissä käytetyistä satunnaismuuttujista.
Koe Satunnaismuuttuja
Heitetään kahta noppaa X = saatujen lukujen summa
Heitetään kolikkoa 25 kertaa X = kruunujen määrä 25:ssä heitossa Viljellään eri maissilajikkeita X = tuotto/aari
Taulukko 1: Esimerkkejä erilaisista satunnaismuuttujista
Tässä tutkielmassa tarkastelun kohteena olevat käsitteet on suurelta osin jaoteltu kahteen tapaukseen sen mukaan, onko satunnaismuuttuja jatkuva vai diskreetti, joten määritellään vielä sekin ominaisuus.
Määritelmä 2.2. Satunnaismuuttuja X onjatkuva, jos sen kertymäfunktio F(x) on jatkuva. Satunnaismuuttuja X on taas diskreetti silloin, kun sen kertymäfunktio F(x) on porrasfunktio. [2, s. 33]
2.2 Riippumattomuus
Erityisesti tutkielman loppupuolella käsitellään toisistaan riippumattomia satunnaismuuttujia. Tässä kappaleessa selvennetään hiukan, mitä riippumat- tomuus satunnaismuuttujien kohdalla tarkoittaa.
Satunnaismuuttujien riippumattomuus pohjaa ehdollisen todennäköisyy- den käsitteestä. Kerrataan se lyhyesti:
Kun A ja B ovat jonkin otosavaruuden tapahtumia, niin tapahtuman B ehdollinen todennäköisyys ehdolla A on
P(B | A) = P(B ∩A)
P(A) , kun P(A)>0.
Kun tapahtumat ovat riippumattomia, on ehdollinen todennäköisyysP(B|A) sama kuin ehdollistamaton todennäköisyys P(B). Siis
P(B) = P(B |A) = P(B ∩A) P(A) . Tästä seuraa riippumattomuuden määritelmä:
Määritelmä 2.3. TapahtumatA ja B ovat riippumattomat, jos P(B∩A) = P(A)P(B)
[10, s. 54]
Satunnaismuuttujien riippumattomuus määritellään vastaavalla tavalla.
Määritelmä 2.4. OlkootX jaY satunnaismuuttujia. Ne ovatriippumatto- mat, jos
P({X ∈A} ∩ {Y ∈B}) =P({X ∈A})P({Y ∈B}), kaikilla A⊂Rja B ⊂R. [9, s. 39]
Määritelmästä seuraa suoraan muun muassa se, että jos ja vain jos X ja Y ovat riippumattomia,
F(x, y) =F1(x)F2(y),
kaikilla (x, y)∈ R2. Tässä F1(x), F2(y) ovat satunnaismuuttujien X, Y ker- tymäfunktioita ja F(x, y) niiden yhdistetty kertymäfunktio. [13, s. 119]
2.3 Odotusarvo
Odotusarvo on yksi tärkeä jakaumien tunnusluku. Tässä kappaleessa ker- rataan siihen liittyviä perusasioita. Odotusarvon kohdalla aloitetaan myös erikseen diskreetin ja jatkuvan tapauksen esittäminen (ks. Määritelmä 2.2).
Olkoon X diskreetin jakauman satunnaismuuttuja, jonka tiheysfunktio onpk =P{X =xk}, k = 1,2, . . .. Jos
(2.1)
∞
X
k=1
|xk|pk <∞,
niin X:n odotusarvo, E(X), on olemassa ja
(2.2) µ=E(X) =
∞
X
k=1
xkpk.
On siis huomattava, että on mahdollista, että jälkimmäinen sarja (2.2) sup- penee, mutta ensimmäinen (2.1) ei. Tällöin määritellään, että E(X) ei ole olemassa.
Esimerkki 2.2. Olkoon X:n tiheysfunktio määritelty seuraavanlaisesti:
pj =P
(
X = (−1)j+13j j
)
= 2
3j, j = 1,2, . . . .
Tällöin ∞
X
j=1
|xj|pj =
∞
X
j=1
2 j =∞ ja E(X) ei ole olemassa, vaikka sarja
∞
X
j=1
xjpj =
∞
X
j=1
(−1)j+12 j onkin suppeneva.
Jos X taas on jatkuva satunnaismuuttuja ja sillä on tiheysfunktio f, saadaan sen odotusarvo integraalin avulla yhtälöstä
E(X) =
Z
xf(x) dx.
Tällöin on vastaavasti oltava
Z
|x|f(x) dx <∞.
Tässä vaiheessa on hyvä palauttaa mieleen, että integraaliR−∞∞ ϕ(x)dxon olemassa vain silloin, kun raja-arvo lima→∞b→∞ R−ba ϕ(x) dx on olemassa. Raja- arvon lima→∞Ra
−aϕ(x)dx on hyvinkin mahdollista olla olemassa ilman, että integraali R−∞∞ ϕ(x) dx on.
Esimerkki 2.3. Tarkastellaan esimerkkinä Cauchyn jakauman tiheysfunk- tiota:
f(x) = 1 π
1
1 +x2, −∞< x < ∞.
Selvästikin
a→∞lim
a
Z
−a
x π
1
1 +x2 dx= 0.
Nyt E(X) ei kuitenkaan ole olemassa, sillä integraali 1
π
∞
Z
−∞
|x|
1 +x2 dx hajaantuu.
Huomautus 1. Sanotaan, että satunnaismuuttujaX onsymmetrinen pisteen α suhteen, jos
P{X≥α+x}=P{X ≤α−x} kaikillax:n arvoilla.
Kertymäfunktiolle F tämä tarkoittaa seuraavaa:
Jos kaikille x∈R pätee
F(α−x) = 1−F(α+x) +P{X =α+x},
niin sanotaan F:n olevan symmetrinen ja α:n olevan sen symmetriakeskus.
Jos α= 0, pätee jokaisella x
F(−x) = 1−F(x) +P{X =x}.
Erityisesti jos X on jatkuva satunnaismuuttuja, se on symmetrinen α:n ollessa sen symmetriakeskus, jos ja vain jos sen tiheysfunktio f toteuttaa seuraavan yhtälön kaikilla x:n arvoilla:
f(α−x) =f(α+x).
Siinä tapauksessa, ettäα = 0 puhutaan yksinkertaisesti, ettäX on symmet- rinen.
Tästä seuraa suoraan se, että kun X on symmetrinen, α symmetriakes- kuksena ja E(X) < ∞, niin E(X) = α. Selkeä esimerkki symmetrisestä jakaumasta on Cauchyn tiheysfunktio, joka esiteltiin tämän kappaleen esi- merkissä 2.3. [13, s. 69-71]
2.4 Momentit
Ennen momentit generoivaa funktiota on hyvä selventää hieman sitä, mitä momentit ovat. Ne ovat myös tärkeitä jakauman tunnuslukuja. Momenttien avulla voidaan luonnehtia satunnaismuuttujan jakaumaa ja ne määritellään odotusarvon avulla.
Määritelmä 2.5. Kunn ∈Z+ ja odotusarvoE(X) on olemassa, satunnais- muuttujan X n:s momentti on
mn=E(Xn).
Satunnaismuuttujan X n:s keskusmomentti taas saadaan seuraavan kaavan avulla:
m0n=E[(X−m)n], missä m=m1 =E(X)
[2, s. 59]
Huomautus 2. Kunα on positiivinen kokonaisluku jaE(|X|)α <∞, saadaan βα =E(|X|)α, jota kutsutaan satunnaismuuttujanX α:ksiitseisarvomomen- tiksi. Tämä esiintyy myöhemmin kappaleessa 4.3 sekä Tsebysevin epäyhtälön että Ljapunovin epäyhtälön yhteydessä. [13, s. 72]
Määritelmästä 2.5 nähdään, että satunnaismuuttujan ensimmäinen mo- mentti on jakauman odotusarvo. Toinen tärkeä ja usein tarpeellinen moment- ti on satunnaismuuttujan toinen keskusmomentti, joka tunnetaan paremmin varianssina. [2, s. 59]
Määritelmä 2.6. JosE(X2) on olemassa, onE[(X−m)2] satunnaisfunktion X varianssi ja voidaan merkitä σ2 =var(X) =E[(X−m)2]. [13, s. 79]
Esimerkki 2.4. Olkoon X tasaisesta jakaumasta luonnollisten lukujen jou- kosta. Olkoon siis
P{X =k}= 1
N, k = 1,2, . . . , N.
Selvästi kaikkien kertalukujen momentit ovat olemassa:
E(X) =
N
X
k=1
k· 1
N = N + 1 2 , E(X2) =
N
X
k=1
k2· 1
N = (N + 1)(2N + 1)
6 jne.
[13, s. 73]
Esimerkki 2.5. OlkoonXeksponenttijakauman satunnaismuuttuja. Tällöin sen tiheysfunktio on
f(x) = 1
λe−x/λ, 0≤x <0 jaλ >0.
Määritetään ensin X:n odotusarvo:
E(X) =
∞
Z
0
1
λxe−x/λ dx
=
∞
0
−xe−x/λ+
∞
Z
0
e−x/λ dx k osittaisintegrointi
=
∞
Z
0
e−x/λ dx=λ.
[2, s. 56]
Määritetään sitten X:n varianssi:
var(X) =E[(X−λ)2] =
∞
Z
0
(x−λ)21
λe−x/λ dx
=
∞
Z
0
(x2−2xλ+λ2)1
λe−x/λ dx=λ2. [3, s. 8-9]
3 Tarvittavia ennakkokäsitteitä
Jatketaan pohjustusta vielä tarpeellisilla esitiedoilla karakteristisesta funk- tiosta ja generoivista funktioista yleensä. Generoivia funktioita on siis muita- kin, kuin tässä tutkielmassa käsittelyyn otettu momentit generoiva funktio.
Käydään tässä kappaleessa läpi yleisellä tasolla generoivien funktioiden tar- koitusta sekä määritellään karakteristinen funktio, jota hyödynnetään myö- hemmin muun muassa Lauseen 4.1 todistuksessa.
3.1 Generoivat funktiot
Oletetaan, että halutaan tutkia lukujonoa (a0, a1, a2, . . .). Tällainen jono saattaa olla määritelty tietyn suhdeluvun avulla tai se saattaa käsittää jonkin joukkoperheen. Erilaisia lukujonojen luokkia, joilla kaikilla on hyvin erilai- set ominaisuudet, on monia. Mitä ovat ne yleiset keinot, joilla lukujonoja voidaan tutkia? Yksi tällainen työväline on generoiva funktio:
A(x) =a0+a1x+a2x2+· · ·=
∞
X
k=0
akxk.
[12, s. 1]
Generoiva funktio on siis keino esittää lukujonoja tiiviimmässä muodossa.
Esimerkiksi geometrinen lukujono voidaan muotoilla seuraavasti:
a+arx+ar2x2+· · ·=
∞
X
k=0
arkxk= a 1−rx. [12, s. 1]
Generoivien funktioiden summa on yksinkertaisesti A(x) +B(x) =
∞
X
k=0
(ak+bk)xk. [7, s. 32]
Generoivien fuktioiden tulo taas on hieman mielenkiintoisempi. Kirjoite- taan siitä määritelmä.
Määritelmä 3.1. OlkoonA(x) =P∞k=0akxkjaB(x) = P∞k=0bkxkgeneroivia funktioita. Niiden tulo AB on generoiva funktio C(x) = P∞k=0ckxk, missä
ck =
k
X
i=0
aibk−i.
[12, s. 5] Tätä tuloa kutsutaan myös Cauchyn tuloksi. [7, s. 32]
Kun generoivia funktioita lähestytään algebrallisesti, symbolillex ei vält- tämättä anneta lukuarvoja, jolloin sen potenssi vain ilmaisee kertoimensa paikan lukujonossa. Tällaisen lähestymistavan etuna on, että sarjan suppe- nemista ei tarvitse tutkia ollenkaan. Generoivia funktioita voi kuitenkin lä- hestyä myös analyyttisesti, kuten tässä tutkielmassa myöhemmin tehdään.
Tällöin sarjan A(x) suppenemisellekin asetetaan tiettyjä ehtoja. [7, s. 32-33]
Toinen generoiva funktio, joka on hyvä tuntea, on eksponentiaalinen ge- neroiva funktio:
∞
X
k=0
akxk k!.
Tietyissä tilanteissa tämä on soveltuvampi työväline.
Esimerkiksi
∞
X
k=0
xk k! =ex,
joka on jonon (1,1,1, . . .) eksponentiaalinen generoiva funktio. [1, s. 60]
Yksinkertaisin generoiva funktio, jota käytetään todennäköisyysteoriassa on diskreetin satunnaismuuttujan X todennäköisyydet generoiva funktio.
Määritelmä 3.2. Olkoon X:n tiheysfunktio pk =P{X =k}, k = 0,1,2, . . . ja
∞
X
k=0
pk= 1.
Tällöin satunnaismuuttujan X todennäköisyydet generoiva funktio on G(s) =
∞
X
k=0
pksk,
mikä suppenee, kun |s| ≤1.
Esimerkki 3.1. Tarkastellaan Poisson-jakautunutta satunnaismuuttujaaX, jonka tiheysfunktio on
P{X =k}=e−λλk
k!, k = 0,1,2, . . . . Tällöin saadaan, että
G(s) =
∞
X
k=0
(sλ)ke−λ
k! =e−λesλ =e−λ(1−s) kaikilla s:n arvoilla.
[13, s. 85-86]
3.2 Karakteristinen funktio
Karakteristinen funktio on kuvaus, jota kutsutaan analyysin puolella myös Fourier-Stieltjes-muunnokseksi. Tässä tutkielmassa sitä tarvitaan Lauseen 4.1 todistuksessa. Karakteristinen funktio on olemassa kaikille jakaumille toisin kuin esimerkiksi momentit generoiva funktio.
Määritelmä 3.3. OlkoonXsatunnaismuuttuja. Kompleksiarvoinen funktio φ on määritelty joukossa R seuraavasti
(3.1) φ(t) = E(eitX), t∈R
ja i = √
−1 on imaginääriyksikkö. Tätä funktiota φ kutsutaan satunnais- muuttujan X karakteristiseksi funktioksi. [13, s. 89]
Kun kyseessä on diskreetti jakauma, φ(t) = X
k
eitxkP{X =xk} ja kun jakauma on jatkuva,
φ(t) =
∞
Z
−∞
eitxf(x) dx.
Esimerkki 3.2. Olkoon X Poisson-jakautunut parametrilla λ. Tällöin φ(t) =e−λ
∞
X
k=0
eitkλk k!
=e−λ
∞
X
k=0
(λeit)k k!
=e−λeλeit
=eλ(eit−1). [15, s. 67]
Esimerkki 3.3. OlkoonXnormaalisti jakautunut satunnaismuuttuja, jonka tiheysfunktio on
f(x) = 1
√2πe−x2/2, x∈R.
Muutetaan ensin Eulerin kaavaa, eix = cosx +isinx, käyttäen kaava (3.1) muotoon
φ(t) = E(eitX) =E(cos(tX)) +iE(sin(tX)).
Nyt
φ(t) = 1
√2π
∞
Z
−∞
cos(tx)e−x2/2 dx+ i
√2π
∞
Z
−∞
sin(tx)e−x2/2 dx.
Huomataan, että sin(tx) on pariton funktio samoin kuin sin(tx)e−x2/2. Näin ollen edellisen funktion oikeanpuoleinen integraali häviää ja saadaan
φ(t) = 1
√2π
∞
Z
−∞
cos(tx)e−x2/2 dx
= 2
√2π
∞
Z
−∞
1
2cos(tx)e−x2/2 dx =e−t2/2, t ∈R. (vrt. [13, s. 90])
4 Momentit generoiva funktio
Nyt päästään vihdoin momentit generoivaan funktioon. Tämä kappale sisäl- tää aluksi tietenkin määritelmän, minkä jälkeen esitellään muutamia esimerk- kejä ja momentit generoivan funktion ominaisuuksia. Näiden jälkeen tarkas- tellaan tietyn jakauman määrittämistä sen momenteista sekä muutamia mo- menttiepäyhtälöitä. Viimeinen luku käsittelee riippumattomien muuttujien summaa.
4.1 Momentit generoivan funktion määritelmä ja pe- rusominaisuuksia
Momentit generoiva funktio on hyödyllinen työkalu todennäköisyyslasken- nassa ja tilastotieteessä. Sen avulla voidaan, nimensä mukaisesti, johtaa sa- tunnaismuuttujan momentit. Tässä tutkielmassa momentit generoivasta funk- tiosta voidaan käyttää myös merkintää MGF.
Määritelmä 4.1. OlkoonX satunnaismuuttuja, jolla on kertymäfunktioF. Funktio
(4.1) M(s) = E(esX)
on tällöin satunnaismuuttujanX momentit generoiva funktio, jos lausekkeen (4.1) oikeanpuoleinen odotusarvo on olemassa jossain nollan ympäristössä.
Toisin sanoen on olemassa h >0 siten, että kaikilla s:n arvoilla−h < s < h, E(esX) on olemassa.
[13, s. 87] ja [2, s. 62]
Tämän pohjalta voidaan tarkentaa, että X:n MGF on M(s) =
∞
X
k=1
esxP{X =x}, kun X on diskreetti ja
M(s) =
∞
Z
−∞
esxf(x) dx, kun X on jatkuva.
Esimerkki 4.1. Olkoon diskreetin satunnaismuuttujanX tiheysfunktio P{X =k}=
( 6
π2 · k12, k = 1,2, . . .
0 muulloin.
Nyt
E(esX) = 6 π2
∞
X
k=1
esk
k2 =∞, kun s >0.
Tästä nähdään, ettäX:n MGF ei ole olemassa. Itse asiassa myösE(X) =∞.
Esimerkki 4.2. Olkoon X:n tiheysfunktio f(x) =
( 1
2e−x/2, x >0
0 muulloin.
Tällöin X on selvästi jatkuva ja M(s) = 1
2
∞
Z
0
e(s−1/2)x dx
= 1
1−2s, s < 1 2.
Tarkastellaan sitten samaa jakaumaa kuin generoivan funktion yhteydes- sä:
Esimerkki 4.3. Olkoon X:n tiheysfunktio (vrt. esimerkki 3.1) P{X =k}=
( e−λ λk!k, k = 0,1,2, . . .
0 muulloin.
Silloin
M(s) =E(esX) = e−λ
∞
X
k=0
eskλk k!
=e−λ(1−es) kaikillas:n arvoilla.
(vrt. [13, s. 87-88])
Esimerkki 4.4. Binomijakauman tiheysfunktio on muotoa f(x) = P{X =x}= n
k
!
px(1−p)n−x, x= 0,1, . . . n, missä n on positiivinen kokonaisluku ja 0≤p≤1.
Nyt
M(s) =
n
X
x=0
esx n k
!
px(1−p)n−x =
n
X
x=0
n k
!
(pes)x(1−p)n−x. Binomikaavan (ks. esim. [2, s. 90]) mukaan
n
X
x=0
n x
!
uxvn−x = (u+v)n. Tällöin, kun u=pes ja v = 1−p, saadaan
M(s) = [pes+ (1−p)]n.
Lause 4.1. Momentit generoiva funktio määrittää aina tietyn kertymäfunk- tion yksikäsitteisesti. [13, s. 88]
Todistus. Tämän lauseen todistus on esitetty tässä pääpiirteittäin. Tarkem- masta esityksestä kiinnostunut lukija voi tutustua esimerkiksi lähteeseen [4].
(i) Tarkastellaan ensin rajoitettua jatkuvaa satunnaismuuttujaa. Tiede- tään, että kun X on jatkuva
M(s) =E(esX) =
∞
Z
−∞
esxf(x) dx.
Jos korvataans it:llä, missäton reaaliluku jai=√
−1, silloin sarja suppenee kaikilla t ja voidaan määritellä funktio
φ(t) =M(it) =
∞
Z
−∞
eitxf(x) dx.
Tämähän onX:n karakteristinen funktio. Tästä nähdään myös, että funktio φ onf:n Fourier-muunnos (ks. esim. [11]). Toisaalta tiedetään, että Fourier- muunnoksen käänteisfunktio saadaan kaavaa
f(x) = 1 2π
∞
Z
−∞
e−itxφ(t) dt
soveltaen.[6, s. 398]
Näin nähdään, että karakteristinen funktio φja sitä kautta momentit ge- neroiva funktio M, määrää tiheysfunktion f yksikäsitteisesti, jolloin myös kertymäfunktio on yksikäsitteisesti määritelty.
(ii) Toisena käsitellään tapaus, kun X on diskreetti satunnaismuuttuja, jolla on äärellinen arvojoukko{x1, x2, . . . , xn}, kertymäfunktioF ja momentit generoiva funktio M.
Tällöin
M(s) =
n
X
j=1
esxjF(xj).
Asetetaan aj =F(xj) ja sitten valitaan n kpl soveltuvia s:n erilaisia arvoja si ja merkitään bi =M(si). Näin saadaan
bi =
n
X
j=1
esixjaj
tai matriisimerkinnöillä
B=MA.
TässäB = (bi) jaA= (aj) ovatn-sarakevektoreita ja M= (esixj) onn×n- matriisi. Saatu matriisiyhtälö voidaan ratkaista A:n suhteen:
A=M−1B,
silloin, kun matriisiMon kääntyvä (ts.M:n determinantin on oltava eri kuin 0).
Tämä voidaan aina järjestää valitsemalla arvot si = i−1, sillä tällöin M:n determinantti on Vandermonden determinantti exi:lle,
det
1 1 1 . . . 1
esx1 esx2 esx3 . . . esxn e2sx1 e2sx2 e2sx3 . . . e2sxn
. . .
e(n−1)sx1 e(n−1)sx2 e(n−1)sx3 . . . e(n−1)sxn
,
jonka arvo on Qi<j(exi −exj).
Tällainen determinantti eroaa aina nollasta, jos sen xj:t ovat eriarvoiset.
Siis sarakevektori A = (aj) saadaan ratkaistuksi matriisiyhtälöstä, jolloin kertymäfunktio tulee yksikäsitteisesti määritetyksi. [6, s. 370]
Huomautetaan vielä, että jos oletus satunnaismuuttujan äärellisyydestä otetaan pois, edellinen todistus ei välttämättä enää päde.
Seuraava lause selittää, miksi funktiota M(s) kutsutaan momentit gene- roivaksi funktioksi.
Lause 4.2. Jos satunnaismuuttujan X momentit generoiva funktio, M(s), on olemassa s:lle välillä [−s0, s0], kun s0 >0, on sen kaikkien asteiden deri- vaatat olemassa, kun s = 0 ja
M(k)(0) =E(Xk), k on positiivinen kokonaisluku.
[13, s. 88]
Todistus. Olkoon M(s) = E(esX) satunnaismuuttujanX momentit generoi- va funktio.
Erotetaan diskreetti ja jatkuva tapaus toisistaan:
Kun X on diskreetti:
d
dsM(s) = d ds
X
x
esxp(x)
=X
x
d
dsesxp(x) k (∗)
=X
x
xesxp(x), jolloin
M0(0) =X
x
xe0xp(x) = X
x
xp(x) = E(X).
(∗) suppenevan potenssisarjan voi derivoida termeittäin
Koska dsdkkesx = xkesx, on selvää, että tulos voidaan yleistää koskemaan myös k. derivaattaa. [5, s. 2]
Kun X on jatkuva ja oletetaan, että integraalimerkin yli voidaan derivoi- da, saadaan
d
dsM(s) = d ds
∞
Z
−∞
esxf(x) dx
=
∞
Z
−∞
(d
dsesx)f(x)dx
=
∞
Z
−∞
(xesx)f(x)dx
=E(XesX).
Näin ollen
M0(0) =E(Xe0X) = E(X).
Kun jatketaan vastaavalla tavalla päädytään tulokseen M(k)(0) = dk
dskM(0) =E(Xke0X) = E(Xk)
[3, s. 10]
Huomautus 3. Vaihtoehtoisesti, jos MGF, M(s), on olemassa s:lle välillä [−s0, s0], kun s0 > 0, voidaan M(s) ilmaista (yksikäsitteisesti) Maclaurin sarjan kehitelmänä:
M(s) =M(0) + M0(0)
1! s+ M00(0)
2! s2+· · · ,
jossa siisE(Xk) on terminsk/k! kerroin. Kun muistetaan alaluvun 2.4 mää- ritelmä 2.5, niin saadaan vielä toinen muotoilu:
M(s) =
∞
X
k=0
mk k! sk.
Viimeistään tästä nähdään selkeästi, mistä momentit generoivan funktion nimi saadaan.
Esimerkki 4.5. Olkoon nytXjatkuva satunnaismuuttuja, jonka arvojoukko on väli [0,∞) ja kertymäfunktiof(x) =λe−λx. Silloin
mn =E(Xn) =
∞
Z
0
xnλe−λx dx=λ(−1)n dn dλn
∞
Z
0
e−λx dx
=λ(−1)n dn dλn
1 λ
= n!
λn. Nyt
M(s) =
∞
X
k=0
mksk k!
=
∞
X
k=0
k!sk λk
1 k!
=
∞
X
k=0
s λ
k
= λ
λ−s. Tämä sarja suppenee vain, jos |s|< λ. [6, s. 396]
Huomautus 4. Satunnaismuuttujan X varianssi voidaan nyt muotoilla myös toisella tavalla (vrt. Määritelmä 2.6), var(X) = E(X2)−(E(X))2.
Esimerkki 4.6. Olkoon X satunnaismuuttuja, jonka tiheysfunktio on f(x) = 1
2e−x/2, x >0.
Esimerkistä 4.2. saadaan, että M(s) = 1
1−2s, kun s < 1 2. Tällöin
M0(s) = 2
(1−2s)2 ja M00(s) = 4·2
(1−2s)3, s < 1 2. Tästä seuraa, että
E(X) = 2, E(X2) = 8 ja var(X) = 4.
Esimerkki 4.7. Olkoon X satunnaismuuttuja, jonka tiheysfunktio on f(x) =
( 1, 0≤x≤1 0 muulloin.
Nyt
M(s) =
1
Z
0
esx dx= es−1
s , kaikillas, M0(s) = es·s−(ss−1)·1
s2 ,
ja
E(X) =M0(0) = lim
s→0
ses−es+ 1 s2 = 1
2. (vrt. [13, s. 89])
Painotetaan vielä, että odotusarvoE(esX) ei ole aina olemassa. Itse asias- sa vaatimus siitä, että M(s) on olemassa nollan läheisyydessä, on kova vaa- timus, jota jotkut yleiset jakaumat eivät täytä. On olemassa generoiva funk- tio, joka on olemassa kaikille jakaumille, karakteristinen funktio. Tarkempaa tietoa siitä löytyy tutkielman pohjatiedoista.
4.2 Jakauman määrittäminen momenteista
Käsitellään nyt jakauman määrittämistä sen momenteista. Annetaan joukko vakioita, {µ0 = 1, µ1, µ2, . . .} ja kysytään, voivatko ne olla tietyn kertymä- funktion F momentteja. Tässä vaiheessa on hyvä huomioida muutama asia.
Ensinnäkin josM(s) =E(esX) on olemassa jollekin satunnaismuuttujalle X,s:n ollessa nollan läheisyydessä, silloinE(|X|n)<∞kaikillan≥1. Mutta oletuksestaE(|X|n)<∞kaikillan≥1 ei kuitenkaan seuraa, ettäX:n MGF on olemassa. [13, s. 90]
Esimerkki 4.8. Olkoon X satunnaismuuttuja, jonka tiheysfunktio on f(x) =ce−|x|α, 0< α <1, −∞< x <∞,
missä con vakio ja määritelty yhtälöstä c
∞
Z
−∞
e−|x|α dx= 1.
Olkoon s >0. Tällöin
∞
Z
0
esxe−xα dx=
∞
Z
0
ex(s−xα−1) dx
ja koska α− 1 < 0, R0∞esxe−xα dx on ääretön kaikilla s > 0. Näin ollen momentit generoivaa funktiota ei ole olemassa. Kuitenkin
E(|X|n) = c
∞
Z
−∞
|x|ne−|x|α dx= 2c
∞
Z
−∞
xne−xα dx <∞ kaikillan ∈Z+. Toiseksi, kahdella (tai useammalla) satunnaismuuttujalla voi olla sama joukko momentteja.
Esimerkki 4.9. Olkoon X:llä lognormaalisti jakautunut tiheysfunktio f(x) = (x−√
2π)−1e−(logx)2/2, x >0, ja f(x) = 0, kun x≤0.
Olkoon Xε:n, |ε| ≤1, tiheysfunktio
fε(x) = f(x)[1 +εsin(2πlogx)], x∈R.
[Huomaa, että fε ≥0 kaikille ε, |ε| ≤1, ja R−∞∞ fε(x) dx= 1, joten fε on tiheysfunktio.] Koska kuitenkin
∞
Z
0
xkf(x) sin(2πlogx) = 1
√2π
∞
Z
−∞
e−(t2/2)+ktsin(2πt) dt
= 1
√2πek2/2
∞
Z
−∞
e−y2/2sin(2πy)dy
= 0, niin nähdään, että
∞
Z
0
xkf(x) dx=
∞
Z
0
xkfε(x) dx,
kaikille ε, kun|ε| ≤1 ja k = 0,1,2, . . .. Mutta f(x)6=fε(x).
[13, s. 91]
Kolmanneksi, jokaisen satunnaismuuttujan X momentit täyttävät tietyt vaatimukset.
Esimerkiksi, josβν =E(|X|ν), myöhemmin esitettävän Ljapunovin epäyhtä- lön (4.7) perusteella nähdään, että (βν)1/ν onν:n kasvava funktio. Yhtä lailla sen neliömuoto
E
n
X
i=1
Xαiti
!2
≥0
antaa X:n eri kertalukujen momenttien välisen suhteen. [13, s. 91]
Aiemmin todistettu Lause 4.1 antaa riittävän ehdon tietyn F:n määrit- tämiseen sen momenteista.
Esimerkki 4.10. Olkoon satunnaismuuttujalla X tiheysfunktio f(x) =
( e−x, kun x≥0 0, kun x <0.
Tällöin
E(Xk) =
∞
Z
0
xke−x dx=k!, ja Huomautuksesta 3 saadaan, että
(4.2) M(s) =
∞
X
k=0
mksk k! =
∞
X
k=0
sk= 1 1−s,
kun 0 < s < 1, mikä on X:n momentit generoiva funktio, jolloin {mk} määrittää F:n yksikäsitteisesti.
Tarkemmin, jos jollakin vakiolla c
|mk| ≤ck, k = 1,2, . . . ,
niin ∞
X
k=1
|mk| k! sk ≤
∞
X
k=1
(cs)k
k! < ecs, kun s >0
ja X:n kertymäfunktio määritetään yksikäsitteisesti. Näin ollen, jos
P{|X| ≤ c} = 1 jollakin c > 0, niin kaikki X:n momentit ovat olemassa täyttäen ehdot |mk| ≤ ck, k ≥ 1 ja X:n kertymäfunktio on yksikäsitteisesti määritetty sen momenteista.
Esitetään vielä riittäviä ehtoja, joilla jono momentteja voi määrittää yk- sikäsitteisesti kertymäfunktion.
(i) Satunnaismuuttujan vaihteluväli on äärellinen.
(ii)P∞k=1(m2k)−1/2k =∞, kun satunnaismuuttujan vaihteluväli on (−∞,∞).
Jos vaihteluväli on (0,∞), riittää ehdoksi P∞k=1(mk)−1/2k =∞.
(iii) limn→∞[(m2n)1/2n/2n] on äärellinen. [13, s. 92]
4.3 Momenttiepäyhtälöitä
Tässä kappaleessa johdetaan muutama epäyhtälö satunnaismuuttujan mo- menteille. Luvun päätulos on Lause 4.3 (sekä seuraus 4.4), joka antaa ylä- rajan häntätodennäköisyydelle (tail probability) jonkin satunnaismuuttujan momentin suhteen. Luku seuraa päälähdettä [13] sivuilta 95-100.
Lause 4.3. OlkoonX satunnaismuuttuja ja olkoonhsellainen, ettäh(X)on ei-negatiivinen satunnaismuuttuja. Jos E(h(X))on olemassa, niin jokaisella ε >0 pätee
(4.3) P{h(X)≥ε} ≤ E(h(X))
ε .
Todistus. Todistetaan tulos, kun X on diskreetti.
Olkoon P{X =xk}=pk, k = 1,2, . . . . Tällöin E(h(X)) =X
k
h(xk)pk
= X
A
+X
Ac
!
h(xk)pk, missä
A={k :h(xk)≥ε}.
Nyt
E(h(X))≥X
A
h(xk)pk≥εX
A
pk
=εP{h(X)≥ε}.
Seuraus 4.4. Olkoon h(X) = |X|r ja ε =Kr, missä r >0 ja K >0. Nyt
(4.4) P{|X| ≥K} ≤ E(|X|r)
Kr .
Tätä kutsutaan Markovin epäyhtälöksi. Jos vielä määritetään, että h(X) = (X−µ)2, ε=K2σ2, saadaan Tsebyshevin epäyhtälö:
(4.5) P{|X−µ| ≥Kσ} ≤ 1
K2, missä µ=E(X) ja σ2 =var(X).
Huomautus 5. Jos halutaan olla tarkkoja kertymäfunktion määritelmän, F(x) =P{X ≤x}suhteen, voidaan kaava (4.3) muotoilla uudelleen seuraa- valla tavalla:
P{h(X)> ε}< E(h(X))
ε .
Sellaisille satunnaismuuttujille, joilla on äärellinen toisen asteen momentti, epäyhtälö (4.5) on tarkin ilmaisu, johon voidaan päästä.
Esimerkki 4.11. Olkoot
P{X = 0}= 1− 1
K2, k K >1 ja vakio P{X =±1}= 1
2K2,
E(X) = 0, E(X2) = 1
K2, σ = 1 K. Näin ollen
P{|X| ≥Kσ}=P{|X| ≥1}= 1 K2, jolloin päästään yhtäsuuruuteen.
Esimerkki 4.12. Olkoon X:n tiheysfunktio f(x) =
( 1, kun 0< x < 1 0 muulloin.
Nyt
E(X) = 1
2, E(X2) = 1
3, var(X) = 1 3− 1
4 = 1 12 ja
P
|X− 1 2|<2
s 1 12
=P
(1 2− 1
√3 < X < 1 2+ 1
√3
)
= 1.
Tsebyshevin epäyhtälöstä saadaan vielä P
|X−1 2|<2
s 1 12
≥1− 1
4 = 0,75.
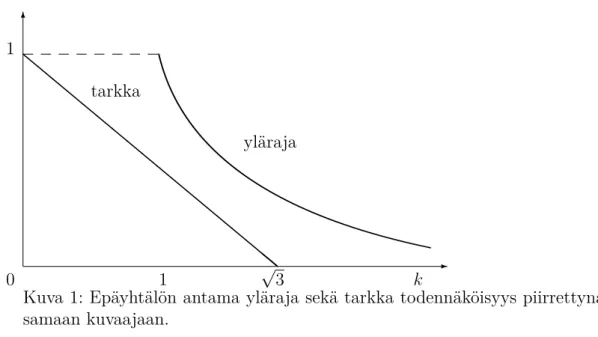
Kuvassa 1 (s. 24) verrataan epäyhtälön P n|X−12| ≥k/√
12o antamaa ylä- rajaa tarkkaan todennäköisyyteen.
Joissakin tapauksissa on mahdollista tarkentaa arviota vielä Tsebyshevin epäyhtälöstä, jos oletetaan, että korkeamman asteen momentteja on olemas- sa. Sitä varten tarvitaan seuraava lemma.
-
k
6
1 √
3 1
0
tarkka
yläraja
l l
l l
l l
l l
l l
l l
l l
l l
ll
Kuva 1: Epäyhtälön antama yläraja sekä tarkka todennäköisyys piirrettynä samaan kuvaajaan.
Lemma 4.5. Olkoon X satunnaismuuttuja siten, ettäE(X) = 0 ja var(X) =σ2. Tällöin
(4.6) P{X ≥x} ≤ σ2
σ2 +x2, jos x >0 ja
(4.7) P{X ≥x} ≥ x2
σ2+x2, jos x <0.
Todistus. Olkoon h(t) = (t+c)2, c > 0. Silloinh(t)≥0 kaikilla t:n arvoilla ja
h(t)≥(x+c)2, kunt ≥x >0.
Tästä seuraa, että
P{X ≥x} ≤P{h(X)≥(x+c)2}
≤ E((X+c)2)
(x+c)2 aina, kun c >0 jax >0.
Kaavan (4.7) todistus menee vastaavalla tavalla.
Lause 4.6. Olkoon E(|X|4)<∞ ja olkoot E(X) = 0, E(X2) =σ2. Silloin P{|X| ≥Kσ} ≤ µ4−σ4
µ4+σ4K4−2K2σ4, kun K >1, missä µ4 =E(X4).
Todistus. Sijoitetaan todistusta varten osamäärän (X2 − σ2)/(K2σ2 −σ2) tilalle X ja asetetaan x= 1 kaavaan (4.6). Siten saadaan, että
P{X2−σ2 ≥K2σ2−σ2} ≤ var[(X2−σ2)/(K2σ2−σ2)]
1 +var[(X2−σ2)/(K2σ2−σ2)]
= µ4−σ4
µ4(K2−1)2+µ4−σ4
= µ4 −σ4
µ4+σ4K4−2K2σ4, K >1.
Esimerkki 4.13. Olkoon X tasaisesti jakautunut ja sen tiheysfunktio f(x) =
( 1, kun 0< x < 1 0 muulloin.
Tällöin
E(X) = 1
2, var(X) = 1
12, µ4 =E
X− 1 2
2!
= 1 80 ja
P
|X−1 2| ≥2
s 1 12
≤
1 80 −1441
1
80 +1441 ·16−81441 = 4 49, mistä saadaan
P
|X− 1 2|<2
s 1 12
≥ 45
49 ≈0,92.
Tämä on paljon tarkempi arvio, kuin mitä saadaan Tsebyshevin epäyhtälöstä esimerkissä 4.12.
Lause 4.7(Ljapunovin epäyhtälö). Olkoonβn=E(|X|n)<∞. Nyt saadaan βk−11/(k−1) ≤βk1/k,
kun k saa mielivaltaisen arvon väliltä 2≤k ≤n.
Todistus. Käsitellään neliömuotoa:
Q(u, v) =
∞
Z
−∞
(u|x|(k−1)/2+v|x|(k+1)/2)2f(x) dx,
missä ollaan oletettu, ettäX on jatkuva ja f on sen tiheysfunktio. Tässä on siis
Q(u, v) =u2βk−1+ 2uvβk+βk+1v2. Selvästikin Q≥0 kaikilla u, v ∈R. Tästä seuraa, että
βk−1 βk βk βk+1
≥0, mikä implikoi, että
βk2k ≤βk−1k βk+1k . Näin ollen
β12 ≤β01β21, β24 ≤β12β32, . . . , βn−12(n−1) ≤βn−2n−1βnn−1, missä β0 = 1. Kun otetaan k−1 peräkkäisen tällaisen tulo, saadaan
βk−1k ≤βkk−1 tai βk−11/(k−1) ≤βk1/k. Tästä seuraa, että
β1 ≤β21/2 ≤β31/3 ≤ · · · ≤βn1/n. Yhtäsuuruus on voimassa, jos ja vain jos
βk1/k =βk+11/(k+1) kun k = 1,2, . . . .
Toisin sanoen{βk1/k}on yhden vakion lukujono, mikä on totta jos ja vain jos
|X| on degeneroitunut. Siis jollain c:n arvolla P{|X|=c}= 1.
(vrt. [13, s. 95-100])
4.4 Riippumattomien muuttujien summa
Tarkastellaan lopuksi vielä tilanteita, joissa on mukana kaksi tai useampi satunnaismuuttuja. Miten momentit generoiva funktio sopii tällöin käytettä- väksi?
Lause 4.8. OlkootXjaY riippumattomia satunnaismuuttujia, joiden MGF:t ovat MX(s) ja MY(s). Tällöin
MX+Y(s) = MX(s)·MY(s)