Cette thèse porte sur l'application des techniques de contrôle optimal et de contrôle géométrique au problème de transfert d'orbite des satellites et à la géométrie quasi-riemannienne. Le chapitre 2 traite du problème de moyenne avec un réglage de poussée faible.
Formulation g´ en´ erale
Dans ce chapitre, nous présentons d'abord des généralités sur le problème du transfert d'orbite des satellites, sa modélisation et les équations dynamiques. Enfin, nous introduisons le cadre géométrique dans lequel s'inscrit le problème du transfert d'orbite, en utilisant le formalisme du principe du maximum de Pontryagin.
Syst` eme consid´ er´ e
Il est aisé de comprendre que l'étude du problème peut varier fortement selon le type de situation (type d'engin spatial, type de moteur, autres contraintes industrielles, coûts... à réduire, type de frottement, changement du champ gravitationnel). , etc.), même si la formulation reste la même. Nous proposons donc une formalisation plus précise et l'introduction d'outils mathématiques adaptés à l'étude de cette classe de problèmes d'optimisation.
Pouss´ ee et contraintes
Cependant, le contrôle d'attitude du satellite permet son orientation, et en pratique la direction de poussée peut souvent être contrôlée. Lorsque cela n'est pas possible, on parle de contraintes de cône directionnel si la poussée reste dans un cône donné et que les directions ne sont pas accessibles.
Equations de la dynamique
Mouvement libre
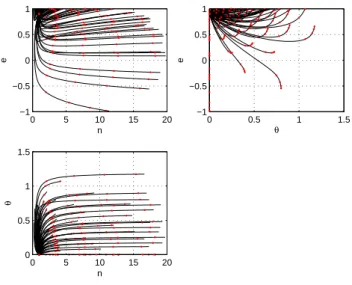
L'argument du périgée θ est l'angle entre le nœud ascendant et le périgée de E, il indique l'angle entre la ligne des nœuds et l'axe focal. La vraie longitude est l= Ω + θ+f, où la vraie anomalie f est l'angle entre le périgée et la position du véhicule en E.
Mouvement contrˆ ol´ e
Le système précédent s’écrit de manière équivalente dans le repère tangentiel/normal comme suit. Le contrôle est décomposé par rapport à u = (un, ut, uc) et dans ce cas on considère le demi-axe majeur au lieu de la coordonnée P à obtenir.
Equation de variation de la masse ´
Crit` eres de minimisation
Crit` ere de temps minimal
De plus, certaines missions visent à rendre l'engin spatial opérationnel très rapidement, voire le plus rapidement possible et la solution sera donnée en utilisant ce critère qui est écrit.
Crit` ere de consommation minimale de carburant
Crit` ere d’´ energie minimale
M´ ethode de continuation
Probl` eme de contrˆ ole
Principe du maximum de Pontryagin
Enonc´ ´ e
On appelle extrémal un triplet (x, p, u) qui est une solution du système hamiltonien (1.8) et qui satisfait la condition du maximum. De plus, si les conditions de transversalité sont vérifiées, l’extrémal est qualifié d’extrémal BC.
Application au probl` eme de l’´ energie minimale pour
Le but de ce chapitre est d'appliquer les techniques de moyenne classiques, dérivées des systèmes dynamiques, au problème de transfert d'orbite à faible poussée à énergie minimale. La méthode de moyenne décrite dans la section 2.2 s'applique très bien au problème de transfert d'orbite dans un contexte de faible poussée.
M´ ethode de moyennation
Mod´ elisation en dimension deux
M´ etriques et outils g´ eom´ etriques
M´ etriques de Liouville
Le cas Clairaut-Liouville peut être défini en lui-même comme une métrique ayant pour première intégrale F, linéaire dans p, qui s'écrit F = a(x, y )px+b(x,y)py. Une généralisation est la classe des métriques de Liouville qui admettent une première intégrale quadratique dans p.
Formes normales de m´ etriques de Liouville
En calculant F aux nouvelles coordonnées F =b01p2u+ 2b02pupv+b03p2v, on obtient, grâce aux conditions de Cauchy-Riemann. Dans les deux cas, la transformation est évidente si la première intégrale est connue.
Probl` eme d’optimalit´ e
Application de la moyennation au probl` eme de transfert or-
La coordonnée θ devient cyclique via la moyenne, elle ne l'est pas pour le problème non moyen.
Cas bientr´ ee et probl` emes riemanniens
- Construction d’une forme normale
- M´ etrique g 1
- Int´ egration du flot extr´ emal
- M´ etrique g 2
Plus précisément, c'est la forme polaire de la métrique plate dx2+ dy2 si l'on pose x=rsinψ,z=rcosψ. En particulier, à partir de cette métrique, on peut récupérer les propriétés d’optimalité locale et globale de la métrique g.
Cas du syst` eme monoentr´ ee dans le rep` ere tangentiel/normal 43
La métrique g1 correspond à la restriction des transferts sur une orbite circulaire et la forme polaire est la métrique plate dx2+ dz2, ses=rsinψ et z=rcosψ. Cependant, la métrique g2 ne peut pas être interprétée comme une métrique lisse sur la sphère S2.
La forme normale du cas tangentiel a les mêmes propriétés d'homogénéité que pour le cas d'entrée de puits, et la métrique g2 peut être utilisée pour une analyse d'optimalité similaire et l'étude des sites d'intersection et de conjugaison.
Int´ egration du flot extr´ emal
Cas du syst` eme monoentr´ ee dans le rep` ere radial/orthoradial 47
Changements de coordonn´ ees
Lieu conjugu´ e
Transferts vers une orbite g´ eostationnaire
Conclusion en dimension deux
Mod´ elisation en dimension trois
La partie perturbatrice l1 de la longitude est due à la composante de poussée hors plan. Ici nous considérons uniquement le cas de la minimisation de l’énergie et nous avons
Moyennation en dimension trois
En utilisant la même transformation, on obtient l'expression résultant du deuxième champ de vecteurs. De la même manière que précédemment, nous introduisons de nouvelles coordonnées dans le mouvement moyen et l’argument du périgée θ.
Hamiltonien hors-plan
L'hamiltonien résultant de l'effet du champ vectoriel orthogonal au plan oscillant est donc induit par le problème sous-riemannien. Le problème sous-riemannien décrit est par construction un problème de contact et dans ce cas le lieu conjugué n'est pas vide et les points conjugués se rassemblent au point d'origine.
Restrictions
Nous retenons les caractéristiques suivantes pour l'orbite osculatrice initiale, associée au point de lancement du premier étage, que nous considérons en première approximation comme le point de sortie de l'atmosphère, à une altitude d'environ 190 km3. Nous considérons des forces de poussée de cet ordre de 100 kN dans la section 3.3 avec une approche de résolution d'arc.
Homotopie ´ energie-consommation et d´ etection d’´ ev´ enements
Homotopie ´ energie-consommation
Structure de l’algorithme
Il s’agit de relier la solution du problème de maximisation de la masse finale à la solution d’un problème plus facile à résoudre. Ainsi, on fausse la solution du problème, qui est a priori plus simple que la solution du problème L1.
D´ etection d’´ ev` enement et localisation des commutations 70
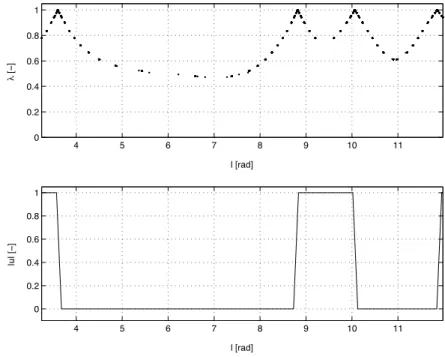
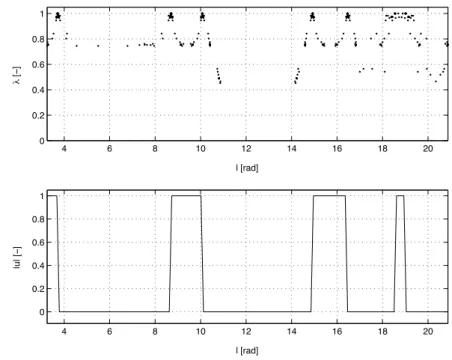
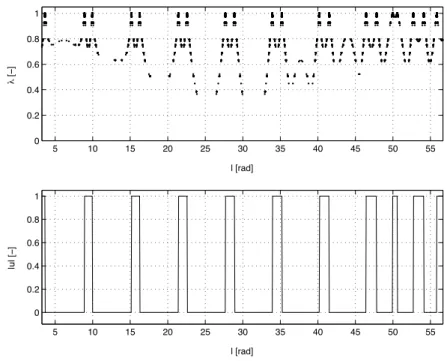
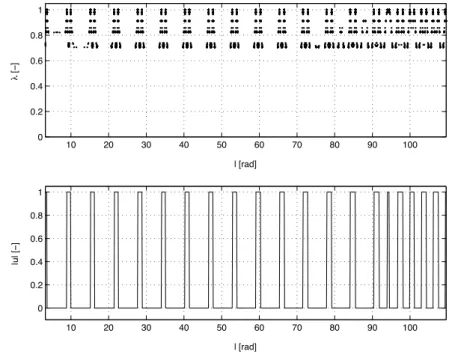
Cette accumulation d'homotopitrine autour de certaines valeurs de λ est particulièrement évidente dans le cas de la figure 3.9. La détection des commutations, combinée à la sortie dense, permet d'améliorer l'intégration pour calculer la fonction de tir à chaque pas de l'homotope.
R´ esolution pour la pouss´ ee forte
Limitations de l’approche homotopique ` a partir de la
3.12 – Evolution des paramètres géométriques de l'orbite osculatrice pour le problème L2 et cinq rotations. 3.15 – Evolution des paramètres géométriques de l'orbite osculatrice pour le problème L2 et demi rotation.
Approche multi-arcs
Ceci est directement possible en mode coplanaire, où le terme de contrôle normal est nul et la dérivée temporelle de la longitude est exprimée. Nous avons encore défini la notation µ pour la constante gravitationnelle dans la section 1.4.1, β comme précédemment et l0 est la valeur de la longitude initiale sur l'arc de poussée considéré.
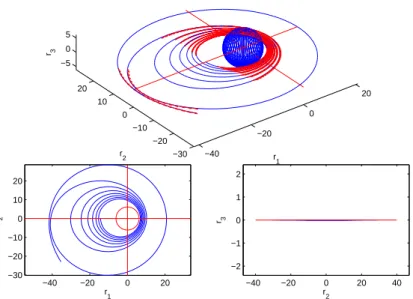
Application
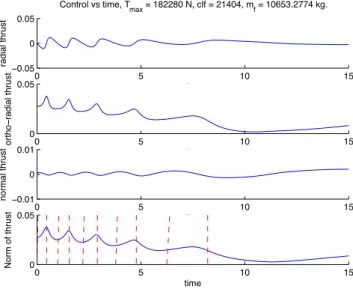
Nous commençons par reformuler le problème en prenant la longitude comme nouvelle variable indépendante au lieu du temps comme dans les chapitres précédents. Notons cependant que l'adéquation de l'approche est confirmée par le fait qu'on parvient à récupérer (dans ce cas sans changer β) la même capacité de consommation (jusqu'à 0,1% es) en substituant à Tmax = 1 kN la séquence d'arcs avec la plus petite longueur à transférer avec la plus faible consommation (voir Figure 3.25).
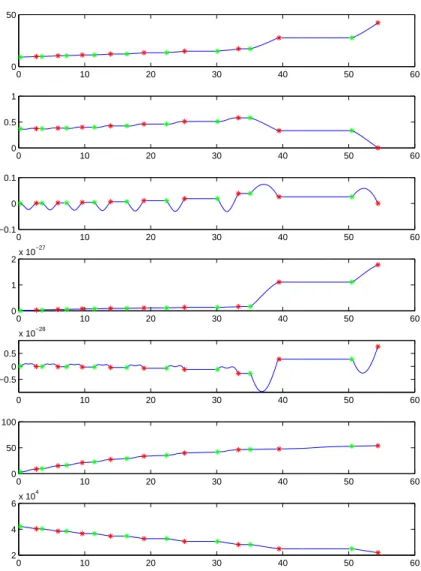
Comparaison des approches
L'étude de telles métriques remonte au problème de Jacobi consistant à calculer des lieux conjugués et sécants pour l'ellipsoïde de révolution. Dans la section 4.4 nous analysons les lieux d'intersection et de conjugaison dans le cas réflexif G(π−ϕ) =G(ϕ).
Lien avec le probl` eme de transfert d’orbite coplanaire
Cela correspond à la déformation (λ = 1) sur la sphère ronde en utilisant l'homotopie Gλ(ϕ) = XR(λX),X = sin2ϕet. Notons cependant que dans ce cas la métrique n'est pas lisse sur toute la sphère pour λ= 1, puisque l'équateur est un pôle d'ordre 2.
M´ etriques presque-riemanniennes sur une 2-sph` ere de r´ evolution 96
- Propri´ et´ es du flot g´ eod´ esique
- Transcendance du probl` eme
- Application premier retour et int´ egration de la variable θ 99
- Calcul du lieu de s´ eparation
- Lieu conjugu´ e
- Singularit´ es
L'intersection d'un pôle est le pôle opposé, celle d'un point de l'équateur est l'équateur moins ce point et sinon c'est un arc antipodal fermé. Dans le cas des Oblats apprivoisés, le lieu d'intersection Cq0 d'un point de l'équateur pour une géodésique telle que pθ ∈[0,p.
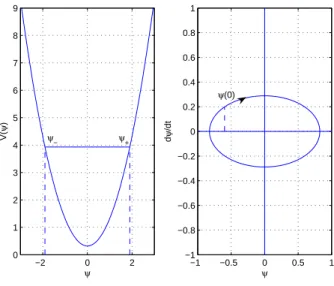
Applications et calculs
G´ en´ eralit´ es sur les fonctions de Jacobi et les int´ egrales
Les propriétés des fonctions trigonométriques fournissent des propriétés correspondantes intéressantes aux fonctions de Jacobi.
Contrˆ ole bientr´ ee pour le transfert d’orbite
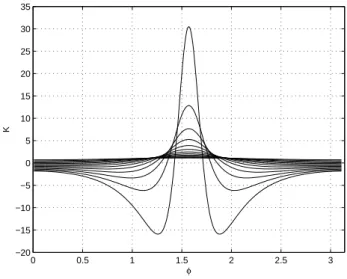
Fig.4.2 – La courbure gaussienne est représentée ici pour différentes valeurs de λ en fonction de l'angle ϕ. Grâce à l'expression de la carte des périodes et en différenciant deux fois on obtient la proposition suivante.
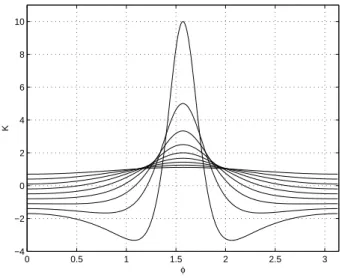
Cas interm´ ediaire de complexit´ e
Fig.4.4 : La courbure est donnée pour différentes valeurs de λ pour ce cas intermédiaire. L'expression intégrale (4.5) donne dans le cas du calcul ci-dessus : X2−X1)/X2 et celui de l'intégrale complète est obtenu pour u=K.
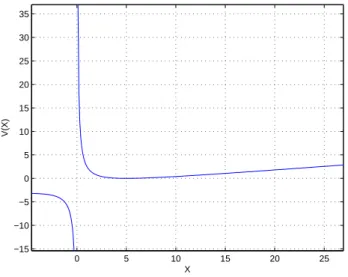
Cas monoentr´ ee tangentiel
Enfin, la Figure 4-14 donne les coefficients de la transformation de M¨obius et le paramètre read−bc qui intervient dans le changement de temps. La construction est donc possible et on cherche à savoir si la singularité de la transformation de M¨obius est dans le domaine [−1,1].
G´ en´ eralit´ es sur les vari´ et´ es sous-riemanniennes
Une première étape dans l'étude des points tangents consiste à rapprocher leur cas du cas Martinet en géométrie sous-riemannienne. On définit alors la distance sous-riemannienne ou distance Carnot-Carath´éodorique entre deux points q1 et q2 de la façon suivante ed(q1, q2) = inf{l(γ), γ est un chemin reliant q1 et q2}.
Structure presque-riemannienne
Un premier exemple fondamental de géométrie quasi-rimannienne est ce que l'on appelle le cas Grushin [2], introduit pour la première fois dans l'article [34]. Le cas de Grushin est un exemple de géométrie proche de riemannienne, l'hamiltonien correspondant étant.
Quelques outils
Sous-analyticit´ e
Comme autre exemple simple de géométrie sous-riemannienne, nous introduisons le cas de Martinet [25] dont le hamiltonien est donné par. En considérant px = 0, nous obtenons un autre exemple d'un cas proche de Riemann avec l'hamiltonien se réduisant à .
Nilpotentisation
Rel` evements de distribution presque-riemannienne en
Points de tangence en deux dimensions
Normalisation du cas tangentiel
Ce théorème donne la normalisation pour le cas quasi-riemannien en dimension deux.
Approximation nilpotente du cas tangentiel
Dans ce qui suit, nous considérons le modèle dit nilpotent donné par la distribution. Un modèle générique d'ordre 0 est appelé structure générée par des champs vectoriels.
Etude des diff´ ´ erents mod` eles
De l’approximation nilpotente du cas des points de
En utilisant les coordonnées de Poincaré q et Pi =< p, Fi> le système d'extrema normaux de l'hamiltonien correspondant. La sphère de petit rayon dans le cas de l’approximation nilpotente est donnée sur la figure 5.1.
De l’ordre 0 ` a Martinet
Dans le cas sous-riemannien de Martinet en dimension trois, les sphères peuvent perdre leur sous-analyticité dans le cas limite k → 1, ce qui n'est pas le cas pour l'approximation nilpotente des tangentes en deux dimensions où k = √. Lors de l’utilisation d’un ascenseur dans une structure sous-Riemannienne, la condition de transversalité originale px = 0 devient moins simple.
Cas r´ eflexif
C'est un modèle intéressant car contrairement au cas générique d'ordre 0, la symétrie est conservée par rapport à l'axe {y = 0} et le modèle est intégrable.
Calcul d’estim´ es g´ eom´ etriques
Front d’onde
Les coordonnées sont comme les poids 1 et 3, et on se donne les poids 0 et -2 pour py et pz pour une forme d'ordre 0. De même, en identifiant terme par terme dans l'ordre 0 et en reparamétrant le temps avec la variable sound on obtenir le système suivant.
Lieu de coupure
L'intersection des deux morceaux du front d'onde donne les deux relations suivantes d'ordre 2 pour la variable y et 4 pour la variable zen η0. Les figures 5.3 et 5.4 montrent plus précisément la déformation du lieu d'intersection dans le cas générique d'ordre 0.
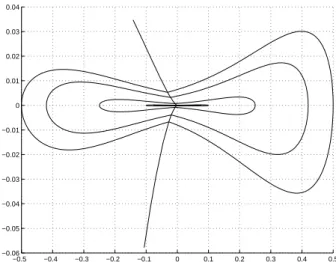
Lieu conjugu´ e
Le chapitre 5 présente les calculs effectués pour l'étude locale des points tangents et des singularités. HABERKORN, Transfert orbital à faible poussée avec minimisation de puissance : résolution par homotopie différentielle.