Étude de paramètres géométriques à partir du code de Freeman

Science et génie de l'environnement Science et génie des matériaux Science et génie des matériaux Génie des procédés. Imagerie des procédés d'ingénierie, vision, science du signal et génie des matériaux Sciences de la Terre.

Quelques codes de contour

La tortue de Papert

QUELQUES CODES DE CONTOUR 3

Le code de Bribiesca

Une chaîne de courbes représentative est obtenue en calculant les changements relatifs de direction autour de la courbe. La longueur L de la courbe sera donc L = (n+2)p avec n le nombre de codes dans la chaîne et p la longueur du segment (ici égale au côté du pixel).

QUELQUES CODES DE CONTOUR 5

Le Vertex Chain Code

Bribiesca [Bri99] a introduit une autre façon d'encoder les contours de formes : le Vertex Chain Code ou VCC. L'alphabet de ces symboles, correspondant respectivement à un, deux et trois sommets dans l'objet, est représenté sur la figure 1.7.

QUELQUES CODES DE CONTOUR 7

Le code de Liu et Zalic

QUELQUES CODES DE CONTOUR 9

Le code de Zeng et Vasseur

Synthèse

Une autre caractéristique de ces codes est qu'ils sont tous indépendants du point de départ sur la frontière dans une permutation circulaire près du code.

Autres codes

Run-Length Encoding

Le code de Huffman

AUTRES CODES 11

Neighbourhood Code

Ce code peut ensuite être réduit pour obtenir la taille d'image souhaitée, par exemple pour passer d'une image 128x128 à une image 16x16. Le caractère sélectionné est celui pour lequel l'erreur (par exemple, l'erreur quadratique moyenne) est la plus faible.

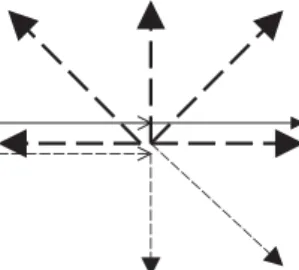
Le code de Freeman

Description et implémentation

Une fois la bonne taille obtenue, il suffit de comparer le code de la vignette avec une base de données et ainsi retrouver le caractère présent dans l'image.

LE CODE DE FREEMAN 13

La frontière interne discrète de l'objet A est notée FI(A) et est définie comme suit. Nous préférons F IV4(A) à F IV8(A) car les indications autorisées pour la surveillance des frontières sont plus nombreuses (8 au lieu de 4) et permettent donc une meilleure surveillance de la frontière.

LE CODE DE FREEMAN 15

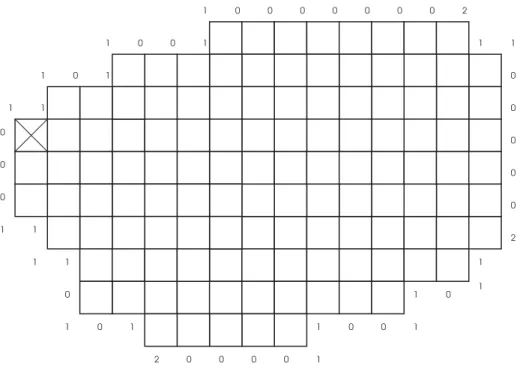
Cet algorithme ne nécessite pas l'extraction de la frontière avant son exécution et a donc l'avantage de travailler sur un objet binaire complet, et pas seulement sur la frontière de l'objet. Un ensemble de codans forme une chaîne, et une chaîne de codans notée a1a2..ai..an donne la représentation du contour d'un objet.

LE CODE DE FREEMAN 17

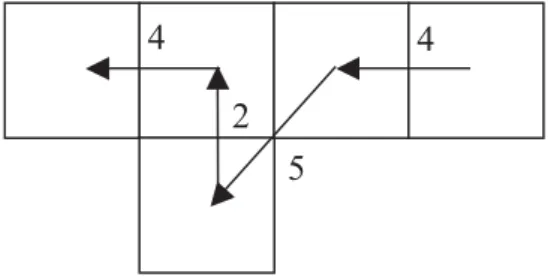
Selon l'algorithme, on cherchera le point suivant de l'encodeur 3 puis 4 ; on retrouve le codage 5. A l'étape (n+2) on va donc chercher à partir du codage 3 et ainsi de suite jusqu'à revenir au point de départ.

LE CODE DE FREEMAN 19

Utilisations du code de Freeman

Le code Freeman est utilisé pour la reconnaissance des caractères chinois écrits à la main par A. A partir du code de Freeman obtenu, une fonction temporelle périodique est en fait générée, sur laquelle le calcul de la FFT est possible.

LE CODE DE FREEMAN 21

Amélioration possible : La détection de segment de ligne doit être possible à partir du code Freeman du contour de l'objet. Ces produits sont recherchés comme points extrêmes locaux sur le code de Freeman du contour du profil.

CONCLUSION 23

Conclusion

68 Après avoir décrit les différents codages des contours de forme existants, nous allons maintenant voir comment on peut utiliser le code de Freeman pour obtenir des informations sur une chaîne de codants puis sur le code de contour d'une forme fermée. Avant d'étudier les paramètres d'une forme on considère un objet, voyons ce qu'il est possible d'étudier sur une chaîne de codants.

Paramètres et opérations sur une chaîne

Inverse d’une chaîne

Longueur d’une chaîne

Largeur et hauteur d’une chaîne

PARAMÈTRES ET OPÉRATIONS SUR UNE CHAÎNE 27

Intégration par rapport à l’axe des x

Pour une chaîne fermée décrivant le contour d'un objet, y0 peut être choisi arbitrairement.

Moments par rapport à l’axe des abscisses

Résidus

PARAMÈTRES ET OPÉRATIONS SUR UNE CHAÎNE 29

Distance entre deux points

PARAMÈTRES GÉOMÉTRIQUES 31

Miroir d’une chaîne

Paramètres géométriques

Périmètre

Avec la circonférence interne et externe, une moyenne des deux peut donner une estimation de la circonférence de l'objet avant numérisation. Pour convexe, la circonférence de Crofton peut donc être obtenue en estimant le diamètre apparent de l'objet A, qui est alors identique aux interceptions.

PARAMÈTRES GÉOMÉTRIQUES 33

Aire

Cet algorithme fournit donc l'aire comprise à l'intérieur de la courbe reliant le centre des pixels décrits par le code. Cela correspond bien à la zone englobée par le polygone décrit par le codage Freeman à quatre voies du contour de l'objet.

PARAMÈTRES GÉOMÉTRIQUES 35

Cependant, dans le cas continu, pour les polygones convexes, l'aire μ du polygone dilaté est donnée par la formule suivante. Une petite vérification s'impose : la zone en jaune moins la zone en bleu nous donne exactement un pixel correspondant à la zone de l'élément structurant de dilatation.

PARAMÈTRES GÉOMÉTRIQUES 37

Centre de masse

Les coordonnées du centre de masse de la frontière d'un objet sont facilement calculées à partir du code de Freeman pour le contour de l'objet. En connaissant les coordonnées du centre de masse du contour de l'objet, les rayons maximum, minimum et moyen pour cet objet peuvent alors être calculés.

Rayon maximum, minimum et moyen

En connaissant x0 et y0 les coordonnées du point de départ du code et en tenant compte de l'orientation du plan selon la figure 1.15 page 13, les coordonnées du point relié par le premier encodeur peuvent être calculées. Ainsi, pas à pas, les coordonnées de tous les points du contour sont calculées.

Diamètre apparent maximal, minimal et moyen

La moyenne en x et la moyenne en y nous donnent respectivement l'abscisse et l'ordonnée du centre de gravité de la frontière de l'objet. Il est important de noter ici que dans la plupart des cas, ce point n'est pas le centre de masse de l'objet solide.

PARAMÈTRES GÉOMÉTRIQUES 39

Rectangle englobant d’aire minimale

La première étape consiste à trouver le plus petit rectangle contenant la courbe et dont les côtés sont parallèles aux axes x et y. Ensuite, chaque segment de ce convexe est divisé de manière itérative pour passer par les points les plus éloignés de la courbe situés à l'extérieur du polygone.

PARAMÈTRES GÉOMÉTRIQUES 41

Dimension fractale

Une équation souvent utilisée pour comprendre ce concept est la mesure de la longueur de la côte bretonne par [Rich], qui donne un résultat surprenant : cette longueur dépend de l'unité avec laquelle elle est mesurée. Certaines des méthodes d'estimation de la longueur d'une courbe sont présentées ici : la méthode du compas, la méthode de la boîte, la méthode de la coupe et enfin la méthode de la saucisse de Minkovski.

PARAMÈTRES GÉOMÉTRIQUES 43

La limite de l'objet est épaissie ici avec un pinceau de largeur 2 ×, représentant une fusée éclairante avec une boule de rayon. Ce phénomène met en évidence le problème de l'unité de mesure généralement inadaptée à l'objet mesuré.

PARAMÈTRES GÉOMÉTRIQUES 45

Cela permet plus de flexibilité, mais oblige μ à être la borne inférieure de la somme des mesures élémentaires. La dimension de Bouligand-Minkowski peut être calculée à partir de la saucisse de Minkovsky, de la méthode de la boîte, de la méthode des boules disjointes ou de la méthode du compas ([Gou]).

PARAMÈTRES GÉOMÉTRIQUES 47

La méthode utilisée ici est inversée en ce sens que nous construisons d'abord le code de Freeman de la courbe puis mesurons sa dimension fractale. Grâce au code de Freeman, nous avons étudié le cas de la courbe de Von Koch pour un angle α= 45◦.

PARAMÈTRES GÉOMÉTRIQUES 49

Les objectifs sont ici les mêmes que pour la courbe de Von Koch : établir le code de Freeman de la courbe et mesurer sa dimension fractale directement à partir du code obtenu. L'algorithme utilisé ici est le même que pour la courbe de von Koch, et nous avons trouvé une dimension fractale de 1,94.

PARAMÈTRES GÉOMÉTRIQUES 51

Paramètres de formes

Paramètres de circularité

PARAMÈTRES DE FORMES 53

Paramètres de symétrie

Seuls le coefficient d'asymétrie de Besicovitch et le coefficient de symétrie de Blaschke sont actuellement directement calculables grâce au code de Freeman. Le coefficient d'asymétrie de Besicovitch [Bes] a pour but de dire si un pointa appartenant à un convexe A est bien ou mal centré en A.

PARAMÈTRES DE FORMES 55

Avant d'étudier ce coefficient de symétrie, nous devons introduire la symétrisation de Minkowski. Le coefficient de symétrie de Blaschke consiste à comparer la surface de la forme étudiée avec celle de sa symétrisation de MinkowskiS(A) et présentée dans [Min].

PARAMÈTRES DE FORMES 57

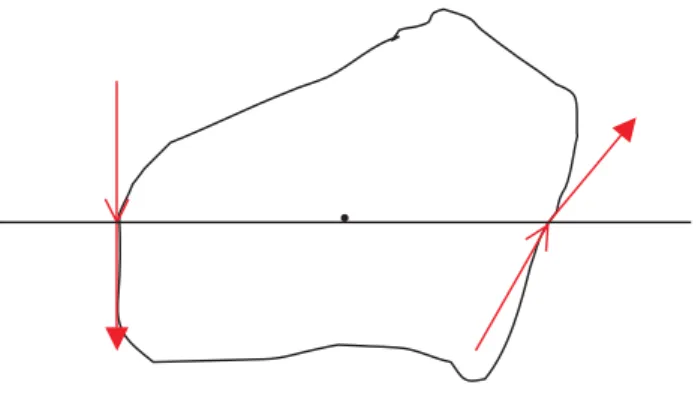
Nous n'avons aucune référence à l'article de Winternitz introduisant ce coefficient, mais seulement l'article de Grünbaum [Grü] le présentant. Le coefficient de Winternitz est basé sur des proportions d'aires délimitées par un axe directionnel θ passant par un point x donné de A (voir Figure 2.33).

PARAMÈTRES DE FORMES 59

Convexité

Pour cette même donnée, alors, on peut dire si toute la forme est n-convexe : une forme est n-convexe si elle est n-convexe en tout point de son contour.

Histogramme d’un code

Axes principaux d’inertie

PARAMÈTRES DE FORMES 61

De plus, toute droite (D) dans le plan est caractérisée par les coordonnées polaires [θ, p] du point H, projection de l'origine O sur (D). On peut garder le même type de raisonnement dans le cas où M0(x0, y0) appartient à la seconde ligne, mais on distingue cette fois les cas p≥ δ ou p < δ, c'est-à-dire les lignes (Dθ,p −δ ).

PARAMÈTRES DE FORMES 63

Si l'on différencie J sous le signe somme par rapport à θ, pour les mêmes raisons que celles énoncées ci-dessus :. xcosθ+ysinθ) (−xsinθ+ycosθ)dxdy=p. xsinθ+ycosθ)dxdy (2.68), ce qui donne après divers développements.

PARAMÈTRES DE FORMES 65

Remarque : Le résultat étant un carré pour tout X, la matrice A est donc symétrique définie positive. Il faut d'abord trouver les valeurs propres de B : en plus de la valeur propre0, ce seront les valeurs propres de la matrice C.

PARAMÈTRES DE FORMES 67

Conclusion

91 Le but de ce chapitre est d'abord de présenter les transformations possibles sur des formes connues par le code de Freeman de leurs contours, puis de comparer deux formes entre elles.

Opérations sur un objet à partir du codage de Free- man

Translation

Homothéties

OPÉRATIONS SUR UN OBJET À PARTIR DU CODAGE DE FREEMAN 71

Le codage courant est en gras, les éventuels prochains codages sont en pointillés longs, et les pointillés courts représentent le chemin et surtout l'arrivée de l'homothétique de la relation deux. Ces cas sont présentés dans le tableau de la figure 3.6 : la première colonne donne les premiers codants possibles et la seconde le début du code de la représentation de l'homothétique.

OPÉRATIONS SUR UN OBJET À PARTIR DU CODAGE DE FREEMAN 73

Le cas des homothéties de rapport 1/k, avec k entier donne des résultats avec perte d'information et n'est pas étudié ici. Cependant, selon [Mai], la contraction est un peu plus complexe et l'information est souvent perdue.

OPÉRATIONS SUR UN OBJET À PARTIR DU CODAGE DE FREEMAN 75

Rotation

Symétries

Calcul de la symétrie de l'objet en calculant le codage symétrique Ci,S de chaque codage de départ Ci (6,6) à droite.

Appartenance d’un point à un objet

La symétrie d'un objet par rapport à un axe θ peut être obtenue facilement et sans distorsion pour des angles multiples de 45◦. Il suffit de remplacer chaque codage par le codage correspondant en se référant au tableau suivant.

OPÉRATIONS SUR UN OBJET À PARTIR DU CODAGE DE FREEMAN 77

Ou si le point limite le plus proche à gauche est dépassé par les encodeurs en montant. Si le point limite le plus proche à gauche est dépassé par les encodeurs descendants.

OPÉRATION SUR DEUX OBJETS À PARTIR DU CODAGE DE FREEMAN 79

Opération sur deux objets à partir du codage de Free- man

Estimation de la distance géométrique entre formes

16 marquage de points entre le point courant et le point suivant : ces points sont extérieurs à l'objet. 22 marquage de points entre le point courant et le point suivant : ces points sont extérieurs à l'objet.

OPÉRATION SUR DEUX OBJETS À PARTIR DU CODAGE DE FREEMAN 81

Intersection et union de deux formes

4 l'intersection des deux objets correspond au code de la forme 1. 6 sinon si un pixel de la forme 2 est à l'intérieur de la forme 1. 7 l'intersection correspond au code de forme 2. 11 Pour chaque point obtenu, stocké en mémoire, pour les 2 courbes d'abscisse, l'ordonnée, l'indice du codeur partant, le codeur arrivant, le codeur partant.

OPÉRATION SUR DEUX OBJETS À PARTIR DU CODAGE DE FREEMAN 83

1 correspond à la forme 1 (l'intersection est donnée par les codeurs de la forme 1 à l'intersection suivante). 2 correspond à la forme 1 (l'intersection est donnée par les codants de la forme 2 à l'intersection suivante).

OPÉRATION SUR DEUX OBJETS À PARTIR DU CODAGE DE FREEMAN 85

4 l'union des deux objets correspond au code de la forme 2. 6 sinon, si un pixel de la forme 2 est à l'intérieur de la forme 1, alors. 7 union correspond au code de forme 1. 11 Pour chaque point obtenu stocké en mémoire, pour 2 courbes abscisse, ordonnée, indice du codeur sortant, futur codeur, codeur sortant.

OPÉRATION SUR DEUX OBJETS À PARTIR DU CODAGE DE FREEMAN 87

Comparaison de deux formes

En utilisant le code de Freeman du périmètre de deux formes étudiées, ce paramètre est obtenu selon l'algorithme 17. L'aire d'un objet est également calculée à partir du code de Freeman du périmètre de la forme étudiée, en utilisant une des méthodes présentées dans §2.2.2 page 33.

OPÉRATION SUR DEUX OBJETS À PARTIR DU CODAGE DE FREEMAN 89

Corrélation entre deux formes

CONCLUSION 91

Conclusion

107 La théorie de la morphologie mathématique binaire est basée sur les opérations ensemblistes de Minkowski et a été présentée dans les années 1960 par Matheron [Mat] et Serra [Ser82] et [Ser88].

Morphologie mathématique binaire

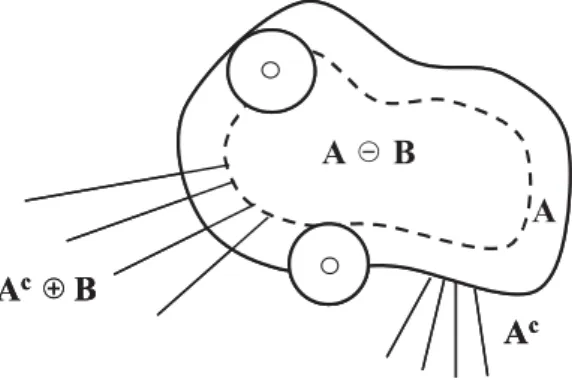
Addition de Minkowski et dilatation

MORPHOLOGIE MATHÉMATIQUE BINAIRE 95

Erosion, ouverture et fermeture

Pour un élément de structure donné, les opérateurs mathématiques de morphologie permettent de compter le nombre de zones entrantes et sortantes d'un objet et ainsi de déterminer, par exemple, le nombre d'objets présents dans un cluster ou de trier les objets en fonction du nombre de zones sortantes. zones dont ils sont propriétaires.

MORPHOLOGIE MATHÉMATIQUE ET CODE DE FREEMAN 97

Morphologie mathématique et code de Freeman

Première approche de la dilatation

Après avoir exécuté l'algorithme, nous obtenons le code de contour "saucisse" de Freeman. Nous avons vu que cette méthode a des limites, nous allons donc travailler à trouver une autre méthode qui permette d'obtenir la dilatation et l'érosion d'un objet en travaillant uniquement sur le code de Freeman de son contour.

MORPHOLOGIE MATHÉMATIQUE ET CODE DE FREEMAN 99

Nouvelle approche de la dilatation

MORPHOLOGIE MATHÉMATIQUE ET CODE DE FREEMAN 101

MORPHOLOGIE MATHÉMATIQUE ET CODE DE FREEMAN 103

Pour cela, il suffit de parcourir le code à la recherche de séquences de codage impossibles compte tenu du sens de rotation choisi au départ. Ensuite, il existe plusieurs possibilités pour déboguer le code, mais la plus intéressante est l'algorithme 18.

MORPHOLOGIE MATHÉMATIQUE ET CODE DE FREEMAN 105

Approches de l’érosion

Cette reconstruction par marqueur nécessite les algorithmes de dilatation et d'intersection que nous avons étudiés. Lors de l'exécution de ces algorithmes, il faut porter une attention particulière à la structure de données utilisée pour stocker le code de Freeman des objets et bien considérer les points isolés introduits par l'algorithme, par exemple, pour le calcul de la section efficace de deux objets.

CONCLUSION 107

Conclusion

Perspectives

• Etude sur différents objets types
• Code de Freeman en niveaux de gris
• Complexité des algorithmes
• Etude des propriétés des autres codages
• Etude du code de Bribiesca
• DESCRIPTEURS TOPOLOGIQUES 111
• Le code de Zeng et Vasseur
• Descripteurs topologiques
• Floating bodies
• Courbure
• Aspect multi-échelle
• Morphologie mathématique binaire
• Supercodage, polygonalisation
• Correction de code après rotation
• Passage bijectif des différents codes au code de Free- manman
• Diamètres apparents
• CONCLUSION SUR LES PERSPECTIVES 113
• Conclusion sur les perspectives

Le code de Freeman que nous avons utilisé ici n'utilise que des images binaires qui sont le résultat d'une segmentation, par exemple. De plus, il est possible d'accéder à ces données grâce au code Freeman et à la signature du contour de la forme étudiée.

Conclusion

Jou84] Jourlin M., Laget B. : Contribution de la morphologie directionnelle à la reconnaissance des formes des coefficients de Fourier du contour de l'écriture arabe pour la normalisation des caractères, Colloque International Francophone Ecriture et Document - CIFEd inria version 1] . édité par) : Imagerie, Hermès Lavoisier IC2, 2003.

GEOMETRIC PARAMETERS COMPUTATION WITH FREEMAN CODE

ETUDE DE PARAMETRES GEOMETRIQUES A PARTIR DU CODE DE FREEMAN