Introduction
A new notion of asymptotic A factorization property allows us to study the convergence in probability of the A moments. The first order asymptotic of the moments of the entries of G(A)- invariant random matrices converging in A-distribution is known.
A -tracial algebras and A -freeness
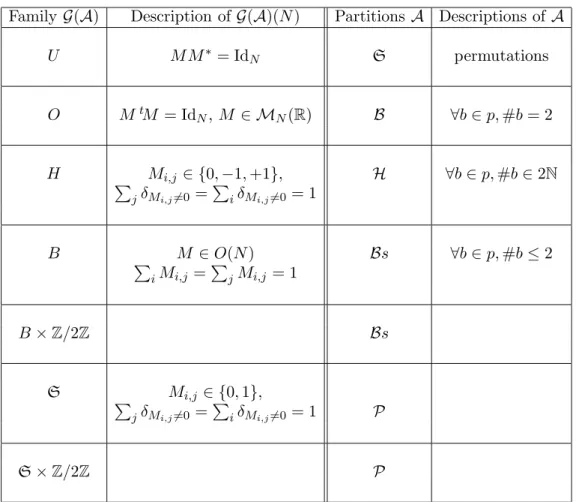
Using the cumulants, we can give a new characterization of the fact that a P trace algebra is deterministic or not. For the sake of simplicity, we first explained the notion of P trace algebra without explaining that for any A ∈ {P, B, S, H,Bs} one can define a notion of A trace algebra. So we already see that two families A1 and A2 of (A,(mp)p∈A2) are A2-free if and only if they are A1-free for the natural extension of A as an A1 trace algebra.
The A1-exclusive moments of (mApc1)p∈P are the P-exclusive moments of the natural extension (A,(mp)p∈A1) as a P-tracial algebra.
Random matrices and A -distribution
Using this discussion, it can be seen that if for any integer N, (MiN)i∈I is a family of symmetric or antero-symmetric matrices, it converges to S-moments if and only if it converges to B-moments. A less trivial result is that if for some integer N, MN is a permutation matrix, then MN converges to the P-distribution if and only if it converges to the S-distribution. For any integer N, let (MiN)i∈I be a family of real random matrices which converges to the distribution A.
If for any integer N, (MiN)i∈I is a family of complex random matrices, the same result holds if we assume that (MiN)i∈I is stable under conjugate or union operations. For any integer N, let (MiN)i∈I be a family of real random matrices which converges to the distribution A. Let us assume that (MiN)i∈I converges to the distribution A, recalling that (C{Xi , i∈ I},(Em(Mp i)i∈I)p∈A) is the algebra of the limiting A-tracial distribution.
By definition, the asymptotic A-cumulants are uniquely characterized by the fact that for any k≥0, anyp inAk and any (i1, .., ik)∈ Ik,. Let us assume that (MiN)i∈I and (LNj )j∈J are asymptotically A-free and satisfy the asymptotic A-factorization property, then the asymptotic A-factorization property holds for (MiN)i∈I ∪(LNj )j ∈J. For any integer N, let (MiN)i∈I and (LNj )j∈J be two families of random matrices which converge in A1 distribution.
Dualities and the finite-dimensional world
Finally, we can prove the asymptotic freedom of the unit invariant matrix and its transfer. For a definition of simple orthogonal groups and proofs of duality theorems, see [2]. When for any integer N (MiN)i∈I is invariant in the conjugation law with G(A)(N), the notions of finite-dimensional exclusive moments and the cumulant become easier.
Moreover, if it satisfies the asymptotic A decomposition property, then it satisfies the asymptotic P decomposition property. We can easily relate the moments of the products of the entries of any S-invariant matrix to the finite-dimensional cumulants: this allows us to calculate the asymptotics of the moments of the products of the entries of any S-invariant matrix to study. The second equation is a consequence of the first and the definition of the order.
In fact, using the forthcoming Section 8, we can get a better understanding of the moments of the inputs as the family converges to a higher order of fluctuations. So we only have to show that E can be written as a linear combination of elements of the form ρN(pc) with p ∈ Dk. Instead of studying the asymptotics of a matrix M, one should study the asymptotics of the matrix Diag[M1, .., Mk] where Mi is independent and has the same law as M: one can see that it leads to the study of partitions of {1, .., k,1′, .., k′}.
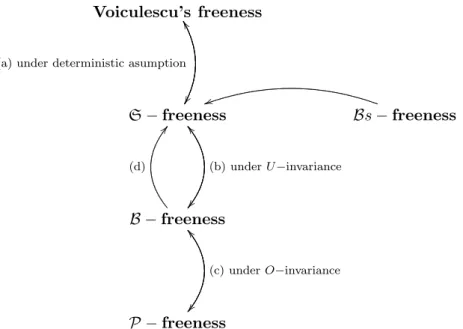
G ( A )-invariance, independence and A -freeness
One may wonder if it is possible to formulate a version of Theorem 5.1 in which the condition of G(A) invariance is replaced by the condition of asymptotic G(A) invariant. Suppose that Theorem 5.1 is true if one replaces the condition of G(A) invariance with the condition of asymptotic G(A) invariance. So (MN)N∈N and (LN)N∈N cannot be P-free: Theorem 5.1 is not true if one simply replaces the condition of G(A) invariance with the condition of asymptotic G(A) invariance .
Actually, one can state a version of Theorem 5.1 where one replaces the notion of G(A)-invariance by the condition of asymptotic strong G(A)-invariance that we are going to define. Let us suppose that the two families(MiN)i∈I and(LNj )j∈J converge in P-distribution and that (LNj )j∈J is asymptotically strongly G(A)-invariant. If for every positive integer N, the two families (MiN)i∈I and (LNj )j∈J are independent, then the two families (MiN)i∈I and (LNj )j∈J are asymptotically A-free.
According to Theorem 3.6, the asymptotic P-freedom of (MiN)i∈I and (LNj )j∈J would imply the asymptotic A-freedom of the two families. Unlike Theorem 5.1, this new Theorem 5.2 is general enough to be used to recover the freedom of general real and complex Wigner matrices. Let us note, however, that Theorem 5.2 is not a generalization of Theorem 5.1, since in this latter we need the families of random matrices to converge in P distribution.
General theorems for convergence of L´evy processes
The family (Gk)k∈N is the only data one needs to calculate E[Xt⊗k] for any positive real. Later we will use the more general fact that for any multiplicative matrix-valued L´evy process (Xt)t≥0, any integers k and l are the family. A consequence of equation (11) is that in the additive case, for any real t0 ≥0, any integer k and any irreducible partition p∈ Pk,.
Using the same notations as in Theorem 6.1, let's assume that for every integer k the sequence (GNk)N≥0 converges: for every p ∈ Pk, κp(GNk) converges. With Theorem 5.1, the family (XtNi+1,ti)ni=0−1 in P-distribution converges to the P-distribution a vector of A-free elements. If for every t ≥ 0 and every integer N the matrices XtN have a complex value, the asymptotic P-factorization possibility does not imply the convergence in probability in P-distribution.
From now until the end of the section, we will assume that for every integer N (XtN)t≥0 is a multiplicative L´evy process. The proof of the following theorem is similar to Theorem 6.1, so we will omit it. If for any positive integers k and l the sequence (GNk,l)N≥0 converges, then the family (XtN)t≥0∪((XtN)∗)t≥0 converges in the P-distribution.
Some examples of L´evy processes and consequences
For any integerN, let (HtN)t≥0 be a Brownian motion ongǫ(N,K) and let (UtN)t≥0 be a Brownian motion onU(N,K). For the second theorem, since we proved the convergence in probability using Theorem 1.1, it is enough to prove that for any integer k, Em(1,..,k)(Ht). For any φ ∈ (C[P2/S2])∗ there exists a sequence of matrices (MN)N∈N such that MN converges in P-distribution to a P-Gaussian whose R-transform is given bye⊞φ .
We can always assume that for any integer N, MN and LN are independent and S-invariant. For any integer N, the process (HtN)t≥0 is an additive L´evy process and its generator (GNk)k∈N can be calculated: it converges and in each case R[G] = p∗ where p is partition taken Considering. A probability measure µ∈ M⊡ is a freely ⊡-infinitely divisible probability measure if for any integer n≥1 there exists a probability measure µ1.
According to Theorem 6.1, we must show that GNk ∈C[ρN(AK,k)] converges for every integer k as N goes to infinity. Using Remark 6.1, it suffices to prove that for every p∈ AK the p-moment GNk converges. For each positive integer N, let (YtN)t≥0 be a L´evy process on U(N,K) with characteristic triple (iarg(ω)IdN, bN, νN).
Using the last statement of Theorem 7.8, for any positive integer N, (YtN)t≥0 is a conjugation-invariant L´evy process with U(N). Using Remark 6.1, it suffices to prove that for every permutation σ ∈ Sk, the p-momentum of GNk converges.
Algebraic fluctuations
From now on, let's assume that (MiN)i∈I converges in A-distribution up to order of fluctuations. For any integer N, let (MiN)i∈I be a family of random matrices that converges in A-distribution to order 1 of fluctuations. Suppose (MiN)i∈I is G(A)-invariant and converges in A-distribution to order no fluctuations, then it converges to order in P-distribution.
A notion of asymptotic A-freedom up to higher fluctuation order can be defined for families that converge in A distribution up to order n of fluctuations. Let us assume that the family (MiN)i∈I ∩(LNj )j∈J converges in A-distribution up to the order of fluctuations. In fact, it is easy to see that the families (MiN)i∈I and (LNj )j∈J are asymptotically A-free up to the order of fluctuations if and only if the algebras generated by (MiN)i∈I and by (LNj) )j∈J is asymptotically A-free up to order n of fluctuations.
Assume that (MiN)i∈I and (LNj )j∈J are asymptotically A-free up to order n oscillations. Then the two families (MiN)i∈I and (LNj )j∈J are asymptotically A-free up to the order of n oscillations. If for any positive integer inl the sequence (GNk,l)N∈N converges to the order of n fluctuations, then the family (XtN)t≥0 ∪((XtN)∗)t≥0 converges in the P-distribution to the order of n fluctuations .
Conclusion
The classical cumulants can be calculated as finite-dimensional cumulants: this shows that there exists a Schur-Weyl interpretation of the fluctuations of the moments of random matrices. It is possible to easily recover the fluctuations of the unitary Brownian motion in this environment, but a general study has yet to be done. Does it exist a good idea that generalizes the idea of asymptotic factorization for higher orders, which will be stable by the asymptotic freedom property of higher orders and will imply probability fluctuations of the moments when N goes to infinity.
In this way, the convergence of fluctuations of Hermitian Brownian motions can be proved, but the general notion is still missing. Male, who encouraged the author to define the abstract concept of P-tracial algebras, a concept that was not present in the first version of the article, and who also presented him with the first negative statement in Theorem 3.7. The first version of this work was created during the author's PhD at Paris 6 UPMC University.
This final version of the paper was completed during his postdoctoral studies at the University of Warwick, where the author is supported by an ERC grant, 'Behavior near criticality', held by Pr. Classical and free infinitely divisible distributions and random matrices. The Annals of Probability, 33, no. A geometric interpretation of the cumulant for random matrices previously defined as convolutions on a symmetric group. Lecture Notes in Mathematics, S´eminaire de Probabilit´es XLI.