Cette application relie le problème classique de recherche opérationnelle d'attribution de fréquences à un problème d'analyse de localisation. L'approche originale de modélisation de cette application en contraintes discrétise entièrement le problème.
Un aper¸cu de la Programmation par Contraintes
Plus formellement, le but de la résolution d'un CSP peut être défini en ces termes : Définition 1.3. Toutes ces façons d'aborder la résolution de problèmes peuvent être satisfaites en DPC.
R´esolution de contraintes discr`etes
Si un algorithme efficace est disponible qui vérifie le respect d'une contrainte globale - par exemple, la contrainte tous différents, l'algorithme de schéma GAC (mentionné sous les cohérences génériques pour les contraintes n-aires) peut être utilisé. La consistance de l'arc de contrainte peut être déterminée en calculant les composantes connexes du graphe résiduel de ce flux.
R´esolution de contraintes continues
L'un des problèmes majeurs rencontrés en arithmétique par intervalles est lié au problème des dépendances entre les variables d'une expression. La notion d'extension d'une fonction à des intervalles que nous venons de voir nous permet maintenant d'introduire des restrictions d'intervalle.
Approches discr`etes-continues en PPC
Ces problèmes impliquent des contraintes discrètes, continues et mixtes (c'est-à-dire affectant simultanément les deux types de variables). Dans un problème de configuration de cuves de mélangeurs industriels : on peut rencontrer des limitations de dilatation en associant le type de cuve à la capacité du récipient.

Conclusion
Nous proposons un premier algorithme de filtrage qui réduit les domaines - représentés par des tuiles - à la simplicité, afin de les réduire à des tuiles plus petites. Un premier algorithme de filtrage est d'abord présenté (Section 2.3), suivi de l'algorithme que nous avons dérivé pour distn (Section 2.4) et pour son extension `adistn var (Section 2.5).
Motivations applicatives
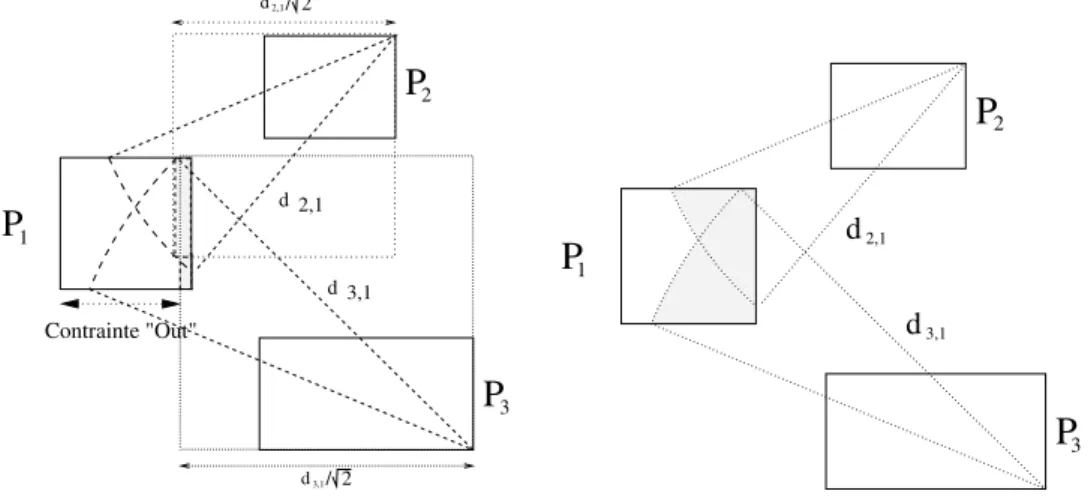
Krippahl et Barahona [71] proposent de combiner une approximation faible de la contrainte de distance euclidienne avec la contrainte globale diffn. Plus précisément, les contraintes In (distance maximale) et Out (distance minimale) sont distinguées et remplacées par une approximation externe (par le carré circonscrit) et interne (par le carré inscrit) de la métrique euclidienne.
Motivations g´eom´etriques
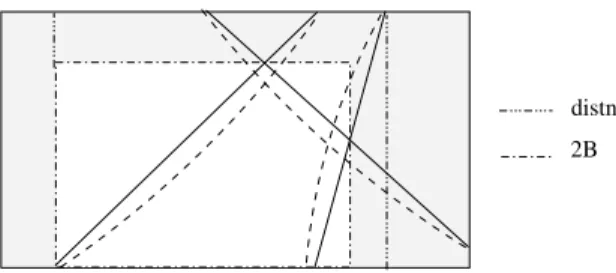
La région autorisée pour une contrainte de distance maximale est définie à l'aide de la somme de Minkowski. Sur le diagramme de gauche de la figure 2.2, on voit qu'avec une représentation des domaines par un produit de deux variables, la cohérence 2B ne parvient à éliminer qu'une très petite partie de la boîte à réduire.
Un premier algorithme de filtrage pour distn
Une stratégie round robin similaire à AC-1 [80] est alors adoptée pour approcher (après M axItérations) le point fixe de propagation des contraintes de distance. La réduction de domaines obtenue par simplexe est montrée dans la figure 2.7 où nous la comparons avec le filtrage de cohérence 2B.
Algorithme de filtrage de distn
Nous donnons maintenant toutes les modifications à apporter à l'algorithme précédent pour son implémentation dans une machine. La condition de stabilité et la justesse de l'algorithme sont préservées par ce calcul.

G´en´eralisation `a distn var
La réduction de la boîte itérative de la boucle principale dans l'algorithme de filtrage de la méthode des zones actives (règle 3, algorithme 7 page 54) utilise un critère d'arrêt statique défini de manière empirique. Pn], dvar) on peut déjà appliquer le filtrage de la contrainte suivante aux variables de position :. 2.10).

Exp´erimentations
Ces contraintes limitent le problème à une seule solution, tout en laissant libres les coordonnées des autres points. Les tableaux 2.4 et 2.5 montrent les capacités de résolution obtenues avec le modèle naïf.

Conclusion
Si les temps entre le modèle naïf et celui utilisant la contrainte globale restent relativement proches, le global permet d'isoler exactement les solutions au problème, alors que l'existence et l'unicité des solutions devraient être vérifiées parmi le grand nombre de cases générées par le modèle naïf. La description de l'application opérationnelle sera suivie d'un modèle mathématique du problème, qui sera réécrit en parallèle en deux modèles de contraintes.
Description du probl`eme applicatif
Si la distance entre les deux antennes est inférieure à dl km, les 2 sites se déformeront si la différence de fréquence entre les émetteurs d'un site et les terminaux de l'autre est plus faible. Si cette distance est comprise entre dl et dh km, les 2 réseaux vont se déformer si l'écart de fréquence entre les émetteurs d'un site et les terminaux de l'autre est inférieur à ∆h, rencontré.

Mod`ele math´ematique du probl`eme
Efi, l'ensemble des couples (tij, fik) pour lesquels une certaine fréquence fik est imposée. Ef6=, l'ensemble des couples (tij, tkl) pour lesquels une fréquence différente est imposée,.
Mod`eles discrets et hybrides en contraintes
L'objectif opérationnel est de minimiser la taille de la bande de fréquence nécessaire pour résoudre le problème, sous réserve de toutes les contraintes imposées. ZI s'écrit comme la disjonction entre les contraintes des inégalités linéaires, et les bornes de ZP I s'expriment par la conjonction des contraintes des inégalités linéaires.
Premi`ere r´esolution et analyse
La solution du RLFAP avec le modèle LocRLFAP ne présente plus de problèmes. De plus, la résolution de LocRLFAP sur les cinq premiers exemples est effectuée plus rapidement que celle du RLFAP dans le même modèle.

Am´eliorations de l’algorithme de recherche
Le modèle hybride bénéficie le plus des raffinements de l'algorithme de recherche et ses performances sont maintenant proches de celles du modèle discret. Cela nous oblige à modifier le modèle LocRLFAP, que nous couvrons maintenant.

Mod´elisation `a l’aide de distn et distn var
Si une contrainte Compat_freq est violée, la nouvelle limite inférieure de distance minimale affecte immédiatement toutes les contraintes de distance de la contrainte distn. Par conséquent, nous pouvons réécrire l'ensemble des contraintes de distance de manière homogène dans le problème.
R´esolution du probl`eme de d´eploiement progressif d’antennes
Sur les cas résolus par les deux modèles, le nombre de backtracks est à peu près équivalent, mais la résolution est en moyenne 2,3 fois plus lente dans le modèle hybride. Dans ces modèles sans contraintes globales, cependant, le modèle hybride parvient à résoudre une instance de plus que le modèle discret.
Conclusion
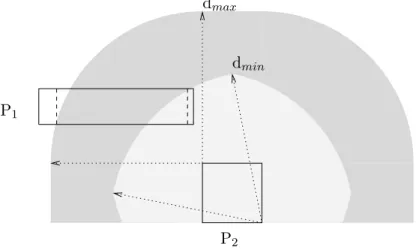
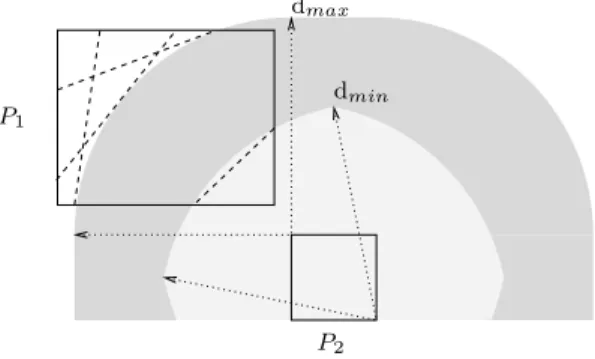
A partir d'un algorithme de conditionnement de cercles, nous avons adopté une interprétation géométrique de la sémantique des domaines de contraintes de distance euclidiens. L'étude au pointo=(X2, Y2) introduit une approximation de la contrainte de distance maximale avec trois tangentes au quart de cercle centré en o.
Exemple du filtrage op´er´e par P 2 sur P 1 avec la 2B-consistance
Filtrage obtenu sur P 1 par la contrainte Out et r´egion d’exclusion approxim´ee par
Filtrage op´er´e par P 2 sur P 1 avec le premier filtrage de distn
Filtrage possible depuis les voisins de la tuile courante
Approximations lin´eaires des arcs
Boˆıte englobante minimale du simplexe calcul´e
Calcul de la chaˆıne de points inactifs sur le bord de P i
Noyau de rayon d d’un polygone
Intersection du noyau de rayon d avec le polytope
Approximation de l’intersection de rayon d avec le polytope par une enveloppe
Calcul par intervalles de la chaˆıne de points inactifs du bord
Distance minimale et maximale entre deux polygones
Utilisation de la diff´erence de Minkowski pour le calcul de la distance minimale
Le manipulateur 3-RPR
Topologie d’un r´eseau `a 10 sites
Mod´elisation d’un probl`eme en contraintes
La modélisation d'un problème de contraintes nécessite de définir un CSP dans un langage de contraintes donné. Résoudre un CSP (en variables discrètes) étant un point dans un espace discret fini, il est commode de voir un CSP discret comme un problème de recherche de solution.
Propagation des contraintes
En général, savoir si un CSP est satisfiable est un problème NP-complet (se réduisant au problème NP-complet SAT [98]), et a priori il n'existe pas d'algorithme générique et efficace pour le résoudre. Pour les CSP en variables continues, on se contente généralement de solutions qui peuvent être représentées dans une machine à intervalles à virgule flottante ; Par conséquent, nous pouvons voir la solution ici comme un problème de recherche de solutions dans un espace fini.
Algorithmes de recherche
Il faut dans ce couplage trouver un bon compromis (défini expérimentalement) entre le temps d'application des techniques de maintien de cohérence locale (plus ou moins fortes) et le temps passé à l'exploration de l'arbre de recherche. 11 on parle de violation d'une contrainte lorsque sa relation sous-jacente ne peut être vérifiée. 12, c'est-à-dire un intervalle contenant au plus deux nombres à virgule flottante.
Modes de r´esolution
Cependant, son champ d'application est limité à de petits problèmes car la consommation mémoire explose très rapidement. Cette dernière approche permet d'obtenir de très bons résultats, par exemple sur de très grands problèmes d'assignation de fréquence [42].
Synth`ese
Leur principe est d'essayer d'améliorer progressivement la valeur de la fonction de coût d'état — par exemple, le nombre de contraintes violées, pour un problème de satisfaisabilité — en explorant son voisinage. Cependant, les principaux inconvénients des méthodes de recherche locale sont qu'elles peuvent rester bloquées au minimum local de l'espace de recherche et qu'elles ne fournissent aucune preuve de l'absence ou de l'optimalité des solutions.
Consistances locales g´en´eriques
Dans certaines situations, la cohérence d'arc ne prend pas en compte les dépendances entre les contraintes, de sorte que le filtrage résultant est très faible. Si le compromis entre complexité de recherche et inférence de contraintes favorise des formes de cohérence plus faibles dans le cas discret, il est parfois différent dans le continuum [102].
Solveurs adapt´es `a la propagation de contraintes sp´ecifiques
Elle assure dans toutes les contraintes que pour toute valeur du domaine d'une variable dans la contrainte il existe une solution de la contrainte à laquelle participe cette affectation.En prenant les exemples de contraintes identifiés ci-dessus, on connaît des algorithmes efficaces pour assurer la (R)-cohérence bornée d'une équation linéaire à variables et coefficients entiers, et la (D)-cohérence bornée du produit de contrainte X.Y = Z [5].
Contraintes globales
Par exemple, la contrainte de distance de Manhattan est une telle relaxation de la contrainte de distance euclidienne. Le coût élevé des appels de contraintes (dans des situations triviales) peut autrement compromettre l'utilité générale de la correspondance des contraintes parentes.
Synth`ese
Probl`emes du calcul r´eel
L'arithmétique d'intervalle effectue des calculs sur des intervalles de nombres (à virgule flottante) et assure par arrondi dirigé l'inclusion de la solution dans l'intervalle calculé. Cependant, le seul qui prouve l'exactitude des calculs avec une efficacité raisonnable est l'arithmétique d'intervalle.
L’arithm´etique d’intervalles
On obtient l'extension naturelle aux intervalles F d'une fonction f en remplaçant chaque variable réelle par une variable d'intervalle et chaque opération arithmétique ou fonction élémentaire par ce qui lui est associé sur les intervalles. Si l'expression d'une fonction f ne contient que de simples occurrences de variables, le développement naturel aux intervalles donne le cadre exact du domaine variationnel de la fonction.
Contraintes d’intervalles
En notant f p(Ni) l'ensemble des points fixes de l'opérateur de contraction Ni, la sémantique approchée de E est définie par. Sa particularité est d'utiliser un opérateur de contraction spécifique pour chaque contrainte.
Op´erateurs de contraction g´en´eriques
On perd alors les propriétés (3) et (4), mais cela est au profit d'une résolution plus rapide. Une alternative qui évite la décomposition en contraintes élémentaires est de se contenter d'une forme de cohérence plus faible : la cohérence de boîte [17].
Solveurs sp´ecialis´es pour des contraintes sp´ecifiques
Une approche intéressante pour résoudre des contraintes d'ordre supérieur (quadratiques, puissances, etc.) est obtenue en effectuant une reformulation linéaire de ces expressions. L'utilisation de reformulations linéaires a été plus récemment généralisée dans l'algorithme de réduction de domaine Quad [78] pour.
Synth`ese
Bien que l'utilisation intensive de l'algorithme du simplexe nécessite son implémentation en virgule flottante, on peut fiabiliser ses résultats [75]. Précisément, on peut déjà définir des approximations linéaires extérieures avec des arrondis dirigés ; puis l'inclusion d'une expression corrective proposée récemment par Neumaier [94] pour les programmes linéaires garantit que l'utilisation des calculs du solveur linéaire préserve la justesse du calcul.
Relaxations continues en PPC
Si en principe, les variables de recherche telles que les variables résolubles peuvent être discrètes ou continues, en pratique, les problèmes traités par Hooker se limitent au cas des contraintes vérifiables liées uniquement aux variables discrètes et des contraintes résolubles limitées aux contraintes linéaires ; par conséquent, ils ne nous aident pas à aborder notre travail. Dans le cas d'une résolution dans un solveur de contraintes discrètes, l'interface d'une contrainte globale permet de gérer la propagation d'un sous-problème continu dans le solveur sans modifier son architecture.
R´esolution de contraintes hybrides en PPC
Elle s'appliquerait également aux contraintes bénéficiant d'un algorithme de filtrage continu spécialisé tel que Quad (cf. Section 1.3.5). Batnini et Rueher [10] présentent une décomposition sémantique des contraintes de distance euclidienne qui accélère l'algorithme Quad [78].
S´emantique de la contrainte distn
Diff´erents domaines d’application de distn
La première contrainte permet de modéliser le sous-problème d'optimisation à travers la variable d'optimisation o et l'encodage de la structure du problème dans la matrice d. On aimerait, pour certaines configurations, pouvoir déterminer la position de la plateforme en fonction de la longueur des pattes.
Synth`ese
Caract´erisation du filtrage par des r´egions permises et interdites
En permettant une représentation des domaines par des polygones, la région interdite de Pi pour la contrainte dist(Pi, Pj)≥di,j est donnée par. En autorisant une représentation des domaines par des polygones, la région autorisée de Pi pour la contrainte dist(Pi, Pj)≤di,j est donnée par.
Filtrage obtenu par une seule contrainte
Cette définition nous intéresse car elle permet de caractériser le support d'une contrainte de distance euclidienne minimale. Par contre, on voit qu'il reste une partie importante du domaine de P1 dont on sait déjà qu'elle ne peut pas contenir de solutions, mais qu'elle ne peut pas être filtrée du fait de la représentation des domaines par un produit de variables indépendantes.
Filtrage obtenu en consid´erant plusieurs contraintes
2} Bien que non présentés comme tels, leur schéma correspond à ce que l'on attend d'une contrainte globale exploitant pleinement la sémantique du problème traité. Ce constat est à l'origine d'une grande partie de la littérature qui traite de cette question, où elle est qualifiée de « méthode des zones actives »4.

La m´ethode des aires actives
Ce dernier schéma est au cœur de notre algorithme global de filtrage par contraintes. Une fois le pavage de l'espace déterminé, un algorithme de filtrage doit être utilisé pour réduire tous les n-tuiles en n-tuiles plus petites (éventuellement les supprimer ou les réduire en points) afin d'éliminer ceux contenant un garnissage avec un rayon supérieur à adinf.
M´ethode des aires actives appliqu´ee `a des domaines rectangulaires
Deux types de procédures de filtrage ont été développés pour la branche et l'algorithme. L'algorithme de propagation considère tour à tour chaque tuile Pi, la décompose temporellement au moyen d'une fonction T empSubT se traduisant en un ensemble de sous-tuiles {Pik}k=1,...,t auxquelles on applique le filtrage M inDistanceP dirigé par chacun des voisins appartenant à Voisins(Pi).
Premier algorithme propos´e pour distn
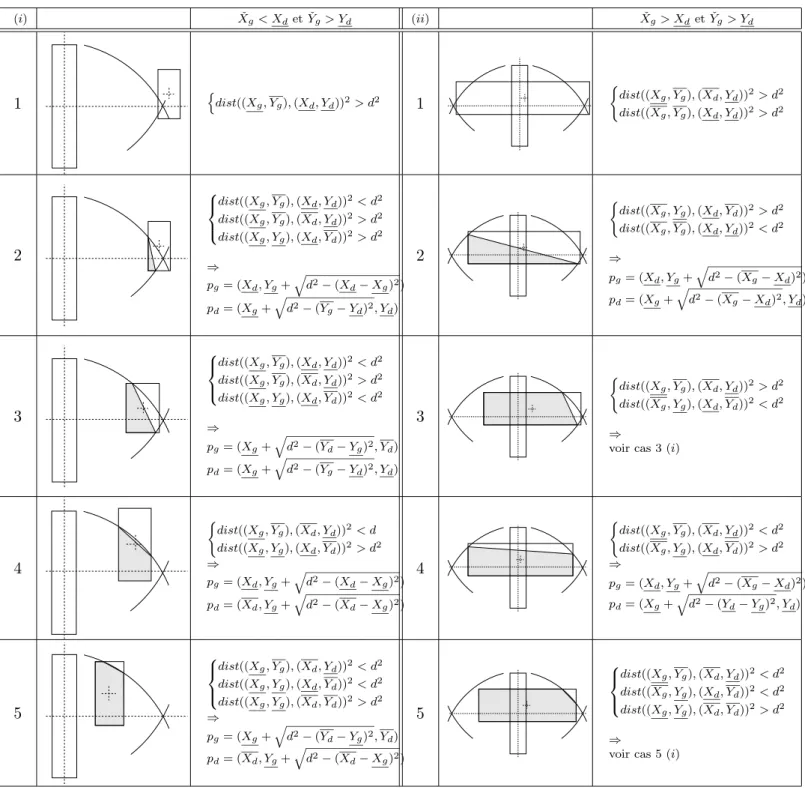
Dans notre approximation de la contrainte de distance minimale ou maximale, nous voulons éliminer uniquement les points de la zone ombrée, nous devons donc nous assurer que les demi-espaces calculés sont bien en deçà de cette limite. Le deuxième point est analogue : lors du calcul du coefficient directeur de la pente des droites supportant ces deux points, il faut utiliser le calcul d'intervalle, et une autre étude de cas détermine alors à quelle borne de l'intervalle adhérer.

Extension aux intervalles de l’algorithme de Seidel
Le premier est résolu en utilisant l'arrondi dirigé de l'arithmétique d'intervalle pour calculer les points d'intersection des arcs avec les carrés : on choisit la limite de l'intervalle. Cette réécriture diffère de l'algorithme original [109] dans ses hypothèses de travail : les inégalités de programme linéaires peuvent être insolubles.
Synth`ese
Cependant, nous avons abandonné cet algorithme au profit de la méthode de l'aire active utilisant des polygones car Mark'ot et Csendes [84] ont récemment montré qu'il est possible d'adapter la méthode des polygones au paradigme de l'arithmétique par intervalles, et la comparaison avec cette nouvelle approche a montré un gain significatif en performance. C'est pourquoi nous avons poursuivi nos travaux basés sur des approximations polygonales de la région active.
Algorithme de filtrage de MinDistance
Nous donnons ici un premier aperçu de la façon dont l'algorithme peut être étendu en 3 dimensions. Nous nous basons sur l'algorithme enO(m+n) pour les polygones ametnside donné dans [38] que nous décrivons en détail dans l'algorithme 11.
Cin´ematique avant d’un robot planaire
Pour rendre cet algorithme efficace, nous combinons le calcul des nombres rationnels avec l'arithmétique des intervalles. Le calcul du prédicat n'implique que des comparaisons de signes et de différences et des produits de vecteurs.
La fractale de Sierpinski
Nous étudions successivement la solution de trois cas avec une seule solution et d'un autre cas contenant plusieurs solutions. En particulier, les consistances locales ordinaires sont trop faibles pour résoudre le problème de Sierpinski(3) en une heure de calcul.

D´efinitions du probl`eme
On définit le domaine ressource d'un chemin comme l'ensemble des couples (fréquence, polarisation) susceptibles de lui être affectés. Nous définissons une solution réalisable au problème d'allocation de fréquence comme l'allocation d'une ressource (fréquence, polarisation) à chaque chemin en satisfaisant toutes les contraintes énoncées.
Description des contraintes radio-´electriques (RLFAP)
L'allocation de fréquences consiste pour l'allocateur à trouver un couple (fréquence, polarisation) pour chaque chemin parmi un domaine de ressources fréquentielles qui lui sont associées (déterminé par des contraintes matérielles, réglementaires ou au choix de l'opérateur) et satisfaisant à toutes les contraintes de compatibilité radio, tout en précisant la localisation des sites associés au sol, en respectant les données associées.
Description des contraintes de d´eploiement (Loc)
Description des contraintes radio´electriques de d´eploiement (LocRLFAP) 75
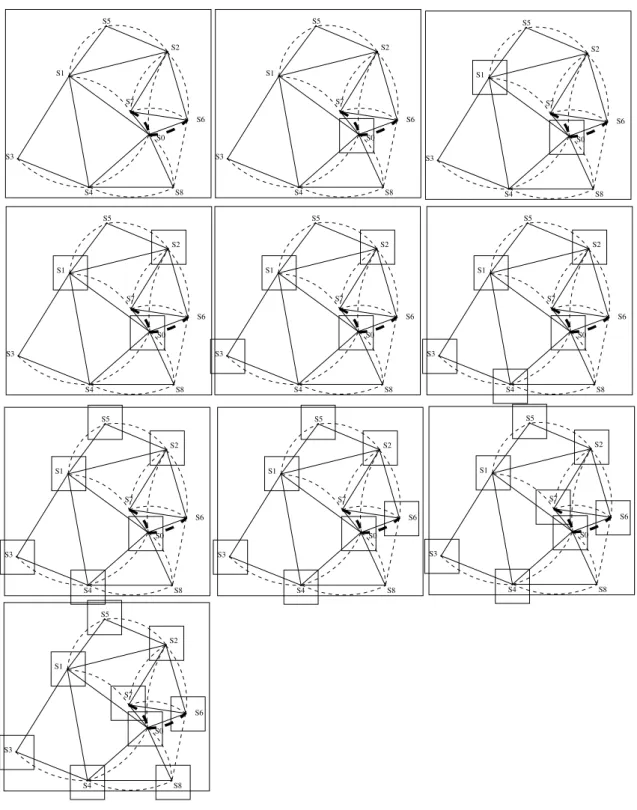
Ces contraintes, appelées contraintes de compatibilité à distance, traduisent le fait que l'écart de fréquence nécessaire entre deux trajets interférents dépend des polarisations qui leur sont respectivement affectées. Les liens sont représentés par des traits pleins, les contraintes de perturbation entre sites à portée sont données par des arcs.

Donn´ees du probl`eme
Mod´elisation des contraintes radio´electriques
Les contraintes de type radio qui peuvent apparaître sur les deux chemins de certains liens lij sélectionnés peuvent alors être modélisées comme suit. On considérera toutes les bandes interdites dans le spectre de fréquence disponible en le définissant à partir de l'union ordonnée de nb bandes acceptables Fbk, 1≤k≤nb.
Mod´elisation des contraintes de d´eploiement
Les fréquences sont contraintes d'être régulièrement espacées dans F d'un pas de fréquence ∆p. Lorsque le polygone est convexe, on peut représenter son intérieur par l'intersection des demi-espaces définis par l'ensemble de ses arêtes, et sans perte de généralité on peut supposer que les ZPI sont convexes1.
Mod´elisation des contraintes de d´eploiement avec allocation de fr´equences 81
Ce critère est atteint en introduisant une variable objectif k qui représente le nombre total de fréquences allouées pour résoudre le problème. A noter que contrairement au problème d'assignation de fréquence, le problème abordé ne se limite plus à minimiser le nombre de couleurs nécessaires pour colorer un graphe.
Mod´elisation des contraintes discr`etes logiques et lin´eaires
Dans notre présentation, nous distinguons les contraintes discrètes simples des contraintes non linéaires discrètes et continues, puis introduisons celles qui représentent la disjonction entre les premières et les deux dernières.
Mod´elisation discr`ete des contraintes non-lin´eaires
Mod´elisation continue des contraintes non-lin´eaires
Les contraintes de distance peuvent donc être fournies directement au solveur en exprimant la formule qui donne la fonction de distance euclidienne. L'algorithme de propagation garantit alors pour tout point de choix la consistance aux bornes de la contrainte et par conséquent la validité de la contrainte en tout point solution dans l'espace continu.
Mod´elisation des disjonctions
Lorsque la branche discrète d'une disjonction hybride devient fausse, la contrainte continue est ajoutée au magasin de contraintes continues, et la propagation de toutes les contraintes continues a lieu jusqu'à ce qu'un point fixe soit atteint ; toutes les disjonctions hybrides sont alors passées en revue pour vérifier qu'aucune de leurs ramifications continues n'a été violée lors de la propagation du stock de contraintes continues. Cependant, on peut noter que si par ex. chacun des termes de gauche de la disjonction est violé, alors le terme de droite le moins restrictif sera mis en place inutilement.
Mod´elisation en contraintes du crit`ere d’optimisation
Simplification et donn´ees du probl`eme
Les liens à établir entre les sites sont matérialisés par des traits pleins sur la figure 3.2, et les limites de compatibilité moyenne et pleine distance sont définies par les constantes dl= 30 et dh= 60.
On peut vérifier que le système de contraintes associé à ces positions ne contient donc pas de contraintes à mi-travée et que l'expression en contraintes du réseau R5 peut ainsi être simplifiée.
Choix du type de domaines utilis´es
L'utilisation de domaines dans l'intension pour limiter la valeur absolue est réalisée par la disjonction de deux limites linéaires. Lors de l'application de la modélisation extensionnelle aux domaines de variables de chemin, les contraintes de valeur absolue garantissent la cohérence d'arc de ce sous-ensemble de contraintes.
Algorithmes de recherche
Avec des domaines donnés en intention, si aucune des branches de la disjonction ne se résout, le filtrage possible pour la contrainte de valeur absolue est nul. Cette dernière était globalement la plus efficace dans nos cas et c'est donc celle qui a été choisie pour résoudre les contraintes discrètes.
R´esultats num´eriques
Cependant, on peut noter que pour les cas plus grands, la résolution est beaucoup plus chère qu'avec le modèle classique. De plus, le modèle rencontre les mêmes difficultés que dans le cas purement discret, à savoir qu'on n'arrive plus à résoudre le scénario à dix pays.
Bilan
En cas de déploiement de neuf sites, il y a un gain de 57% en fréquences. Nous avons en(n−1) disjonctions dans le modèle, étant donné que toute la clique de sites est considérée et que pour chaque paire, les contraintes de compatibilité d'étendue et de mi-portée sont fixées.
Branchement sur les disjonctions dans l’algorithme de recherche
Heuristiques de choix de variables
De plus, la résolution du LocRLFAP est plus facile que celle du RLFAP sur les cas de 5 à 9 sites, mais ce n'est pas vrai sur le plus gros exemple que nous sommes alors étonnamment incapables de résoudre. Si ce choix seul n'est pas bénéfique, le combiner avec mindomain peut produire de bons résultats ; exactement, celui avec le plus petit domaine le plus restreint était le meilleur sur nos exemples.
Heuristique de choix de valeurs
Bessi`ere et Régin présentent dans [21] des arguments qui suggèrent de privilégier l'heuristique mindomain/maxdegree plutôt que mindomain pour effectuer la sélection des variables, mais dans nos expérimentations cette heuristique ne s'est pas avérée intéressante dans nos exemples.
R´esultats num´eriques
Maintien des contraintes de distance min et max par la contrainte globale
Il est également avantageux d'ajouter au système de contraintes – de manière redondante – l'expression de distn par des contraintes élémentaires de distance, car cela permet d'accélérer la propagation du modèle.
Maintien des contraintes de distance min et max par la contrainte globale
Ici, nous fournissons à nouveau une expression redondante pour distn var par contraintes.
R´esultats num´eriques sur les mod`eles simples
Dans six cas sur dix, le modèle hybride atteint l'optimum avec un peu moins de boucles de rétroaction, mais l'écart n'est pas suffisant pour accélérer le calcul. Rappelons que l'une des principales lacunes du modèle et du mode de résolution précédents était qu'ils n'avaient pas réussi à augmenter le déploiement à 10 endroits.
R´esultats num´eriques avec distn var
En revanche, dans trois autres cas, le modèle hybride permet de résoudre le problème en moins de dix minutes, alors que le modèle discret n'arrive même pas à trouver une solution réalisable en quelques heures. C'est l'association du modèle hybride utilisant distn var avec l'heuristique mindomain-maxconstraints qui est essentielle pour résoudre tous nos exemples.

Analyse qualitative des r´esultats
Cette option, bien qu'assez spécifique au cas du placement d'antennes radio, pourrait augmenter l'importance de la limitation et l'efficacité d'al-. En particulier, le passage aux trois dimensions permettrait de comprendre l'applicabilité de la contrainte à des problèmes importants.