HAL Id: hal-01276815
https://hal.archives-ouvertes.fr/hal-01276815
Submitted on 20 Feb 2016
HAL
is a multi-disciplinary open access archive for the deposit and dissemination of sci- entific research documents, whether they are pub- lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire
HAL, estdestinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
EL-Labelings and Canonical Spanning Trees for Subword Complexes
Vincent Pilaud, Christian Stump
To cite this version:
Vincent Pilaud, Christian Stump. EL-Labelings and Canonical Spanning Trees for Subword Com-
plexes. Karoly Bezdek; Antoine Deza; Yinyu Ye. Discrete Geometry and Optimization, 69, Springer
International Publishing, pp.213-248, 2013, Fields Institute Communications Series, 978-3-319-00199-
9. �10.1007/978-3-319-00200-2_13�. �hal-01276815�
FOR SUBWORD COMPLEXES
VINCENT PILAUD AND CHRISTIAN STUMP
Abstract. We describe edge labelings of the increasing flip graph of a sub- word complex on a finite Coxeter group, and study applications thereof. On the one hand, we show that they provide canonical spanning trees of the facet-ridge graph of the subword complex, describe inductively these trees, and present their close relations to greedy facets. Searching these trees yields an efficient algorithm to generate all facets of the subword complex, which extends the greedy flip algorithm for pointed pseudotriangulations. On the other hand, when the increasing flip graph is a Hasse diagram, we show that the edge labeling is indeed an EL-labeling and derive further combinatorial properties of paths in the increasing flip graph. These results apply in particular to Cambrian lattices, in which case a similar EL-labeling was recently studied by M. Kallipoliti and H. M¨uhle.
Contents
1. Introduction 2
2. Edge labelings of graphs and posets 2
2.1. ER-labelings of graphs and associated spanning trees 2
2.2. EL-labelings of graphs and posets 3
3. Subword complexes on Coxeter groups 4
3.1. Coxeter systems 4
3.2. Subword complexes 5
3.3. Inductive structure 7
3.4. Flips and roots 7
3.5. Restriction of subword complexes to parabolic subgroups 9 4. EL-labelings and spanning trees for the subword complex 11 4.1. EL-labelings of the increasing flip graph 11
4.2. Greedy facets 15
4.3. Spanning trees 17
4.4. Greedy flip algorithm 22
5. Further combinatorial properties of the EL-labelings 24
5.1. Double root free subword complexes 24
5.2. Two relevant examples 28
Acknowledgments 31
References 31
V. P. was supported by the spanish MICINN grant MTM2011-22792, by the french ANR grant EGOS 12 JS02 002 01, by the European Research Project ExploreMaps (ERC StG 208471), and by a postdoctoral grant of the Fields Institute of Toronto.
1
1. Introduction
Subword complexes on Coxeter groups were defined and studied by A. Knutson and E. Miller in the context of Gr¨obner geometry of Schubert varieties [KM04, KM05]. Type A spherical subword complexes can be visually interpreted using pseudoline arrangements on primitive sorting networks. These were studied by V. Pilaud and M. Pocchiola [PP12] as combinatorial models for pointed pseudo- triangulations of planar point sets [RSS08] and for multitriangulations of convex polygons [PS09]. These two families of geometric graphs extend in two different ways the family of triangulations of a convex polygon.
The greedy flip algorithm was initially designed to generate all pointed pseudo- triangulations of a given set of points or convex bodies in general position in the plane [PV96,BKPS06]. It was then extended in [PP12] to generate all pseudoline arrangements supported by a given primitive sorting network. The key step in this algorithm is to construct a spanning tree of the flip graph on the combinatorial objects, which has to be sufficiently canonical to be visited in polynomial time per node and polynomial working space.
In the present paper, we study natural edge lexicographic labelings of the in- creasing flip graph of a subword complex on any finite Coxeter group. As a first line of applications of these EL-labelings, we obtain canonical spanning trees of the flip graph of any subword complex. We provide alternative descriptions of these trees based on their close relations to greedy facets, which are defined and studied in this paper. Moreover, searching these trees provides an efficient algorithm to generate all facets of the subword complex. For type A spherical subword com- plexes, the resulting algorithm is that of [PP12], although the presentation is quite different.
The second line of applications of the EL-labelings concerns combinatorial prop- erties ensuing from EL-shellability [Bj¨o80, BW96]. Indeed, when the increasing flip graph is the Hasse diagram of the increasing flip poset, this poset is EL- shellable, and we can compute its M¨obius function. These results extend recent work of M. Kallipoliti and H. M¨uhle [KM12] on EL-shellability of N. Reading’s Cambrian lattices [Rea04, Rea06, Rea07a, Rea07b], which are, for finite Coxeter groups, increasing flip posets of specific subword complexes studied by C. Ceballos, J.-P. Labb´e and C. Stump [CLS11] and by the authors in [PS11].
2. Edge labelings of graphs and posets
In [Bj¨o80], A. Bj¨orner introduced EL-labelings of partially ordered sets to study topological properties of their order complexes. These labelings are edge labelings of the Hasse diagrams of the posets with certain combinatorial properties. In this paper, we consider edge labelings of finite, acyclic, directed graphs which might differ from the Hasse diagrams of their transitive closures.
2.1. ER-labelings of graphs and associated spanning trees. LetG:= (V, E) be a finite, acyclic, directed graph. For u, v ∈ V, we write u v if there is an edge from u to v in G, and u v if there is apath u=x1 x2 · · · x`+1=v from u to v in G (this path has length `). The interval [u, v] in G is the set of verticesw∈V such that u w v.
An edge labeling of G is a map λ: E → N. It induces a labeling λ(p) of any path p : x1 x2 · · · x` x`+1 given by λ(p):=λ(x1 x2)· · ·λ(x` x`+1).
The path pis λ-rising (resp.λ-falling) if λ(p) is strictly increasing (resp. weakly decreasing). The labelingλis anedge rising labelingofG(orER-labelingfor short) if there is a uniqueλ-rising pathpbetween any verticesu, v∈V withu v.
Remark 2.1 (Spanning trees). Let u, v ∈ V, and λ: E → Nbe an ER-labeling of G. Then the union of all λ-rising paths from u to any other vertex of the interval [u, v] forms a spanning tree of [u, v], rooted at and directed away from u.
We call it theλ-source treeof [u, v] and denote it byTλ([u, v]). Similarly, the union of allλ-rising paths from any vertex of the interval [u, v] tovforms a spanning tree of [u, v], rooted at and directed towards v. We call it the λ-sink tree of [u, v] and denote it byTλ∗([u, v]). In particular, ifGhas a unique source and a unique sink, this provides two canonical spanning treesTλ(G) andTλ∗(G) for the graphGitself.
Example 2.2(Cube). Consider the 1-skeletondof thed-dimensional cube [0,1]d, directed from0:= (0, . . . ,0) to1:= (1, . . . ,1). Its vertices are the elements of{0,1}d and its edges are the pairs of vertices which differ in a unique position. Note thatε:= (ε1, . . . , εd) ε0:= (ε01, . . . , ε0d) if and only ifεk ≤ε0k for allk∈[d].
For any edgeε ε0 ofd, letλ(ε ε0) denote the unique position in [d] whereε andε0 differ. Then the mapλis an ER-labeling ofd. Ifε∈ {0,1}dr0, then the father ofεin Tλ(d) is obtained fromε by changing its last 1 into a 0. Similarly, ifε∈ {0,1}dr1, then the father ofεinTλ∗(d) is obtained fromεby changing its first 0 into a 1. See Figure1.
111
110 101
011
100 001
010 000
000 100
010 110
001 101
011 111
3 3
3 3
1
1 1
1
2 2
2
2 111
3 3
3
2 3
2 1
011 101 001
110 010
100 000
3
1
1 1
1
2 2
Figure 1. An ER-labeling λof the 1-skeleton 3 of the 3-cube, theλ-source treeTλ(3) and theλ-sink tree Tλ∗(3).
2.2. EL-labelings of graphs and posets. Although ER-labelings of graphs are sufficient to produce canonical spanning trees, we need the following extension for further properties. The labeling λ: E →N is anedge lexicographic labelingof G (orEL-labelingfor short) if for any verticesu, v∈V withu v,
(i) there is a uniqueλ-rising pathpfrom uto v, and
(ii) its labeling λ(p) is lexicographically first among the labelings λ(p0) of all pathsp0 fromutov.
For example, the ER-labeling of the 1-skeleton of the cube presented in Example2.2 is in fact an EL-labeling.
Remember now that one can associate a finite poset to a finite acyclic directed graph andvice versa. Namely,
(i) thetransitive closureof a finite acyclic directed graphG= (V, E) is the finite poset (V, );
(ii) theHasse diagramof a finite posetPis the finite acyclic directed graph whose vertices are the elements of P and whose edges are thecover relationsin P, i.e.u v ifu <P v and there is now∈P such thatu <P w <P v.
The transitive closure of the Hasse diagram ofP always coincides withP, but the Hasse diagram of the transitive closure of Gmight also be only a subgraph ofG.
AnEL-labelingof the posetP is an EL-labeling of the Hasse diagram ofP. If such a labeling exists, then the poset is calledEL-shellable.
As already mentioned, A. Bj¨orner [Bj¨o80] originally introduced EL-labelings of finite posets to study topological properties of their order complex. In particular, they provide a tool to compute the M¨obius function of the poset. Recall that the M¨obius functionof the poset P is the mapµ:P×P →Zdefined recursively by
µ(u, v):=
1 ifu=v,
−P
u≤Pw<Pvµ(u, w) ifu <P v,
0 otherwise.
When the poset is EL-shellable, this function can be computed as follows.
Proposition 2.3([BW96, Proposition 5.7]). Letλbe an EL-labeling of the posetP.
For everyu, v ∈P withu≤P v, we have
µ(u, v) = evenλ(u, v)−oddλ(u, v),
whereevenλ(u, v)(resp.oddλ(u, v)) denotes the number of even (resp. odd) length λ-falling paths fromutov in the Hasse diagram ofP.
Example 2.4(Cube). The directed 1-skeletondof thed-dimensional cube [0,1]d is the Hasse diagram of the boolean poset. The edge labelingλofdof Example2.2 is thus an EL-labeling of the boolean poset. Moreover, for any two verticesε ε0 ofd, there is a uniqueλ-falling path betweenεandε0, whose length is the Ham- ming distance δ(ε, ε0):=| {k∈[d]|εk6=ε0k} |. The M¨obius function is thus given byµ(ε, ε0) = (−1)δ(ε,ε0). In particular,µ(0,1) = (−1)d.
3. Subword complexes on Coxeter groups
3.1. Coxeter systems. We recall some basic notions on Coxeter systems needed in this paper. More background material can be found in [Hum90].
Let V be an n-dimensional Euclidean vector space. Forv ∈V r0, we denote bysv the reflection interchangingv and−v while fixing pointwise the orthogonal hyperplane. We consider afinite Coxeter groupW acting onV,i.e.a finite group generated by reflections. We assume without loss of generality that the intersection of all reflecting hyperplanes ofW is reduced to 0.
A root system for W is a set Φ of vectors stable under the action of W and containing precisely two opposite vectors orthogonal to each reflection hyperplane of W. Fix a linear functional f : V → R such that f(β) 6= 0 for all β ∈ Φ. It splits the root system Φ into the set ofpositive rootsΦ+ :={β∈Φ|f(β)>0}and the set ofnegative roots Φ−:=−Φ+. Thesimple roots are the roots which lie on the extremal rays of the cone generated by Φ+. They form a basis ∆ of the vector spaceV. Thesimple reflectionsS:={sα|α∈∆}generate the Coxeter group W. The pair (W, S) is afinite Coxeter system. Fors∈S, we letαs∈∆ be the simple root orthogonal to the reflecting hyperplane ofs.
Thelengthof an elementw∈W is the length`(w) of the smallest expression ofw as a product of the generators inS. An expressionw=s1· · ·sp, withs1, . . . , sp∈S, is reducedifp=`(w). The length ofw is also known to be the cardinality of the inversion setofw, defined as the set inv(w):= Φ+∩w(Φ−) of positive roots sent to
negative roots byw−1. Indeed, inv(w) ={αs1, s1(αs2), . . . , s1· · ·s`−1(αs`)}for any reduced expression w=s1· · ·s` of w. The (right) weak orderis the partial order onW defined byu≤wif there existsv∈W withuv=wand`(u) +`(v) =`(w).
In other words,u≤v if and only if inv(u)⊆inv(v).
Example 3.1 (Type A — Symmetric groups). The symmetric group Sn+1, act- ing on the linear hyperplane1⊥:=
x∈Rn+1
h1|xi= 0 by permutation of the coordinates, is the reflection group oftypeAn. It is the group of isometries of the standard n-dimensional regular simplex conv{e1, . . . , en+1}. Its reflections are the transpositions of Sn+1 and the set {ei−ej|i6=j} is a root system for An. We can choose the linear functionalf such that the simple reflections are the adjacent transpositionsτi:= (i i+ 1), and the simple roots are the vectors ei+1−ei. 3.2. Subword complexes. We consider a finite Coxeter system (W, S), a word Q:= q1q2· · ·qm on the generators of S, and an elementρ∈ W. A. Knutson and E. Miller [KM04] define the subword complex SC(Q, ρ) to be the simplicial com- plex of those subwords of Q whose complements contain a reduced expression forρ as a subword. A vertex of SC(Q, ρ) is a position of a letter in Q. We denote by [m]:={1,2, . . . , m} the set of positions in Q. A facet ofSC(Q, ρ) is the comple- ment of a set of positions which forms a reduced expression forρin Q. We denote byF(Q, ρ) the set of facets ofSC(Q, ρ). We writeρ≺Q when Q contains a reduced expression ofρ,i.e.whenSC(Q, ρ) is non-empty.
Example 3.2. Consider the type A Coxeter group S4 generated by {τ1, τ2, τ3}.
Let Qex :=τ2τ3τ1τ3τ2τ1τ2τ3τ1 andρex := [4,1,3,2]. The reduced expressions ofρex are τ2τ3τ2τ1, τ3τ2τ3τ1, and τ3τ2τ1τ3. Thus, the facets of the subword complex SC(Qex, ρex) are given by {1,2,3,5,6}, {1,2,3,6,7}, {1,2,3,7,9}, {1,3,4,5,6}, {1,3,4,6,7}, {1,3,4,7,9}, {2,3,5,6,8}, {2,3,6,7,8}, {2,3,7,8,9}, {3,4,5,6,8}, {3,4,6,7,8}, and{3,4,7,8,9}. Let Iex :={1,3,4,7,9} and Jex :={3,4,7,8,9} de- note two facets ofSC(Qex, ρex). We will use this example throughout this paper to illustrate further notions.
Example 3.3 (TypeA— Primitive networks and pseudoline arrangements). For typeACoxeter systems, subword complexes can be visually interpreted using prim- itive networks. AnetworkN is a collection ofn+ 1 horizontal lines (calledlevels, and labeled from bottom to top), together with m vertical segments (called com- mutators, and labeled from left to right) joining two different levels and such that no two of them have a common endpoint. We only consider primitive networks, where any commutator joins two consecutive levels. See Figure2(left).
4 3 2 1
4 3
1 1 2
2 4 8
5 7
3 6 9
4 3 2 1
2 3
4 1
34 3
4 2
2 2
1 1
2 4
1 4
1 43
32
Figure 2. The network NQex (left) and the pseudoline arrange- ment ΛIex for the facetIex={1,3,4,7,9}ofSC(Qex, ρex) (right).
Apseudolinesupported by the network N is an abscissa monotone path onN. A commutator ofN is acrossingbetween two pseudolines if it is traversed by both pseudolines, and a contact if its endpoints are contained one in each pseudoline.
Apseudoline arrangement Λ is a set ofn+ 1 pseudolines onN, any two of which have at most one crossing, possibly some contacts, and no other intersection. We label the pseudolines of Λ from bottom to top on the left of the network, and we defineπ(Λ)∈Sn+1to be the permutation given by the order of these pseudolines on the right of the network. Note that the crossings of Λ correspond to the inversions ofπ(Λ). See Figure2(right).
Consider the typeACoxeter groupSn+1generated byS ={τi |i∈[n]}, whereτi
is the adjacent transposition (i i+ 1). To a word Q:= q1q2· · ·qm with mletters onS, we associate a primitive networkNQ withn+ 1 levels andm commutators.
If qj =τp, thejth commutator ofNQis located between thepthand (p+ 1)thlevels of NQ. See Figure2 (left). For ρ∈Sn+1, a facetI of SC(Q, ρ) corresponds to a pseudoline arrangement ΛI supported byNQ and withπ(ΛI) =ρ. The positions of the contacts (resp. crossings) of ΛI correspond to the positions ofI(resp. of the complement ofI). See Figure 2(right).
Example 3.4 (Combinatorial models for geometric graphs). As pointed out in [PP12], pseudoline arrangements on primitive networks give combinatorial models for the following families of geometric graphs (see Figure3):
(i) triangulations of convex polygons;
(ii) multitriangulations of convex polygons [PS09];
(iii) pointed pseudotriangulations of points in general position in the plane [RSS08];
(iv) pseudotriangulations of disjoint convex bodies in the plane [PV96].
For example, consider a triangulationT of a convex (n+ 3)-gon. Define the di- rection of a line of the plane to be the angleθ∈[0, π) of this line with the horizontal axis. Define also a bisector of a triangle 4 to be a line passing through a vertex of4and separating the other two vertices of4. For any directionθ∈[0, π), each triangle ofT has precisely one bisector in directionθ. We can thus order then+ 1
Figure 3. Primitive sorting networks are combinatorial models for triangulations, multitriangulations, and pseudotriangulations of points or disjoint convex bodies.
triangles ofT according to the orderπθof their bisectors in directionθ. The pseu- doline arrangement associated to T is then given by the evolution of the order πθ
when the direction θ describes the interval [0, π). A similar duality holds for the other three families of graphs, replacing triangles by the natural cells decomposing the geometric graph (stars for multitriangulations [PS09], or pseudotriangles for pseudotriangulations [RSS08]). See Figure 3 for an illustration. Details can be found in [PP12].
Remark 3.5. There is a natural reversal operation on subword complexes. Namely, SC(qm· · ·q1, ρ−1) ={{m+ 1−i|i∈I} |I∈ SC(q1· · ·qm, ρ)}.
We will use this operation to relate positive and negative labelings, facets and trees.
3.3. Inductive structure. We denote by Q`:= q2· · ·qm and Qa:= q1· · ·qm−1 the words on S obtained from Q:= q1· · ·qm by deleting its first and last letters, respectively. We denote by X→ the right shift {x+ 1|x∈X} of a subset X ofZ. For a collection X of subsets ofZ, we write X→ for the set{X→|X∈ X }.
Moreover, we denote by X? z (or by z ?X) the join{X∪z|X ∈ X } of X with somez∈Z. Remember that`(ρ) denotes the length ofρand that we writeρ≺Q when Q contains a reduced expression ofρ.
We can decompose inductively the facets of the subword complexSC(Q, ρ) de- pending on whether or not they contain the last letter of Q. Denoting by ε the empty word and by ethe identity of W, we have F(ε, e) ={∅} andF(ε, ρ) =∅ ifρ6=e. Moreover, for a non-empty word Q onS, the set F(Q, ρ) is given by
(i) F(Qa, ρqm) ifmappears in none of the facets ofSC(Q, ρ) (i.e.ifρ6≺Qa);
(ii) F(Qa, ρ)? mifmappears in all the facets ofSC(Q, ρ) (i.e.if`(ρqm)> `(ρ));
(iii) F(Qa, ρqm)t F(Qa, ρ)? m
otherwise.
By reversal (see Remark3.5), there is also a similar inductive decomposition of the facets of the subword complexSC(Q, ρ) depending on whether or not they contain the first letter of Q. Namely, for a non-empty word Q, the setF(Q, ρ) is given by
(i) F(Q`, q1ρ)→if 1 appears in none of the facets of SC(Q, ρ) (i.e.ifρ6≺Q`);
(ii) 1?F(Q`, ρ)→ if 1 appears in all the facets ofSC(Q, ρ) (i.e.if`(q1ρ)> `(ρ));
(iii) F(Q`, q1ρ)→ t 1?F(Q`, ρ)→
otherwise.
Although we will only use these decompositions for the facetsF(Q, ρ), they extend to the whole subword complexSC(Q, ρ) and are used to obtain the following result.
Theorem 3.6([KM04, Corollary 3.8]). The subword complexSC(Q, ρ)is either a simplicial sphere or a simplicial ball.
3.4. Flips and roots. Let I be a facet of SC(Q, ρ) and i be a position in I. If there exists a facetJ ofSC(Q, ρ) and a position j∈J such thatIri=Jrj, we say thatIandJ areadjacentfacets, thatiisflippablein I, and thatJ is obtained from Ibyflippingi. Note that, if they exist,J andj are unique by Theorem3.6.
We say that the flip fromIto J flips out iandflips inj.
We denote byG(Q, ρ) the graph of flips, whose vertices are the facets ofSC(Q, ρ) and whose edges are pairs of adjacent facets. That is,G(Q, ρ) is the ridge graph of the simplicial complexSC(Q, ρ). This graph is connected according to Theorem3.6.
This graph can be naturally oriented by the direction of the flips as follows. LetI andJ be two adjacent facets ofSC(Q, ρ) withIri=Jrj. We say that the flip from I to J is increasing ifi < j. We consider the flip graphG(Q, ρ) oriented by increasing flips.
12356 23568 23678 12367
23789 12379
34789 13479
34678 13467
34568 13456
Figure 4. The increasing flip graphG(Qex, ρex).
Example 3.7. Figure 4 represents the increasing flip graph G(Qex, ρex) for the subword complexSC(Qex, ρex) of Example3.2. The facets ofSC(Qex, ρex) appear in lexicographic order from left to right. Thus, all flips are increasing from left to right.
Remark 3.8. The increasing flip graph of SC(Q, ρ) was already considered by A. Knutson and E. Miller [KM04, Remark 4.5]. It carries various combinatorial informations about the subword complex SC(Q, ρ). In particular, since the lex- icographic ordering of the facets of SC(Q, ρ) is a shelling order for SC(Q, ρ), the h-vector of the subword complexSC(Q, ρ) is the in-degree sequence of the increasing flip graphG(Q, ρ).
Throughout the paper, we consider flips as elementary operations on subword complexes. In practice, the necessary information to perform flips in a facet I ofSC(Q, ρ) is encoded in its root functionr(I,·) : [m]→Φ defined by
r(I, k):= ΠQ[k−1]rI(αqk),
where ΠQX denotes the product of the reflections qx ∈ Q for x ∈ X. The root configuration of the facetI is the multiset R(I):={{r(I, i)|iflippable inI}}. The root function was introduced by C. Ceballos, J.-P. Labb´e and C. Stump [CLS11], and we extensively studied root configurations in [PS11] in the construction of brick polytopes for spherical subword complexes. The main properties of the root function are summarized in the following proposition, whose proof is similar to that of [CLS11, Lemmas 3.3 and 3.6] or [PS11, Lemma 3.3].
Proposition 3.9. Let I be any facet of the subword complex SC(Q, ρ).
(1) The mapr(I,·) :i7→r(I, i)is a bijection from the complement of I to the inversion set ofρ.
(2) The mapr(I,·) sends the flippable positions inI to {±β|β ∈inv(ρ)} and the unflippable ones toΦ+rinv(ρ).
(3) IfIandJ are two adjacent facets ofSC(Q, ρ)withIri=Jrj, the position jis the unique position in the complement ofIfor whichr(I, j)∈ {±r(I, i)}.
(4) In the situation of(3), we have r(I, i) =r(I, j)∈Φ+ if i < j (increasing flip), whiler(I, i) =−r(I, j)∈Φ− if i > j (decreasing flip).
(5) In the situation of(3), the map r(J,·)is obtained from the mapr(I,·)by:
r(J, k) =
(sr(I,i)(r(I, k)) if min(i, j)< k≤max(i, j), r(I, k) otherwise.
We callr(I, i) =−r(J, j) thedirectionof the flip from the facetI to the facetJ. Example 3.10. In typeA, roots and flips can easily be described using the prim- itive network interpretation presented in Example3.3. Consider a word Q on the simple reflections{τi|i∈[n]}, an elementρ∈Sn+1, and a facetIofSC(Q, ρ). For anyk∈[m], the rootr(I, k) is the differenceet−ebwheretandbare the indices of the pseudolines of ΛI which arrive respectively on the top and bottom endpoints of thekth commutator ofNQ. A flip exchanges a contact between two pseudolines t andb of ΛI with the unique crossing betweentand bin ΛI (when it exists). Such a flip is increasing if the contact lies before the crossing, i.e. if t > b. Figure 5 illustrates the properties of Proposition 3.9on the subword complex SC(Qex, ρex) of Example3.2.
4 3 2 1
2 3
4 1 24
42
43 3
1 1
3 4
1 4
1 32
23 4
3 2 1
2 3
4 1
34 3
4 2
2 2
1 1
2 4
1 4
1 43
32
Figure 5. The increasing flip from facet Iex = {1,3,4,7,9} to facet Jex = {3,4,7,8,9} of the subword complex SC(Qex, ρex), illustrated on the networkNQex.
3.5. Restriction of subword complexes to parabolic subgroups. In the proof of our main result, we will need to restrict subword complexes to dihedral parabolic subsystems. The following statement can essentially be found in [PS11, Proposi- tion 3.7], we provide a proof here as well for the sake of completeness.
Proposition 3.11([PS11, Proposition 3.7]). LetSC(Q, ρ)be a subword complex for a Coxeter system(W, S)acting onV, and letV0 ⊆V be a subspace ofV. The sim- plicial complex given by all facetsJ ofSC(Q, ρ)reachable from a particular facetI by flips whose directions are contained in V0 is isomorphic to a subword complex SC(Q0, ρ0)for the restriction of(W, S)toV0. The order of the letters is preserved by this isomorphism. In particular, the restriction of the increasing flip graph G(Q, ρ) to these reachable facets is isomorphic to the increasing flip graph G(Q0, ρ0).
Proof. To prove this proposition, we explicitly construct the word Q0onS0 and the elementρ0∈W0 where (W0, S0) is the restriction of (W, S) to the subspace V0.
First, the elementρ0 only depends onρand onV0: it is given by the projection ofρontoW0. This is to say thatρ0 is the unique element inW0whose inversion set is inv(ρ0) = inv(ρ)∩V0. To see that inv(ρ)∩V0 is again an inversion set, remember that a subsetI of Φ+ is an inversion set for an element inW if and only if for all α, β, γ∈Φ+ such thatγ=aα+bβ for somea, b∈R≥0,
α, β∈ I =⇒ γ∈ I =⇒ α∈ I orβ ∈ I ,
seee.g.[Pap94]. Moreover this property is preserved under intersection with linear subspaces.
We now construct the word Q0 and the facet I0 of SC(Q0, ρ0) corresponding to the particular facet I of SC(Q, ρ). For this, let X:={x1, . . . , xp} be the set of
4 6 5
3 2 1
4 1 5
6 2 3 31
65
65 54
14 5
4 4
4 2 3 3
2 2
1 3
2 31
64 41
51 6
5 61
⇓ restriction to the spaceV0= vecthe3−e1, e4−e3, e6−e5i ⇓
5 6
4 3 1
6 5
1 4 3 31
65 6
5
14
43 31
41
65
Figure 6. Restricting subword complexes.
positionsk∈[m] such thatr(I, k)∈V0. The word Q0 haspletters corresponding to the positions inX, and the facetI0 contains precisely the positionsk∈[p] such that the position xk is in I. To construct the word Q0, we scan Q from left to right as follows. We initialize Q0 to the empty word, and for each 1 ≤ k ≤ p, we add a letter q0k ∈ S0 to Q0 in such a way that r(I0, k) = r(I, xk). To see that such a letter exists, we distinguish two cases. Assume first that r(I, xk) is a positive root. Let I be the inversion set of w:= ΠQ[xk−1]rI and I0 = I ∩V0 be the inversion set of w0:= ΠQ0[k−1]rI0. Then the set I0∪ {r(I, xk)} is again an inversion set (as the intersection ofV0with the inversion setI ∪ {r(I, xk)}ofwqxk) which contains the inversion set I0 of w0 together with a unique additional root.
Therefore, the corresponding element ofW0 can be written asw0q0kfor some simple reflection qk0 ∈S0. Assume now that r(I, xk) is a negative root. Then xk ∈ I, so that we can flip it with a positionxk0 < xk, and we can then argue on the resulting facet.
By the procedure described above, we eventually obtain the subword complex SC(Q0, ρ0) and its facet I0 corresponding to the facet I. Finally observe that se- quences of flips in SC(Q, ρ) starting at the facetI, and whose directions are con- tained in V0, correspond bijectively to sequences of flips in SC(Q0, ρ0) starting at the facetI0. In particular, let J andJ0 be two facets reached fromI and fromI0, respectively, by such a sequence. We then have that the root configuration of J0 is exactly the root configuration of J intersected with V0, and that the order in which the roots appear in the root configurations is preserved. This completes the
proof.
Example 3.12. To illustrate different possible situations happening in this restric- tion, we consider the subword complexSC(Q, ρ) on the Coxeter groupA5=S6gen- erated by S = {τ1, . . . , τ5}, the word Q:=τ1τ2τ4τ2τ5τ3τ1τ3τ4τ2τ5τ3τ1τ2τ4τ4τ3 and the elementρ:= [3,2,6,4,5,1] =τ1τ2τ3τ4τ5τ1τ4τ3. The sorting network correspond- ing to the subword complexSC(Q, ρ) and the pseudoline arrangement corresponding to the facetI:={2,3,5,7,8,10,12,14,15} ofSC(Q, ρ) are shown in Figure 6(top).
Let V0 be the subspace of V spanned by the roots e3−e1, e4−e3 and e6−e5. LetX ={x1, . . . , x8}={2,4,5,6,8,10,15,16}denote the set of positions k∈[17]
for whichr(I, k)∈V0. These positions are circled in Figure6(top).
We can now directly read off the subword complexSC(Q0, ρ0) corresponding to the restriction of SC(Q, ρ) to all facets reachable from I by flips with directions in V0. Namely, the restriction of (W, S) to V0 is the Coxeter system (W0, S0) where W0 is generated byS0 ={τ10, τ20, τ30}={(1 3),(3 4),(5 6)}, and thus of type A2×A1. Moreover, we have Q0 =τ10τ10τ30τ20τ20τ10τ30τ30, corresponding to the roots at positions inX, andρ0 =τ10τ20τ30, with inversion set given by the positive roots corre- sponding to the roots at positions inXrI. Finally, the facetI0corresponding toI is given byI0 ={1,3,5,6,7}. The sorting network corresponding to the restricted subword complexSC(Q0, ρ0) and the pseudoline arrangement corresponding to the facetI0 ofSC(Q0, ρ0) are shown in Figure6(bottom).
As stated in Proposition 3.11, the map which sends a facet J of SC(Q0, ρ0) to the facet {xj|j∈J} ∪(IrX) of SC(Q, ρ) defines an isomorphism between the increasing flip graphG(Q0, ρ0) and the restriction of the increasing flip graphG(Q, ρ) to all facets reachable fromI by flips with directions inV0.
4. EL-labelings and spanning trees for the subword complex 4.1. EL-labelings of the increasing flip graph. We now define two natural edge labelings of the increasing flip graphG(Q, ρ).
LetI and J be two adjacent facets of SC(Q, ρ), withIri=J rj and i < j.
We label the edge I J of G(Q, ρ) with the positive edge label p(I J):=i and with the negative edge label n(I J):=j. In other words, p labels the position flipped out while n labels the position flipped in during the flip I J. We call p : E(G(Q, ρ)) → [m] the positive edge labeling and n : E(G(Q, ρ)) → [m] the negative edge labeling of the increasing flip graph G(Q, ρ). The terms “positive”
and “negative” emphasize the fact that the rootsr(I,p(I J)) and r(J,n(I J)) are always positive and negative roots respectively.
The positive and negative edge labelings are reverse to one another (see Re- mark3.5). Namely,I J is an edge in the increasing flip graphG(qm· · ·q1, ρ−1) if and only ifJ0:={m+ 1−j|j∈J} I0:={m+ 1−i|i∈I}is an edge in the increasing flip graphG(q1· · ·qm, ρ), and in this casen(I J) =m+ 1−p(J0 I0).
However, we will work in parallel with both labelings, since we believe that certain results are simpler to present on the positive side while others are simpler on the negative side. We always provide proofs on the easier side and leave it to the reader to translate to the opposite side.
Example 4.1. Consider the subword complexSC(Qex, ρex) of Example3.2. We have represented on Figure7the positive and negative edge labelingspandn. Since we have represented the graphG(Qex, ρex) such that the flips are increasing from left to right, each edge has its positive label on the left and its negative label on the right.
12356 23568 23678 12367
23789 12379
34789 13479
34678 13467
34568 13456
2 4 2
4
1 8
1 8
2 1 4 8 2 4
1 8
2 4 2
4
1 8
1 8
6 9
5 7 6
9
5
7 6
9
5 7 6
9
5 7
Figure 7. The positive and negative edge labelings p and n of G(Qex, ρex). Each edge has its positive label on the left (or- ange) and its negative label on the right (blue).
The central result of this paper concerns the positive and negative edge labelings of the increasing flip graph.
Theorem 4.2. The positive edge labeling p and the negative edge labeling n are both EL-labelings of the increasing flip graph.
For Cambrian lattices, whose Hasse diagrams were shown to be particular cases of increasing flip graphs in [PS11, Section 6], a similar result was recently obtained by M. Kallipoliti and H. M¨uhle in [KM12]. See Section5.2.1for details.
In Sections4.2to4.4, we present applications of Theorem4.2to the construction of canonical spanning trees and to the generation of the facets of the subword complex. Further combinatorial applications of this theorem are also discussed in Section 5. We prove Theorem 4.2 only for the positive edge labelingp, and leave it to the reader to translate the proof to the negative edge labeling n (through the reversal operation of Remark3.5). Let IandJ be two facets ofSC(Q, ρ) such thatI J. To show thatpis indeed an EL-labeling, we have to show that (i) there is ap-rising path fromItoJ inG(Q, ρ) which is (ii) unique and (iii) lexicographically first among all paths fromI toJ inG(Q, ρ). We start with (ii) and (iii), which are direct consequences of the following proposition.
Proposition 4.3. Let I1 · · · I`+1 be a path of increasing flips, and define the labels pk:=p(Ik Ik+1)andnk:=n(Ik Ik+1). Then, for allk∈[`], we have
min{pk, . . . ,p`}= min(IkrI`+1) and max{n1, . . . ,nk}= max(Ik+1rI1).
Moreover, the path is p-rising if and only if pk = min(IkrI`+1) for all k ∈ [`], while the path is n-rising if and only ifnk = max(Ik+1rI1)for allk∈[`].
Proof. The position min{pk, . . . ,p`}is inIkrI`+1since it is flipped out and never flipped in along the path fromIktoI`+1(because all flips are increasing). Moreover, min{pk, . . . ,p`} has to coincide with min(IkrI`+1) otherwise this position would never be flipped out along the path.
This property immediately yields the characterization ofp-rising paths. Indeed, if the path is p-rising, then we have pk = min(pk, . . . ,p`) = min(Ik rI`+1) for all k ∈ [`]. Reciprocally, if pk = min(Ik rI`+1) for all k ∈ [`], then we have pk= min(IkrI`+1)<min(Ik+1rI`+1) =pk+1 so that the path isp-rising.
The proof is similar for the negative edge labelingn.
We now need to prove the existence of a p-rising path from I to J. Before proving it in full generality, we prove its crucial part in the particular case of dihedral subword complexes.
Lemma 4.4. Let SC(Q, ρ) be a subword complex for a dihedral reflection group W =I2(m). Let I and K be two of its facets such that there is a pathI J K fromI toK inG(Q, ρ)withp(I J)>p(J K). Then there is as well ap-rising path from I toK inG(Q, ρ).
Proof. First, we remark that we construct a path only using letters in Q at posi- tions not used inI(those positions corresponding to the reduced expression forρ), together with the two positionsi:=p(I J) andj:=p(J K). Observe here that bothiandj are already contained inI.
We distinguish two cases: the roots r(I, i) andr(I, j) generate either a 1- or a 2-dimensional space. In the first case, we haver(I, i) =r(I, j) and we can directly flip position j in the facet I to obtain the facet K. In the second case, it is straightforward to check that we can perform ap-rising path fromI toK, starting with positionj, followed by position i, and finishing by a possibly emptyp-rising
sequence of flips.
We are now ready to prove Theorem 4.2. Restricting subword complexes to dihedral parabolic subgroups as presented in Section3.5, we will reduce the general case to several applications of the dihedral situation treated in Lemma4.4.
Proof of Theorem 4.2. Let I and J be two facets of SC(Q, ρ) related by a path I=I1 · · · I`+1=Jof increasing flips. Letpk:=p(Ik Ik+1). Assume that this path is notp-rising, and letkbe the smallest index such thatpk6= min{pk, . . . ,p`}, and letk0> ksuch thatpk0 = min{pk, . . . ,p`}. We now prove that we can flippk0
instead ofpk0−1inIk0−1, and still obtain a path fromItoJ wherepk0 is still smaller than all positive edge labels appearing after it. In Example 4.5, we illustrate this procedure on an explicit example.
Clearly pk0−1>pk0, and we have a p-falling sequence of two flips given by Ik0−1 Ik0 Ik0+1. Using Proposition 3.11, we can now see these two flips as well in a subword complex for the dihedral parabolic subsystem. For this, re- strict (W, S) to the subspace V0 spanned by the two roots r(Ik0−1,pk0−1) and r(Ik0−1,pk0) = r(Ik0,pk0). This restricted subword complex corresponds to all facets of SC(Q, ρ) reachable from the particular facet Ik0−1 by flips whose direc- tions are contained inV0. Applying Lemma4.4, we can thus replace the subpath Ik0−1 Ik0 Ik0+1 by a p-rising path fromIk0−1 toIk0+1 flipping first positionpk0 and then a (possibly empty) sequence of positions larger than or equal topk0−1.
Repeating this operation, we construct a path from I to J such that pk = min{pk, . . . ,p`}. By this procedure, we obtain eventually a p-rising path from I to J. This path is unique and lexicographically first among all paths fromI toJ inG(Q, ρ) according to the characterization given in Proposition4.3. This concludes the proof thatpis an EL-labeling ofG(Q, ρ). The proof is similar for the negative edge labelingn(by the reversal operation in Remark3.5).
Example 4.5. Consider the subword complexSC(Qex, ρex) of Example3.2, whose labeled increasing flip graph is shown in Figure7. Consider the path
12356 5 12367 6 12379 2 13479 1 34789,
in G(Q, ρ), where the numbers on the arrows are the positive edge labels. In the language of the proof of Theorem 4.2, we have k = 1, k0 = 4, and therefore we replace the subpath 12379 2 13479 1 34789 by the subpath 12379 1 23789 2 34789, thus obtaining the path
12356 5 12367 6 12379 1 23789 2 34789.
Applying this operation again and again produces the sequence of paths given by 12356 5 12367 1 23678 6 23789 2 34789,
12356 1 23568 5 23678 6 23789 2 34789, 12356 1 23568 5 23678 2 34678 6 34789, 12356 1 23568 2 34568 5 34678 6 34789.
The resulting path isp-rising. In this example, all paths happen to have the same length. This does not hold in general, compare Figure 15on page 29, where the path 123 2 137 3 178 1 678 7 689 is, for example, replaced by the path 123 2 137 1 357 3 567 5 678 7 689.
In contrast to the rising paths, we can have none, one, or more than onep-falling andn-falling paths between two facetsIandJ ofSC(Q, ρ). Even if we will not need it in the rest of the paper, we observe in the next proposition that there are always as manyp-falling paths asn-falling paths fromItoJ. Remember that we say that a pathI1 I2 · · · I`+1 flips out the multisetP:={{p(Ik Ik+1)|k∈[`]}}and flips in the multisetN:={{n(Ik Ik+1)|k∈[`]}}. Note that a p-falling (resp. n- falling) path is determined by the multisetP(resp.N) of positions that it flips out (resp. in).
Proposition 4.6. Let I andJ be two facets ofSC(Q, ρ). Then there are as many p-falling paths asn-falling paths fromItoJ. More precisely, for any multisubsetsP and Nof [m], there exists a p-falling path from I to J which flips out Pand flips inN, if and only if there exists ann-falling path with the same property.
Proof. Consider ap-falling pathI=I1 · · · I`+1=J. Definepk:=p(Ik Ik+1) and nk:=n(Ik Ik+1). We want to prove that there is as well an n-falling path which flips outP:={{pk|k∈[`]}}and flips in N:={{nk |k∈[`]}}.
If the path I = I1 · · · I`+1 = J happens to be n-falling, we are done.
Otherwise, consider the first positionk such thatnk−1 <nk. Since the path isp- falling, we thus have pk < pk−1 < nk−1 < nk. By Proposition 3.9(3), we know that r(Ik−1,pk−1) =r(Ik−1,nk−1) andr(Ik,pk) =r(Ik,nk). According to Proposi- tion3.9(5) and to the previous inequalities, we therefore obtain
r(Ik−1,pk) =r(Ik,pk) =r(Ik,nk) =r(Ik−1,nk).
Thus, in the facet Ik−1, flipping out pk flips in nk. We denote by Ik0 the facet ofSC(Q, ρ) obtained by this flip. Using again Proposition3.9(5) and the previous inequalities, we obtain that
r(Ik0,pk−1) =sr(Ik−1,pk)(r(Ik−1,pk−1)) =sr(Ik−1,pk)(r(Ik−1,nk−1)) =r(Ik0,nk−1).
Therefore, in the facet Ik0, flipping outpk−1 flips in nk−1. After these two flips, we thus obtain Ik+1 (since we flipped out pk and pk−1, while we flipped in nk
and nk−1). In other words, we can replace the subpath Ik−1 Ik Ik+1 by the path Ik−1 Ik0 Ik+1 where we flip first pk to nk and then pk−1 to nk−1. The
new path still flips out P and flips in N, and the first k positions it flips in are in decreasing order. Repeating this transformation finally yields an n-falling path from Ito J which still flips outPand flips inN. Observe that this path does not necessarily coincide with thep-falling path we started from.
Since a p-falling (resp. n-falling) path is determined by the set of positions it flips out (resp. in), we obtain a bijection betweenp-falling paths andn-falling paths
fromI toJ. They are thus equinumerous.
Remark 4.7. Observe that Proposition 4.6 can be deduced from the following observations in the situation of double root free subword complexes studied in Section 5. In this situation, the flip graph is the Hasse diagram of its transitive closure and thep- andn-labelings are both EL-labelings thereof. By Theorem5.4, allp- andn-falling paths have the same length. Therefore, Proposition2.3implies that they are equinumerous. A similar topological construction in the situation of subword complexes having double roots is yet to be found.1
4.2. Greedy facets. We now characterize the unique source and sink of the in- creasing flip graphG(Q, ρ).
Proposition 4.8. The lexicographically smallest (resp. largest) facet of SC(Q, ρ) is the unique source (resp. sink) of G(Q, ρ).
Proof. The lexicographically smallest facet is a source of G(Q, ρ) since none of its flips can be decreasing. We prove that this source is unique by induction on the word Q. Denote byP(Qa, ρ) (resp.P(Qa, ρqm)) the lexicographically smallest facet ofSC(Qa, ρ) (resp.SC(Qa, ρqm)) and assume that it is the unique source of the flip graphG(Qa, ρ) (resp.G(Qa, ρqm)). Consider a sourcePofG(Q, ρ). We distinguish two cases:
• If`(ρqm)> `(ρ), thenqm cannot be the last reflection of a reduced expression forρ. ThusSC(Q, ρ) =SC(Qa, ρ)? mandP=P(Qa, ρ)∪m.
• Otherwise,`(ρqm)< `(ρ). Ifmis inP, then
r(P, m) =ρ(αqm)∈Φ−∩ρ(Φ+).
Since Φ− ∩ ρ(Φ+) = −inv(ρ), we obtain that m is flippable (by Proposi- tion3.9(3)) and its flip is decreasing (by Proposition3.9(4)). This would con- tradict the assumption that P is a source of G(Q, ρ). Consequently, m /∈ P.
Since the facets of SC(Q, ρ) which do not contain m coincide with the facets ofSC(Qa, ρqm), we obtain thatP=P(Qa, ρqm).
In both cases, we obtain that the source Pis the lexicographically smallest facet ofSC(Q, ρ). The proof is similar for the sink.
We callpositive(resp.negative)greedy facetand denote byP(Q, ρ) (resp. N(Q, ρ)) the unique source (resp. sink) of the graph G(Q, ρ) of increasing flips. The term
“positive” (resp. “negative”) emphasizes the fact thatP(Q, ρ) (resp.N(Q, ρ)) is the unique facet ofSC(Q, ρ) whose root configuration is a subset of positive (resp. neg- ative) roots, while the term “greedy” refers to the greedy properties of these facets underlined in Lemmas4.10and4.11.
These greedy facets are reverse to one another (see Remark3.5). Namely, N(qm· · ·q1, ρ−1) ={m+ 1−p|p∈P(q1· · ·qm, ρ)}.
We still work with both in parallel to simplify the presentation in the next section.
1We thank an anonymous referee for raising this question.
Example 4.9. Consider the subword complex SC(Qex, ρex) presented in Exam- ple3.2. Its positive and negative greedy facets are P(Qex, ρex) ={1,2,3,5,6} and N(Qex, ρex) ={3,4,7,8,9}, respectively, see Figure8. They appear respectively as the leftmost and rightmost facets in Figure4.
4 3 2 1
2 3
4 1 24
42
43 3
1 1
3 4
1 4
1 32
23 4
3 2 1
2 3
4 1
43 3
4 2 4 2 2 2 2 1
1 4
1 43
32
Figure 8. The positive and negative greedy facets ofSC(Qex, ρex).
The following two lemmas provide two (somehow inverse) greedy inductive pro- cedures to construct the greedy facets P(Q, ρ) and N(Q, ρ). These lemmas are direct consequences of the definition of the greedy facets and of the induction for- mulas for the facetsF(Q, ρ) presented in Section3.3. Remember that we denote by Q`:= q2· · ·qmand Qa:= q1· · ·qm−1the words onSobtained from Q:= q1· · ·qm by deleting its first and last letters respectively, and byX→:={x+ 1|x∈X}the right shift of a subsetX ⊂Z.
Lemma 4.10. The greedy facetsP(Q, ρ)andN(Q, ρ)can be constructed inductively fromP(ε, e) =N(ε, e) =∅using the following formulas:
P(Q, ρ) =
(P(Qa, ρ)∪m ifm appears in all facets ofSC(Q, ρ), P(Qa, ρqm) otherwise.
N(Q, ρ) =
(1∪N(Q`, ρ)→ if1 appears in all facets of SC(Q, ρ), N(Q`, q1ρ)→ otherwise.
Lemma 4.11. The greedy facetsP(Q, ρ)andN(Q, ρ)can be constructed inductively fromP(ε, e) =N(ε, e) =∅using the following formulas:
P(Q, ρ) =
(P(Q`, q1ρ)→ if 1 appears in none of the facets ofSC(Q, ρ), 1∪P(Q`, ρ)→ otherwise.
N(Q, ρ) =
(N(Qa, ρqm) if mappears in none of the facets of SC(Q, ρ), N(Qa, ρ)∪m otherwise.
Lemmas 4.10and 4.11can be reformulated to obtain greedy sweep procedures on the word Q itself, avoiding the use of induction. Namely, the positive greedy facetP(Q, ρ) is obtained:
(1) either sweeping Q from right to left placing inversions as soon as possible, (2) or sweeping Q from left to right placing non-inversions as long as possible.
The negative greedy facet is obtained similarly, reversing the directions of the sweeps.
We have seen in Theorem4.2 that for any two facets I, J ∈ F(Q, ρ) such that I J, there is ap-rising (resp.n-rising) path fromI to J. In particular, there is always ap-rising (resp.n-rising) path fromP(Q, ρ) toN(Q, ρ). We will now show that there is also at least onep-falling (resp.n-falling) path fromP(Q, ρ) toN(Q, ρ) if the subword complexSC(Q, ρ) is spherical.
Proposition 4.12. For any spherical subword complexSC(Q, ρ), there is always a p-falling and ann-falling path fromP(Q, ρ) toN(Q, ρ).
Proof. Since the subword complex SC(Q, ρ) is spherical, recall that any position in any facet ofSC(Q, ρ) is flippable. We will prove that starting from the positive greedy facet P(Q, ρ) and successively flipping all its positions in decreasing order yields the negative greedy facetN(Q, ρ), thus providing ap-falling path fromP(Q, ρ) toN(Q, ρ).
Let `:=|Q| −`(ρ) denote the size of each facet of SC(Q, ρ). Let p1>· · ·>p`
denote the positions of the positive greedy facetP(Q, ρ) in decreasing order. We consider the p-falling path P(Q, ρ) =I1 · · · I`+1 defined byp(Ik Ik+1) =pk. We also setnk:=n(Ik Ik+1). By definition, we haveIk ={n1, . . . ,nk−1,pk, . . . ,p`}.
We will prove that the rootr(Ik,nj) is negative for anyj < k∈[`+ 1]. This implies in particular thatI`+1 is the negative greedy facetN(Q, ρ).
To see this, fix j ∈ [`]. For any k ∈ [j + 1, `+ 1], denote by xk the po- sition in the complement of Ik such that r(Ik,xk) = ±r(Ik,nj). We prove by induction on k that pk < xk < nj, and thus (by Proposition 3.9(4)) that the rootr(Ik,nj) =−r(Ik,xk) is negative for anyj < k≤`+ 1. First, this is immediate fork=j+ 1 sincexj+1=pj (because we just flipped outpjto flip innj inIj) and pj+1<pj<nj. Assume now that we proved thatpk<xk<nj for a certaink. We distinguish two cases:
(i) Ifnk <nj, thenr(Ik+1,nj) =r(Ik,nj) by Proposition3.9(5). Since this root is negative, Proposition3.9(4) ensures thatxk+1<nj. Moreover, ifxk+1≤pk+1, then we would havexk+1<pk, and thus Proposition3.9(5) would give
r(Ik,xk+1) =r(Ik+1,xk+1) =−r(Ik+1,nj) =−r(Ik,nj).
By definition, this would imply thatxk=xk+1<pk, contradicting the induc- tion hypothesis.
(ii) If nk>nj, then we have pk <xk <nj < nk. Therefore, Proposition 3.9(5) ensures that
r(Ik+1,xk) =sr(Ik,pk)(r(Ik,xk)) =−sr(Ik,pk)(r(Ik,nj)) =−r(Ik+1,nj).
By definition, this implies that xk+1=xk.
In both cases, we obtained thatpk+1 <xk+1 <nj, thus concluding our inductive argument.
The proof for then-falling path is similar.
Note that this proposition fails if we drop the condition thatSC(Q, ρ) is spherical, as illustrated in the subword complex SC(Qex, ρex) of Example 3.2. A smaller example is given by the subword complexSC(τ1τ2τ1τ2, τ1τ2).
4.3. Spanning trees. As discussed in Remark 2.1, the edge labelings p and n automatically produce canonical spanning trees of any interval of the increasing flip graphG(Q, ρ). SinceG(Q, ρ) has a unique sourceP(Q, ρ) and a unique sinkN(Q, ρ),
we obtain in particular four spanning trees of the graphG(Q, ρ) itself. The goal of this section is to give alternative descriptions of these four spanning trees.
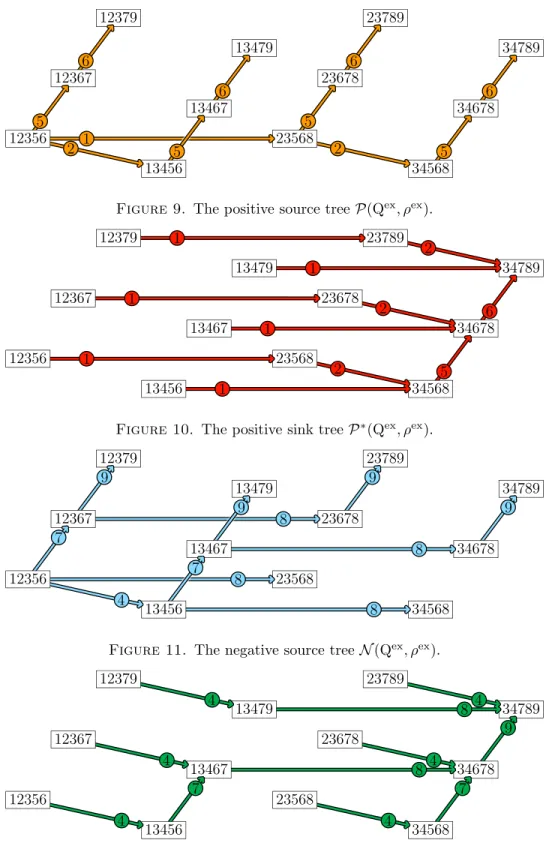
We call respectively positive source tree,positive sink tree,negative source tree, and negative sink tree, and denote respectively by P(Q, ρ), P∗(Q, ρ), N(Q, ρ), and N∗(Q, ρ), the p-source, p-sink, n-source, and n-sink trees of G(Q, ρ). The treeP(Q, ρ) (resp.N(Q, ρ)) is formed by allp-rising (resp.n-rising) paths from the positive greedy facetP(Q, ρ) to all the facets ofSC(Q, ρ). BothP(Q, ρ) andN(Q, ρ) are rooted at and directed away from the positive greedy facet P(Q, ρ). The treeP∗(Q, ρ) (resp.N∗(Q, ρ)) is formed by allp-rising (resp.n-rising) paths from all the facets ofSC(Q, ρ) to the negative greedy facetN(Q, ρ). Both P∗(Q, ρ) and N∗(Q, ρ) are rooted at and directed towards the negative greedy facetN(Q, ρ).
The positive source and negative sink trees (resp. the positive sink and the nega- tive source trees) are reverse to one another (see Remark3.5). Namely, as we already observed,I J is an edge in the increasing flip graphG(qm· · ·q1, ρ−1) if and only ifJ0:={m+ 1−j|j∈J} I0:={m+ 1−i|i∈I} is an edge in the increasing flip graphG(q1· · ·qm, ρ). Moreover, I J belongs toP(qm· · ·q1, ρ−1) if and only ifJ0 I0 belongs toN∗(q1· · ·qm, ρ). Similarly,I J belongs toP∗(qm· · ·q1, ρ−1) if and only ifJ0 I0 belongs toN(q1· · ·qm, ρ).
Example 4.13. Consider the subword complex SC(Qex, ρex) from Example 3.2.
Figures9,10,11, and12represent respectively the treesP(Qex, ρex),P∗(Qex, ρex), N(Qex, ρex), and N∗(Qex, ρex). Observe that these four canonical spanning trees ofG(Q, ρ) are all different in general.
We now give a direct description of the father of a facetIinP∗(Q, ρ) andN(Q, ρ) in terms ofIrN(Q, ρ) andIrP(Q, ρ).
Proposition 4.14. Let I be a facet of SC(Q, ρ). If I 6=N(Q, ρ), then the father ofI inP∗(Q, ρ)is obtained fromI by flipping the smallest position inIrN(Q, ρ).
Similarly, if I 6= P(Q, ρ), then the father of I in N(Q, ρ) is obtained from I by flipping the largest position inIrP(Q, ρ).
Proof. Since the father ofIin P∗(Q, ρ) (resp. inN(Q, ρ)) is the facet next toIon the uniquep-rising path towardsN(Q, ρ) (resp. the facet previous toIon the unique n-rising path fromP(Q, ρ)), this is a direct consequence of Proposition4.3.
We now focus on the positive source treeP(Q, ρ) and on the negative sink tree N∗(Q, ρ), and provide two different descriptions of them. The first is an inductive description ofP(Q, ρ) and N∗(Q, ρ) (see Propositions4.17and4.18). The second is a direct description of the father of a facetIinP(Q, ρ) andN∗(Q, ρ) in terms of greedy prefixes and suffixes ofI(see Propositions4.19and4.20). These descriptions mainly rely on the following property of the greedy facets.
Proposition 4.15. If m is a flippable position of N(Q, ρ), then N(Qa, ρqm) is obtained fromN(Q, ρ)by flippingm. Similarly, if1is a flippable position ofP(Q, ρ), thenP(Q`, q1ρ)is obtained from P(Q, ρ)by flipping 1and shifting to the left.
Proof. Although the formulation is simpler for the negative greedy facets, the proof is simpler for the positive ones (due to the direction chosen in the definition of the root function). Assume that 1 is a flippable position ofP(Q, ρ). LetJ ∈ F(Q, ρ) andj∈J be such thatP(Q, ρ)r1 =Jrj. Consider the facetJ←ofSC(Q`, q1ρ)