The complex Coxeter∆(W, S) associated with a system Coxeter(W, S) is a nice simple complex that encodes the structure of Weyl rooms for W. Another immediate consequence is the following description of high homology as a intersection of nuclei.
Unitary reflection groups
Since the elements of S are involutions, and the map sender, sto−1andt na+1 extends to a homomorphism of G that sends all elements ofSto−1, we must have that ∆(G, S) is an orientable surface, and then a quick Euler characteristic calculation shows that it has genusn−1. Nevertheless, a happy situation occurs when the unit reflection group G is generated by unit reflections of order two (involutions). Perhaps surprisingly, there are many cases where this occurs, even when the group is not the complexification of some Euclidean reflection group (see e.g. the tables at the end of [9]).
Any minimal choice of generating involutive reflections S for such a group G will give rise to an orientable pseudomanifold ∆(G, S)(via Proposition 2.9), since the determinant representation is a well-defined homomorphismǫ:G→Z×. A closer look at the case of G=G(4,2,2) also illustrates how the Boolean complex∆(G, S) cannot be a simple complex. However, ∆(G, S) is not a simple complex, since one can check, for example, that the two cosets1G{s2,s3}= s3s1G{s2,s3}andG{s1,s3}index two vertices, which are the endpoints of two distinct edges, indexed by cosetss1G{s3}ands3s1G{s3}.
Unipotent groups over F 2
Biss [2] has shown that all relations between theses are generated by the following Coxeter-like relations s2i = 1. Consequently, Corollary 2.15 implies that ∆(G, S) is a quotient of the Coxeter complex ∆( ˆW ,S) ˆ for Coxeter system described by the relations (3.1), where one quotients with the normal subgroupKofWˆ generated by the elements(ˆsiˆsi+1ˆsi+2)4. By Proposition 2.9, ∆(G, S) will be a non-orientable surface, and an Euler characteristic calculation shows that it is indeed the real projective plane.
The left side in this relation happens to coincide with the image of the longest element w0 inWˆ under the surjection Wˆ . G, so the Kof kernel of this assumption must contain the cyclic group of order two generated by aw0inWˆ. Since Wˆ is the symmetry group of the regular cube or octahedron, ∆(W, S) is the a2-sphere isomorphic to the barycentric subdivision of the boundary of the cube or octahedron. The longest element that happens to act in this case as the antipodal map on the 2-sphere ∆( ˆW ,S) andˆ ∆(G,S) is the triangulation of the real projective plane arising from the antipodal identification.
Here we study in more detail the case where = An is treated as a reflection group and S is the minimal generated set of reflections.
Trees and forests
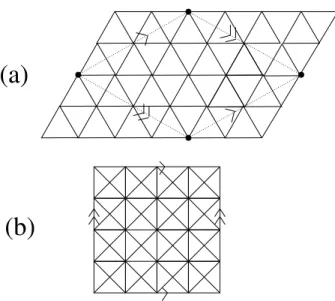
ˆW ,S)ˆ is a regular tessellation of the 2-plane with isosceles right triangles and K acts as a 2-dimensional grid of translations, giving the quotient ∆(G, S) that triangulates the a2-torus, as in Figure 3.1 (b). For every spanning tree T on [n], the pair (Sn, ST) satisfies the intersection condition (2.1), so ∆T is a simplicial complex. Bn−|J|are the blocks of splitting [n] into vertices of trees in the subforest T induced by the edge subset J.
Sort the labeled subforests by saying (F, w)≤(F′, w′) if the vertex set of each tree in Fi is the union of the vertex sets of the trees in F′ and the corresponding label sets are the unions of the label sets inw ′. CosetwGJ corresponds to a pair (F, w) in which F is a subforest of T induced by the edge setJ. Here we show how to relabel the nodes of T and thus also how to label the sets of subtree nodes in F.
For other spanning treesT on[n] less is known, although the case where T is the star graph (so that∆T is the chessboard complex∆n−1,nas in Example 4.5) has been considered in [14,§5], and studied more extensively in [23].
Deletion-contraction and flossing
The flossing induction relates T to a tree Tˆ which either has fewer vertices, or the same number of vertices but fewer leaves, or the same number of vertices and leaves but with δ( ˆT)< δ(T); see Figure 4.2 for an example. Let (ℓ,ℓ, v)ˆ be a triple such that distT(ℓ, v) reaches the minimumδ(T), and is defined to be the first edge on the ngavtoℓ path. ThenTˆ is formed in two steps: first contracting T together to create T /e, with a sequence of natural multiplicity/ assigning multiplicity2 to the contracted vertex and multiplicity1 to all other vertices, and then obtaining Tˆ by “uncontracting” or “stretching " this shrunken climax. to a new edgeˆthat lies along the path toℓ'(equivalently, one can think of Tˆas obtained from T /eby dividing the first edge along the path from the contracted vertex at ℓ).ˆ.
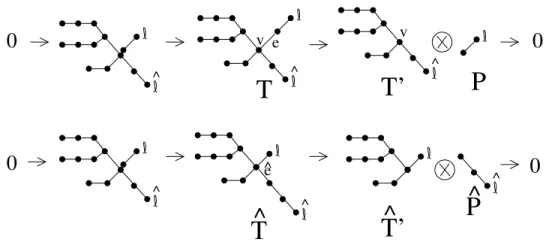
Note that in this process, T /ˆˆ e = T /e, so a spanning tree with sets (T /e,m/e) fits two short exact sequences that follow from Proposition 4.7,. Here we denote by T′, P(=T′′) two components of T −e and by Tˆ′,Pˆ(= ˆT′′), two components of Tˆ−ˆe, emphasizing the fact that the components P,Pˆ containing ℓ, ℓ are paths.ˆ. We will say that a proof proceeds by string induction if it tries to prove the homology property ∆T as follows.
When T is not a path, one applies induction simultaneously on the number of vertices inT, the number of leavesℓ(T), and on the setδ(T): one assumes that the property holds for any tree that has either.
Constraints on the homology representations
All that remains is to show ∂k(Vk)6= 0, for which it is sufficient to check that the coefficient of the identity permutationidinγ{v+. In fact, we only need this in the special case of the Littlewood-Richardson rule known as Pieri's formula, where V2 is the character representation S1n2; this is due to the fact that P,Pˆ are paths, and therefore have only the sign representation that occurs in the homology of the Coxeter complexes. ∆P,∆Pˆ). Since T′, P,Tˆ′, Pˆ all have fewer vertices than T, induction holds for them, and so the K¨unneth formula together with the previous fact shows that the homology of the third term in both short exact sequences ( 4.1) and (4.2) ) contain no occurrence of S(r,1n−r)forr≥3.
This implies from the exact long sequence in the homology that the homology of the first term in (4.2) contains no occurrences of S(r,1n−r) for r≥3. But since T /ˆˆ e=T / implies that this is the same as the homology of the first term in (4.1), we can conclude that the homology of the middle term in (4.1) has the same property, as desired. A similar thread induction argument gives a bound on the length of the longest row of λ for any Sλ occurring in the homology of ∆T.
We use flossing induction, as in the last proof, exploiting the fact that P,Pˆ are paths, so that their homology contains only irreducible representations S1n′′,S1nˆ′′, respectively.
Some examples
However, see the discussion of checkerboard complexes in Example 4.15 below as an illustration of the looseness of this assumed connectivity boundary in general. Finally, we mention a somewhat trivial constraint on the homology representations of∆T,mwhich ignores the tree structureT. Recall from Example 4.5 that when this ann-vertex star and massignsrto the central vertex and1to the remaining vertices,∆T, the checkerboard complex∆n−1,n+r−1 is missing.
There has also been an assumption (as recently demonstrated by Shareshian and Wachs [26]) that this connectivity is tight. This shows that the above assumption about the connectivity ∆T,m for a T star and m as above is very far from tight: these known results show that in this checkerboard case ∆T,m is approx. The checkerboard examples also illustrate how far homology with complex coefficients can deviate from integral homology for ∆T,m.
The homology with complex coefficients on ∆m,n was fully described by Friedman and Hanlon [15], even as aC[Sm×Sn] module.
A general lower bound
In this section, we study in more detail the simplicial complexes ∆T (and in general ∆T,m), presented in the previous section, in the case where a tree having at most one branch vertex, i.e. we use induction on the number of edges in T and apply Proposition 4.7, choosing to be any edge of T that is incident to a branch vertexv. Therefore, the induction holds for showhHi(∆T /e,m/e),Sλi= 0, so that Sλ does not appear in the i-dimensional homology of the first term of the short exact sequence of Proposition 4.7.
We want to show that Sλ also does not appear in the i-dimensional homology of the third term of this short exact sequence, so that the desired disappearance would follow from the corresponding long exact sequence in homology. Therefore, according to the K¨unneth formula, Sλ can only occur in the i-dimensional homology of the third term if it occurs in the decomposition of a tensor product Sµ′⊗ Sµ′′in irreducible numbers wheren′+n′′=n, µ′ ⊢n ′, µ′′⊢n′′. On the other hand, the Littlewood-Richardson rule for factoring this tensor product easily implies that λ1≥µ′1.
The case of three leaves
However, the presence of min(r, s) in formula (5.1) for V(p,q),(r,s) would make this somewhat awkward. In fact, these results would be sufficient to imply all the vanishing homology claims in the theorem except the lack of torsion. From Proposition 2.9, we know that the assertion of the theorem for i=n−2 is correct and that this above homology gives the unique occurrence of S1n.
Since for any tree T the complex ∆T is an orientable pseudomanifold that bears the sign representation of Snon its top homology (Theorem 2.9), the homology of the Coxeter complex for Sn (i.e. ∆Pn) trivially gives a lower bound for the multiples of irreducible Sn representations in each homology group H·(∆T,C). On the other hand, fort=m, this labeled subforest is no longer a vertex because it does not divide the path into two sets (the second set has cardinality n−t+r−1 =n−m+r−1 = 0) , and in fact the intersection of all the stars of the vii is the empty face. Then∆isk-connected if and only if the nerve of the covering{∆i}si=1isk-connected.
We use a nerve argument as in the proof of the previous theorem, but apply Lemma 7.2. As before, one can check this for anyt≤min(a1, m−1), the intersection of the stars orvi1,. Fort in the range a1 < t < m, one can check whether the intersection of the stars of vi1,.