In many engineering optimization problems, the calculation of the objective functions is affected by error arising from the model used for the calculation. This ultimately allows for a further reduction in the cost of computing the Pareto front by approximating the objective functions at a negligible cost. In many real applications, the evaluation of the objective function may be affected by a source of uncertainty, noise, or error.
Such errors can also be linked to the variability of the measure of the objective values, in the context of noise optimization. However, in the literature, the main strategy to account for uncertainty about the objective functions is to use a probabilistic ranking of the individuals. This is done to assess whether the current surrogate model can be used to bypass the calculation of the objective functions.
Second, the convergence of the method is demonstrated when using the surrogate strategy.
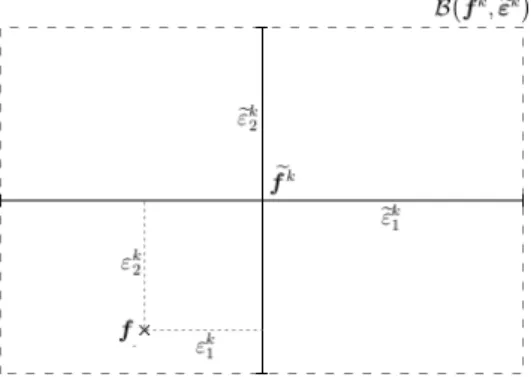
Bounding-Box definition and convergence analysis
As shown below, the assumption that this error is conservative is necessary to demonstrate the convergence of the proposed approach. Let us now define the classical and recursive (BB) approaches introduced to obtain the refined discrete front approximation. Note that the following development is written in design space, but can easily be extended to target space.
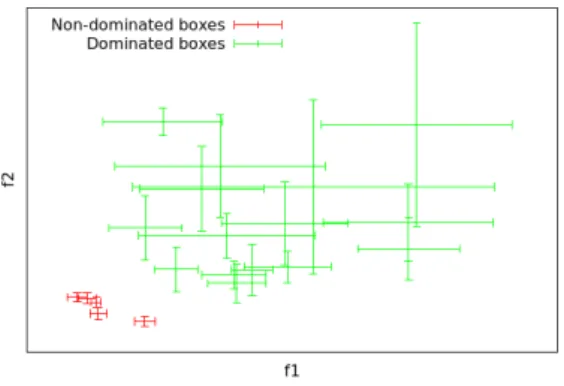
The difference with the Bounding-Box approach is in the recursive aspect of the BB sequence, which is very important. Then, as can be seen from the proof of this claim, any unfulfilled non-domination condition implies a strict inclusion between two sets of sequences. More precisely, the goal is to demonstrate the convergence of a continuous Pareto frontPec built on the approximated merahfek Xef,k.
A novelty of this paper compared to Fusi's Bounding-Box approach in [35] is the possibility of imposing a precision threshold for the convergence of the objective functions. Note that the convergence of the discrete approximate preextension Pec fek Xef,k. towards the real continuous front PC remains to be proven. This would imply the convergence of the example, due to the continuity hypothesis related to Assumption 3. Pe ∈ XN, approximation set fek. k∈N+ and conservative error set series εek. k∈N+, the following convergence is verified:. where the classical Hausdorff distance is denoted as dH.
Convergence of tightest boxes is not required here, as the concept of boxes is robustly extended to the Pareto optimum. One of the main conclusions of [35] was a significant drop in the performance of the Bounding-Box strategy throughout the execution as the designs approach the Pareto optimum. This finding was the starting point for an additional feature of the framework, which is presented in the next section.
Surrogate-assisted model
From a numerical point of view, due to the noise on the training points xi,fekmin(xi) the evolutionary surrogate model is built, a regression appears to be more accurate a-priorion than an interpolation. On the contrary, a genetic algorithm or any classical sequential optimization process will allow a refinement of the surrogate model at each generation or repetition of the optimization. We think that the mathematical convergence of the coupled strategy can be easily demonstrated since the only difference is that the limitk→+∞.
The drawback of joining the evolutionary surrogate is an increase in the box sizes associated with the designs whose values are calculated with the surrogate. On the contrary, the main advantage is a significant reduction of the global computational cost, especially at the end of the run, when the surrogate is considered converged to the true function. Rather, s2 is compared to the approximation error of the objective functions, providing the accuracy at which the bins are no longer refined.
Here, these thresholds are defined as a percentage of the range of the objective functions, where this value is improved and updated throughout the optimization. The set D is initialized at the beginning of the algorithm and contains all non-dominated models and is updated whenever the objective functions are improved. This set was introduced in Definition 10 and is updated at the end of execution, along with the associated fields.
It returns first approximations of the objective functions, the combined objective functionsofOBJ, the size of the r-boxes, and the set of non-dominated designs (which can potentially be refined). For each new design, the error of the evolutionary surrogate is compared to thresholds1. This section is devoted to the application of the framework to several test cases and performance analysis.
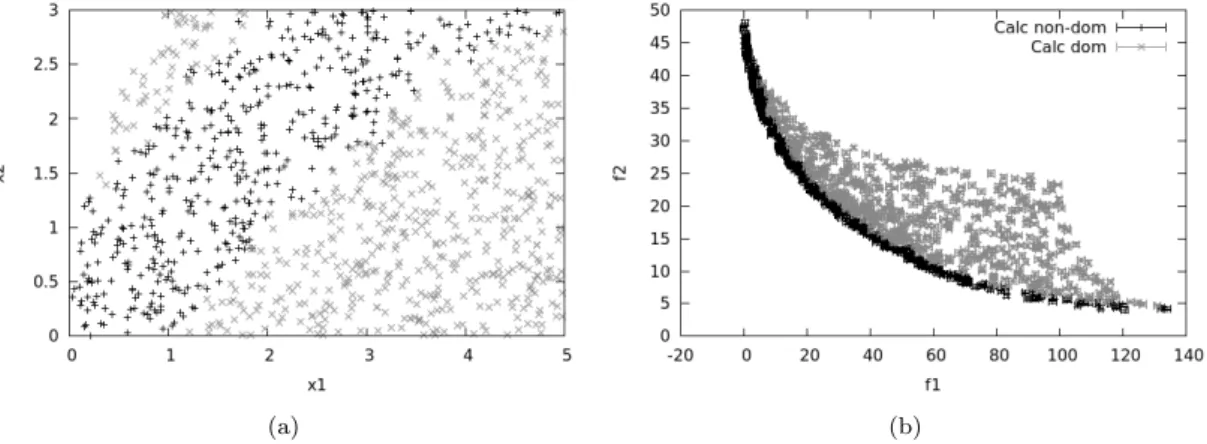
Test-case 1: The BNH problem
The effect of convergence on the optimal area will be studied in test cases 2 and 3. Note also that the extent se2 of the conservative error in the interpolated boxes is simply taken equal to thresholds2, which implies that only the non-dominated interpolated boxes are provided conservative. Obviously, the difference lies in the objective space, where a significant fraction of boxes do not converge to 2 in the recursive approach, thus reducing the number of function evaluations and subsequently the computational cost of the optimization.
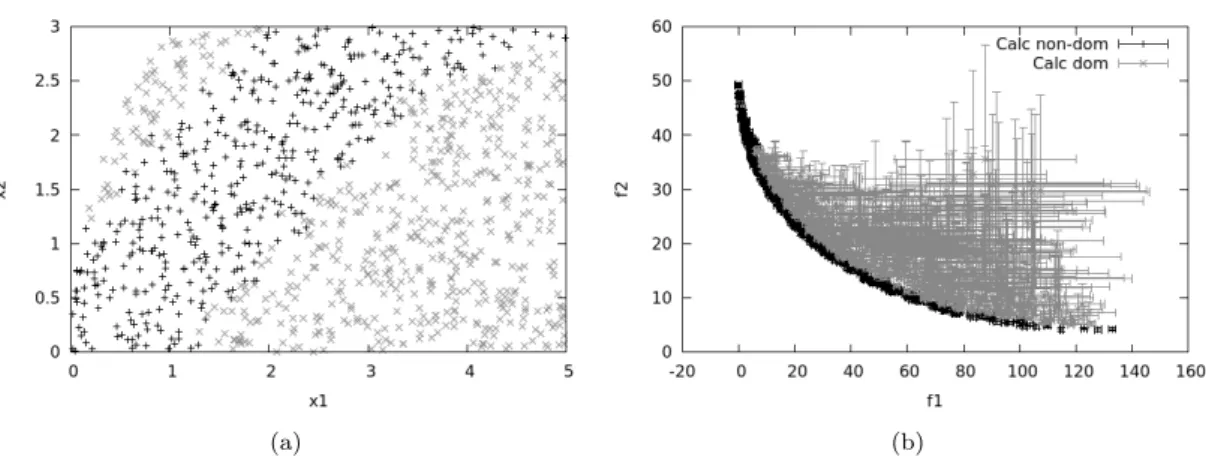
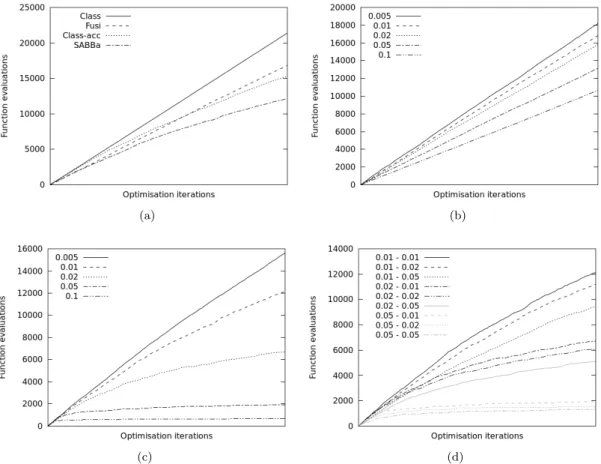
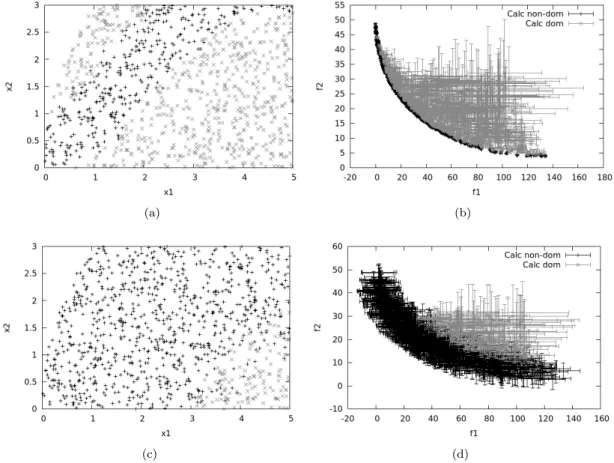
In Figures 6 and 7, the effect of the evolutionary replacement model is illustrated for the classical approach and the proposed framework, respectively. More importantly, the non-dominated area is similar to the classical fully computed approach shown in Figure 5, and so is the Pareto front. More precisely, it improves the slope of the cost curve by a ratio that can be interpreted as the average computational cost in the recursive strategy compared to the full convergence cost.
Since almost half of the designs in this test case are non-dominated, the gain is quite limited. Therefore, the slope of the cost curve during the first iterations is the same as for the unsupported strategies. To highlight the influence of the tuning parameters, further comparisons are performed by varying s2 in Fusi's approximation, and then s1 and both s2 and s1 with SABBa.
However, this threshold has a huge impact on the accuracy of the Pareto optimal set in the design space. Finally, Figures 8c and 8d illustrate how it is possible to extremely reduce the computational cost by bypassing multiple evaluations using the surrogate model. Globally, the framework appears to be effective as a cost-reduction strategy, but by requiring some adaptation of the thresholds to provide the best.
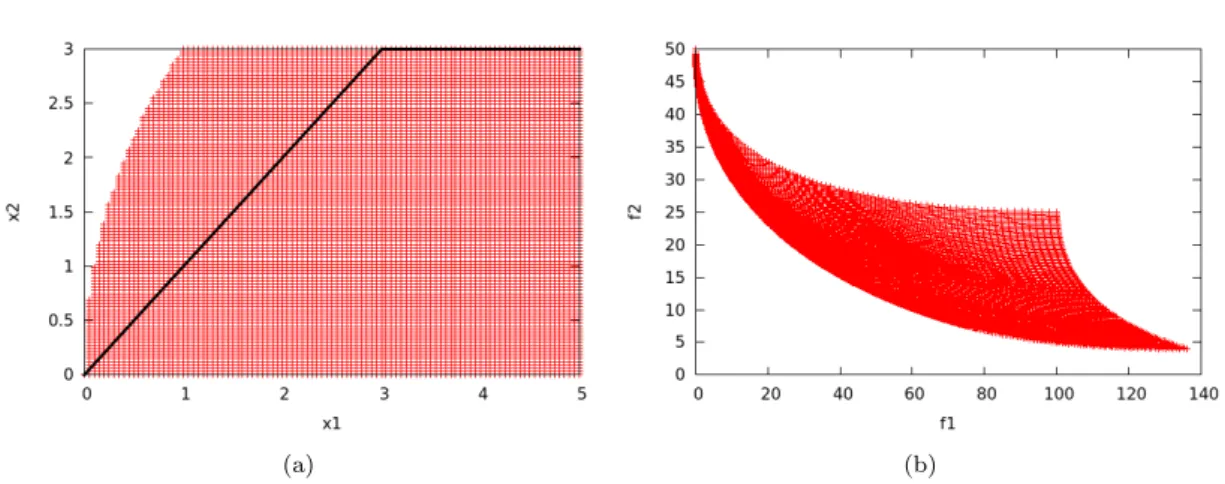
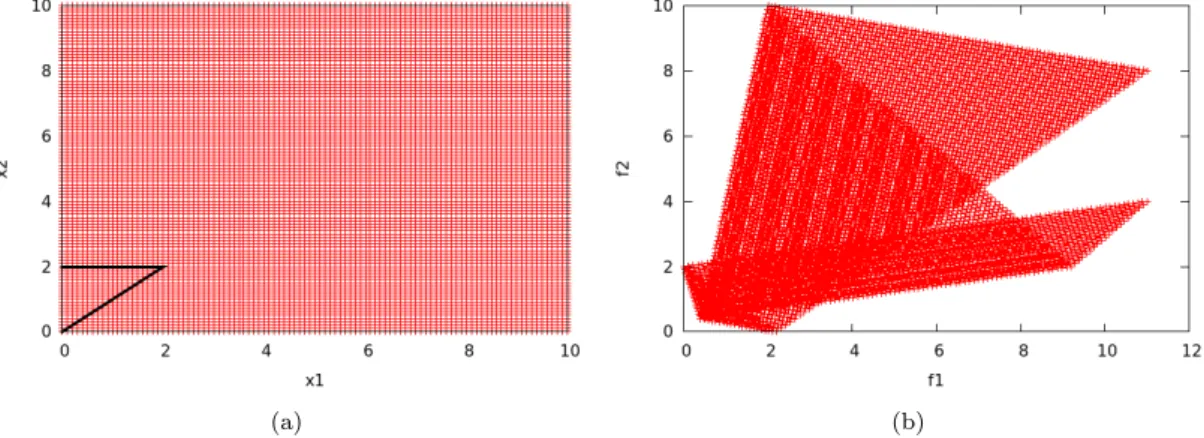
Test-case 2: The Triangle problem
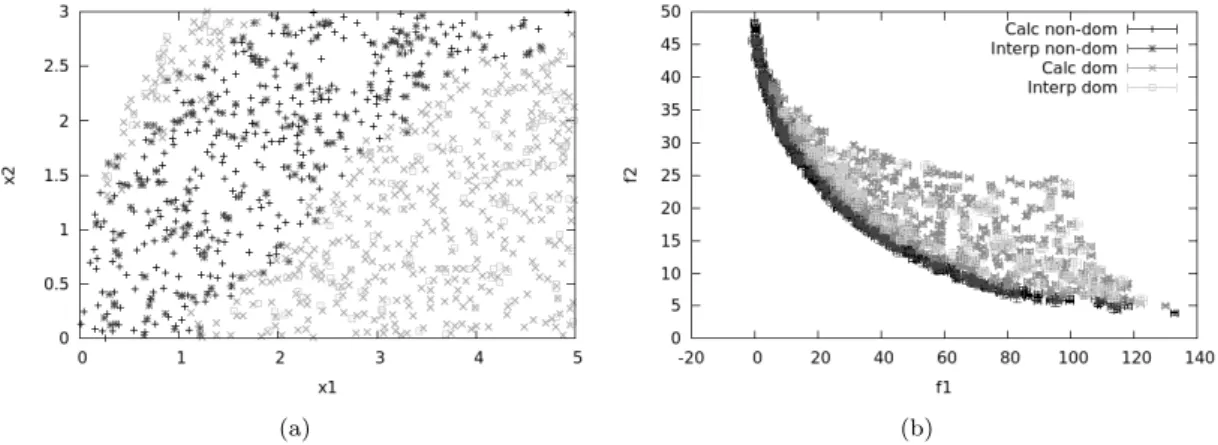
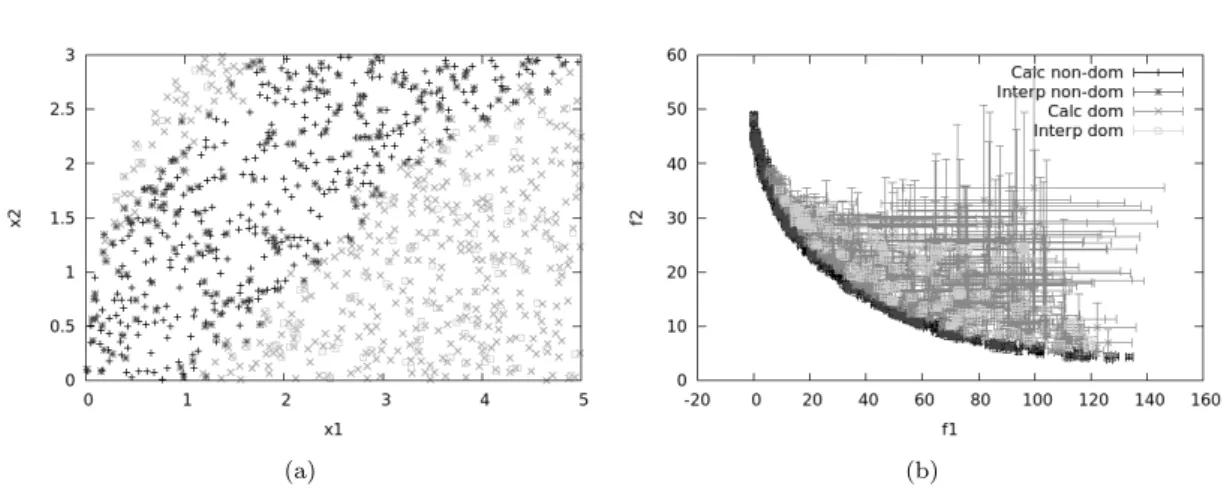
The next test case concerns a function with an optimal area, which is small with respect to the entire variation space. case 2: Classical approach, non-convergent domain for new designs: a) Design space, b) Objective space. For this case, new designs are randomly selected in a domain that converges to the optimal region. In practice, with k iterations of the optimization, new designs are chosen as follows, for i in {1,2},. a) (b).
The main effect of the convergence to the optimal region is a better refinement of the Pareto optima. As concluded in [35], it can be seen that the convergence to the optimal region induces a decreasing impact of the recursive strategy. This is due to the increasing number of non-dominated designs within the convergent search domain.
Therefore, SABBa relies on the evolutionary surrogate to quickly become accurate on the optimal area, which is highly sampled, eventually bypassing all function evaluations in this area. Despite the cost increase of the Fusi strategy alone, SABBa allows fewer evaluations and a much reduced final slope. a) (b). 12a has more and more non-dominated designs throughout the iterations, which alone explains the decreasing gains from the recursive approach.
This can also be understood by the influence of s2 on the cost of convergent and non-convergent optimization. 14a, the number of non-dominated models is low enough that the threshold s2 has a negligible impact on the computational cost. Conversely, convergence towards the optimal region increases the number of fully converged models and thus increases the influence of s2 in all iterations, which explains the separation of the curves in Figure 1.

Test-case 3: The Kursawe problem
This problem is known to have a rather complex Pareto front with multiple discontinuities associated with a small region of the design space. The Pareto representation of the functions and the corresponding Pareto front are given in fig. We can see that the front is highly discontinuous and that the scope of the objective functions must allow a large influence of the recursive strategy through the poorly refined dominant fields.
However, it can be used to get a first approximation of the optimal set as the computational cost is reduced here to 3546 evaluations (gain = 93%). 13 and 14, with a reduction of the impact of the recursive strategy alone and an increasing sensitivity to s2. The plateau is reached in this test case before the end of the optimization process, and Fig. 19c illustrates the influence of the threshold s1 when the plateau is reached.
It can be seen that, due to the variable impact of s2 on the recursive approximations of the computational cost, the influence of this threshold value increases. a) (b). In this case, many non-dominated boxes are calculated and s2 has a non-negligible impact on global costs, as shown in the first three curves of the same figure. First, we provided a mathematical proof of the robustness of the framework and of its convergence under some assumptions.
Then, a numerical validation has been performed to validate the convergence, quantify the computational cost reduction, and make explicit the main behavior of the strategy. The accuracy of the output has been qualitatively analyzed with respect to the associated cost reduction. Finally, the influence of the user-defined thresholds has been investigated, to provide the keys to tune them effectively.
Future developments will be directed towards applying the proposed framework to an uncertainty-based multi-objective optimization problem in engineering applications. An Adaptive Strategy on the Error of Objective Functions for Uncertainty-Based Derivative-Free Optimization.