For the sake of simplicity of presentation we consider in the rest of the article that the data is always of type integer (and therefore it is possible to take as abstract data domains the standard octagons or polyhedra abstract domains). Because all data updates only affect the first symbol of the words, in the following we will refer to the head of a word (i.e. the first symbol) and the tail (i.e. the suffix that begins with the second symbol) separately. They use variables that represent words (which have the same name as the nodes of the graph) and terms that are interpreted as integers: hd(n) denotes the first symbol in the word represented by n, len(n)de its length and the sum tl(n). ) is the sum of the symbols in its tail.
The integer variable init sum specifies the sum of the integers in the initial list. To make the definitions of all abstract domain operators uniform, we assume that for each abstract heap. AH for which we cannot find an isomorphic abstract heap in A′H we add the abstract heap (N,S,V,⊥W) to A′H and vice versa.
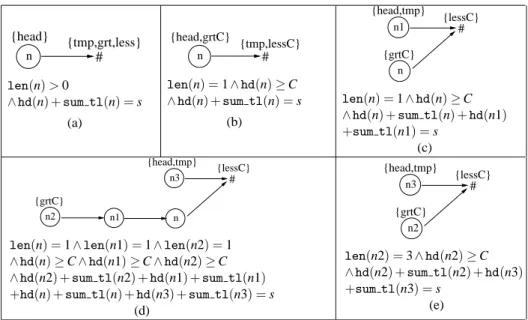
For example, an abstract version of the Uncover procedure, denoted Uncover#, used in post#k(free(p),AH) is given in Figure 6. Constraints on the length of the list and the data in the list are given by an abstract value written below the graph. Two of the abstract heaps obtained after the first iteration of the loop are given in Fig. 7(b) and (c).
After two more iterations, one of the resulting abstract heaps is the one in Figure 7(e).

4 A DW -domain over universally-quantified formulas
Syntax of formulas
Syntax of patterns The patterns describe a set of positions that belong to the tails of different words. They specify the word to which the positions belong, they fix an order between the positions belonging to the same word, and they place arithmetic constraints on some of these positions (which are the first on each word).
Semantics of formulas
Lattice operators
Also, ⊔Uand⊓U are the least upper bound and greatest lower bound, respectively, and∇U is a broadening operator. The proof for the extension operator relies on the extension operator∇Zen on the fact that the set of patterns P is fixed.
Closed sets of patterns
2 The Galois connection between the lattice C(DWVars,DVar) andAU is defined according to the semantics given in Section 4.2. Intuitively, Tuples(PRi,v1, . . ,vm) shows all possible ways to choose j positions that satisfy the order constraint in PRi on the word representing the concatenation of the words v1. Roughly speaking, all possible ways are considered to choose any number of positions on the word v1, any number of positions on the word v2, etc.
Otherwise, if m≥2, we start by considering the case where we choose positions that are not the first symbols of the words v1,. Above, φ1 characterizes the q1 positions belonging to the word vs1, for some 1≤s1≤ m, which obey the same constraints as the first q1 positions in PRi. Obviously, the positions yqi1 and yqi1+1 cannot be immediate successors, because we have considered the case where yqi1+1 cannot be the first symbol of vs2.
Above, ψ1 describes q1−t0 positions associated with the word vs1, for some 1≤s1≤ m, which satisfy the same constraints as the positions yti0,. It is assumed that the first t0−1 positions are assigned to the first symbols of some of the words v2,. Then ψ2 describes q2−(q1+t1) positions belonging to the word vs2, for some 1≤s2≤m, which satisfy the same constraints as the positions yqi1+t1,.
If t1=1, then between yqi1 and yqi1+1 there is at least one symbol (the first symbol of vs2). We denote by yi′⊆y the set of variables y for which there exists a variable u∈u and some vector y⊆yi with y∈y, such that y∈tl(u) is an atomic formula in QiR(yi ,ui). Let QiR(yi,ui∩u) denote the relation of atomic formulas in QiR(yi,ui) over positional variables in yi′.
Note that if the model P contains no arithmetic constraints, then Closure(P,k) = Closure(P,k+1), for every k greater than or equal to the number of position variables in P. Taking all groupsClosure(P ,u1, . . . ,uq) which correspond to the attachments of at most words C, where C is the constant mentioned in remark 1, we get Closure (P,k).
Abstract transformers
In some of the results that follow, we need a canonical representation for the abstract values in LU. This implies thatαZ(γU(W)|f st∪len)⊑ZE, which implies by the property of the Galois connection. The projection operator First we give the definition of the projection operator and then we present correctness and precision results.
The correctness and accuracy of the projection operator is proven in the following results. The following results prove the correctness of the abstract transformer updateFirst# and identify conditions under which it is a best abstract transformer. If the command abstract transformer inAZ is exact for data expressions of the form dt then.
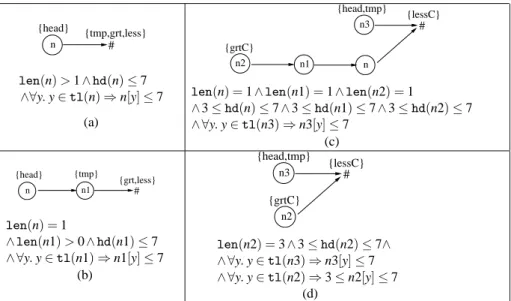
Then, during the first iteration of the loop, the output oftmp=head→nextis shown in Figure 8(b). Update universal formulas: Regarding universal formulas, we retain those that do not characterize the tail of the data word marked with x or that do not use the term len(x) for the length of x. The following results prove the correctness of the separation of abstract transformers# and identify the conditions under which it is the best abstract transformer.
Then concat#(We,V1, . . . ,Vt) transforms W so that the first variable in Ve i will represent a word that is the concatenation of the words labeled by the variables in Vi for each 1≤i≤t. After several iterations of the loop, we get the abstract heap in Fig. 8(d), which is obtained by applying Normalizek# to the abstract heap in Fig. 8(c). Since the length of the words labeled n2, n1, and n is 1, we need to use the second inconcat# step.
We are looking for the formula∀y.y∈tl(n2)⇒U which holds when n2 is interpreted as a concatenation of single elements represented by n2, n1 and n. Since the chain length is 3, there are only two values for y, so y∈tl(n2), y=1 and y=2. The word represented by n1 satisfies the same constraints as in W and the word represented by not 2 is an abstraction of the concatenation of the individual elements denoted by n2, n3, n4 and n5.
The value U is the aggregation of several numerical abstract values representing properties of three consecutive positions on the concatenation of the words labeled n1 and n2. For example, the abstract value representing the property of the last symbol in n1 and the first two symbols in n2 is the meeting of the abstract value associated with P1(n1), the quantifier-free part where hd(n1) has been replaced by n[y2 ], and the right part associated with P2(n2).
5 Experimental results
Fortunately, given the simple patterns, all abstract transformers retain the closure property, meaning that they output closed values when applied to closed values. Using more complex patterns not yet implemented in our domain, we manually synthesize the postcondition of a program that copies two lists A and Bin in sequence to a third list C, i.e. ∀y1,y2.(B−→y∗ 1∧C−→ ∗ y2∧y2=len(A−→null) +∗ y1)⇒data(y1) =data(y2). Constraint (D) given in the introduction is generated using a pattern with three consecutively ordered universals (and patterns in its conclusion).
Using a pattern with two universals we get that the list head is sorted and using a pattern with one universal we get at∀y.head−−+→y⇒ (data(y) +1≥len(head− −→ y)). Performance: Each of the examples is executed in less than 1 second with between 4KB and 63MB.
6 Conclusion and related work
Analysis with AHS(AΣ) of the program that creates a copy of a list generates the back state 2×len(head−→null). Complex Arithmetic Relationships: We have applied our tool to the example of Fibonacci using AHS(AU) over different sets of patterns. In contrast, our approach adjusts the formulas on the left-hand side of the implication and synthesizes the right-hand side.
The class of invariants they can generate is included in that handled by our approach using AHS(AU). The analysis introduced in [18] for programs with arrays can synthesize invariants on multisets of the elements of array fragments. This technique differs from our domain-basedAHS(AU) in that it cannot be applied directly to programs with dynamic lists.
It is not limited by the class of data structures, but it only takes into account properties related to the shape and size of the memory, provided that data has been abstracted away. Our approach is less general with respect to shape properties, but it is more expressive with respect to properties on data.