Then the segment point cannot be in the corresponding direction cones, which is a contradiction. These lines are also transversal to the interior of the spheres in F, from which it follows that K≺(F) is strictly strongly convex. If u is the direction of the boundary K≺(F), then there exists a unique line ` transverse to F with direction u.
By the convexity theorem, the projection, in the direction space, of the sets of line surfaces onto disjoint spheres is quite simple, since it consists of a disjoint union of convex regions. The equivalence of statements (i) and (ii) follows from the relation between the set of line transversals to F-realization. B5} of 5 disjoint spheres tangent to a line ` in that order, and consider the projection of the spheres on a plane perpendicular to `.
Let's mark the projection of the line, that is, the point common to the projected disks. Let S be the screen of (B,`) and denote by T(B) and T(S) the set of transversal lines to Pas and S. It was previously known that the number of geometric permutations of n disjoint unit balls, when sufficiently large, maximum 4, regardless of dimension [HXC01,HXC04,KSZ03, ZS01].
Our proof of Theorem 4.1 uses the different approach of identifying compatible pairs of patterns for geometric permutations of the same set of disjoint unit balls.

Every minimal attachment of a line with possible intersection of convex polytopes in R3 whose face is not coplanar with the line has.
First we note that C cuts T ∩M exactly at the origin, otherwise we can find a line through the origin in C∩T∩M. We can ensure, by perturbing v if necessary, that the segment does not contain the origin. The wt point of M on the segment joining and extending to the origin goes to 0, contradicting the assumption that the origin is isolated to C∩M.
Since Fpins`0 the origin is an isolated point of C∩M and we are in one of the cases (i)–(iii) of Lemma5.5. In this setup, the solid line of lines satisfying an orthogonal constraint is a half-space with the origin on its boundary. Such a family intersects in a single point if and only if the convex hull of their outer normal vectors contains the origin in its interior.
We give a description of minimal families of vectors (or equivalently points) in R4 that contain the origin in the interior of its convex hull. A set of points in Rd is said to surround the origin if the origin lies inside their convex hull. Our first goal is to characterize the sets that minimally surround the origin in R4 as unions of (not necessarily distinct) critical simplices.
This proves that every point surrounding at least the origin in R4 is of one of types (i)–(iv). It follows that any closed half-space containing the origin on its boundary is missing at least one point S. We say that a family of vectorsu0,. ukforms a critical simplex if the points O+u0,. the intersection of the half-spaces with the origin at their boundary and the outer normalsu0. uk should have the dimension exactly 4−k.
We now turn our attention to situations where constraints that are not necessarily orthogonal are fixed "at first order", that is, when the origin remains isolated at the intersection of the linearizations of the solids Ug. The limit of Ug is a quadric through the origin and its normal ηgin the origin is given by equation 5.2. Since the volumes Ug are bounded by algebraic surfaces of constant degree, the origin 0 is isolated at the intersection of such volumes if and only if there exists no smooth path moving away from 0 inside that intersection.

Any higher-order minimal pinning of a line by con- straints in R 3 has size at most six
In this case, if there is no single point, the four normals are linearly dependent on the constraints in F⊥. The space of oriented lines touching S is diffeomorphic to the unit tangent bundle of the sphere S2, which is a smooth 3-dimensional polyhedron. Let p denote the contact point A with `0 and r the inverse Gaussian curvature of A inp.
A⊥`0i continuously in the parameters (angle of the rotation and amplitude of the translation) of the screw. Recall that, as argued in the proof of Theorem 2.1, a family of convex sets inR3 has a line transversal with directionuif and only if any three members of the family have a line transversal with directionu; indeed, it is. Name a family of sets that is not additive if any union of disjoint members of the family is not in the family.
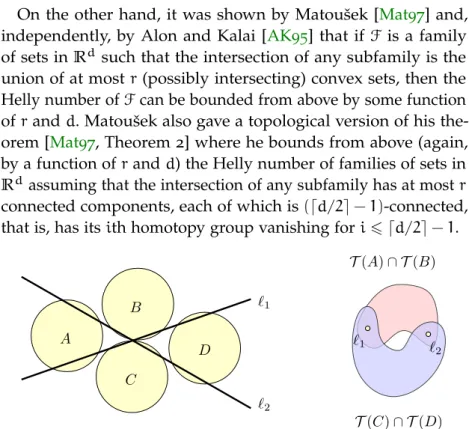
Let F be a (G,r) family and let C denote the union, for all elements A ∈ F, of the set of components of A. We call a simplicial map dimension-preserving if any simplex is mapped to a simplex of same dimension. Lemma8.7 implies that the Helly number of a family is at most ∆(α) +1, where α is any good gradation of the nerve of F.
Finally, we turn to the proof of the Grünbaum-Motzkin conjecture by Eckhoff and Nischke [EN09]. In their proof, they use the property that the union of good covering in Rd has trivial homology in dimension j > d. The name of the game is to compute a basis H such that w(H) = w(Γ), and this can be done efficiently when the combinatorial dimension is bounded [Cla95,MSW96,Sei91].
The map that associates with each face ofτthe set of vertices of that face is a bijection between[0,τ]and2V. Under this assumption, M(F) can be identified with the set of all connected components of the intersection of a subfamily of F, equipped with the opposite of the inclusion order. We bound L(M(F)) from above via the following analogue of the nervous theorem for acyclic families.
The nature of the surrounding space is used in two places in the proof of Theorem 9.1. First, it ensures, in the proof of Theorem 9.3, that the connected components and the arc-connected components of any open subset of the space agree; the same is indeed true in any locally arc-connected topological space.

What configurations of four smooth rotund convex sets in R 3 have infinitely many common tangent lines?
The main problem is that some non-convexity is hidden in situations where an immobilized line passes through the face of a polytope, since the set of lines intersecting this polytope near the line is isometric to (the intersection of the Klein quadric with) the union of the two half-spaces. Helly numbers are related, as mentioned in the notes to Chapter 8, to the notion of combinatorial dimension of LP-type problems. Given the robustness of the pinning theorems, the sparsity condition (association of the radius C with the minimum interpoint distance inP) may be unnecessary.
Although the geometry of lines has been studied for quite some time, as evidenced by Euclid's Elements, the modern view of line geometry, which studies the space of line as an object in itself, is more recent; it has its origins in the second half of the 19th century, with the work of people such as Plücker, Klein and Grassmann. This parameterization can be very useful (as shown in Chapter 5), but it only works if you only care about what happens near a line that intersects the planes at two different points; however, lines parallel to either plane or passing through the intersection of the two planes are not displayed. However, one can map the line `=p+Ru, where pis is a point-andua vector, to the sixfoldξ(`) = (u;−→ . Op×u), where (a;b) is the juxtaposition of the coordinates of two vectors db.
This representation is, in a nutshell, the affine reformulation of the standard coordinate system introduced by Julius Plücker, and thus known as Plücker coordinates, and their interpretation, due to Felix Klein, as a map between lines in RP3 and a hyperquadric in RP5 (often referred to as the Klein quadric). Our aim here is simply to equip the reader who is not already familiar with this branch of mathematics with the definitions and basic intuition of the objects manipulated in Chapters 8 and 9. For a more thorough exposition of this subject refer we to one of the classic textbooks, e.g.
By linearity, any 0-chain of X consisting of two vertices of the same connected component with opposite weights is a limit. In fact, the a0 chain is a limit if and only if the coefficients (in the chain) of γs vertices for each connected componentγafS are to 0. The open lower interval [0,σ) is by definition isomorphic to the limit of thed-simplex; we simply glue a geometric-simplex to the realization of this limit.
This leads to the definition of these simple homology groups of the space Γ, and the simple homology groups of a simple complexX can be shown to be isomorphic to the simple homology group of any realization|X|ofX. To each simplicial poset X we can associate a topological space |X|, its realization, by the same procedure as above: first create a single point for each vertex of X and then, since the open lower interval [0,σ) is isomorphic to the boundary of the d-simplex, glue a geometric-simplex to realize that boundary. In terms of simple complexes, the simple homology groups of a simplicial poset are isomorphic to the simple homology groups of any of its realizations.