Durant ces trois années, j'ai eu l'occasion de profiter de l'excellente ambiance de travail qui règne à l'UMR Gulliver. Je souhaite chaleureusement la bienvenue à tous les membres de la société Science Ouverte, lycéens et mentors, avec qui j'ai travaillé durant les deux dernières années de ma thèse.
Solides colloïdaux
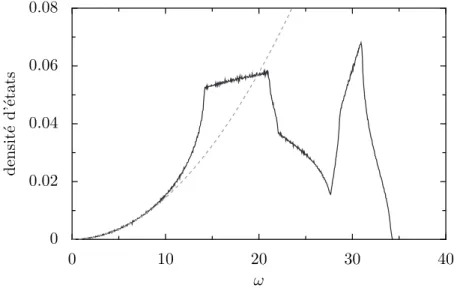
À partir de la matrice de corrélation par paires hui(R)uk(R′)i dans l’espace réel, la densité d’états peut être obtenue. Ceci est impossible à partir de la matrice de corrélation de déplacement huˆi(K)ˆu∗k(K)i pour le même vecteur K dans l'espace de Fourier. Ceci est réalisé sur la figure 2.8 en utilisant la matrice de corrélation de déplacement dans un cristal bidimensionnel.
On trouve les résultats de la littérature obtenus dans le contexte de l'élasticité linéaire homogène. Densités de probabilité des états propres de la matrice de corrélation de déplacement v. L'évolution de la pression en fonction de la fraction volumique dans le domaine de coexistence est représentée sur la figure 3.27.
Ceux-ci sont représentés en fonction de la fraction volumique dans le domaine de coexistence sur la figure 3.28.

Apport de la diffusion dynamique de la lumière
Microscopie confocale
Mais la matrice de corrélation des paires dans l’espace réel n’est accessible expérimentalement que par observation directe dans l’espace réel. Dans ce deuxième cas, le terme densité d'états sera réservé à la densité de probabilité de fréquences propres dérivée de la matrice de corrélation par paires dans l'espace réel.
Modes localisés
La question qui se pose alors est la suivante : comment interpréter correctement les données expérimentales obtenues à partir du déplacement projeté sur une couche bidimensionnelle. L'objectif du chapitre 2 est de déterminer les propriétés élastiques effectives accessibles à partir de l'observation des corrélations du déplacement projeté sur une couche d'un cristal tridimensionnel.
Propriétés élastiques d’un cristal métastable
Les valeurs propres de la matrice de propagation ˆD(K) sont donc inverses de celles de la matrice de corrélation huˆi(K)ˆu∗k(K)i, avec le coefficient de proportionnalité kBT N/vm. Cela montre clairement que la fonction de Green ˆGkm(K) est l'inverse de la matrice de propagation ˆD(K). Le calcul de l'effet de la projection sur la matrice de propagation ˆD(K) peut être résumé dans le diagramme suivant.
De plus, une inversion de la matrice de propagation cubique ˆDcub(K) est possible dans le cas général. La relation de dispersion résultant de la matrice de corrélation de déplacement est donnée dans la section suivante. Il y a au total neuf composantes différentes dans le tenseur de la dérivée des déplacements uij.
La ligne continue représente la densité d'états correspondant à la diagonalisation de la matrice de corrélation de paires dans l'espace réel.
Obtention de cristaux surchauffés
Mécanisme de la fusion homogène à l’échelle d’une particule . 18
La fréquence au carré ω2 est proportionnelle aux valeurs propres de la matrice de propagation ˆDik(K). C’est notamment le cas de la notion de chute critique qui sera développée au chapitre 5. Les traits donnent la hauteur du plateau de la fonction de répartition dans le cas d'une chute sphérique pour nl = 6 etns = 7 (trait plein) et pour nl = 7 et ns = 8 (traits pointillés).
Déformation, équation d’onde et constantes élastiques
Ondes acoustiques et modes élastiques statistiques
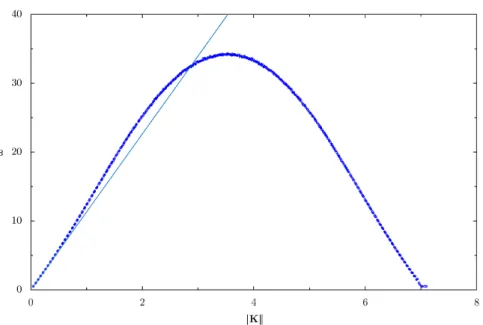
Leur fréquence et leur direction de propagation peuvent être comprises à partir de la matrice de propagation ˆD(K). En introduisant cette forme de matrice de propagation dans l’expression (2.54), on obtient
Principe de la projection
Ce qui frappe d’abord dans la figure 3.2, c’est que la pression augmente avec la polydispersité. La dépendance linéaire de 1/qln(hτMDi) en fonction de la fraction volumique n'est vérifiée qu'approximativement sur la figure 4.4. Les caractéristiques de la densité de probabilité du temps de fusion sont discutées en fonction de l'état initial dans des simulations cinétiques de Monte Carlo et de dynamique moléculaire.
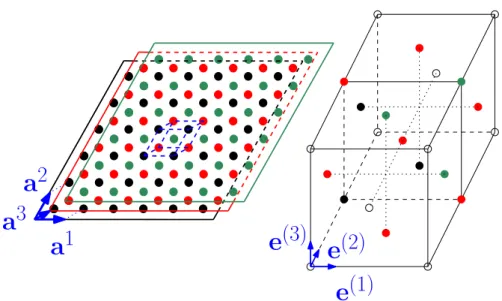
Calcul exact dans un milieu isotrope effectif
Caractéristiques du code de dynamique moléculaire
Enfin, l’algorithme événementiel s’affranchit de la nécessité de définir un pas de temps court. Ceci est nécessaire pour que les vecteurs du réseau réciproque introduits par la périodicité de la boîte de simulation coïncident avec les vecteurs du réseau réciproque associé au cristal.
Relations de dispersion projetées de trois à deux dimensions . 53
Cependant, la variation de pression avec la polydispersité dans les liquides est comprise théoriquement [106]. L'augmentation de pression avec la polydispersité dans le cristal des sphères dures peut néanmoins être décrite numériquement. La méthode présentée dans le paragraphe précédent permet d'obtenir les valeurs des coefficients contrainte-déformation en fonction de la polydispersité.
Figure 5.2 – Densité de probabilité pour une composante de la vitesse d'une particule dans le solide métastable déduite de la dynamique moléculaire (cercles).

Choix de la distribution des rayons
Pression et constantes élastiques
Deuxièmement, l'effet de la polydispersité sur la densité de probabilité des états propres de la matrice de corrélation des déplacements dans l'espace de Fourier sera étudié. Figure 3.2 – Variation de pression avec polydispersitéδ exprimée en pourcentage, pour un système de N = 9261 sphères dures, à la fraction volumique φ = 0,57. Il fournit une expression explicite de la pression Ppoly dans un système polydispersé de sphères dures.

Modes élastiques localisés
Ce coefficient de corrélation est tracé sur la figure 3.20 en fonction de la valeur seuil prc choisie pour le taux de participation local. Comme le montre la figure 4.4, le temps d'attente moyen hτMDi dépend fortement de la fraction volumique φ. Dans le prochain chapitre, le modèle cinétique de Monte Carlo établi ici sera utilisé pour étudier les propriétés de la chute critique.
Premièrement, le caractère bimodal de la densité de probabilité du temps de fusion est observé à la fois dans les simulations MCC et de dynamique moléculaire. Le caractère bimodal de la densité de probabilité équivaut à l'existence d'un plateau dans la fonction de distribution correspondante. Figure 5.4 – Densité de probabilité du temps de fusion τM D dérivée de simulations de dynamique moléculaire (symboles) pour les trois configurations spatiales différentes de la figure 5.3.
Comme dans les résultats cinétiques de Monte Carlo, la bimodalité de la densité de probabilité du temps de fusion correspond à l'existence d'un plateau dans la fonction de distribution.

Différence dynamique entre les cristaux stable et surchauffé
Détermination des constantes élastiques du cristal surchauffé . 115
Il n'est pas surprenant que la variation des constantes élastiques en fonction de la fraction volumique dans le solide métastable soit continuellement liée à sa variation dans le domaine du cristal stable. Figure 3.28 – Evolution des coefficients de Lamé λ, µ et ν en fonction de la fraction volumique φ dans le domaine de coexistence 0,494< φ < 0,545, issus de simulations de dynamique moléculaire pour un système de N = 1 728 particules. L'utilisation de simulations MCC pour étudier la dynamique de fusion homogène est possible mais reste rare [ 78 ].

Paramètre d’ordre local de liaison et nature d’une particule
Enfin, les effets de la taille finie sur les propriétés des gouttelettes et le temps de fusion sont analysés dans des simulations cinétiques de Monte Carlo et de dynamique moléculaire. 5.1) où λg, kg, λd et kd sont des paramètres réglables et où h est la hauteur du plateau de la fonction de distribution des temps de fusion [89]. Le nombre de particules liquides présentes dans la gouttelette initiale a donc peu d'influence sur le temps de fusion final, qui dépend de la nucléation d'une autre gouttelette.
La hauteur du plateau de la fonction de distribution du temps de fusion correspondante fournit une mesure sensible de la nature critique d'une gouttelette. Par exemple, la dépendance du temps de coalescence sur la taille du système est plus complexe dans les simulations de dynamique moléculaire que dans les simulations cinétiques de Monte Carlo.

Paramètres d’ordre globaux et temps de fusion
Approche de champ moyen
Le premier état stationnaire, où le nombre de particules fluides est faible, peut être comparé à l’état métastable obtenu en dynamique moléculaire. L'accord entre le nombre de particules liquides dans les deux états stationnaires stables de l'approche en champ moyen ainsi que dans les états métastables et d'équilibre des simulations de dynamique moléculaire encourage l'utilisation du mécanisme de réaction proposé dans l'équation (4.17) pour prédire le temps de fusion stochastique. Pour atteindre ce temps d'attente, il faut prendre en compte les fluctuations du nombre total de particules fluides et donc dépasser l'approche champ moyen.

Méthode de Monte-Carlo cinétique
Tableau 4.1 – Variation du temps d'attente moyen avant fusion, hτMCCi, dérivé des simulations cinétiques de Monte-Carlo pour différentes valeurs des coefficients stoechiométriques limites nsetnlet pour les mêmes paramètres que sur la Figure 4.10. Le temps d'attente hτMCCi est moyenné en utilisant différentes graines pour le générateur de nombres aléatoires. Le tableau 4.1 montre les temps d'attente moyens hτMCCi trouvés dans MCC pour différentes valeurs des paramètres nl etns.

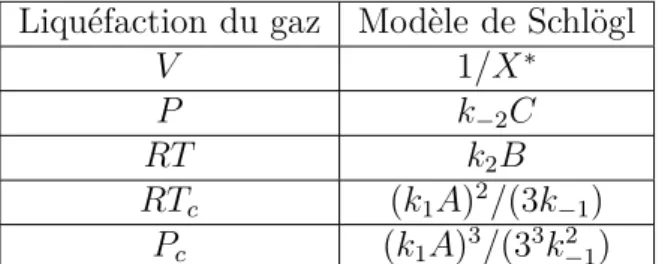
Lien avec le modèle de Schlögl
Identifier ces deux définitions de la vallée spino revient à dire que l'état métastable n'est clairement identifiable que si l'état d'équilibre final contient les deux phases. L'analogie avec le modèle de Schlögl peut donc être étendue, et les deux états stationnaires stables du modèle de Schlögl correspondent à l'état métastable et à l'état d'équilibre final de la transition de phase du premier ordre. Figure 4.11 – Schéma des courbes spinodale et isotherme de la transition de phase liquide-vapeur dans l'espace (P, V).
Simulations de Monte-Carlo cinétique
Cela correspond bien à l’idée selon laquelle la goutte critique a l’une des deux options suivantes : se propager ou se résoudre. Les fonctions de distribution du temps de fusion sont également représentées sur la figure 5.1abcd pour les quatre configurations initiales (a), (b), (c) et (d). Les fonctions de distribution du temps de fusion obtenues dans MCC sont approximées par des lois de type Weibull comme au chapitre 4.
Simulations de dynamique moléculaire
Tableau 5.1 – Valeurs de la hauteur de plaque h et des paramètres λl,kl, λr,kr pour les fonctions de distribution du temps de fusion données dans la figure 5.3abc pour les trois configurations spatiales différentes (a), (b), ( vs. ) . Les deux pics présents dans la densité de probabilité du temps de fusion peuvent être comparés un peu plus en détail pour les différentes configurations initiales (a), (b) et (c). Pour ce faire, les trois densités de probabilité de temps de fusion sont tracées sur le même graphique pour les trois configurations initiales (a), (b) et (c) de la figure 5.4.

Forme de la goutte
C'est pourquoi, dans la suite, les caractéristiques de la chute critique obtenues dans les simulations MCC seront étudiées plus en détail. La taille de la goutte critique est indépendante de la taille du système et le temps de fusion moyen dérivé des simulations cinétiques de Monte Carlo varie comme l'inverse de la taille N du système. Dans le chapitre 5, la dynamique de fusion homogène est étudiée plus en détail à travers l'idée de chute critique, dans les simulations de dynamique moléculaire et dans celle de Monte Carlo cinétique.

Influence des coefficients stœchiométriques limites
Taille du système
Les simulations cinétiques de Monte Carlo et de dynamique moléculaire révèlent le caractère bimodal de la distribution de probabilité du temps de fusion lorsque la configuration initiale inclut une chute critique. Plus précisément, la complexité de la dynamique de fusion observée dans Cependant, le modèle cinétique minimal de Monte Carlo ne prend pas en compte toutes les propriétés de la dynamique de fusion.