In the early days of the theory's development, manifestations of entanglement caused many physicists to dislike the probabilistic interpretation of quantum theory. We then characterize the local unitary invariants using the representation theory of unitary groups and also propose a concrete method for con-.
Quantum correlations
This motivates our study of fermionic entanglement measures with the tools of the second chapter. One or both of these assumptions must therefore be removed from the picture we have of the world.
Entanglement classification problem
These states are special in that they cannot be written as tensor products of vectors from the Hilbert spaces of individual subsystems. The standard construction [13] in the theory of order allows us to pass to equivalence classes with respect to - ∩ -−1, and on the set of quotients this induces a partial order.
Quantification of entanglement
The classification problem can thus be divided into two parts: First we want to identify equivalently entangled states, then we want to find out if we are able to convert representatives of two given equivalence classes into each other via local transformations. For example, it is not known how the distillable entanglement of a mixed bipartite state can be calculated.
Bipartite quantum systems
In this case, we can describe the algebra of polynomial LU invariants explicitly: it is generated by elementary symmetric polynomials of at most min{n1, n2} of the eigenvalues. The state space of a composite quantum system of distinguishable subsystems is the tensor product of the Hilbert spaces of the individual subsystems (see sections A.3 and A.4 in the appendix for the definition and properties of the tensor product).
Time evolution
Semigroups of local transformations
In the previous section we saw that any element of End(H) can be applied to a quantum system with state space H with a non-zero success probability, and that any unitary operator in End(H) can be applied with probability one . The LU (local unitary) group is the subgroup of unitary elements in the SLOCC group.
Monoid actions
SLOCC-equivalently entangled if ψ ∼ ϕ where ∼ is the equivalence relation induced by the SLOCC group action. Confused LU-equivalent if ψ ∼ϕwhere ∼is the equivalence relation induced by the action of the LU group.
Invariant polynomials
This vector space is the dual of the tensor algebra (see Sections A.2 and A.5 in the Appendix). Conversely, a function f :V →C, which is a polynomial in the coefficients, can be uniquely represented by a vector inS(V∗).
The symmetric algebra of a Hilbert space
Note that the same program would fail in the case of the SLOCC group at several points: when G is the SLOCC group with the usual action, there are no G-invariant inner products on H; we cannot limit ourselves to a compact subset, and therefore polynomials are not dense in the space of continuous functions; there is no averaging operator, because the SLOCC group is not compact, and thus there is no normalized Haar measure; and worse, a dense orbit may exist, in which case even continuous invariant functions are unable to separate the orbits. It is known from the representation theory of the unitary groups (see section B.4 in the appendix) that in this way every Sm(H) becomes an irreducible unitary representation of U(H), and thus the induced inner product essentially becomes the only immutable under this group action.
Local unitary invariants
Fourth order invariants
Elements of the symmetric algebra S(H) are polynomials in these vectors, in particular a vector of Sm(H) is a degree m homogeneous polynomial. We claim that it is an element of VA, moreover, vectors of this type form a basis of VA and are pairwise orthogonal.
Invariants of higher order
Fourth order invariants with permutation symmetry
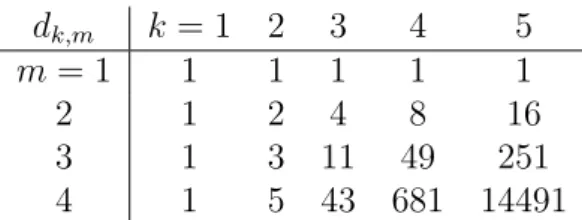
Since there seems to be no simple formula for the norm square of these vectors, we cannot give the general form of the corresponding invariant, but it can be computed without any difficulty for any concrete value of m and k and any subset A Therefore, the dimension of the vector space of permutation invariant degree four unitary invariants is 1 +bk2c.
Dimensions of subspaces of LU-invariants
Note first that the Hilbert series of the tensor product of scalar algebras is the product of their Hilbert series. When working with stabilized dimensions, only two parameters remain: the number of subsystems k and the degree of polynomials 2m. Another possibility is to fix m and determine the behavior of the dimension of the subspace of polynomial invariants of degree 2m as a function of k.
Stable dimensions of the spaces of LU-invariant polynomials . 41
The order of centralization of an element in the conjugation class labeled bya is given by[22]. Jn1 is their product, therefore f in the ideal is generated by n1-fold products of the coordinate functions. Note that the special case where the dimensions of the individual Hilbert spaces are equal was studied in ref.[15].
Local unitary invariants for mixed states
The inclusions ιn,n0 : Hn → Hn0 in this case also induce the maps %n,n0 : Ik,nmixed0 → Ik,nmixed with similar compositional properties as in the case of pure states. Note that according to our previous notions introduced in the case of distinguishable subsystems, states as in Eq. We would like to follow a similar program as with the distinguishable subsystems.
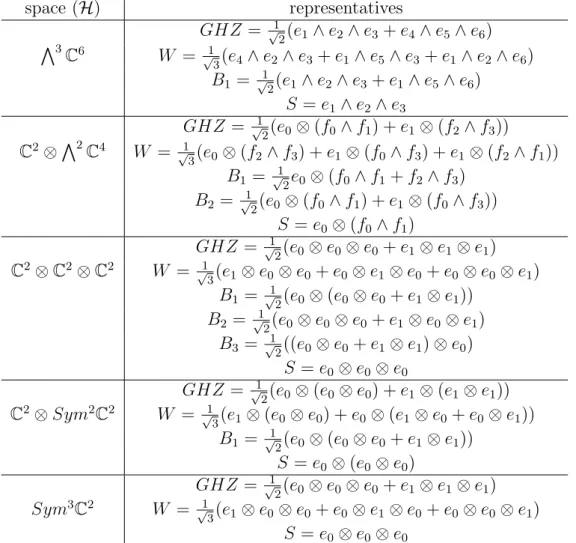
Special three-particle quantum systems
- Three fermions with six single particle states
- One qubit and two fermions with four single particle
- Three qubits
- One distinguished qubit and two bosonic qubits
- Three bosonic qubits
We see that the injection of the space of three-qubit states into the space of three-fermion states can be done at the Jordan algebra level. It is therefore not surprising that the three-tangle of a three-qubit state can also be obtained by first taking the associated special three-fermion state and then computing the value of the quartic invariant on it. The state space of these systems can naturally be seen as subspaces of that which describes three qubits, so one can expect that these can be injected into the latter, just as the three-qubit system is injected into the three-fermion system.
Local unitary invariants of fermionic pure states
In the following, we will consider only the fermionic case, because it is the orthonormal basis of the fermionic. Interestingly, this decay is independent of n (except for the disappearance of subrepresentations associated with partitions involving more than n parts, but for n≥km this certainly cannot happen). Note also that if the multiplicity of the representation SλH in Sm(ΛkH) is cλ, then the dimension of the space is invariant of degree 2m P .
Invariant subspaces with maximal highest weight
Keeping track of the character that occurs could cause some problems, but this can be overcome by leaving eabc. The coefficient sl contains exactly those terms in the expansion in which the number of replaced j-indices is l. b) d is the (total) number of occurrences of index j in each term w. The coefficient of the term sd−r is therefore proportional to the image of the coefficient sr in the case of the transposition exchange of ei and ej. c) The constant term is w. d) Let π∈Sn≤U(H) be such an element that Cw=Cπ·w0 holds.
Examples
If we wanted to compute the projectors of other isotype subspaces, we simply had to take the orthogonal complement of W and find the weight vectors corresponding to the largest weight, and proceed in the same way as we did zem12..k . We are done with the corollary of the lemma, but it is instructive to check the dimension of the generated subspace. The third type in the generated set is {eijelk+eikelj}, which generates a two-dimensional space for each set of four indices, and these subspaces are pairwise orthogonal and also orthogonal to other elements.
In this case, orthogonalization turns out to be a bit lengthy, especially in the case of six-term vectors as in equation (3.68). Using these data, the value of the invariant I(3,3) can be calculated in a straightforward manner, but the full formula is too long to be presented explicitly. The orthogonal complement of W clearly has a highest weight of (22,12), and we could find a generator of the unique one-dimensional weight space corresponding to it, and compute the projector of its invariant subspace.
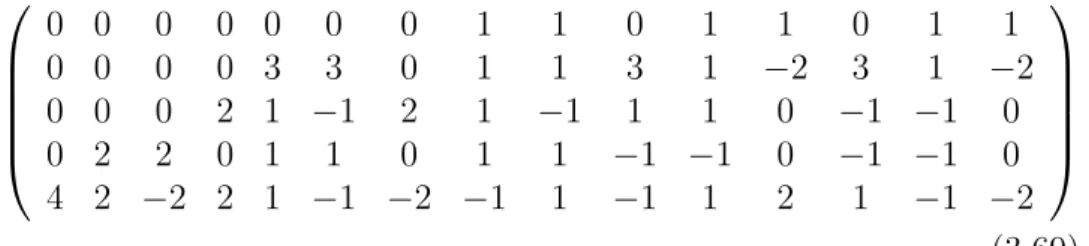
Our invariant corresponding to the subrepresentation indexed by the partition (16) must be proportional to it. These two invariants are linearly independent and they sum to 1 with the one associated with the third irreducible subspace. For a fixed subset of six indices, the vectors of the form as in (3.76) span a five-dimensional subspace.

Fermionic SLOCC invariants
Fourth order LU-invariants of multipartite systems with iden-
Finally, let's look at the symmetric square of the state space of a quantum system of k bosons. An object a together with a family of morphisms πi : a → ai is called the product of the family (ai)i∈I if for every object b ∈ Ob(C) and every set of morphisms fi : b → ai a exists uniquely morphism f : b → a creating the diagram. An object a together with a family of morphisms ιi : ai → a is called the co-product of the family (ai)i∈I if for every object b ∈ Ob(C) and every set of morphisms fi : ai → b there are there exists a unique morphism f : a → b in creating the diagram.
Vector spaces
Let C and I be a two categories, and F : I → C a covariant functor, called a diagram of type I in C. A.3) for a visualization of the morphisms appearing in the definition). Note that when the only morphisms in I are the identity morphisms, then the limit reduces to the product. Let Ibe consider a partially ordered set as a small category, that is, objects of I are elements of a partially ordered set, Hom(i, j) has exactly one element if i≤j, and it is otherwise empty .
Tensor products
Due to the universal property in the definition of the tensor product, there exists a unique linear map TrV : V ⊗V∗ → K such that TrV(v⊗ϕ) =ϕ(v) The map TrV : HomVectK(V, V) →K is called the track.
Tensor products of Hilbert spaces
Graded algebras
In N−AlgK products and coproducts always exist, and are called direct products and free products, respectively. Two spaces G-V and W are said to be isomorphic if there exists a G-equivariant isomorphism in HomVect. If G and H are groups, V is a G-space, and W is an H-space, then the tensor product V ⊗W comes with a representation G×H defined by (g, h)·(v⊗w) : = (g·v)⊗(h·w) in elementary and linearly extended tensors.
Character theory of finite groups
In the case of finite groups, the theory of finite dimensional representations can therefore be encoded in a table containing the values of irreducible signs of each conjugacy class, which also indicates the sizes of the conjugacy classes. In this case, the value of the sign of a group element g is the number of elements in S fixed by g. In the special case where S =G and α : G×G→ G is the group multiplication, the resulting representation is called the left regular representation .
Representations of the symmetric group
In principle, this theorem allows us to compute the characters of the irreducible representations of Sd. A permutation of the set [d] can always be written essentially uniquely as the product of cycles. The set of these numbers is called the group element cycle type, where fixed elements are considered to be cycles of length 1.

Rational representations of the unitary and the general linear
In addition, there is a noble sub-C∗-algebra A ≤End(H) of the C∗-algebra of bounded linear operators of H. Then the appropriate permutation group acts on the Hilbert space of the composite system by permuting the factors of the tensor product and observables are invariant under this action, giving rise to superselection sectors. Hk, we easily see that Sk acts on the tensor product and on End(H), and the action of the observables is equivariant.
Time evolution with restricted interactions
Hk then the Hilbert space associated with the composite system is their tensor product H := H Hk. In this case the corresponding Hilbert spaces are isomorphic via a distinct isomorphism and can thus be identified. If the initial state of the joint system is %⊗ψψ∗, where % ∈ End(H) and ψ ∈ HEN V is a unit vector, then after an elapsed time interval is the state of the quantum system. C.5) Second, every continuous function on the spectrum of H can be uniformly approximated by polynomials, from which the conclusion follows.
