Opracowywanie danych doświadczalnych - Wydział Fizyki PW

Treść skryptu i rozkład materiału

Dopiero pierwszy rozdział, który wprowadza zasady wyznaczania niepewności, wykorzystuje pojęcia, które zostaną wyjaśnione później. Sugeruję, abyś przeczytał scenariusz w dwóch etapach, najpierw przeczytaj rozdział 5 „Wyrażanie niepewności”, następnie przestudiuj podstawy matematyki (prawdopodobieństwo i statystyka matematyczna), a następnie wróć do rozdziału 5 i dokładnie go przestudiuj.

Model pomiaru, definicja pomiaru

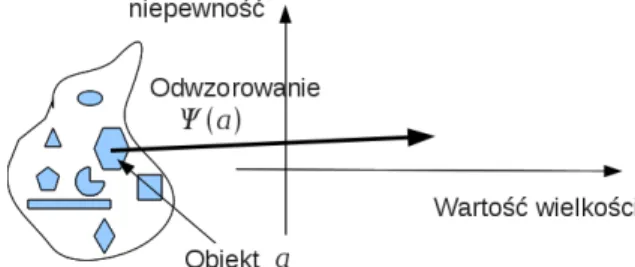
Czytając po raz pierwszy, można pominąć rozdziały matematyczne i po wstępie rozpocząć czytanie od rozdziału 5: „Wyrażenia niepewności”, w którym opisano zasady wyznaczania wartości i niepewności pomiaru. Odróżniamy więc wielkość oznaczoną jako Φκ od wartości wielkości Φκ(a), wartość wielkości jest wynikiem pomiaru wielkości Φκ dla przedmiotu a.

Fazy eksperymentu

• Planowanie eksperymentu pomiarowego
• Zorganizowanie zespołu badawczego
• Zestawienie układu pomiarowego i zapew-
• Wykonanie pomiarów
• Przetworzenie danych pomiarowych
• Ocena niepewności
• Interpretacja wyników pomiarów i wnioski 11
• Model obiektu
• Weryfikacja modelu

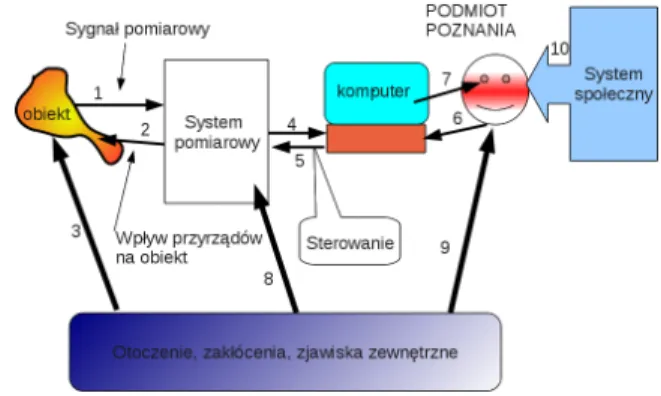
Przedmiotem badań (zwanym obiektem) może być dowolne ciało, proces, pole fizyczne lub zjawisko, które można wydobyć. Na podstawie modelu obiektu (czyli wiedzy o obiekcie) można rozwijać produkcję masową, jakość produkcji zależy od dokładności modelu i dokładności pomiaru.

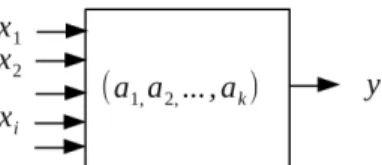
Schemat układu pomiarowego

Strategia eksperymentu

Strategie wyznaczanie parametrów modelu 18

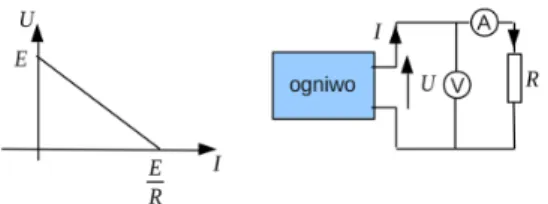
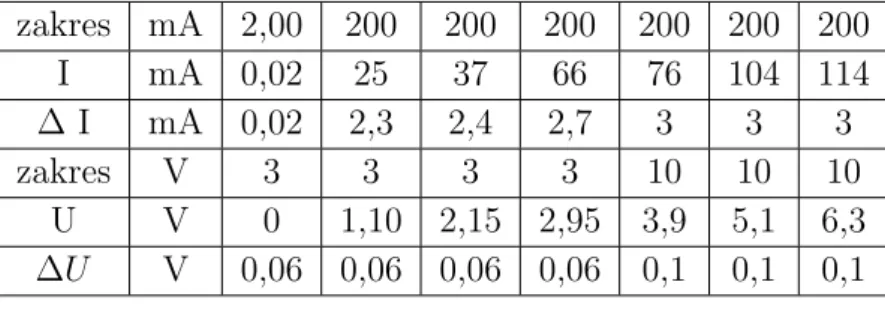
Przykładem pomiarów, w których odczyt przyrządu pomiarowego jest traktowany jako wartość pomiaru, jest pomiar masy wagą, pomiar prądu elektrycznego amperomierzem, pomiar braku napięcia woltomierzem lub pomiar temperatury za pomocą termometru. Załóżmy, że wykonano pomiary zależności natężenia prądu I od napięcia U dla miniaturowego opornika metalizowanego o mocy 0,25 W i wartości nominalnej 56 Ω z tolerancją.

Błąd, wartość prawdziwa, błąd systematyczny i

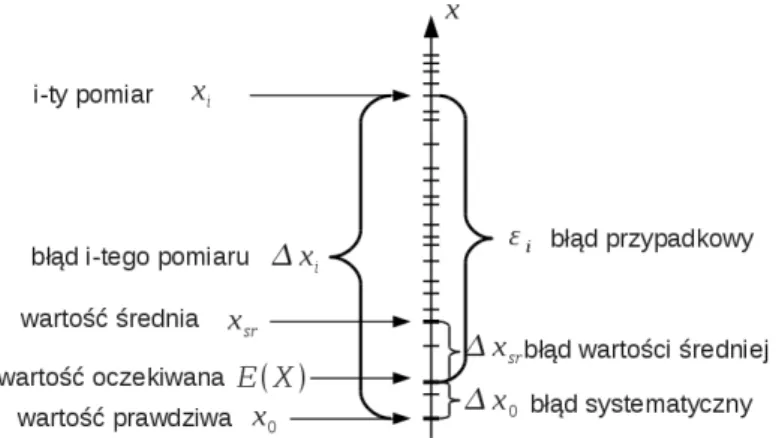
Zatem błąd losowy opisuje odchylenie od wartości oczekiwanej, natomiast błąd systematyczny – odchylenie wartości oczekiwanej od wartości prawdziwej, jak pokazano na rys. 6. Xxi (23) Błąd wartości średniej ∆xsr dla każdej serii pomiarowej jest inny, więc jest to zmienna losowa.

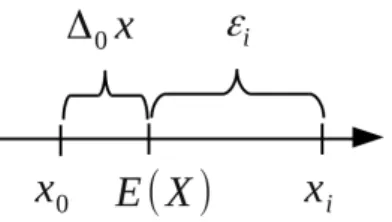
Modele niepewności i metody jej wyznaczania

Zwykle przyjmuje się, że błąd całkowity jest sumą błędów składowych różnych zjawisk (patrz Równanie (177) w sekcji 5.5). Zatem jeśli w opisie urządzenia podana jest wartość błędu: „błąd wynosi ∆x”, oznacza to, że błąd jest graniczny.

Elementy teorii pomiaru 29

Pomiar jako komparacja

Sygnał wyjściowy ma zwykle inny charakter niż sygnały wyjściowe, jest wyczuwalny zmysłami lub steruje układem kompensacji. Polega na porównaniu sygnału przetwarzanego przez przetwornik (czujnik, czujnik) ze wzorcem przetwarzanej wielkości (wyjściem przetwornika).

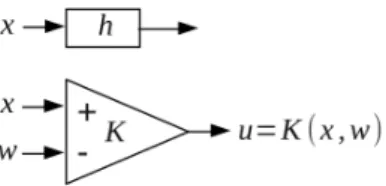
Teoria reprezentacji

• Struktura algebraiczna, relacje, działania . 34
• Pomiar idealny, reprezentacja liczbowa
• Środek i promień sumy przedziałów, propa-

Homomorfizm to mapowanie zachowujące strukturę, to znaczy mapowanie, które odwzorowuje porządek w jednym zbiorze na porządek w innym zbiorze i odwzorowuje akcję na akcję. gdzie < jest relacją pierwszeństwa w zbiorze M, + jest operacją w M. W następnym podrozdziale zostaną przedstawione dwa przypadki, pomiar idealny, gdy nie ma błędu pomiaru, oraz przypadek reprezentacji przedziałowej, gdy występują tylko błędy systematyczne. Reprezentacja interwałowa, błąd systematyczny Jeśli można pominąć zjawiska losowe, wynik pomiaru jest reprezentowany przez interwał.

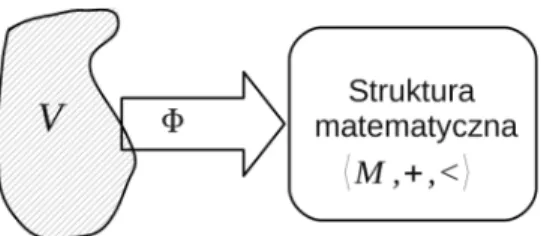
Podstawy teorii prawdopodobieństwa 39

Zmienna losowa, zbiór zdarzeń elementarnych

• Prawdopodobieństwo
• Zmienna losowa dyskretna

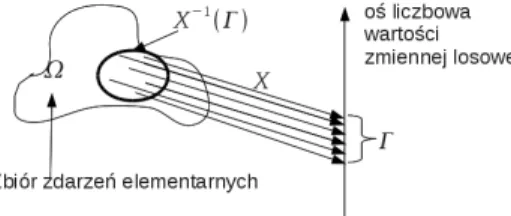
Podkreślmy, że założenie jest takie, że każde zaobserwowane zdarzenie (nazwijmy je A) jest podzbiorem zbioru zdarzeń elementarnych, tj. A⊂Ω. Pojęcie zdarzenia elementarnego oznacza, że ​​wszystkie zdarzenia nieelementarne mogą składać się ze zdarzeń elementarnych. W praktyce trudno jest ponumerować elementy zbioru zdarzeń elementarnych, a wygodniej jest posługiwać się wartościami wielkości charakteryzujących zdarzenia.

Jak wynika z zapisu, prawdopodobieństwo jest funkcją, która każdemu podzbiorowi zdarzeń elementarnych przypisuje wartość liczbową z przedziału [0,1]. Jeżeli zbiór zdarzeń elementarnych Ω jest przeliczalny (składający się z przeliczalnej liczby elementów), to zbiór 2Ω wszystkich podzbiorów Ω jest zawsze ciałem σ35. Formuła (49) oznacza, że ​​każdemu zdarzeniu A, rozumianemu jako podzbiór zbioru zdarzeń elementarnych Ω, przyporządkowane jest prawdopodobieństwo bycia liczbą z przedziału [0,1].

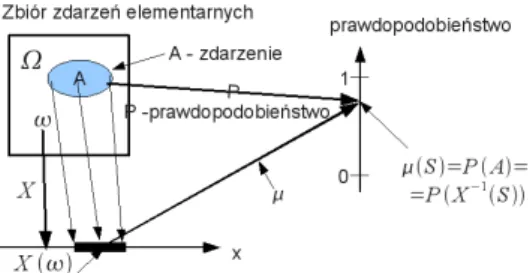
Niezależność zdarzeń i zmiennych losowych

Przypadek jednakowo prawdopodobnych zdarzeń

Rozkład zmiennej losowej

• Dystrybuanta

Najczęściej stosowanym rozkładem zmiennej losowej jest funkcja rozkładu, zwana także skumulowanym rozkładem prawdopodobieństwa [23], definiowana jako prawdopodobieństwo zdarzenia X(ω) ≤ x, tj. prawdopodobieństwo, że wartości zmiennej losowej są mniejsze lub równe x.

Zmienna losowa ciągła, gęstość rozkładu prawdo-

Większość wielkości fizycznych, takich jak masa, długość czy czas, to wielkości ciągłe, a opisywane przez nie zmienne losowe są ciągłymi zmiennymi losowymi. Prawdopodobieństwa, że ​​wartość zmiennej losowej jest równa całce, można zapisać jako różnicę wartości rozkładu F(b)−F(a), ponieważ ta różnica jest równa różnicy pól.

Wartość oczekiwana

• Wartość oczekiwana zmiennej losowej dys-
• Wartość oczekiwana funkcji zmiennej loso-
• Właściwości wartości oczekiwanej
• Przykłady obliczania wartości oczekiwanej 50

Oczekiwanie dyskretnej zmiennej losowej OczekiwanieE(X) to funkcja, która przypisuje liczbę zmiennej losowej X (opisanej rozkładem prawdopodobieństwa). Wartość oczekiwana jest parametrem modelu prawdopodobieństwa opisanego rozkładem prawdopodobieństwa pk i jest równa średniej ważonej o wagach równych prawdopodobieństwu pk. Wartość oczekiwana jest również nazywana wartością średnią i należy jeszcze raz podkreślić, że definicja w 3.7.1 uwzględnia, że ​​udział w sumie (68) jest proporcjonalny do prawdopodobieństwa tego zdarzenia.

Oblicz oczekiwaną wartość (EK) =EK energii kinetycznej EK = mv22, mając dany rozkład prawdopodobieństwa prędkości f(v):

Odchylenie standardowe – miara rozrzutu

• Odchylenie standardowe sumy zmiennych
• Odchylenie standardowe sumy zmiennej lo-
• Uzasadnienie wzoru na wariancję

Jeśli te zmienne są niezależne, to pi,j = pX,ipY,j, gdzie pX,i i pY,i są odpowiednio rozkładami X i Y. Dodanie stałej liczby do zmiennej losowej zmienia wartość oczekiwaną o tę liczbę (3.7.3), ponieważ dodanie stałej przesuwa cały rozkład (patrz właściwość opisana w rozdziale 3.7. Ponieważ błąd różni się od wartości mierzonej wartością prawdziwą x0 (tj. przy stałej wartości x x = x −x0 (x0- wartość prawdziwa)) odchylenie standardowe wielkości mierzonej jest równe odchyleniu standardowemu błędu: σ(x) = σ(∆x).

Całkowita odległość to suma składowych: P.. idi, a średnia ścieżka to średnia z wartości ścieżki di, gdzie każdy krok miał długość di. Wariancja jest więc średnią ważoną kwadratów odległości (xk − E(X))2 o wagach równych prawdopodobieństwom pk, gdzie xk=X(ωk). Na rysunku 19 przedstawiono odchylenie X−E(X) oraz wagę pk proporcjonalną do pola f(x)dx zaznaczonego na wykresie dla ciągłej zmiennej losowej.

Mediana, kwantyle

Mediana ma właściwość dzielenia zbioru obserwacji na pół: połowa obserwowanych wartości jest niższa od mediany, a druga połowa wyższa, mediana to kwantyl 0,5.

Najczęściej wykorzystywane rozkłady prawdopo-

• Rozkład dwupunktowy
• Rozkład dwumianowy
• Rozkład normalny
• Rozkład jednostajny
• Rozkład Weibulla

Wynik ten nie zależy od badanego rozkładu i opisuje niepewność zaobserwowanej empirycznie liczby wystąpień określonej wartości zmiennej losowej w dowolnym pomiarze. W fizyce statystycznej zwykle przyjmuje się, że wielkości fizyczne, takie jak prędkości cząstek, mają rozkład normalny. Jeśli uważamy, że zdarzenia z określonego obszaru mogą wystąpić z równym prawdopodobieństwem, używamy rozkładu jednorodnego, zwanego również rozkładem jednorodnym lub prostokątnym.

Rozkład jednorodny ma zastosowanie tam, gdzie można założyć, że wszystkie zdarzenia są jednakowo prawdopodobne. Jeżeli weźmiemy pod uwagę przyrząd pomiarowy o rozdzielczości lub błędzie granicznym ∆x, to można przyjąć, że błąd pomiaru wynikający z ograniczonej rozdzielczości ma rozkład równomierny w przedziale [−∆x,∆x]. Stosuje się go w przypadkach, gdy wartości zmiennej losowej (wartości pomiarowe) są dodatnie i istnieją przesłanki, by sądzić, że rozkład prawdopodobieństwa nie jest symetryczny.

Elementy statystyki matematycznej 60

• Konstrukcja histogramu w przypadku ob-
• Konstrukcja histogramu w przypadku ob-
• Estymatory wartości oczekiwanej
• Zasady doboru próby w badaniach staty-
• Własności wartości średniej z próby. Śred-
• Przykłady obliczania średnich
• Wartość oczekiwana i odchylenie standar-
• Estymator odchylenia standardowego w
• Rozstęp
• Estymacja przedziałowa, przedział ufności

Zwykle parametr opisujący przeżycie zależy od wieku osoby, w takim przypadku rozkład normalny nie może być użyty do opisania tego zjawiska. Średnia nie jest jedynym estymatorem wartości oczekiwanej, ale jest najlepszym estymatorem podczas badania zmiennej losowej o rozkładzie normalnym. Załóżmy, że powtórzymy obserwację zmiennej losowej X N razy o rozkładzie ciągłym f(x) lub dyskretnym p(xk) i otrzymamy próbkę losową x˜i (i = 1,.

E(Xn) = E(X) i σ(Xn) = σ(X) (132) Fakt, że X i Xn mają ten sam rozkład, nie oznacza, że ​​są to te same zmienne losowe (tj. X 6 = Xn), to dlatego, że X jest silnie skorelowane, podczas gdy Xn i Xm (które opisują kolejne pomiary) nie muszą być skorelowane. Estymacja przedziałowa, przedział ufności Tak jak poprzednio zakładamy, że wynikiem pomiaru jest v ), gdzie odchylenie standardowe σ(¯X) wartości średniej zostało zastąpione estymatorem (158).

Zasady wyznaczania wartości mezurandu i jego

• Estymacja wartości mierzonej
• Niepewność
• Metody wyznaczania niepewności
• Niepewność względna
• Klasa dokładności
• Metoda statystyczna oceny niepewności
• Niepewność rozszerzona
• Niestatystyczne metody szacowania nie-
• Wyznaczanie niepewności na podstawie da-
• Niepewność złożona (całkowita) w przy-
• Niepewność sumy dwóch wielkości - propa-
• Źródła błędów i składowe niepewności
• Niepewność funkcji dwóch zmiennych
• Budżet niepewności
• Zasady zapisu wyniku pomiaru

Niepewność rozszerzona obliczona ze wzoru (162) opisuje tylko składową niepewności reprezentującą rozrzut wyników pomiarów. Składowa związana z przyrządem pomiarowym, obliczona na podstawie danych producenta, nazywana jest niepewnością instrumentalną lub instrumentalną. Dodatkowo przyjmiemy, że składowe błędu wynikające z poszczególnych składowych są niezależne, tak że kwadrat odchylenia standardowego sumy zmiennych losowych jest równy sumie kwadratów odchyleń standardowych (wzór (86) w rozdziale 4).

Aby określić składową związaną z zaburzeniami losowymi, należy powtórzyć pomiar co najmniej 12 razy i obliczyć odchylenie standardowe średniej. Wzór (182) jest konsekwencją założenia, że ​​składowe błędu we wzorze (181) są niezależnymi zmiennymi losowymi. Przyjmuje się, że błędy są addytywne (dla pomiarów bezpośrednich jest to opisane wzorem (177)), a niepewność podlega regułom składu wariancji.

Metoda najmniejszych kwadratów 89

Kryteria dopasowania rodziny funkcji do danych

Zakładamy, że gdyby pomiary były doskonałe, zależność byłaby opisana funkcją z rodziny fα (np. jedną z funkcji liniowych). Aby znaleźć równanie najlepiej pasujące do danych pomiarowych, należy zastosować metody statystyczne (nie może to być metoda polegająca na rozwiązaniu układu równań typu yi =fα0(xi)). Jeżeli niepewność każdej wartości yi jest różna i równa U(yi), miarę χ2(α) należy zmodyfikować tak, aby punkty pomiarowe o dużych niepewnościach miały niewielki wkład w wyznaczoną χ2(α).

56 Można wykazać, że taka miara daje najlepsze dopasowanie (w sensie najmniejszego błędu) parametrów, jeśli rozkład błędu jest normalny [5]. Spójrzmy na najprostszy przykład dopasowania jednoparametrowej funkcji liniowej f(x) = ax do danych pomiarowych {xi, yi}Ni=1 wykonanych z tą samą niepewnością (wszystkie u(yi) są identyczne). Zakładając, że każdy pomiar yi miał niepewność u(yi) = σi, należy zastosować warunek minimalizacji funkcji (196) i otrzymujemy:

Testowanie hipotez statystycznych 95

Moc testu, błąd drugiego rodzaju

Taki rozkład może znacznie różnić się od rozkładu P(A|H0), a obszar krytyczny dla odrzucenia hipotezy H0 może leżeć w obszarze nieodrzucenia hipotezy alternatywnej H1.

Test zgodności chi-kwadrat

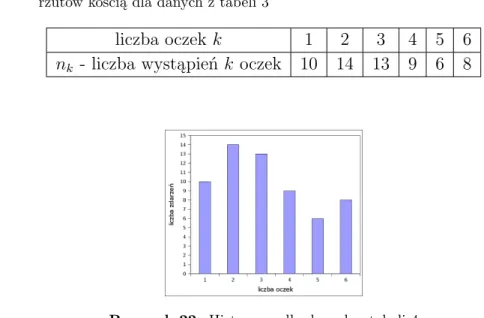
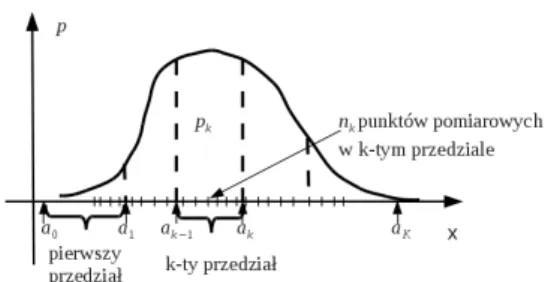
Jeżeli liczba wystąpień nk pomiarów w k-tym przedziale jest większa niż 10, to można przyjąć, że zdefiniowana w ten sposób zmienna χ2 ma rozkład chi-kwadrat z K −1 stopniami swobody (stąd test nazywa się „test chi-kwadrat hipotezy rozkładu statystycznego”) [16]. W celu wyznaczenia nk i pk osie liczb rzeczywistych reprezentujących wyniki pomiarów dzieli się na K przedziałów [ak−1, ak], k = 1 , Test hipotezy rozkładu normalnego szumu generowanego przez diodę Zenera Seria pomiarów napięcia generowanego przez diodę Zenera (generator szumu wykorzystujący diodę Zenera) za pomocą przetwornika analogowo-cyfrowego.

Zadaniem jest zweryfikowanie hipotezy o rozkładzie normalnym procesu poprzez wygenerowanie zestawu danych, które traktujemy jako losową próbkę badanego rozkładu. Aby zweryfikować hipotezę, że dane pomiarowe są losową próbą badanego rozkładu, w tym przypadku normalnego, należy porównać wartość statystyki χ2 obliczoną ze wzoru (216) z wartościami krytycznymi rozkładu χ2 dla stałe . 10) - co dziesiąta wartość pomiaru z tabeli 5 (ostatnia kolumna), F(y) - funkcja rozkładu rozkładu normalnego dla wartości w kolumnieak,pk - prawdopodobieństwo dla przedziałów (ak−1,ak)wg wzór (217) ,χ2 – wartości cząstkowe statystyki χ2 ze wzoru (216), ostatni wiersz kolumny χ2 – suma składowych zapisanych w kolumnie. Można zatem argumentować, że przy poziomie istotności 0,05 nie ma podstaw do odrzucenia hipotezy, że dane pomiarowe są próbą losową o rozkładzie normalnym.

Pojęcia podstawowe i ważniejsze definicje 102

Wzorce głównych wielkości fizycznych

• Czas
• Długość
• Masa
• Natężenie prądu i napięcie elektryczne
• Rezystancja elektryczna
• Temperatura
• Światłość
• Ciśnienie

Wielkości fizyczne dzielą się na pierwotne i wtórne, do pierwotnych należą czas, długość, masa, prąd, temperatura, kąt i jasność [3]. W 1983 roku XVII Generalna Konferencja Miar i Wag ustaliła, że ​​wzorcem metra jest odległość przebyta przez światło w próżni w s. Temperatura jest parametrem stanu układu fizycznego określonym w termodynamice stanu, który jest zwana zerową zasadą termodynamiki [4]: ​​dwa ciała będące w równowadze termicznej mają tę samą temperaturę59.

Jednostką jasności jest kandela (cd), jednostką strumienia świetlnego jest lumen (lm), a jednostką kąta bryłowego jest steradian (sr). Kandela to jasność źródła emitującego promieniowanie monochromatyczne o częstotliwości 5,4⋅1014 Hz i mocy na steradian równy 6831 Wsr. Starym standardem dla kandeli było światło emitowane przez doskonałą czerń podgrzaną do temperatury topnienia platyny.

Podstawowe przyrządy pomiarowe

• Suwmiarka
• Mikrometr
• Waga
• Częstościomierz i zegar
• Multimetr

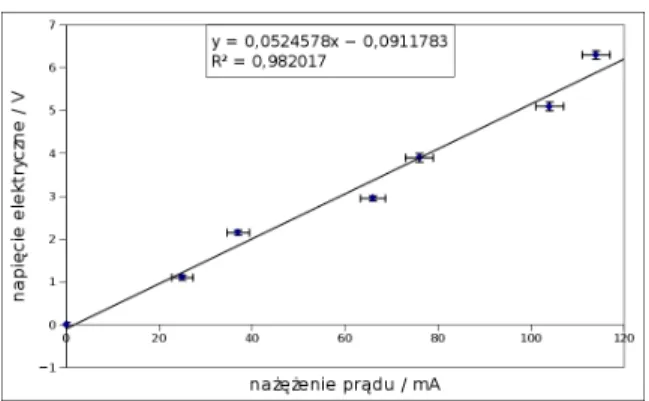
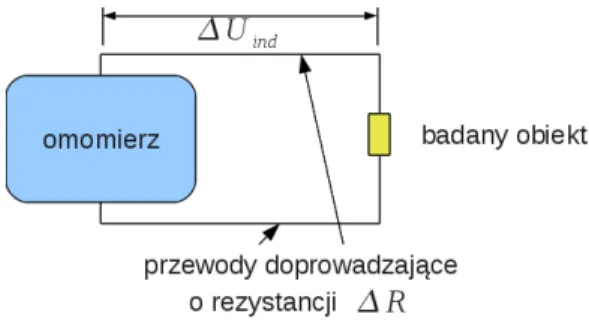
Mikrometr jest zwykle tak skonstruowany, że jeden obrót śruby powoduje przesunięcie o 0,5 mm, a podziałka na śrubie pozwala na odczyt z dokładnością do 0,01 mm. 9.3.3. Jeśli nie zastosujemy się do tych zasad, błąd pomiaru może wzrosnąć wielokrotnie, nawet do kilku mg. Wyniki pomiarów nanieść na wykres U=f(I), zaznaczyć słupki błędów, narysować (wzrokowo) linię prostą najlepiej pasującą do danych i określić błąd (graniczny) wyznaczenia rezystancji na rysunku.

Długość cienia belki wynosiła h1 = 1m, rozmycie cienia ∆h1 = 1cm, natomiast długość cienia budynku h2 = 10m, a rozmycie tego cienia ∆h2 = 10cm. cień budynku taśmą mierniczą o długości 1 cm. Wyznacz całkowitą niepewność przy założeniu, że rozmycie cienia można traktować jako błąd graniczny, a składowe błędów są niezależnymi zmiennymi losowymi (a więc sumowanie odbywa się zgodnie z pierwiastkiem kwadratowym). Klasa obu przyrządów wynosi 0,2% (błąd przyrządu cyfrowego składa się z dwóch składowych: błędu kwantyzacji i błędu systematycznego wynikającego z klasy przyrządu).