The lecture presents new results and hypotheses about the structure of the cut locus in Euler's elastic problem. Its identity with the curvature of a cloth completed by the weight of the included liquid.
On identical resonance in stability problem of pendulum periodic motions of a heavy rigid body in the Hess case
Centrally symmetric periodic solutions in Hill problem
The condition for the existence of generating solutions is written in the form F(e, p, q) sink= 0, (4) where is an eccentricity, is an argument of the center, p+q ∈ {1,2,4}. The specificity of the generalized Hill problem leads to the proof that it is possible to successfully continue such generative solutions to periodic orbits of the Hill problem whose semi-major axes are less than 1, or, equivalently, for p, q ∈N.
The Chaplygin ball on a rotating table
Moreover, it was shown in [1] that in the system under consideration one can construct an integral similar to the Jacobi integral in mechanics. For the system (7) to be integrable, we also need (with suitable parameter values of the system) pairs of tensor invariants, for example two integrals, or an integral and a symmetry field.
Vortex and mass dynamics over surfaces
Maxwell laws, geometry and surface topology
Symplectic invariants of integrable Hamiltonian systems
Strange attractors in the problem of the motion of a rigid body in a fluid
Borisov was supported by the Ministry of Education and Science of the Russian Federation under grant.
Rational integrability of trigonometric polynomial potentials on the flat torus
On a class of integrable Lotka–Volterra equations
Sub-Finsler problem on the Heisenberg group
Billiards within quadrics and extremal polynomials
Moving energies and integrability of symmetric mechanical nonholonomic systems with affine constraints
Time Reparametrisations in Nonholonomic Dynamics and Integrability of the n -Dimensional Rolling Ball Over a
Sphere
Dynamics of a homogeneous sphere on a rotating plane
Also, an experimental study of ball movement on an inclined and horizontal plane was carried out using high-speed cameras and modern computer data processing methods. The comparison of numerical and experimental results has shown a good qualitative agreement and has made it possible to determine the values of the coefficient of friction for the pair of materials used.
On the locomotion of a slider with internal moving masses
Prym varieties and generalisation of Jacobi–Mumford systems
For the development of the dynamic rolling model, the nonholonomic rolling model [11, 12] is modified with the addition of viscous rolling friction similarly to the work [10]. Dynamic model of rolling friction of spherical bodies on a no-slip plane // Russian Journal of Nonlinear Dynamics, 2017, vol.

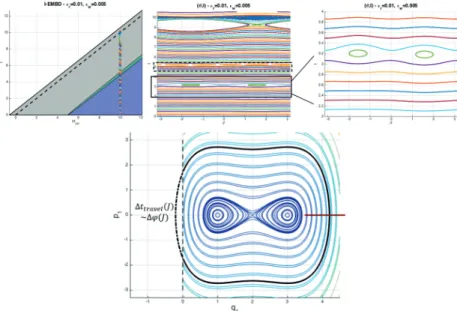
Liouville foliation of topological billiards, bounded with segments of confocal quadrics in Minkowski plane in terms
Liouville foliation of topological billiards bounded by segments of confocal quadrics in the Minkowski plane in terms. Fomenko-Zieschang invariants for different topological billiards: billiards in the left column and corresponding invariants in the right column. Topological invariants for elliptical billiards and geodesics on ellipsoids in Minkowski space // Journal of Mathematical Sciences, 2017, vol.
Topological classification of billiards in locally planar domains bounded by arcs of confocal quadrics// Sb.
Any three-dimensional bifurcation of an integrable Hamiltonian system is a neighborhood of the critical level of
Every three-dimensional bifurcation of an integrable Hamiltonian system is a neighborhood of the critical level of. A topological classification of billiards in local planar domains bounded by arcs of confocal quadrilaterals // Matematika Sbornik.
Topological invariants of Liouville foliation for analogs of the Kovalevskaya integrable case
A nonholonomic model of the Paul trap
The results of linear stability analysis are compared with the known results obtained earlier for the classical Brower problem. A three-dimensional Poincar'e map generated by the phase flow of the problem of interest is numerically investigated and the existence of a region of bounded trajectories in the vicinity of the saddle point of the paraboloid is shown. It is shown that a similar problem of a ball rolling on a rotating paraboloid, considered within the framework of the rubber model, can be reduced to a Lagrangian system with the Lagrangian.
Qualitative analysis of the dynamics of two vortex lattices
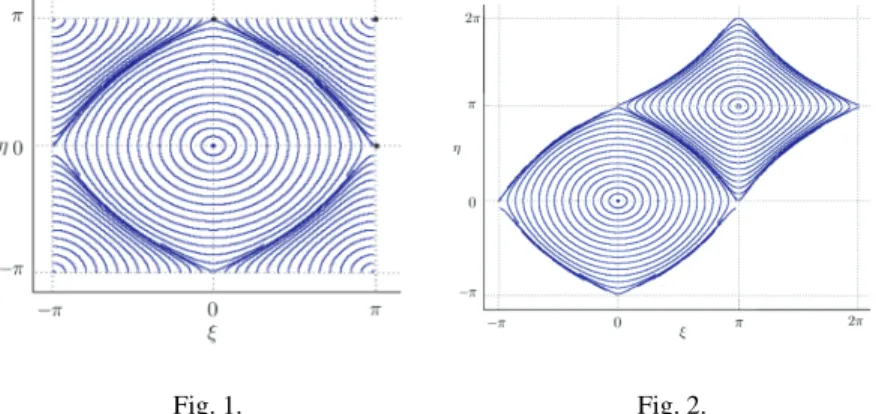
In this case, the paths in absolute space become discontinuous, and different parts of the path correspond to different parts of the path of different vortices of the same lattice. To reconstruct the trajectory of a vortex from a particular vortex lattice, it is necessary to consider the reduced system as a system on the plane (without taking into account periodicity) (see Figure 2), then the trajectories in absolute space will be continuous. In Figure 1, dots indicate the positions of three fixed points: two unstable and one stable, which correspond to stationary configurations of vortices.
From the similarity of the trajectories of the reduced system with trajectories in absolute space, as well as the boundary of the trajectory in the phase portrait, the boundary of the vortex trajectory follows.
Stabilization of the motion of a spherical robot using feedbacks
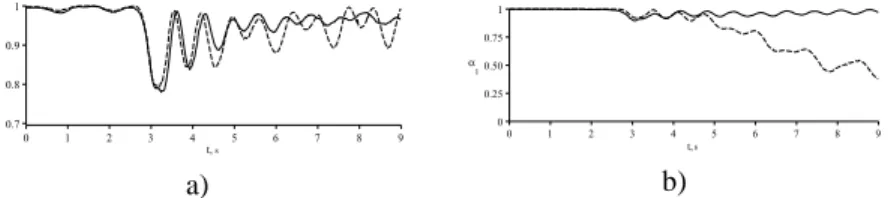
2a and 2b respectively. γ3 and α1 are the components of the basic orthogonal vectors that determine the orientation of the combined-type spherical robot. The time dependence of the components γ3 and α1 during the stabilization of the motion of the combined-type spherical robot is shown as solid lines in Fig. Videos showing the movement of the combined-type spherical robot can be found at: https://www.youtube.com/.
Non-holonomic dynamics and control of a spherical robot with an internal omniwheel platform: theory and experiments // Proceedings of the Steklov Institute of Mathematics, 2016, vol.
Vortex pairs on genus zero surfaces: stability of equilibria and the triaxial ellipsoid
The system is invariant with respect to the Moebius transformation S2. ii) Every equilibrium pair in Σ × Σ can be represented by an antipodal pair (north, south) in the sphere, even if Σ has no symmetries at all. iii) Furthermore, if Σ has antipodal symmetry X→ −X, then the antipodal pairs form an invariant submanifold. We analyze the stability of the balance of pairs placed at the end points of the three axes. The conformal mapping from ellipsoid to sphere uses confocal square coordinates in the ellipsoid and sphero-conical coordinates in S2.
In the limits → 0, composing with the stereographic projection of the sphere, it reproduces the well-known conformal map from the elliptic region to the unit disk.
Instability, asymptotic trajectories and dimension of the phase space
Realization of Jordan–Kronecker invariants by Lie algebras
The Jordan–Kronecker invariants of a pair of compatible Poisson brackets are: . 1) number of different eigenvalues λi of Jordan blocks, 2) number and sizes of Jordan blocks for each eigenvalue λi, 3) number and sizes of Kronecker blocks. We are interested in the Jordan–Kronecker invariants for the pencil shift of arguments on Lie coalgebras. The constraints are derived from the canonical form of the compatible non-degenerate Poisson bracket described in [4].
Smale–Williams attractor in a system of alternately oscillating coupled Froude pendulums
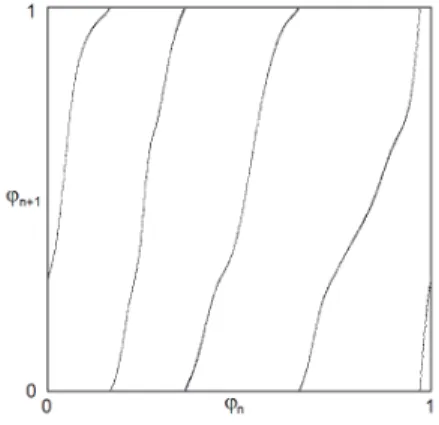
Consequently, as the second pendulum approaches sustained self-oscillation, its phase appears to double compared to the initial phase of the first pendulum. 2 shows a diagram for the phases determined on the final parts of the successive stages of excitation of one of the pendulums, obtained in numerical calculations for a sufficiently large number of modulation periods. A diagram showing the phase transformation in successive stages of operation of one of the pendulums.
Its value is close to a constant equal toln which agrees with the approximate description of the phase variable from the expanding circle map.
Modelling and bifurcation dynamics of a rattleback situated on vibrating platform
In this work there are analyzed dynamics of the ratchet placed on vibration translation in three directions inclined base, possibility to move uphill of the stone and influence of specific elements of contact forces on bifurcation dynamics of the system. 2 shows two bifurcation diagrams of the teeter-totter, where frequencyωzof vibrations of the base in a direction perpendicular to its surface with constant acceleration amplitude plays a role of bifurcation parameter and whereω3 is a component along axis x3 of body-fixed frame of reference of angular velocity of the body. 2a a bifurcation diagram is presented corresponding to friction model considering finite size of the contact (bT =bM = 1), while Fig.
Dry friction model in the rolling problem of rigid bodies // Journal of Applied Mathematics and Mechanics, 1998, vol.
First integral and exact solutions of the Duffing – Van der Pol equation
Superintegrable Bertrand natural mechanical systems
Self-acceleration of Chaplygin sleigh
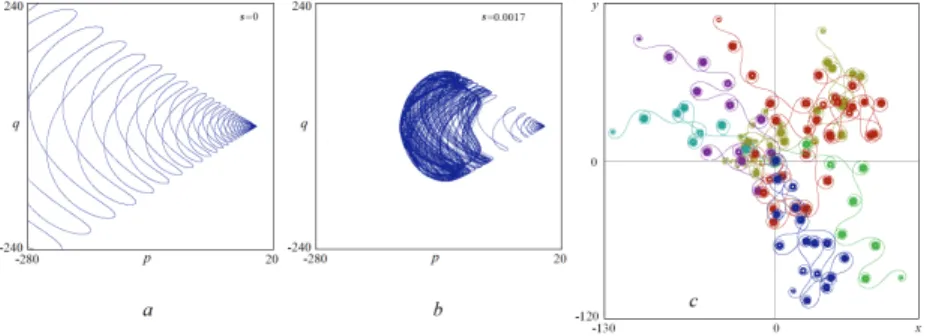
One mechanism, observed with small oscillations of the internal mass, leads to a regular unidirectional motion. Another mechanism is effect of parametric instability observed when the moving internal mass is of value comparable to the mass of the platform; this leads to oscillatory movements of the sled. So, the momentum asymptotically follows the power law1/3, and the same is true for the translational velocity of the sled.
Unbounded acceleration of the sled (a) and bounded acceleration where the trajectory approaches a chaotic attractor (b) accompanied by random walk in the laboratory frame (c).
Dynamics of constrained many body problems in constant curvature two-dimensional manifolds
The Chaplygin sleigh with parametric excitation: chaotic dynamics and nonholonomic acceleration
The last four quantities are given functions of time, which are expressed in system parameters as follows:. In the general case, system (4) has no additional tensor invariants (first integral, invariant measure). Since in this case the dependence on time is periodic, system (4) generates a Poincare map of the plane after each period.
Chaotic and quasi-periodic oscillations – the system has a strange attraction, which can coexist with invariant tori.
Sub-Riemannian geodesics on the group of motions of Euclidean space
Liouville foliation topology of integrable billiard with nonconvex angles on the boundary
Generalisation of Chaplygin’s reducing multiplier theorem with an application to multi-dimensional nonholonomic
Intermediate integrable model: a strategy to apply the averaging method
For small ε, the behavior of the variables σ and pin solutions of system (2) can be described as a Cassini cycle with slowly changing parameters sh, ω. Using these evolution equations, we draw phase portraits in each of the regions and analyze how the trajectories cross the separatrixes that exist in the intermediate system. Further analysis of possible transitions through separatrixes allows us to classify evolutionary scenarios according to transitions between regions.
This work was supported by RFBR, grants Simulation of the attitude movement of large-sized space debris object”.
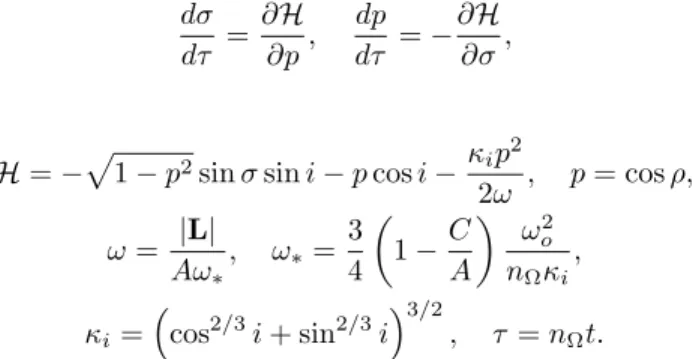
On semi-local classification of non-degenerane rank 0 singularities for integrable Hamiltonian systems with three
Bi-homogeneity and integrability of rational potentials
Geometric theory of flexible and expandable tubes conveying fluid
On the optimal control of a rolling ball robot actuated by internal point masses
On some near integrable impact systems
The return map is defined by a cross-section Σ (red line on right panel) corresponding to the crossing branch in the subphase space of the Duffing oscillator. For regular bang-bang trajectories, the phase portrait on the smooth surface is described by the maximized Hamiltonian or Pontryagin maximum principle. For other types of extremal trajectories, second-order optimality condition is applied, and upper bounds on the number of links are obtained.
Probabilistic properties of random Hamiltonian systems
Canonoid and Poissonoid transformations, symmetries and bi-Hamiltonian structures
Scattering maps and global instability in Hamiltonian systems
Dynamics and Control of UAV with Variable Geometry
We then leave in the right-hand sides of the equations only those terms that explicitly depend on the chosen control parameters u, moving all other terms to the left-hand side. Calculation of the left side of (4) requires the estimates of the state vector variables rI,qIB,r˙I,ΩBand the controller (3)'s output – ¨r(t)andΩ˙ (t). By substituting the balance equations in (4), we obtain a system of eight equations that can be divided into two subsystems of four equations, both of which allow an analytical solution with respect to the control parameters. 5) whereεT is the balance equation tuning parameter, Biis a quadratic form in the components of F and T.
If the solution is not found, we can go back to the controller (3) and scale its output.
Dynamics of Stars in “Disk+Halo” Galaxy Model
On the integrability of non-autonomous Li´enard–type equations
Explicit integration the second critical subsystem for the integrable case of Adler and van Moerbeke in rigid body
Explicit integration is the second critical subsystem for the integrable case of Adler and van Moerbeke in a rigid body. Note that the expression forK differs from the forms of the auxiliary integral used in the original works devoted to the proof of algebraic integrability (see [3], [5]). In the paper [10], invariant relations are obtained in which the rank of the momentum map is 1.
In this report, we present a specific setαin the second critical subsystem for the rest of the edges of the bifurcation diagram.
Planar three-body problem in the pairwise strong potential
Nonholonomic constraints and limit cycles in the swimming of a Joukowski foil
Draft classification of 2D and 3D superintegrable systems with natural Hamiltonians and higher order integrals of
The Liouville foliation of nonconvex topological billiards bounded by arcs of confocal conics
Description of singularities for billiard systems bounded by confocal ellipses or hyperbolas, Moscow Univ.
Vortex streets and solitons
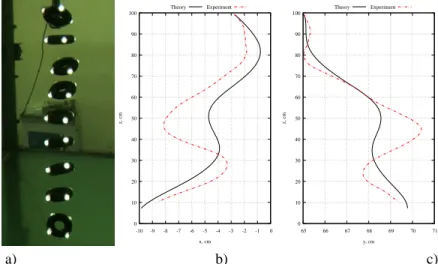
Determination of the hydrodynamic resistance of a toroidal body using experimental data
To determine the coefficients of use,gi and vectorsa,b, we reduce the deviation between the calculated trajectory and the experimental one by using a real coded genetic algorithm. Vetchanin was supported by the Ministry of Education and Science of the Russian Federation within the framework of the grant and grant RFBR no. Identification of Toroidal Body Motion Model Parameters Using Experimental Data, Russian Journal of Nonlinear Dynamics, 2018, vol.
Relative periodic solutions of the N -vortex problem via the variational method
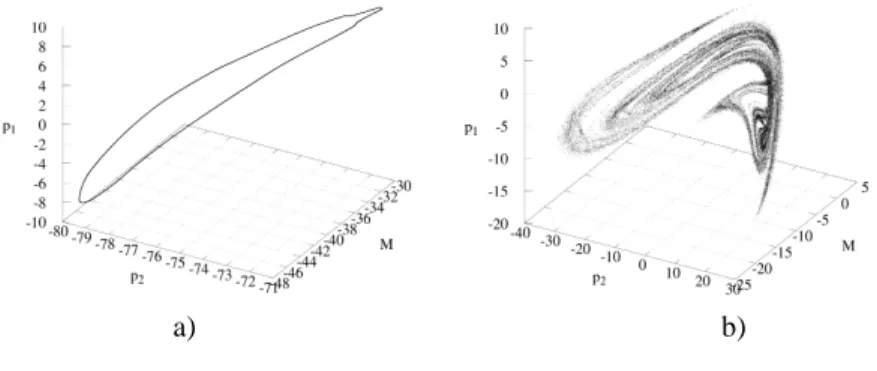
Acceleration of a Chaplygin Top Using Rotors
In this plane, each point corresponds to the average energy value of the system for a sufficiently large time interval T, divided by this time interval, and has a corresponding color. Such a diagram for G= 5 is shown in Figure 1b. a) Time dependence of system energy with initial conditions (3) and parameters (2). The second is the solid red region, which corresponds to linear energy growth.
And under all other initial conditions corresponding to the third region, due to chaotic regimes, the system exhibits either a linear growth of the energy (red regions) or chaotic motion (blue and yellow regions).
