Essas análises, aliadas aos estudos clínicos, podem oferecer mais uma alternativa aos órgãos de saúde e auxiliá-los na elaboração de ações que possam efetivamente reduzir o número de suicídios. Os autores alertam para o aumento da taxa de suicídio no mesmo período em que a austeridade econômica é imposta à população. Os dados sobre as taxas de suicídio por gênero foram obtidos no banco de dados do Instituto de Pesquisa Econômica Aplicada (IPEA) e do Instituto Brasileiro de Geografia e Estatística (IBGE).
Para o ajuste dos modelos, foi utilizada a metodologia de Box & Jenkins, que consiste em modelos autorregressivos integrados com médias móveis, para as séries de taxas de suicídio em Minas Gerais.
Séries temporais
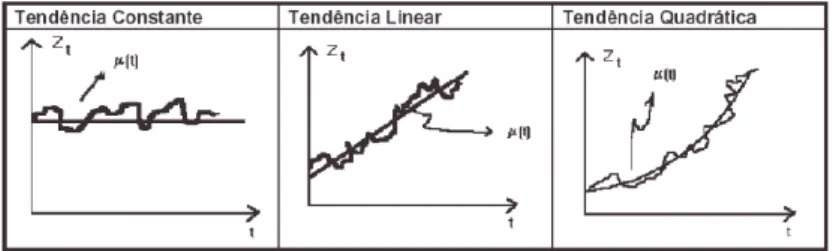
Segundo Morettin e Toloi (2006), uma das suposições mais frequentes feitas sobre uma série temporal diz respeito à sua sazonalidade, ou seja, se o seu comportamento, ao longo do tempo, evolui aleatoriamente em torno de uma média. A forma mais tradicional de analisar uma série é decompô-la em componentes de tendência, ciclo e sazonalidade. A tendência de uma série indica se ela aumenta, diminui ou permanece estável e a velocidade dessas mudanças.
Segundo Campos (2008), uma tendência em uma série temporal é a mudança gradual observada através da mudança de seus valores ao longo do tempo e que se preserva durante o movimento dos componentes dos ciclos, sazonalidade e fatores aleatórios. Segundo Fonseca, Martins e Toledo (1985), o componente cíclico é entendido como a parte da série temporal que representa um movimento em torno da tendência ao longo do tempo. A análise espectral é uma decomposição de séries temporais em componentes cíclicos, e isso pode ser feito usando transformadas de Fourier ou wavelets.
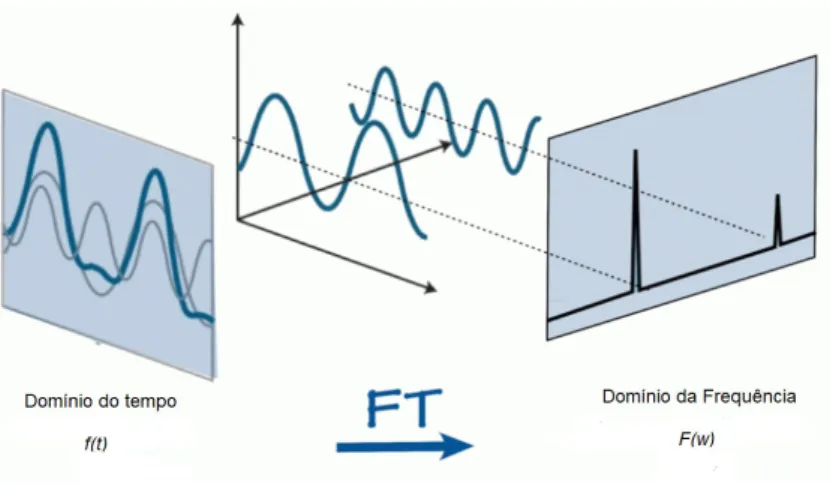
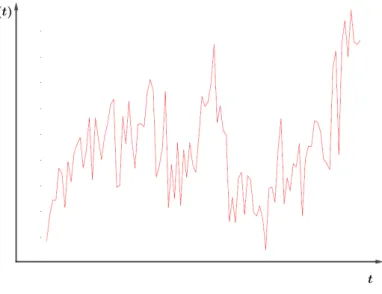
Na Figura 3, uma série temporal decomposta em seus componentes cíclicos é mostrada, usando a transformada de Fourier (FT). A sazonalidade em uma série temporal, muitas vezes confundida com ciclos, são as oscilações para cima e para baixo que ocorrem regularmente em um determinado período de tempo. Ao estudar uma série temporal, estamos interessados em analisar e modelar a série, a fim de descrever e verificar as características mais relevantes e possíveis relações com outras séries.
Metodologias estatísticas de previsão
Estacionalidade
Uma das suposições mais comuns sobre uma série temporal é que ela é estacionária, ou seja, ela se desenvolve aleatoriamente no tempo em torno de uma média constante, refletindo alguma forma de equilíbrio estável (MORETTIN; TOLOI, 2006). Uma série temporal pode ser estacionária por um longo ou curto período de tempo, se mudar de nível ou inclinação, então é não estacionária. Consequentemente, uma série não estacionária apresenta ambas as componentes, tendência e sazonalidade, ou uma delas (SÁFADI, 2004).
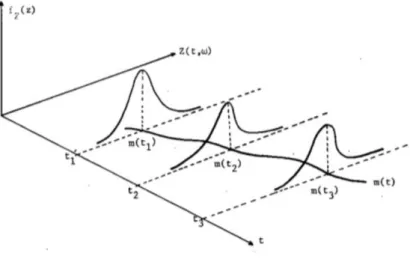
Segundo Morettin e Toloi (2006), há uma sazonalidade fraca, uma série ampla de segunda ordem e uma série forte e mais rígida. Um processo estocástico Z = Z(t), t∈T, é dito estritamente estacionário se todas as distribuições de dimensão finita permanecem as mesmas sob translações de tempo, ie. A ideia inicial para analisar uma série temporal, ou seja, o primeiro passo é construir um gráfico da série para entender características importantes como tendência e sazonalidade.
O teste Augmented Dickey Fuller (ADF) relaciona a presença de uma tendência à existência de uma raiz dentro de um círculo unitário no polinômio autorregressivo. Segundo Dickey e Fuller (1979), o teste é utilizado para verificar se a série é estacionária, por meio do estudo das raízes dos operadores atrasados dentro de um círculo de raio um. Uma série temporal é estacionária se as características de sua média, variância ou covariância não variam ao longo do tempo, ou seja, é estacionária se evolui ao longo do tempo dentro de uma média constante, (GUJARATI; PORTER, 2011).
Função de autocorrelação
Um dos pressupostos do teste afirma que as variáveis em cada amostra devem ser independentes e que as amostras são independentes entre si, o que não ocorre em séries temporais.
Função de autocorrelação parcial
Metodologia Box & Jenkins
Etapas da modelagem
Ao utilizar modelos de Box & Jenkins, com o objetivo de fazer previsões em séries temporais, a primeira etapa consiste em identificar o processo aleatório que gera os dados e, a seguir, estimar os parâmetros que os caracterizam e verificar se as hipóteses do modelo são atendidas. Caso contrário, uma nova fase de identificação deve ser considerada até que o teste de hipóteses seja finalmente satisfatório, permitindo fazer previsões. i) Identificação do modelo. A identificação do modelo ARIMA usa técnicas que podem identificar a estrutura do modelo para permitir a identificação dos valores p, d e q que caracterizam o processo estocástico.
Para que a utilização do modelo seja eficaz na predição da variável dependente sob investigação, o pesquisador deve primeiramente examinar os pressupostos da regressão, bem como identificar as consequências de sua violação. O AIC avalia o ajuste do modelo pelo método da máxima verossimilhança, determina os logaritmos das razões comparando os modelos e penaliza os modelos com os parâmetros utilizados (GUJARATI; PORTER, 2011). Os dados sobre o número de suicídios por gênero no estado de Minas Gerais, entre 1992 e 2019, foram obtidos no banco de dados do Instituto de Pesquisa Econômica Aplicada (IPEA, 2020), vinculado ao Ministério da Economia.
Dados relativos à população por sexo no estado de Minas Gerais, também entre 1992 e 2019, foram obtidos por meio de estimativas feitas pelo Instituto Brasileiro de Geografia e Estatística (IBGE, 2010). Os testes de Dickey Fuller (ADF) e Kruskall-Wallis aumentados foram aplicados para tendência e sazonalidade, então as funções de autocorrelação (f ac) e autocorrelação parcial (f acp) na série livre de tendência foram analisadas para estimar a ordem do modelo. Nesta seção, os modelos de adaptação são obtidos utilizando a metodologia de Box et al. 1994) com o objetivo de fazer previsões para as taxas específicas de suicídio por sexo nos estados de Minas Gerais, para que ações sociais sejam direcionadas a esse tema.
Identificação dos modelos
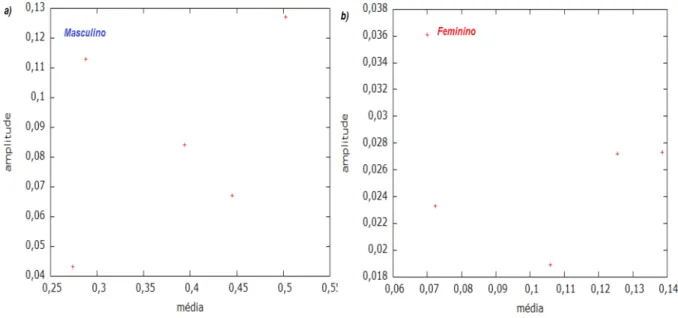
Para verificar a necessidade de transformar os dados nas séries, foram feitos gráficos de amplitude versus média mostrados na Figura 9. Verificou-se que não houve necessidade de transformar os dados, pois as médias não são diretamente proporcionais às amplitudes. Essas informações podem ser observadas analisando o gráfico da Figura 9, onde as séries foram divididas em subgrupos de cinco observações consecutivas, e para cada grupo são calculadas médias e amplitudes com o objetivo de verificar visualmente a necessidade ou não da transformação logarítmica no Series. Em seguida, a série foi submetida ao Augmented Dickey Fuller Unit Root Test (ADF) para verificar a existência ou não de nível sazonal.
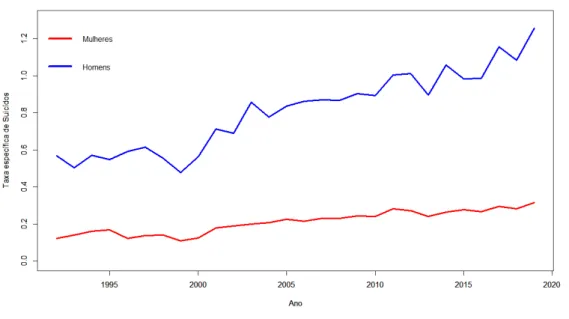
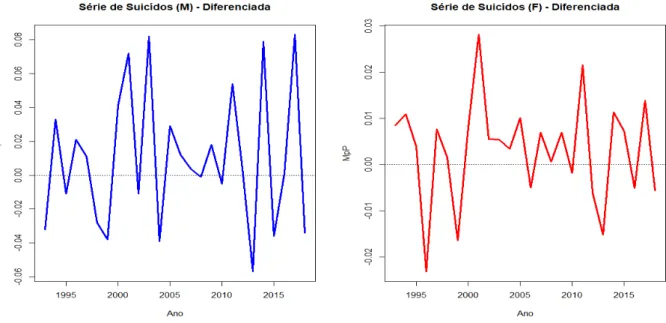
A Tabela 1 apresenta os resultados dos testes, que mostram que as séries não são estacionárias, ou seja, a taxa de suicídio por 10.000 habitantes tem aumentado ao longo dos anos para ambas as populações (mulheres e homens). Após a aplicação da primeira diferença, o gráfico da Figura 10 mostra que as séries diferenciadas apresentam influências sazonais. A Tabela 2 mostra os resultados dos testes, indicando que as séries diferenciadas são estacionárias, portanto as séries são integradas na ordem d = 1.
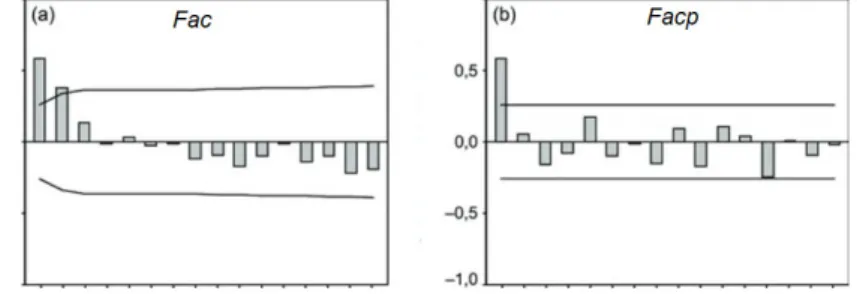
A próxima verificação realizada foi a presença ou ausência de sazonalidade, para a qual foi aplicado o teste de Kruskall Wallis, apresentado na Tabela 3, ao nível de significância de 5%, concluímos que temos evidências estatísticas de que as séries não possuem sazonalidade. Na Figura 11 são apresentadas as funções de autocorrelação e autocorrelação parcial para as séries de suicídios masculinos e femininos em Minas Gerais. As funções de autocorrelação, Figura 11, mostram a correlação existente no tempo com a mesma série defasada em relação ao tempo inicial, ou seja, há uma dependência temporal da taxa específica de suicídio ao longo do tempo.
Estimação dos modelos
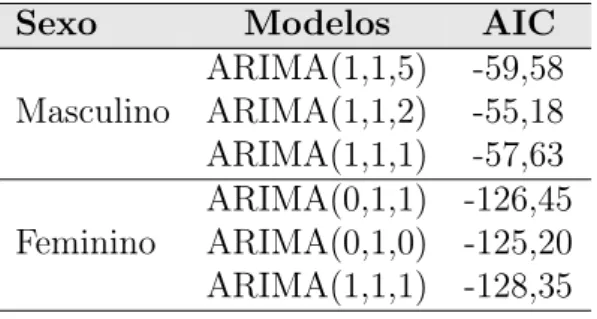
Ao analisar a Tabela 4, o critério AIC mostra que os melhores resultados foram o modelo ARIMA(1,1,5) para a série masculina e ARIMA (1,1,1) para a série feminina. A Figura 13 mostra gráficos que mostram o poder preditivo de cada série quando as taxas específicas de suicídio são comparadas com os valores previstos pelos modelos ajustados. As previsões feitas usando o modelo ARIMA (1,1,5) para a série masculina e ARIMA (1,1,1) para a série feminina são próximas entre si.
Verificação dos modelos
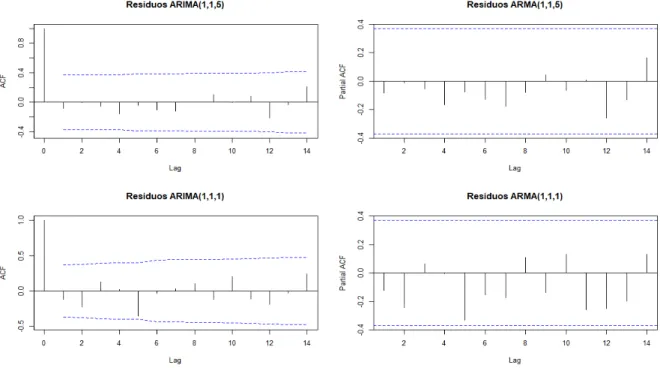
A Tabela 6 apresenta os resultados do teste de Ljung-Box, que mostram que as séries ajustadas não apresentam correlação nos resíduos, o que confirma o que já observamos para as funções de autocorrelação, Figura 14. Outra forma de verificar a qualidade do modelo fit é realizar uma análise do gráfico de normalidade dos resíduos. Na Figura 15, podemos ver que os valores estimados estão distribuídos em uma linha diagonal, o que indica linearidade satisfatória, as hipóteses de normalidade foram aceitas com base no teste de Shapiro-Wilk, onde os p-valores de p = 0,1785 e p = 0 foram obtidos 0,4263 para as séries de suicídio masculino e feminino.
Previsões
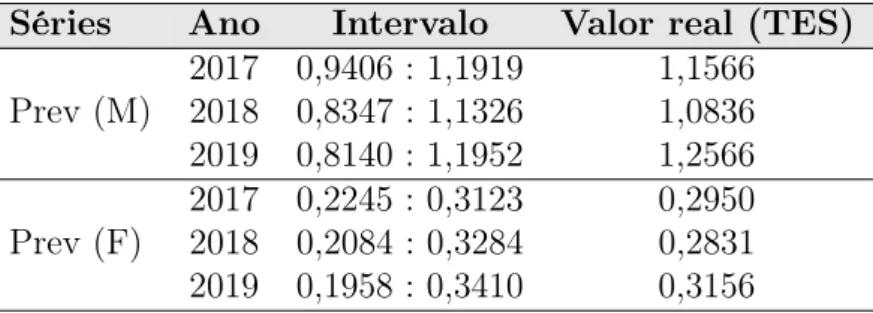
Como podemos ver, a maioria dos valores das taxas específicas de suicídios verdadeiros se enquadram no intervalo de confiança previsto pelos modelos, sugerindo que os modelos se ajustam bem às séries analisadas. A Tabela 8 mostra os valores previstos para cada percentual específico e também por intervalo, ao nível de significância de 5%. De acordo com a Tabela 8, nota-se que as projeções para a taxa de suicídio da população masculina e feminina apontam para uma taxa média de crescimento anual de 2,1% e 1,3%, respectivamente, com crescimento mais acentuado de 2021 a 2022 na população masculina.
Considerando o aumento da incidência de suicídio para ambas as populações, um aspecto também é observado por Ribeiro et al. 2018) na cidade de Uberaba em Minas Gerais, é importante direcionar políticas públicas com mais atenção a esta temática para diminuir o sofrimento com perda de vidas humanas. Portanto, antes de concluir as análises dos dados, a Figura 17 apresenta os gráficos do resumo diagnóstico dos modelos ajustados. No geral, os modelos de Box & Jenkins foram encontrados para ajustar os dados bem o suficiente para fazer previsões confiáveis em um nível de significância de 5%.
Observou-se uma tendência histórica de crescimento para as duas séries de suicídios e conclui-se que a tendência de crescimento das taxas específicas de suicídios nas duas populações (masculina e feminina) se mantém para os anos e 2022. uma análise múltipla de séries que podem ser correlacionadas com taxas específicas de suicídio, a fim de compreender possíveis causas do aumento ao longo do tempo. O impacto dos eventos de austeridade econômica e prosperidade no suicídio na Grécia: uma análise de série temporal interrompida de 30 anos.