This work has as objective to present what é a Geometry Fractal and its relevance when working on Basic Education. The purpose of this work is to present what fractal geometry is and their relevance when used in basic education. We concluded that fractals and fractal geometry, when inserted into basic education and functioning correctly, can greatly help the teacher and the student in the teaching-learning process.
INTRODUÇÃO
A terceira apresenta reflexões sobre a utilização desta nova geometria no contexto de sala de aula, onde apresentamos conceitos de pesquisadores sobre este tema no que diz respeito à sua utilização no ensino fundamental. A segunda e terceira atividades destinam-se ao ensino básico e tratam dos temas de potenciação e cálculo de área e perímetro de figuras fractais.
FRACTAIS E A GEOMETRIA FRACTAL
Fractais
A complexidade infinita está relacionada ao fato do processo de geração fractal ser recursivo, com um número infinito de iterações. Segundo Alves (2007), as aplicações dos fractais podem ser catalogadas em três grupos: aplicações a objetos ou fenômenos da natureza, aplicações a criações humanas e aplicações voltadas à modelagem de situações nas áreas das ciências econômicas, sociais e humanísticas. É surpreendente quantas formas na natureza podem ser melhor modeladas por fractais.
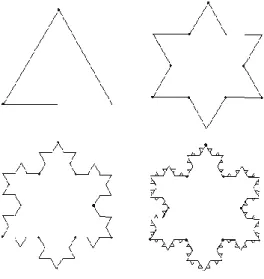
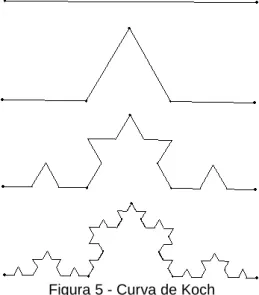
A dimensão fractal nos sistemas fluviais é um exemplo da presença de fractais na ecologia, um batimento cardíaco saudável não é regular, mas sim caótico e representa auto-similaridade em diferentes escalas de tempo na sua representação gráfica. A construção do floco de neve é feita a partir de um polígono convexo regular e uma curva de Koch é construída em cada um de seus lados.Vejamos um exemplo de construção a partir de um triângulo equilátero. No cinema, como relata Alves (2007, p. 158), “as imagens geradas por computador foram uma das primeiras aplicações dos fractais”, os fractais revolucionaram a criação de imagens.
Em documentário, exibido pela BBC (British Broadcasting Corporation), The Code relata como a indústria da animação conseguiu através do uso de fractais para a produção cinematográfica, a Pixar, uma das maiores produtoras de filmes infantis digitais, utiliza fractais em suas produções para alcançar mais realismo e beleza nas imagens. A presença dos fractais nas ciências económicas, sociais e humanas remonta ao início dos estudos do próprio Mandelbrot, quando trabalhava na IBM em questões económicas e estudava distribuições de rendimentos e salários.

Geometria não euclidiana e a geometria fractal
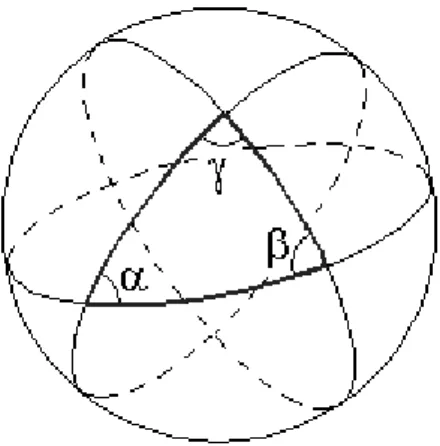
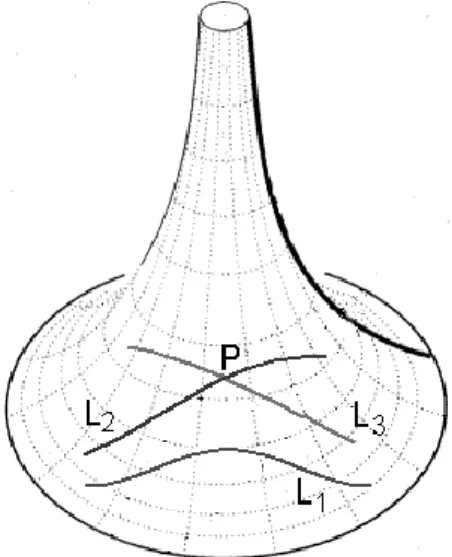
A seguir faremos algumas considerações sobre geometrias não euclidianas e o estudo de fractais, geometria fractal. Historicamente, a geometria fractal não surgiu da mesma forma que outras geometrias, porém é classificada como "não euclidiana" por se diferenciar da geometria euclidiana clássica. Durante séculos, os objetos e conceitos da filosofia e da geometria euclidiana foram considerados os que melhor descrevem o mundo em que vivemos.
Em todos estes exemplos, existem componentes cujas formas representam predominantemente irregulares e caóticas, e tentar simplificá-los usando modelos de geometria euclidiana não seria apropriado. Nesse sentido, Alves (2007) alerta que nem tudo na natureza pode ser considerado fractal e que existem situações em que a geometria euclidiana é necessária, ou seja, a presença da geometria fractal não exclui o uso da geometria euclidiana, que continua ser importante para a modelagem de formas que surgem do mundo humano. Dada a quantidade de aplicações já mencionadas, a geometria fractal é uma ferramenta muito flexível para trabalhar com educação.
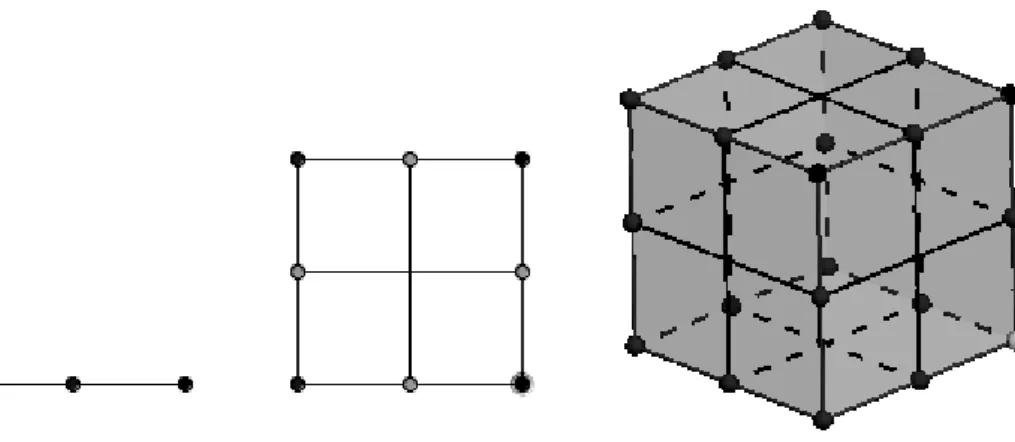
Um exemplo de aplicação da geometria fractal no ensino fundamental é utilizar a questão da dimensão fractal para desenvolver atividades envolvendo logaritmos. Este é um exemplo em que podemos desenvolver ou aplicar um tema matemático no ensino primário através da geometria fractal, neste caso logaritmos.
Reflexões do ensino da geometria fractal na educação
Nunes (2006) destaca vários pontos importantes para justificar a inclusão da geometria fractal nos currículos de matemática do ensino básico, pois ao ser introduzida na aula torna-se um tema motivador tanto para professores como para alunos, bem como é um tema integrador de diferentes conceitos matemáticos. A geometria fractal pode proporcionar aos alunos uma visão diferenciada da matemática, pois permite suavizar a abordagem dos conteúdos curriculares, permitindo a conexão de conceitos que muitas vezes são considerados pelos alunos como desconectados e sem qualquer correlação. Barbosa (2005) elenca alguns dos pontos positivos da utilização da geometria fractal em sala de aula, tais como: a conexão entre a geometria fractal e diferentes ciências; a possibilidade de difundir o acesso à informática nos diferentes níveis de ensino; apresentar aos alunos o mundo da arte, despertando e desenvolvendo o seu sentido estético com construções fractais; evocar uma sensação de admiração pela ordem no caos.
A inclusão da geometria fractal no ensino permite uma maior reflexão sobre a própria geometria euclidiana, pois amplia discussões de conceitos e resultados que muitas vezes não são discutidos em sala de aula. No âmbito estadual, o estado do Paraná é pioneiro no ensino de geometrias não euclidianas no ensino fundamental, neste caso incluindo a geometria fractal. No 8º ano, a geometria fractal é introduzida na grade curricular, para que o aluno “conhece os fractais através da visualização e manipulação de materiais e discute suas propriedades” (PARANÁ, 2008, p. 79); e também no ensino médio, espera-se que o aluno “conhecer os conceitos básicos da Geometria Elíptica, Hiperbólica e Fractal (Geometria da superfície esférica)” (PARANÁ, 2008, p.81).
Levando em consideração os argumentos acima mencionados, percebe-se que a inclusão da geometria fractal no ensino fundamental pode ser benéfica ao processo de ensino e aprendizagem, auxiliando os professores na sua prática e os alunos na compreensão do currículo. No próximo capítulo apresentaremos algumas atividades e suas sequências didáticas que envolvem o uso da geometria fractal para ensinar outros conceitos matemáticos.
ATIVIDADES E SUAS SEQUÊNCIAS DIDÁTICAS
Atividade 1 – Probabilidade Geométrica
- Apresentação da atividade 1
- Sequência didática da atividade 1
Resposta Qual é a probabilidade de escolher qualquer ponto do triângulo se ele pertencer a um buraco? Qual é a probabilidade de escolher um ponto aleatório do quadrado mesmo que não pertença ao buraco? As construções que você acabou de fazer são conhecidas como fractais, respectivamente o triângulo de Sierpinski e o tapete de Sierpinski.
Um destaque da atividade é a utilização de construções geométricas para resolução de problemas. Depois que o aluno concluir a construção, ele tornará o problema menos abstrato, pois poderá raciocinar por meio de seu desenho. Se tivermos uma região B do plano contida em uma região A, admitimos que a probabilidade de um ponto de A também pertencer a B é proporcional à área de B e não depende da posição ocupada por B em A leva. A solução do exercício (4) é: (a) 64 quadrados; (b) a área de cada quadrado é de 1 cm2, o que corresponde à octogésima primeira parte do quadrado original.
Portanto, podemos generalizar que a área de qualquer triângulo gerado no enésimo passo é ( ) da área original e, portanto, a área do triângulo tenderá a zero. Recomenda-se que nesta fase o professor explique brevemente e dê um exemplo do que é a geometria fractal e que as figuras dos dois primeiros exercícios sejam: Triângulo de Sierpinski e Tapete de Sierpinski.
Atividade 2 – Fractais e potenciação
- Apresentação da atividade 2
- Sequência didática da atividade 2
Ambos os exercícios envolvem situações em que os alunos terão que raciocinar sobre a quantidade de objetos em cada etapa das seções com o objetivo de concluir que estão trabalhando com a multiplicação de fatores iguais. Os alunos utilizarão a tabela para responder à questão (2), onde verificarão que a cada novo passo o número de passos duplica, ou seja, é multiplicado pelo mesmo fator 2. É importante destacar que caso não seja possível completar a quarta etapa, etapa de ambos os cartões, não deve interferir no preenchimento da tabela, pois os alunos entendem a sequência de números dobrados a cada nova etapa.
Nesta fase, tem um papel importante o professor, que auxiliará os alunos na construção do cartão “Passos Centrais”, e à medida que os alunos concluírem a dobragem, eles próprios irão completar a tabela de exercícios (1). É fundamental que o professor não ajude a completar a tabela, pois nesta fase os alunos devem encontrar formas de resolver as duas primeiras questões. Se achar apropriado, você também pode dar aos alunos um exemplo do conceito fractal antes de começar a criar o cartão do Triângulo de Sierpinski.
A diferença nesta fase é que os alunos terão que utilizar o conceito de potenciação para preencher a tabela de exercícios (3) e responder corretamente à última questão. O professor avaliará os alunos de acordo com o desempenho nos exercícios; avaliará a participação ativa dos alunos e os seus contributos para o desenvolvimento da atividade.
Atividade 3 – Fractais, perímetro e área
- Apresentação da atividade 3
- Sequência didática da atividade 3
Nesta etapa, com base nas respostas do aluno às questões (1) e (2), o professor formalizará o conceito de exponenciação e ensinará o conceito de base e expoente. É bastante provável que neste nível de escolaridade a maioria dos alunos não consiga resolver o problema originalmente colocado sobre a reprodução de bactérias, pelo que neste nível o professor demonstrará aos alunos a função de potenciação utilizando as conclusões obtidas no desenvolvimento de exercícios (1) e (2) para generalizar e responder o problema das bactérias junto com a turma. O destaque da atividade é a utilização do computador para a construção de figuras de geometria fractal que servirão de apoio aos alunos no raciocínio a partir delas.
O exercício (3) exigirá maior abstração por parte dos alunos, então esperamos que eles respondam que a área do triângulo de Sierpinski ficará cada vez menor à medida que aumentarmos o número de passos. Após as sugestões dadas pelos alunos, o professor poderá explicar o conceito de geometria fractal com alguns exemplos. Nesta fase os alunos terão que completar a tabela do primeiro exercício após a construção do fractal em GSP.
Neste ponto, o professor será capaz de explicar e ilustrar aos alunos o conceito de auto-similaridade presente nos fractais, bem como a questão da recursividade na construção fractal. Depois de construírem juntos o Triângulo de Sierpinski no GSP, os alunos resolverão os demais exercícios.
CONSIDERAÇÕES FINAIS
Disponível em:
Com a ferramenta “seta” selecione o ponto central e clique com o botão direito do mouse, selecione a opção Ocultar Ponto ou utilize o atalho de teclado Ctrl + H. Com a ferramenta “reto”, opção de segmento reto, clicaremos nos pontos A e C para construir o segmento AC e nos pontos B e C para construir o segmento BC. Utilizando a ferramenta seta, selecione os três lados do triângulo (é importante que apenas os lados sejam selecionados) e a seguir, no menu Construir, selecione a opção Ponto Médio ou utilize o atalho de teclado Ctrl + M.