Therefore, a gauge theory is constructed from the gauge fields (as fundamental objects) of the theory. Moreover, this is a topological equation because the solution is the definition of the gauge potential, i.e. the algebra of the group is the tangent space of the group at the identity[1].
DRAFT
QUANTIZATION OF GAUGE THEORIES
A general result is that BRST doublets belong exclusively to the trivial sector of the cohomology [43]. In practice, any BRST doublet can be introduced because they are harmless to the physical content of the theory. In non-Abelian theories, the BRST symmetry must be taken in favor of gauge symmetry due to the presence of the Faddeev–Popov ghosts.
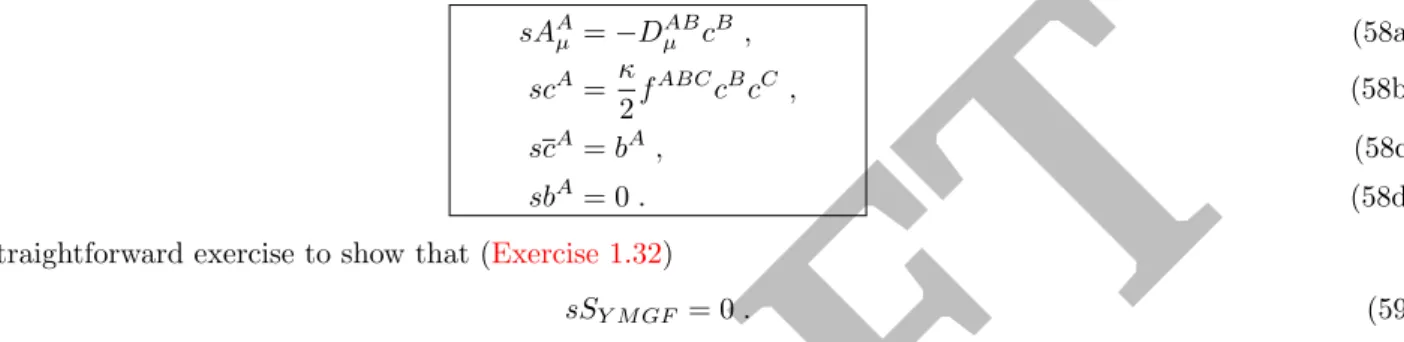
GRIBOV AMBIGUITIES
Basically, the factor V(Ω) is a Heaviside function that limits the functional integral to the Gribov horizon. However, some remarks (focused on QCD) are important: Restricting the path integral to the region of the Mushrooms brings profound changes to the gluon propagator. Then, a local and renormalization action is needed, which effectively implements the constraint on the Mushroom region Ω.
In particular, the restriction to the area of Gribov is implemented by imposing that the functional integral must be performed in the area of the configuration space where the smallest eigenvalue is M=MAA/(N2−1), i.e. the result for the modified path integral that takes into account the restriction to the area of the Mushrooms Ω is given by. Therefore, the explicit violation of BRST symmetry is a direct consequence of the restriction of the domain of the path integral to the region of Gribov.
It is important to mention that the Gribov-Zwanziger action is renormalizable for all orders in perturbation theory. Therefore, the restriction to the Gribov region brings more non-trivial features to the non-perturbative level. The proposal is to account for these instabilities of the Gribov-Zwanziger action from the outset by introducing them.
As presented here, the (refined) Gribov-Zwanziger action may appear to be restricted to the Landau track.
GRAVITY AS A GAUGE THEORY
EQUIVALENCE PRINCIPLE AND GEOMETRODYNAMICS
Because the covariant derivative defines parallel transport, the curvature measures the error in the parallelogram law. In other words, parallel transport of a vector along two different directions will differ by swapping the order of the directions. These isometries are described by the Lorentz group SO(1,3), but the local version of the Lorentz group, i.e.
Thus eaµ is not unique because there are infinitely equivalent virbeins related to the elements of the local group SO(1,3). An important observation is that the effect of the Lorentz group on the vierbein leaves the spacetime coordinates xµ unchanged, but affects the vierbein. The two-form of the curvature is easily defined by the double action of the covariant derivative (Exercise 2.12).
By the vanishing torsion condition we see that it is possible to describe GR in the first order formalism, despite the fact that gµν is not considered as the fundamental field in favor of the quadrilateral. We emphasize here that the set of equations (134a-134c) are natural consequences of the geometry we are constructing. The main difference is related to the geometric structures of both theories: The gauge group of gravity has an intimate connection with spacetime, that is, the gauge group is identified with the local isometries of the spacetime tangent space.
In fact, the absence of the Hodge operator opens the possibility for gµν to be interpreted as an induced quantity.
GENERALIZED THEORIES
Furthermore, recalling that the Yang-Mills curvature, in differential form notation, is F =dA+κAA, another similarity appears with respect to the curvature (128). The Einstein-Hilbert action (138) has no relation to the Yang-Mills action, which reads in differential form notation. This feature is not only related to the fact that we have many different actions, but also because the quadruped is dimensionless with respect to canonical dimensions, i.e.
The first term is known as the cosmological constant term while the second term is the well-known EH term. However, in four dimensions, this term is actually topological and, therefore, makes no contribution to the field equations. Again, the first term is the cosmological constant term and the second is the EH term.
The third term is the Chern-Simons three-form of the vierbein, and the fourth term is the usual topological Chern-Simons three-form of the compound. It is known that in certain situations the last term corresponds to the first two terms [104]. The fourth term is the topological term Pontryagin and is related to the connection CS term through.
Moreover, for b2 = −b3 the last two terms become the Nieh-Yang topological term, which is related to the CS vierbein term [105].
QUANTIZATION ATTEMPTS
EFFECTIVE GRAVITY FROM YANG-MILLS THEORIES
GENERAL IDEAS
This fact is important because it prevents the measurement field, which has dimension 1, from being directly associated with the vierbein, which has a vanishing dimension. This means that at the quantum level, gauge theory and spacetime are completely decoupled. The gauge field is a 1-form with an algebra value and thus contains dimG components related to the algebra of the gauge group.
As a result, the gauge components can be identified by spin coupling and vierbein. It is important to note that depending on the gauge group, symmetry breaking may not be necessary. This happens if the gauge transformations can be partially identified by local Lorentz transformations and partially identified by diffeomorphisms.
The theory has two sectors, the UV, which is a massless gauge theory in Euclidean four-dimensional space, and the IR sector, which presents soft BRST symmetry breaking and dynamically generated mass parameters. One possibility is thus to identify the H gauge field with the spin connection and the Q field with vierbein. Both theories present soft BRST breaking and need to be redefined to establish the physical content at the infrared regime.
In the case of QCD, the physical content is confined states identified with hadrons and glue balls.
SO(5) YANG-MILLS THEORY
Moreover, a reparameterization of the SO(5) generators is required due to the existence of a mass scale, i.e. a stereographic projection is now allowed if one identifies the mass parameter with the radius of the measuring manifold R5S, see [39]. Action (158) is exactly the original action (155) with a specific decomposition of the fields and a very simple rescaling of the fields. At this point this is just an assumption, but due to asymptotic freedom it is not an unlikely hypothesis45.
If we consider this limit in the transformed algebra (159), the In¨on¨u-Wigner contraction46 [109] occurs, which forces the group SO(5) to shrink down into the Euclidean Poincar´e group (Exercise 3.10). The gauge symmetry is then dynamically deformed into the Euclidean Poincar´e group, SO(5) −→ ISO(4), for some values of κ in the strong coupling regime. An In¨on¨u-Wigner contraction is a deformation of a group into another group that is not a subgroup of the first.
Since the Poincar´e group is not a symmetry of action (158), a dynamic symmetry breaking occurs. After the contraction, field A thus becomes the only gauge field with respect to the Lorentz group, while θ has migrated to the matter sector (it undergoes group rotations only under infinitesimal Lorentz transformations, i.e. it is a vector representation of the group). 44We note that, due to the hierarchy of fundamental interactions, a low energy scale for gravity would be much higher compared to all other fundamental interactions.
46Perhaps the most famous example of an In¨onu-Wigner contraction in Physics is the deformation of the Lorentz group to the Galileo group forv/c7−→0 (Exercise 3.9).
INDUCED GRAVITY
QUANTUM ASPECTS
The linearized version of GR, on the other hand, is also a gauge theory and the same first-case principles apply [110]. In this way, the resulting geodynamical theory is obtained from the full dynamical content of the original gauge theory. Another question can be raised at this point: Where are the spin-2 excitations of the graviton.
Another way to think about changing the rotation count lies in the map R4 7−→ M4 where the local set of gauges is identified with the isometries of the tangent spaces of M4. A remarkable feature of the current theory is that Newton and the cosmological constants are related through Λ2 = κ2/16πG. In perturbative QFT, the function of the parameters can be defined by the renormalization factors of the fields and parameters.
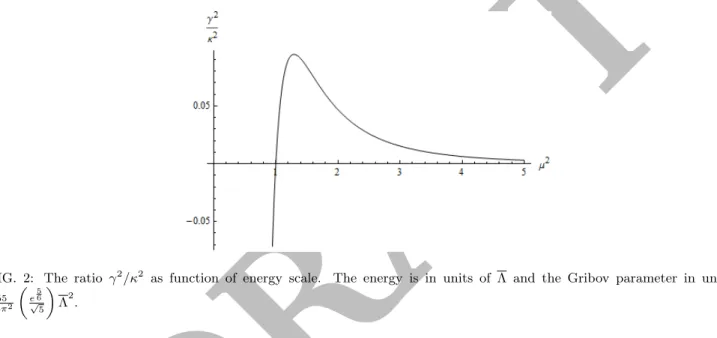
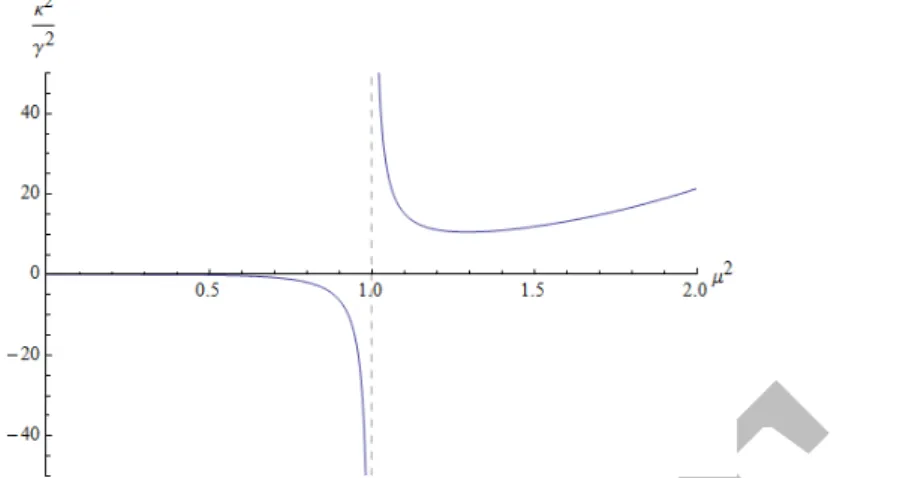
In the case of the Gribov parameter, it is determined by a gap equation obtained from the minimization of the quantum effect with respect to γ2, see Sect. On the other hand, we can write bearing in mind that the coupling parameter is determined through the renormalization group equations [66, 67]. This kind of enhancement can affect the infrared sector of the Gribov parameter in such a way that it can also be limited.
In this region, BRST soft breaking dominates and rescaling of the fields (157) is allowed.

CLASSICAL ASPECTS Let us now study some classical aspects of the theory
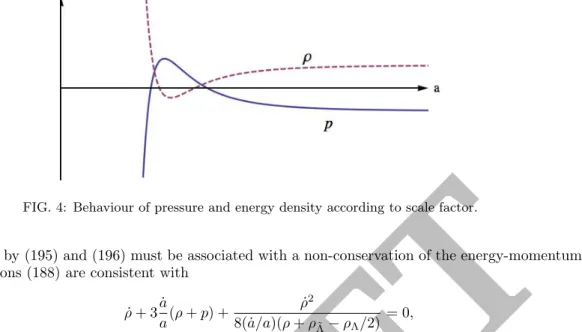
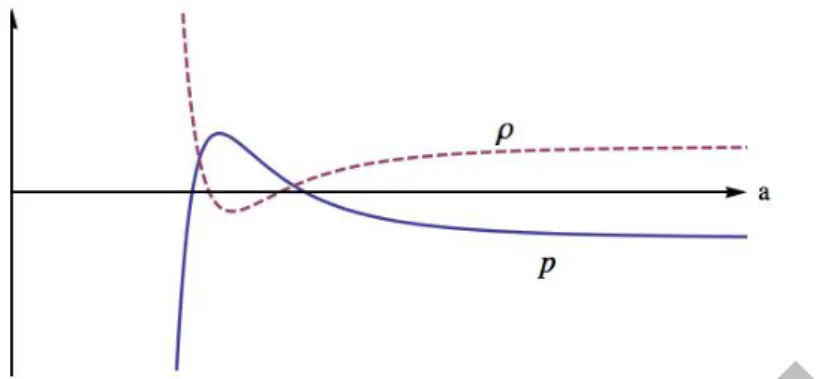
XB, the cosmological constant term in (175) will sum with all vacuum terms of the matter field action. Equations (175) and (176) are the full field equations, valid in all sectors of the geometric phase. In this case, the equation of state of the fluid is of great importance to fully specify the dynamic system.
Finally, let us only comment that the characteristic of the general solution (198) depends on the interaction between the constant, R0 and ξ0. In this case, the extra sector of the gauge group manifests itself in the geometric sector as a matter field that interacts only with gravity. Since the dimension of the spacep shape is given by dimEp=. it is straightforward to see. i.e. the dimension of the dual space has the same dimension as the space of p-forms.
An important property using the integration of p-forms is contained in the definition of the inner product. The correct action is mapFp7−→Fp and is possible due to the closure property of groups. The basic structure of the gauge theories we consider in these lectures is the principal bundle P(G,R4) where the base space is the four-dimensional Euclidean spacetime, G is the gauge group.
Let's look at the argument against commuting the covariant derivative of the first term, c = u−1δu, its derivative reads57. Wald, Space, Time and Gravity: The Theory of the Big Bang and Black Holes, Chicago, USA: Univ. Le Delliou, Dark energy–dark matter interaction and violation of the equivalence principle from the cluster Abell A586, Phys.