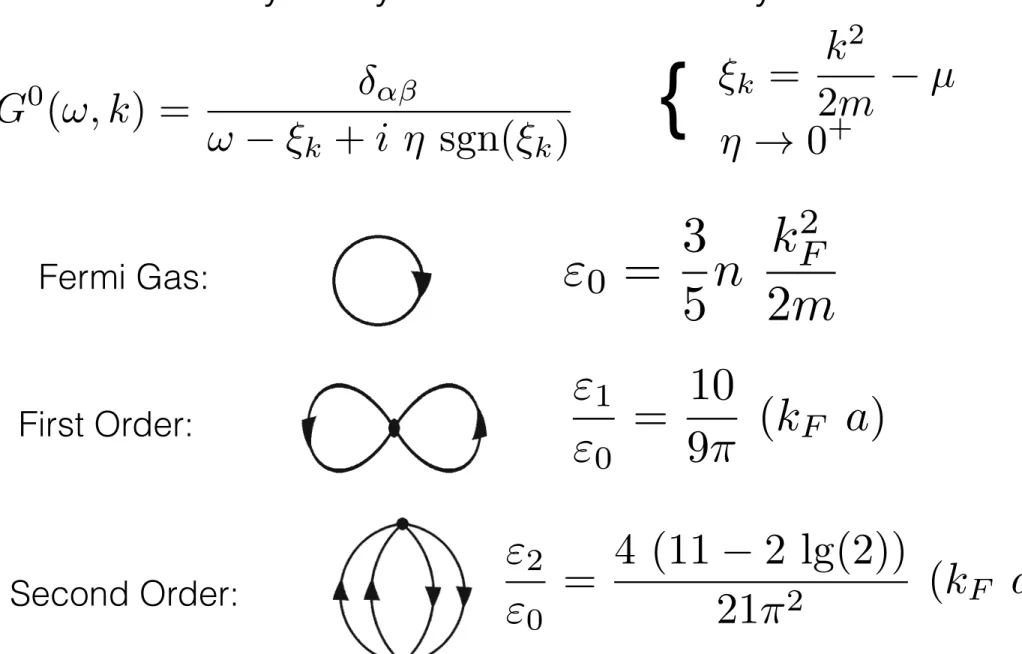Lecture I:
!
1. Stability of things big and small: why atoms, nuclei and compact stars do not collapse. [20]2. Degenerate Fermi gases: Ideal and interacting [10]
3. Non interacting dense nucleonic matter: Charge neutrality and beta-equilibrium. [15]
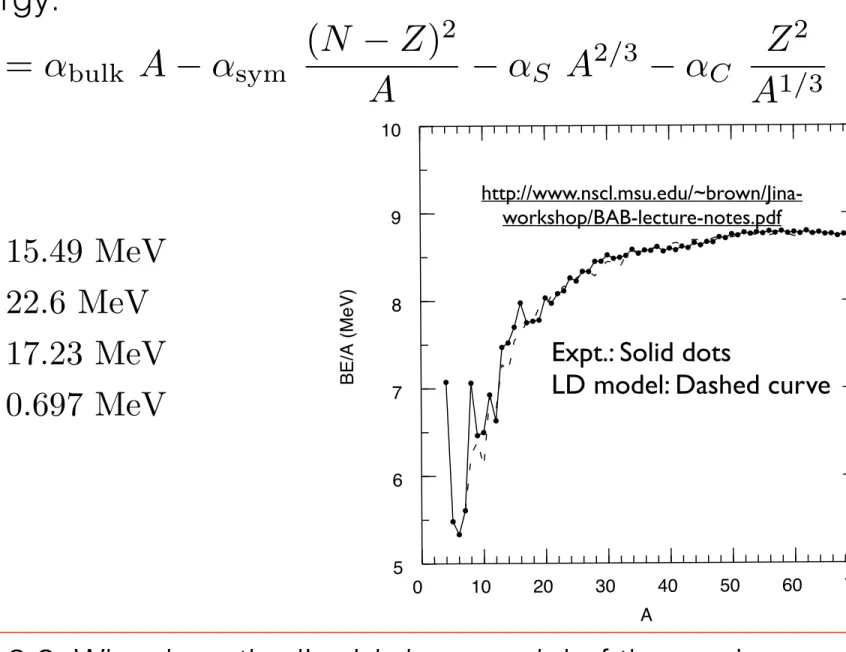
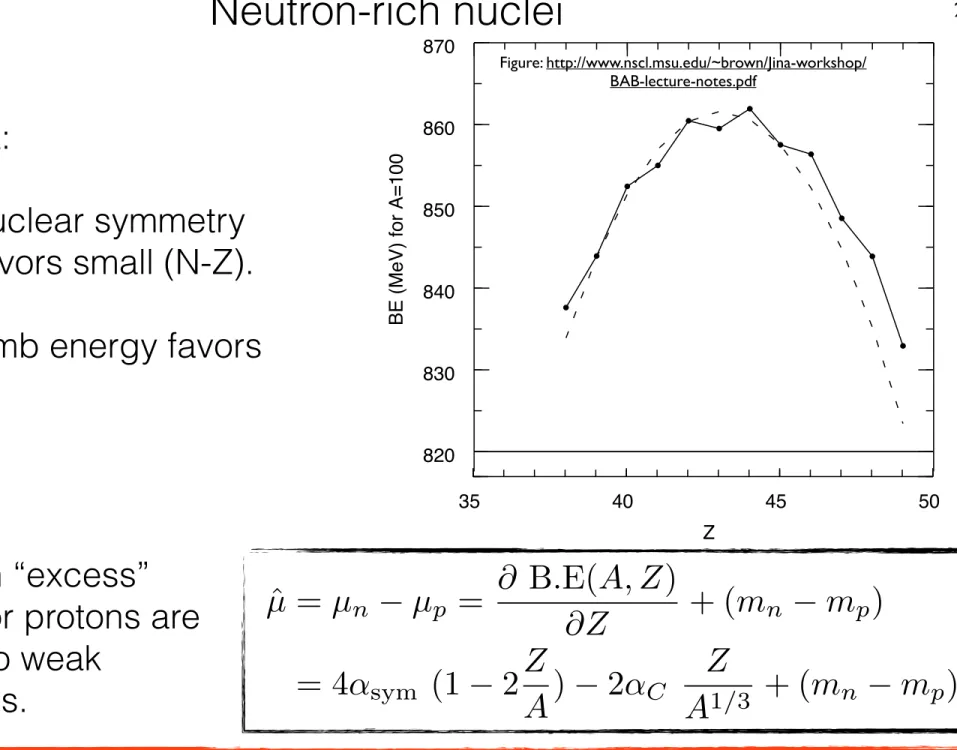
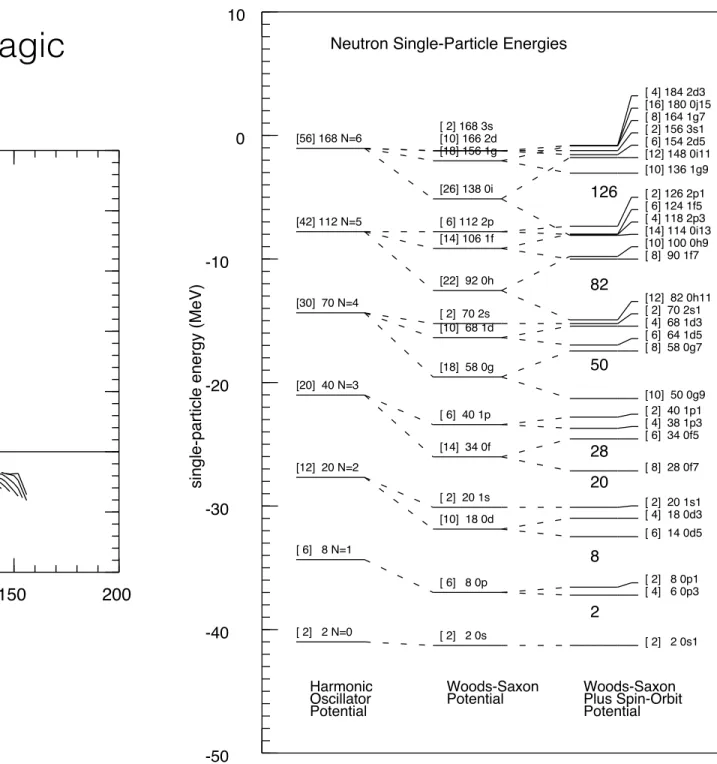
4. Nuclei as drops of nuclear matter: Liquid drop model and nuclear masses. [15]
5. Low density matter: Nuclei embedded in an electron gas [10]
6. Neutron drip: Nuclei embedded in a gas of electrons and neutrons [10].
7. Uniform Interacting Nuclear matter. [10]
Lecture II:
!
1. Neutron star structure: Hydrostatic equilibrium & Tolman-Oppenheimer-Volkoff equation [20]2. Equation of state of dense matter: Nucleons, hyperons, condensates, quarks. [45]
3. Neutron star mass-radius and dense matter constraints. [25]
Lecture III:
!
1. Low temperature properties: Heat capacity of liquids, solids, and superfluids [30]
2. Neutrino cooling: URCA reactions [20]
3. Cooling and transport in dense matter: Correlations in low energy processes [20]
4. Future: Looking ahead to what we might learn in the next 10 years [20]
Structure of neutron stars and basic properties of dense matter
Sanjay Reddy, INT, University of Washington, Seattle
Look and Listen, Mexican Astrophysics School, 2014 !1
Atomic Stability
!2
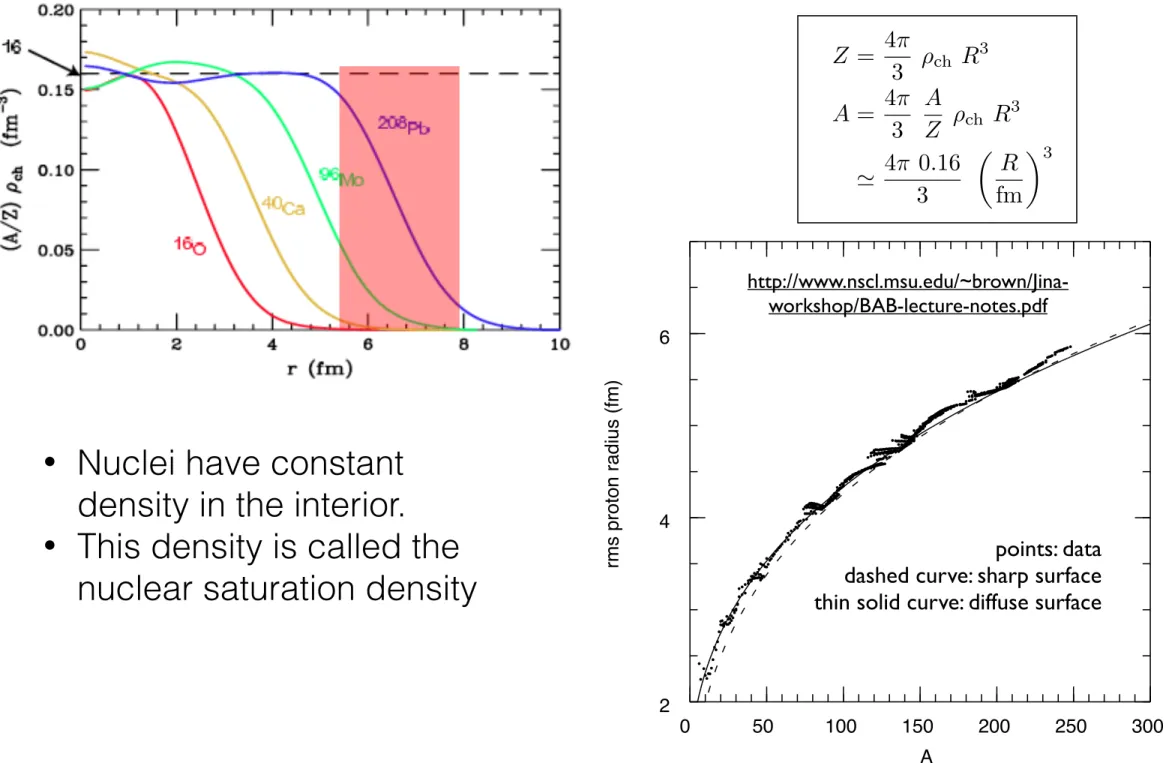
•
Energy of an atom:
Quantum mechanics:
p = — r
•
Zero point energy grows as 1/r
2: non-relativistic kinetic energy
•
Natural units: ~ = 1 & c = 1
c = 2.99792 10 8 m s
~ = 6.582119 ⇥ 10 16 eV s ~ c = 1.9733 ⇥ 10 7 eV m
= 197.33 MeV fm
}
E
Atom= 1
2 m
ev
2- k e
2r = p
22 m
e- k e
2r
E
Atom= —
22 m
er
2- k e
2r
•
Electrostatic units: V (r) = k Z
1Z
2e
2r
↵ em = ke 2
~ c = 1 137
k = 1, ~ = 1, c = 1
e 2 = ↵ em
Atomic Size & Energy
•
Minimizing with respect to the radius:
∂ EAtom
∂r = aem r2
- 1 r3 me
= 0 rmin = a0 HBohr radiusL = 1 aem me
E
AtomH r
minL = 1
2 a
em2m
e•
Relativistic correction (an order of magnitude estimate):
DEAtom = p2 +me2 -me - p2
2me = - 1 8
p4 me3
+ OBp6
me5 F = -1 8me3 rmin4
+ OBp6
me5 F = - 1
8 aem4 me + OAaem6 meE
•
A relativistic atom ?
EAtom ? = p - aemr = 1
r - aem r
•
Dense atomic systems - pressure ionization:
When distance between atoms d << 137/(Z m
e)or p >> Z m
e/137 they delocalize to form a uniform degenerate gas. Eventually, at higher density electrons will become relativistic.
!3
Dense Electron Gas
•
Mean kinetic energy of N electrons confined in a sphere of radius R:
!4
r
zr
yr
xR
p
xp
yp
yp
Fe.
/
Matter at 10
6g/cm
3•
Distance between electrons: = /
•
Electron Fermi momentum: = ( )
// /
. MeV
•
Total energy per electron:
+ + ( )
+ + ( )
Problem 1.0: What have we ignored in the above estimate of the energy per electron ?
!5
White Dwarfs: A Bound Dense Electron Gas
•
Fermi degeneracy resists gravity
!6
= ( )
/= .
/
•
Fermi momentum of N electrons in a spheres
•
Energy per electron in the star:
=
Non-relativistic electrons:
Relativistic electrons: =
•
Gravitational Potential
(Binding) Energy: = =
Mass and Radius of a White Dwarf
!7
•
non-relativistic case:
•
For a given value of N (or M) the preferred radius is obtained by minimizing the energy per electron.
( ) =
( ) .
/
.
( ) .
/Problem 1.1: Estimate the radius of a white dwarf with M = 0.5 M
⊙?
•
relativistic case: ( ) .
/
.
( ) = = .
Problem 1.2: Estimate the maximum mass of a white dwarf.
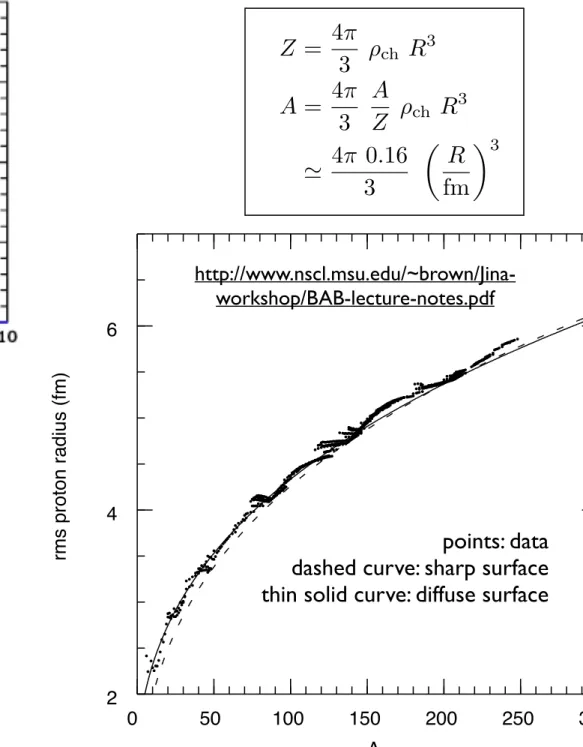
Getting Big Numbers from Small Ones:
= = .
. .
. .
= .
Estimating white dwarf radii and maximum masses:
( ) = . .
.
.
. .
= = . . .
Neutron Star Prototype:
free neutron gas bound by gravity
•
Neutron Fermi energy resists gravity:
( ) . /
( ) .
/
.
replace electrons (on slide 7)
by neutrons
( ) = . .
.
.
.
•
Neutron Star Radius:
neutrons are also the
source of mass
Maximum Mass
= .
( ) = = .
•
A simple and wrong estimate of the neutron star maximum mass:
(assume neutrons are relativistic when calculating the kinetic energy and non- relativisitic when calculation the
gravitational energy)
( ) .
/
.
. .
better estimate is:
•
A better estimate:
(correct the gravitational energy by including kinetic contribution to the energy density.
General and Special Relativity !)
( ) .
/
.
•
Are you troubled by the estimates we have made so far ?
If our estimates of maximum masses of white dwarfs and neutron stars were correct which of the following statements are false:
1. Neutron stars would not exist in the universe.
2. Carbon based life would still be possible.
3. Oppenheimer would be best known for his work on neutron stars.
4. Nucleons repel each other at short distances (< 1 fm).
5. We would have solved the dark matter problem.
True or False:
Scales in Strong Interaction Physics
4 Effective Theories of Dense and Very Dense Matter 217
For comparison, the density of a free Fermi gas in d dimensions is n = 2
(4π)
d/2k
dFΓ !
1 +
d2" . (4.98)
This equation determines the relation between ϵ
F≡ k
2F/(2m ) and the density.
We get
ϵ
F= 2 π m
# n 2 Γ
$ d
2 + 1
%&
2/d. (4.99)
We determine ϵ
Ffor the interacting gas by inserting nfrom Eq. (4.97) into Eq. (4.99).
The universal parameter is ξ = µ/ϵ
F. We find ξ = 1
2 ϵ
3/2+ 1
16 ϵ
5/2log(ϵ) − 0.025 ϵ
5/2+ . . . = 0.475 (ϵ = 1), (4.100) which agrees quite well with the result of fixed node quantum Monte Carlo calcula- tions. The calculation has been extended to O (ϵ
7/2) by Arnold et al. [47]. Unfortu- nately, the next term is very large and it appears necessary to combine the expansion in 4 − ϵ dimensions with a 2 + ϵ expansion in order to extract useful results. The ϵ expansion has also been applied to the calculation of the gap [45 ], the critical temperature [48] and the critical chemical potential imbalance [46 , 49].
4.5 QCD and its Symmetries 4.5.1 Introduction
Before we discuss QCD at large baryon density we would like to provide a quick review of QCD and the symmetries of QCD. The elementary degrees of freedom are quark fields ψ
α,a fand gluons A
aµ. Here, a is color index that transforms in the fundamental representation for fermions and in the adjoint representation for gluons.
Also, f labels the quark flavors u , d , s , c, b, t . In practice, we will focus on the three light flavors up, down and strange. The QCD lagrangian is
L =
Nf
'
f
ψ ¯
f(i D / − m
f)ψ
f− 1
4 G
aµνG
aµν, (4.101) where the field strength tensor is defined by
G
aµν= ∂
µA
aν− ∂
νA
aµ+ g f
abcA
bµA
cν, (4.102)
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
% (ψψ)
†(ψ ∇
↔2ψ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants,
↔∇ =
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4 πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
%
( ψψ )
†( ψ ∇
↔2ψ ) + h .c &
+ . . . , (4.1)
where m is the neutron mass, C
0and C
2are dimensionful coupling constants, ∇
↔=
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
%
( ψψ )
†( ψ
↔∇
2ψ ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants,
↔∇ =
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
218 T. Schäfer
and the covariant derivative acting on quark fields is i D / ψ = γ
µ!
i ∂
µ+ g A
aµλ
a2
"
ψ . (4.103)
QCD has a number of remarkable properties. Most remarkably, even though QCD accounts for the rich phenomenology of hadronic and nuclear physics, it is an essen- tially parameter free theory. To first approximation, the masses of the light quarks u , d , s are too small to be important, while the masses of the heavy quarks c, b , t are too heavy. If we set the masses of the light quarks to zero and take the masses of the heavy quarks to be infinite then the only parameter in the QCD lagrangian is the coupling constant, g. Once quantum corrections are taken into account g becomes a function of the scale at which it is measured. If the scale is large then the coupling is small, but in the infrared the coupling becomes large. This is the famous phenomenon of asymptotic freedom. Since the coupling depends on the scale the dimensionless parameter g is traded for a dimensionful scale parameter Λ
QC D. Since Λ
QC Dis the only dimensionful quantity in QCD with massless fermions it is not really a parameter of QCD, but reflects our choice of units. In standard units, Λ
QC D≃ 200 MeV ≃ 1 fm
−1.
Another important feature of the QCD lagrangian are its symmetries. First of all, the lagrangian is invariant under local gauge transformations U (x ) ∈ SU (3)
cψ ( x ) → U (x ) ψ (x ), A
µ(x ) → U (x ) A
µU
†(x ) + iU ( x ) ∂
µU
†(x ), (4.104) where A
µ= A
aµ( λ
a/2). In the QCD ground state at zero temperature and density the local color symmetry is confined. This implies that all excitations are singlets under the gauge group.
The dynamics of QCD is completely independent of flavor. This implies that if the masses of the quarks are equal, m
u= m
d= m
s, then the theory is invariant under arbitrary flavor rotations of the quark fields
ψ
f→ V
fgψ
g, (4.105)
where V ∈ SU (3). This is the well known flavor (isospin) symmetry of the strong interactions. If the quark masses are not just equal, but equal to zero, then the flavor symmetry is enlarged. This can be seen by defining left and right-handed fields
ψ
L,R= 1
2 (1 ± γ
5) ψ . (4.106)
In terms of L / R fields the fermionic lagrangian is
L = ¯ ψ
L(i D / ) ψ
L+ ¯ ψ
R(i D / ) ψ
R+ ¯ ψ
LM ψ
R+ ¯ ψ
RM ψ
L, (4.107)
!!!!!!####"
%%%%%)
"
"
"
"
"
"
"
"
"
'
(MeV)
Nucleon-nucleon Potentials, Chiral EFT Integrate-out quark and gluons
Integrate-out nucleons
A Prototypical Fermi System
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
%
( ψψ )
†( ψ
↔∇
2ψ ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants,
↔∇ =
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4 π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
%
( ψψ )
†( ψ ∇
↔2ψ ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants, ∇
↔=
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [ 3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
% (ψψ )
†(ψ ∇
↔2ψ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants, ∇
↔=
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
%
( ψψ )
†( ψ ∇
↔2ψ ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants, ∇
↔=
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
p cot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4πa
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
% (ψψ)
†(ψ ∇
↔2ψ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants, ∇
↔=
→
∇ −
←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4π a
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
194 T. Schäfer
4.2 Fermi Liquids
4.2.1 Effective Field Theory for Non-Relativistic Fermions
If the relevant momenta are small neutrons and protons can be described as point- like non-relativistic fermions interacting via local forces. Effective field theories for nuclear systems have been studied extensively over the past couple of years [3, 9– 11].
If the typical momenta are on the order of the pion mass pions have to be included as explicit degrees of freedoms. For simplicity we will consider neutrons only and focus on momenta small compared to m
π. The effective lagrangian is
L
0= ψ
†!
i ∂
0+ ∇
22m
"
ψ − C
02
# ψ
†ψ $
2+ C
216
% (ψψ)
†(ψ
↔∇
2ψ) + h .c &
+ . . . , (4.1) where m is the neutron mass, C
0and C
2are dimensionful coupling constants, ∇
↔=
∇ −
→ ←∇ is a Galilei invariant derivative, and . . . denotes interactions with more deriv- atives. We have only displayed terms that act in the s-channel. The coupling constant are determined by the neutron-neutron scattering amplitude. For non-relativistic scat- tering the amplitude is related to the scattering phase shift δ by
A = 4π m
1
pcot δ − i p . (4.2)
For small momenta the quantity pcot δ can be expanded as a Taylor series in p . This expansion is called the effective range expansion
pcot δ = − 1
a + 1 2
'
∞ n=0r
np
2(n+1), (4.3)
where a is the scattering length, and r
0is the effective range. The situation is simplest if the scattering length is small. In this case the scattering amplitude has a perturbative expansion in C
i. At tree level
C
0= 4π a
m , C
2= C
0ar
02 . (4.4)
However, there are many systems of physical interest in which the scattering length is not small. This happens whenever there is a two-body bound state with a very small binding energy, or if the two-body system is very close to forming a bound state. For neutrons a
nn= − 17 fm, much larger than typical strong interaction length scales.
Non-relativistic Fermions interacting with finite-range forces.
Effective Lagrangian Two-body observables
renormalization
scheme
Many-Body Perturbation Theory
4 Effective Theories of Dense and Very Dense Matter 197
Fig. 4.1 Leading order Feynman diagrams for the ground state energy of a dilute gas of fermions interacting via a short range potential
empty. The possible excitation of the system are particles above the Fermi surface or holes below the Fermi surface, corresponding to the first and second term in Eq. (4.13). The particle density is given by
ρ = ⟨ ψ † ψ ⟩ =
! d 4 p
(2π) 4 S αα 0 ( p )e i p
0δ "
"
δ → 0
+= 2
! d 3 p
(2π) 3 Θ ( p F − p ) = p 3 F 3π 2 .
(4.14) Tadpole diagrams require an extra i δ prescription which can be derived from a careful analysis of the path integral representation at µ ̸= 0. As a first simple application we can compute the energy density as a function of the fermion density. For free fermions, we find
E = 2
! d 3 p
(2π ) 3 E p Θ ( p F − p ) = 3
5 ρ p 2 F
2m . (4.15)
We can also compute the corrections to the ground state energy due to the interac- tion (C 0 /2)(ψ † ψ) 2 . The first term is a two-loop diagram with one insertion of C 0 , see Fig. 4.1. There are two possible contractions and the spin-factor of the diagram is (δ αα δ ββ − δ αβ δ αβ ) = g (g − 1) where g = (2s + 1) is the degeneracy and s is the spin of the fermions. In the following we will always set g = 2. The diagram is proportional to the square of the density and we get
E 1 = C 0
# p 3 F 6π 2
$ 2
. (4.16)
We observe that the sum of the first two terms in the energy density can be written as E = ρ p 2 F
2m
% 3
5 + 2
3π ( p F a ) + . . .
&
, (4.17)
which shows that the C 0 term is the first term in an expansion in p F a , suitable for a dilute, weakly interacting, Fermi gas.
4E ffecti veT
heoriesof Dense andVery
Dense Matter
197
Fig.4.1 Leadingorder
Feynman diagramsfor
the groundstate
energy ofa dilutegas
offermions
interactingvia ashort
range potential
empty.The possibleexcitation
ofthe systemare
particlesabo vethe
Fermisurf ace
orholes below
theFermi surface,
correspondingto thefirst
andsecond termin
Eq.(
4.13).The particledensity
isgi ven by
= ρ
⟨
† ψ
⟩ ψ
= d !
p 4
π (2
4 )
0 αα S p ( e )
ip δ
0"
"
→ δ
+
0
= 2 d !
p 3
π (2
3 ) Θ p (
− F
p
= )
3 p
F
π 3 . 2
(4.14)
Tadp oled iag ram sre quir ean extr a δ i prescriptionwhich
canbe derived
fromacareful
analysisof thepath
integral representationat
̸= µ 0.A sa first sim ple app lica
tion
wecan computethe
energy densityas
afunction ofthe
fermiondensity .For
free
fermions,we find
= E 2 d !
p 3
π (2
3 ) E Θ p
p (
− F
) p 3 =
ρ 5
2 p
F
. 2m (4.15)
Weca nal soc omp ute the corr ecti ons tot heg rou nds tate ene
rgy due tot hei nter ac-
tion (C /2 0
ψ )(
ψ † 2 ) .The firstterm
isa two-loop
diagramwith oneinsertion
of C , 0
seeFig.
4.1.Th ere
are two poss
ible con
trac tion san dth esp in-f acto rof the diag ram
is δ ( δ αα
− ββ
δ δ αβ
) αβ
= g g (
− 1) where
= g + (2s
1 isthe ) degenerac
yand is s
thespin ofthe
fermions.In thefollo
wingwe willal
ways g set
= 2.The diagramis
proportionalto thesquare
ofthe densityand
weget
1 E
= C
0
#
3 p
F 2 6π
2 $ (4.16) .
Weob serv eth atth esu mof
the first two term sin
the ene rgy den sity can bew ritte nas
= E p ρ
2 F
2m 3 % + 5 2 π 3 p ( a) F
+ ...
&
(4.17) ,
whichsho wsthat
the C termis 0
thefirst termin
anexpansion in
p a,su F
itab lef ora
dilute,weakly interacting,Fermi
gas.
4 Effective Theories of Dense and Very Dense Matter 197
Fig. 4.1 Leading order Feynman diagrams for the ground state energy of a dilute gas of fermions interacting via a short range potential
empty. The possible excitation of the system are particles above the Fermi surface or holes below the Fermi surface, corresponding to the first and second term in Eq. (4.13). The particle density is given by
ρ = ⟨ ψ
†ψ ⟩ =
! d
4p
(2π)
4S
αα0( p )e
i p0δ" "
δ→0+
= 2
! d
3p
(2π)
3Θ ( p
F− p ) = p
3F3π
2.
(4.14) Tadpole diagrams require an extra i δ prescription which can be derived from a careful analysis of the path integral representation at µ ̸= 0. As a first simple application we can compute the energy density as a function of the fermion density. For free fermions, we find
E = 2
! d
3p
(2π)
3E
pΘ ( p
F− p ) = 3
5 ρ p
2F2m . (4.15)
We can also compute the corrections to the ground state energy due to the interac- tion (C
0/2)(ψ
†ψ)
2. The first term is a two-loop diagram with one insertion of C
0, see Fig. 4.1. There are two possible contractions and the spin-factor of the diagram is (δ
ααδ
ββ− δ
αβδ
αβ) = g(g − 1) where g = (2s + 1) is the degeneracy and s is the spin of the fermions. In the following we will always set g = 2. The diagram is proportional to the square of the density and we get
E
1= C
0# p
3F6π
2$
2. (4.16)
We observe that the sum of the first two terms in the energy density can be written as E = ρ p
2F2m
% 3
5 + 2
3π ( p
Fa ) + . . .
&
, (4.17)
which shows that the C
0term is the first term in an expansion in p
Fa , suitable for a dilute, weakly interacting, Fermi gas.
G 0 (⌅ , k) = ⇥
⌅ ⇤ k + i ⇥ sgn(⇤ k )
k = k 2
2m µ
⌘ ! 0 +
0 = 3
5 n k F 2 2m
{
Fermi Gas:
First Order:
Second Order:
⇥ 2
⇥ 0 = 4 (11 2 lg(2))
21 2 (k F a) 2
⇥ 1
⇥ 0 = 10
9 (k F a)
Nucleon-nucleon Potential
• One can make different assumptions at short-
distance and generate other potentials.
• Difficult to decouple short and long distance.
V ij = X
p
v p (r ij ) O ij p
Intricate spin, isospin and tensor structure.
Interaction is scale
dependent:
Chiral Effective Field Theory
Weinberg, van Klock (1994), Epelbaum (2002)
Construct a momentum space potential with contact interactions and pion exchange.
!
Order the interaction in powers of the momentum.
!
Choose procedure to regulate the sum over intermediate states.
!
!
+... +... +...
+...
2N Force 3N Force 4N Force
LO (Q/ )0
NLO (Q/ )2
NNLO (Q/ )3
N3LO (Q/ )4
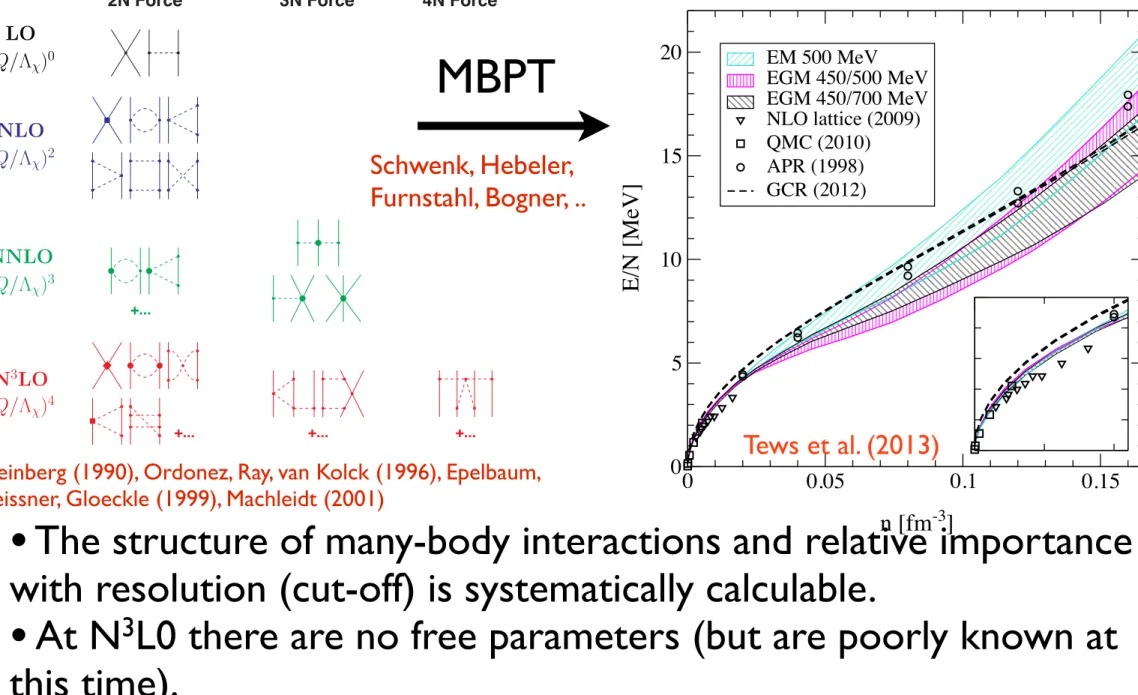
Figure 1: Hierarchy of nuclear forces in ChPT. Solid lines represent nucleons and dashed lines pions. Small dots, large solid dots, solid squares, and solid diamonds denote vertices of index = 0, 1, 2, and 4, respectively. Further explanations are given in the text.
The reason why we talk of a hierarchy of nuclear forces is that two- and many-nucleon forces are created on an equal footing and emerge in increasing number as we go to higher and higher orders. At NNLO, the first set of nonvanishing three-nucleon forces (3NF) occur [70, 71], cf. column ‘3N Force’ of Fig. 1. In fact, at the previous order, NLO, irreducible 3N graphs appear already, however, it has been shown by Weinberg [52]
and others [70, 127, 128] that these diagrams all cancel. Since nonvanishing 3NF contributions happen first at order (Q/ )3, they are very weak as compared to 2NF which start at (Q/ )0.
More 2PE is produced at = 4, next-to-next-to-next-to-leading order (N3LO), of which we show only a few symbolic diagrams in Fig. 1. Two-loop 2PE graphs show up for the first time and so does three-pion exchange (3PE) which necessarily involves two loops. 3PE was found to be negligible at this order [57, 58].
Most importantly, 15 new contact terms Q4arise and are represented by the four-nucleon-leg graph with a solid diamond. They include a quadratic spin-orbit term and contribute up toD-waves. Mainly due to the increased number of contact terms, a quantitative description of the two-nucleon interaction up to about 300 MeV lab. energy is possible, at N3LO (for details, see below). Besides further 3NF, four-nucleon forces (4NF) start at this order. Since the leading 4NF come into existence one order higher than the leading 3NF, 4NF are weaker than 3NF. Thus, ChPT provides a straightforward explanation for the empirically known fact that 2NF⇥3NF⇥4NF . . . .
4. Two-nucleon interactions
The last section was just an overview. In this section, we will fill in all the details involved in the ChPT development of theN N interaction; and 3NF and 4NF will be discussed in Section 5. We start by talking
19
Chiral EFT and Neutron Matter Calculations
Weinberg (1990), Ordonez, Ray, van Kolck (1996), Epelbaum, Meissner, Gloeckle (1999), Machleidt (2001)
arXiv:1206.0025v3 [nucl-th] 4 Feb 2013
Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory
I. Tews,1, 2 T. Kr¨uger,1, 2 K. Hebeler,3 and A. Schwenk2, 1
1Institut f¨ur Kernphysik, Technische Universit¨at Darmstadt, 64289 Darmstadt, Germany
2ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum f¨ur Schwerionenforschung GmbH, 64291 Darmstadt, Germany
3Department of Physics, The Ohio State University, Columbus, OH 43210, USA
Neutron matter presents a unique system for chiral effective field theory (EFT), because all many-body forces among neutrons are predicted to next-to-next-to-next-to-leading order (N3LO).
We present the first complete N3LO calculation of the neutron matter energy. This includes the subleading three-nucleon (3N) forces for the first time and all leading four-nucleon (4N) forces.
We find relatively large contributions from N3LO 3N forces. Our results provide constraints for neutron-rich matter in astrophysics with controlled theoretical uncertainties.
PACS numbers: 21.65.Cd, 21.30.-x, 26.60.Kp, 12.39.Fe
The physics of neutron matter ranges from universal properties at low densities to the structure of extreme neutron-rich nuclei and the densest matter we know to exist in neutron stars. For these extreme conditions, con- trolled calculations with theoretical error estimates are essential. Chiral EFT provides such a systematic expan- sion for nuclear forces [1]. This is particularly exciting for neutron matter and neutron-rich systems, because all three- and four-neutron forces are predicted to N3LO [2].
Neutron matter based on chiral EFT has been studied using lattice simulations [3] at low densities, n ! n0/10 (with saturation density n0 = 0.16 fm−3), and following an in-medium chiral perturbation theory approach [4, 5], where low-energy couplings are adjusted to empirical nu- clear matter properties. In addition, the renormalization group (RG) has been used to evolve chiral EFT interac- tions to low momenta [6], which has enabled perturbative calculations for nucleonic matter [2, 7]. While these con- strain the properties of neutron-rich matter to a much higher degree than is reflected in neutron star model- ing [8], the dominant uncertainties are due to 3N forces, which were included only to N2LO. A consistent inclusion of higher-order many-body forces is therefore key.
Here we present the first calculations at nuclear den- sities based directly on chiral EFT interactions without RG evolution. To this end, we have studied the per- turbative convergence of chiral two-nucleon (NN) poten- tials for neutron matter in detail, and found that the available N2LO and N3LO potentials with lower cutoffs Λ = 450−500 MeV are perturbative. This is supported by small Weinberg eigenvalues at low energies indicat- ing the perturbative convergence in the particle-particle channel [6]. In neutron matter, it comes as a result of effective range effects [9], which weaken NN interactions at higher momenta, combined with weaker tensor forces among neutrons, and with limited phase space at finite density due to Pauli blocking [10].
At the NN level we use the N2LO and N3LO po- tentials developed by Epelbaum, Gl¨ockle and Meißner (EGM) [11] with Λ/Λ! = 450/500 and 450/700 MeV (Λ/Λ! denotes the cutoff in the Lippmann-Schwinger equation
and in the two-pion-exchange spectral-function regular- ization, respectively). We also use the Λ = 500 MeV N3LO NN potential of Entem and Machleidt (EM) [12], which is most commonly used in nuclear structure calcu- lations. The larger Λ = 550 −600 MeV NN potentials of EGM and EM have been found to be nonperturbative [13]
and are therefore not included. Moreover, the LO NN contact couplings in the 600/600 and 600/700 EGM po- tentials break Wigner symmetry perturbatively (at the interaction level), with a repulsive spin-independent CS
0 0.05 0.1 0.15
n [fm-3] 0
5 10 15 20
E/N [MeV]
EM 500 MeV EGM 450/500 MeV EGM 450/700 MeV NLO lattice (2009) QMC (2010) APR (1998) GCR (2012)
FIG. 1. (Color online) Neutron matter energy per particle as a function of density including NN, 3N and 4N forces at N3LO. The three overlapping bands are labeled by the differ- ent NN potentials and include uncertainty estimates due to the many-body calculation, the low-energy ci constants and by varying the 3N/4N cutoffs (see text for details). For com- parison, results are shown at low densities (see also the inset) from NLO lattice [3] and Quantum Monte Carlo (QMC) sim- ulations [22], and at nuclear densities from variational (APR;
the different points are with/without boost corrections) [23]
and Auxiliary Field Diffusion MC calculations (GCR) [24]
based on adjusted nuclear force models.
Schwenk, Hebeler, Furnstahl, Bogner, ..
Tews et al. (2013)
• The structure of many-body interactions and relative importance with resolution (cut-off) is systematically calculable. !
• At N
3L0 there are no free parameters (but are poorly known at this time). !
• Current EOS calculations are based on many-body perturbation theory. Convergence is plausible but needs to be checked.
MBPT
Energy of Nuclear Matter
•
Nucleons are bound - by about 15 MeV per nucleon.
•
There is a saturation density.
•
Three nucleon forces are important.
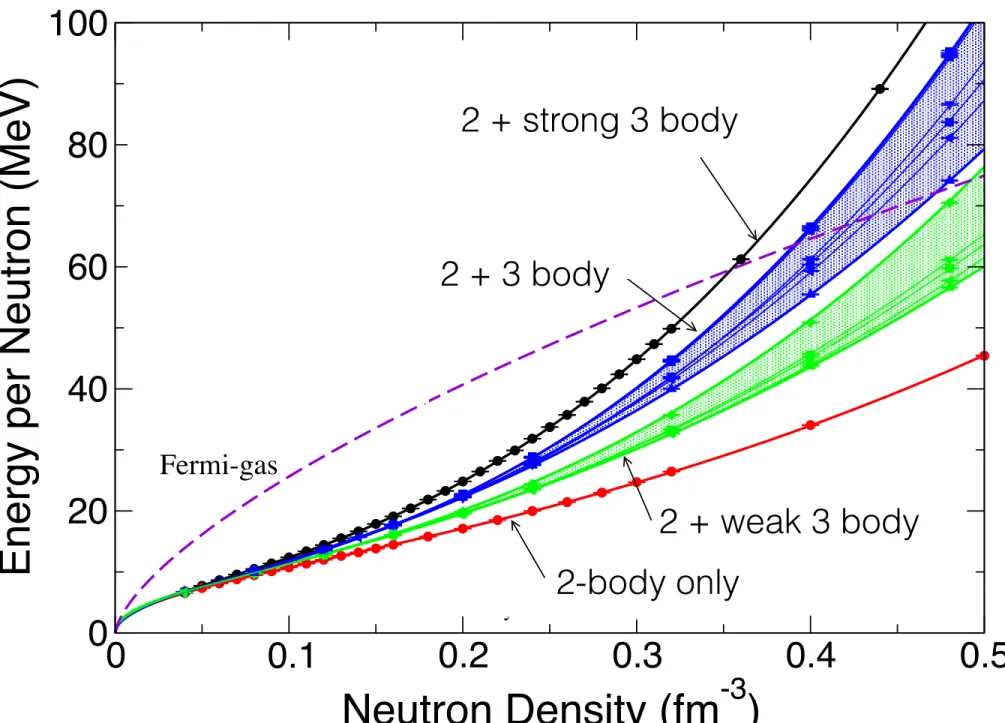
Neutron Matter & 3N Forces
0 0.1 0.2 0.3 0.4 0.5
Neutron Density (fm -3 )
0 20 40 60 80 100
Energy per Neutron (MeV)
30 32 34 36
E
sym(MeV)
30 40 50 60 70
L (MeV)
35.1
33.7
32
E
sym= 30.5 MeV (NN) Fermi-gas
Figure 1: The energy per particle of neutron matter for different values of the nuclear symmetry energy (E sym ). For each value of E sym the corresponding band shows the effect of different spatial and spin structures of the three-neutron interaction. The inset shows the linear correlation between E sym and its density derivative L .
strength of the short-range 3n interaction A R is taken to be a free parameter adjusted to yield the experimentally accessible nuclear symmetry energy. This procedure will attribute missing effects such as relativistic and four and higher nucleon forces to the strength of the 3n inter- action. Although not proven, we make two reasonable assumptions: 1) relativistic effects in neutron matter show a similar density dependence to the short-range three-nucleon interaction as carefully studied in Ref. (25); and 2) four-nucleon force contributions are suppressed rela- tive to the 3n force for densities up to 2-3 0 . This assumption can be justified at nuclear density by the high precision fits to light-nuclei obtained with only 3n forces (21), at higher density this model assumption can be tested by its predicted correlation between properties of neutron-rich nuclei and neutron stars.
Our assumption is that the symmetry energy is defined as the difference between the en- ergy per particle in symmetric nuclear and neutron matter at nuclear density and is denoted by E sym = E neutron ( 0 ) E nuclear ( 0 ). It is determined from model fits to nuclear masses favors
7
2-body only
2 + weak 3 body 2 + 3 body
2 + strong 3 body
"20
-16 MeV 14 MeV
0.5 1.0 1.5
E/A